Geometry of Mediating Protein Affects the Probability of Loop Formation in DNA

Abstract

Recent single molecule experiments have determined the probability of loop formation in DNA as a function of the DNA contour length for different types of looping proteins. The optimal contour length for loop formation as well as the probability density functions have been found to be strongly dependent on the type of looping protein used. We show, using Monte Carlo simulations and analytical calculations, that these observations can be replicated using the wormlike-chain model for double-stranded DNA if we account for the nonzero size of the looping protein. The simulations have been performed in two dimensions so that bending is the only mode of deformation available to the DNA while the geometry of the looping protein enters through a single variable which is representative of its size. We observe two important effects that seem to directly depend on the size of the enzyme: 1), the overall propensity of loop formation at any given value of the DNA contour length increases with the size of the enzyme; and 2), the contour length corresponding to the first peak as well as the first well in the probability density functions increases with the size of the enzyme. Additionally, the eigenmodes of the fluctuating shape of the looped DNA calculated from simulations and theory are in excellent agreement, and reveal that most of the fluctuations in the DNA occur in regions of low curvature.

INTRODUCTION

Since its discovery in the 1980s, enzyme-mediated DNA looping has been implicated as the key to many important biological processes. For example, the activity of the lac, gal, and λ-operons in E. coli is known to be regulated by the formation of DNA loops mediated by their respective repressor proteins (1). Similarly, the functioning of many restriction enzymes is known to be controlled by the formation of loops in DNA (2). A subclass of these enzymes called two-site restriction endonucleases efficiently cleave double-stranded DNA only if they interact with the DNA at two distant sites. In fact, a majority of reactions on DNA that include transcription, replication and repair, site-specific recombination etc., are mediated by multimeric proteins that interact with DNA at multiple sites (2). As a result, the biochemistry and biophysics of these reactions have been the subject of many experimental, computational, and theoretical investigations. A key question in this context is, “What molecular machinery or mechanism governs the rate at which two distant sites on the DNA are brought close to each other?”

The quest to address this question has produced several studies (3), through which a reasonably clear picture has emerged for the related process of DNA cyclization in which two sticky ends (short regions of single-stranded DNA with complementary basepairs) of a piece of linear double-stranded DNA are juxtaposed to produce a circular DNA loop in the absence of any mediating protein. The equilibrium constant for the cyclization reaction is governed by the length of the DNA involved (4). For DNA lengths longer than 300 basepairs (bp), this has been proved by the remarkable agreement of bulk biochemical experiments (5), Monte Carlo (MC) simulations (6), and theories based on the wormlike-chain (WLC) models of DNA (4,7). There is still some debate (5,6) about the cyclization propensity of short (∼100 bp) DNA fragments—the data from some bulk biochemical experiments have been explained on the basis of nonlinear models that require the formation of flexible hinges (or kinks) in the DNA (7,8) while those from another set of bulk experiments seem to agree quite well with the traditional WLC model of DNA, without any need for nonlinearities such as kinks or hinges (6).

On the other hand, enzyme-mediated DNA loops have been studied primarily by single molecule techniques that burst onto the scene approximately two decades ago. The majority of experiments involving DNA looping are carried out using the tethered particle assay in which one end of the DNA is immobilized by attaching it to a coverslip or to an optically trapped bead while the Brownian motion of the other end, also attached to a bead, reports on the formation/breakage of enzyme-mediated loops (9). The bead at the other end can be trapped optically or magnetically (10), allowing for the possibility of exerting forces and moments on the DNA that can attenuate the rate of the looping reaction. This technique has been used to study the kinetics of formation/breakage of loops formed by the lac, gal, and λ-repressors (9–11) as well those by the restriction enzymes NaeI and NarI (12). The constant formation/breakage of the loops (over timescales of ∼10 s for NaeI (12), for instance) in these experiments, which typically span several minutes or hours, ensures that this process is well described by equilibrium binding statistics. Once again, an important question that arises in this context concerns the effect of the length of the DNA loop on the rates of the forward/backward reaction or equivalently, on the equilibrium constant of looping. This question of length dependence was addressed in a recent single molecule experiment in which the probability of loop formation was measured as a function of DNA length for several two-site restriction enzymes (13). The key results of this experiment were that, 1), the probability of forming short DNA loops (∼100 bp or less) is much higher than predicted by a theory based on the WLC theory of DNA mechanics alone; 2), the data agree better with theories of DNA with kinks and hinges; and 3), the probability density as well as the optimal loop length is highly dependent on the looping protein. In this set of experiments, large forces were required to accelerate the rate of the loop breaking reaction for some proteins, implying that the results report on the probability of loop formation alone and not on the equilibrium constant of the loop formation/breakage reaction.

It is our goal in this article to explore a possible explanation for these observations by accounting for the geometry of the looping protein. We do not invoke nonlinear theories of DNA involving kinks or hinges. We also assume that the protein acts as a coupler and has no elasticity of its own. The calculations presented here have been carried out in two dimensions so that the only mode of deformation available to the DNA is bending in a plane. As a result, other sources of nonlinearities such as coupling between twisting and bending modes (14,15) are not considered in this model. In contrast to the work of Merlitz et al. (16), we also do not account for the electrostatic interaction and the stretching energy of the DNA. These calculations are a precursor to more comprehensive three-dimensional calculations where the DNA can bend and twist (15). An advantage of two-dimensional calculations is that the analytical theory remains tractable while not sacrificing the important concept of the competition between elasticity and entropy that governs the physics of DNA cyclization and looping reactions at equilibrium. For example, the peak in the Jacobson-Stockmayer factor (17) for DNA cyclization can be seen both in two- as well as three-dimensional MC simulations although it is shifted to longer DNA lengths in the two-dimensional setting since entropic forces are relatively weaker in this case (18). We show in this article that the mere introduction of the span of the protein complex (denoted by the length scale a throughout this article) together with the competition of elastic and entropic forces results in probability density functions (probability of loop formation as function of length) that can vary significantly with protein geometry. A battery of MC methods have been employed to arrive at the probability density functions presented in this article. The details are explained in Simulation Methods. In some cases, we have also verified our MC calculations by comparison with analytical calculations based on the treatment of DNA as a fluctuating elastic rod.

We observe two important effects that seem to directly depend on the size of the protein complex: 1), the overall propensity of loop formation at any given value of the DNA contour length increases with the size of the protein complex; and 2), the contour length corresponding to the first peak as well as the first well in the probability density functions increases with the size of the protein complex. Another interesting outcome of the MC simulations of DNA loops presented in this article is the visualization of the fluctuating shape. For loop lengths which are small multiples of the DNA persistence length, we find that the shape fluctuates close to an equilibrium shape that can be calculated from the Kirchhoff theory of rods. The fluctuations around the equilibrium shape contribute to the configurational entropy. If the fluctuations are small enough, we can expand the elastic energy functional up to quadratic order in the fluctuations around equilibrium and obtain a fluctuation operator. The eigenmodes of this operator show us the collective motions of the DNA molecule. We have analytically calculated the slowest eigenmode of this fluctuation operator and compared our expressions with the results of a numerical eigenfunction analysis of the MC data. Remarkably, we find good agreement between the two methods. To our knowledge, this is the first time the shape fluctuations have been computed using analytical techniques for this problem. We note that a similar computation of eigenfunctions for boundary conditions involving a given force and zero moments at the ends was performed by Kulic et al. (19). Such shape fluctuations in macromolecules are now known to play a key role in determining the free energy change associated with binding two species (20).

THEORY

Mechanics of the DNA loop

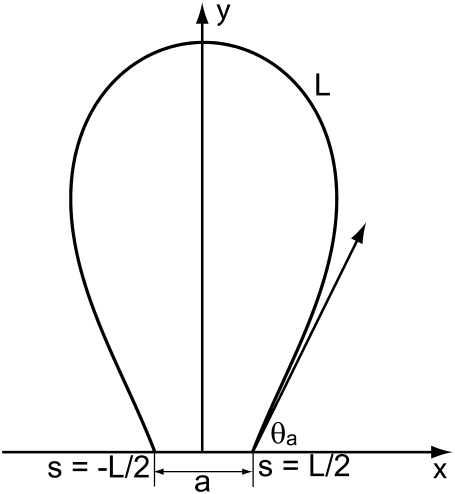
In this article, we model the DNA as an inextensible, homogeneous, isotropic rod with bending stiffness K_b. The value K_b can be determined from the persistence length ξ_p through the relation 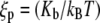where k_B is the Boltzmann constant and T is the absolute temperature. In this article, we take ξ_p = 50 nm (21) for double-stranded DNA and k_BT = 4.1 pN nm, which corresponds to value at room temperature. The protein complex is modeled as a coupler of size a. For example, a dimer of the restriction enzyme BfiI has size of 10 nm (PDB ID: 2C1L). More precisely, a is the spatial distance between the points at which the protein binds to the DNA. The protein is usually a dimer, tetramer, etc., and is often symmetric. We therefore expect the DNA loop to be symmetric as well and choose the y axis as the axis of symmetry (Fig. 1). The protein exerts a force F on the DNA which, by symmetry, has to lie along the x axis in our model. With no other forces being exerted on the DNA in the looped region, we know that equilibrium demands that

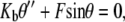(1)

where θ (s) is the angle made by the tangent at any point s to the positive x axis and the prime (′) denotes differentiation with respect to the arc-length s. Recalling that K_bθ ′(s) = M(s) is the bending moment we can see that Eq. 1 is a second-order nonlinear differential equation in θ (s), which expresses a balance of moments at every point on the DNA. The solution of Eq. 1 requires that we specify two boundary conditions. We will consider several possibilities here. If the protein is a rigid jig, then we will require

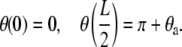(2)

The first of these conditions is required by the assumption of symmetry while the second one will be dictated by the constraint posed by the protein-DNA interaction. We assume that the angle θ_a can be reasonably determined from the co-crystal structure of the protein bound to the DNA and that the protein is rigid enough to exert a moment on the DNA to ensure that the boundary condition is obeyed. If, on the other hand, the protein is flexible (for example, lac-repressor (22,23) and AraC (24)), then the appropriate boundary conditions would be that the protein does not exert any moments on the DNA. In such a scenario the boundary conditions would be

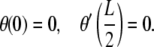(3)

Finally, the constant F is determined by enforcing the constraint on the end-to-end distance

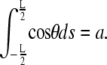(4)

The boundary value problem consisting of the differential equation (Eq. 1) together with boundary conditions given by Eqs. 2 and 4 (as well as its three-dimensional version) has been solved analytically by Purohit and Nelson (14). For solving the problem with boundary conditions (Eq. 3), it is useful to recall that the solution to Eq. 1 can be written in terms of elliptic functions to obtain

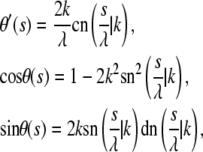(5)

where 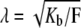and k are constants. Clearly, 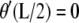requires 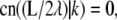which is possible only if 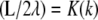where K(k) is the complete elliptic integral of the first kind. This constraint together with the following can be solved to determine λ and k for given values of L and a,

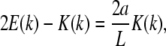(6)

where E(k) is the complete elliptic integral of the second kind. Equation 6 above results from the constraint 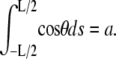It is clear that the angle θ_a at the ends of the loop is then determined through

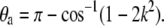(7)

Viewed differently, k (with 0 ≤ k ≤ 1) parameterizes the dependence of the angle θ_a on 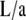through Eqs. 6 and 7. (This dependence has been plotted later in Fig. 4.)

FIGURE 1.

Schematic of protein-mediated two-dimensional DNA loop; a is the size of the protein holding the loop.

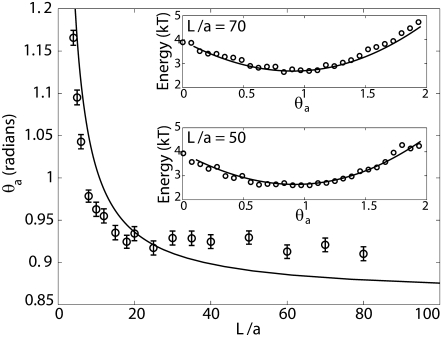
FIGURE 4.

Most probable angle θ_a plotted as function of L/a. Error bars represent standard error in the reported values. As a → 0, we see that θ_a → 49.5°, which corresponds to a loop opening angle of 81° predicted by Shimada and Yamakawa (4). The most probable angle was obtained from the probability distribution of the end angles of the loops generated by the MC simulations. The line is the result of a calculation based on a minimization of elastic bending energy which predicts that the optimal loop is the one whose curvatures are zero at the ends. This condition corresponds to a situation in which the protein exerts no moments on the DNA. The inset shows the energy of an elastic rod plotted as a function of θ_a for L = 5ξ_p and two different values of L/a. In both the panels we also plot −log(P(θ_a;L/a)) + C, where C is an arbitrary constant using data from MC simulations and find good agreement. We note that the energy wells in both the panels are shallow (which implies that we should expect a large variance), which explains why the MC data for most probable θ_a for large values of L/a does not agree too well with the curve.

The equilibrium shapes of the loop obtained above do not account for the role of fluctuations. In general, this is a difficult exercise, but in the limit of small fluctuations around the equilibrium configuration, we can make considerable progress by expanding the energy up to quadratic order in the fluctuations. In the case of the DNA loop, we expand the energy up to quadratic order in the fluctuations δθ (s) of the angle θ (s) made by the tangent to the x axis. In other words, we write

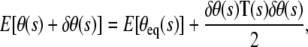(8)

where the stiffness T (also called the fluctuation operator) contains information about fluctuations, and E[θ_eq(s)] is the elastic energy corresponding to the equilibrium shape of the loop. Note that there is no first-order term in δθ, since equilibrium implies that 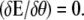The eigenmodes of the fluctuation operator ultimately contribute to the entropy. In the Appendix, we explicitly compute the fluctuation operator for a DNA loop and determine its lowest eigenmode. We then compare the analytical expressions with our MC simulations (and plot the results later in Fig. 5).

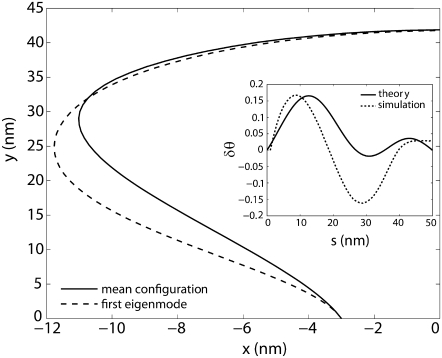
FIGURE 5.

The first eigenmode of the fluctuating loop obtained from MC simulations. The solid line represents the mean configuration and the dashed line represents the deformation due to the fluctuations along the first eigenmode. The end-to-end distance of the loop is fixed and so are the angles made by the tangents (to the x axis) at the ends. The inset shows the corresponding change in the tangent angle δθ as a function of the arc-length s calculated using theory (solid line plotted using Eq. 23) and using MC simulations (dotted line) calculated as described in Eigenmode Calculation.

SIMULATION METHODS

Summary

We employ a battery of MC methods to quantify the behavior of the DNA loop in two dimensions. We calculate the loop formation probability, P(L;a) of a fragment of the DNA of length L and given end-to-end distance, a when the opening angle is allowed to vary, using the method (described in P(L;a) Calculation) proposed by Czapla et al. (15). A Metropolis-based Monte Carlo method (described in Eigenmode Calculation) is used to quantify fluctuations of the DNA loop while density-of-states Monte Carlo (DOSMC) (see Validation of the Quasiharmonic Assumption) is used to validate the quasiharmonic assumption employed in our theory. Our methods are checked for consistency by comparing mean potential energy of an ensemble of fluctuating configurations of a given DNA loop by all three methods. In the above simulation protocols, we discretize the double-stranded DNA of fixed L and a into N rigid links, each of length Δs. Unless specified, the link length is taken to be 1 nm, i.e., ξ_p/50. Following Klenin (25), we also calculate the correction to the persistence length due to discretization of DNA. This correction is small since the chosen link length is small compared to the DNA persistence length, and hence, it is neglected. To treat the angles at the boundaries, we use the boundary condition that θ′(± L/2) = 0, which corresponds to a flexible protein (see Eq. 3). In our simulations, we use ξ_p = 50 nm and k_BT = 4.1 pN m. We describe the potential energy of each conformation of the DNA loop as

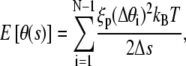(9)

where we have replaced the derivative 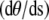by 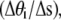the bending modulus K_b by ξ_pk_BT, and summed over all the links.

P(L;a) calculation

We employ a methodology, termed as Gaussian sampling, from the work of Czapla et al. (15). This MC method is superior to the more traditional Metropolis MC method for calculating P(L;a) because it is computationally efficient, and it does not suffer from correlations between trial configurations. In the Gaussian sampling protocol, the DNA chain is grown link-by-link by adding a new link to the preexisting chain at the growing end until the desired DNA length is reached. Adding a new link at an angle Δθ_i to the growing end demands an energy Hence, this angle is sampled from the following Gaussian distribution dictated by a Boltzmann distribution at equilibrium:

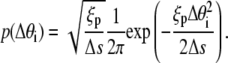(10)

Because rigid body (overall) translation and rotation of the DNA loop do not contribute to loop formation probability, we effectively remove them by constraining the first link in a vertical orientation at the origin. Once the DNA has grown to a total length of L, the distance between the first and the last link is computed. If this distance lies in the interval [a − δ, a + δ], we record it as a “hit” (where δ is the tolerance). This process is repeated one billion times (N_try) yielding N_hits hits. P(L;a) is simply the ratio of N_hits to N_try. Results are reported as an average over four different runs with different initial conditions for the random number seed to generate p(Δθ_i) in Eq. 10. To quantify the dependence of the angle θ_a on L/a, for every hit, the observed value of θ_a is recorded, and a mean is computed over the N_hits values after each simulation run.

Figs. 2 and 3 report the equilibrium probability of loop formation P(L;a) for different values of L and a while Fig. 4 reports the equilibrium value of average opening angle (defined as π − 2θ_a) over all conformations recorded as hits as a function of L/a.

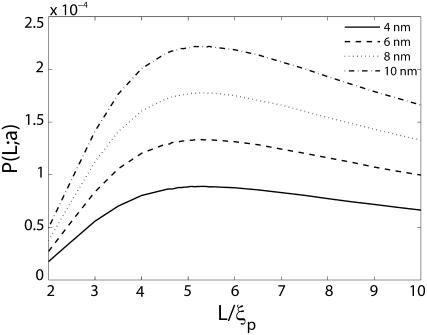
FIGURE 2.

Probability of loop formation P(L;a) plotted as a function of nondimensionalized length L/ξ_p for various values of the end-to-end distance a. The probability is peaked at L/ξ_p ≈ 5. There is also a second peak at much smaller values of L/ξ_p, which is depicted in Fig. 3. A peak at L/ξ_p ≈ 5 is expected from the classical WLC model of DNA, which does not account for the presence of the protein. The location of this peak shows only a weak dependence on a. Link length = 2.5 nm; tolerance in a = 0.5 nm. Coefficient of variation of P(L;a) (not shown in the figure) is <1%.

FIGURE 3.

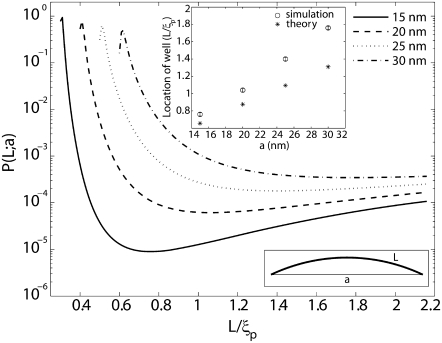
Probability of loop formation P(L;a) plotted as a function of nondimensionalized length L/ξ_p for various values of the end-to-end distance a. The presence of a new length-scale a imposed by the protein results in a second peak at small values of L. The WLC theory for cyclization does not predict this peak. The wells in the probability distributions correspond to lengths at which the elastic energy required to bend a short fragment of DNA to satisfy the constraint on end-to-end distance is a local maximum. The inset on the top shows that there is good correlation between the locations of the well, determined from the MC simulations versus the locations of maximum bending energy. The disagreement between these two calculations increases with increasing length due to the increasing effects of fluctuations. The inset in the bottom depicts the shape of a DNA loop when L ≈ a. Link length = 1.0 nm; tolerance in a = 0.5 nm. Coefficient of variation of P(L;a) (not shown in the figure) is <1%.

Eigenmode calculation

Eigenmodes of the DNA thermal fluctuations can be extracted based upon the knowledge of various loop configurations. In our model, we sample DNA loop configurations from a constant length-constant separation-constant temperature ensemble. New loop conformations are generated from the existing one by crankshaft rotation (26). A subchain containing a random number of links is flipped about an axis joining the end points of this segment. This new conformation is selected with a probability of acceptance 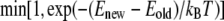to satisfy the Metropolis criterion (27), where E_new and E_old are the energies of the new and old conformations, respectively, and the min function selects the minimum of the two terms in parenthesis. In our model, overlap of DNA segments is not allowed and therefore, trial moves generating loop-segment overlap (E_new = ∞) are automatically discarded by the acceptance criteria. The eigenmode calculations can be performed by either imposing fixed end-angles or variable end-angles in the simulation. However, the theoretical calculation of the first eigenmode (see Appendix) is performed for the case when the end-angles are fixed. Therefore, to make the explicit comparison with the theoretical result, we impose that the end-angles are fixed in our Metropolis MC simulations. Rigid body translation and rotation are removed by holding the end-points of the DNA loop fixed. Each MC run is carried out one billion times to ensure that the system reaches equilibrium and the properties (average energy) converge.

The initial geometry of the links of the DNA loop, to begin the MC simulations, is obtained from the minimum energy configuration by solving the following discrete version of Eq. 1:

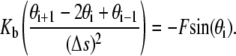(11)

This equation is a boundary value problem and is solved numerically using a shooting method (28) by varying the force, F (Lagrange multiplier), to satisfy the constraint of end-to-end distance.

To calculate the eigenmodes of DNA loop fluctuations from the MC data, a covariance matrix 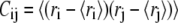is constructed (29), where r_i is the position vector of each link, and 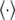represents average over conformations sampled from the MC run. Eigenvectors of this matrix represent the principal modes of loop fluctuations, while each eigenvalue indicates the squared amplitude of the fluctuations along each eigenmode. Because the eigenvectors are orthogonal, they represent independent modes (basis functions) for describing the collective DNA loop fluctuations in the equilibrium ensemble of the conformations.

Fig. 5 reports the calculated shape of the first (slowest) eigenmode resulting from the covariance analysis (see above).

Validation of the quasiharmonic assumption

To calculate the eigenfunctions of the fluctuation operator, T (see Eigenmode Calculation), we expanded the potential energy functional to quadratic order in δθ, thus treating the DNA loop as a quasiharmonic system. In this section, we describe a method to validate this assumption by comparing the configurational density of states (DOS) of the DNA loop against that of n-independent harmonic oscillators. To this end, we use the DOSMC method, developed by Wang and Landau (30), to calculate DOS of the DNA loop. DOSMC is an enhancement over conventional MC techniques since it directly produces the DOS, g(E) instead of the canonical distribution generated by conventional techniques. DOSMC achieves this task by performing a random walk in energy space instead of random walk in the conformational space. Starting from g(E) = 1 and energy histogram, h(E) = 0, random walks in the energy space are performed by generating new loop conformations by crankshaft rotation (see Validation of the Quasiharmonic Assumption). The new conformation is accepted with a probability 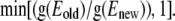Each time an energy state is visited, the corresponding DOS and energy histogram are updated according to g(E) = g(E) × f and h(E) = h(E) + 1, where f is a modification factor >1 (in our simulations, we take f = e¹). The random walk in energy space is continued until the accumulated energy histogram is flat within a predefined tolerance (we define a histogram to be flat when h(E) is within ±5% of average h(E)). To increase the accuracy of g(E) (which is proportional to ln f), f is reduced according to the rule 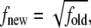and the histogram is reset to zero, i.e., h(E) = 0. These steps are performed until the desired accuracy in g(E) is obtained. In this work, simulations are performed until f reduces to 10⁻⁷. To speed up the simulations, the energy space is divided into overlapping energy windows. Any walk outside the corresponding energy window is rejected. To satisfy the boundary condition imposed by Eq. 3, the energy cost to change the terminal angle that the last/first link makes with the positive x axis is set to zero. At the end, resultant pieces of g(E) in the respective windows are merged together so as to minimize the error between g(E) in the overlapping regions. The obtained g(E) is an accurate estimate of the configurational DOS of the system up to a constant multiplicative factor.

For a DNA loop of n links (i.e., length nΔs) in two dimensions, a total of 2n + 2 coordinates need to be specified. However, the following constraints on the system reduce the degrees of freedom available to the DNA loop: 1), absence of rigid body translation and rotation defines three constraints; 2), each link length being constant defines n constraints; and 3) distance between first and last link being constant defines one constraint. Hence, the DNA loop effectively has only (n − 2) degrees of freedom. The quasiharmonic treatment of the DNA loop assumes that DNA motion can be treated as a collection of (n − 2) independent harmonic oscillators. For a system comprised of m independent harmonic oscillators, the number of states with a total configurational energy between energy E and E + dE is N(E)dE, where N(E) is given by (31)

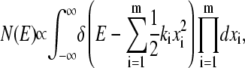(12)

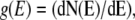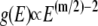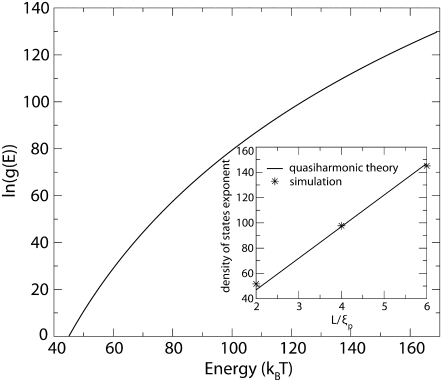
where δ is the Dirac δ-function, and k_i and x_i are, respectively, the spring constant and the displacement of the i^th oscillator. The DOS for this system is then yielding (in deriving this relation, we first performed the integration in Eq. 12 (32)). Hence, if the quasiharmonic approximation holds for a DNA loop of n links, its DOS should obey 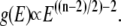By comparing the slope of the ln g(E)-versus-E plot (Fig. 6) from the DOSMC simulations to the slope, which is equal to the density-of-states exponent, from the above expression, i.e., (n − 2)/2 − 2 (Fig. 6 inset), we can assess the validity of quasiharmonic approximation for the DNA loop.

FIGURE 6.

DOS for the 200-nm fluctuating DNA loop plotted as a function of the energy. The inset shows the DOS exponent as a function of the nondimensionalized length L/ξ_p. The excellent agreement between the slope predicted from quasiharmonic theory of independent oscillators with that from DOSMC simulations shows that expanding the energy up to quadratic order in the fluctuations in θ (s) is a good approximation for the lengths of the DNA considered in this article.

RESULTS AND DISCUSSION

The main message of this article is that the probability of loop formation in DNA is affected by the geometry of the looping protein. This result is manifest in Figs. 2–4. Fig. 2 shows the probability of loop formation P(L;a) as a function of the length L of the loop and the size of the protein complex a. As expected from the classical WLC model (33) of DNA there is a peak in the probability of loop formation for L/ξ_p ≈ 5. This is a result of the competition between elastic bending and entropy. The probability is not much affected by the protein size a at these lengths, since a ≪ L. Similar conclusions were reported also by Merlitz et al. (16), who showed (using a Brownian dynamic simulation) that the effect of the finite size of the looping protein is most dramatic for contour lengths <300 bp and small for lengths >500 bp. This does not imply, however, that the size of the protein complex is irrelevant for these loop lengths. This can be better appreciated from Fig. 4, which summarizes the effect of protein size on the value of the loop opening angle. For example, the optimal opening angle of a DNA loop is known to be 81° when a → 0 (4), but for a = 10 nm at L ≈ 250 nm we find an optimal opening angle of 75°. Fig. 4 also suggests that the most probable shape of the loop corresponds to the case in which the curvatures at the ends are zero. Evidence for this assertion comes from the strong correlation between the continuous line obtained from an argument resting on the minimization of elastic energy of the loop and the data obtained from MC simulations, and the fact that an opening angle of 81° for a = 0 calculated by Shimada and Yamakawa (4) does actually correspond to the zero end-curvature condition. This observation implies that the most probable loop shape is one in which the protein exerts no moments on the DNA at their points of contact. The agreement between the curve obtained from the elastic calculation and the data obtained from MC simulations seems to get poorer as L → ∞. The reason for this can be understood by looking at the insets of Fig. 4. The continuous lines in the inset were obtained by calculating (following (14)) the elastic energy of the loop as a function of the end-angle θ_a for L = 5ξ_p and two different values of a. The open circles are data from MC simulations for the same values of L and a. The probabilities were converted into energies (up to an additive constant) through the Boltzmann law. It is remarkable that the data from the MC simulations agree so well with the elasticity calculation. This suggests that the shapes of the loop corresponding to different values of the fluctuating variable θ_a are such that the corresponding energies are not too different from the equilibrium shape for those boundary conditions. We also see that for large values of L/a the probability of having an end-angle θ_a is peaked at the value of θ_a corresponding to zero end moments. However, the energy well is shallow, implying that the variance is large. This is the reason behind the relatively poorer agreement between the two methods used for determining the most probable value of the end angles. One has to do an impractically large MC calculation to obtain better agreement.

The most significant effects of the size of the protein complex are felt at small values of the length L. The probability of loop formation is peaked at values of L that are comparable to a as seen from Fig. 3. This peak is significantly higher than the peak observed at L/ξ_p ≈ 5 and has not been predicted by the classical WLC model of DNA. Some researchers have suggested that looping probabilities will necessarily be high when the DNA contour length is comparable to the span of the protein complex, but a quantitative prediction is still lacking (34). In fact, most studies which predict high probability of loop formation at short DNA lengths do so only after the introduction of defects, such as, kinks or hinges in the DNA, thus deviating from the WLC model (7,34–36). A notable exception is a study by Merlitz et al. (16) which shows, through Brownian Dynamics simulations based on the classical WLC model of DNA, that the probability of loop formation is enhanced >10-fold at L ≈ 40 nm when we go from a = 0 to a = 10 nm. They also analyzed the effects of nonlinearities such as permanent bends in the DNA, and showed how these defects can greatly enhance looping probabilities and rate constants for contour lengths L in the interval 40 nm < L < 100 nm for various values of the span a. Merlitz et al. do not report results for lengths shorter than 40 nm, but it would not be unreasonable to expect that to obtain high looping probabilities in this regime would require introduction of nonlinearities in the DNA. However, this is exactly the regime where we have obtained a second peak and valley in the looping probabilities. In the light of this observation the significance of the results summarized in Fig. 3 is that high looping probabilities for short DNA contour lengths (L < 40 nm) can be explained with the classical WLC model of DNA (without nonlinearities such as kinks or permanent bends) if we account for the geometry of the looping protein. At these short contour lengths, shape fluctuations make only a small contribution to the free energy so that the peak in probability is simply a result of the low elastic bending energy required to satisfy the constraint on the end-to-end distance placed by the looping protein. In fact, the location of the well in the probability distribution between the two peaks (at L ≈ a and L ≈ 5ξ_p) is strongly correlated with the length at which the elastic bending energy has a local maximum (see Fig. 3, inset).

The results summarized in Figs. 2 and 3 could also provide an alternative interpretation for the experimental results of Smith et al. (13). In this experiment, the probability of loop formation was measured as a function of the length of the loop for several enzymes which interact with DNA at two separate sites (13). The main results of these experiments were that the probability distribution was different for different proteins and that looping at short contour lengths was far more probable than predicted by the WLC theory alone. The authors had also found two peaks in the probability distribution for looping by some proteins. Qualitatively similar observations in bulk experiments were made by Reuter et al. (37), who found that the propensity of cutting by certain two-site restriction enzymes (EcoRII) was peaked at two different contour lengths with the highest propensity occurring at the peak at short lengths. They had suggested that at short contour lengths the DNA is slightly bent to meet the constraints placed by the enzyme while at longer lengths it was looped. All of these observations are replicated in our model which accounts for the effects of protein size. A direct comparison of our results with those of Smith et al. (13) is not possible, since our calculations have been carried out only in two dimensions, whereas the experiments are fully three-dimensional. Also, despite our results which rely solely on an elastic rod model of DNA, the possibility of kink or hinge formation at high curvatures still remains open.

An important by-product of our MC simulations is that we have decomposed the fluctuating shapes of the loop into eigenmodes. Such a decomposition is possible when the fluctuations around equilibrium are small so that the energy of an arbitrary shape can be expressed as the sum of the energy of the equilibrium shape and a term that is quadratic in the small fluctuations. For the case of the DNA loop, the shape can be written in terms of the angle θ (s), which is the angle made by the tangent to the loop to the positive x axis. Fig. 5 shows the deviations in the shape of the loop and the angle δθ (s) as a function of the arc-length s. The first eigenmode (corresponding to the largest eigenvalue of covariance matrix) is shown together with comparison to an analytical result. The analytical calculation is performed in a slightly different context in which the force at the ends (as opposed to the end-to-end distance) as well as the angles made by the tangents at the ends are held fixed. Despite this difference in the boundary condition, the theory and simulations yield similar variation for the change in the tangent angle along the arc length of the DNA (see Fig. 5, inset). Movies showing the projection of the MC data on the two slowest eigenmodes are available as Supplementary Material data. Both the results show that the shape fluctuations are large in the regions of the loop which are nearly straight (low curvature) and small in the highly curved regions. This would imply that the entropic contributions to the free energy of the loop have their origin in the low curvature regions. A similar conclusion was also reached by Fain et al. (38) in their analysis of plectonemes in DNA where it was determined that most of the free energy of the plectonemes was elastic bending and twisting energy while the entropic part was always negligible. To the best of the authors' knowledge, this is the first report on the fluctuating modes of a DNA loop subjected to clamped boundary conditions. Calculations such as these could be important building blocks for determining the free energies of binding/unbinding reactions of biological entities which have only recently been shown to depend strongly on configurational entropy.

Finally, from our DOSMC simulations, we have confirmed that expanding the potential energy of the DNA loop to quadratic order in fluctuations is a good approximation (see Fig. 6). The assumption of quasiharmonicity simplifies a variety of thermodynamic property calculations, the most prominent example being the entropy. Based on the conformational sampling of metropolis MC and its subsequent eigenvector decomposition, we can calculate the quasiharmonic configurational entropy of the DNA loop (29). Furthermore, the DOS can be directly used to compute the free energy and entropy, quantities which are not directly available in conventional MC methods.

CONCLUSIONS

In this article, we have summarized the effects of the size of the mediating protein on the propensity of loop formation in DNA. Many of the qualitative features observed in recent single molecule experiments on enzyme-mediated DNA looping are reproduced by the WLC theory if we take into account the nonzero size of the looping enzyme. Two important effects that seem to directly depend on the size of the enzyme complex are that, 1), the overall propensity of loop formation at any given value of the DNA contour length increases with the size of the enzyme complex; and 2), the contour length corresponding to the first peak as well as the first well in the probability density functions increases with the size of the enzyme complex. These qualitative features of the results can be readily tested by performing the looping experiments with looping proteins of known sizes. Also, of special interest are the eigenmodes of DNA fluctuations. Our theoretical calculations and MC simulations have shown that the fluctuations in the DNA are large where the curvature is small. Perhaps this observation can also be verified from experiments where real-time motions of DNA are recorded (39).

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

APPENDIX: FLUCTUATION OPERATOR

To visualize the fluctuations away from the equilibrium shape θ_eq(s), we vary the shape by δθ (s) and expand the following potential energy functional (see Eq. 13) characterizing a bent rod up to quadratic order in δθ (s):

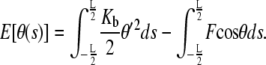(13)

The first term in the above potential energy is the elastic bending energy and the second term is the potential energy of the applied force F. We assume here that a known force F is applied at the ends of the loop. This is different from specifying a given end-to-end distance on the loop as a constraint as summarized by Eq. 4. In that case, F should be interpreted as a Lagrange multiplier enforcing the constraint on the end-to-end distance. Here we will work with the case when the force F is specified since the mathematics in this situation is relatively simpler. We now wish to compute T which is the so-called “fluctuation operator” and is given by

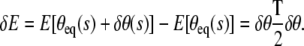(14)

Fortunately, this exercise has been carried out by Kulic et al. (19), who have shown that the fluctuation operator is given by

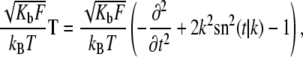(15)

and t = s/λ and the equilibrium shape of the loop is described by Eq. 5. We are interested in the eigenvalues ν_p and eigenfunctions f_p(s) of this operator, which satisfy

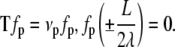(16)

The second condition is a result of requiring that 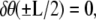which would be the case if the angle at the ends of the loop were constrained by a rigid protein. If, on the other hand, the protein was flexible, then we would require 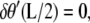which leads to

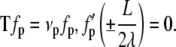(17)

Real numbers ν_p and corresponding functions f_p(s) satisfying the equation Tf_p = ν_pf_p for the operator T given by Eq. 15 are known (see (19)). The eigenvalues and corresponding eigenfunctions are

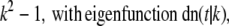(18)

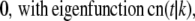(19)

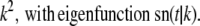(20)

The values ν_p = 0 and 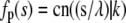satisfy the conditions summarized by Eq. 17. However, none of these eigenfunctions satisfy Eq. 16. But, fortunately, the operator T also has a continuous spectrum apart from the discrete eigenvalues given above. The spectrum was determined as part of a one-dimensional problem in solid-state physics regarding the valence and conduction bands in solids (40). The eigenvalues and eigenfunctions of the continuous spectrum are

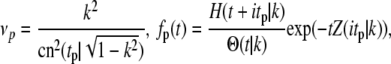(21)

where H(t|k),Θ(t|k) and Z(t|k) are Jacobi's η, θ, and ζ-functions, and 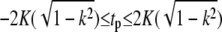and K(k) are the complete elliptic integrals of the first kind. The lower bound on the continuous spectrum of eigenvalues is obtained when t_p = 0 or 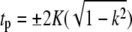resulting in ν_p = k², which leads to the eigenfunctions 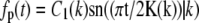and 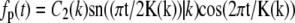where C₁(k) and C₂(k) are real numbers that depend only on k. We note, however, that the eigenvalue ν_p = k² also has another eigenfunction f_p(t) = sn(t|k). In other words, the eigenspace corresponding to the eigenvalue k² is spanned by three eigenfunctions and we can satisfy the boundary condition that 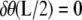by finding constants α and β such that

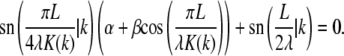(22)

The required eigenfunction corresponding to eigenvalue k² is then simply a linear combination of these eigenfunctions:

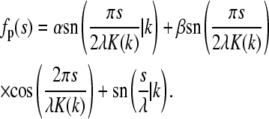(23)