Cytoskeletal Bundle Mechanics

Abstract

The mechanical properties of cytoskeletal actin bundles play an essential role in numerous physiological processes, including hearing, fertilization, cell migration, and growth. Cells employ a multitude of actin-binding proteins to actively regulate bundle dimensions and cross-linking properties to suit biological function. The mechanical properties of actin bundles vary by orders of magnitude depending on diameter and length, cross-linking protein type and concentration, and constituent filament properties. Despite their importance to cell function, the molecular design principles responsible for this mechanical behavior remain unknown. Here, we examine the mechanics of cytoskeletal bundles using a molecular-based model that accounts for the discrete nature of constituent actin filaments and their distinct cross-linking proteins. A generic competition between filament stretching and cross-link shearing determines three markedly different regimes of mechanical response that are delineated by the relative values of two simple design parameters, revealing the universal nature of bundle-bending mechanics. In each regime, bundle-bending stiffness displays distinct scaling behavior with respect to bundle dimensions and molecular composition, as observed in reconstituted actin bundles in vitro. This mechanical behavior has direct implications on the physiological bending, buckling, and entropic stretching behavior of cytoskeletal processes, as well as reconstituted actin systems. Results are used to predict the bending regimes of various in vivo cytoskeletal bundles that are not easily accessible to experiment and to generate hypotheses regarding implications of the isolated behavior on in vivo bundle function.

INTRODUCTION

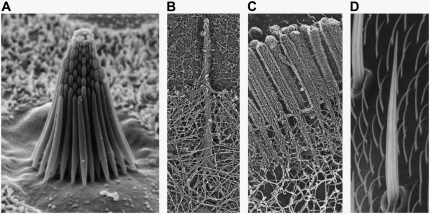
Cytoskeletal actin bundles comprise numerous vital cellular processes including stereocilia, cytoskeletal stress fibers, the sperm acrosome, microvilli, and filopodia (Fig. 1) (1–3). The mechanical properties of these processes play essential roles in cell function—the bending stiffness of stereocilia mediates the senses of hearing and equilibrium (4,5), the elasticity of cytoskeletal stress fibers enhance cellular resistance to mechanical deformation (6–13), the buckling resistance of the sperm acrosome facilitates egg cell penetration during fertilization (14,15), and filopodial buckling resistance facilitates filopodial protrusion (16–20) and mediates actin turnover during neuronal growth and wound healing (21,22). In addition to the preceding actin-based cytoskeletal bundles, cells also align microtubules (MTs) to actively regulate nuclear positioning during mitosis (23,24) and stabilize cell shape in the neuronal axon process (21) and outer pillar cells in the mammalian ear (25). Thus, a quantitative understanding of the molecular design principles responsible for the mechanical behavior of these ubiquitous cytoskeletal modules is important for gaining a mechanistic understanding of cell function (21,26,86).

FIGURE 1.

Fiber bundles consisting of F-actin. (A) Ciliary bundle from the sensory epithelium of a bullfrog saccule consisting of ∼60 stereocilia (courtesy of David P. Corey and John A. Assad). (B) Filopodium protruding from the lamellipodium of a mouse melanoma cell (reproduced from Svitkina et al. (81) by copyright permission of The Rockefeller University Press). (C) Epithelial microvilli. (D) Drosophila neurosensory micro- and macrochaete bristles (reproduced from Tilney et al. (82) with the permission of The American Society for Cell Biology).

Bundle dimensions and internal constitution vary considerably depending on physiological function. Bundle length varies from several microns in microvilli and stress fibers to tens of microns in the sperm acrosome and hundreds of microns in neurosensory bristles (2,3). Similarly, bundle diameters range from tens of filaments in filopodia to hundreds of filaments in stereocilia. Interestingly, actin bundle dimensions and the predominant cross-linking protein associated with various cytoskeletal processes are highly conserved across otherwise widely divergent species (27), suggesting specific and possibly mechanically related functional constraints imposed during evolution (26,28). Fascin is the predominant actin-binding protein (ABP) in filopodia and neurosensory bristles, fimbrin is prevalent in microvilli and stereocilia, scruin is present exclusively in the limulus sperm acrosome, and α-actinin predominates in cytoskeletal stress fibers. Despite the fundamental importance of actin bundle mechanical properties to cell function, the effects of bundle dimensions and cross-link composition on bundle mechanics remain poorly understood. Direct measurement of in vivo bundle mechanical response is limited by a number of complicating factors, rendering a systematic investigation of the effects of bundle dimensions and cross-linking protein composition on bundle mechanics impracticable.

As an alternative, the bending stiffness of reconstituted actin bundles was recently measured in a controlled in vitro assay (29). This enabled the systematic and broad exploration of the effects of bundle dimensions and ABP type and concentration on the bending stiffness of actin bundles. Bundle-bending stiffness is the fundamental mechanical property of interest for inextensible bundles because once it is known, other physiologically relevant mechanical properties such as the critical buckling load or entropic stretching stiffness may be derived. In Claessens et al. (29), the bending stiffness was found to depend in a complex manner on bundle composition, varying by orders of magnitude depending on cross-linking protein type and concentration and bundle dimensions.

In this article, we employ a molecular-based model of cross-linked fiber bundles to explore the range of mechanical behavior of cytoskeletal actin bundles. The bending stiffness, 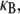is found to depend on only two simple design parameters: the number of constituent filaments in the bundle, N, and a measure of the effectiveness of cross-links in mechanically coupling neighboring filaments, denoted α. The values of N and α are shown to delineate three distinct mechanical regimes that differ markedly in their dependence on bundle dimensions and internal constitution, highlighting the importance of the former on cytoskeletal bundle mechanics. The isolated mechanical behavior has direct implications on a number of disparate fields of biophysical research involving the physiological bending, buckling, and entropic stretching response of cytoskeletal processes involved in mechanosensation, fertilization, cell motility, and neuronal growth, and may be used to predict the bending regime of in vivo cytoskeletal bundles that are not easily amenable to experimental measurement.

MATERIALS AND METHODS

Model

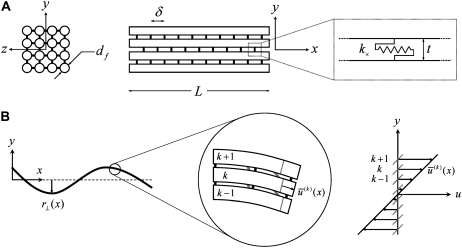
We consider the linear bending response of fiber bundles of length L that consist of N cubically or hexagonally packed fibers, as is typical of highly cross-linked filamentous actin (F-actin) (15,31,32) (Fig. 2 A). Each fiber is characterized geometrically at a coarse-grained molecular scale by its cross-sectional dimension, 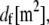and contour length, 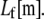Fibers run the full length of the bundle 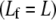and are modeled mechanically as extensible Euler-Bernoulli beams (or extensible wormlike polymers) with stretching stiffness 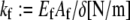and isotropic transverse bending stiffness 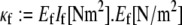is the effective Young's modulus of the fiber, 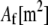is its cross-sectional area, 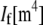is the moment of inertia of its cross-sectional area with respect to its neutral axis, and 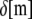is the mean spacing between discrete cross-links with effective shear stiffness 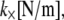and length, 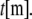(For molecular-scale objects, 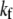and 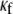are fundamental independent observables that may be measured experimentally, whereas, 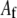and 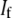are macroscopic geometric properties that are ill defined at the molecular scale and thus only effective in their nature). Cross-links are assumed to be transversely inextensible, thereby constraining transverse fiber deflections to be equal but allowing interfiber relative slip. Bundle torsional stiffness is assumed to be of the same order as the bundle-bending stiffness so the effects of twist are of higher order and may safely be ignored in analyzing the linear bending response of stiff bundles for which the apparent bundle persistence length 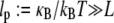(33–36). In-plane bending of 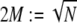fiber layers cross-linked to their nearest neighbors in- and out-of-plane may then be considered, where the corresponding three-dimensional (3D) bundle-bending stiffness is related to its 2D counterpart by 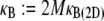(Fig. 2 A). (Effects of out-of-plane shear deformations present in hexagonally packed bundles during planar bending, as well as finite-size geometric boundary effects, are ignored to leading order.) Various types of biological fiber bundles have been modeled previously along similar lines (25,32,37,38).

FIGURE 2.

Theoretical bundle model. (A) Cross-linked fiber bundle with N = 16 fibers. Discrete cross-links couple nearest-neighbor fibers mechanically in stretching and bending. (B) (left) Deformed backbone of a fiber bundle subject to in-plane bending; (middle) close-up view of three typical fibers showing fiber and cross-link deformations in (faded gray lines) decoupled and (solid black lines) fully coupled bending; (right) transverse distributions of fiber axial displacement, 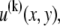and (arrows) mean axial displacement, 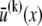in (faded gray lines) decoupled and (solid black lines) fully coupled bending.

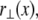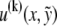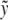Bundle deformations are characterized by the transverse deflection of the bundle neutral surface at axial position x along its backbone and internal axial extensions of the constituent fibers. Let be the axial displacement field in the kth fiber at a distance from the fiber neutral axis. The associated local strain field 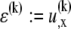then consists of a linear superposition of fiber bending and stretching contributions, 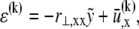where, 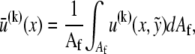a subscript comma is used to denote differentiation, and the standard small displacement approximation, 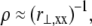is used for the neutral surface radius of curvature, ρ (Fig. 2 B).

Cross-link shear displacements, ν, result from stretching and plane cross-section rotations of neighboring fibers, 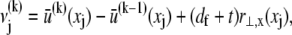where j labels the cross-link at axial position 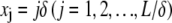and 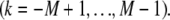The shear displacement may be written equivalently in terms of the local fiber mean axial strain and inverse radius of curvature,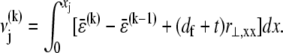

Although the enthalpic stretching and bending stiffnesses of F-actin (39–41) and MTs (40,42) are experimentally known, the shear stiffness of a given cross-link is often unknown. One exception is provided by the recent measurements of Claessens et al. (29), in which an apparent 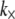was inferred for the ABPs fimbrin, fascin, and α-actinin in thermodynamic equilibrium. In other cases, 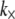in principle may be calculated directly using atomistic-based simulation methods or measured using micromanipulation techniques. The effective length of the cross-linker, t, may be approximated using crystal structures (15,43,44), and δ may be estimated from chemical equilibrium and fiber packing considerations (31).

Biological cross-links such as the ABPs fascin and fimbrin have finite off-rates, 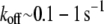(45,46,87) and are therefore irreversibly bound only on loading or deformation timescales that are shorter than 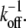On longer timescales cross-links may dissociate and rebind, thereby relaxing their shear deformation energy, such as in the coiled packing of the actin bundle of the sperm acrosome in which kinking via cross-link unbinding and subsequent interfilament slip occur (47). Although the effects of cross-link unbinding/rebinding are of interest for understanding the viscoelastic response of cytoskeletal bundles, this work is limited to conditions in which the loading timescale is shorter than the cross-link off-rate, which may be mediated by force. The model may also be applied to conditions in which thermal fluctuations excite bundle-bending modes provided that the relaxation time of the slowest (longest) wavelength mode is shorter than the cross-link off-rate and the appropriate mean number of bound cross-links is employed (29). Extension of this model to include dynamic cross-links, molecular motors that mediate filament sliding, and filament (de)polymerization provide important model extensions that will be pursued as suitable experimental data become available to validate such developments (48,49).

In addition to their finite shear stiffness, cross-links have a finite extensibility 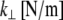that in principle could allow peristaltic (out-of-phase) fiber-bending modes. Typical cross-linking proteins have an extensional stiffness, 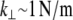(50), however, that restricts the wavelength of these peristaltic modes to lengths at or below the typical cross-link distance, δ, and ensuing transverse fluctuations are negligibly small. (Cross-links suppress fiber peristaltic modes to wavelengths, 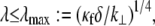where 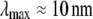for F-actin with 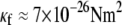(39,40). The minimum axial distance between coplanar cross-links in hexagonally packed actin bundles is 37.5 nm (31). The associated transverse fluctuations are 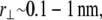which is much less than the interaxial spacing between fibers, 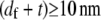(31).) Thus, actin bundles are tightly packed and ordered, as demonstrated by electron microscopy (31,51), and the assumption of inextensible cross-links is justified in analyzing their mechanical response.

The three-dimensional bundle-bending stiffness can in general be expressed as a function of all the independent parameters of the model, 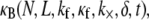which in dimensionless form may be written, 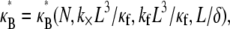in the limit of small cross-links, where 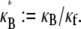We will demonstrate, however, that 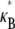depends only on the two independent dimensionless parameters, N, and the fiber coupling parameter,

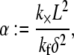(1)

which is evidently a measure of the competition between cross-link shearing and fiber stretching.

Finite element modeling

Fibers are discretized identically in two dimensions (2D) using two-node Hermitian beam elements with nodal degrees of freedom, 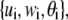where 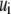is axial displacement, 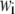is transverse deflection, and 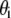is in-plane rotation (30). Nodes on adjacent fibers are constrained to have equal transverse deflection. Cross-link shear stiffness is modeled using a general two-node finite element (FE) that couples nearest-neighbor fibers k and (k−1) via the cross-link shear energy function, 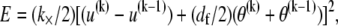where 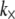is normalized properly to account for discretization. 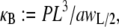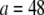Three-point bending is simulated by applying pinned or clamped boundary conditions to the bundle ends and applying a transverse unit point load at the bundle midpoint, yielding the apparent wormlike chain bending stiffness, where and 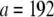for pinned and clamped ends, respectively. Simulations are performed using the commercial FE software ADINA (version 8.2.0; Adina R&D, Watertown, MA). Experimental methods are as described in Claessens et al. (29).

Numerical analysis

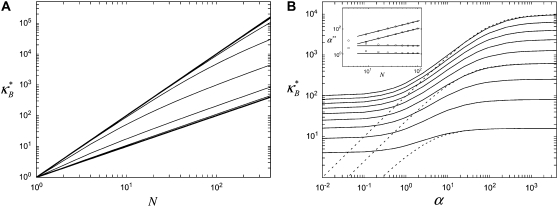
To elucidate the mechanics of bundle bending, we begin by examining the bending response of model fiber bundles subject to simple three-point bending computationally using the FE method. Analogous with experiment, 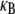is evaluated as a function of increasing fiber number, N, for bundles of fixed α, which is akin to fixing the fiber and cross-link properties (Fig. 3 A). Decoupled bending characterized by linear scaling is observed for small α and fully coupled bending for large α. Interestingly, between these two limits we also observe an intermediate range of α that displays a smooth crossover from quadratic to linear scaling in N. This is in contrast to a bending stiffness that is characterized simply by an α-dependent exponent, a, 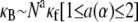(16,37). Replotting 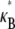as a function of α for a series of values of N indicates that this range is in fact part of a distinct intermediate regime where 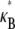increases with increasing α (Fig. 3 B). Moreover, any bundle that exhibits fully coupled bending behavior at any given α necessarily transitions into this regime with increasing bundle diameter. In what follows, we perform a scaling analysis that considers the energetic competition between fiber stretching and cross-link shearing to elucidate the physical origin of the crossovers between each regime and to delineate their boundaries in (N, α)-space.

FIGURE 3.

Theoretical bundle-bending stiffness. (A) Dependence of normalized bending stiffness, 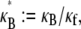on filament number, N, for various constant values of the fiber coupling parameter, α = 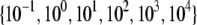(bottom to top). Thick lines denote (bottom) decoupled and (top) fully coupled bending regimes. (B) Dependence of 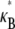on α at constant 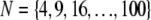(bottom to top). Dotted lines correspond to Timoshenko theory predictions. Inset: Dependence of the crossover values, α, of the fiber coupling parameter on bundle filament number, N, at the (bottom curves) decoupled-to-intermediate and (top curves) fully coupled-to-intermediate regime crossovers for (squares) pinned and (circles) clamped boundary conditions. Solid lines indicate N-independent and linear-in-N scaling. Crossover values of α are defined by the value of α at which 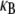is within a factor of two of its limiting decoupled and fully coupled values.

Scaling analysis

Consider a generic fiber bundle with a fixed characteristic radius of curvature, 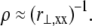In the decoupled limit, individual fibers bend equally without stretching, whereas in the fully coupled limit cross-links resist shear deformation so fibers are forced to stretch and compress in addition to bend (Fig. 2 B). Differences in fiber deformations in the decoupled, fully coupled, and intermediate regimes are thus manifest at a fixed radius of curvature solely in differences in mean fiber stretching.

Accordingly, to isolate the crossover from the fully coupled to the intermediate regime, we impose an infinitesimal stretching deformation, 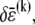that extensionally relaxes the fibers and thereby reduces the total fiber-stretching energy, 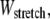at the expense of an increase in cross-link shearing energy, 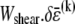is a characteristic deformation that is constant along the bundle axis but may differ between fiber layers, k. The crossover between the fully coupled and intermediate regimes is then determined by the point at which cross-link shearing becomes favorable to fiber stretching, 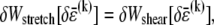where 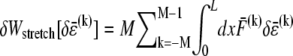is the variation in stretching energy and 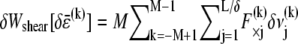is the variation in cross-link shearing energy associated with the imposed relaxation 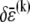that results in the cross-link displacement, 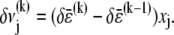The calculation of these energy variations requires that the mean fiber stretching, 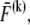and cross-link force, 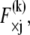conjugate to the deformations 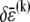and 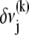be evaluated, which we turn to next.

The mean axial force in the kth fiber is related linearly to its mean axial strain by 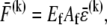which in the fully coupled regime increases linearly with distance, y, from the bundle neutral axis, 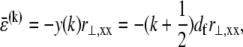so 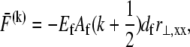as in a homogeneous Euler-Bernoulli beam (Fig. 2 B). The limit of small cross-links 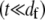is assumed here for simplicity without loss of generality. It is precisely this fiber-stretching force that gives rise to the additional bundle-bending moment and higher associated bundle-bending stiffness in the fully coupled regime. The cross-link force, 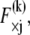is linearly related to its shear displacement via 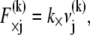which is given by 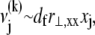so 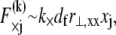where a constant characteristic radius of curvature is assumed in evaluating ν, consistent with the scaling picture here. Note the differences between the expressions for the fiber axial force and the cross-link shear force: The former increases through the bundle cross section, whereas the latter increases along the bundle axis.

Variations in fiber stretching and cross-link shearing energy associated with the imposed relaxation 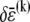may now be calculated using the above results to yiel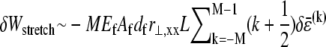d and 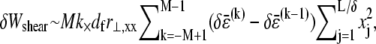which may be rewritten after evaluation of the summation over cross-links. Equating the resultant increase in cross-link shear energy with the decrease in fiber-stretching energy and imposing arbitrary 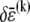determines the location of the crossover, 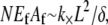which may be rewritten, 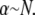Thus, the crossover from the fully coupled regime to the intermediate regime occurs at higher α for larger diameter bundles. This result is because in the fully coupled regime the fiber-stretching energy scales with bundle diameter whereas the cross-link shearing energy scales with bundle length.

A similar analysis applies to the decoupled limit except that fibers are initially unstressed axially in the ground state. FE results indicate that axial stretching is first induced in fibers at the outer boundary of the bundle to minimize the associated increase in 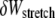because inner fibers then remain in their relaxed state. This leads directly to a crossover that is bundle diameter independent and thus N independent, which is given by the condition 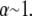Comparison of the crossovers between the decoupled-intermediate 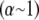and fully coupled-intermediate 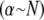regimes computed with the FE model confirms the validity of the foregoing scaling arguments (Fig. 3 B), with some deviations for small N. Introduction of the finite size, t, of the cross-links increases the absolute value of the fully coupled bending stiffness, but it does not affect this scaling behavior.

Closed form bundle-bending stiffness expression

The fiber bundle model admits an analytical solution employing a continuum energetic approach (Appendix). As in the FE model, the total elastic energy of the bundle, 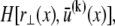is given by fiber bending, 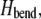fiber stretching, 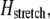and cross-link shearing, 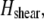contributions. The bending contribution is given by a linear superposition of the standard wormlike chain bending energy for each independent fiber, 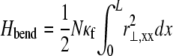because transverse fiber displacements are equal. The fiber-stretching energy is given by the axial strain energy, 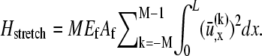Finally, cross-link shear energy is associated with cross-link deformation that results from neighboring fiber bending and stretching,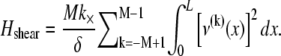

The theoretical model contains 2M internal stretching degrees of freedom 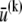in addition to the transverse bundle deflection, 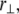which is the principal observable of interest in measuring bundle response. Accordingly, the fiber-stretching degrees of freedom are integrated over to obtain an effective bundle-bending energy that depends solely on from which the mode number dependent effective bundle-bending stiffness is (Appendix)

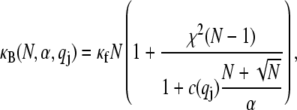(2)

where 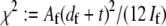accounts for the finite thickness of the cross-links. The mode number dependent bending stiffness depends on the wave numbers 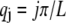through the nondimensional factor 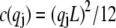and on the design parameters N and α isolated previously using scaling analysis. In three-point bending at zero temperature, the analytical solution for the bundle-bending stiffness is well approximated by Eq. 2 with a constant factor 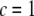for pinned ends and 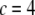for clamped ends, in quantitative agreement with the FE results. In the limits of 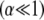and 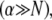Eq. 2 reduces to decoupled and fully coupled bending, respectively, and in the intermediate regime 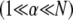it exhibits the scaling 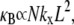which is independent of the mechanical properties of the underlying fibers. This demonstrates that the intermediate regime is dominated by shear deformation of the cross-links so intermediate and shear dominated may be used interchangeably. This is in contrast to the decoupled and fully coupled regimes in which the cross-link shear stiffness is effectively equal to zero and infinity, respectively.

The mode number dependence of 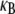demonstrates that in addition to being state dependent 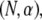bundle-bending stiffness is an apparent material property that depends on how the bundle is probed. This is in stark contrast to a standard wormlike polymer, which is defined as having an intrinsic bending stiffness that is state and mode number independent (52,53). Thus, inference of 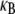from “macroscopic” bundle observables—such as the mean square end-to-end distance, the zero temperature force-deflection relation, or the fluctuation spectrum by associating the bundle with an equivalent wormlike polymer—will yield different apparent values for 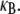Of course, cytoskeletal bundles present in cellular processes are typically stiff 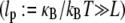so the lowest mode dominates their mechanical response. Accordingly, our primary interest is in the relative values of the isolated design parameters, N and α, which delineate the state dependence of the bundle-bending stiffness. The consequences of the mode number dependence of 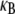on the statistical mechanical properties of bundles of wormlike chains are examined in a separate work (54).

Connection to Timoshenko theory

Fiber bundles consisting of MT protofilaments (42,55) and single-walled carbon nanotubes (56,57) have recently been analyzed using Timoshenko beam theory. (MTs have been analogized to fiber bundles by treating protofilaments as individual fibers and interprotofilament interactions as effective cross-links.) In this approach, the heterogeneous microstructure of the bundle is ignored so the bundle can instead be treated as a single homogeneous medium with effective macroscopic geometric and mechanical properties. 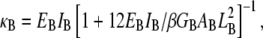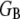The bundle stiffness computed from Timoshenko theory for three-point bending with pinned boundary conditions may be written (58) where is the effective bundle shear modulus and β is a cross-section dependent shear-correction factor. To make a connection with the microscopic fiber bundle theory employed in this work, interlayer shear displacements are assumed to be constant through the bundle cross section and related to the macroscopic bundle shear strain by 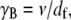where the limit of small cross-links is assumed 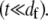Setting the macroscopic bundle shear stress equal to the effective interlayer shear stress, 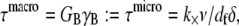then yields 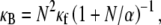which is identical to the fiber-based model result when the limit 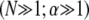is applied. Thus, Timoshenko theory converges to the same fully coupled bundle-bending stiffness as the microscopic-based theory when 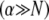and crosses over to the shear-dominated regime when 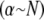(Fig. 3 B). Unlike the microscopic theory, however, Timoshenko theory is asymptotically correct only in the intermediate regime for large bundles 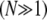and it fails drastically when 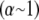because it does not account explicitly for the heterogeneous underlying fiber structure of the bundle (Fig. 3 B). Moreover, consideration of the underlying molecular structure of cytoskeletal bundles facilitates a connection to atomistic modeling to investigate the source of mesoscopically observed parameters such as the cross-linker shear stiffness as well as to examine the effects of underlying structural properties of the bundle such as fiber fracture, which we consider next.

Effect of fiber fracture

In certain cases, such as Drosophila bristles in their developmental phase (59) and cytoskeletal stress fibers (10,11), actin bundles are formed from short overlapping segments of fractured fibers that do not run the full length of the bundle. We tested the effect of fiber fracture on 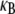numerically by dividing each original mother fiber in the FE model into m daughter fibers of equal length, 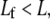where nearest neighbor mother fibers were randomly aligned with respect to one another (Supplementary Material). The primary mechanical consequence of fracture is that the fiber tension/compression propagation that is present in the fully coupled regime is eliminated. Instead, the preexisting axial load carried by a fractured fiber is transferred to its nearest neighbors via cross-link shear coupling. Intuitively, this transfer is most effective for high cross-link shear stiffnesses, low fracture densities, and large diameter bundles.

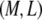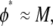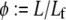Quantitatively, for any bundle size we find two distinct regimes delineated by the critical ratio, where is the fracture number density per fiber. As expected, for 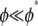the bending response of the bundle is unaffected by fiber fracture. For 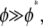however, the bundle response is strongly affected by fiber fracture and characterized by a renormalized coupling parameter 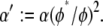In this regime, the bundle behaves like m smaller subbundles of length 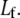Although the critical density 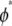is derived from a planar 2D model, the fact that parallel planar fiber layers are assumed to bend independently implies that the same critical density applies to 3D bundles. This scaling behavior is also expected to apply to situations in which fractured segments are not monodisperse in length, as assumed here, as long as fractures are not aligned transversely but instead exhibit significant transverse disorder.

Application to in vitro actin bundles

The bending stiffness of actin bundles cross-linked by fascin, fimbrin, and nonspecific polyethylene glycol-induced depletion forces was recently measured experimentally using an in vitro droplet assay in which actin bundles form compact stable rings (29). In that work, bundle-bending stiffness was analyzed using an existing analytical theory that depends in a complex manner on the numerous bundle parameters, 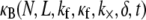(25,29). Using the analytical bending stiffness (Eq. 2) to fit each bending stiffness data point, 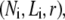at a given fascin/actin concentration ratio 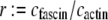yields a concentration-dependent effective interlayer shear modulus, 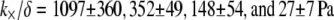for r = 0.5, 0.2, 0.05, and 0.02, respectively, over the range of bundle diameters 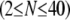and lengths 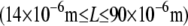examined. The preceding dependence of 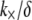on r is consistent with a constant apparent cross-linker shear stiffness of 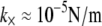and a mean spacing between cross-links that depends on cross-linker concentration as 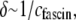as expected from equilibrium binding considerations (29), where a minimum in-plane axial cross-link spacing of 39 nm, 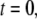and c = 5 appropriate to the periodic boundary conditions used to model the ring bundle examined experimentally is assumed (Appendix). Employing a cross-linker dimension of 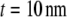results in an apparent stiffness of 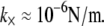The uncertainty in model parameters including t and δ renders the estimate of 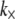valid only to within an order of magnitude. 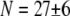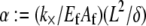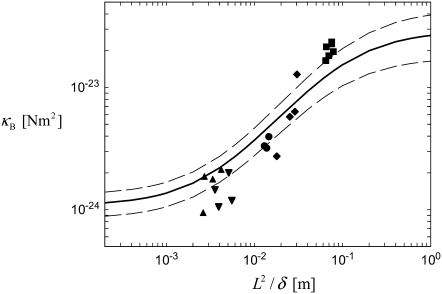The dependence of bundle-bending stiffness on bundle length, L, at fixed filament number provides additional evidence for the validity of the proposed mechanical model in which mediates the bending regime of cross-linked actin bundles within the limited range of L capable of being probed experimentally at fixed N 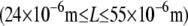(Fig. 4).

FIGURE 4.

Experimental and theoretical bending stiffness of fascin cross-linked actin bundles for N = 27 ± 6. Experimental bundle stiffness (symbols) is measured using a microemulsion droplet system for a range of fascin concentrations with corresponding mean spacings, δ: (squares) 40 nm, (circles) 56 nm, (diamonds) 68 nm, (pointed-up-triangles) 225 nm, (pointed-down-triangles) 412 nm, as described in Claessens et al. (29). Bundle length is varied in an uncorrelated fashion by a factor of over two. Cross-linker axial spacing is calculated using a simple Langmuir isotherm approximation, 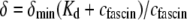(83,84), where 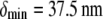is the minimum in-plane spacing between ABPs in hexagonally ordered actin bundles (31) and 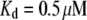is the fascin-actin dissociation constant (83,84). Theoretical bundle stiffness (solid line) is calculated using Eq. 2 with c = 5 (Appendix) assuming N = 27, and bounding curves (dashed lines) that account for experimental uncertainty are calculated using N = 21 and N = 33.

In the absence of detailed information regarding the fine structure of the actin bundles examined, the preceding analysis assumes fiber fracture to be below the critical fracture density, 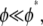and fibers to be ordered transversely. Although the former assumption is consistent with the observation that phalloidin tends to anneal actin into stable, continuous filaments (60) and the latter is consistent with observations of the hexagonally ordered packing of actin bundles (3,31,61), direct examination of the fine structure of the in vitro ring bundles are needed to fully justify these assumptions.

Unlike fascin cross-linked bundles, bundles cross-linked by fimbrin and nonspecific depletion forces exhibit a bending stiffness that is independent of the cross-linker concentration, where fimbrin cross-linked bundles exhibit decoupled bending and depletion force induced bundles exhibit fully coupled bending over the range of bundle dimensions and cross-linker concentrations examined (29). Although nonspecific depletion forces are likely to induce tight packing between helical actin filaments (43) that would explain the fully coupled bending observed, the decoupled bending behavior observed for fimbrin may be hypothesized to be due either to an enhanced F-actin shear compliance associated with actin monomer tilting (62) mediated by fimbrin binding or facile modes of shear deformation involving the actin-fimbrin binding interface (43). We believe that direct bundle stiffness measurements using optical or magnetic tweezers to actively probe the nonlinear and nonequilibrium bending response of actin bundles are required together with molecular modeling of cross-linked actin bundles (63) to understand the origin of the observed behavior as well as to further validate the interpretation of cytoskeletal bundle-bending mechanics proposed here.

Bending stiffness state diagram

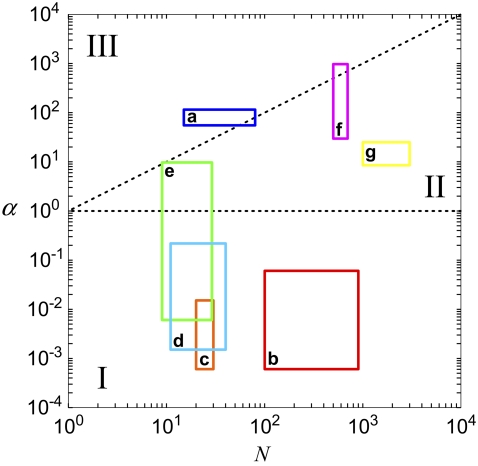
The bending regime of in vivo cytoskeletal bundles may be predicted by evaluating the design parameters N and α using the apparent values of 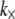determined experimentally (29) and known bundle dimensions (2,3) (Fig. 5). Maximal bundle compliance is achieved by decoupled bending 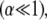whereas maximal bundle stiffness is achieved with fully coupled bending 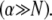In the shear-dominated regime 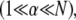bundle length or cross-link concentration may be varied to tune bundle-bending stiffness by orders of magnitude.

FIGURE 5.

Bundle-bending stiffness state diagram for various cytoskeletal bundles. Dashed lines denote crossovers between (I) decoupled, (II) shear-dominated, and (III) fully coupled bending regimes. (a) Acrosomal process of the horseshoe crab sperm cell (64); (b) vertebrate hair cell stereocilia (2,3,66); (c) brush-border microvilli (2,3,85); (d) stress fibers; (e) filopodia (16); (f) Drosophila neurosensory bristles (59); and (g) outer pillar hair cell MT bundles (25). Spacing between ABPs is taken to be the minimal in-plane value for hexagonally packed bundles, 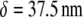(31). Extensional stiffnesses are 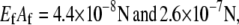for F-actin (41) and MTs (40), respectively.

The sperm acrosomal process is required to mechanically penetrate the outer jelly coat of the egg cell during fertilization (64,65). The limulus (horseshoe crab) sperm acrosome consists of a tapered bundle of 15–80 hexagonally packed F-actin fibers that are tightly cross-linked by scruin and run the full length (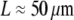) of the bundle. Macroscopic measurements of its bending stiffness have been made using hydrodynamic flow (64), where it was determined that the bundle exhibits fully coupled bending. This independent macroscopic observation is consistent with the a priori prediction of the fiber-based model, in which the ranges in N and α are determined from the parameters probed experimentally (Fig. 5). The shear stiffness of fascin is used as a lower-bound estimate for the unknown shear stiffness of scruin because the molecular structure and interfilament packing of the latter suggest that it is considerably stiffer (15).

Vertebrate hair cell stereocilia are finger-like projections in the inner ear that serve as mechanochemical transducers for sound and motion (Fig. 1). Ranging 1–10 μm in length, each stereocilium consists of up to 900 hexagonally packed F-actin filaments cross-linked predominantly by fimbrin (2,3,66). Together with their short length, the low apparent shear stiffness of fimbrin places the predicted bending stiffness of stereocilia deep in the decoupled regime, consistent with independent experimental observations of native stereocilia (32,37) (Fig. 5).

Brush border microvilli 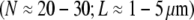are passive cellular processes that predominate in fimbrin and serve primarily to increase the apical surface area of intestinal epithelial cells (2,3) (Fig. 1). Cytoskeletal stress fibers 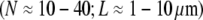predominant in α-actinin (8,10,11,13) function mechanically to enhance the tensile stiffness of cells. Each of these processes is predicted to exhibit decoupled bending due to its relatively short length. Filopodia are active actin bundles present at the leading edge of motile cells and neuronal growth cones that increase in length during locomotion and growth (3) (Fig. 1). Consisting of at least 10–30 filaments, they are predominantly cross-linked by fascin and typically range 1–10 μm but may reach lengths of up to 30–40 μm in certain cases such as in the sea urchin embryo (16,67). As a final actin-based example, we consider the 11 fascin cross-linked bundles constituting the Drosophila neurosensory bristle. Each bundle is ≈400 microns long and contains 500–700 filaments in macrochaetes (59,68) (Fig. 1). Using their full length, these bundles are predicted to lie at the interface of the fully coupled and intermediate regimes, despite their large diameter. Early in development, however, bristles consist of short overlapping bundle modules 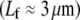(59). At this early stage the fiber fracture density, 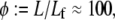is on the order of the critical fracture density at which we find the fully coupled-intermediate regime transition to be affected by fracture (Supplementary Material). Thus, direct bending stiffness measurements are needed to verify this prediction. Finally, noting that the bundle model employed in this work is generic to ordered fiber bundles, we also include in the state diagram MT bundles from outer pillar hair cells for which the interlayer shear modulus was measured using micromanipulation and a fiber-based model 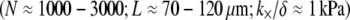(25).

The bending stiffness state diagram in Fig. 5 provides preliminary, ab initio estimates for the bending regime of in vivo cytoskeletal actin bundles based on apparent values for 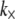that have been inferred from a single type of in vitro experimental assay that probes the linear, equilibrium mechanical response of actin bundles. As noted earlier, significant further experimentation on in vitro and in vivo bundles using active measurement probes are needed to further validate these predictions as well as to explore the nonlinear and nonequilibrium mechanical response of actin bundles. For example, an actin bundle that exhibits fully coupled or intermediate bending behavior on loading timescales that are much shorter than the cross-link unbinding timescale necessarily relaxes to the decoupled bending regime as cross-links dissociate under far-from-equilibrium loading conditions (69). Additionally, the rate of this relaxation will be accelerated in a manner that depends on the rate of bundle deformation (70,71). Notwithstanding, the importance of this work is to isolate the generic design parameters N and α that reveal the universal nature of static cytoskeletal bundle mechanics, as well as their strong dependence on bundle geometry and cross-linker properties. Although the quantitative values of N and α corresponding to specific cytoskeletal processes should be refined and further validated in the future and modified to include effects of cross-link unbinding and nonlinear mechanical response present in situ, the importance of N and α in mediating both the regime of cytoskeletal bundle bending and crossovers between these regimes is expected to apply.

Implications for in situ mechanical function

The isolated mechanical behavior of cytoskeletal bundles has direct implications on the in situ bending, buckling, and entropic-stretching behavior of cytoskeletal bundles.

Decoupled bending exhibited by stereocilia and microvilli not only maximizes the bending compliance of these cellular processes but also relieves the actin filament stretching/compression that grows linearly with distance from the bundle centerline in fully coupled bending, 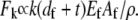Thus, fragility of actin filaments under axial strain that leads to filament fracture (72) may provide an alternative criterion to design cytoskeletal bundles that exhibit decoupled bending in cellular processes such as these.

In contrast, fully coupled bending maximizes the mechanical resistance of the sperm acrosome to axial compressive forces that lead to structural failure at the critical buckling load, 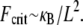The isolated crossover from fully coupled to intermediate bending at the critical ratio 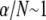provides a constraint on the design of cytoskeletal bundles for maximal mechanical stability under compressive loading. Also subject to compressive loading are invadopodia and filopodia, fascin cross-linked actin bundles involved in tissue invasion, cell motility, and axonal growth (16,17). The results of this work suggest that as the length of these processes increases they transition from decoupled to intermediate regime bending, where 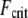becomes independent of length because 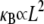there. This is in stark contrast to a standard wormlike chain for which 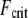decreases strongly with increasing length. Thus, dynamic cytoskeletal processes such as filopodia may potentially increase their length without compromising their buckling stability in the intermediate regime until they finally reach fully coupled bending, where 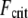becomes length-dependent again.

The entropic stretching response of actin bundles is suggested to play a role in the elasticity of reconstituted actin networks (46,73,74), biological tissues (75), and potentially cells (76,77). Importantly, decoupled cytoskeletal actin bundles have an entropic stretching stiffness, 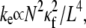that is substantially lower than its fully coupled counterpart, 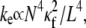with a markedly different dependence on filament number or bundle diameter. Additionally, the mode number dependence of 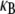renders the dependence of 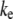on bundle length relatively weak 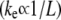in the intermediate regime (54,74).

Taken together, these examples illustrate the direct implications that the state-dependent bending stiffness of cytoskeletal actin bundles isolated in this work has on their in situ biomechanical behavior. Significant further experimentation is clearly warranted to better understand the complex nature of cytoskeletal bundle-bending mechanics in cells and in reconstituted actin networks, in particular under the physiological conditions of nonlinear and nonequilibrium loading present during active processes such as cell migration (78). Additionally, extension of the model in this article to include the active, nonequilibrium stretching response of individual cytoskeletal stress fibers as mediated by myosin, tropomyosin, and α-actinin provides an important, yet challenging avenue of development to facilitate the bottom-up prediction of cellular mechanics (8,10,11,79).

CONCLUSIONS

Cytoskeletal bundles of cross-linked actin filaments form key structural components of a broad range of cellular processes. To date, a common conception has been that cytoskeletal bundles display two limiting bending behaviors, namely decoupled or fully coupled bending. Here, we demonstrate that their bending behavior is considerably more intricate, depending on global bundle dimensions, the shear stiffness of intervening cross-links, and the stretching stiffness and fracture density of constituent fibers. We isolate two generic design parameters, N and α, that delineate the three distinct bending regimes of cytoskeletal bundles with markedly different scaling properties. Experimental bending stiffness of in vitro fascin cross-linked actin bundles, as well as existing in vivo measurements of the bending stiffness of the limulus sperm acrosome and of the stereocilium, validate our interpretation of actin bundle mechanics. The isolated state dependence of fiber bundles has important implications for the physiological bending, buckling, and potential entropic-stretching behavior of cytoskeletal processes, some of which are highlighted in this work. Finally, ab initio predictions for the bending regime of various cytoskeletal processes are presented in the form of a bending stiffness state diagram, which emphasizes the importance of bundle dimensions and internal composition on bundle mechanical response, as well as the generic nature of the proposed description.

Future experimentation using active mechanical probes will facilitate the extension of the static molecular-based model here to include nonequilibrium effects of force-induced cross-link unbinding, filament dynamics including rupture and disassembly, and molecular motor mediated filament sliding and translocation as present in cytoskeletal stress fibers. Although considerable additional experimentation in close collaboration with multiscale modeling is needed to fully understand the intricate nature of cytoskeletal bundle mechanics, this challenging line of research should eventually facilitate a mechanistic, molecular-level understanding of the interplay between cellular mechanics and active cytoskeletal remodeling that has remained elusive to date.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

APPENDIX: DERIVATION OF THE MODE NUMBER DEPENDENT BUNDLE-BENDING STIFFNESS

The bundle Hamiltonian,

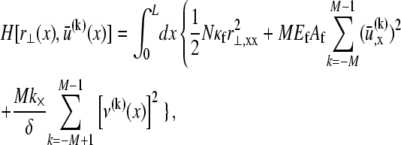(A1)

may be simplified to depend only on 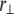and the relative degree-of-stretching between fibers, 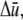by employing the approximation that fiber stretching varies linearly through the bundle cross section (25),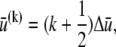

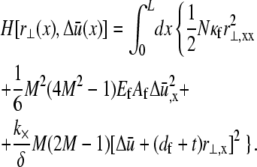(A2)

Fourier transformation of the Hamiltonian in Eq. A2 then results in the decomposition 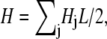where the contribution of mode j to H is

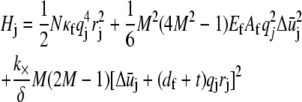(A3)

and r_j, 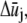and q_j denote the Fourier coefficients and wavenumber associated with mode j. Minimization of Eq. A3 with respect to 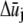yields the minimum value,

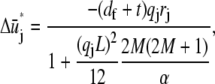(A4)

and the corresponding reduced Hamiltonian,

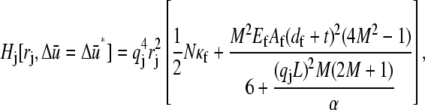(A5)

which yields the mode number dependent effective bundle-bending stiffness,

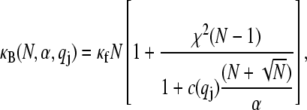(A6)

where 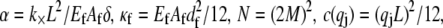and 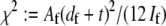have been defined, where 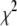accounts for the finite thickness of the cross-links.

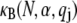may subsequently be employed to calculate the transverse deflection 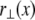corresponding to transverse loading 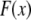via back-transformation to real space of

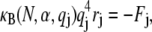(A7)

where 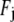is the jth Fourier component of the applied force. The transverse deflection is given by

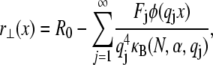(A8)

where the eigenfunction 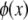is given by sine and cosine for hinged and clamped boundary conditions, respectively, and 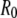is chosen such that the transverse deflection vanishes at the bundle ends.

Although an exact evaluation of the sum in Eq. A8 in general yields a complex analytical expression, performing the sum without the “1” in the denominator of Eq. A6 and adding it back to the final result yields an approximate solution that is nearly identical to the exact result. The deflection of the bundle midpoint 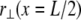may then be recast into the standard result from Euler–Bernoulli beam theory,

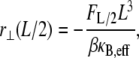(A9)

where β = 48 and 192 for pinned and clamped ends, respectively. The effective bending stiffness, 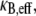then has the same form as in Eq. A6 except with the (mode number dependent) factor c substituted by the constant factors 1 and 4, as verified by comparison with the FE results.

Calculation of the equilibrium mean-square transverse displacement of the bundle backbone due to thermal fluctuations requires evaluation of

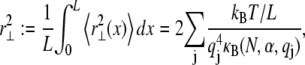(A10)

where 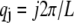for periodic boundary conditions applicable to the ring-bundle system examined experimentally. This yields, 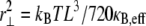(80), where the effective bundle-bending stiffness is again given by Eq. A6 with c = 5.