Intracellular Microrheology of Motile Amoeba proteus

Abstract

The motility of Amoeba proteus was examined using the technique of passive particle tracking microrheology, with the aid of newly developed particle tracking software, a fast digital camera, and an optical microscope. We tracked large numbers of endogeneous particles in the amoebae, which displayed subdiffusive motion at short timescales, corresponding to thermal motion in a viscoelastic medium, and superdiffusive motion at long timescales due to the convection of the cytoplasm. Subdiffusive motion was characterized by a rheological scaling exponent of 3/4 in the cortex, indicative of the semiflexible dynamics of the actin fibers. We observed shear-thinning in the flowing endoplasm, where exponents increased with increasing flow rate; i.e., the endoplasm became more fluid-like. The rheology of the cortex is found to be isotropic, reflecting an isotropic actin gel. A clear difference was seen between cortical and endoplasmic layers in terms of both viscoelasticity and flow velocity, where the profile of the latter is close to a Poiseuille flow for a Newtonian fluid.

INTRODUCTION

Viscoelasticity is closely associated with motility in a wide range of biological organisms. Examples include slugs sliding on mucin trails, skin coatings on fish, the hinge joints of dragon flies, the gait of kangaroos, swimming motion in protists and bacteria, and the amoeboid crawling of many eukaryotes, including mammalian cells. The viscoelasticity of the substrate, the environment, the organs or cellular compartments of the organism, and the individual biological molecules all have a direct effect on the form of motility.

Amoeboid locomotion is the general term describing the motility exhibited by adherent eukaryotic cells that move by extending pseudopodia, cytoplasmic streaming, and changing their shape. Amoeboid locomotion is exhibited by many types of cell, including free-living amoebae and mammalian cells. In the latter, amoeboid locomotion is vital for the development of the embryo, the repair of wounds, and the action of the immune system. It is also responsible for the spread of tumors. Physical theories of amoeboid locomotion have developed since the mid-19th century, when the role of contractions of the cell cortex was recognized (reviewed in de Bruyn (1)). Eventually the fundamental chemistry of this contractility was understood in terms of the actomyosin system and its interaction with the cell membrane and other cellular components (2,3). In recent years, the motion and rheology of cells as well as reconstituted cytoskeletal systems have been an active research field in physics. New techniques have allowed measurements of the forces exerted and experienced by cells (4–7), as well as the forces and dynamics of individual cytoskeletal molecules (8). Theoretical progress has been made on the rheology and force generation of the cytoskeleton (8–11), and on integrated models of specific examples of amoeboid and amoeboid-like motion (12–16).

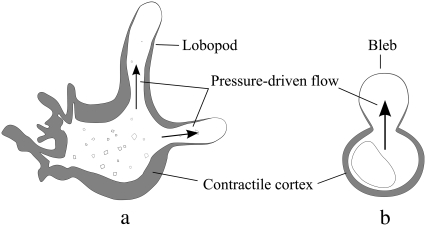
Amoeboid locomotion has different characteristics in different cell types, and sometimes different characteristics in the same cell type in different environments (3). Large free-living amoebae such as Amoeba and Chaos exhibit lobopodia, with a clear distinction between the ectoplasmic gel layer and endoplasmic sol, which streams freely as the amoeba moves. Many mammalian cells on two-dimensional tissue-culture substrates exhibit flat lamellipodia and thin filopodia, and comparatively slow locomotion. However, these cells often behave differently in three-dimensional tissue, where their extending pseudopodia may have closer resemblance to lobopodia. The similarity between motion in mammalian cells and amoebae has been further highlighted by observations of phagocyte motion, cortical oscillations in cells lacking microtubules (17), and cytokinesis (13,18). In both cortical oscillations of mammalian cells and crawling large amoebae, movement is generated by the contraction of the cytoskeleton in the cortical layer, which forces the cytoplasm into an expanding lobopod or bleb, respectively (see Fig. 1).

FIGURE 1.

We have the same broad understanding of the mechanics of motion in a large amoeba (a) and cortical oscillations in a mammalian cell (b). Both are driven by contractions in the cortical cytoskeleton, causing pressure-driven flow into lobopodia or blebs. A. proteus is a useful model for microrheology, due to its thick cortical gel layer, and the large number of visible embedded particles.

We present what we believe is a novel perspective on amoeboid locomotion using a new experimental technique—passive particle-tracking microrheology (PTM). In PTM, the thermal motion of tracer particles is tracked, yielding information on the rheology of the material (19–23). A new advance is that we have developed software that allows endogeneous particles to be accurately tracked against a complex optical background, i.e., the cell. This software functions well with a fast digital camera (10 kHz) and a high resolution oil immersion light microscope (24). Our experimental subject is Amoeba proteus, which has been a popular model of amoeboid locomotion for more than a century (3). For our technique, A. proteus is especially useful due to its large number of endogeneous particles, which are visible in the light microscope, and its thick cortical gel layer.

METHODS

Amoeba culture

Specimens of A. proteus were cultured by setting up a food chain according to Page (25). The culture medium consisted of 200 ml of Prescott's and James's solution with two boiled rice grains. Samples of A. proteus and the cryptomonad flagellate Chilomonas were obtained from Blades Biological (Kent, UK) and added to the medium in a glass dish. A. proteus fed on the abundant Chilomonas cells, which fed on bacteria in the medium. The culture was kept at room temperature.

Particle tracking microrheology

Individuals of A. proteus were observed in an Olympus IX71 inverted microscope (Olympus UK, London, UK) in bright field mode, with a 100× oil-immersion lens and a 1.6× magnifier. Images were captured using a Photron FastCam PCI charge-coupled device camera (Photron (Europe), Bucks, UK), at frame rates up to 3000 Hz. Tracking of endogeneous particles was performed using our recently developed particle tracking software (24), which is especially suited for tracking low-contrast particles against a complicated background. The use of endogenous granules is much more elegant biologically than introducing particles exogenously, which can damage or kill many cells. We can be certain with endogenous particle tracking that we are not perturbing the cellular processes that we want to study. Several large and small individuals were examined, all at 21°C, in Prescott's and James's solution, and at a similar light intensity. We note that the amoebae could be at different stages of their life cycle, but since the life cycle and biochemistry of A. proteus are not well understood, it is not trivial to define its state in an experiment. Measurements presented below are representative of all sampled amoebae.

To extract rheological information from the particle tracks, we follow the well-established single-particle analysis (21,26,27). The more subtle two-particle correlation analysis offers the advantage that its result is independent of the interactions between the particle and the medium (20,28). Unfortunately, however, we find that the two-particle technique does have some disadvantages, particularly with respect to intracellular work. The correlation between probe fluctuations is sensitive to the boundary conditions in the confined environments (e.g., the boundaries of the cell and glass surface) bringing the derivation used into question (the cell thickness is comparable to the interparticle separation). We did not observe the required (interparticle separation)⁻¹ decay for the correlation to use the Lubensky-Levine theory, and note that Lau et al. (29) measured only a rough agreement with the theory over the range of interparticle distances probed. In our case, we find below that the cytoplasm is inhomogeneous and that part of that inhomogeneity is due to spatial organization and flow-thinning. Therefore, to apply the two-particle analysis to our particle tracks, we would be forced either to take an average over an inhomogeneous set of particles, or to select subsets of particles between which to calculate the correlations, thus introducing extra complications. We prefer the single-particle analysis in the current work, since it is simpler to use, provides reliable measurements with lower statistical error, and still provides a clear robust probe of sample dynamics: a number of single-particle microrheology methods provided the first good evidence for t^3/4 fluctuations of a variety of semiflexible fibers (21,26,30–32).

Confocal laser scanning microscopy

Confocal fluorescence images were taken with a Leica SP2 AOBS confocal microscope (Leica Microsystems, Wetzlar, Germany). TubulinTracker (taxol conjugated to Oregon Green 488, Molecular Probes, Invitrogen, Paisley, UK) was added directly to the culture medium containing live amoebae. Staining of F-actin was performed with Alexa Fluor 633 phalloidin (Molecular Probes), after fixing amoebae in 3.7% formaldehyde in phosphate-buffered saline for 10 min at room temperature, and permeabilizing with 0.1% Triton in phosphate-buffered saline for 3 min.

RESULTS

Endogenous particles were tracked in several live A. proteus cells at frame rates of up to 3000 Hz. Large and small specimens were examined, and robust quantitative characterization of viscoelasticity from point to point was possible.

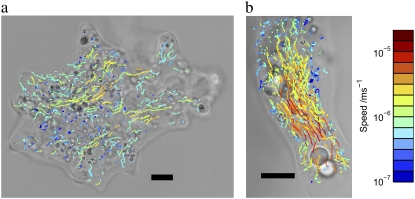
Fig. 2 shows (a) one small and (b) one large individual of A. proteus. The large individuals are polytactic: they extend and contract lobopodia in several directions simultaneously. Fig. 2 b shows a single pseudopod. Tracks of endogeneous particles are superposed on images a and b, captured at 2000 Hz and 3000 Hz, respectively. The average speed of each particle is represented by colors from blue (slowest) to red (fastest). It is clear that the flow of cytoplasm in the amoebae is inhomogeneous: the small amoeba shows localized fast currents surrounded by slow or gelled cytoplasm, whereas the large amoeba shows fast flow in a central channel (the endoplasm), surrounded by a much slower layer (the cortex or ectoplasm). These measurements reflect previous observations of intracellular velocities (33).

FIGURE 2.

(a) Small individual of A. proteus and (b) lobopod of a large polytactic individual. 10 μm scale bars are plotted on each, and the trajectories of all tracked particles are superposed, colored according to their speed on the scale shown at the right.

From the particle tracks, we calculate the mean-squared displacement (MSD) of each track, as a function of timescale t, according to

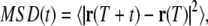(1)

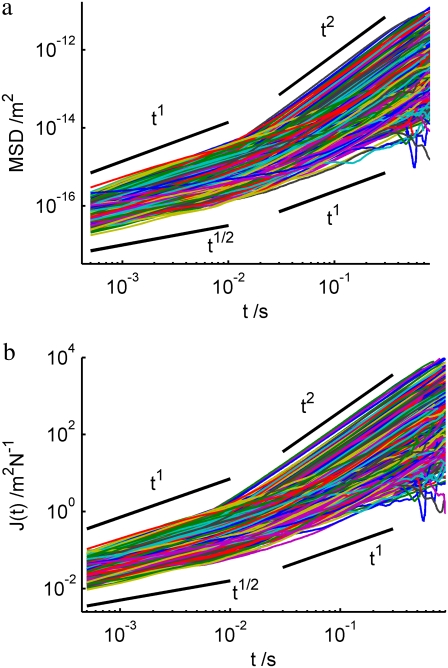
where r(T) is the position at time T, and the average is performed over T. Fig. 3 a shows MSDs of all tracked particles in the small amoeba above. Two power-law regimes can be identified at different timescales. At large t, most particle tracks are superdiffusive—i.e., dominated by active motion—since they have exponents >1 and indeed as large as 2, which corresponds to steady, directed motion. At small t, motion is subdiffusive—corresponding to thermal motion in a viscoelastic medium—since the MSDs have exponents <1. The crossover takes place at t ∼ 0.02 s, which reflects the rheology of the medium and the speed of the flow. The exponents at small t may be understood according to the theoretical models of the rheology of stiff filaments: in particular, an exponent of 3/4 is expected for a network of tethered semiflexible filaments, and 1/2 is expected for semiflexible filaments under a sufficiently large tension (10,22,34).

FIGURE 3.

(a) MSD and (b) compliance J(t) of all tracked particles in the small amoeba in Fig. 2 a as a function of time. Two regimes are identified: a subdiffusive regime at small t, indicative of thermal motion in a viscoelastic medium, and a superdiffusive regime at large t, indicative of active motion.

As t decreases to 0.5 ms, the MSD curves decrease steadily with no apparent leveling off due to the “static” error of measuring the particle positions (35). Therefore, our static error is insignificant compared to particle displacements, and must be significantly less than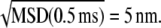

We examined the particle tracks for step-like motion but found none, in contrast to our previous observations of mammalian cells (24). Neither did we find rapid directional movements of single particles while their neighbors remained stationary, which would be a clear sign of motor-driven motion along protein filaments. Therefore, we can conclude that the particle motion really is dominated by thermal forces in the subdiffusive region that we have identified.

The MSD is related to the rheology of the material around each particle by the generalized Stokes-Einstein relation. We calculate the time-dependent shear compliance J(t), which is directly related to the MSD (26). In the case of a two-dimensional MSD:

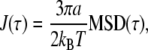(2)

where a is the radius of each particle, which can be measured from the image (calculated according to Rogers et al. (24)). Fig. 3 b shows J(t) for the same data as Fig. 3 a. There is a large variation in absolute values of J(t) between particles, even when the scaling exponent is the same. This variation is approximately a factor of 10 at t = 1 ms. This is likely to be due, in part, to the local heterogeneity of the cellular environment (23) or the heterogeneity of contacts between the particle and the cytoskeleton (36).

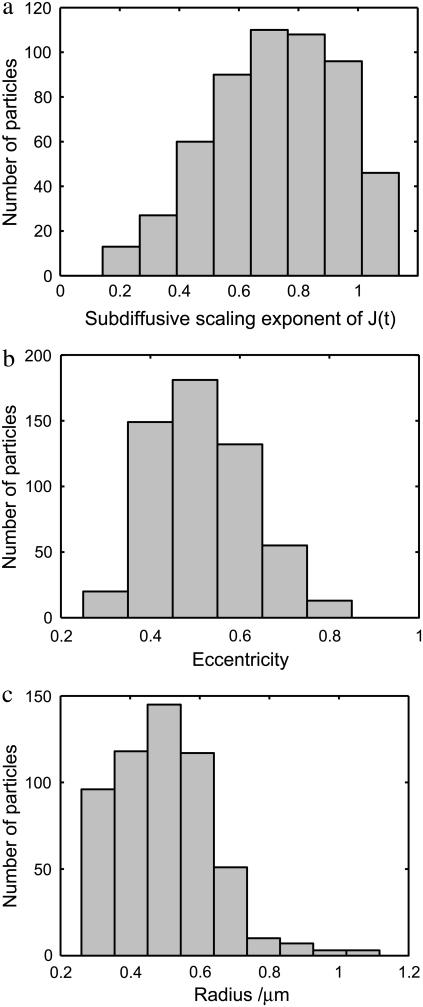
A histogram of the scaling exponents, fitted to each curve of J(t) in the range 0.5 ≤ t ≤ 3 ms, is presented in Fig. 4 a. The histogram is peaked at 0.75, corresponding to the tracked particles being attached or closely associated with a network of semiflexible filaments (10). We also plot histograms of the radii and eccentricity of the tracked particles. The radii are peaked at 0.5 μm, and the eccentricities at 0.5. By using Eq. 2, we have treated all particles as spherical; therefore, the eccentricity of the particles will cause an error in the analysis. Using the drag coefficients for a prolate ellipsoid (37), taking eccentricity = 0.5, we obtain a ratio of the drag coefficients, perpendicular and parallel to the principle axis, of 1.03. The error is therefore negligible compared to the heterogeneity of the cytoplasm observed above. Very few particles actually appear to change their radii significantly during the captured movies (see the Supplementary Material). Typical particles only vary by ∼30 nm: much less than the typical radius—only 0.5% of the particles vary more than 100 nm (data not shown). We expect that these apparent variations are mainly caused by out-of-plane displacements and variations in the image background intensity. Although we do not expect that the radii measured from the image are accurate, neither do we expect that they are biased. Moreover, we are fortunate that the compliance is only linearly dependent on the particle radius. Thus, even a 50% error in the radius of a particle will lead to an error far smaller than the observed factor-of-10 variation in the magnitude compliance from point to point seen in Fig. 3 b. More importantly, the scaling exponent is unaffected by an error in the prefactor.

FIGURE 4.

(a) Histogram of scaling exponents in the subdiffusive region of J(t) for each tracked particle in the small amoeba of Fig. 2 a. The histogram is peaked at 0.75, corresponding to a network of semiflexible filaments. (b and c) Histograms of radii and eccentricity of all tracked particles, calculated according to Rogers et al. (24).

The same features of Fig. 3 were observed in all measured amoebae, i.e., a subdiffusive and a superdiffusive region, with approximately the same range of exponents and a similar range of absolute values.

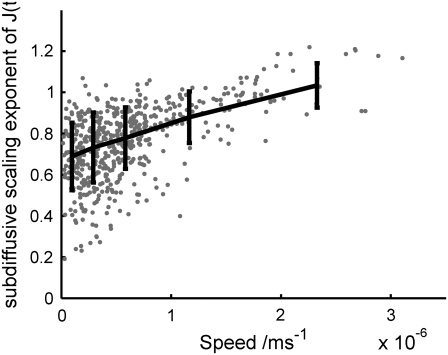
We investigated the dependence of the scaling exponent in the subdiffusive region on position and velocity within the cell to elucidate the effect of cellular structure on rheology. Fig. 5 shows the speed plotted against the scaling exponent, calculated as above, for all tracked particles in the small amoeba above. The data points are binned, and the mean of each bin plotted, with error bars showing the standard deviation from each mean. A clear trend is apparent: the scaling exponent increases with speed, with a mean of ∼0.7 at zero speed, and reaching a mean of 1, corresponding to a viscous liquid, at ∼2 μm s⁻¹.

FIGURE 5.

Scaling exponent in the subdiffusive region of J(t) for each tracked particle in Fig. 2 a, plotted against particle speed (circles). The data are binned and the mean of each bin plotted as a line graph, with error bars calculated from the standard deviation of each bin. The scaling exponent shows a clear increase with rising speed.

Note that the expected error in the subdiffusive scaling exponent due to a particle's drift velocity can be calculated as follows. For a typical particle in Fig. 3 a, MSD = Ct^0.75 + (Vt)², where V is speed in the range 0–3 μm s⁻¹, and typical values of MSD ≈ 10⁻¹⁶ m² at t = 1 ms set the parameter C ≈ 3 × 10⁻¹². By taking the differences of the terms in this equation over the interval 0.5 ≤ t ≤ 3 ms, we calculate an error in the scaling exponent of the order 10⁻⁷, which is insignificant compared to its measured increase as a function of particle speed.

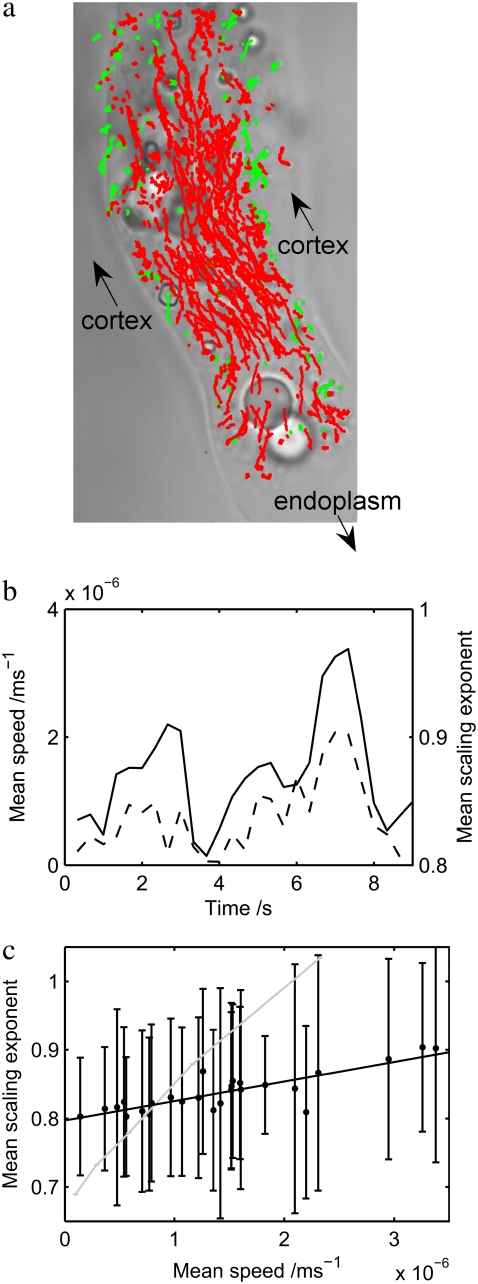
The same effect is apparent in large amoebae. Fig. 6 a shows the same extending lobopod of the large individual shown in Fig. 2 b. Here we highlight each particle depending on its velocity component with respect to the direction of lobopodial movement: red for positive and green for negative. Particles embedded in the endoplasm are forced by the cytoplasmic pressure in the direction of the lobopod, whereas particles embedded in the cortex tend to have a small velocity in the opposite direction. This well-known but counterintuitive phenomenon, known as the fountain effect (14,38), is due to the cortex of the lobopod being connected directly to the cortex of the entire cell: since the cortex is contracting everywhere, it draws the lobopodial cortex back toward the cell body. Separating the particle data by this direction of drift, we plot the speed and mean subdiffusive scaling exponent of the particles, in the endoplasm only, against time (Fig. 6 b). Here the data are broken up into time steps of 1000 frames (i.e., 1/3 s). The average speed of flow can be seen to pulsate rhythmically, as is also apparent from the video of the lobopodial extension (see the Supplementary Material). The mean subdiffusive scaling exponent, calculated as above, rises and falls in tandem with the speed, and both are plotted against each other in Fig. 6 c. Here, a clear trend is shown by the linear least-squares fit (solid line): the data points follow this line much more closely than the plotted error bars, which show the standard deviation of the sample of particles at each time point. Indeed this standard deviation is an overestimate of the statistical error in this plot, since it is due to the inhomogeneity in the local environment of each particle, which does not necessarily change between successive time points. In the lobopod endoplasm only, the trend is significantly shallower than in the data for the entire small amoeba, of Fig. 5 above, which is superposed here (shaded line). These data show an analogous phenomenon to shear thinning, and are further discussed below, along with the differences between the measurements.

FIGURE 6.

(a) Endoplasmic (red) and cortical regions (green) in the lobopod of the large amoeba of Fig. 2 b, identified by the direction of particle drift with respect to the direction of the lobopod. (b) Mean particle speed of endoplasmic particles (solid line), plotted simultaneously with mean subdiffusive scaling exponent (dotted line), as a function of time, in steps of 1/3 s. The speed and scaling exponent rise and fall in tandem. (c) Mean particle speed and mean scaling exponent, from b, are plotted against each other. A clear trend is shown by the linear least-squares fit (solid line): the data points follow this line much more closely than the error bars, which show the standard deviation of the sample of particles at each time point. The trend is significantly shallower here than in the data for the entire small amoeba (shaded line), of Fig. 5.

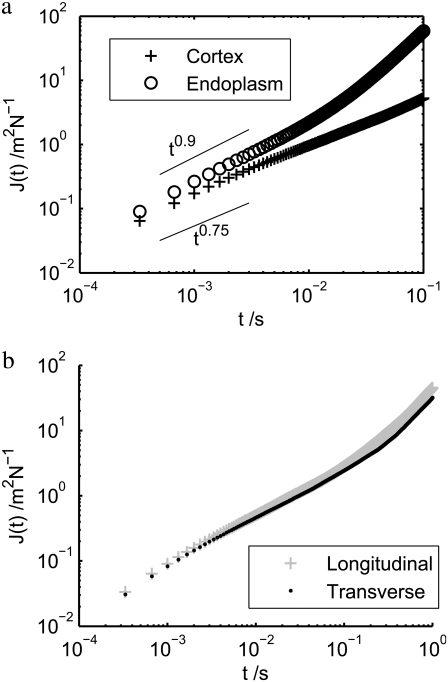
The effect of structure on rheology within the lobopod can be further investigated. In Fig. 7 a, we plot the compliance within the cortex and endoplasm, respectively, averaged over all particles separated as shown in Fig. 6 a. A simple mean of the compliance was calculated from each particle track, weighted by the number of time points N_i in track i, so that each measured event contributes equally to the average compliance: 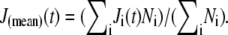Looking only at the subdiffusive regime, we see that there is a small difference: the mean scaling exponents are close to 0.75 and 0.9 for cortex and endoplasm, respectively. Indeed, the difference in the absolute value of J(t) is fairly small: the endoplasm is 54% more compliant than the cortex on a timescale of 1 ms, and the compliances of both sections appear as if they will converge to the same value if extrapolated to ∼10⁻⁴ s. We can fit endoplasmic compliance with a linear function of time, since its scaling exponent of the endoplasm is so close to 1. Fitting J(t) in the range 0.5 ≤ t ≤ 3 ms, we obtain J(t) ≈ 220 × t Pa⁻¹s⁻¹. Thus the effective viscosity is given by η = t/J(t) = 4.5 mPa s. The rheology within a lobopod section is further explored below in a different individual.

FIGURE 7.

(a) Compliance within the cortex and endoplasm of the lobopod shown in Fig. 6 a. There is a small difference in the subdiffusive regime: the mean scaling exponents are close to 0.75 and 0.9 for the cortex and endoplasm, respectively. (b) Rheological anisotropy in the cortex shown as effective compliance in the longitudinal and transverse directions with respect to the lobopod. There is a negligible difference: the rheology of the cortex is effectively isotropic.

Besides rheological inhomogeneity, there may be rheological anisotropy within the cytoplasm. In particular, we may expect the actin filaments within the cortex to have an anisotropic arrangement, such as a preferred orientation, parallel or perpendicular to the lobopod. Any such anisotropy in cortical structure would surely be reflected in the rheology. Following Hasnain and Donald (39), we analyze rheological anisotropy by treating the MSD as a tensor: 〈(r_i(T + t) − r_i(T))(r_j(T + t) − r_j(T))〉, where i, j = {x, y}. By rotating the coordinate axes to the directions parallel and perpendicular to the lobopod, and treating each direction independently, we may use Eq. 2 to obtain the effective compliance in each direction. Fig. 7 b shows the result: there is negligible difference between the compliance in each direction; indeed the difference is very much smaller than the standard deviation of compliances among different particles. Therefore, the cortex may be considered rheologically isotropic. The same result was obtained on two other measured lobopodia.

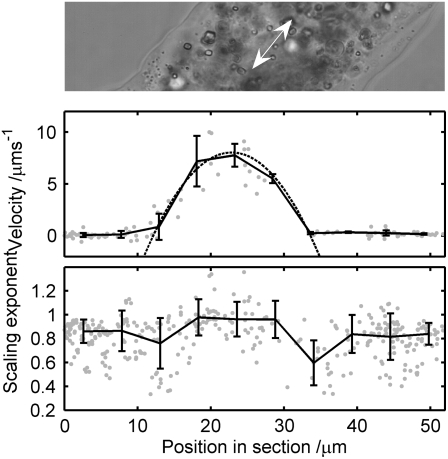
The velocity profile and subdiffusive scaling exponent profile are plotted simultaneously for the midsection of another A. proteus lobopod in Fig. 8 (top). The data were taken from an 8-s movie captured at a frame rate of 3000 Hz, during which the flow rate varied continually. The velocity profile was calculated from all tracked particles during the last 2 s of the movie, when the flow rate was approximately constant. We plotted the component of the velocity parallel to the lobopod (Fig. 8, center): here we can see the nearly sessile cortical layer, ∼15 μm thick, and the flowing endoplasm, with a diameter of ∼20 μm. The data points are rebinned, and the mean and standard deviation in each bin are plotted as a solid line with error bars. The velocity of the endoplasm shows good correspondence to a parabolic fit (dotted line), which would be indicative of a Poiseuille flow in a Newtonian fluid in contrast to the plug flow (flattened parabola) exhibited by strongly elastic suspensions (40). The scaling exponent profile is calculated as above, from all tracked particles in the entire movie (Fig. 8, bottom). Again, the data are rebinned and the means and standard deviations plotted as a solid line with error bars. This profile shows two regions of scaling exponent ≈0.8 and 1.0, respectively: these correspond to the cortex and endoplasm as identified from the velocity profile. Although the statistics of each bin limit our resolution to ∼5 μm in analyzing the spatial variation of the rheology, it appears here that the boundary between cortex and endoplasm is fairly abrupt: no gradual change in the mean-scaling-exponent is apparent, and the boundary itself has an upper thickness limit of 5 μm.

FIGURE 8.

Midsection of an A. proteus lobopod is displayed (top), showing the direction of flow. From tracked particles in this image, we calculate a velocity profile (center) and a scaling exponent profile (bottom). Individual data points (circles) are plotted on each graph, with the rebinned and averaged data plotted with error bars, showing each standard deviation from the mean (solid line). The velocity of the endoplasmic layer is fitted well with a parabola (dotted line), which corresponds to Poiseuille flow in a Newtonian fluid. The scaling exponent profile shows two regions of scaling exponent ≈0.8 and 1.0, respectively, corresponding to the cortex and endoplasm as identified from the velocity profile. The boundary between the layers seems abrupt; there is no gradual change in the mean-scaling-exponent, as far as the local inhomogeneity in the data permits us to discern.

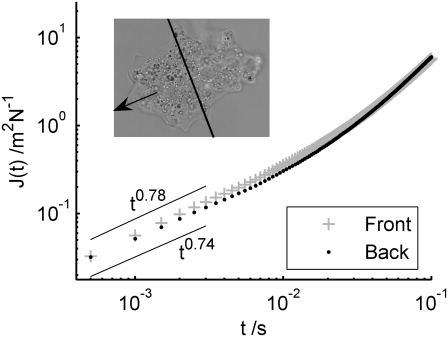
We looked for differences in the rheology of the cortex and endoplasm in extending and retracting parts of A. proteus. The small amoebae could be completely observed in a single field of view under the microscope, so that it was simple to bisect the images into front (extending) and back (receding) halves, and measure the microrheology of each. Fig. 9 (inset) shows the bisection of the data from the individual of Fig. 2 a, thence the mean compliance in each region is plotted. There is a very small difference in average rheology between the extending and receding regions—far less than the standard deviation from the mean (not shown). In this amoeba, the fitted scaling exponents were 0.78 and 0.74 in the front and back regions, respectively, but this small difference was within the error bars on repeated measurements with different amoebae (not shown).

FIGURE 9.

Particle tracks from the individual of Fig. 2 a are bisected into front (extending) and back (receding) halves. Then the mean compliance in each region is plotted. There is a small difference in average rheology between the extending and receding regions: in this amoeba, the fitted scaling exponents were 0.78 and 0.74 in the front and back regions, respectively, but this difference varied among different amoebae (not shown).

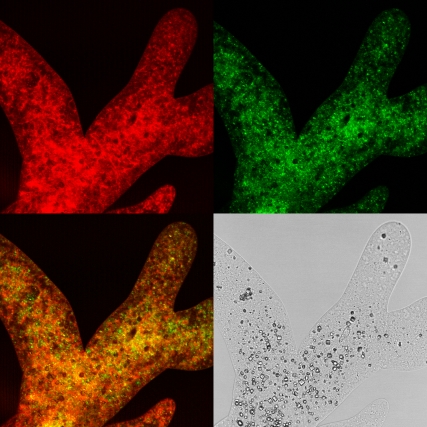
Samples of A. proteus were fixed and stained for microtubules and filamentous actin as described above. Fig. 10 shows representative images. Phalloidin-stained actin is found throughout the cell, whereas fluorescently labeled taxol seems to have stained particulate matter rather than extended microtubules. This confirms previous observations of the lack of microtubules in the cytoplasm (3). The observed particular matter is likely to be short microtubules and microtubule-organizing centers (41). No layer of high actin concentration is observed at the cell periphery—indeed, the observation of its absence in immobilized cells has been noted previously (42). Only in live cell fluorescence images does a layer of high actin concentration develop transiently near the cell periphery and continually change during cell movement (42,43). It seems that filamentous actin is present throughout the cell, and concentrated layers of actin only appear during cortical contractions before disintegrating again.

FIGURE 10.

Large individual of A. proteus fixed in formaldehyde and stained for microtubules (green) and F-actin (red). The fluorescence images are overlaid (bottom left), and a corresponding bright field image is shown (bottom right). F-actin is distributed throughout the cell, whereas tubulin is predominantly found deeper within the cell.

DISCUSSION

Although the studies of amoeboid motion in general and A. proteus in particular are very old topics, our application of microrheology to them has yielded what we believe are novel results. One of the advantages of particle tracking microrheology is that it allows us to distinguish thermal from active motion. Directional motion, e.g., convection or motion along a protein fiber, leads to MSD ∼ t². However, thermal motion with MSD ∼ t^α; 0 ≤ α ≤ 1, will always dominate if we can examine short enough timescales, and that is what we saw in Fig. 3.

First we identified a power law viscoelastic regime in J(t) at short timescales, similar to that observed in cultured animal cells and reconstituted actin networks. Although there was a large variability in the absolute value of J(t) due to inhomogeneity of the cytoplasm and presumably heterogeneity of interactions between each particle and the cytoskeleton, we found that the exponent of the power law regime of J(t) gave illuminating results. The mean of the distribution of exponents was near 3/4 in all cases where the cytoplasm was at rest. A similar result has been obtained several times in reconstituted actin networks (44–46), but rarely in cultured mammalian cells, where very different exponents are reported (47), although the famous exponent of 3/4 has been found by some authors (48,49). We feel that these discrepancies highlight the difficulties of accurate intracellular microrheology. However, the exponent of 3/4 can be observed more clearly in our data than any other published data of which we are aware. This success is due to the size of A. proteus, the large number of trackable particles it contains, the use of a fast digital camera, and our new tracking method (24).

We then examined the effect of flow on the rheology of the cytoplasm, finding in each case that the J(t) scaling exponent increased with flow speed, i.e., the cytoplasm became more fluid-like. In the case of pulsating flow in the large amoeba lobopod, the shear rate can be estimated by assuming Poiseuille flow in a cylinder of diameter 10 μm, the approximate diameter of the endoplasm in Fig. 2 b. Thus the range of speeds 0–3.4 μm s⁻¹ maps onto the range of shear rates 0–0.7 s⁻¹. One obvious reason that the measurements of shear-thinning in Fig. 6 c do not agree with each other is that the geometry of the flow is not the same in the different amoebae, although unfortunately we cannot estimate the shear rates in the small amoeba because we lack data on the velocity of the flow as a function of height above the substrate. In the endoplasm of the large amoeba, the flow rate rose and fell on a timescale of ∼1 s, and the scaling exponent followed it without a measurable delay. On that timescale, the change in rheology could be due to either passive or active remodeling of the cytoskeleton (49). We should additionally expect that the active remodeling of the cytoskeleton occurs on a range of longer timescales; for example, the active cycling of material between the cortex and endoplasm in the course of cell migration occurs on a timescale of minutes (42).

These measurements join very few previous reports of shear-thinning in living cytoplasm, which measured the apparent viscosity under forces applied with magnetic tweezers (50,51) and micropipettes (52). However, our measurements of the effect of flow on the rheological scaling exponent are new, and reveal information that could be compared with theories of viscoelasticity of semiflexible fiber networks. To our knowledge, no such theories exist of how the rheology of these networks changes with deformation. But heuristic models of the shear-thinning response of cells are already in use, as they are necessary to explain the measured deformations of whole cells under applied forces, such as during micropipette aspiration (53).

Comparing the rheology of cortex and endoplasm, we found that the absolute values of compliance were similar in both, and may be expected to converge to the same value at timescales ≲10⁻⁴ s. (Fig. 7 a). The similarity in compliance between the two regions is perhaps unsurprising, given the fairly uniform distribution of filamentous actin throughout the cell (Fig. 10). The rheology of the endoplasm was found to be close to a Newtonian liquid with a viscosity of 4.5 mPa s. Although reported values of cytoplasmic viscosity are known to vary by six orders of magnitude (quoted in Valberg and Feldman (50) and Yamada et al. (54)), our value is similar to several measurements at the lower end of the scale. It is not surprising that these techniques accessing different parts of the cell machinery at different timescales, length scales, and deformation rates have yielded such different values of effective viscosity. But our measurement is notable in that we know it describes the flowing endoplasm only, whose rheology we have found to be approximately Newtonian. If we use this value to obtain the Reynolds number and Péclet number of the endoplasmic flow, we obtain Re = ρVR/η ≈ 10⁻⁵ and Pe = LV/D ≈ 10³, taking the radius of the channel as R = 10 μm, the velocity as V = 5 μm s⁻¹, the density ρ of water, and the typical diffusivity of a tracked particle as D = k_bT/6πaη with a ≈ 1 μm. The Reynolds number is low—there is no turbulence, and the Péclet number is high—convection dominates the particle motion over the length scale R. A typical pressure drop can be estimated along a lobopod of length L = 100 μm: ΔP = 4ηVL/R² ≈ 0.1 Pa, using the equation for Poiseuille flow. We note that the pressure difference within the endoplasm is very much smaller than the pressure differences of 10²–10³ Pa required to stall the amoeba's motion (55–57): although large stresses are generated within the cortex, the endoplasm transmits the pressure hydrostatically.

In Fig. 7 b, we were surprised to find that the rheology of the cortex is effectively isotropic, suggesting that the actin filaments in the cortical cytoskeleton are arranged isotropically, rather than with orientational order with respect to the cell geometry. This novel result provides reassuring evidence that theories and measurements in vitro of model isotropic actin networks correspond to the system in vivo, at least in the case of A. proteus.

The velocity profile and scaling exponent profile in the lobopod section (Fig. 8) show that the streaming amoeba endoplasm flows like a Newtonian fluid, with a parabolic velocity profile and a scaling exponent of 1 throughout the endoplasm. The boundary between the endoplasm and cortex seems intriguingly abrupt in both profiles: we are not aware that the physics of this boundary has been studied. The scaling exponent was near 0.75 within the cortex as found previously.

Finally, we saw that the average rheology of a small amoeba did not differ significantly when bisected into front and back halves. In both halves, the average was dominated by the particles embedded in the cortex, shown by the exponent of ≈0.75. Although the back half of the cortex must have a larger tension than the front half to produce the observed motion, there is no significant difference in the rheology of the two halves. This result suggests that the difference in tension is not caused by a difference in the structure of the cytoskeletal network, which would surely affect the microrheology. Rather, it is likely to be caused simply by the difference between the thicknesses of the cortex in the two halves. We note that the result contrasts with the microrheology of migrating animal fibroblasts: Kole et al. (58) found that the leading part (the lamellipodium) of 3T3 cells is significantly less compliant than the trailing part, which contains the nucleus and most of the cytoplasm. Following them, we found that the lamellipodia of 3T3 and HeLa cells have lower rheological scaling exponents than the perinuclear region (S. S. Rogers, T. A. Waigh, and J. R. Lu unpublished data). It is not clear if these differences within animal cells are due to the structure of the cytoskeleton or the confinement of the particle and tight association to the substrate within a thin lamellipodium.

We may compare the measurements of compliance in A. proteus with previous PTM studies on mammalian cells and F-actin solutions. Measurements on COS7 cells (54) and 3T3 (58) yielded compliance in the range 0.01–0.1 m²N⁻¹ on a timescale of 0.1 s. In the different individuals of A. proteus that we have sampled, we have found compliances in the range 1–10 m²N⁻¹ on a timescale of 0.1 s, similar to measurements of F-actin solutions, at physiological concentrations (54,59). The cytoplasm of A. proteus is therefore less stiff than these typical mammalian cell lines by a factor of ∼100.

CONCLUSION AND OUTLOOK

Our application of PTM to crawling A. proteus has yielded what we believe are novel results on the structure and rheology of the cytoskeleton in living cells. In particular, we have seen variations (or lack of variations) of the rheological scaling exponent with flow rate and position or orientation within the cortex, endoplasm, and extending or contracting parts of the cell. A. proteus has always been one of the major organisms for studying amoeboid motility. Its resemblance to mammalian cells in many types of motion, such as cortical oscillations, makes our results on its microrheology relevant to the wider field of cell motility. The endoplasm of A. proteus behaves as Newtonian fluid at fast flow rates, and has a velocity profile close to Poiseuille flow. The compliance of the cortex displays a clear t^3/4 scaling, which is indicative of the bending fluctuations of actin filaments.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.