Evidence for a Common Mode of Transcription Factor Interaction with Chromatin as Revealed by Improved Quantitative Fluorescence Recovery after Photobleaching

Abstract

How site-specific transcription factors scan the genome to locate their target sites is a fundamental question in gene regulation. The in vivo binding interactions of several different transcription factors with chromatin have been investigated recently using quantitative fluorescence recovery after photobleaching (FRAP). These analyses have yielded significantly different estimates of both the binding rates and the number of predicted binding states of the respective transcription factors. We show here that these discrepancies are not due to fundamental differences among the site-specific transcription factors, but rather arise from errors in FRAP modeling. The two principal errors are a neglect of diffusion's role and an oversimplified approximation of the photobleach profile. Accounting for these errors by developing a revised FRAP protocol eliminates most of the previous discrepancies in the binding estimates for the three different transcription factors analyzed here. The new estimates predict that for each of the three transcription factors, ∼75% of the molecules are freely diffusing within the nucleus, whereas the remainder is bound with an average residence time of ∼2.5 s to a single type of chromatin binding site. Such consistent predictions for three different molecules suggest that many site-specific transcription factors may exhibit similar in vivo interactions with native chromatin.

INTRODUCTION

Fluorescence recovery after photobleaching (FRAP) has been used extensively in recent years to show that most nuclear proteins are highly dynamic (1). These studies have been aided by the development of mathematical models for FRAP that provide estimates of the binding rates of nuclear proteins to chromatin (1–8). As a result, we now have in vivo chromatin binding estimates for histones, histone-associated proteins, mRNA-binding proteins, DNA repair proteins, and transcription factors.

In vivo binding measurements have advantages over their in vitro counterparts since the latter cannot easily account for the complexities of the in vivo cellular milieu, such as the packaging of DNA into higher order chromatin, the potential association of a nuclear protein with other cellular factors that could modulate its binding, or molecular crowding (9–11). Thus in vivo assays have the potential to provide more accurate measurements.

However, in vivo assays for binding are still in their infancy, so the quantitative results from such procedures cannot as yet be validated against a “gold standard” to determine how accurate they are. Establishing a gold standard requires applying different in vivo binding procedures to the same molecule to determine if similar estimates are obtained, and if not, then why not. When different procedures yield different estimates for the same molecule, then the procedures should be modified to eliminate the differences by identifying and correcting inaccurate assumptions. Iteration of this approach with different in vivo binding procedures will ultimately identify errors and limitations in the different procedures, and should eventually yield a consensus estimate for the molecule in question.

This is the approach that we have begun here, focusing on one set of nuclear proteins, the site-specific transcription factors. These molecules must scan all possible DNA binding sites within the nucleus to locate the much smaller subset of promoter sequences whose downstream genes are under their regulatory control. This scanning process can be assayed by quantitative FRAP. Three different studies have employed this approach on three different site-specific transcription factors, arriving at very different binding estimates.

Sprague et al. (8) predicted for live mouse nuclei that ∼85% of the total glucocorticoid receptor (GR) molecules were bound with an average residence time of ∼0.01 s to a single type of chromatin binding site, which they argued was nonspecific DNA (8). Hinow et al (6) predicted for human nuclei that ∼43% of the total p53 molecules were bound with an average residence time of ∼2.5 s to a single type of chromatin binding site, which they also argued was nonspecific DNA (6). Phair et al. (7) examined seven different site-specific transcription factors in mouse and human nuclei, and argued that each was bound to two different types of chromatin binding sites, which they suggested might reflect specific and nonspecific DNA sites (7). For a representative transcription factor, Max, Phair et al. predicted that ∼98% of Max molecules were bound in one of the two chromatin binding states, with a residence time of ∼5 s for the weak binding state and ∼14 s for the tight binding state. Thus these three different FRAP studies have yielded vastly different estimates for either the fraction of bound transcription factor (from 43% to 98%), the number of distinct binding states (either one or two), and the residence time of the transcription factor on chromatin (from 0.01 s to 14 s).

Although each of the preceding studies used FRAP to quantify transcription factor binding, the details of the FRAP procedures differed in numerous ways, including the size and shape of the bleached region, the number of iterations used to perform the bleach, the temporal sampling rate for collecting recovery data, and the cell type examined. In addition, the mathematical and computational procedures applied to extract quantitative binding estimates also differed in their assumptions about the intensity profile of the photobleach and the role of diffusion in the recovery.

Thus it is not clear whether the vastly different predictions in binding reflect intrinsic differences among the transcription factors or simply differences in the FRAP procedures. To address this, we applied the three different procedures to the same transcription factor in the same cell line, and obtained three completely different binding estimates. We then scrutinized the three FRAP protocols to identify potentially incorrect assumptions, which led us to adapt two of the existing procedures such that they differed only in the bleach-spot geometry. The new procedures then yielded the same binding estimates for the same transcription factor in the same cell line. Interestingly, the estimates for the three transcription factors were now also similar to each other, suggesting a common mode of interaction of site-specific transcription factors with chromatin.

METHODS

Cells

Mouse adenocarcinoma cell line 3134 was grown in Dulbecco's modified Eagle's medium (GIBCO BRL, Grand Island, NY) supplemented with 2 mM glutamine (GIBCO BRL, Grand Island, NY) and 10% FBS (HyClone, Logan, UT). For p53 or Max FRAPs, the 3134 cells were transiently transfected by electroporation (BTX T820 Square Porator with three square wave pulses 140 V, 10ms, BTX Instrument Division, Holliston, MA) with either p53-green fluorescent protein (GFP) (12) or Max-GFP (13) DNA, and then subjected to FRAP 6 h (p53) or 12 h (Max) later.

For GFP-GR FRAPs, a stably transfected form of 3134 cells containing GFP-GR (mouse 3617 cells) was used. These cells were prepared for FRAP experiments as previously described (8).

Generic FRAP conditions

FRAP experiments were performed on a Zeiss 510 confocal microscope (Carl Zeiss, Thornwood, NY) with a 100×/1.3 NA oil-immersion objective and a 40 mW argon laser. Cells were imaged in LabTek II chambers (Nalgene) kept at 37°C using an air-stream stage incubator (Nevtek, Burnsville, Rochester, NY). Recovery data were binned logarithmically (14) generating relatively uniform spacing of points along the FRAP curve so as not to bias one phase of the curve when fitting with a FRAP model.

The FRAP model equations were programmed in MATLAB (The MathWorks, Natick, MA), and the routine nlinfit was used to fit the models to experimental data. A simplified pure diffusion form of the models was tested first, and then if this failed to yield a good fit, the full model equations were employed (8). The full model fit was performed with a grid search (8) to identify starting guesses for the nlinfit routine. Bound and free concentrations were calculated using the estimated association (k*_on) and dissociation (k_off) rates: bound, C_eq = k*_on/(k*_on + k_off) and free, F_eq = k_off/(k*_on + k_off) (8). Average residence time was calculated as 1/k_off. The MATLAB source code for the newly developed circle FRAP procedure with documentation is available upon request.

Implementation of the original circle, strip, and half-nuclear FRAP procedures

Three different bleach spot geometries were used in the original studies: a small circle (performed originally for GR (8)), a narrow rectangular strip (performed originally for p53 (6)), or a large, roughly semicircular region covering half of the nucleus (performed originally for Max (7)). Since we have applied these procedures to different transcription factors, we refer to them here based on their bleach-spot geometry, namely as circle, strip, or half-nuclear FRAPs.

Circle FRAP recovery data were obtained, corrected for observational photobleaching, and fit to a FRAP model, all as originally described (8).

Strip FRAP recovery data were also obtained as described, except that we used 5 instead of 10–50 iterations for the photobleach (6), since with our 40 mW argon laser 10 or more iterations induced excessive bleaching. Unlike the original study, we also detected observational photobleaching during the FRAP. We corrected for this effect using the same observational photobleaching correction procedure described below for the new strip FRAP.

Half-nuclear FRAP was also performed as described (7), but with the following adjustments. To achieve the published ∼0.5 s acquisition time per frame, we used zoom 4 and unidirectional scanning at speed 7. For image acquisition, we used an acousto-optical tunable filter (AOTF) setting of 0.5 instead of 0.1, which led to some observational photobleaching. This was corrected using a custom ImageJ macro from the European Molecular Biology Laboratory (Heidelberg, Germany) available at http://www.embl-heidelberg.de/eamnet/html/body_bleach_correction.html. For application of this macro, we defined the whole nucleus in the first postbleach image as the reference region. All succeeding images were then corrected such that the fluorescence in the nucleus was conserved. As in the published study, we also used two iterations of the photobleach, except for the measurements in Fig. 2 E, where one iteration was used. To fit the published Max FRAP data, we used simplified forms of the original model (Eqs. 14 and 15 in Appendix 4 with and ) that captured its essential features, namely one or two different binding states with no contribution from diffusion. The same equations were used to fit the GR half-nuclear FRAP data in Fig. 1.

FIGURE 2.

Test for diffusion-dependence of the FRAP. Schematic of the measurement for half-nuclear FRAP (A) and strip FRAP (B). The photobleach was performed in the dotted region. Intensity profiles were measured in the solid rectangle by starting at the base of the arrows (distance, 0 μm) and averaging pixels along lines perpendicular to the direction of the arrows. All postbleach profiles were normalized by the prebleach profile. Correction for observational photobleaching was performed as described in Methods. Scale bars, 5 μm. (C–H) Plots display averaged fluorescence intensity versus distance for Max, GR, and p53. The insets show the same profiles normalized between 0 and 1. Normalized profiles change in all cases indicating that diffusion should be incorporated into the FRAP model for Max, GR, and p53.

FIGURE 1.

FRAP with GR using the original circle, strip, and half-nuclear procedures. (A) Experimental data (gray circles) collected according to the original procedures are well fit (solid line) by the original FRAP models. Insets show a schematic illustrating the FRAP procedures. (B) The estimated values for k*_on and k_off are, however, radically different for each procedure (note the log scale). (C) Published estimates for each procedure (Circle FRAP for GR, strip FRAP for p53, half-nuclear FRAP for Max) are in the same range as the parameters estimated by each of the procedures for GR. This suggests that the FRAP procedure itself could significantly influence the binding estimates.

Implementation of the new circle and strip FRAP procedures

Data collection

Recovery data were acquired with the argon laser operating at 95% laser power and the AOTF set at 0.5%. The confocal pinhole was set to 3.0 Airy units corresponding to an optical slice of 2.5 μm, which yields a good signal/noise ratio without extending the depth of field outside the nucleus. The zoom factor was 4 yielding a pixel size of 0.045 μm for both circle and strip FRAP. Images were 512 × 50 pixels for strip FRAP (23 × 2.25 μm) and 512 × 90 pixels for circle FRAP (23 × 4.0 μm). Scanning was bidirectional with scan speed 12, yielding 44 ms per circle FRAP image and 25 ms per strip FRAP image. Prebleach images were acquired for ∼12 s (300 images for circle FRAP or 500 images for strip FRAP) to ensure that observational photobleaching was in a regime that could be accurately described by a single exponential decay (see “Data processing” below and Appendix 1). Then intentional photobleaching with a single iteration was performed with the 488 nm line from the 40 mW argon laser with the AOTF set to 100%. For circle FRAP, the photobleach was performed in a circle of 1.35 μm radius in the center of the image (bleach duration: 24 ms). For strip FRAP the photobleach was performed in a strip of 0.68 μm height centered vertically in the image but spanning its width (bleach duration 6.8 ms). In both procedures, postbleach images were acquired for 25 s.

Data processing

For circle FRAP, the recovery was measured in a circle of radius 2.0 μm, whereas for strip FRAP, the recovery was measured from a 2.25 μm strip spanning the nucleus. Background intensity was measured separately by finding a region of the LabTek II chamber containing no cells, and then this background value was subtracted from the measured FRAP data.

Next, the detector blinding effect was corrected. As described in Appendix 3, this effect led to a temporary loss of detector sensitivity after the photobleach. This was calibrated by photobleaching fixed cells containing GFP-GR using the photobleaching parameters described in the preceding section. Normalizing this response curve to its final recovery level produced a correction curve for this detector blinding effect, which was then divided into the FRAP data to yield a corrected recovery curve. Under our conditions, detector blinding occurred only in strip FRAP not circle FRAP, so the correction was only applied to the strip FRAP data.

After correction for detector blinding, observational photobleaching was accounted for using a new procedure to generate a calibration curve by collecting a second time series identical to the FRAP but without a photobleach (see Appendix 1 for details and justification). Specifically, upon completion of the FRAP, we waited 1 min to ensure that fluorescence had completely reequilibrated, and then collected images for ∼37 s (900 images for circle FRAP and 1500 images for strip FRAP) using the FRAP data collection parameters defined in the preceding section. This second time series was used to generate a calibration curve for observational photobleaching by measuring the fluorescence decay at the same location and in the same way as for FRAP. During the period corresponding to the FRAP recovery (from 12 s to 37 s), this decay was well described by a single exponential (see Appendix 1), and so the FRAP curve was corrected by dividing it with this fitted exponential decay function (see Supplementary Material 2 for justification).

Finally these background-subtracted data that had been corrected for detector blinding and observational photobleaching were normalized such that the prebleach intensity was 1.

FRAP modeling

We derived a new circle FRAP model (see Appendix 4) to account for both the nonuniform spatial distribution of the photobleach and for the finite size of the nucleus, since these are more realistic conditions than the previous circle FRAP presumption of a uniform photobleach within an infinite nucleus. We used the published version of the strip FRAP model, except that we used the measured spatial profile of the photobleach as the initial condition (Appendix 4 includes a description of this minor extension of the published strip FRAP model).

For both the circle and strip FRAP models, we used the measured photobleach profile as the initial condition. We then used the measured final recovery level of the FRAP curve to determine either the radius (circle FRAP) or length (strip FRAP) of the model nucleus that was required to account for the reduction in fluorescence predicted by the photobleach profile. The details of this procedure are in Appendix 5.

RESULTS

Application of the three different FRAP procedures to the same transcription factor

We refer to the three different FRAP procedures by the geometry of the photobleach: circle FRAP for the original GR procedure, strip FRAP for the original p53 procedure, and half-nuclear FRAP for the original Max procedure. When we applied these different procedures (see Methods) to the same transcription factor (GR) in the same cell line (mouse 3617 cells), we obtained good fits to the FRAPs, but three completely different sets of binding estimates (Fig. 1, A and B).

Both the circle and strip FRAP procedures predicted a single binding state for GR, but the circle FRAP binding estimates were more than two orders of magnitude larger than the strip FRAP binding estimates. These circle FRAP estimates for GR were, however, close to the published circle FRAP estimates for GR (8), whereas the strip FRAP estimates for GR were close to the published strip FRAP estimates for p53 (6) (Fig. 1 B versus 1 C). The half-nuclear FRAP estimates for GR yielded two binding states instead of the one binding state predicted by the circle and strip procedures. This was consistent with the predictions of two binding states for all of the seven transcription factors analyzed in the original Max study (7). Together, these results suggested that the details of the FRAP procedure might account for many of the differences between the published binding estimates for GR, p53, and Max.

Differences among the FRAP procedures

To understand how different FRAP procedures could yield radically different estimates, we identified key differences among the procedures. First, we focused on why the approaches differed in the number of predicted binding states (one for circle and strip FRAP, two for half-nuclear FRAP). An obvious difference was that the circle and strip FRAP models incorporated terms for both diffusion and binding, whereas the half-nuclear FRAP model incorporated only a term for binding, presuming that diffusion could be neglected.

To investigate this assumption, we performed a half-nuclear FRAP of Max, GR, and p53, and then plotted the spatial profile of fluorescence intensities as a function of time across the entire nucleus (Fig. 2 A). This profile changed its shape over time (2) (Fig. 2, C, E, and G), suggesting that diffusion contributed to these half-nuclear FRAPs. These measurements argue that it was improper to ignore diffusion both in the original Max analysis and in the preceding analysis of the GR half-nuclear FRAP (Fig. 1 B).

Although diffusion appeared to contribute to half-nuclear FRAPs, it was not clear whether it would also play a role for smaller bleach spots. The smaller the bleach spot, the more likely it is that diffusion can be neglected (8). We therefore performed FRAPs of Max, GR, and p53, photobleaching a very narrow strip (Fig. 2 B, 0.68 μm in width) through the nucleus. We found even in these cases evidence for shape changes in the fluorescence profiles of Max, GR, and p53 over time (Fig. 2, D, F, and H), arguing that diffusion should not be neglected for these transcription factors even with bleach spots close to the diffraction limit. In sum, these measurements support the inclusion of diffusion in any form of FRAP model for GR, p53, and Max.

Based on these data implicating a role for diffusion, we focused our attention on the circle and strip FRAP procedures, since these had already incorporated diffusion into the FRAP model. Although these procedures both predicted a single binding state, the predicted binding rates differed by more than two orders of magnitude (Fig. 1 B). This discrepancy could be explained by a variety of differences between the circle and strip procedures.

Modifications in the strip and circle FRAP procedures

We identified the primary procedural differences between circle and strip FRAP (other than the bleach spot geometry), decided on an optimal approach, and then implemented that. The principle changes are summarized here and outlined in Table 1:

1. The two original methods differed in their correction for observational photobleaching. In strip FRAP, no correction was applied because observational photobleaching was negligible. In circle FRAP, a correction was applied based on the rate of fluorescence loss at a site some distance away from the intentional photobleach (15). We found that choice of this measurement site could yield variable corrections (data not shown). Thus, we developed an improved procedure based on measurement of fluorescence decay at the same site as the intentional photobleach (see Appendix 1), and then applied this procedure to the new circle FRAP. We also applied it to the new strip FRAP, since under our conditions we detected observational photobleaching in strip FRAP.

2. The two original methods differed in how the initial conditions were determined. Although in both strip and circle FRAP the spatial profile of the photobleach was presumed uniform across the bleached region, the size of the bleached region was determined differently. In strip FRAP, the bleach-spot size was indirectly deduced based on conservation of total fluorescence, i.e., the width of the bleached strip was calculated such that it could account for the destruction of fluorescence corresponding to the final recovery level of the FRAP curve. In circle FRAP, the bleach spot size was measured from fixed cells that were photobleached. We found that both of these procedures might be flawed, since our measurements indicated that the photobleach pattern in strip or circle FRAP was not spatially uniform. In the new strip and circle FRAP, we used the spatial distribution of fluorescence measured from the first postbleach image as an approximation for the real photobleach profile (see Appendix 2).

3. Neither the original strip nor circle FRAP accounted for a phenomenon that we have called detector blinding, in which the photomultiplier tube on the confocal microscope can suffer a transient loss in sensitivity after the photobleach. We found under our conditions that detector blinding occurred in strip but not circle FRAP. This is probably due to the larger bleached area in strip FRAP, which more easily saturates the detector. We calibrated detector blinding using fixed cells, and used these data to correct strip FRAP recoveries at early time points (see Appendix 3).

4. The two original mathematical models differed in the presumed size of the nucleus, with strip FRAP presuming a finite nucleus and circle FRAP presuming an infinite nucleus. We developed a new circle FRAP model for the more realistic case of a finite nucleus (see Appendix 4). The new model also allowed for an arbitrary initial photobleach profile to incorporate the measured nonuniform photobleach profiles (point No. 2 above).

5. The two original methods differed in how the models conserved fluorescence. In circle FRAP, an infinite nucleus was modeled and so the fluorescence destroyed by the photobleach was negligible, which automatically guaranteed conservation of fluorescence. This was not the case in strip FRAP, which modeled a finite nucleus. Here a measurable amount of fluorescence was destroyed by the photobleach. In this model, the profile of this initial photobleach was calculated to ensure conservation of fluorescence based on two measured parameters: the “length” of the nucleus and the final recovery level of the FRAP curve. (Note that this approach requires an independent experiment demonstrating that there is no immobile fraction, guaranteeing that the final recovery level of the FRAP reflects only the fluorescence destroyed by the photobleach (6).) In the new circle and strip FRAP, we measured the initial photobleach profile and then conserved fluorescence by calculating the size of the model nucleus that would be consistent with the final recovery level of the FRAP curve (this also requires a demonstration that there is no immobile fraction). This new approach has the advantage that the photobleach profile is more easily measured than the size of the model nucleus. Nuclear size in the model corresponds to the accessible fluorescent volume of the real nucleus. Since the real nucleus contains nucleoli and does not extend uniformly along the optical axis, its total fluorescence is not simply given by a measurement of its “length” or “radius” (see Appendix 5).

TABLE 1.

Comparison of the main features of the original and new FRAP procedures: principal differences between the original procedures, and their reconciliation in the new procedures

	Original FRAP		New circle and strip FRAP
Correction for observational photobleaching (Appendix 1)	Circle	Correction derived from an adjacent region of the nucleus	Correction derived from the photobleached region
	Strip	No correction, since observational photobleaching not detected
Initial conditions (Appendix 2)	Circle	Uniform circular photobleach	Gaussian photobleaching profile measured from the first postbleach image
	Strip	Uniform rectangular photobleach of a computed width to satisfy conservation of fluorescence
Detector blinding (Appendix 3)	Circle	Not considered	Circle	Not detected
	Strip	Not considered	Strip	Present and corrected for
Mathematical model (Appendix 4)	Circle	Infinite nucleus Applicable only to uniform circular photobleach	Finite nucleus
	Strip	Finite nucleus Applicable to an arbitrary photobleach pattern	Applicable to an arbitrary photobleach pattern
Conservation of fluorescence (Appendix 5)	Circle	Guaranteed (Infinite nucleus)	Enforced (Bleach-spot profile measured, nuclear “size” deduced)
	Strip	Enforced (Nuclear “size” measured, bleach-spot size deduced)

Application of the new strip and circle FRAP procedures

After implementing the preceding changes, we applied the new circle and strip procedures to GR, p53, and Max. None of the FRAP data could be fit with a simplified pure diffusion form of the new models (see Appendix 4), but all of the data could be fit with a full model that presumed a single type of chromatin binding state (Fig. 3 A). This yielded estimates for the diffusion constant (D_f), the association rate (k*_on), and the disassociation rate (k_off) for each transcription factor that were similar, whether obtained by circle or strip FRAP (Fig. 3 B). This result suggests that the modifications made in the two FRAP procedures eliminated the principal differences between them.

FIGURE 3.

FRAP with GR, p53, and Max using the new circle and strip procedures. (A) Experimental single-cell data (shaded circles) collected according to the two new procedures are well fit (solid line) by the new FRAP models. (B) The estimated values for D_f, k*_on, and k_off from such fits show good agreement between circle and strip procedures for the same proteins, and also among different proteins. Average values from 10 to 15 cells are shown with standard deviations.

Importantly, not only did we find consistent estimates for the same transcription factor with circle and strip FRAP, we also found that the binding estimates for the three different transcription factors were similar compared to each other (Fig. 3 B). The average bound fraction was 25% and the average residence time was 2.5 s. We did find that Max recoveries were somewhat faster than either GR or p53, yielding a higher disassociation rate for Max. This might reflect a small difference in the interactions of Max with chromatin compared to GR or p53. Overall, our average estimates are close to the original estimates for p53 (Figs. 3 B and 6 A), indicating that the changes we made in the FRAP procedures had their biggest impact on Max and GR.

FIGURE 6.

Influence of presuming uniform initial conditions for strip FRAP of p53. The original and new estimates were reasonably close (A), yet the original strip FRAP for p53, like the original circle FRAP for GR, presumed uniform initial conditions for the photobleach. The much smaller impact of this incorrect presumption on the p53 estimates was due to the presumed size of the uniformly bleached region for p53 versus GR. A simulated strip FRAP curve was generated with the estimated binding rates for p53 (k*_on = 0.15 s⁻¹, k_off = 0.4 s⁻¹) and Gaussian initial conditions (length of nucleus = 20 μm, σ = 1 μm, bleach depth θ = 0.2). Then this curve was fit with a strip FRAP model using a uniform photobleach profile of two different sizes. When the size (3 μm) was chosen to match the amount of fluorescence destroyed by the simulated Gaussian photobleach, then the residuals plot yielded a global minimum close to the global minimum produced with the Gaussian initial conditions (C, middle versus bottom, analog of p53 scenario). When the presumed size of the uniformly bleached area was too small (2.25 μm) to account for the fluorescence destroyed by the Gaussian photobleach, then a new global minimum appeared at much larger binding rates that yielded a slightly better fit than the original minimum (C, top, analog of GR scenario—compare to Fig. 5 C).

Comparison of the original and new procedures

Max

The most striking disparity between the original and new results for Max was that the new procedures predicted a single binding state whereas the original procedure predicted two binding states (Fig. 4 A). As we discuss below, this difference most likely arises because diffusion was omitted from the original FRAP model for Max. This omission appears to be improper based on our current measurements (Fig. 2 C), which suggest that diffusion was not negligible during the Max FRAP recovery.

FIGURE 4.

Reaction-diffusion FRAPs with one binding state are well described by a reaction-dominant model with two binding states, explaining the major difference in the old and new estimates for Max (A). A pure diffusion curve ((B) D_f = 10 μm²/s, shaded circles) or a full model curve ((C) D_f = 10 μm²/s, k*_on = 0.5 s⁻¹, k_off = 0.5 s⁻¹, shaded circles) are not well fit by a reaction-dominant model with one binding state (dashed line). However, both curves are well fit with a two binding state reaction-dominant model (solid line). Data from the original Max study (shaded circles) are also well fit by a two-binding state reaction-dominant model (D). The fit in D yields estimated off rates (k_off,1, k_off,2) and estimated bound fractions (C_eq,1, C_eq,2) for the two predicted binding states that are in good agreement with the published values (compare to A).

To evaluate the consequences of improperly ignoring diffusion, we used the new circle FRAP model to generate simulated FRAP curves that spanned a large range of reaction-diffusion FRAP curves (k*_on and k_off ranging from 10⁻⁴ s⁻¹ to 10⁺⁴ s⁻¹ with D_f = 5 μm²/s). We found that every one of these simulated curves could be well fit with a two-binding state reaction dominant model, i.e., a model neglecting diffusion, which is comparable to the model used by Phair et al. (7) (see Fig. 4, B and C, for examples, and Appendix 4 for the reaction-dominant model). These simulations illustrate that FRAP curves exhibiting reaction-diffusion behavior can be well fit with an improper model that lacks diffusion, if the model erroneously presumes there are two binding states rather than one. This improper model then yields incorrect predictions about the number of binding states and their binding rates.

To specifically evaluate Max, we used the published FRAP curve for Max, and attempted to fit it with a reaction-dominant model. Consistent with our simulations, we achieved a good fit of the Max data using a two binding state reaction-dominant model (Fig. 4 D). The binding estimates for this fit were similar to the published estimates from the original study (Fig. 4 D versus 4 A). These results suggest that excluding diffusion from the original FRAP model for Max led to the prediction of a second binding state.

GR

The most striking disparity between the new and original estimates for GR was that although in both cases a single binding state was predicted, the new estimates were more than two orders of magnitude smaller than the original estimates (Fig. 5 A). We found that nearly all of this difference could be explained simply by the change in the model's initial conditions from a uniform photobleach to one with Gaussian edges (Fig. 5 B).

FIGURE 5.

Differences in the old and new circle FRAP estimates for GR (A) are primarily due to changes in the initial conditions. To test the contribution of the initial conditions and the photobleaching correction (the other major difference between the old and new circle FRAP procedure), we collected FRAP data with the new acquisition procedure and fit the same data with different variants of the new circle FRAP model. First we processed the data with the original photobleaching correction procedure and fit these data with a form of the new circle FRAP model designed to mimic the old model: the nuclear radius was set to 50 μm to approximate an infinite nucleus, and the initial conditions were set to a uniform circular bleach to match the old initial conditions. (Each fitted data set is shown by an “×” and the mean of these fits by a dot). By themselves, these changes in analysis of the new circle FRAP data yielded estimates for k*_on and k_off (rows labeled Original Original) that were close to the original estimates. Then we used the new initial conditions (Gaussian edges in the photobleach) instead of the old uniform initial conditions but still corrected the data with the old photobleaching correction procedure. This converted the k*_on and k_off estimates from the same data set to values (rows labeled New Original) much closer to those from the new procedure (rows labeled New New). The “New New” estimates were obtained from the same data by applying the new photobleaching correction procedure and using a model with a finite nucleus with the same Gaussian initial conditions. This yielded some change in the average value of the estimates and a tightening in the spread of the estimated values. The sum of squared residual plots for these fits reveals how the initial conditions corrupted the original estimates (C). Shown for each of the conditions in B are corresponding one-dimensional profiles through the residuals plot along a path in (k*_on, k_off) space (corresponding to the gray line in the colored plot) that yielded the minimum sum of residuals for each k*_on. The old initial conditions created a global minimum (Original Original) that disappeared with the new initial conditions (New Original). The new photobleaching correction and finite nucleus yielded a more pronounced version of the new global minimum.

The evidence for this came from examining individually the consequences of the two main differences between the old and new circle FRAP procedures: the initial conditions and the correction for observational photobleaching. We did this by analyzing the same FRAP data sets (collected with the new FRAP protocol; see Methods) with three variants of the new circle FRAP model. First, we mimicked the original FRAP procedure, then we changed just the initial conditions and then finally we added the new correction method for observational photobleaching.

We mimicked the original circle FRAP procedure by applying the original photobleaching correction, and then fitting the corrected FRAP data, presuming a large nuclear radius (to mimic the infinite nucleus in the original procedure) and a uniform photobleach as the initial condition (to match the initial condition of the original procedure). The best fit yielded binding rates close to the original estimates (Fig. 5 B, Original Original), demonstrating that we could use this modified form of the new procedure to capture the essence of the original procedure. Interestingly, when we plotted the sum of squared residuals for the fits (Fig. 5 C, Original Original), we discovered a well separated local minimum away from the global minimum. The binding rates of this local minimum were close to the new estimates and yielded reasonable fits to the FRAP data (data not shown). This indicated that the original and the new estimates could both give reasonable fits to the FRAP data, but under conditions mimicking the original procedure, the original estimates produced a somewhat better fit.

Strikingly, this situation reversed itself when we used Gaussian instead of uniform initial conditions but still applied the original photobleaching correction (Fig. 5 C, New Original). We discovered again two well separated minima, but now the global minimum was close to the estimates obtained by the new FRAP procedure, whereas the former global minimum changed to a local plateau. This demonstrated that changing just the initial conditions was sufficient to convert the FRAP estimates from the original values to ones close to the new values.

Finally, when we added the other principal features of the new procedure, namely the new photobleaching correction and the finite nucleus, the global minimum became somewhat sharper and deeper, but its location shifted only slightly (Fig. 5 C, New New). This indicated that the new photobleaching correction and finite nucleus had only a modest influence on the magnitude of the binding estimates. Their principal effect was to reduce their variability (compare the variability in individual estimates in Fig. 5 B, New Original and New New). This is probably because the new photobleaching correction was calibrated from the same spot at the same location as the intentional photobleach, whereas the original procedure was calibrated from a spot at a different, arbitrarily chosen location.

Hence in contrast to the effects of the photobleaching correction and finite nucleus, the wrong initial conditions had a much larger effect on the magnitude of the estimates. This arose because these improper initial conditions created a specious global minimum that suppressed the real global minimum. In simple terms, the wrong model was capable of producing a good fit to the data with parameters that bore no relationship to the parameters obtained using a more accurate initial condition.

p53

There were relatively small differences between the new and old estimates for p53 (Fig. 6 A), with only the estimates for D_f outside of the error bounds. This minor difference in D_f estimates may have arisen from some combination of the approximations made by each approach in the initial conditions (Appendix 2) or in the possible effects of detector blinding (Appendix 3).

Overall, the relative agreement in p53 binding estimates was encouraging because it suggested that the original and new procedures were reasonably robust. At the same time, this agreement was puzzling given the sensitivity of the GR estimates to the model's initial conditions (see preceding section). Like GR, the original p53 procedure incorrectly presumed a uniform photobleach, yet unlike GR this had minimal effect on the p53 estimates.

We found that this differential sensitivity to the incorrect initial conditions arose from differences in the presumed size of the uniformly bleached region (Fig. 6 B). Evidence for this came from simulating a strip-FRAP curve with the new binding estimates for p53 and typical Gaussian initial conditions for the new strip FRAP procedure. We then fit this curve assuming different uniform initial conditions. In the original strip-FRAP, the presumed uniform photobleach was set to a size that destroyed the same amount of fluorescence as the actual Gaussian photobleach. When we used this approach, only a single global minimum appeared in the residuals plot (Fig. 6 C, middle), and the estimates obtained were close to those with the true Gaussian initial conditions (Fig. 6 C, bottom). This replicated the situation for the original versus new p53 strip FRAPs. However, when the presumed uniform photobleach destroyed less fluorescence than the actual Gaussian photobleach, then a second minimum appeared in the residuals plot, well separated from the first (Fig. 6 C, top). This second minimum was stronger than the original global minimum and yielded binding estimates that were two orders of magnitude larger than those obtained with the correct Gaussian initial conditions. This replicated the behavior seen above not only for circle FRAP, but now for strip FRAP.

Motivated by this analysis, we found that the original GR circle FRAP procedure could yield estimates only 50% smaller than the current GR estimates, simply by increasing the presumed size of the uniformly bleached circle used to fit the GR FRAP data (from 1.35 μm to 1.85 μm; data not shown). Errors of roughly similar magnitude (in this case for D_f and k*_on) were detected by simulating the original p53 strip FRAP procedure that presumed a uniform bleach profile, and comparing its predictions to the true parameters used to generate the simulated FRAP data with its actual Gaussian bleach profile (data not shown). We conclude that uniform initial conditions are only slightly detrimental if they are set to match the amount of fluorescence destroyed by the real photobleach.

DISCUSSION

Errors in previous FRAP analyses

We found that applying the wrong FRAP model could lead to major errors in the model's predictions about binding.

Diffusion was presumed to be negligible in the original FRAP model for Max (7). This assumption was based on the fact that the recovery time for Max was significantly longer than the recovery time for unconjugated GFP, suggesting that diffusion of Max would occur much faster than binding of Max. However, it is now recognized that diffusion can contribute to very slow FRAP recoveries as long as the time to associate with a binding site is fast compared to the time to diffuse across the bleach spot (2,8,16). Thus recovery time itself cannot be used to rule out a role for diffusion. As a direct test of diffusion's role, we found that the spatial fluorescence intensity profile for Max changed its shape during the recovery, suggesting that diffusion contributed substantively to the FRAP (2). We showed that excluding diffusion from the FRAP model led to the prediction that Max was bound to two distinct chromatin binding states instead of just one.

Though diffusion had been accounted for in the FRAP model for GR, the original study made another significant error. The photobleach profile was presumed spatially uniform with discontinuous edges (8), whereas the actual profile had Gaussian edges. We showed that ignoring the Gaussian edges changed the estimates for the binding parameters by more than two orders of magnitude. Correcting this error resulted in a change of the GR estimates that brought them into the range of the original p53 estimates.

Interestingly, the original p53 estimates also ignored the Gaussian edges of the photobleach, yet the binding estimates were not grossly different from our new estimates. We found that this agreement arose because in the original p53 study, the width of the presumed uniform photobleach was set to match the amount of fluorescence destroyed by the actual Gaussian-edged photobleach. Thus our results now show that if uniform initial conditions lead to conservation of total fluorescence after the photobleach, then the error in the binding estimates will be small.

In addition to these errors in FRAP modeling, we also detected an instrumental defect that under some conditions could alter FRAP estimates. This occurred on our confocal microscope when we photobleached a large enough fraction of the imaged area, as in strip FRAP. The photobleach introduced a transient loss of sensitivity in the photomultiplier tube, probably reflecting a partial “blinding” of the detector due to the bright burst of fluorescence produced by photobleaching. This led to an underestimate of the fluorescence intensity at a few early time points, thereby reducing the depth of the FRAP curve. If we ignored this defect, it led to a fivefold overestimate of the diffusion constant in the new strip FRAP (Appendix 3). Since this defect depends on the laser power, it is impossible to know if it played any role in the original strip FRAP; however, it seems prudent to test for this effect in future FRAP studies. We now provide a method to identify the defect and in principle correct it using a fixed specimen as a calibration standard (Appendix 3).

Prospects for further improvement in quantitative FRAP

Our current binding estimates were obtained using two different FRAP procedures (circle and strip FRAP), and so should be more robust than previous estimates. In addition, our estimates are close to those obtained by another laboratory for one of the proteins (p53) (6).

Despite this progress in obtaining consistent estimates, it is important to realize that the circle and strip procedures are not completely orthogonal, since they share some assumptions that may not be correct. Both methods presume that the FRAP can be described by a set of two-dimensional, reaction-diffusion equations with an instantaneous photobleach performed at the center of a homogeneous distribution of fluorescence. Although the consequences of some of these approximations have been investigated (2,4,17,18), at least five fundamental assumptions still remain largely unexplored.

First, the reduction of the model equations from three to two dimensions is only valid if the bleach distribution along the optical axis (z axis) is homogeneous (8). Although this is a reasonable first approximation (17), some deviation is expected since the three-dimensional illumination profile of the bleaching laser beam is only cylindrical for relatively low numerical aperture objectives and conical otherwise (19). This will produce a conical photobleach profile that may be further exacerbated by fluorescence saturation effects, which can occur at the high laser powers used for photobleaching (20). It has been shown that ignoring just these saturation effects can introduce up to a 60% underestimate in the diffusion coefficient for the case of simple diffusion (21). The effects of these factors in the more complex reaction diffusion case are at present unknown, but could be addressed by numerical models for FRAP that account for the actual three-dimensional photobleach profile.

Second, the presumption of homogeneously distributed fluorescence throughout the nucleus is obviously violated by the actual fluorescence distribution of most transcription factors. These molecules are found at low concentrations within nucleoli, and at higher concentrations elsewhere, and their distribution outside of nucleoli is somewhat punctate. The impact of these inhomeogeneities can also be addressed by using numerical models of FRAP that in this case account for the actual distribution of nuclear fluorescence (2).

Third, the presumption of simple diffusion in the reaction-diffusion equations for FRAP is subject to question. Although a number of FRAP studies have been able to fit unconjugated GFP recoveries using a simple diffusion model, several FCS studies (22,23) and a single-molecule study (24) suggest that anomalous diffusion may occur in the nucleus. If so, then the current reaction-diffusion equations for FRAP should be modified to incorporate a more accurate diffusion model. This issue could be resolved by future studies of transcription factors using FCS and single molecule tracking.

Fourth, although binding reactions in FRAP models have been presumed to occur in a single step, some evidence suggests that other factors could either inhibit or catalyze the binding process (9,10,25). If so, then the rate equations describing binding would be more complex than those in current use, and this could also influence the binding estimates derived. Detection of intermediate binding states might be addressed in part by future single molecule tracking of transcription factors.

Fifth, most FRAP experiments are performed in cells with a GFP-tagged protein that is usually expressed at higher levels than the endogenous protein. Competition between tagged and untagged proteins has no effect on the binding estimates. This is because FRAP is typically performed at times when tagged protein levels are constant, and so competition for free binding sites has reached an equilibrium that is unchanged by the photobleach. Of course, if the tag itself interferes in any way with normal binding, then the measured binding affinity will not reproduce that of the endogenous protein. A further complication is that overexpression of the tagged protein will lead to occupation of more binding sites than normal. This reduces the concentration of free sites, which in turn reduces the estimated association rate (k*_on, which is the product of the concentration of free sites and the on rate (8)). This effect will be significant only if the overexpression levels are high enough to substantially change the normal concentration of free binding sites. This issue can be addressed using knock-in systems combined with more sensitive detection to enable measurement of FRAP recoveries at endogenous protein levels.

In addition to these potential inaccuracies in the FRAP model, there are also shortcomings in FRAP data acquisition that might be overcome in future studies. We found that the correction method for observational photobleaching had some influence on the binding estimates. Reducing or eliminating observational photobleaching by utilizing more sensitive detectors should improve future FRAP estimates. We also found that a more accurate determination of the initial photobleach profile markedly altered the binding estimates. Even better estimates of this initial condition could be achieved in the future with instrumentation permitting faster photobleaching and more rapid data acquisition after the photobleach.

Until all of these uncertainties can be resolved, some caution is advisable in accepting the quantitative estimates of binding reported here and elsewhere by FRAP. Our results have shown quite strikingly that the good fits obtained for FRAP curves in some previous analyses do not guarantee that the quantitative estimates derived from the fits are correct. However, even if our current best estimates are revised once again, they will likely change concordantly for p53, GR, and Max, since we found that the same FRAP procedure produced very similar FRAP curves for each of these transcription factors.

Evidence for a common mode of transcription factor interaction with chromatin

The evidence to date has suggested that transcription factor interactions with chromatin might be specific to the molecule and cell type in question (6–8). However, our results demonstrate that these reported differences for GR, p53, and Max are due primarily to differences in FRAP modeling rather than intrinsic differences among these three transcription factors. This suggests that at least a subset of transcription factors will share common interaction behaviors at chromatin sites.

We favor the model that the single binding state detected by FRAP for these three different transcription factors reflects interactions at nonspecific DNA sites (i.e., a DNA sequence other than the promoter sequences for which the factor is designed to bind). This seems likely because for most transcription factors, the number of nonspecific sites available within the genome is probably orders of magnitude larger than the number of specific sites, and so FRAP at a random location is likely to sample primarily these nonspecific sites.

Some experimental data support this hypothesis of nonspecific binding. Mutations in p53 that abolish only binding to specific DNA sites did not alter the p53 FRAP curve (6). Conversely, mutations in the DNA binding domain of the yeast transcription factor Ace1p did alter its FRAP curve, even though this factor binds specifically to only three promoters in the entire yeast genome (10). Our observation that FRAP curves for GR, p53, and Max are similar is also consistent with the hypothesis of nonspecific binding, since it might be expected that the interaction of different transcription factors with generic DNA sequences would be similar.

Understanding the mechanisms of nonspecific binding of transcription factors is vital because every transcription factor must sample nonspecific DNA sites to search for its correct target sequence (26). Based on their very similar diffusion and binding characteristics, our results suggest that within the same cell the search times for GR, p53, and Max to locate their respective targets should be roughly the same. Analysis of other transcription factors and further improvement of the procedures developed here should help determine if other transcription factors share the properties we have detected for GR, p53, and Max.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

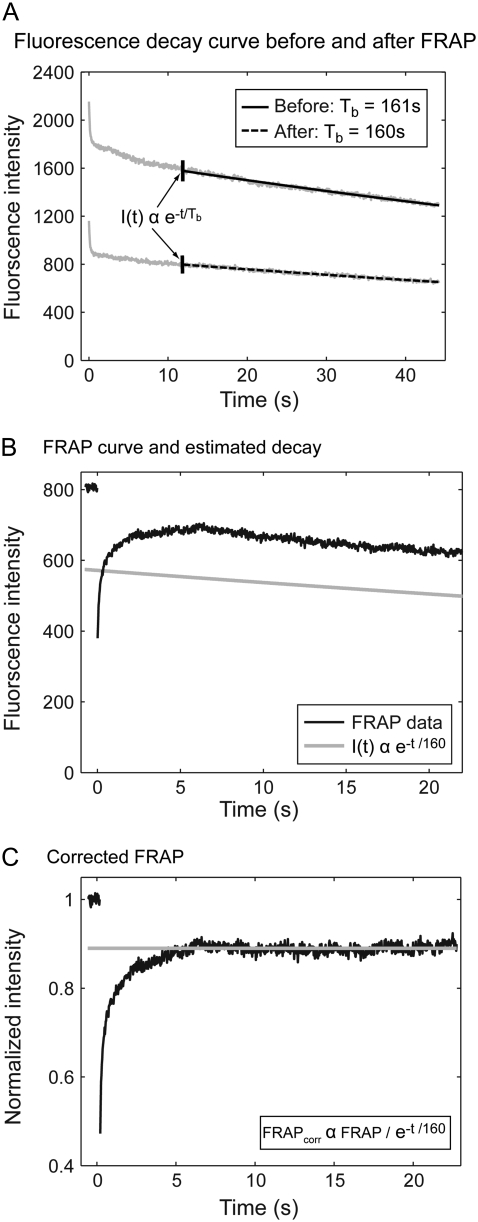
APPENDIX 1: CORRECTION FOR OBSERVATIONAL PHOTOBLEACHING

To characterize observational photobleaching, we acquired time-lapse images of live cells with the same imaging conditions used to acquire FRAP data. Average intensities within a spot (whose size was equivalent to that used for the intentional photobleach) consistently showed an initial rapid decay lasting ∼2 s followed by a simple, single exponential decay (Fig. 7 A). For a given location within a cell, the exponential time constant describing this decay remained the same whether measured before or after a FRAP experiment (Fig. 7 A). We measured the rate of observational photobleaching after the FRAP, otherwise considerable fluorescence was depleted before the FRAP resulting in a poorer signal/noise ratio during the FRAP.

FIGURE 7.

Observational photobleaching. (A) Fluorescence decay curves of GFP-GR in live cells consistently show a faster decay followed by a slower decay. The slower decay can be described by a single exponential (time constant shown in the box). When the decay is measured after a FRAP experiment has been performed, the slower fraction of the decay curve yields the same decay rate, indicating that this rate is not affected by the intervening FRAP experiment. (B) The fitted exponential function exhibits similar decay behavior as the equilibrated FRAP curve (both curves are shown 10 s after the start of image acquisition). (C) The FRAP curve is divided by the fitted exponential decay curve to correct for observational photobleaching. This yields a corrected curve that plateaus at a constant level, which is <1 due to the fluorescence destroyed by the intentional photobleach.

To ensure that observational photobleaching was in the single exponential regime during FRAP, we acquired time-lapse images for 12 s before performing the FRAP, and then we measured the recovery for an additional 25 s. Image acquisition was stopped, and then 60 s later we acquired the second sequence of time-lapse images to quantify observational photobleaching. The decay time constant was calculated from these data over the same period corresponding to the FRAP recovery (from 12 s to 37 s). As expected, an overlay of the FRAP curve and the corresponding segment of the observational photobleaching calibration curve showed comparable decay behavior (Fig. 7 B). We then corrected the FRAP curve for observational photobleaching by dividing it with this calibration curve (Fig. 7 C).

This correction procedure was tested by incorporating observational photobleaching directly into the FRAP model. We found that this decay could be factored out of the equations for the FRAP recovery, demonstrating that it is appropriate to divide the FRAP curve by the exponential decay curve (Supplementary Material 2).

APPENDIX 2: ESTIMATION OF THE INITIAL PHOTOBLEACH PROFILE

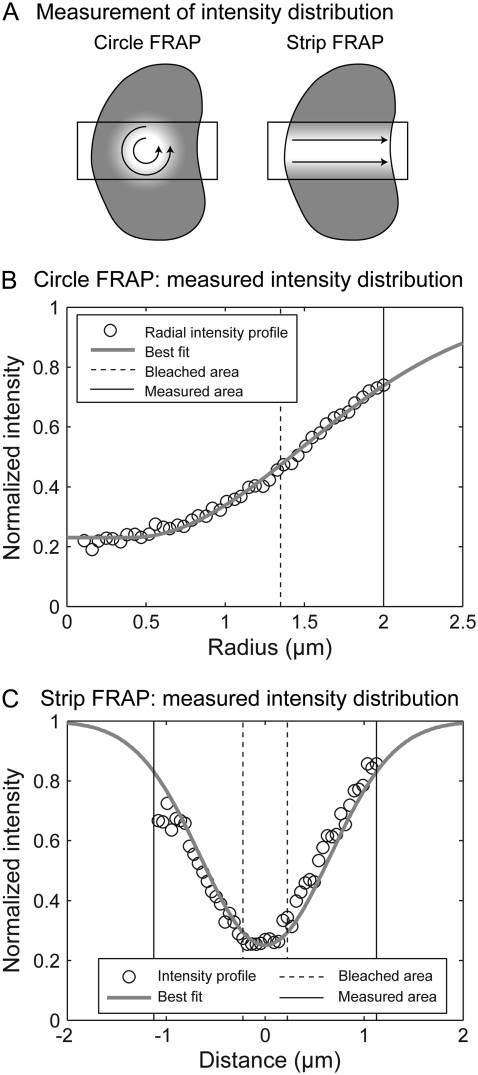
Neither the original circle nor strip FRAP procedures directly assayed the initial photobleach profile. Although both original procedures presumed a uniform profile, in reality the profile is broadened for several reasons: the finite time for the photobleaching and imaging (27), the Gaussian intensity distribution of the bleaching laser beam (18,19), and fluorescence saturation (20). To obtain a more direct estimate of the photobleach profile for the new FRAP procedures, we measured the fluorescence intensity profile in the first postbleach image. For circle FRAP we calculated the averaged radial intensity about the center of the bleach spot (Fig. 8 A), and for strip FRAP we calculated the averaged line intensity at different distances parallel to the long axis of the strip (Fig. 8 A).

FIGURE 8.

Determination of the initial condition. (A) Schematic illustrating the measurement procedure. The rectangle delineates the imaged area. Intensities were averaged along the directions indicated by the arrows. (B) Averaged radial intensity profile of a circle FRAP experiment (circles) was fitted (shaded line) with a central constant function with a Gaussian distribution at the edge. (C) Averaged linear intensity profile of a strip FRAP experiment (circles) was fit (shaded line) with a Gaussian distribution. The dashed lines mark the bleached regions, solid lines the measured regions. Both measured intensity profiles have been normalized by the prebleach intensity profile.

In our measurements, the circle FRAP photobleach profile was well described by a constant function with Gaussian edges:

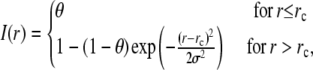where θ is the depth of the bleach, σ is the width of the Gaussian, and 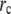is the radius of the constant portion (Fig. 8 B). The strip FRAP photobleach profile was well described by a Gaussian distribution (Fig. 8 C). To factor out any systematic local fluctuations in intensity, the averaged spatial profiles for the circle and strip FRAP were renormalized with the respective prebleach profiles.

The estimated photobleach profiles were used as the initial condition (t = 0 s) in the FRAP models. This is an approximation since these images were not acquired at t = 0 s, but at t = 22 ms for circle FRAP and t = 13 ms for strip FRAP. To determine the error introduced by this approximation, we used the circle FRAP model with different values of D_f, k*_on, and k_off to produce simulated FRAP data, including a spatial intensity profile at t = 22 ms after the photobleach. We then fit the simulated FRAP curve assuming that the spatial intensity profile at t = 22 ms actually corresponded to t = 0 s. We found that this introduced small errors in the estimated D_f, and larger errors in the estimated k*_on and k_off values depending on the FRAP regime and the time for full recovery. For the full model regime and short recovery times, k*_on and k_off values could be overestimated by as much as 70%. For the parameter range of the transcription factors studied here, the predicted overestimate in k*_on was 25%, and <10% for D_f and k_off . FRAPs with long recovery times (>50 s), or FRAPs in the pure-diffusion regime showed very little error in D_f, k*_on, or k_off.

APPENDIX 3: CORRECTION FOR DETECTOR BLINDING

In the course of analyzing photobleach profiles, we discovered that the spatial integral of the fitted Gaussian intensity distribution versus time remained constant for the circle (data not shown) but not the strip FRAP (Fig. 9 A). This spatial integral measures the amount of bleached fluorescence and so should remain constant, since the transcription factors remain in the nucleus and observational photobleaching is negligible on the timescale over which the spatial integral was calculated (0.25 s).

FIGURE 9.

Correction for detector blinding in strip FRAP. (A) Integrating the intensity profile at a series of time points after the intentional photobleach yields changing values (open circles) instead of a constant over time. This contradicts conservation of total fluorescence. Correction for detector blinding (see below) yields the expected response (solid circles). (B) FRAP on a fluorescent plastic slide reveals that detector sensitivity transiently decreases immediately after the intentional photobleach. Intensity was averaged in the right quarter of the slide, whereas increasing portions on the left side of the slide were photobleached (over the full height of the image). The loss of sensitivity increases with increasing bleached areas, but still occurs even when the photobleached area is completely separate from the measured area, thus ruling out reversible photobleaching. (solid curve, full width bleached; shaded curve, half width bleached; dotted curve, quarter width bleached). (C) A comparable effect is seen with typical cellular intensities under our new strip FRAP conditions, as revealed by FRAP performed on fixed cells containing GFP-GR. A detector response curve (inset) was obtained by dividing the data by its final postbleach intensity. This response curve was used to correct strip FRAP data. (D) Early time points for uncorrected and corrected strip FRAP curves are shown, along with the parameter estimates obtained. For this p53 recovery, the principal error arising from neglecting detector blinding is in the estimated diffusion constant.

We investigated this phenomenon by performing a strip FRAP on a fluorescent plastic slide (Fig. 9 B). The fluorescent dye molecules in the plastic were immobile and also resistant to photobleaching. Nevertheless, when subjected to a high intensity laser pulse comparable to that used in strip FRAP, we detected a transient reduction in fluorescence intensity from the plastic slide. This effect was not caused by reversible photobleaching (28) of the dye, since the same effect arose if we bleached only one portion of the slide image and recorded exclusively from the adjacent unbleached portion of the slide image (Fig 9 B). The reduction in detector sensitivity increased when larger areas were exposed to the laser pulse, suggesting that the loss of sensitivity was related to the amount of fluorescence produced by the pulse. We speculate that this behavior reflects a transient loss in detector sensitivity most likely induced by a temporary saturation of the detector. It was detected only in strip FRAP because it probably depended on photobleaching a large enough area to induce sufficient saturation of the detector (Fig. 9 B).

To generate a correction for strip FRAP data, we calibrated the detector blinding effect using fixed GFP-GR (3617) cells (fixed in 3.5% paraformaldehyde for 15 min at room temperature). When the cells were photobleached with the new strip FRAP settings, a transient response in detector sensitivity was again detected (Fig. 9 C). This curve was normalized to the final asymptotic intensity value after the photobleach, yielding a detector response curve under the strip FRAP conditions (Fig. 9 C, inset). This response curve was used to correct the spatial fluorescence intensity profile at each of the affected time points after the photobleach. The corrected profiles were then used to compute the corrected FRAP curve. This correction procedure eliminated most of the detector blinding artifact, as the spatial integral of the Gaussian photobleach profile was nearly constant over time after the correction had been applied (Fig. 9 A).

To evaluate the impact of ignoring this effect on FRAP estimates, we fitted p53 strip FRAP data with and without the correction for detector blinding (Fig. 9 D). We found the largest effect on the estimated diffusion constant, which was fivefold overestimated when the detector blinding effect was improperly ignored (Fig. 9 D).

APPENDIX 4: MATHEMATICAL MODELS

Circle FRAP models

The published model for circle FRAP (8) assumed an infinite nucleus and a uniform circular photobleach. The new model presented below accounts for a finite nucleus and an arbitrary initial bleach profile. We assume a circular nucleus of radius that is photobleached at its center with an arbitrary, radially symmetric bleach profile. Intensity measurements are made within a centered circle of radius We adopt the assumption of previous FRAP studies that the photobleach profile does not change appreciably along the optical axis (see Sprague et al. (17) for experimental evidence for this). This allows modeling the FRAP in the plane of focus, i.e., in two dimensions.

Outline of the derivation of the circle FRAP model

In the mathematical model, the concentrations of the free and bound proteins are defined by a set of coupled reaction-diffusion equations. We obtain a particular solution to these equations using separation of variables (29), where the time dependence is described by two decaying exponential functions and the spatial dependence by Bessel functions of the first kind. The general solution is then defined as a series expansion of the particular solution. The unknown coefficients of the series solution are then calculated using the boundary condition (no flux at the nuclear membrane) and the initial condition (the radial distribution of fluorescence produced by the photobleach). The actual FRAP curve is then calculated by spatial averaging of the sum of the free and bound fluorescence intensities in the measured area. A more detailed outline of the derivation is given in Supplementary Material 1. Shown below for clarity are just the starting differential equations and their final solutions for each model used in this study.

Full model for circle FRAP

We use the model described in Sprague et al. (8) for freely diffusing proteins 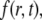which undergo transient binding events with immobile nuclear structures resulting in a concentration of bound proteins 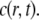Before the bleach, the system is at equilibrium, and and 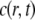have achieved steady-state values and We assume the concentrations are normalized such that 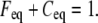The dynamics of the system can be described by a system of partial differential equations:

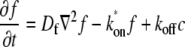(1)

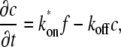(2)

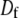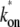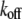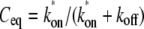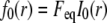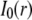where is the diffusion constant and and are the association and dissociation rates of the binding, respectively. The binding rates define equilibrated concentrations and (8). The initial conditions are given by and where is the arbitrary, radial distribution of total fluorescence at the start of the recovery. The boundary conditions are no flux at the nuclear membrane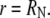

The FRAP recovery curve is calculated by spatial averaging the concentration of fluorescent particles in the measured region:

(3)

where 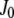are Bessel functions and the brackets symbolize spatial averaging over the measurement region :

(4)

The constants in Eq. 3 are defined as

(5)

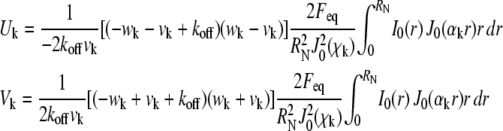(6)

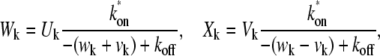(7)

where 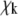is the kth zero of the Bessel function of the first kind and 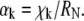For typical fitting of FRAP curves, the sum in Eq. 3 is truncated at 500 terms.

Pure-diffusion model for circle FRAP

The pure-diffusion equation is

(8)

with the initial condition 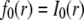and the same boundary condition as for the full model above. The solution for the FRAP recovery is

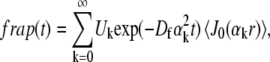(9)

where

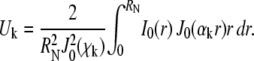(10)

Adaptation of the published strip FRAP model

For consistency with our new circle FRAP procedure, we adapted the published strip FRAP model so that Gaussian bleach profiles could be considered.

Hinow et al. (6) derived a series solution for the FRAP curve. Using different initial conditions does not influence the theoretical derivation of the FRAP solution, but only influences the calculation of the coefficients.

For the full model, Gaussian initial conditions for the mobile fraction 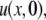and the immobile fraction convert Eqs. 10 and 11 in Hinow et al. (6) to

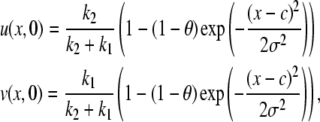(11)

where c is the center of the bleach, θ is the bleach depth, σ is the width of the Gaussian distribution, and k₁ and k₂ are the association and disassociation rates, respectively. For the pure diffusion model, Gaussian initial conditions, convert Eq. 4 in Hinow et al. (6) to

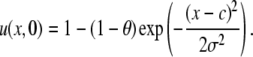(12)

Simplification of the published half-nuclear FRAP model

The published model for half nuclear FRAP (7) was based on ordinary differential equations containing terms for binding and no term for diffusion. In this section, we present a simplified version of this model. The simplest equation describing one binding state in a finite nucleus is

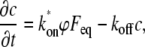(13)

where ϕ is the percent of fluorescence remaining after the photobleach. The solution for the FRAP recovery is

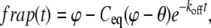(14)

where θ is the bleach depth of the FRAP. For the case of two binding states in a finite nucleus, the solution is

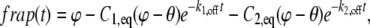(15)

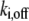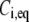where and are the dissociation rates and the equilibrated bound concentrations for the two binding sites (i = 1,2). With knowledge of the bleach depth θ, and 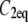can be extracted from the constants preceding the exponential terms, which in turn enables calculation of the association rates with Eq. 54 in Sprague et al. (8).

APPENDIX 5: DETERMINATION OF THE AREA OF THE MODEL NUCLEUS

The new FRAP models use a simplified, finite geometry for the nuclear cross section: a circle is assumed for the circle FRAP and a rectangle for the strip FRAP. Along the optical axis, both models assume an infinite nucleus with a homogeneous internal fluorescence distribution. Both models then compute the FRAP recovery only in the plane of focus (see Appendix 4), and so fluorescence is conserved in this two-dimensional region. The real nucleus is ellipsoidal in x,y,z and contains large regions (nucleoli) that are mostly devoid of fluorescence. Nevertheless, the model nucleus can be a reasonable approximation to the real nucleus if its size is set such that the photobleach destroys the same proportion of fluorescence as in the real nucleus.

The size of the model nucleus can be estimated from two measurable parameters: the profile of the photobleach, I(·), and the final recovery level of the FRAP, ϕ. Since intensities are normalized to one, the amount of fluorescence before the photobleach, equals the area of the nucleus, whereas the amount of fluorescence after the photobleach, equals the integral of I(·) over the nuclear area. For circle or strip FRAP, these parameters are related by

where is the radius of the nucleus in the circle FRAP model and 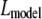is the length of the nucleus in the strip FRAP model. We solved these equations for eithe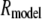r or using the value for ϕ determined from the measured FRAP curves and the value of I(·) determined from measuring the photobleach profile in the first postbleach image (see Appendix 2).

Note that the preceding approach presumed no immobile fraction in the FRAP recovery. We tested this with the published procedure of Hinow et al. (6), and found no evidence for an immobile fraction for GR, p53, or Max (data not shown).