Abstract
We report a theoretical investigation of the electrohydrodynamic properties of spherical soft particles composed of permeable concentric layers that differ in thickness, soft material density, chemical composition, and flow penetration degree. Starting from a recent numerical scheme developed for the computation of the direct-current electrophoretic mobility (μ) of diffuse soft bioparticles, the dependence of μ on the electrolyte concentration and solution pH is evaluated taking the known three-layered structure of bacteriophage MS2 as a supporting model system (bulk RNA, RNA-protein bound layer, and coat protein). The electrokinetic results are discussed for various layer thicknesses, hydrodynamic flow penetration degrees, and chemical compositions, and are discussed on the basis of the equilibrium electrostatic potential and hydrodynamic flow field profiles that develop within and around the structured particle. This study allows for identifying the cases where the electrophoretic mobility is a function of the inner structural and chemical specificity of the particle and not only of its outer surface properties. Along these lines, we demonstrate the general inapplicability of the notions of zeta potential (ζ) and surface charge for quantitatively interpreting electrokinetic data collected for such systems. We further shed some light on the physical meaning of the isoelectric point. In particular, numerical and analytical simulations performed on structured soft layers in indifferent electrolytic solution demonstrate that the isoelectric point is a complex ionic strength-dependent signature of the flow permeation properties and of the chemical and structural details of the particle. Finally, the electrophoretic mobilities of the MS2 virus measured at various ionic strength levels and pH values are interpreted on the basis of the theoretical formalism aforementioned. It is shown that the electrokinetic features of MS2 are to a large extent determined not only by the external proteic capsid but also by the chemical composition and hydrodynamic flow permeation of/within the inner RNA-protein bound layer and bulk RNA part of the bacteriophage. The impact of virus aggregation, as revealed by decreasing diffusion coefficients for decreasing pH values, is also discussed.
INTRODUCTION
Over the years, growing attention has been devoted to the fundamental understanding of electrokinetic phenomena and their applications in various fields of science such as microfluidics (1,2), environmental science (3), advanced oil recovery issues (4), and modern ceramic materials preparation (5), to mention only a few. Understanding the concept, definition, measurement, and interpretation of electrokinetic potentials, and the role played by surface conduction (6) in accounting for electrokinetic data on hard, rigid particles, has seen substantial progress (7–15). For the sake of illustration, we mention the “dynamic Stern layer model” now frequently used to reconcile zeta potentials as obtained from independent electrokinetic techniques, e.g., electrophoresis and dielectric spectroscopy. We may state that for “simple” surfaces the slip process, and for that matter, the physical notion of zeta potential, are now well established even though molecular interpretation is still the subject of ongoing research (16). The theoretical problems are now shifting toward the interpretation of the electrokinetics of “complex” soft colloidal systems such as bacterial particles (17–23), humic acids (24), or polysaccharides (25,26).
Contrary to their hard counterparts, soft particles are generally characterized by a hard core covered by a (charged) polyelectrolyte type of layer of given hydrodynamic permeability (27,28). The electrokinetic properties of such particles have been the subject of recent extensive theoretical developments. In a pioneering work by Ohshima (27,29), the flow permeability within the soft layer was considered by assuming a discontinuous description of the interface, i.e., the density of the polymer chains was found constant in the soft surface layer and dropped sharply to zero at the very interface formed with the electrolyte side. This interfacial description is thus based on a step-function-like or homogeneous profile for the soft material density throughout the permeable part of the particle. Analytical solutions of the governing transport and electrostatic equations were so provided, mainly by Ohshima (27,29), for a variety of soft colloids under the conditions that polarization and relaxation of the electrical double layer are absent. More advanced (numerical) analyses integrate polarization/relaxation of electric double layer under the action of applied field (30–35) and allow for the evaluation of the electrophoretic mobility over a wide range of electrolyte concentrations, coating thicknesses, and polyelectrolyte charges. Recently, Hill et al. (30,31,34) introduced arbitrary segment and charge density distributions in their electrokinetic model for soft particles. Later, Duval and Ohshima (35) systematically investigated the impact of such a continuous polymer material density profile within the soft layer on the electrophoretic mobility. Based on a diffuse representation of the soft interface, they quantified the important discrepancies between mobilities as evaluated from a discontinuous modeling of the interface and a diffuse, continuous interface where the density of polymer segments gradually decays from bulk values within the heart of the soft layer to zero in the electrolytic solution. Use of this theory is particularly relevant for interpreting electrokinetic data collected for colloidal systems such as microgel particles (36,37), humic acids (24), or polysaccharides (25,26), which undergo deformation via swelling/shrinking processes (36–39) or aggregation under the effect of electrolyte concentration, variations in solvent quality, or temperature.
Despite the advances brought about by this formalism, it applies to particles for which the chemical composition (nature of ionogenic sites) of the soft layer remains constant in space, thus focusing only on the spatial anisotropy in polyelectrolyte chains distribution. Basically, this comes to state that the local charge distribution within the soft layer follows that dictated by the spatial profile for the polyelectrolyte chains density. Successful application of the model (35) is reported in (21) for the examination of the electrokinetic properties of Gram-positive bacteria of the oral type Streptococcus salivarius covered by pili of length 60–200 nm. The typical hydrodynamic penetration length (of magnitude ∼1 nm) within the pili is too small for the electroosmotic flow to probe the different chemical compositions of the outer pili layer and of the inner peptidoglycan layer; therefore, the electrokinetics is determined by the chemical and hydrodynamic permeation properties of the outer pili layer only.
For a number of bioparticles, viruses being the paradigms (10–50 nm in radius), the spatial anisotropy in polymer segment distribution is strongly accompanied by position-dependent chemical heterogeneities (40–42), the length scales of those being of the same order of magnitude than typical flow penetration lengths reported for soft bioparticles. In such cases, the assumption of similar spatial functionalities for the distribution of the volume charge density and polymer segment density within the soft layer is clearly inadequate and needs to be revisited, which is essentially the purpose of this study.
For MS2 bacteriophage (40–42), one may clearly distinguish three concentric soft layers that differ in composition: a bulk RNA region (center part of the virus, radius ∼8 nm), an RNA protein-bound layer (thickness ∼3 nm), and a proteic capsid that forms the outer shell of the virus (thickness ∼2 nm). To our knowledge, the understanding of the electrokinetic properties of such type of permeable particles has received only marginal attention despite the fundamental foundations laid down by the recent theories for the electrokinetics of soft particles (27–35). In Schaldach et al. (43), the analysis of the electrokinetic features of various bacteriophages relies on the application of the Helmholtz-Smoluchowski equation and on the notion of zeta potential, ζ, which is assimilated to the “average surface potential” (43) of a spherical, hard particle within the Debye-Hückel approximation. That average surface potential is evaluated by summing over the surface the corresponding local surface potentials as obtained from the interaction potentials between the considered surface position and all charges located within the particle. The analysis disregards the flow permeation properties of the bacteriophage, which is a priori inconsistent with the subsurface viral structure that exhibits pores (41,44), the size of which exceeds tens of angstroms. For such soft particles, the very notion of ζ-potential has no physical meaning, since the gradual decay of the flow field within the particle makes the location of any slip plane irrelevant (45). Only for particles with moderate hydrodynamic permeability, one may use the ζ-potential concept for interpreting electrokinetic data, providing, however, that tangential surface conduction processes are taken into account in the electrokinetic model. This was shown in a recent study by Dukhin et al. (46), who reconciled the soft particle approach first proposed by Ohshima and the surface conduction phenomena that typically take place at the interface between hard particles and aqueous solution. None of those elements are considered in the electrokinetic analysis reported in Schaldach et al. (43).
In view of the preceding elements, the objectives of our work are essentially twofold:
Extend the formalism reported in Duval and Ohshima (35) to the case of particles where spatial structural and chemical anisotropy concomitantly govern their electrokinetic response. For that purpose, we shall reason on the basis of a three concentric layers composition for the particle, taking the example of MS2 bacteriophage as a supporting model. Rigorous numerical solutions of the key electrohydrodynamic equations will be provided for a number of situations that underline the complex interplay among the respective layer thicknesses, the overall flow permeability, the local polymer segment densities within the particle layers, and their chemical properties.
Analyze specifically the electrokinetic peculiarities of MS2 bacteriophage. To do this, the reported chemical composition (GenBank accession numbers NP 040648 for MS2 coat protein and NC 001417 for MS2 complete genome) of the layers that constitute the virus will be taken into account in the model developed in (i), and so will be the soft material (RNA bulk, RNA protein-bound, and coat protein) density profile from the center of the virus to its outer periphery, as recently measured by cryoelectron microscopy (cryoEM) (41,42) and small-angle x-ray scattering (40). The analysis will allow for the determination of the contribution of the bulk RNA and RNA protein-bound layer to the overall electrophoretic mobility.
The information derived from the study reported here forms the basis for a quantitative description of the electrostatic and hydrodynamic features of isolated MS2 bacteriophage. Knowledge of these interfacial characteristics is of outmost relevance for understanding on a fundamental level the interfacial phenomena of practical importance that MS2 are involved in, such as transport through groundwater (47–52), virus filtration through membranes (53–55), bioadhesion (53,56–62), and virus aggregation (63,64).
MATERIALS AND METHODS
Preparation of viruses suspension
MS2 phages (ATCC 15597-B1) were replicated according to standard procedure (ISO 10705-1, 1997) without a CHCl3 lysis step and using Escherichia coli Hfr K12 (ATCC 23631) as bacterial host. After replication, the viral suspension was centrifuged (Beckman (Fullerton, CA), model J2-22, 27,000 × g, 60 min, 4°C) and the supernatant filtered through a 0.22 μm membrane (Millipore (Billerica, MA), SLGP033RS). All suspensions were dialyzed (100 kDa molecular weight cutoff, Spectrum (Gardena, CA), 131420) against deionized water (0.1 μS.cm−1) for 14 h and dialyzed for a second time against NaNO3 1 mM, pH 6.7, (150 μS.cm−) for 14 h. Suspensions were then filtered again (0.22 μm). The viral suspensions were observed by electron microscopy to make sure that suspensions contained no aggregates. The final viral concentrations were 1011 plaque-forming units ml−1 and were stored as stock suspension at 4°C before any measurements.
Light scattering and electrokinetic measurements
Diffusion coefficients and electrophoretic mobilities were measured at 23 ± 0.1°C using the Zetasizer Nano ZS instrument (He-Ne red laser (633 nm, Malvern Instruments, Malvern, UK). The apparatus is equipped with an automatic laser attenuator and an avalanche photodiode detector. The position of the latter is located 173° relative to the laser source so that backscattering detection is ensured. Experiments were driven by the Dispersion Technology Software provided by Malvern Instruments. The distribution of the diffusion coefficient was evaluated by fitting the measured correlation curves according to available fitting algorithms. Electrophoretic mobilities were measured by laser Doppler electrophoresis also known as phase analysis light scattering. The rate of change of the phase shift between the scattered light and a reference beam is correlated to the particle velocity and thus allows for evaluating the particular electrophoretic mobility.
THEORY
Modeling the polymer segment density and chemical composition profiles for soft multilayer particles
Spatial anisotropy for the density of polymer segments
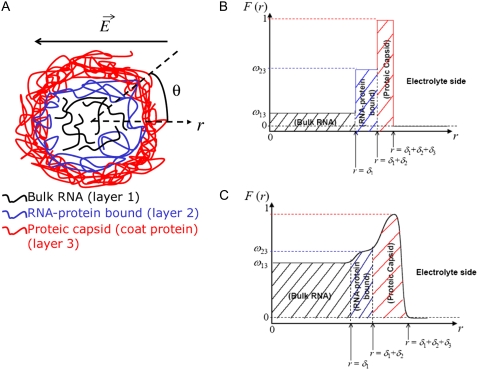
We consider the geometrical situation of a permeable bioparticle composed of three concentric soft layers as depicted in Fig. 1 A. The spherical coordinates 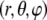 are adopted with the position
are adopted with the position 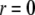 marking the center of the particle. This soft particle structure is selected in view of the application of the theoretical formalism for interpreting electrokinetic data on MS2 bacteriophage (see below). Without loss of generality, the theoretical modeling could be developed for an n-layer particular composition with
marking the center of the particle. This soft particle structure is selected in view of the application of the theoretical formalism for interpreting electrokinetic data on MS2 bacteriophage (see below). Without loss of generality, the theoretical modeling could be developed for an n-layer particular composition with 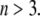 The thicknesses of the layers numbered 1, 2, and 3 are denoted in the following as
The thicknesses of the layers numbered 1, 2, and 3 are denoted in the following as 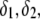 and
and 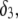 respectively, where the subscripts 1, 2, and 3 pertain to the inner, intermediate, and outer layer of the particle. The spatial distribution of the polymer segment density within the soft layer i
respectively, where the subscripts 1, 2, and 3 pertain to the inner, intermediate, and outer layer of the particle. The spatial distribution of the polymer segment density within the soft layer i 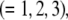 denoted as
denoted as 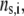 is chosen to be dependent on the radial position r only, and is written for the sake of generality as
is chosen to be dependent on the radial position r only, and is written for the sake of generality as
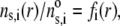 |
(1) |
where 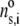 is the nominal segment density of the layer i, that is with homogeneously distributed chains. Within the framework of the Debye-Bueche theory (65), polymer segments constituting layer i may be assimilated to resistance centers of radius
is the nominal segment density of the layer i, that is with homogeneously distributed chains. Within the framework of the Debye-Bueche theory (65), polymer segments constituting layer i may be assimilated to resistance centers of radius 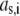 that exert frictional forces on the fluid flowing through layer i. The r-dependence of the hydrodynamic volume fraction
that exert frictional forces on the fluid flowing through layer i. The r-dependence of the hydrodynamic volume fraction 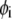 of polymer segments within layer i, is simply
of polymer segments within layer i, is simply
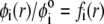 |
(2) |
with 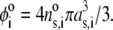 To obtain the spatial distribution of the friction coefficient
To obtain the spatial distribution of the friction coefficient 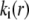 within the layer i, we reason on the basis of the Brinkman equation (66) that relates
within the layer i, we reason on the basis of the Brinkman equation (66) that relates 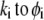 by considering the flux of fluid across the group of spheres of radius
by considering the flux of fluid across the group of spheres of radius 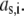 For sufficiently large water content within the various soft layers of interest, one may show that the result simply reads as (35)
For sufficiently large water content within the various soft layers of interest, one may show that the result simply reads as (35)
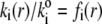 |
(3) |
with 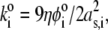 η denoting the dynamic viscosity of water. Stochastic calculations further demonstrate that Eq. 3 is valid for
η denoting the dynamic viscosity of water. Stochastic calculations further demonstrate that Eq. 3 is valid for 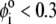 (67). To go further, explicit expressions are required for the functions
(67). To go further, explicit expressions are required for the functions 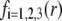 that characterize the spatial profiles of polymer segments densities within the layer of thickness
that characterize the spatial profiles of polymer segments densities within the layer of thickness 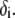 These expressions may be empirical, may derive from computational thermodynamics or be inferred from spectroscopic, imaging, or electronic measurements (35). Following the route detailed in Duval and Ohshima (35), we shall adopt here the spatial functionalities as expressed by
These expressions may be empirical, may derive from computational thermodynamics or be inferred from spectroscopic, imaging, or electronic measurements (35). Following the route detailed in Duval and Ohshima (35), we shall adopt here the spatial functionalities as expressed by
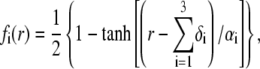 |
(4) |
where the 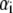 denote the typical length over which the polymer segment density distribution within the layer i deviates from the step function-like profile. The local hydrodynamic volume fraction of polymer segments within the soft particle, denoted as
denote the typical length over which the polymer segment density distribution within the layer i deviates from the step function-like profile. The local hydrodynamic volume fraction of polymer segments within the soft particle, denoted as 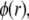 may be written in the form
may be written in the form
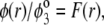 |
(5) |
where we have arbitrarily chosen to normalize 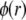 with respect to
with respect to 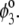 One may easily show that
One may easily show that 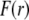 is given by
is given by
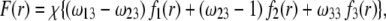 |
(6) |
where the 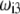 are defined by
are defined by 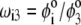 and the scalar χ ensures the constancy of the total number of polymer segments within the particle upon variation of the heterogeneity of the various layers, that is when varying the ratios
and the scalar χ ensures the constancy of the total number of polymer segments within the particle upon variation of the heterogeneity of the various layers, that is when varying the ratios 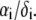 As such, χ satisfies the relationship
As such, χ satisfies the relationship
 |
(7) |
Function F essentially refers to the radial polymer segment density distribution throughout the soft particle. In Fig. 1, B and C, we show the dependence of function F (Eqs. 6 and 7) on the radial position r for homogeneous distribution of polymer segments (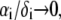 panel B) and diffuse segment density distribution (
panel B) and diffuse segment density distribution (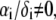 panel C) in the inner, intermediate, and outer soft layers of the particle. Fig. 1 C corresponds to the spatial profile of the polymer segment density measured by cryoEM (41,42) for the bacteriophage MS2 (see discussion below).
panel C) in the inner, intermediate, and outer soft layers of the particle. Fig. 1 C corresponds to the spatial profile of the polymer segment density measured by cryoEM (41,42) for the bacteriophage MS2 (see discussion below).
FIGURE 1.
(A) Simplified representation of a MS2 viral particle placed in an external electric field 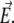 For the sake of readability, the charges that stem from the ionogenic sites distributed throughout the virus are not indicated, nor are the ions located within and around the particle. Based on the work reported in (40–42),
For the sake of readability, the charges that stem from the ionogenic sites distributed throughout the virus are not indicated, nor are the ions located within and around the particle. Based on the work reported in (40–42), 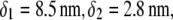 and
and 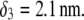 The scheme is not to scale. (B) Radial profile
The scheme is not to scale. (B) Radial profile 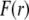 (Eq. 6) for the volume density of polymer segments with
(Eq. 6) for the volume density of polymer segments with  (see Eqs. 4–6). The interfaces between layer i and i + 1
(see Eqs. 4–6). The interfaces between layer i and i + 1  and that between layer 3 and the electrolytic solution are step-function like. (C) Typical example of polymer segments density distribution with
and that between layer 3 and the electrolytic solution are step-function like. (C) Typical example of polymer segments density distribution with  (
(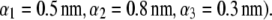 The interfaces between layer i and i + 1
The interfaces between layer i and i + 1 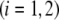 and that between layer 3 and the electrolytic solution are diffuse (35).
and that between layer 3 and the electrolytic solution are diffuse (35).
Based on the same arguments that allowed the derivation of Eq. 3 from Eq. 2, the local friction coefficient 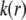 within the particle is written
within the particle is written
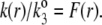 |
(8) |
In the following, we shall introduce the local softness parameter of the particle, the spatial distribution of which is given by
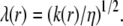 |
(9) |
The quantity 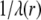 has the dimension of a length and denotes the local flow penetration degree within the particle. Combining Eqs. 8 and 9, we have
has the dimension of a length and denotes the local flow penetration degree within the particle. Combining Eqs. 8 and 9, we have
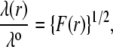 |
(10) |
where 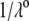 represents the nominal hydrodynamic penetration length within the particle for homogeneous polymer chains distribution, that is
represents the nominal hydrodynamic penetration length within the particle for homogeneous polymer chains distribution, that is 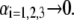
Spatial anisotropy for the volume charge density within the soft particle
Under the assumption that the density of ionogenic sites within the particle is directly proportional to the polymer segment density 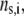 the spatial distribution of the volume density of fixed charges, denoted as
the spatial distribution of the volume density of fixed charges, denoted as 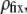 is simply given by
is simply given by
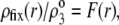 |
(11) |
where 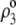 is the nominal charge density within the polymeric layer 3 and the function F is given by Eq. 6. Relaxing this assumption is required for analyzing the electrohydrodynamic properties of the particles of interest here where chemical heterogeneity compounds the structural anisotropy evoked in the preceding section. For those cases that come closer to practical situations, adopting the scheme of the previous section, the local volume charge density may be written
is the nominal charge density within the polymeric layer 3 and the function F is given by Eq. 6. Relaxing this assumption is required for analyzing the electrohydrodynamic properties of the particles of interest here where chemical heterogeneity compounds the structural anisotropy evoked in the preceding section. For those cases that come closer to practical situations, adopting the scheme of the previous section, the local volume charge density may be written
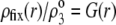 |
(12) |
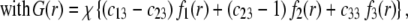 |
(13) |
where the scalars 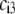 are defined by the relationships
are defined by the relationships 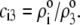 Function G denotes the chemical composition profile throughout the soft particle. Equation 11 is recovered from Eq. 13 under the condition
Function G denotes the chemical composition profile throughout the soft particle. Equation 11 is recovered from Eq. 13 under the condition 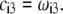 Equations 12 and13 are strictly valid within the condition of complete dissociation of the ionogenic groups located at position r. As such, the quantity
Equations 12 and13 are strictly valid within the condition of complete dissociation of the ionogenic groups located at position r. As such, the quantity 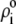 can be viewed as the overall net charge that arises from the complete dissociation of
can be viewed as the overall net charge that arises from the complete dissociation of 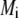 types of ionizable sites within the soft polymeric layer i. In the more general case, the degree of dissociation of these groups depends on the nature of the site considered and varies with the solution pH and the local equilibrium potential, denoted as
types of ionizable sites within the soft polymeric layer i. In the more general case, the degree of dissociation of these groups depends on the nature of the site considered and varies with the solution pH and the local equilibrium potential, denoted as 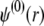 (35). Recognizing for the necessity of introducing these elements, the coefficients
(35). Recognizing for the necessity of introducing these elements, the coefficients 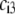 become pH and position dependent according to
become pH and position dependent according to
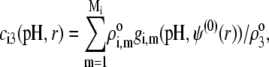 |
(14) |
where the function 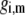 is the isotherm describing the protolytic properties of the site of type m within the polyelectrolyte layer i and the quantity
is the isotherm describing the protolytic properties of the site of type m within the polyelectrolyte layer i and the quantity 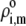 represents the maximal charge density as reached upon complete dissociation of the sites of type m present in layer i. For the case of MS2 bacteriophage (see below), the function
represents the maximal charge density as reached upon complete dissociation of the sites of type m present in layer i. For the case of MS2 bacteriophage (see below), the function 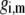 takes the form
takes the form
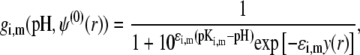 |
(15) |
where 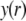 is the dimensionless electrostatic potential
is the dimensionless electrostatic potential 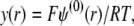 with F the Faraday number, R the gas constant, and T the absolute temperature, and
with F the Faraday number, R the gas constant, and T the absolute temperature, and 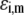 takes the values +1 or −1 depending on the sign of the charge carried by the site considered. Equation 15 stands for the Langmuir isotherm derived for the following equilibria:
takes the values +1 or −1 depending on the sign of the charge carried by the site considered. Equation 15 stands for the Langmuir isotherm derived for the following equilibria:
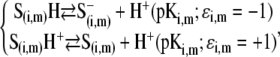 |
(16,17) |
where the subscript 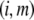 denotes the layer and type of site S considered. It is stressed here that the developments above neglect the local positioning of the
denotes the layer and type of site S considered. It is stressed here that the developments above neglect the local positioning of the 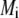 charged sites within a given layer i. The formalism adopted here is thus “smeared-out” in the sense that it regards the very distribution of all ionizable sites within the layer i as homogeneous for a given r-position. Such approximation is legitimate for typical separation distances between adjacent charges that do not exceed the characteristic spatial extension of the electrical double layer, which will be basically the case for the bacteriophage MS2 analyzed in this study. Abandoning this approximation requires the use of ab initio formalisms where interaction potential between neighboring sites are accounted for. Retaining such a detailed picture of the electrostatics imposes tackling the flow permeation properties of the particle at a detailed molecular scale.
charged sites within a given layer i. The formalism adopted here is thus “smeared-out” in the sense that it regards the very distribution of all ionizable sites within the layer i as homogeneous for a given r-position. Such approximation is legitimate for typical separation distances between adjacent charges that do not exceed the characteristic spatial extension of the electrical double layer, which will be basically the case for the bacteriophage MS2 analyzed in this study. Abandoning this approximation requires the use of ab initio formalisms where interaction potential between neighboring sites are accounted for. Retaining such a detailed picture of the electrostatics imposes tackling the flow permeation properties of the particle at a detailed molecular scale.
Segment density and chemical composition profiles for bacteriophage MS2
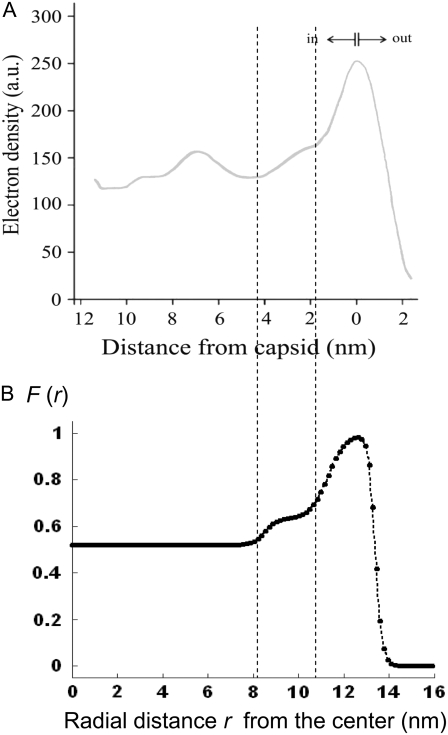
MS2 bacteriophage is an RNA virus with an icosahedral capsid measuring 22–29 nm in diameter (68–70). The genome encodes four proteins: a major coat protein, which builds up the capsid of the virus; a maturation protein (or A-protein), which is a minor constituent of the virion involved in pilus recognition; a replicase (a RNA polymerase necessary for genome multiplication); and a lysis protein. Recent detailed small-angle x-ray scattering and cryoEM analyses (40–42) revealed two spheres of RNA density below the shell of capsid density, as schematically depicted in Fig. 1 A. From (40,70,71), the bulk RNA virion is ∼8.5 nm in radius, and the RNA protein-bound layer and the proteic capsid 2.8 nm and 2.1 nm thick, respectively. The radial distribution of the virus, obtained from the cryoEM analysis reported in van den Worm et al. (42), is represented in Fig. 2 A. It could be satisfactorily reconstructed using Eqs. 4, 6, and 7 with 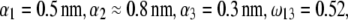 and
and 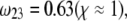 as shown in Fig. 2 B. We stress that the uniqueness of this set of parameters in reconstructing the cryoEM data in van den Worm et al. (42) from Eqs. 4, 6, and 7 is ensured by the fact that i),
as shown in Fig. 2 B. We stress that the uniqueness of this set of parameters in reconstructing the cryoEM data in van den Worm et al. (42) from Eqs. 4, 6, and 7 is ensured by the fact that i), 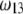 and
and 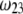 pertain to the bulk values of the normalized density distributions within layer 1 (bulk RNA) and layer 2 (RNA protein-bound layer), respectively, and ii), the variables
pertain to the bulk values of the normalized density distributions within layer 1 (bulk RNA) and layer 2 (RNA protein-bound layer), respectively, and ii), the variables 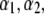 and
and 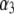 allow a refined description of the segment density distributions at the interfaces layer 1/layer 2, layer 2/layer 3, and layer 3/electrolyte solution, respectively. As such, the determination of each of the parameters involved in the expression for the segment density distribution (Eqs. 4–6) may be done independently. Also, the local details (oscillations) of the density distribution within the heart of the virus (
allow a refined description of the segment density distributions at the interfaces layer 1/layer 2, layer 2/layer 3, and layer 3/electrolyte solution, respectively. As such, the determination of each of the parameters involved in the expression for the segment density distribution (Eqs. 4–6) may be done independently. Also, the local details (oscillations) of the density distribution within the heart of the virus (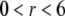 with r in nm, see Fig. 2 B) have been omitted because they refer to the spatial region where the electroosmotic flow within the virus is the most attenuated (as verified from the calculated flow profiles, not shown). As such, this part of the viral particle is the least determinant in governing the electrophoretic mobility of the virus, and an account of small local details therein does not affect our results. The percentage of solvent in the RNA inner region and in the proteic capsid are ∼75% and 98%, respectively (40,71), which justifies the use of Eq. 3 that identifies the soft material density distribution (Fig. 2) to that for the friction coefficient k (Eqs. 5 and 8).
with r in nm, see Fig. 2 B) have been omitted because they refer to the spatial region where the electroosmotic flow within the virus is the most attenuated (as verified from the calculated flow profiles, not shown). As such, this part of the viral particle is the least determinant in governing the electrophoretic mobility of the virus, and an account of small local details therein does not affect our results. The percentage of solvent in the RNA inner region and in the proteic capsid are ∼75% and 98%, respectively (40,71), which justifies the use of Eq. 3 that identifies the soft material density distribution (Fig. 2) to that for the friction coefficient k (Eqs. 5 and 8).
FIGURE 2.
Reconstruction (panel B) of the radial density distribution as derived from cryoEM data (panel A, adapted from Fig. 3 in van den Worm (42)) on the basis of Eqs. 4, 6, and 7. The data are normalized with respect to the largest proteic capsid density (outer shell of the virus). See text for further detail. The dashed lines mark the spatial transitions among the inner RNA, RNA protein-bound layer, and proteic capsid.
To picture the chemical composition of the virus, we started from the three dimensional viral representation as given in ((69,70,72); Protein Data Bank entry 2MS2). We then inventory the various types of amino-acids in the free-RNA proteic capsid (layer 3) (protein ID in GenBank: NP_040648) with lateral ionizable chains and their apparition frequency, and subsequently assign to each indexed site a pK value as provided by the computer simulation program PROPKA (73). The latter evaluates the dissociation constants of a given site taking into account its chemical environment. The reader is referred to Li et al. (73) for further details. Comparison with tabulated pK data (74) that ignore the dependence of the dissociation constants on the detailed molecular environment reveals small to significant (1 pH unit) variations, depending on the type of site considered. Regarding the RNA part of the virus (layers 1 and 2), we considered the integrality of the MS2 genomic sequence and listed all ionogenic sites of which the dissociation generates a charge, and we associated a pK value for the corresponding acido-basic equilibria (75). Contrary to the proteic capsid, the tabulated pK values for the nucleobases do not take into account their specific environment within the virus. To our knowledge, no computation program is available for that purpose. As done in Schaldach et al. (43), we modeled the virus as a spherical particle. From the geometrical details of the virus illustrated in Fig. 1 and from the apparition frequencies of the sites, the nominal charge densities 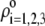 could be easily evaluated. We specify here that the count of the RNA ionizable sites could not be performed by discriminating the bulk RNA from the RNA protein-bound layer, which comes to set
could be easily evaluated. We specify here that the count of the RNA ionizable sites could not be performed by discriminating the bulk RNA from the RNA protein-bound layer, which comes to set 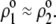 The underlying approximation is, however, acceptable in view of
The underlying approximation is, however, acceptable in view of  All results pertaining to
All results pertaining to 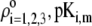 and
and 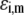 (see Eqs. 14–17) are collected in Tables 1 and 2. The remaining parameter required for the theoretical analysis of the electrokinetic data (numerical theory, Eqs. 1–10 and Eqs. 12–34 given below) is the nominal hydrodynamic permeability
(see Eqs. 14–17) are collected in Tables 1 and 2. The remaining parameter required for the theoretical analysis of the electrokinetic data (numerical theory, Eqs. 1–10 and Eqs. 12–34 given below) is the nominal hydrodynamic permeability 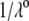 of the virus, which serves as an adjustable parameter.
of the virus, which serves as an adjustable parameter.
TABLE 1.
Chemical composition of the outer proteic capsid of MS2 bacteriophage and corresponding parameters 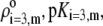 and
and 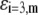 as involved in Eqs. 15–17; see text for further detail
as involved in Eqs. 15–17; see text for further detail
| Amino acids | 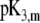 |
ɛ3,m |
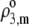 F3,m/mM F3,m/mM |
|---|---|---|---|
| Glutamic acid (−COOH) | 2.79 | −1 | −370 |
| Tyrosine (−COOH) | 2.95 | −1 | −74 |
| Aspartic acid (−COOH) | 3.30 | −1 | −296 |
Alanine ( ) ) |
7.93 | +1 | +74 |
| Cysteine (−SH) | 9.35 | −1 | −148 |
| Tyrosine (−OH) | 10.00 | −1 | −296 |
Lysine ( ) ) |
10.89 | +1 | +444 |
Arginine ( ) ) |
12.22 | +1 | +296 |
TABLE 2.
Chemical composition of the inner RNA part of MS2 bacteriophage and corresponding parameters 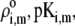 and
and 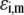 as involved in Eqs. 15–17; see text for further detail
as involved in Eqs. 15–17; see text for further detail
| Nucleobases | pKi,m | ɛi,m |
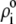 Fi,m/mM Fi,m/mM |
|---|---|---|---|
| Phosphodiester | 1.5 | −1 | −976 |
Adenine ( ) ) |
3.725 | +1 | +225 |
Cytosine ( ) ) |
4.24 5 | +1 | +255 |
Uracile (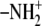 ) ) |
9.26 | +1 | +240 |
Guanine ( ) ) |
9.29 | +1 | +255 |
(i=1,2)
Governing electrohydrodynamic equations of soft multilayer particles
The particle described above is placed in a uniform direct current electric field 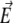 and thereby moves with a velocity
and thereby moves with a velocity 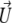 in an electrolyte of dielectric permittivity
in an electrolyte of dielectric permittivity 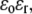 composed of N types of ionic, mobile species with valences
composed of N types of ionic, mobile species with valences 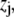 bulk concentrations
bulk concentrations 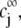 and limiting ionic conductivities
and limiting ionic conductivities 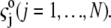 The origin of the spherical coordinate system
The origin of the spherical coordinate system 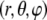 is placed at the center of the particle and the polar axis
is placed at the center of the particle and the polar axis 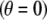 is set parallel to
is set parallel to 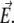 The set of governing electrokinetic equations for a core-diffuse (mono)shell particle (i.e., for
The set of governing electrokinetic equations for a core-diffuse (mono)shell particle (i.e., for 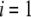 ) has been extensively discussed in recent studies (35). We present here the basic steps in the derivation of the fundamental equations for a diffuse soft particle composed of three concentric soft layers.
) has been extensively discussed in recent studies (35). We present here the basic steps in the derivation of the fundamental equations for a diffuse soft particle composed of three concentric soft layers.
The Navier-Stokes equation that determines the flow velocity, 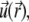 at the position
at the position 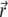 relative to the particle, is written in its general form (27)
relative to the particle, is written in its general form (27)
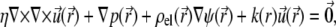 |
(18) |
where 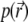 is the pressure,
is the pressure, 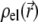 and
and 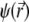 are the space charge density (resulting from the mobile ionic species) and the electrostatic potential in the presence of the applied electric field, respectively.
are the space charge density (resulting from the mobile ionic species) and the electrostatic potential in the presence of the applied electric field, respectively. 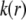 is the position-dependent friction coefficient as given by Eq. 8. The quantity
is the position-dependent friction coefficient as given by Eq. 8. The quantity 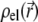 is related to the local ionic concentrations, denoted as
is related to the local ionic concentrations, denoted as 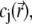 by
by
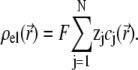 |
(19) |
The continuity equation for a steady incompressible flow further imposes that
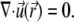 |
(20) |
The local velocity, 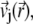 of an ion j is determined by that of the liquid flow,
of an ion j is determined by that of the liquid flow, 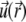 (convection), and by the gradient in electrochemical potential, denoted as
(convection), and by the gradient in electrochemical potential, denoted as 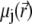 (diffusion), so that
(diffusion), so that
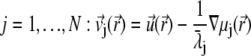 |
(21) |
with 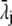 the drag coefficient of ion j.
the drag coefficient of ion j. 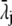 is related to the limiting conductivity
is related to the limiting conductivity 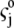 by the simple expression
by the simple expression 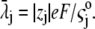 The continuity equation written for an ion j leads to
The continuity equation written for an ion j leads to
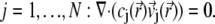 |
(22) |
For sufficiently weak electric fields E, as commonly considered within the framework of electrokinetic phenomena of the first kind, we may expand 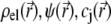 and
and 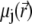 as follows:
as follows:
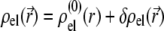 |
(23) |
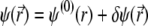 |
(24) |
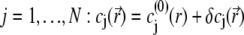 |
(25) |
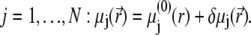 |
(26) |
In Eqs. 23–26, the quantities indicated by the superscript 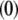 refer to those at equilibrium (i.e., in the absence of the applied electric field) and the variables
refer to those at equilibrium (i.e., in the absence of the applied electric field) and the variables 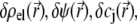 and
and 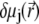 indicate small perturbations of the corresponding equilibrium values due to the presence of the applied field E.
indicate small perturbations of the corresponding equilibrium values due to the presence of the applied field E.  and
and 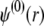 are given by the Poisson-Boltzmann equations
are given by the Poisson-Boltzmann equations
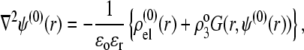 |
(27) |
where the function G, which depends on 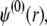 is defined by Eqs. 13–14, and
is defined by Eqs. 13–14, and
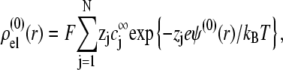 |
(28) |
where 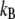 is the Boltzmann constant. The electrochemical potential of ion j,
is the Boltzmann constant. The electrochemical potential of ion j, 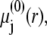 is related to
is related to 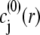 via the relationship
via the relationship
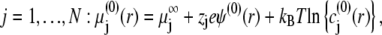 |
(29) |
where 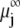 is the electrochemical potential of ion j at some reference state. Using Eqs. 23–26, one may linearize the governing electrokinetic Eqs. 18–22 with respect to the electric field E. The method is essentially the same as that adopted in (27,34,35). The results read as
is the electrochemical potential of ion j at some reference state. Using Eqs. 23–26, one may linearize the governing electrokinetic Eqs. 18–22 with respect to the electric field E. The method is essentially the same as that adopted in (27,34,35). The results read as
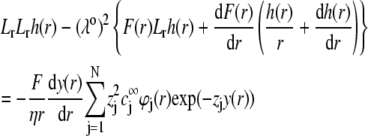 |
(30) |
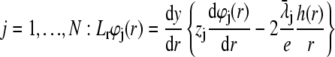 |
(31) |
with 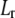 the differential operator defined by
the differential operator defined by 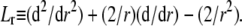 The radial functions h and
The radial functions h and 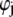 depend on
depend on 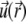 and
and 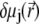 according to (27,35):
according to (27,35):
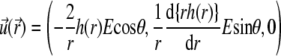 |
(32) |
and
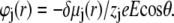 |
(33) |
Boundaries pertaining to the functions h, 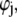 and
and 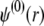 are derived and extensively discussed in Duval and Ohshima (35). In particular we have
are derived and extensively discussed in Duval and Ohshima (35). In particular we have
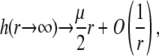 |
(34) |
where μ is the searched electrophoretic mobility.
The complexity of the problem requires a numerical solution for the computation of functions h, 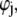 and
and 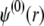 and the evaluation of μ. The reader is referred to Duval and Ohshima (35) for the details of the numerical scheme.
and the evaluation of μ. The reader is referred to Duval and Ohshima (35) for the details of the numerical scheme.
Isoelectric point of multilayer soft particles: an analytical development
The developments detailed above allow for the estimation of μ for any values of the electrolyte concentration, pH solution, and physicochemical (protolytic, electrostatic, and hydrodynamic) determinants of the particle investigated which consists of three concentric soft layers. A parameter of special interest—particularly for the virologists community—(76,77) is the so-called isoelectric point (iep) defined by the pH value where 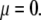 Experimental determination of the iep is rather easy and provides a rough prediction of the pH range where, e.g., i), a given bacteriophage will be active in infecting a target bacterium of known charge (in sign and magnitude), ii), virus trapping by a charged membrane will be effective (78–90), iii), viral surface colonization will take place, or iv), virus aggregation will interfere with biological activity measurements (91). Unfortunately, there are no available analytical or semianalytical expressions for the electrophoretic mobility and isoelectric point of complex three-layer soft polyelectrolytic type of particles such as MS2.
Experimental determination of the iep is rather easy and provides a rough prediction of the pH range where, e.g., i), a given bacteriophage will be active in infecting a target bacterium of known charge (in sign and magnitude), ii), virus trapping by a charged membrane will be effective (78–90), iii), viral surface colonization will take place, or iv), virus aggregation will interfere with biological activity measurements (91). Unfortunately, there are no available analytical or semianalytical expressions for the electrophoretic mobility and isoelectric point of complex three-layer soft polyelectrolytic type of particles such as MS2.
Instead, the only integral equation for the electrophoretic mobility where chemical composition and segment density profiles may be included is that given by Ohshima (27) for a soft particle with a hard core, under the assumption that the radius of that rigid component of the particle well exceeds the Debye layer thickness. For the sake of simplicity, we choose to include in the integral equation by Ohshima (see Eq. 45) a two-layer structure for the soft component of this core-shell particle and subsequently derive analytically the expression of the isoelectric point as a function of the relevant electrohydrodynamic parameters of the particle. Within this section, we thus tackle the case of a core-shell particle of core radius 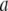 where the soft component is composed of two concentric layers (thickness
where the soft component is composed of two concentric layers (thickness 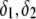 ) with step functions
) with step functions 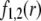 (homogeneous distribution of polymer segments density). The particle is further characterized here by a hydrodynamic penetration length distribution that satisfies
(homogeneous distribution of polymer segments density). The particle is further characterized here by a hydrodynamic penetration length distribution that satisfies 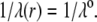 We shall see that the simple analytical model developed below for the isoelectric point of such a particle illustrates the complex ionic strength and flow permeation dependences of the iep value for the soft particle as a whole, dependences that have been largely overlooked in the literature so far. For the sake of simplicity, the derivations are done in the case where the layers
We shall see that the simple analytical model developed below for the isoelectric point of such a particle illustrates the complex ionic strength and flow permeation dependences of the iep value for the soft particle as a whole, dependences that have been largely overlooked in the literature so far. For the sake of simplicity, the derivations are done in the case where the layers 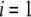 and
and 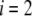 contain amphoretic sites
contain amphoretic sites 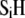 that may accept or give protons according to the following equilibria:
that may accept or give protons according to the following equilibria:
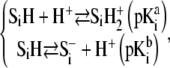 |
(35,36) |
where 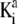 and
and 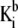 are the thermodynamic equilibrium constants associated with Eqs. 35 and 36, respectively. The corresponding Langmuir isotherms are expressed as
are the thermodynamic equilibrium constants associated with Eqs. 35 and 36, respectively. The corresponding Langmuir isotherms are expressed as
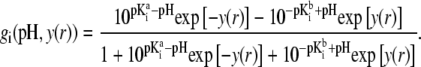 |
(37) |
After straightforward arrangements (92), Eq. 37 may be rewritten in the form
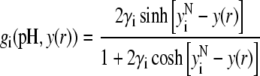 |
(38) |
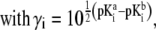 |
(39) |
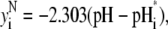 |
(40) |
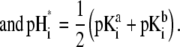 |
(41) |
In the limit of low potentials 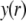 (Debye-Hückel approximation), a first-order Taylor expansion of Eq. 38 provides
(Debye-Hückel approximation), a first-order Taylor expansion of Eq. 38 provides
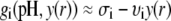 |
(42) |
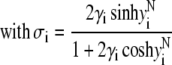 |
(43) |
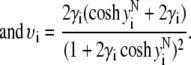 |
(44) |
For a core-shell particle with 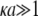 (where
(where 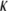 is the classical reciprocal screening Debye length) and a flow permeation degree
is the classical reciprocal screening Debye length) and a flow permeation degree 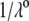 that fulfills the condition
that fulfills the condition 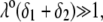 the mobility expression by Ohshima (27) is rewritten for the particle of interest here
the mobility expression by Ohshima (27) is rewritten for the particle of interest here
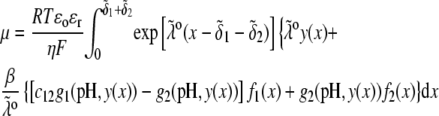 |
(45) |
with the dimensionless variables 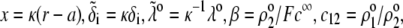 and
and 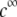 pertaining to the 1:1 bulk electrolyte concentration. Solving for the Poisson-Boltzmann equation (Eqs. 27 and 28) with appropriate boundaries (see the Appendix for details), we show that the pH value satisfying the condition
pertaining to the 1:1 bulk electrolyte concentration. Solving for the Poisson-Boltzmann equation (Eqs. 27 and 28) with appropriate boundaries (see the Appendix for details), we show that the pH value satisfying the condition 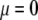 is the solution of the transcendental equation
is the solution of the transcendental equation
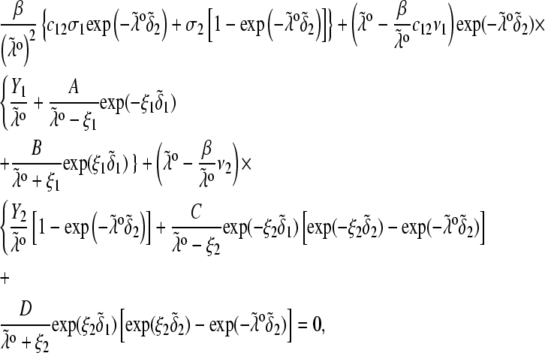 |
(46) |
where the quantities 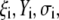 A, B, C, and D are pH-dependent variables defined by Eqs. A7–A19 in the Appendix.
A, B, C, and D are pH-dependent variables defined by Eqs. A7–A19 in the Appendix.
ELECTROKINETICS OF MULTILAYER SOFT PARTICLES: THEORETICAL ILLUSTRATIONS
Impact of the polymer segment density and chemical composition profiles on the electrophoretic mobility μ (numerical theory, three-layer particle structure)
To unravel the necessarily coupled dependences of the electrophoretic mobility μ of the soft particle depicted in Fig. 1, on the polymer segment density distribution 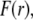 and the chemical composition profile
and the chemical composition profile 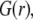 we first report results obtained for completely dissociated ionogenic sites (the coefficients
we first report results obtained for completely dissociated ionogenic sites (the coefficients 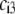 and Eq. 14 are thus pH and position independent) under the condition that
and Eq. 14 are thus pH and position independent) under the condition that 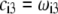 so that
so that 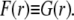
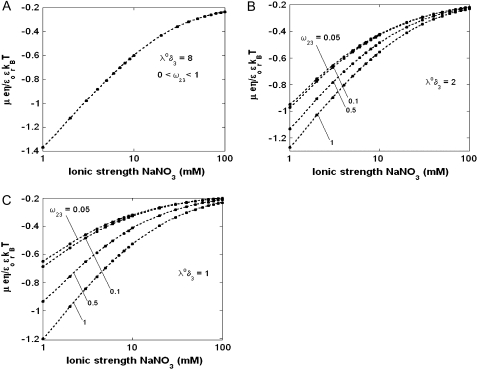
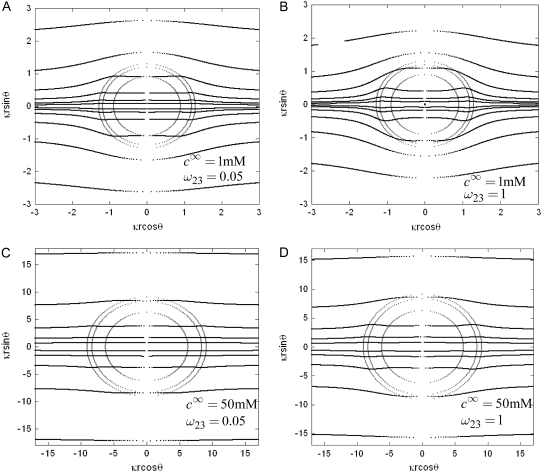
In Fig. 3, the dimensionless mobility 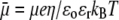 is examined as a function of NaNO3 electrolyte concentration (denoted as
is examined as a function of NaNO3 electrolyte concentration (denoted as 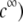 for various values of the ratio
for various values of the ratio 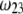 and thickness
and thickness 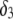 of the outer shell layer of the particle, the other parameters kept constant. In all cases analyzed, the decrease (in magnitude) of
of the outer shell layer of the particle, the other parameters kept constant. In all cases analyzed, the decrease (in magnitude) of 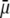 upon increasing
upon increasing 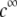 is according to expectation and has been discussed in previous communications (35). It is related to the screening of the fixed charges within the soft particle by the mobile ions. The mobility asymptotically tends for
is according to expectation and has been discussed in previous communications (35). It is related to the screening of the fixed charges within the soft particle by the mobile ions. The mobility asymptotically tends for 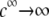 to a nonzero constant value, which is characteristic of the presence of permeable soft layer that carries a given volume charge density (27). For
to a nonzero constant value, which is characteristic of the presence of permeable soft layer that carries a given volume charge density (27). For 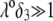 (Fig. 3 A), the flow penetration within the particle is too small for
(Fig. 3 A), the flow penetration within the particle is too small for 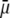 to depend on the details of the polymer segment density distribution within the inner layers 1 and 2. As a result,
to depend on the details of the polymer segment density distribution within the inner layers 1 and 2. As a result, 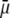 remains independent of
remains independent of 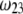 over the entire range of electrolyte concentrations considered. This limiting situation is actually that explicitly examined in Duval and Ohshima (35), the electrokinetic features of the particle as a whole being determined by the electrohydrodynamic properties of the outer layer only (classical core/shell particle). The situation changes drastically upon decrease of
over the entire range of electrolyte concentrations considered. This limiting situation is actually that explicitly examined in Duval and Ohshima (35), the electrokinetic features of the particle as a whole being determined by the electrohydrodynamic properties of the outer layer only (classical core/shell particle). The situation changes drastically upon decrease of 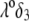 (panels B and C), i.e., when the Darcy number that pertains to layer 3,
(panels B and C), i.e., when the Darcy number that pertains to layer 3, 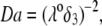 becomes of order 1. In those cases,
becomes of order 1. In those cases, 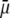 increases (in magnitude) with
increases (in magnitude) with 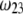 at fixed
at fixed 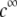 and this dependence of
and this dependence of 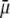 on
on 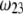 gradually vanishes when increasing
gradually vanishes when increasing 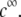 Let us comment on this. In the low electrolyte concentration regime where
Let us comment on this. In the low electrolyte concentration regime where 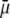 is significantly influenced by the presence of the inner layer 2, the double layer encompasses the whole particle and develops within the particle well beyond layer 3 (
is significantly influenced by the presence of the inner layer 2, the double layer encompasses the whole particle and develops within the particle well beyond layer 3 (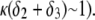 As a result, the electroosmotic flow i), probes the local potential distribution within layer 2, and ii), experiences the local friction forces exerted by the polymer segments distributed according to the profile
As a result, the electroosmotic flow i), probes the local potential distribution within layer 2, and ii), experiences the local friction forces exerted by the polymer segments distributed according to the profile 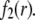 Features (i) and (ii) are both
Features (i) and (ii) are both 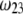 -dependent (see Eqs. 3, 8,and 11). Increasing
-dependent (see Eqs. 3, 8,and 11). Increasing 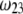 is expected to increase (in magnitude) the local potential within layer 2 and thereby increase
is expected to increase (in magnitude) the local potential within layer 2 and thereby increase 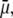 which is indeed observed (increase of the driving electrostatic force). On the other hand, increasing
which is indeed observed (increase of the driving electrostatic force). On the other hand, increasing 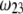 should lead to an increase of the drag force and thus a slowing down of the particle (decreasing
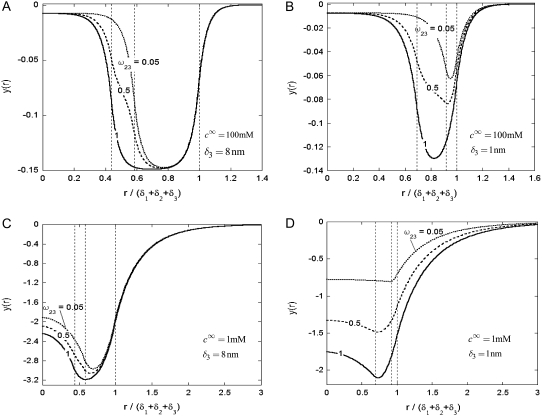
should lead to an increase of the drag force and thus a slowing down of the particle (decreasing 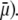 In Fig. 3, B and C, the electrostatic effect aforementioned overwhelms the hydrodynamic effect essentially because the flow field has significantly decreased in magnitude when passing from layer 3 to layer 2, whereas the potential distribution, on the contrary, increases (in magnitude) drastically in layer 2, especially at low ionic strengths. Those elements are illustrated in Fig. 4, where the potential distributions are reported under the conditions of Fig. 3. Also, in Fig. 5, A–D, we give the typical flow streamlines within and around the soft particle for
In Fig. 3, B and C, the electrostatic effect aforementioned overwhelms the hydrodynamic effect essentially because the flow field has significantly decreased in magnitude when passing from layer 3 to layer 2, whereas the potential distribution, on the contrary, increases (in magnitude) drastically in layer 2, especially at low ionic strengths. Those elements are illustrated in Fig. 4, where the potential distributions are reported under the conditions of Fig. 3. Also, in Fig. 5, A–D, we give the typical flow streamlines within and around the soft particle for 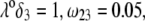 and
and 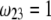 at two electrolyte concentrations
at two electrolyte concentrations 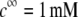 (panels A and B) and
(panels A and B) and 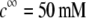 (panels C and D). From Fig. 5, A and B, it is clear that the deflection of the streamlines in the inner region of the particle becomes more important upon increase of the friction exerted by layer 2 on the flow, i.e., when increasing
(panels C and D). From Fig. 5, A and B, it is clear that the deflection of the streamlines in the inner region of the particle becomes more important upon increase of the friction exerted by layer 2 on the flow, i.e., when increasing 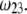 When increasing
When increasing 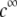 (Fig. 5, C and D), the parameter
(Fig. 5, C and D), the parameter 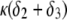 increases, the fixed charges within the particle are screened, the potential distribution therein decreases in magnitude, and the electroosmotic flow hardly depends on
increases, the fixed charges within the particle are screened, the potential distribution therein decreases in magnitude, and the electroosmotic flow hardly depends on 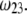 As a result, the electrophoretic mobility becomes determined to a lesser extent by the details of the polymer segment density profile within the inner layers of the soft particle. For sufficiently large
As a result, the electrophoretic mobility becomes determined to a lesser extent by the details of the polymer segment density profile within the inner layers of the soft particle. For sufficiently large 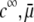 thus becomes independent on
thus becomes independent on 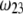 and reaches the plateau value given by reference (27),
and reaches the plateau value given by reference (27),
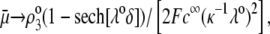 |
(47) |
(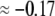 in the conditions of Fig. 3), with
in the conditions of Fig. 3), with 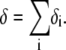 Equation 47 is in line with the prediction made in Duval and Ohshima (35) on the mobility plateau value reached at high ionic strengths for a diffuse interface between a core/(mono)shell particle and an electrolyte solution under the assumption that the charge density distribution matches that of the polymer segment density distribution.
Equation 47 is in line with the prediction made in Duval and Ohshima (35) on the mobility plateau value reached at high ionic strengths for a diffuse interface between a core/(mono)shell particle and an electrolyte solution under the assumption that the charge density distribution matches that of the polymer segment density distribution.
FIGURE 3.
Dimensionless electrophoretic mobility 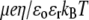 as a function of NaNO3 electrolyte concentration, ratio
as a function of NaNO3 electrolyte concentration, ratio 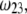 and dimensionless number
and dimensionless number 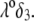 Equations 1–10, 12, 13, and 18–34 are used with
Equations 1–10, 12, 13, and 18–34 are used with 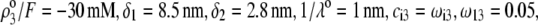 and
and 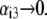
FIGURE 4.
Dimensionless equilibrium potential distribution within and around the soft particle depicted in Fig. 1 A at 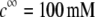 (panels A and B) and
(panels A and B) and 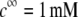 (panels C and D) for various values of
(panels C and D) for various values of 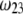 (indicated) and
(indicated) and 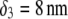 (panels A and C) and
(panels A and C) and 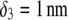 (panels B and D). Other model parameters as in Fig. 3. The dashed lines indicate the positioning of the interfaces between layers 1 and 2, 2 and 3, and between layer 3 and the electrolyte solution.
(panels B and D). Other model parameters as in Fig. 3. The dashed lines indicate the positioning of the interfaces between layers 1 and 2, 2 and 3, and between layer 3 and the electrolyte solution.
FIGURE 5.
Flow streamlines within and around the soft particle depicted in Fig. 1 for 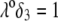 (
(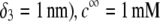 (panels A and B), 50 mM (panels C and D), and
(panels A and B), 50 mM (panels C and D), and 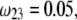 1 (indicated). Other model parameters as in Fig. 3. The flow streamlines are obtained from the numerical solution
1 (indicated). Other model parameters as in Fig. 3. The flow streamlines are obtained from the numerical solution 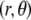 of the implicit equation
of the implicit equation 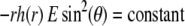 (24). The concentric layers represent the various components of the soft particle.
(24). The concentric layers represent the various components of the soft particle.
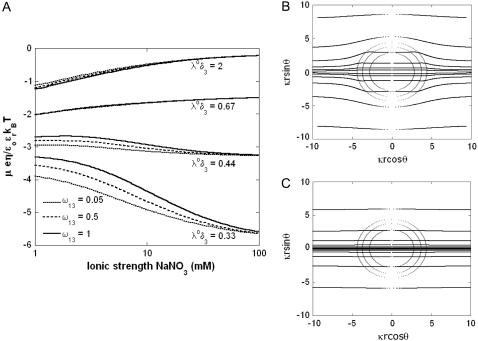
Fig. 6 illustrates the dependence of 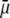 on
on  for various values of
for various values of 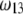 and
and 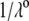 at fixed
at fixed 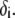 Consistent with the results shown previously,
Consistent with the results shown previously, 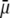 hardly depends on
hardly depends on 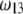 at large electrolyte concentrations and/or reduced flow permeation within the particle (large
at large electrolyte concentrations and/or reduced flow permeation within the particle (large 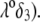 The values reached at
The values reached at 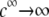 are all consistent with Eq. 47. Whereas
are all consistent with Eq. 47. Whereas 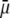 increases in magnitude with decreasing ionic strengths for
increases in magnitude with decreasing ionic strengths for 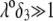 (see corresponding streamline distribution in panel B), Fig. 6 reveals that for sufficiently low
(see corresponding streamline distribution in panel B), Fig. 6 reveals that for sufficiently low 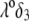 or equivalently large hydrodynamic permeability (panel C), the trend is reversed. This feature is due to the polarization of the electric double layer that becomes increasingly important upon decreasing
or equivalently large hydrodynamic permeability (panel C), the trend is reversed. This feature is due to the polarization of the electric double layer that becomes increasingly important upon decreasing 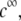 that is when increasing (in magnitude) the local potentials throughout the particle. Polarization of the double layer leads to a dissymmetry in the ionic cloud distribution within and around the particle and is accompanied by a polarization field that retards the particle motion (decreasing magnitude of
that is when increasing (in magnitude) the local potentials throughout the particle. Polarization of the double layer leads to a dissymmetry in the ionic cloud distribution within and around the particle and is accompanied by a polarization field that retards the particle motion (decreasing magnitude of 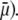 The lower
The lower 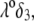 i.e., the more free-draining is the particle, the more the electroosmotic flow probes the variations of the large potentials in the inner part of the particle and the more significant is the polarization process evoked before. Along this line, the polarization of the electric double layer is enhanced when increasing
i.e., the more free-draining is the particle, the more the electroosmotic flow probes the variations of the large potentials in the inner part of the particle and the more significant is the polarization process evoked before. Along this line, the polarization of the electric double layer is enhanced when increasing 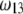 since it leads to increasing (in magnitude) the local potentials within layer 3.
since it leads to increasing (in magnitude) the local potentials within layer 3.
FIGURE 6.
(A) Dimensionless electrophoretic mobility 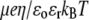 as a function of NaNO3 electrolyte concentration, ratio
as a function of NaNO3 electrolyte concentration, ratio 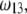 and dimensionless number
and dimensionless number 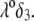 Equations 1–10, 12, 13, and 18–34 are used with
Equations 1–10, 12, 13, and 18–34 are used with 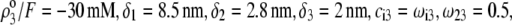 and
and 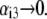 (B and C) Flow streamlines within and around the soft particle under the conditions of panel A for
(B and C) Flow streamlines within and around the soft particle under the conditions of panel A for 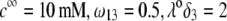 (B), and
(B), and 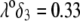 (C).
(C).
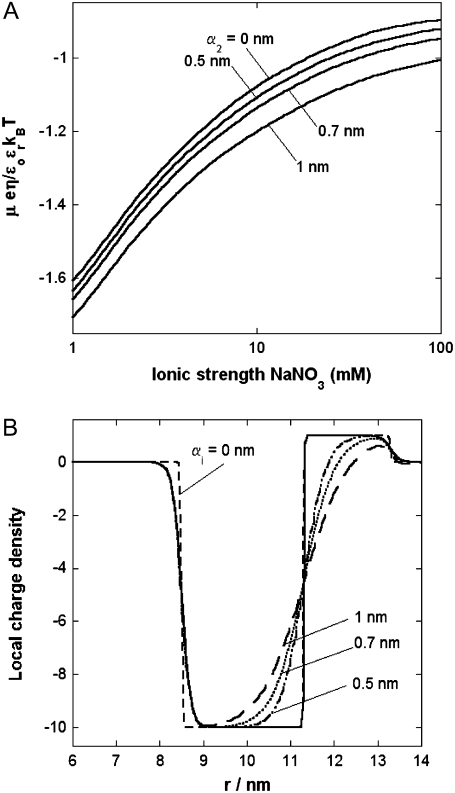
In Fig. 7, we briefly discuss the impact of the diffuseness of the interface between layers 2 and 3, that is the dependence of 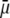 on
on 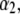 set to zero in all previous cases. In the set of results collected in Fig. 7, layer 1 is uncharged (
set to zero in all previous cases. In the set of results collected in Fig. 7, layer 1 is uncharged (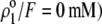 and layer 2 carries a pH-independent nominal charge density
and layer 2 carries a pH-independent nominal charge density 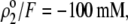 whereas
whereas 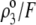 is positive (
is positive (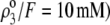 so that
so that 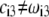 (see details in caption). The situation now tackled is thus that of a particle with soft layers that contain completely dissociated ionogenic sites of opposite signs (Eq. 13). The variation of
(see details in caption). The situation now tackled is thus that of a particle with soft layers that contain completely dissociated ionogenic sites of opposite signs (Eq. 13). The variation of 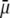 with
with 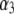 —which pertains to the spatial anisotropy of the polymer segment density distribution at the interface layer 3/electrolyte solution—has already been examined in detail in Duval and Ohshima (35) within the framework of the analysis of the electrokinetics of classical core/diffuse shell particles. Instead, we focus here on the effect of the variation of the inner soft material density distribution of the particle on its overall electrohydrodynamic features. From Fig. 7, the mobility increases in magnitude upon increase of
—which pertains to the spatial anisotropy of the polymer segment density distribution at the interface layer 3/electrolyte solution—has already been examined in detail in Duval and Ohshima (35) within the framework of the analysis of the electrokinetics of classical core/diffuse shell particles. Instead, we focus here on the effect of the variation of the inner soft material density distribution of the particle on its overall electrohydrodynamic features. From Fig. 7, the mobility increases in magnitude upon increase of 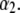 This trend is easily interpreted from the charge density profiles depicted in Fig. 7 B: increasing
This trend is easily interpreted from the charge density profiles depicted in Fig. 7 B: increasing 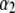 results in increasing
results in increasing 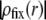 in layer 3 such that the local charge density therein eventually changes sign. In the meantime, the friction coefficient decreases significantly (Eq. 8) so that the resulting picture is an increase in magnitude of the electrophoretic mobility when increasing
in layer 3 such that the local charge density therein eventually changes sign. In the meantime, the friction coefficient decreases significantly (Eq. 8) so that the resulting picture is an increase in magnitude of the electrophoretic mobility when increasing 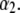 It is noted that those concomitant changes in the electrostatic and hydrodynamic features of layer 3—as a result of increasing diffuseness for the interface layer 2/layer 3—impact more significantly on the mobility
It is noted that those concomitant changes in the electrostatic and hydrodynamic features of layer 3—as a result of increasing diffuseness for the interface layer 2/layer 3—impact more significantly on the mobility 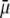 as compared to the electrohydrodynamic changes observed for layer 2. This is so because in the example of Fig. 7, we have in layer 2 an increase of
as compared to the electrohydrodynamic changes observed for layer 2. This is so because in the example of Fig. 7, we have in layer 2 an increase of 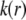 with
with 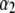 (Eq. 8), which accounts for the fact that the electroosmotic flow probes to a lesser extent the electrohydrodynamic details within layer 2. Similar situations arise when varying
(Eq. 8), which accounts for the fact that the electroosmotic flow probes to a lesser extent the electrohydrodynamic details within layer 2. Similar situations arise when varying 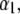 though with very limited impact on
though with very limited impact on 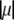 since spatial anisotropy (in charge and friction) now concerns the most internal region of the particle thus made less accessible by the hydrodynamic flow. As a final remark, we note that Eq. 47 is clearly inadequate for particles with different spatial distributions for
since spatial anisotropy (in charge and friction) now concerns the most internal region of the particle thus made less accessible by the hydrodynamic flow. As a final remark, we note that Eq. 47 is clearly inadequate for particles with different spatial distributions for 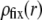 and
and 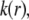 in line with the expectations laid out in Duval and Ohshima (35).
in line with the expectations laid out in Duval and Ohshima (35).
FIGURE 7.
(A) Dimensionless electrophoretic mobility 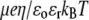 as a function of NaNO3 electrolyte concentration and parameter
as a function of NaNO3 electrolyte concentration and parameter 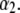 Equations 1–10, 12, 13, and 18–34 are used with
Equations 1–10, 12, 13, and 18–34 are used with 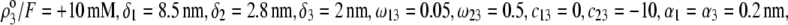 and
and 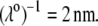 (B) Profiles of the local charge density
(B) Profiles of the local charge density 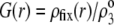 (Eq. 13) under the conditions of panel A.
(Eq. 13) under the conditions of panel A.
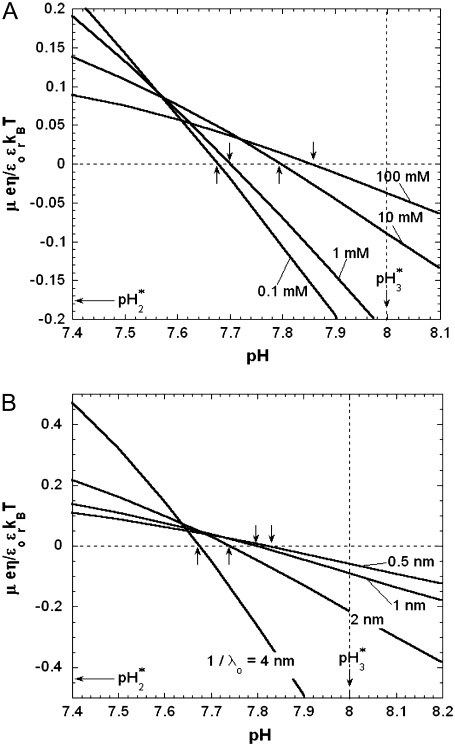
Physical meaning of the isoelectric point of a multilayer soft particle (the results are obtained from Eq. 46 if not explicitly specified)
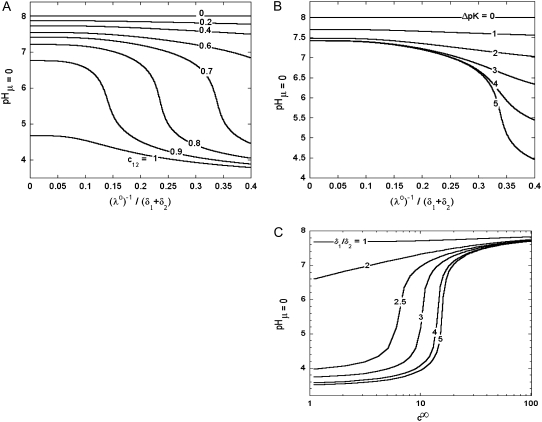
In Fig. 8, we report the variation of the iep of a chemically anisotropic, two-layer soft particle as a function of its hydrodynamic flow permeation properties, chemical composition, ratio 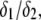 and electrolyte concentration. The results are derived from the semianalytical formalism detailed in the section “Isoelectric point … development” (Eq. 46). As a general comment, the situation is more complex than for a hard particle in the presence of indifferent electrolyte, the iep of the latter being simply the pH value where the surface potential, or the zeta potential, equates zero. This limiting situation corresponds to the case
and electrolyte concentration. The results are derived from the semianalytical formalism detailed in the section “Isoelectric point … development” (Eq. 46). As a general comment, the situation is more complex than for a hard particle in the presence of indifferent electrolyte, the iep of the latter being simply the pH value where the surface potential, or the zeta potential, equates zero. This limiting situation corresponds to the case 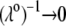 in panels A and B of Fig. 8. For such a hard particle in the absence of any specific ion adsorption, the iep does not depend on the ionic strength (93), which is obviously not the case for a multilayer soft particle with chemical heterogeneities and significant hydrodynamic permeability (panels A and B,
in panels A and B of Fig. 8. For such a hard particle in the absence of any specific ion adsorption, the iep does not depend on the ionic strength (93), which is obviously not the case for a multilayer soft particle with chemical heterogeneities and significant hydrodynamic permeability (panels A and B, 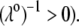 Let us discuss those distinguishing characteristics in some more detail. In the absence of charge for the layer 1 (
Let us discuss those distinguishing characteristics in some more detail. In the absence of charge for the layer 1 (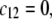 where
where 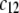 is the nominal charge density ratio for the two layers) or dissymmetry in chemical composition between layers 1 and 2, the expected results
is the nominal charge density ratio for the two layers) or dissymmetry in chemical composition between layers 1 and 2, the expected results 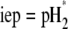 and
and 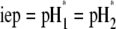 (93), respectively, are recovered by the model. In other cases, the iep decreases significantly upon increasing the hydrodynamic permeability and verifies the inequality
(93), respectively, are recovered by the model. In other cases, the iep decreases significantly upon increasing the hydrodynamic permeability and verifies the inequality 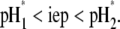 The electroosmotic flow then probes the inner layer of the particle, which is, in the situations examined, more acidic than layer 2
The electroosmotic flow then probes the inner layer of the particle, which is, in the situations examined, more acidic than layer 2 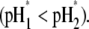 The larger
The larger  (Fig. 8 A) and/or
(Fig. 8 A) and/or 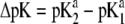 (Fig. 8 B), the lower is the iep for a given permeability. In panel C, the variation of the iep with the electrolyte concentration may be explained as follows. In the high ionic strength regime where
(Fig. 8 B), the lower is the iep for a given permeability. In panel C, the variation of the iep with the electrolyte concentration may be explained as follows. In the high ionic strength regime where 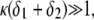 the local electrostatic potentials approach zero throughout the particle, and the asymptotic value of the electrophoretic mobility is determined by the electrohydrodynamic and chemical features of the most external parts of the particle, i.e., by the quantity
the local electrostatic potentials approach zero throughout the particle, and the asymptotic value of the electrophoretic mobility is determined by the electrohydrodynamic and chemical features of the most external parts of the particle, i.e., by the quantity 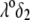 and the ratio
and the ratio 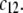 Upon decrease of the ionic strength, the electrophoretic mobility becomes more sensitive to the details of the inner particle (see Figs. 3 and 4), in particular to the ratio
Upon decrease of the ionic strength, the electrophoretic mobility becomes more sensitive to the details of the inner particle (see Figs. 3 and 4), in particular to the ratio 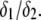 Increasing the latter at constant
Increasing the latter at constant 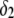 leads to diminishing the curvature effects on the potential distribution and thus to increasing the magnitude of the electrostatic potential in layer 1 (see analogies with Fig. 4, C and D). The double layer spans significantly over the region 1, which becomes more acidic with, as a result, a lowering of the iep of the particle at a given ionic strength. Of course, this feature is possible because the permeability set in the calculations is large enough for the electroosmotic flow to probe the subtle variations of the potential distribution within the particle as induced by changes in electrolyte concentrations.
leads to diminishing the curvature effects on the potential distribution and thus to increasing the magnitude of the electrostatic potential in layer 1 (see analogies with Fig. 4, C and D). The double layer spans significantly over the region 1, which becomes more acidic with, as a result, a lowering of the iep of the particle at a given ionic strength. Of course, this feature is possible because the permeability set in the calculations is large enough for the electroosmotic flow to probe the subtle variations of the potential distribution within the particle as induced by changes in electrolyte concentrations.
FIGURE 8.
Variation of the isoelectric point as a function of the flow penetration degree, for various values of the nominal charge density ratio 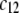 for layers 1 and 2 (panel A) and different values of
for layers 1 and 2 (panel A) and different values of 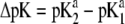 (panel B). Model parameters, panel A:
(panel B). Model parameters, panel A: 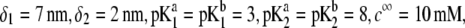 and
and 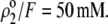 Model parameters, panel B: the same as in A with
Model parameters, panel B: the same as in A with 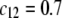 and variable
and variable 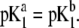 (C) Variation of the isoelectric point as a function of the electrolyte concentration and the ratio
(C) Variation of the isoelectric point as a function of the electrolyte concentration and the ratio 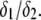 Model parameters, panel C: as in A with
Model parameters, panel C: as in A with 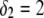 nm,
nm, 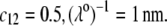 In all these calculations, Eqs. 35–46 are used (particle composed of two concentric soft layers, Eq. 46).
In all these calculations, Eqs. 35–46 are used (particle composed of two concentric soft layers, Eq. 46).
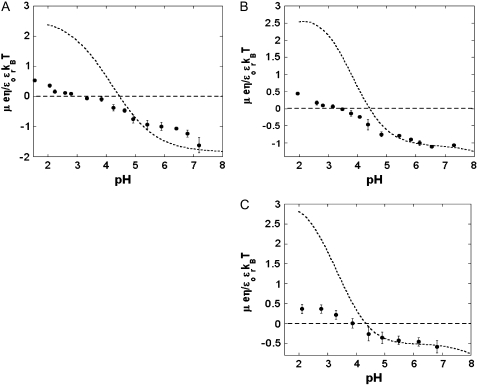
The basic trends discussed above on the impacts of ionic strength and flow permeability on the iep value for a two-layer particle structure (use of the semianalytical expression given by Eq. 46) are essentially the same as those computed for a three-layer soft particle by means of the numerical theory previously discussed (Eqs. 18–34). This is shown in Fig. 9 for a three-layer particle characterized by different chemical compositions for layers 2 and 3 (Eqs. 1–10, 12–14, and 18–37 with 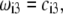 ionic exchange equilibria given by Eqs. 35–36 as detailed in the legend). Upon increase of the electrolyte concentration and/or flow penetration degree within the soft particle, the isoelectric point (indicated by arrows in Fig. 9) decreases because the electroosmotic flow extends significantly within layer 2, which is more acidic than layer 3.
ionic exchange equilibria given by Eqs. 35–36 as detailed in the legend). Upon increase of the electrolyte concentration and/or flow penetration degree within the soft particle, the isoelectric point (indicated by arrows in Fig. 9) decreases because the electroosmotic flow extends significantly within layer 2, which is more acidic than layer 3.
FIGURE 9.
(A) Dimensionless electrophoretic mobility 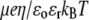 as a function of pH solution and ionic strength NaNO3 (indicated). Equations 1–10, 12–14, and 18–37 are used with
as a function of pH solution and ionic strength NaNO3 (indicated). Equations 1–10, 12–14, and 18–37 are used with 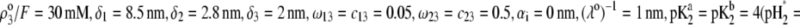 and
and 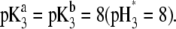 (B) Dimensionless electrophoretic mobility
(B) Dimensionless electrophoretic mobility 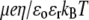 as a function of pH solution for various values of
as a function of pH solution for various values of 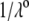 (indicated) at
(indicated) at 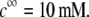 Other model parameters as in panel A. It is emphasized that the ionic exchange equilibria as given by Eqs. 35–36 are considered for the calculations set in this figure. The arrows indicate the location of the isoelectric point.
Other model parameters as in panel A. It is emphasized that the ionic exchange equilibria as given by Eqs. 35–36 are considered for the calculations set in this figure. The arrows indicate the location of the isoelectric point.
We devote the next section to the explicit analysis of the electrohydrodynamic features of MS2 bacteriophage on the basis of the numerical formalism detailed above.
APPLICATION TO THE BACTERIOPHAGE MS2
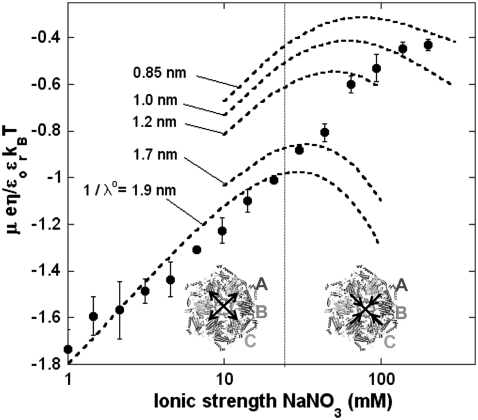
Impact of the ionic strength on the electrokinetic features of MS2 bacteriophage
We measured the electrophoretic mobility of MS2 bacteriophage as a function of ionic strength over a wide range of salt concentrations. As shown in Fig. 10, the magnitude of measured 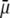 decreased monotonically with increasing electrolyte concentration at pH 7. At that pH and over the whole range of electrolyte concentrations examined, the mobility
decreased monotonically with increasing electrolyte concentration at pH 7. At that pH and over the whole range of electrolyte concentrations examined, the mobility 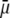 is negative, which deserves some comments. On the basis of the data collected in Tables 1 and 2, one easily shows that the overall (nominal) charge density carried by the layer i at pH 7 may legitimately be approximately by
is negative, which deserves some comments. On the basis of the data collected in Tables 1 and 2, one easily shows that the overall (nominal) charge density carried by the layer i at pH 7 may legitimately be approximately by 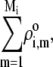 essentially because the conditions
essentially because the conditions 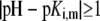 are valid for all sites present (Eqs. 14 and 15). This yields net nominal charge densities of +74 mM and −480 mM for the proteic capsid and for the RNA part, respectively. The inner RNA constituent of the virus impacts significantly on the MS2 electrophoretic mobility. This is confirmed by the modeling of the experimental data on the basis of Eqs. 1–10 and 12–34 with the spatial distributions of charge and soft material densities as discussed in preceding sections (Eqs. 4 and 12–17). Excellent agreement between theoretical and experimental data is achieved with
are valid for all sites present (Eqs. 14 and 15). This yields net nominal charge densities of +74 mM and −480 mM for the proteic capsid and for the RNA part, respectively. The inner RNA constituent of the virus impacts significantly on the MS2 electrophoretic mobility. This is confirmed by the modeling of the experimental data on the basis of Eqs. 1–10 and 12–34 with the spatial distributions of charge and soft material densities as discussed in preceding sections (Eqs. 4 and 12–17). Excellent agreement between theoretical and experimental data is achieved with  over the ionic strength range 1–20 mM. This value denotes an important flow penetration within the capsid shell of thickness 2.1 nm. Such a characteristic is, for a large part, due to the presence at the virus surface of cylindrical pores that perforate the entire outer shell of the virus (41,69,70,72) thus connecting the inner RNA part of the virus to the outer medium. Bacterial infection by the MS2 bacteriophage takes place with the injection of its RNA into the genomic material of the bacterium. The transport could occur via the channel structure of the aforementioned pores. In the high ionic strength regime, good agreement between experiment and theory is obtained upon decreasing
over the ionic strength range 1–20 mM. This value denotes an important flow penetration within the capsid shell of thickness 2.1 nm. Such a characteristic is, for a large part, due to the presence at the virus surface of cylindrical pores that perforate the entire outer shell of the virus (41,69,70,72) thus connecting the inner RNA part of the virus to the outer medium. Bacterial infection by the MS2 bacteriophage takes place with the injection of its RNA into the genomic material of the bacterium. The transport could occur via the channel structure of the aforementioned pores. In the high ionic strength regime, good agreement between experiment and theory is obtained upon decreasing  from 1.7 nm at 20 mM to ∼1 nm at 100 mM. As demonstrated in previous analysis dealing with the relationship between electrohydrodynamic features and structural organization of core/shell particles (26), the observed variation of the hydrodynamic permeability must necessarily be related to the modulation of the viral structure as induced by changing the electrolyte concentration.
from 1.7 nm at 20 mM to ∼1 nm at 100 mM. As demonstrated in previous analysis dealing with the relationship between electrohydrodynamic features and structural organization of core/shell particles (26), the observed variation of the hydrodynamic permeability must necessarily be related to the modulation of the viral structure as induced by changing the electrolyte concentration.
FIGURE 10.
Measured electrophoretic mobility 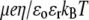 for bacteriophage MS2 as a function of NaNO3 electrolyte concentration at pH = 7 (solid circles) and theoretical predictions for various values of
for bacteriophage MS2 as a function of NaNO3 electrolyte concentration at pH = 7 (solid circles) and theoretical predictions for various values of 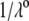 (dashed lines). See text for further detail. In inset, the morphological unit composed of three proteins A, B. and C with the arrows that indicate the modulations of the pore size as governed by the electrolyte concentration level. For the modeling, Eqs. 1–10 and 12–34 are used with the
(dashed lines). See text for further detail. In inset, the morphological unit composed of three proteins A, B. and C with the arrows that indicate the modulations of the pore size as governed by the electrolyte concentration level. For the modeling, Eqs. 1–10 and 12–34 are used with the 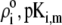 and
and 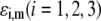 as reported in Tables 1 and 2.
as reported in Tables 1 and 2.
A first possible hypothesis is that the shrinking/swelling of the virus is a result of the decreased/increased intramolecular interactions among neighboring charged sites. Said differently, upon lowering the ionic strength, the increase in size (electrostatic swelling) is accompanied by an increase in the radius of the resistance centers (Eq. 3) and thus a decrease of the friction coefficient, or equivalently an increase of 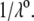 This mechanism is, however, not realistic for MS2 viruses because i), no significant size variations were measured upon lowering the ionic strength at pH 7 (94) and ii), important changes in
This mechanism is, however, not realistic for MS2 viruses because i), no significant size variations were measured upon lowering the ionic strength at pH 7 (94) and ii), important changes in 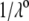 should be observed in the low ionic strength regime where the interfacial osmotic pressure is the most significant (26).
should be observed in the low ionic strength regime where the interfacial osmotic pressure is the most significant (26).
Those elements lead us to formulate another explanation for the electrokinetic features depicted in Fig. 10. Recall the spatial organization of the proteins that constitute the proteic capsid of the MS2 virus. It consists of 60 similar morphological units, each of which is composed of three capsid proteins (commonly denoted as A, B, and C in view of their different conformations) that form a triangle (base = 6 nm, height 2 nm) (70). The most significant difference among the three subunits A, B, and C in MS2 is found in a long loop, called the FG loop, that connects the F and G strands of the β-sheet. The FG loops of the A and C subunits are very similar and have an extended conformation, whereas that in the B subunit is folded back and has a closer contact with the rest of the protein (68). The result of this arrangement is the formation of a channel into the core of the particle with a diameter of ∼17 Å and a length of ∼14 Å; one of these channels may be a site of RNA extrusion during infection (68,95,96). Mutation and deletions in the FG loop have shown to reduce the efficiency of the capsid assembly (97,98). The propensity of those FG loops to adopt distinct conformations is due to a conserved Pro-78, which is preceded by a peptide that can easily switch between a trans and cis conformation (95). The pore size is basically modulated by the respective separation distances between those flexible loops.
One hypothesis is that at equilibrium, these separation distances are determined by the balance among the various interactions forces among the (charged) loops, e.g., electrostatic, van der Waals, hydrophobic, entropic, and elastic forces. At low ionic strengths, the electrostatic interactions are very important and it is expected that the loops significantly repel each other: the pore size is then large and so is 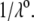 The fact that
The fact that 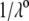 does not vary from 1 mM to 20 mM indicates that the flexible loops belonging to the proteins A, B, and C are stuck to the most rigid part of the protein, thus rendering impossible any further extension of the pore cavity. For sufficiently large ionic strengths, the situation can be reversed: the loops can approach each other and gradually obstruct the channel with the decrease of
does not vary from 1 mM to 20 mM indicates that the flexible loops belonging to the proteins A, B, and C are stuck to the most rigid part of the protein, thus rendering impossible any further extension of the pore cavity. For sufficiently large ionic strengths, the situation can be reversed: the loops can approach each other and gradually obstruct the channel with the decrease of 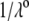 as a result.
as a result.
The theoretical computations of the electrophoretic mobility of MS2 bacteriophage as a function of electrolyte concentration exhibit a maximum that is more or less pronounced depending on the value of 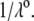 This may be explained as follows. For a given
This may be explained as follows. For a given 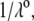 the decrease in magnitude of the mobility upon increase of the electrolyte concentrations up to 20 mM is the result of screening of the fixed charges carried by the ionogenic sites within and at the surface of the virus. Roughly speaking, at infinitely large ionic strengths and at fixed
the decrease in magnitude of the mobility upon increase of the electrolyte concentrations up to 20 mM is the result of screening of the fixed charges carried by the ionogenic sites within and at the surface of the virus. Roughly speaking, at infinitely large ionic strengths and at fixed 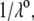 the mobility tends to a nonzero asymptotic value, which is the specific signature of flow permeation within charged soft particles (27,46). For MS2 particles, this value of the dimensionless mobility is ∼
the mobility tends to a nonzero asymptotic value, which is the specific signature of flow permeation within charged soft particles (27,46). For MS2 particles, this value of the dimensionless mobility is ∼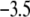 at
at 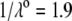 nm and is reached for electrolyte concentrations well above 100 mM because of the large contribution in charge brought about by the inner viral part (see Tables 1 and 2 and the discussion above on the net charges carried by the proteic capsid and the RNA part at pH 7). This charge makes the electrostatics still operative at ionic strengths around 100 mM. As a result of the electrokinetic behavior at low and infinite electrolyte concentrations, a maximum in theoretical mobility is observed at intermediate ionic strengths. The nonmonotonous variation of the electrophoretic mobility of soft particles with large charge density is discussed in more details in Duval and Ohshima (35) (see Supporting Information therein). The lower
nm and is reached for electrolyte concentrations well above 100 mM because of the large contribution in charge brought about by the inner viral part (see Tables 1 and 2 and the discussion above on the net charges carried by the proteic capsid and the RNA part at pH 7). This charge makes the electrostatics still operative at ionic strengths around 100 mM. As a result of the electrokinetic behavior at low and infinite electrolyte concentrations, a maximum in theoretical mobility is observed at intermediate ionic strengths. The nonmonotonous variation of the electrophoretic mobility of soft particles with large charge density is discussed in more details in Duval and Ohshima (35) (see Supporting Information therein). The lower 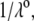 the lesser the contribution of the inner viral part to the mobility of the particle, the lesser the charge probed by the electroosmotic flow within the particle, and the lower the magnitude of
the lesser the contribution of the inner viral part to the mobility of the particle, the lesser the charge probed by the electroosmotic flow within the particle, and the lower the magnitude of 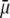 at
at 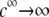 with a maximum that becomes less marked.
with a maximum that becomes less marked.
Impact of solution pH
The dependence of the electrophoretic mobility on pH is given in Fig. 11 for NaNO3 ionic strengths of 1, 10, and 100 mM. Unsurprisingly, the mobility becomes more negative when increasing pH because of the deprotonation of the various sites listed in Tables 1 and 2. The results reveal a slight decrease of the iep upon decrease of the electrolyte concentration (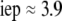 for
for 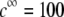 mM and
mM and 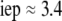 for
for 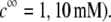 From the values of
From the values of 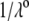 obtained in the analysis of
obtained in the analysis of  as a function of ionic strength, the theoretical variations of
as a function of ionic strength, the theoretical variations of 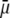 with pH were computed and are collected in Fig. 11. It is emphasized that no further adjustable parameters are required for these computations. Reasonable (1 mM) to excellent agreement (10 mM, 100 mM) is met for all three concentrations in the pH range
with pH were computed and are collected in Fig. 11. It is emphasized that no further adjustable parameters are required for these computations. Reasonable (1 mM) to excellent agreement (10 mM, 100 mM) is met for all three concentrations in the pH range 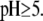 The theoretical values of the iep are somewhat larger than those determined experimentally but do not vary significantly with ionic strength
The theoretical values of the iep are somewhat larger than those determined experimentally but do not vary significantly with ionic strength 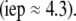 For pH < 5, the model systematically overestimates the electrophoretic mobility. To clarify this, we performed size measurements at various pH values and
For pH < 5, the model systematically overestimates the electrophoretic mobility. To clarify this, we performed size measurements at various pH values and 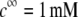 and
and  mM NaNO3 electrolyte concentrations (94). Those results clearly indicate the occurrence of a significant aggregation of viral particles at
mM NaNO3 electrolyte concentrations (94). Those results clearly indicate the occurrence of a significant aggregation of viral particles at 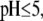 which is exactly in the pH range where the theoretical predictions—obtained for a strictly isolated and noninteracting virus—deviate from the experimental data. By “significant aggregation”, we mean the pH range below which the number of isolated viruses becomes less predominant as compared to the various aggregate populations appearing due to diminished electrostatic (repulsive) interactions at lower pH. The determination of the mobility for viral aggregates is an extremely complex matter because the structure of the aggregate intimately influences the hydrodynamic flow field profiles within and around the pool of aggregated particles as well as the electrostatic potential distribution therein. On the basis of the studies reported in Duval et al. (24), one may expect for an aggregate an increase of the overall hydrodynamic permeability as compared to that for an isolated virus. Such an increase in permeability would thus contribute in probing more efficiently the RNA distributed within the viral particles that constitute the aggregate, and doing so, lead to a decrease in the iep value, which is indeed observed (ieptheory > iepexperiment). However, aggregation may also result in strong denaturation of the capsid proteins at the outer surface of the viruses and therefore induce significant modulation (reduction) of the pore size. It is noted that for the set of pK values reported in Tables 1 and 2, the point of zero charge at infinite electrolyte concentration (
which is exactly in the pH range where the theoretical predictions—obtained for a strictly isolated and noninteracting virus—deviate from the experimental data. By “significant aggregation”, we mean the pH range below which the number of isolated viruses becomes less predominant as compared to the various aggregate populations appearing due to diminished electrostatic (repulsive) interactions at lower pH. The determination of the mobility for viral aggregates is an extremely complex matter because the structure of the aggregate intimately influences the hydrodynamic flow field profiles within and around the pool of aggregated particles as well as the electrostatic potential distribution therein. On the basis of the studies reported in Duval et al. (24), one may expect for an aggregate an increase of the overall hydrodynamic permeability as compared to that for an isolated virus. Such an increase in permeability would thus contribute in probing more efficiently the RNA distributed within the viral particles that constitute the aggregate, and doing so, lead to a decrease in the iep value, which is indeed observed (ieptheory > iepexperiment). However, aggregation may also result in strong denaturation of the capsid proteins at the outer surface of the viruses and therefore induce significant modulation (reduction) of the pore size. It is noted that for the set of pK values reported in Tables 1 and 2, the point of zero charge at infinite electrolyte concentration (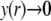 ) is for the RNA part and for the proteic capsid, if considered separately, 2.9 and about 9, respectively (values obtained from the solutions of the implicit equations
) is for the RNA part and for the proteic capsid, if considered separately, 2.9 and about 9, respectively (values obtained from the solutions of the implicit equations 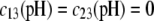 and
and 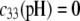 with the
with the 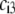 defined by Eq. 14). In the light of the discussion laid out in the section “Physical meaning of the isoelectric point of a multilayer soft particle”, the measured and theoretical values for the iep of the virus as a whole—which are closer to that of the RNA constituent than that of the proteic capsid—confirm that flow permeation within MS2 bacteriophage is so high that the electroosmotic flow significantly probes the inner RNA part. The fact that the iep of the isolated viruses does not depend much on ionic strength is basically due to the combination of
defined by Eq. 14). In the light of the discussion laid out in the section “Physical meaning of the isoelectric point of a multilayer soft particle”, the measured and theoretical values for the iep of the virus as a whole—which are closer to that of the RNA constituent than that of the proteic capsid—confirm that flow permeation within MS2 bacteriophage is so high that the electroosmotic flow significantly probes the inner RNA part. The fact that the iep of the isolated viruses does not depend much on ionic strength is basically due to the combination of 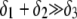 and large
and large 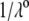 (see analogies with the trends in Fig. 8 C).
(see analogies with the trends in Fig. 8 C).
FIGURE 11.
Measured electrophoretic mobility 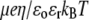 (solid circles) for bacteriophage MS2 as a function of pH for NaNO3 electrolyte concentration 1 mM (panel A), 10 mM (panel B), and 100 mM (panel C) and theoretical predictions (dashed lines) with the values of
(solid circles) for bacteriophage MS2 as a function of pH for NaNO3 electrolyte concentration 1 mM (panel A), 10 mM (panel B), and 100 mM (panel C) and theoretical predictions (dashed lines) with the values of 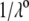 as derived from Fig. 10 (
as derived from Fig. 10 (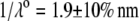 for
for 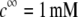 and
and  mM and
mM and 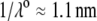 for
for 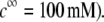 See text for further detail.
See text for further detail.
CONCLUSIONS
An original theoretical formalism is proposed for understanding on a quantitative level the electrokinetic properties of soft particles built up by concentric layers that differ in thickness, soft material density distribution, chemical composition, and flow penetration degree. The analysis is illustrated with numerical simulations of the electrophoretic mobility under various conditions. Those clearly show the complex interplay between the coupled electrostatic and hydrodynamic properties of the whole particle as governed by the physicochemical characteristics of its constituting layers. In particular, it is unambiguously demonstrated that the concept of zeta potential is inappropriate for such type of particles whose electromigration in an external field is influenced by the structural and chemical details of the inner layers. Also, the notion of isoelectric point is revisited and we prove that it is generally a function of the ionic strength, flow permeation degree, and extent of dissymmetry in the chemical compositions of the various soft layers.
On the basis of this formalism, strictly valid for sufficiently diluted suspensions of multi layer soft particles (absence of interparticular interactions), we interpret the dependence of measured electrophoretic mobility on pH and ionic strength for bacteriophage MS2 composed of inner RNA encapsulated by an outer proteic shell. The results indicate a strong flow permeation within the virus with a large impact of the RNA constituents of MS2 on its overall electrohydrodynamic properties. At pH 7, where viruses are isolated, two ionic strength regimes may be distinguished: a low electrolyte concentration range where the typical flow penetration length within MS2 remains constant, and a large ionic strength range where the viral permeability gradually decays. Those trends are qualitatively in line with the dynamics of pore size as conditioned by the intermolecular repulsion among flexible loops of proteins within the shell capsid. The theoretical predictions are further in excellent agreement with size measurements of MS2 viruses that picture the occurrence of aggregation at sufficiently low pH values 
From the conclusions laid out in this study, one may expect the propensity of infecting bacteria by MS2 viruses to be a strong function of the physicochemical conditions of their close environment (pH and ionic strength). For this reason, understanding the biological activity of viruses as well as their interactions with other mineral or organic components—as occurring in filtration processes and transport through groundwater—necessarily require reasoning beyond the too simplistic concept of zeta or surface potential (as involved in the Helmholtz-Smoluchowski equation). This concept is strictly valid for homogeneous and impermeable (hard) particles. Scrupulous analysis of the electrohydrodynamic properties of the (soft) virus is instead the first mandatory prerequisite to achieve such degree of understanding.
APPENDIX
Details of the derivation of the semianalytical expression for the isoelectric point of a soft particle composed of two concentric step-like soft layers (Eq. 46)
After arrangements, the linearized form of the Poisson-Boltzmann equation (Eqs. 27–28) is written for a soft particle that satisfies the condition 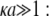
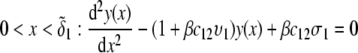 |
(A1) |
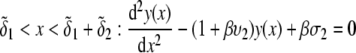 |
(A2) |
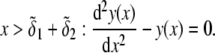 |
(A3) |
The boundaries associated to Eqs. A1–A3 express the zero charge at the surface of the particle core 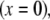 the zero potential as a reference at
the zero potential as a reference at 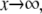 and the continuity of the electrostatic potential and electric field at
and the continuity of the electrostatic potential and electric field at 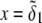 and
and 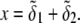 After calculations, the solution is given by
After calculations, the solution is given by
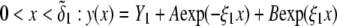 |
(A4) |
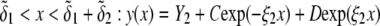 |
(A5) |
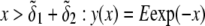 |
(A6) |
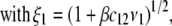 |
(A7) |
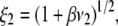 |
(A8) |
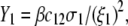 |
(A9) |
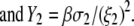 |
(A10) |
The constants A, B, C, D, and E are determined from the boundaries and are yielded by the algebraic equations
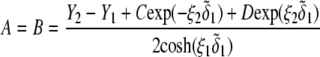 |
(A11) |
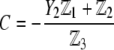 |
(A12) |
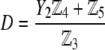 |
(A13) |
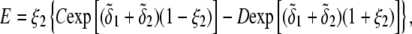 |
(A14) |
where  are defined by the expressions
are defined by the expressions
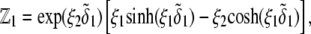 |
(A15) |
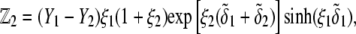 |
(A16) |
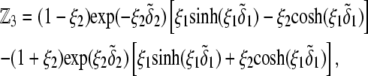 |
(A17) |
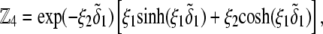 |
(A18) |
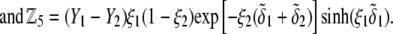 |
(A19) |
Substituting in Eq. 45 the expressions for the potential distribution derived above and computing the integral leads to the result given in Eq. 46 in the main text.
Editor: David P. Millar.
References
- 1.Stone, H. A., and S. Kim. 2001. Microfluidics: basic issues, applications, and challenges. AIChE J. 47:1250–1254. [Google Scholar]
- 2.Beebe, D. J., G. A. Mensing, and G. M. Walker. 2002. Physics and applications of microfluidics in biology. Annu. Rev. Biomed. Eng. 4:261–286. [DOI] [PubMed] [Google Scholar]
- 3.Cox, C. D., M. A. Shoesmith, and M. M. Ghosh. 1996. Electrokinetic remediation of mercury contaminated soils using iodine/iodide lixiviant. Environ. Sci. Technol. 30:1933–1938. [Google Scholar]
- 4.Sharma, M. M., and Y. C. Yortsos. 1987. Transport of particulate suspensions in porous media: model formulation. AIChE J. 33:1636–1643. [Google Scholar]
- 5.De Beer, E., J. F. L. Duval, and E. Meulenkamp. 2000. Electrophoretic deposition: a quantitative model for particle deposition and binder formation from alcohol-based suspensions. J. Colloid Interface Sci. 222:117–124. [DOI] [PubMed] [Google Scholar]
- 6.Lyklema, J. 2001. Surface conduction. J. Phys. Condens. Matter. 13:5027–5034. [Google Scholar]
- 7.Overbeek, J. Th. G. 1943. Theorie der elektrophorese. Kolloid-Beih. 54:287–364. [Google Scholar]
- 8.Booth, F. 1950. The cataphoresis of spherical, solid non-conducting particles in a symmetrical electrolyte. Proc. Roy. Soc. Lond. 203:533–551. [Google Scholar]
- 9.Wiersema, P. H., A. L. Loeb, and J. Th. G. Overbeek. 1966. Calculation of the electrophoretic mobility of a spherical colloid particle. J. Colloid Interface Sci. 22:78–99. [Google Scholar]
- 10.Dukhin, S. S., and N. M. Seminikhin. 1970. Theory of double layer polarization and its effect on the electrokinetic and electrooptical phenomena and the dielectric permeability of dispersed systems. Kholloid Zh. 32:360–368. [Google Scholar]
- 11.O'Brien, R. W., and L. R. White. 1978. Electrophoretic mobility of a spherical colloidal particle. J. Chem. Soc. Faraday Trans. II. 74:1607–1626. [Google Scholar]
- 12.DeLacey, E. H. B., and L. R. White. 1981. Dielectric response and conductivity of dilute suspensions of colloidal particles. J. Chem. Soc. Faraday Trans. II. 77:2007–2039. [Google Scholar]
- 13.O'Brien, R. W., and R. J. Hunter. 1981. The electrophoretic mobility of large colloidal particles. Can. J. Chem. 59:1878–1887. [Google Scholar]
- 14.Dukhin, S. S. 1993. Non-equilibrium electric surface phenomena. Adv. Colloid Interface Sci. 44:1–134. [Google Scholar]
- 15.Lyklema, J. 1995. Electrokinetics and related phenomena. In Fundamentals of Interface and Colloid Science: Solid-Liquid Interfaces, Vol. 2. Academic Press, London. Chapter 4.
- 16.Lyklema, J., S. Rovillard, and J. L. De Conninck. 1998. Electrokinetics: The properties of the stagnant layer unraveled. Langmuir. 14:5659–5663. [Google Scholar]
- 17.Van der Wal, A. 1996. Electrochemical characterization of the bacterial cell surface. PhD thesis. Wageningen Universiteit, Wageningen, The Netherlands.
- 18.Poortinga, A. T. 2001. Electric double layer interactions in bacterial adhesion and detachment. PhD thesis. Rijksuniversiteit Groningen, Groningen, The Netherlands.
- 19.Bos, R., H. C. van der Mei, and H. J. Busscher. 1998. ‘Soft-particle’ analysis of the electrophoretic mobility of a fibrillated and non-fibrillated oral streptococcal strain: Streptococcus salivarius. Biophys. Chem. 74:251–255. [DOI] [PubMed] [Google Scholar]
- 20.de Kerchove, A. J., and M. Elimelech. 2005. Relevance of electrokinetic theory for “soft” particles to bacterial cells: Implications for bacterial adhesion. Langmuir. 21:6462–6472. [DOI] [PubMed] [Google Scholar]
- 21.Duval, J. F. L., H. J. Busscher, B. van de Belt-Gritter, H. C. van der Mei, and W. Norde. 2005. Analysis of the interfacial properties of fibrillated and non-fibrillated oral streptococcal strain from electrophoretic mobility and titration measurements: evidence for the shortcomings of the “classical soft particle approach”. Langmuir. 21:11268–11282. [DOI] [PubMed] [Google Scholar]
- 22.Gaboriaud, F., E. Dague, S. Bailet, F. Jorand, J. F. L. Duval, and F. Thomas. 2006. Multi-scale dynamics of the cell envelope of Shewanella putrefaciens as a response to pH change. Colloids Surf. B Biointerfaces. 52:108–116. [DOI] [PubMed] [Google Scholar]
- 23.Dague, E., J. F. L. Duval, F. Jorand, F. Thomas, and F. Gaboriaud. 2006. Probing surface structures of Shewanella spp. by microelectrophoresis. Biophys. J. 90:2612–2621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Duval, J. F. L., K. J. Wilkinson, H. P. van Leeuwen, and J. Buffle. 2005. Humic substances are soft and permeable: evidence from their electrophoretic mobilities. Environ. Sci. Technol. 39:6435–6445. [DOI] [PubMed] [Google Scholar]
- 25.Duval, J. F. L., V. I. Slaveykova, M. Hosse, J. Buffle, and K. J. Wilkinson. 2006. Electrohydrodynamic properties of Succinoglycan as probed by fluorescence correlation spectroscopy, potentiometric titration and capillary electrophoresis. Biomacromolecules. 7:2818–2826. [DOI] [PubMed] [Google Scholar]
- 26.Rotureau, E., F. Thomas, and J. F. L. Duval. 2007. Relationship between swelling and electrohydrodynamic properties of functionalized carboxymethyldextran macromolecules. Langmuir. 23:8460–8473. [DOI] [PubMed] [Google Scholar]
- 27.Ohshima, H. 1995. Electrophoresis of soft particles. Adv. Colloid Interface Sci. 62:189–235. [DOI] [PubMed] [Google Scholar]
- 28.Saville, D. A. 2000. Electrokinetic properties of fuzzy colloidal particles. J. Colloid Interface Sci. 222:137–145. [DOI] [PubMed] [Google Scholar]
- 29.Ohshima, H. 1994. Electrophoretic mobility of soft particles. J. Colloid Interface Sci. 163:474–483. [DOI] [PubMed] [Google Scholar]
- 30.Hill, R. J., and D. A. Saville. 2005. ‘Exact solutions of the full electrokinetic model for soft spherical colloids: electrophoretic mobility. Colloids Surf. A. Physicochem. Eng. Aspects. 267:31–49. [Google Scholar]
- 31.Hill, R. J., D. A. Saville, and W. B. Russel. 2003. Electrophoresis of spherical polymer-coated particles. J. Colloid Interface Sci. 258:56–74. [Google Scholar]
- 32.Lopez-Garcia, J. J., C. Grosse, and J. J. Horno. 2003. Numerical study of colloidal suspensions of soft spherical particles using the network method: 1. DC electrophoretic mobility. J. Colloid Interface Sci. 265:327–340. [DOI] [PubMed] [Google Scholar]
- 33.Lopez-Garcia, J. J., C. Grosse, and J. J. Horno. 2003. Numerical study of colloidal suspensions of soft spherical particles using the network method: 2. AC electrokinetic and dielectric properties. J. Colloid Interface Sci. 265:341–350. [DOI] [PubMed] [Google Scholar]
- 34.Hill, R. J. 2004. Hydrodynamics and electrokinetics of spherical liposomes with coatings of terminally anchored poly(ethylene glycol): numerically exact electrokinetics with self-consistent mean-field polymer. Phys. Rev. E. 70:051406. [DOI] [PubMed] [Google Scholar]
- 35.Duval, J. F. L., and H. Ohshima. 2006. Electrophoresis of diffuse soft particles. Langmuir. 22:3533–3546. [DOI] [PubMed] [Google Scholar]
- 36.Mason, T. G., and M. Y. Lin. 2005. Density profiles of temperature sensitive microgel particles. Phys. Rev. E. 71:040801. [DOI] [PubMed] [Google Scholar]
- 37.Fernandez-Nievez, A., F. J. de las Nieves, and A. Fernandez-Barbero. 2004. Static light scattering from microgel particles: model of variable dielectric permittivity. J. Chem. Phys. 120:374–378. [DOI] [PubMed] [Google Scholar]
- 38.Gao, C., S. Leporatti, S. Moya, E. Donath, and H. Mohwald. 2003. Swelling and shrinking of polyelectrolyte microcapsules in response to changes in temperature and ionic strength. Chem. Eur. J. 9:915–920. [DOI] [PubMed] [Google Scholar]
- 39.Garcia-Salinas, M. J., M. S. Romero-Cano, and F. J. de Las Nieves. 2001. Electrokinetic characterization of poly(N-isopropylacrylamide) microgel particles: effect of electrolyte concentration and temperature. J. Colloid Interface Sci. 241:280–285. [DOI] [PubMed] [Google Scholar]
- 40.Kuzmanovic, D. A., I. Elashvili, C. Wick, C. O'Connell, and S. Krueger. 2006. Quantification of RNA in bacteriophage MS2-like viruses in solution by small-angle X-ray scattering. Radiat. Phys. Chem. 75:359–368. [Google Scholar]
- 41.Koning, R., S. van den Worm, J. R. Plaisier, J. van Duin, J. P. Abrahams, and H. Koerten. 2003. Visualization by cryo-electron microscopy of genomic RNA that binds to the protein capsid inside bacteriophage MS2. J. Mol. Biol. 332:415–422. [DOI] [PubMed] [Google Scholar]
- 42.Van den Worm, S. H. E., R. I. Koning, H. J. Warmenhoven, H. K. Koerten, and J. van Duin. 2006. Cryo electron microscopy reconstructions of the Leviviridae unveil the densest icosahedral RNA packing possible. J. Mol. Biol. 363:858–865. [DOI] [PubMed] [Google Scholar]
- 43.Schaldach, C. M., W. L. Bourcier, H. F. Shaw, B. E. Viani, and W. D. Wilson. 2006. The influence of ionic strength on the interaction of viruses with charged surfaces under environmental conditions. J. Colloid Interface Sci. 294:1–10. [DOI] [PubMed] [Google Scholar]
- 44.Valegard, K., J. Murrary, N. J. Stonehouse, S. van den Worm, P. G. Stockely, and L. Liljas. 1997. Three-dimensional structures of two complexes between recombinant MS2 capsids and RNA operator fragments reveal sequence-specific protein–RNA interactions. J. Mol. Biol. 270:724–738. [DOI] [PubMed] [Google Scholar]
- 45.Duval, J. F. L. 2007. Electrophoresis of soft colloids: basic principles and applications, Chapter 7. In Environmental Colloids and Particles: Behaviour, Separation and Characterization. K .J. Wilkinson and J. Lead, editors. Vol. 10 IUPAC Series on Analytical and Physical Chemistry of Environmental Systems. J. Buffle and H. P. van Leeuwen, Senior Editors. John Wiley & Sons, Chichester, England.
- 46.Dukhin, S. S., R. Zimmermann, and C. Werner. 2006. Electrokinetic fingerprinting of grafted polyelectrolyte layers—a theoretical approach. Adv. Colloid Interface Sci. 122:93–105. [DOI] [PubMed] [Google Scholar]
- 47.Berger, P. 1994. In Ground Water Contamination and Control. U. Zoller, editor. Dekker, New York.
- 48.Redman, J. A., S. B. Grant, T. M. Olson, and M. K. Estes. 2001. Pathogen filtration, heterogeneity, and the potable reuse of wastewater. Environ. Sci. Technol. 35:1798–1805. [DOI] [PubMed] [Google Scholar]
- 49.Yoshino, K., and T. Morishima. 1971. Filtration of viruses through Millipore membranes coated with polyvinylpyrrolidone. Arch. Virol. 35:399–401. [Google Scholar]
- 50.Yahya, M. T., L. Galsomies, C. P. Gerba, and R. C. Bales. 1993. Survival of bacteriophages MS-2 and PRD-1 in ground water. Water Sci. Technol. 27:409–412. [Google Scholar]
- 51.Schulze-Makuch, D., H. Guan, and S. D. Pillai. 2003. Effects of pH and geological medium on bacteriophage MS2 transport in a model aquifer. Geomicrobiol. J. 20:73–84. [Google Scholar]
- 52.Guan, H., D. Schulze-Makuch, S. Schaffer, and S. D. Pillai. 2003. The effect of critical pH on virus fate and transport in saturated porous medium. Ground Water. 41:701–708. [DOI] [PubMed] [Google Scholar]
- 53.Farrah, S. R. 1982. Chemical factors influencing adsorption of bacteriophage MS2 to membrane filters. Appl. Environ. Microbiol. 43:659–663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Hu, J. Y., S. L. Ong, L. F. Song, Y. Y. Feng, W. T. Liu, T. W. Tan, L. Y. Lee, and W. J. Ng. 2003. Removal of MS2 bacteriophage using membrane technologies. Water Sci. Technol. 47:163–168. [PubMed] [Google Scholar]
- 55.Jacangelo, J. G., R. Rhodes Trussell, and M. Watson. 1997. Role of membrane technology in drinking water treatment in the United States. Desalination. 113:119–127. [Google Scholar]
- 56.You, Y., G. F. Vance, D. L. Sparks, J. Zhuang, and Y. Jin. 2003. Sorption of MS2 bacteriophage to layered double hydroxides: effects of reaction time, pH, and competing anions. J. Environ. Qual. 32:2046–2053. [DOI] [PubMed] [Google Scholar]
- 57.Chattopadhyay, S., and R. W. Puls. 1999. Adsorption of bacteriophages on clay minerals. Environ. Sci. Technol. 33:3609–3614. [Google Scholar]
- 58.Dowd, S. E., S. D. Pillai, S. Wnag, and M. Y. Corapcioglu. 1998. Delineating the specific influence of virus isoelectric point and size on virus adsorption and transport through sandy soils. Appl. Environ. Microbiol. 64:405–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Dizer, H., A. Nasser, and J. M. Lopez. 1984. Penetration of different human pathogenic viruses into sand columns percolated with distilled water, groundwater, or wastewater. Appl. Environ. Microbiol. 47:409–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Lytle, C. D., and L. B. Routson. 1995. Minimized virus binding for tests of barrier materials. Appl. Environ. Microbiol. 61:643–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Meschke, J. S., and M. D. Sobsey. 1998. Comparative adsorption of Norwalk virus, poliovirus 1 and F+ RNA coliphage MS2 to soils suspended in treated wastewater. Water Sci. Technol. 38:187–189. [PubMed] [Google Scholar]
- 62.Shields, P. A., and S. R. Farrah. 2002. Characterization of virus adsorption by using DEAE-sepharose and octyl-sepharosedagger. Appl. Environ. Microbiol. 68:3965–3968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Herath, G., K. Yamamoto, and T. Urase. 1999. Removal of viruses by microfiltration membranes at different solution environments. Water Sci. Technol. 40:331–338. [Google Scholar]
- 64.Langlet, J., F. Gaboriaud, and C. Gantzer. 2007. Effects of pH on plaque forming unit counts and aggregation of MS2 bacteriophage. J. Appl. Microbiol. n press. [DOI] [PubMed]
- 65.Debye, P., and A. J. Bueche. 1948. Intrinsic viscosity, diffusion and sedimentation rate of polymers in solution. J. Chem. Phys. 16:573–579. [Google Scholar]
- 66.Brinkman, H. C. 1949. Problems of fluid through swarms of particles and through macromolecules in solution. Research. 2:190–194. [PubMed] [Google Scholar]
- 67.Sangani, S. A., and C. Yao. 1988. Transport processes in random arrays of cylinders. II. Viscous flow. Phys. Fluids. 31:2435–2444. [Google Scholar]
- 68.Valegård, K., L. Liljas, K. Fridborg, and T. Unge. 1991. Structure determination of the bacteriophage MS2. Acta Crystallogr. B. 47:949–960. [DOI] [PubMed] [Google Scholar]
- 69.Golmohammadi, R., K. Valegård, K. Fridborg, and L. Liljas. 1993. The refined structure of bacteriophage MS2 at 2.8 A resolution. J. Mol. Biol. 234:620–639. [DOI] [PubMed] [Google Scholar]
- 70.Valegård, K., L. Liljas, K. Fridborg, and T. Unge. 1990. The three-dimensional structure of the bacterial virus MS2. Nature. 345:36–41. [DOI] [PubMed] [Google Scholar]
- 71.Kuzmanovic, D. A., I. Elashvili, C. Wick, C. O'Connell, and S. Krueger. 2003. Bacteriophage MS2: molecular weight and spatial distribution of the protein and RNA components by small-angle neutron scattering and virus counting. Structure. 11:1339–1348. [DOI] [PubMed] [Google Scholar]
- 72.Valegård, K., L. Liljas, K. Fridborg, and T. Unge. 1991. Structure determination of the bacteriophage MS2. Acta Crystallogr. Sect. B-Struct. Sci. 47:949–960. [DOI] [PubMed] [Google Scholar]
- 73.Li, H., A. D. Robertson, and J. H. Jensen. 2005. Very fast empirical prediction and rationalization of protein pKa values. Proteins. 61:704–721. [DOI] [PubMed]
- 74.Kyte, J., and R. Doolittle. 1982. A simple method for displaying the hydropathic character of a protein. J. Mol. Biol. 157:105–132. [DOI] [PubMed] [Google Scholar]
- 75.Acharya, P., P. Cheruku, S. Chatterjee, S. Acharya, and J. Chattopadhyaya. 2004. Measurement of nucleobase pKa values in model mononucleotides shows RNA-RNA duplexes to be more stable than DNA-DNA duplexes. J. Am. Chem. Soc. 126:2862–2869. [DOI] [PubMed] [Google Scholar]
- 76.Gerba, C. P. 1984. Applied and theoretical aspects of virus adsorption to surfaces. Adv. Appl. Microbiol. 30:133–168. [DOI] [PubMed] [Google Scholar]
- 77.Jin, Y., and M. Flury. 2002. Fate and transport of viruses in porous media. Adv. Agron. 77:39–102. [Google Scholar]
- 78.Sobsey, M. D., and B. L. Jones. 1979. Concentration of poliovirus from tap water using positively charged microporous filters. Appl. Environ. Microbiol. 37:588–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Logan, K. B., G. E. Rees, N. D. Seeley, and S. B. Primrose. 1980. Rapid concentration of bacteriophages from large volumes of freshwater: evaluation of positively charged, microporous filters. J. Virol. Methods. 1:87–97. [DOI] [PubMed] [Google Scholar]
- 80.Sobsey, M. D., and J. S. Glass. 1980. Poliovirus concentration from tap water with electropositive adsorbent filters. Appl. Environ. Microbiol. 40:201–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Chang, L. T., S. R. Farrah, and G. Bitton. 1981. Positively charged filters for virus recovery from wastewater treatment plant effluents. Appl. Environ. Microbiol. 42:921–924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Raphael, R. A., S. A. Sattar, and V. S. Springthorpe. 1985. Rotavirus concentration from raw water using positively charged filters. J. Virol. Methods. 11:131–140. [DOI] [PubMed] [Google Scholar]
- 83.Shields, P. A., T. F. Ling, V. Tjatha, D. O. Shah, and S. R. Farrah. 1986. Comparison of positively charged membrane filters and their use in concentrating bacteriophages in water. Water Res. 20:145–151. [Google Scholar]
- 84.Lukasik, J., T. M. Scott, D. Andryshak, and S. R. Farrah. 2000. Influence of salts on virus adsorption to microporous filters. Appl. Environ. Microbiol. 66:2914–2920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Farrah, S. R., C. P. Gerba, C. Wallis, and J. L. Melnick. 1976. Concentration of viruses from large volumes of tap water using pleated membrane filters. Appl. Environ. Microbiol. 31:221–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Sobsey, M. D., C. Wallis, M. Henderson, and J. L. Melnick. 1973. Concentration of enteroviruses from large volumes of water. Appl. Microbiol. 26:529–534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Gerba, C. P., S. R. Farrah, S. M. Goyal, C. Wallis, and J. L. Melnick. 1978. Concentration of enteroviruses from large volumes of tap water, treated sewage, and seawater. Appl. Environ. Microbiol. 35:540–548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Morris, R., and W. M. Waite. 1980. Evaluation of procedures for recovery of viruses from water. I. Concentration systems. Water Res. 14:791–793. [Google Scholar]
- 89.Sobsey, M. D., S. E. Oglesbee, and D. A. Wait. 1985. Evaluation of methods for concentrating hepatitis A virus from drinking water. Appl. Environ. Microbiol. 50:1457–1463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Payment, P., A. Berube, D. Perreault, R. Armon, and M. Trudel. 1989. Concentration of Giardia lamblia cysts, Legionella pneumophila, Clostridium perfringens, human enteric viruses, and coliphages from large volumes of drinking water, using a single filtration. Can. J. Microbiol. 35:932–935. [DOI] [PubMed] [Google Scholar]
- 91.Gassilloud, B., and C. Gantzer. 2005. Adhesion-aggregation and inactivation of poliovirus 1 in groundwater stored in a hydrophobic container. Appl. Environ. Microbiol. 71:912–920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Lyklema, J., and J. F. L. Duval. 2005. Heterointeraction between Gouy-Stern double layers. Charge and potential regulation. Adv. Colloid Interface Sci. 114-115:27–45. [DOI] [PubMed] [Google Scholar]
- 93.Lyklema, J. 1995. Electric double layers. In Fundamentals of Interface and Colloid Science: solid-liquid interfaces, Vol. 2. Academic Press, London. Chapter 3.
- 94.Langlet, J., F. Gaboriaud, J. F. L. Duval, and C. Gantzer. 2008. Electrophoresis and aggregation of F-specific bacteriophages: dependence on pH and ionic strength conditions. Water Res. In press.
- 95.Stonehouse, N. J., K. Valegård, R. Golmohammadi, S. van den Worm, C. Walton, P. G. Stockley, and L. Liljas. 1996. Crystal structures of MS2 capsids with mutations in the subunit FG loop. J. Mol. Biol. 256:330–339. [DOI] [PubMed] [Google Scholar]
- 96.Reference deleted in proof.
- 97.Peabody, D. S., and K. R. Ely. 1992. Control of translational repression by protein-protein interactions. Nucleic Acids Res. 20:1649–1655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Stockley, P. G., N. J. Stonehouse, and K. Valegård. 1994. Molecular mechanism of RNA phage morphogenesis. Int. J. Biochem. 26:1249–1260. [DOI] [PubMed] [Google Scholar]