Abstract
Molecular dynamics simulations and 31P-NMR spin-lattice (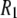 ) relaxation rates from 0.022 to 21.1 T of fluid phase dipalmitoylphosphatidylcholine bilayers are compared. Agreement between experiment and direct prediction from simulation indicates that the dominant slow relaxation (correlation) times of the dipolar and chemical shift anisotropy spin-lattice relaxation are ∼10 ns and 3 ns, respectively. Overall reorientation of the lipid body, consisting of the phosphorus, glycerol, and acyl chains, is well described within a rigid-body model. Wobble, with
) relaxation rates from 0.022 to 21.1 T of fluid phase dipalmitoylphosphatidylcholine bilayers are compared. Agreement between experiment and direct prediction from simulation indicates that the dominant slow relaxation (correlation) times of the dipolar and chemical shift anisotropy spin-lattice relaxation are ∼10 ns and 3 ns, respectively. Overall reorientation of the lipid body, consisting of the phosphorus, glycerol, and acyl chains, is well described within a rigid-body model. Wobble, with 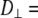 1–2 × 108 s−1, is the primary component of the 10 ns relaxation; this timescale is consistent with the tumbling of a lipid-sized cylinder in a medium with the viscosity of liquid hexadecane. The value for
1–2 × 108 s−1, is the primary component of the 10 ns relaxation; this timescale is consistent with the tumbling of a lipid-sized cylinder in a medium with the viscosity of liquid hexadecane. The value for 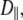 the diffusion constant for rotation about the long axis of the lipid body, is difficult to determine precisely because of averaging by fast motions and wobble; it is tentatively estimated to be 1 × 107 s−1. The resulting D‖/D⊥ ≈ 0.1 implies that axial rotation is strongly modulated by interactions at the lipid/water interface. Rigid-body modeling and potential of mean force evaluations show that the choline group is relatively uncoupled from the rest of the lipid. This is consistent with the ratio of chemical shift anisotropy and dipolar correlation times reported here and the previous observations that 31P-NMR lineshapes are axially symmetric even in the gel phase of dipalmitoylphosphatidylcholine.
the diffusion constant for rotation about the long axis of the lipid body, is difficult to determine precisely because of averaging by fast motions and wobble; it is tentatively estimated to be 1 × 107 s−1. The resulting D‖/D⊥ ≈ 0.1 implies that axial rotation is strongly modulated by interactions at the lipid/water interface. Rigid-body modeling and potential of mean force evaluations show that the choline group is relatively uncoupled from the rest of the lipid. This is consistent with the ratio of chemical shift anisotropy and dipolar correlation times reported here and the previous observations that 31P-NMR lineshapes are axially symmetric even in the gel phase of dipalmitoylphosphatidylcholine.
INTRODUCTION
The rotational relaxation (as described with correlation times) of lipids in bilayers is a sensitive indicator of both lipid structure and the membrane environment. This relaxation can be estimated by NMR and, in principle, be related to changes in membrane composition or ambient conditions. In particular, recent advances in 31P-NMR have enabled measurement of the nuclear spin-lattice relaxation rate (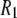 ) over a wide range of magnetic field strengths (1), thereby allowing a new experimental frequency-dependent analysis of the dynamical parts of the lipids near the water/lipid interface (2,3). For such measurements to be fully informative, however, the molecular origin of the individual motions must be deduced. This is especially critical for 31P
) over a wide range of magnetic field strengths (1), thereby allowing a new experimental frequency-dependent analysis of the dynamical parts of the lipids near the water/lipid interface (2,3). For such measurements to be fully informative, however, the molecular origin of the individual motions must be deduced. This is especially critical for 31P 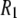 's because contributions to the relaxation arise from both dipolar interactions with nearby hydrogens on the glycerol and the choline groups, and chemical shift anisotropy (CSA).
's because contributions to the relaxation arise from both dipolar interactions with nearby hydrogens on the glycerol and the choline groups, and chemical shift anisotropy (CSA).
This report focuses on determining the motional contributions to 31P 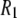 rates in dipalmitoylphosphatidylcholine (DPPC) bilayers using molecular dynamics (MD) simulations. The results are compared with newly obtained experimental measurements on DPPC near the temperature of the simulation. Of special interest is the degree to which a rigid-body diffusion model is applicable to lipids and the values of the rotational diffusion constants. If the dynamics of different regions (chains, glycerol, phosphate, and choline groups) is largely uncoupled, the relaxation times obtained from NMR measurements would necessarily be interpreted differently than if a rigid-body model were appropriate.
rates in dipalmitoylphosphatidylcholine (DPPC) bilayers using molecular dynamics (MD) simulations. The results are compared with newly obtained experimental measurements on DPPC near the temperature of the simulation. Of special interest is the degree to which a rigid-body diffusion model is applicable to lipids and the values of the rotational diffusion constants. If the dynamics of different regions (chains, glycerol, phosphate, and choline groups) is largely uncoupled, the relaxation times obtained from NMR measurements would necessarily be interpreted differently than if a rigid-body model were appropriate.
A specific target of this study is the 5–10 ns “slow” correlation time 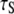 extracted phenomologically from a model-free analysis of recently published 31P data relaxation data from a variety of membranes (2). A similar ∼10 ns correlation time was observed in a sample in which the lipids were cross-linked at the ends of their acyl chains (2). This latter observation suggests that the dominant slow relaxation does not arise from rotation of the entire lipid about its long axis (axial rotation). If it did, cross-linking would dramatically lengthen
extracted phenomologically from a model-free analysis of recently published 31P data relaxation data from a variety of membranes (2). A similar ∼10 ns correlation time was observed in a sample in which the lipids were cross-linked at the ends of their acyl chains (2). This latter observation suggests that the dominant slow relaxation does not arise from rotation of the entire lipid about its long axis (axial rotation). If it did, cross-linking would dramatically lengthen 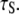 There are three plausible alternatives. The first is that isomerizations in the glycerol and phosphate regions randomize the projection of the vectors on the bilayer surface. In the extreme, the tails of the lipids could be frozen in place. In this case, the measurement of
There are three plausible alternatives. The first is that isomerizations in the glycerol and phosphate regions randomize the projection of the vectors on the bilayer surface. In the extreme, the tails of the lipids could be frozen in place. In this case, the measurement of 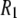 provides information on the bilayer surface but not on the interior. The next alternative entails “wobble in a cone”, or restricted diffusive reorientation of the lipid long axis with respect to the bilayer normal (4); wobble may be pictured as Brownian motion of a two-dimensional pendulum. Wobble involves the chains and glycerol group and thereby probes the bilayer interior as well as the surface. The third possibility is that the lipids in the sample were not fully cross-linked.
provides information on the bilayer surface but not on the interior. The next alternative entails “wobble in a cone”, or restricted diffusive reorientation of the lipid long axis with respect to the bilayer normal (4); wobble may be pictured as Brownian motion of a two-dimensional pendulum. Wobble involves the chains and glycerol group and thereby probes the bilayer interior as well as the surface. The third possibility is that the lipids in the sample were not fully cross-linked.
There are two basic steps in the logic of this study. In the first, reorientational correlation functions for the appropriate internal vectors are evaluated from four recently reported (5) MD simulations of DPPC, each of 50 ns. Three contain 72 lipids, and a fourth contains 288. Correlation times and other averages are extracted, and 31P relaxation rates are calculated and compared with experiment. None of the simulation results were scaled or otherwise altered to achieve a better fit to the 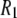 data.
data.
The overall very good agreement with experiment enables the second step: fitting the correlation functions of the P-H and other vectors to a relaxation model containing wobble, axial rotation, and fast internal motion. The model, sketched in Fig. 1 and described in detail in the following section, has been applied with good success to the acyl chains of DPPC bilayers (6–8). This study extends the modeling to the headgroup region. The similarity of the rigid-body parameters for different vectors suggests the applicability of such models for lipids. The values of the parameters yield insight into the underlying motions contributing to 31P R1 and the microenvironment of the bilayer.
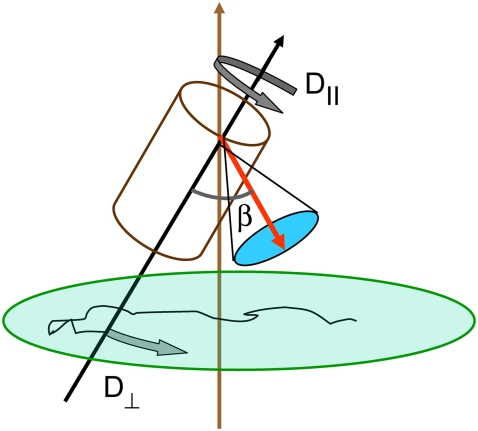
FIGURE 1.
Model for lipid dynamics including rotation about the long axis (axial rotation), described by 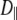 ; restricted rotation of the long axis (wobble), described by
; restricted rotation of the long axis (wobble), described by 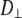 ; and internal reorientation (including isomerizations of dihedral angles). β is the average angle between the vector of interest (in red) and the long (or symmetry) axis of the lipid. The bilayer normal is shown in brown. The average extent of lipid wobble and internal reorientation of the vector is depicted by the green and blue disks, respectively. A hypothetical trajectory is projected onto the green disk to illustrate wobble.
; and internal reorientation (including isomerizations of dihedral angles). β is the average angle between the vector of interest (in red) and the long (or symmetry) axis of the lipid. The bilayer normal is shown in brown. The average extent of lipid wobble and internal reorientation of the vector is depicted by the green and blue disks, respectively. A hypothetical trajectory is projected onto the green disk to illustrate wobble.
METHODS
Simulations and nomenclature
Three fully hydrated (30.4 waters/lipid) systems of 72 DPPC and one of 288 DPPC were simulated for 50 ns after equilibration with the CHARMM (9) and NAMD (10) programs, respectively, and the parameter set C27r (11). In all cases, areas (A) were fixed at 64 Å2/lipid, and a constant normal pressure (P) of 1 atm was maintained with an extended system piston (12) with a mass of 2000 amu. Temperatures (T) of the 72-lipid systems were maintained at 323.15 K with a Hoover thermostat (13) with a coupling constant of 20,000 kcal mol−1 ps−2. The temperature of the 288-lipid system was not fixed after equilibration, but drift was <1.3 K over 50 ns. Hence, the ensembles of the 72 and 288 systems are NPAT and NPAH (H is enthalpy) (14,15). Long-range electrostatics were evaluated using particle mesh Ewald with a real-space cutoff set to 10 Å (16); Lennard-Jones interactions were shifted to zero from 8–10 Å, and a long-range correction applied to the normal pressure (17). See Klauda et al. (5) for further details. Simulations were performed at 323.15 K because the surface area per lipid has been determined at that temperature for DPPC (18).
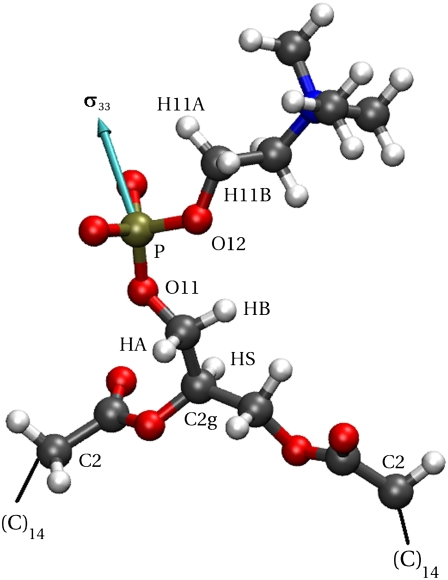
Fig. 2 labels the headgroup atoms relevant for calculations of the 31P relaxation rates: the glycerol hydrogens that neighbor the phosphorus (HA and HB) and the neighboring hydrogens of the choline (H11A and H11B). Atoms relevant for later analysis include O11 of the glycerol, O12 of the choline, the CH group of the glycerol (C2g-HS vector), and carbon 2 of each acyl chain (C2-C2 vector). The other acyl chains atoms are not shown.
FIGURE 2.
Relevant atoms in the headgroup region of DPPC. The principal axis of the phosphorus chemical shift tensor is shown in cyan. Atom positions are from a snapshot of a trajectory.
Experimental procedures
DPPC was obtained from Avanti Polar Lipids (Alabaster, AL) and used without further purification. Large unilamellar vesicles were prepared in two ways: i), sonicating the DPPC suspension in 50 mM HEPES, pH 7.5, 40% D2O, at 318 K, then cooling the sample to 281 K and letting it sit at this temperature overnight (this generates a fairly homogeneous sample of 1000 Å diameter vesicles); or ii), extrusion of the sample (at least 10 times) using a Lipofast extruder and 0.1 μm filters. Smaller (250–300 Å diameter) highly curved DPPC vesicles (3), produced by sonication, are unstable at the lower temperatures used for sealing samples and tend to fuse over time. Therefore, these smaller structures were not examined by field cycling.
High-resolution 31P field cycling, covering the range 0.022–11.74 T, was carried out in a custom-built system attached to a Varian (Palo Alto, CA) 500 MHz spectrometer described in detail previously (1). The DPPC sample (1 ml) was sealed in a shortened 8 mm NMR tube and attached to a plastic shuttle piston that moved up and down the magnet bore by suction or pressure. 31P relaxation data at 14.04 and 18.78 T were obtained on a Varian INOVA 600 spectrometer, and on the Bruker (Billerica, MA) 800 MHz spectrometer at the Boston area NMR facility. The relaxation rate at 21.13 T was obtained by Dr. Klaas Hallenga on the Varian 900 MHz spectrometer at the National Magnetic Resonance Facility at Madison, WI. Data were taken down only to 0.022 T. Below this field an interesting and useful extra  dispersion has been reported previously (3). This field regime was not explored because
dispersion has been reported previously (3). This field regime was not explored because  rises too rapidly to provide useful information about the 1000 Å vesicles studied (3). Lastly, data were collected at 318 K (rather than the simulated temperature of 323 K) due to concerns with the integrity of the epoxy cement used to seal the samples.
rises too rapidly to provide useful information about the 1000 Å vesicles studied (3). Lastly, data were collected at 318 K (rather than the simulated temperature of 323 K) due to concerns with the integrity of the epoxy cement used to seal the samples.
NMR relaxation rates predicted from simulation
The NMR 31P  rates arise from dipolar and CSA contributions:
rates arise from dipolar and CSA contributions:
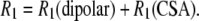 |
(1) |
Cross correlations between these mechanisms were not calculated because they would be averaged to zero by the rapid cross-relaxation flips of the protons.
The dipolar contribution for each P-H interaction was calculated from
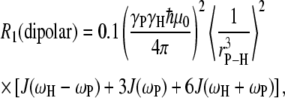 |
(2) |
where γP (1.08297 × 108 T−1s−1) and γH (2.6753 × 108 T−1s−1) are the phosphorus and hydrogen gyromagnetic ratios, ωP and ωH are, respectively, the product of these gyromagnetic ratios and the applied field, μ0 is the permittivity of a vacuum, ℏ is Planck's constant divided by 2π, 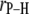 is the phosphorus-hydrogen distance at each point in the trajectory, and the
is the phosphorus-hydrogen distance at each point in the trajectory, and the 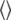 signifies the time average over the trajectory. The spectral density,
signifies the time average over the trajectory. The spectral density, 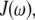 is the one-sided Fourier transform of the reorientational correlation function
is the one-sided Fourier transform of the reorientational correlation function
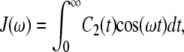 |
(3) |
with
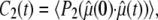 |
(4) |
where 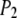 is the second Legendre polynomial
is the second Legendre polynomial 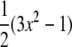 and
and 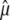 is the particular P-H unit vector. Use of Eq. 4, rather than a correlation function including full angular dependence (19), is appropriate because the relaxation rate is measured as the spherical average (20) over the vesicles which tumble slowly with respect to lipid reorientation but rapidly with respect to spin relaxation. Furthermore, evaluations of
is the particular P-H unit vector. Use of Eq. 4, rather than a correlation function including full angular dependence (19), is appropriate because the relaxation rate is measured as the spherical average (20) over the vesicles which tumble slowly with respect to lipid reorientation but rapidly with respect to spin relaxation. Furthermore, evaluations of  based on the more rigorous correlation function
based on the more rigorous correlation function 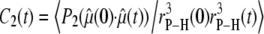 did not yield statistically significant differences from Eq. 2. This implies that fluctuations in
did not yield statistically significant differences from Eq. 2. This implies that fluctuations in 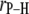 and
and 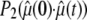 are sufficiently uncorrelated so that they can be averaged separately.
are sufficiently uncorrelated so that they can be averaged separately.
Dipolar relaxation of the phosphorus arises from interactions with all nearby hydrogens. Because of the 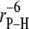 dependence in Eq. 2, only the closest hydrogens on the glycerol (HA and HB) and the choline (H11A and H11B) need be considered here.
dependence in Eq. 2, only the closest hydrogens on the glycerol (HA and HB) and the choline (H11A and H11B) need be considered here.
The CSA contribution to the relaxation rate was calculated as
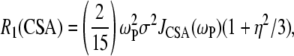 |
(5) |
where σ and η are the CSA interaction size and asymmetry (21). Their values were set to 160 ppm and 0.57, respectively (2). Based on solid-state 31P-NMR measurements of related lipids and model compounds (22), variations in σ and η are 3 ppm and 0.02, respectively. From Eq. 5, variations of this size could lead to shifts of ∼±5% in calculated 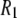 's. The spectral density
's. The spectral density 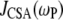 is obtained from
is obtained from 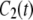 of the principal axis of the 31P chemical shift tensor. This principal axis was determined by Herzfeld et al. (22) and is denoted
of the principal axis of the 31P chemical shift tensor. This principal axis was determined by Herzfeld et al. (22) and is denoted 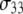 (see Fig. 2). The reorientational correlation functions for the other two principal axes,
(see Fig. 2). The reorientational correlation functions for the other two principal axes, 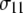 and
and 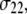 were found to be qualitatively similar to that of
were found to be qualitatively similar to that of 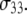 Hence, the
Hence, the 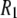 calculated at high field are insensitive to small variations in the orientation of
calculated at high field are insensitive to small variations in the orientation of 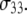
Correlation functions for the assorted vectors determined from the simulations were fit to a function with three exponentials and a constant:
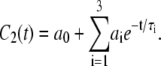 |
(6) |
Here, 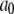 is the plateau or long-time value of the correlation function, and was calculated directly as the average
is the plateau or long-time value of the correlation function, and was calculated directly as the average 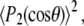 where
where 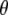 is the instantaneous angle between the vector and the bilayer normal (assumed here to be the z axis). Spectral densities for
is the instantaneous angle between the vector and the bilayer normal (assumed here to be the z axis). Spectral densities for 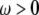 are then given by the Fourier transform of Eq. 6:
are then given by the Fourier transform of Eq. 6:
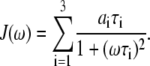 |
(7) |
The time-independent term 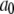 in Eq. 6 is not included in the Fourier transform, Eq. 7, because it would lead to a meaningless singularity at zero frequency. If a simulation of the entire vesicle for many microseconds could be performed, the correlation function evaluated would contain a very slow component given by
in Eq. 6 is not included in the Fourier transform, Eq. 7, because it would lead to a meaningless singularity at zero frequency. If a simulation of the entire vesicle for many microseconds could be performed, the correlation function evaluated would contain a very slow component given by 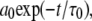 where
where 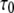 is the rotational correlation time associated with vesicle tumbling and lateral diffusion; for the 1000 Å vesicles studied here
is the rotational correlation time associated with vesicle tumbling and lateral diffusion; for the 1000 Å vesicles studied here 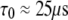 (see the Supplementary Material in Roberts and Redfield (3)). The full Fourier transform of Eq. 6 would then contain the low frequency dispersion (3). As already noted, this region could not be studied for these large vesicles. A 25 μs correlation time has no expected observable effect at 0.022 T and above, and therefore is ignored.
(see the Supplementary Material in Roberts and Redfield (3)). The full Fourier transform of Eq. 6 would then contain the low frequency dispersion (3). As already noted, this region could not be studied for these large vesicles. A 25 μs correlation time has no expected observable effect at 0.022 T and above, and therefore is ignored.
Motional models
The two dynamical models utilized here to represent the motion provided by the simulation include rigid-body rotation and internal dynamics. The underlying assumption of such a treatment is that internal dynamics is rapid compared to overall rotation and averages the molecule into an effective shape that can be treated as if it were a rigid body with a unique rotational diffusion tensor. In the case of a lipid in a membrane, simulations indicate that this shape is remarkably cylindrical (7).
In both models the vector of interest (shown in red in Fig. 1) is attached to a rigid cylinder with an angle β with respect to the cylinder axis. The rotational diffusion constants of the cylinder are denoted 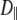 (describing rotation about the long axis of the cylinder) and
(describing rotation about the long axis of the cylinder) and 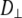 (for rotation of the long axis, or wobble). In Model I the lipid is allowed to axially rotate and wobble. The geometry of the bilayer limits the extent of wobble and leads to order parameters
(for rotation of the long axis, or wobble). In Model I the lipid is allowed to axially rotate and wobble. The geometry of the bilayer limits the extent of wobble and leads to order parameters 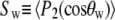 and
and 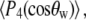 where
where 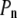 are Legendre functions and
are Legendre functions and 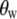 is the instantaneous angle between the cylinder axis and the bilayer normal. A very good approximation to the exact second rank Legendre polynomial correlation function for a vector rigidly attached to the cylinder was derived by Szabo (23):
is the instantaneous angle between the cylinder axis and the bilayer normal. A very good approximation to the exact second rank Legendre polynomial correlation function for a vector rigidly attached to the cylinder was derived by Szabo (23):
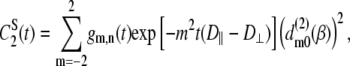 |
(8) |
where 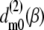 are Wigner rotation matrix elements, and
are Wigner rotation matrix elements, and 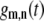 are functions of
are functions of 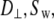 and
and 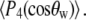 After accounting for symmetry, there are as many as nine exponential decays in Eq. 8 (see Szabo (23) for full details). When
After accounting for symmetry, there are as many as nine exponential decays in Eq. 8 (see Szabo (23) for full details). When 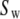 = 0 (no restriction on the rotation), Eq. 8 reduces to the formula of Huntress for diffusive relaxation of a symmetric top (24). When there is no wobble (the cylinder is fixed along the bilayer normal),
= 0 (no restriction on the rotation), Eq. 8 reduces to the formula of Huntress for diffusive relaxation of a symmetric top (24). When there is no wobble (the cylinder is fixed along the bilayer normal), 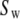 = 1,
= 1, 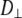 does not contribute to the relaxation, and it reduces to the Woessner model (25), which is the basis of Model II:
does not contribute to the relaxation, and it reduces to the Woessner model (25), which is the basis of Model II:
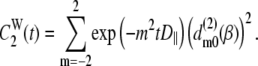 |
(9) |
Internal dynamics primarily arises from isomerization of the dihedral angles and leads to fast decays of the observed or simulated correlation functions. The correlation function for such fast motions is assumed to be
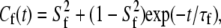 |
(10) |
where 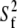 is the generalized order parameter and
is the generalized order parameter and 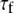 is the correlation time. This fast dynamics is also sketched in Fig. 1. Hence, there are two important order parameters in the model:
is the correlation time. This fast dynamics is also sketched in Fig. 1. Hence, there are two important order parameters in the model: 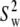 for lipid wobble and
for lipid wobble and 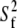 for internal dynamics.
for internal dynamics.
Under the assumption that the fast and overall motions are independent, the second rank correlation functions for Models I and II are then defined by
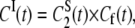 |
(11a) |
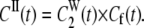 |
(11b) |
The plateau, or long-time, values of the correlation functions are given by
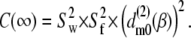 |
(12) |
Correlation functions from the simulation were fit for each model. 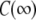 was set to the plateau calculated directly from the simulation (
was set to the plateau calculated directly from the simulation (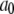 ) and used as a constraint for Model I.
) and used as a constraint for Model I.
RESULTS AND DISCUSSION
Comparison of simulation and experiment
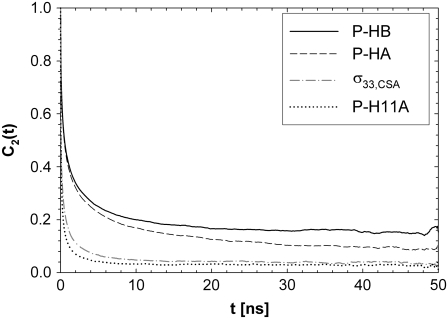
Fig. 3 plots the correlation functions obtained from the simulation for the vectors between phosphorus and nearby hydrogens (to evaluate the dipolar contribution to 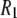 ) and for the principal axis
) and for the principal axis 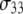 (for the CSA contribution); the fitted amplitudes and decay times (Eq. 6) of these correlation functions are listed in Table 1. The decays of the P-HA and P-HB vectors are not identical. The longest decay times,
(for the CSA contribution); the fitted amplitudes and decay times (Eq. 6) of these correlation functions are listed in Table 1. The decays of the P-HA and P-HB vectors are not identical. The longest decay times, 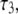 of P-HA and P-HB are 7 and 12 ns, respectively, and are in the range previously estimated by field cycling for other lipids (2). The correlation functions for P-H11A, P-H11B, and
of P-HA and P-HB are 7 and 12 ns, respectively, and are in the range previously estimated by field cycling for other lipids (2). The correlation functions for P-H11A, P-H11B, and 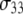 are similar, and their three fitted decay constants are 3–5 times smaller than the corresponding
are similar, and their three fitted decay constants are 3–5 times smaller than the corresponding 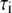 of P-HA and P-HB;
of P-HA and P-HB; 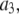 the amplitude of the slowest motion of this set, is also smaller than
the amplitude of the slowest motion of this set, is also smaller than 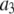 of P-HA and P-HB. The origin of these differences is suggested by Fig. 2: if the glycerol region of the lipid is substantially more rigid than the choline group, rotation about the P-O11 bond could relax
of P-HA and P-HB. The origin of these differences is suggested by Fig. 2: if the glycerol region of the lipid is substantially more rigid than the choline group, rotation about the P-O11 bond could relax 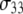 but leave P-HA and P-HB relatively unchanged. Isomerizations in the choline region would then lower relaxation times of P-H11A and P-H11B with respect to
but leave P-HA and P-HB relatively unchanged. Isomerizations in the choline region would then lower relaxation times of P-H11A and P-H11B with respect to 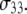 Hence, torsional motions about P-O11 bond could partially decouple the choline group and the rest of the lipid. This is demonstrated explicitly in the following section.
Hence, torsional motions about P-O11 bond could partially decouple the choline group and the rest of the lipid. This is demonstrated explicitly in the following section.
FIGURE 3.
Reorientational correlation functions of the phosphorus hydrogen and 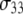 unit vectors. P-H11B is omitted for clarity because it overlaps with P-H11A.
unit vectors. P-H11B is omitted for clarity because it overlaps with P-H11A.
TABLE 1.
Parameters from three exponential fits of fits of correlation functions from the MD simulations
| Vector | 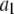 |
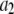 |
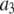 |
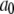 |
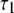 (ps) (ps) |
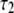 (ns) (ns) |
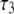 (ns) (ns) |
|---|---|---|---|---|---|---|---|
| P-HA | 0.403 (0.03) | 0.318 (0.02) | 0.190 (0.01) | 0.089 (0.005) | 87.1 (15.5) | 1.350 (0.25) | 12.12 (2.0) |
| P-HB | 0.336 (0.03) | 0.313 (0.02) | 0.195 (0.01) | 0.156 (0.005) | 61.3 (15.5) | 0.874 (0.25) | 6.83 (2.0) |
| P-H11A | 0.477 (0.03) | 0.376 (0.02) | 0.118 (0.01) | 0.029 (0.005) | 16.2 (2.7) | 0.212 (0.047) | 2.07 (0.60) |
| P-H11B | 0.473 (0.03) | 0.368 (0.02) | 0.119 (0.01) | 0.030 (0.005) | 15.8 (2.7) | 0.205 (0.047) | 1.93 (0.60) |
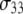 |
0.490 (0.021) | 0.335 (0.024) | 0.136 (0.003) | 0.040 (0.001) | 20.6 (2.5) | 0.372 (0.061) | 3.17 (0.58) |
The standard errors are in parentheses.
Table 2 lists the average lengths (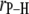 ) and angles (
) and angles (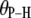 ) with respect to the bilayer normal for each of the P-H vectors. The values of
) with respect to the bilayer normal for each of the P-H vectors. The values of 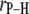 (2.92–2.99 Å) are comparable to those obtained for other lipids from fits to the experimental 31P relaxation data (2.80–2.88 Å) (2). Recently, a combination of 31P measurements and the Woessner model were used to obtain tentative values of
(2.92–2.99 Å) are comparable to those obtained for other lipids from fits to the experimental 31P relaxation data (2.80–2.88 Å) (2). Recently, a combination of 31P measurements and the Woessner model were used to obtain tentative values of 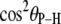 for assorted lipids (3), leaving two ranges for
for assorted lipids (3), leaving two ranges for 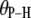 : 41.1–46.3° and 64.4–71.5°. The results here indicate that the former range is very likely correct when relaxation is dominated by P-HA and P-HB.
: 41.1–46.3° and 64.4–71.5°. The results here indicate that the former range is very likely correct when relaxation is dominated by P-HA and P-HB.
TABLE 2.
The average lengths, 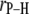 (evaluated as
(evaluated as 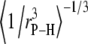 ) of relevant P-H vectors and their angles with respect to the bilayer normal,
) of relevant P-H vectors and their angles with respect to the bilayer normal,
| Vector |
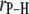 (Å) (Å) |
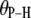 (deg) (deg) |
|---|---|---|
| P-HA | 2.92 | 43.3 |
| P-HB | 2.96 | 39.3 |
| P-H11A | 2.99 | 88.9 |
| P-H11B | 2.97 | 89.2 |
The P-H vector is pointing toward the center of the bilayer when 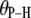 = 0. Standard errors are 0.001–0.002 Å for
= 0. Standard errors are 0.001–0.002 Å for 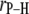 and 0.3° for
and 0.3° for 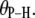
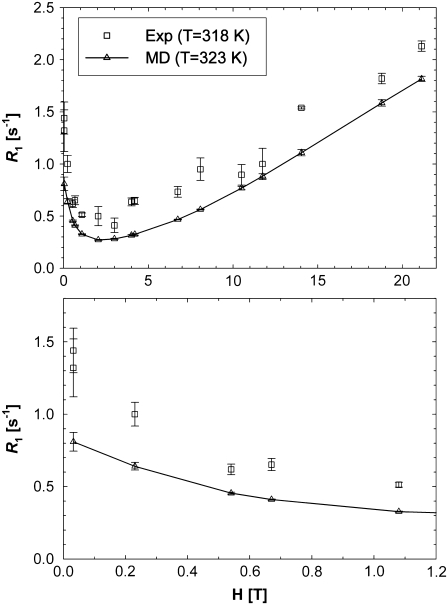
Fig. 4 plots the 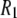 's calculated from the MD generated correlation functions and those obtained experimentally. (Table 4 includes the individual components of
's calculated from the MD generated correlation functions and those obtained experimentally. (Table 4 includes the individual components of 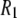 's from simulation at each field examined.)
's from simulation at each field examined.)
FIGURE 4.
NMR 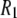 rates from experiment and MD simulation over all fields measured (top) and, in an expanded scale, at lower field (bottom). Dipolar relaxation dominates at low fields, and CSA relaxation dominates the region above 5 T. The contribution of CSA relaxation is negligible below 0.5 T.
rates from experiment and MD simulation over all fields measured (top) and, in an expanded scale, at lower field (bottom). Dipolar relaxation dominates at low fields, and CSA relaxation dominates the region above 5 T. The contribution of CSA relaxation is negligible below 0.5 T.
TABLE 4.
Fitted values of parameters for assorted vectors in the lipid for Models I (Eq. 11a) and II (Eq. 11b)
| Vector | Model |
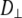 (108 s−1) (108 s−1) |
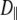 (108 s−1) (108 s−1) |
β(°) | 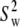 |
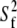 |
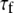 (ps) (ps) |
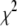 |
|---|---|---|---|---|---|---|---|---|
| P-HA | I | 0.59 | 0.01 | 33 | 0.580 | 0.504 | 165 | 0.0446 |
| II | 1.32 | 35 | 0.405 | 256 | 0.1128 | |||
| P-HB | I | 0.90 | 0.07 | 28 | 0.587 | 0.598 | 110 | 0.0288 |
| II | 2.08 | 31 | 0.464 | 205 | 0.0733 | |||
| P-O11 | I | 1.20 | 0.04 | 24 | 0.622 | 0.562 | 44 | 0.0118 |
| II | 2.77 | 28 | - | 0.446 | 85 | 0.0474 | ||
| P-O12 | I | 4.14 | 0.19 | 36 | 0.565 | 0.512 | 36 | 0.0081 |
| II | 7.08 | 39 | 0.375 | 58 | 0.0222 | |||
| P-N | I | 3.80 | 0.27 | 42 | 0.551 | 0.674 | 49 | 0.0079 |
| II | 5.85 | 44 | 0.487 | 107 | 0.0244 | |||
| C2g-HS | I | 1.56 | 0.10 | 41 | 0.594 | 0.713 | 61 | 0.0236 |
| II | 2.33 | 42 | 0.539 | 187 | 0.0732 | |||
| C2-H | I | 1.71 | 0.00 | 41 | 0.597 | 0.276 | 41 | 0.0245 |
| II | 2.14 | 40 | 0.198 | 57 | 0.0641 | |||
| C3-H | I | 3.20 | 0.00 | 36 | 0.557 | 0.256 | 38 | 0.0233 |
| II | 7.67 | 38 | 0.212 | 43 | 0.0334 | |||
| C〈9–14〉-H | I | 2.25 | 0.00 | 30 | 0.610 | 0.133 | 22 | 0.0024 |
| II | 5.53 | 33 | 0.112 | 23 | 0.0054 | |||
| C14-H | I | 3.03 | 0.00 | 28 | 0.594 | 0.057 | 15 | 0.0012 |
| II | 15.58 | 36 | 0.068 | 1 | 0.0025 | |||
| C15-H | I | 2.40 | 0.00 | 27 | 0.624 | 0.032 | 14 | 0.0009 |
| II | 18.75 | 36 | 0.045 | 0 | 0.0010 | |||
| C2-C2 | I | 1.43 | 0.05 | 38 | 0.610 | 0.803 | 74 | 0.0116 |
| II | 2.14 | 38 | 0.594 | 281 | 0.0484 |
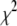 is the sum of squared errors of each fit to the simulated correlation function over 0–50 ns.
is the sum of squared errors of each fit to the simulated correlation function over 0–50 ns.
Before presenting more analysis, the major features of the experimental curves in Fig. 4 and their correspondences to the parameters in Table 1 are discussed qualitatively. The large rise in 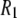 at low field is due to the phosphorus-proton dipolar interaction. The same interaction is well known as a contributor to 15N
at low field is due to the phosphorus-proton dipolar interaction. The same interaction is well known as a contributor to 15N 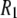 in proteins. However, the correlation time in rigid proteins that dominates dipolar
in proteins. However, the correlation time in rigid proteins that dominates dipolar 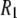 is that for overall rotational diffusion of the entire protein. Much of what follows in this work is devoted to identifying what gives rise to this motion. The terms in the simulation that give rise to the sharp increase in
is that for overall rotational diffusion of the entire protein. Much of what follows in this work is devoted to identifying what gives rise to this motion. The terms in the simulation that give rise to the sharp increase in 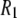 seen below 1 T are almost exclusively the
seen below 1 T are almost exclusively the 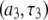 terms of the P-HA and P-HB vectors in Table I. The remaining dipolar terms in Table 1 are too broad to produce any distinctive peaks in the predicted
terms of the P-HA and P-HB vectors in Table I. The remaining dipolar terms in Table 1 are too broad to produce any distinctive peaks in the predicted 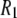 curve, although some of them may contribute enough to visibly increase the magnitude of
curve, although some of them may contribute enough to visibly increase the magnitude of 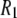 in the region around 2 T.
in the region around 2 T.
The predicted 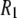 behavior above 2 T is dominated by the
behavior above 2 T is dominated by the 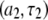 term of the CSA interaction, with an increase proportional to the square of the field due to the
term of the CSA interaction, with an increase proportional to the square of the field due to the 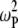 term in the numerator of Eq. 5. The denominator of
term in the numerator of Eq. 5. The denominator of 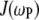 (see Eq. 7, whose dipolar terms are similar to the CSA term
(see Eq. 7, whose dipolar terms are similar to the CSA term 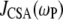 in Eq. 5) is nearly 1 over the entire field range, because
in Eq. 5) is nearly 1 over the entire field range, because 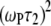 = 0.04 for the highest field measured. There is also a nearly field-independent relaxation contribution from the
= 0.04 for the highest field measured. There is also a nearly field-independent relaxation contribution from the 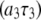 CSA term (it is field independent because
CSA term (it is field independent because 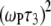 ≫ 1 above 2 T, so the
≫ 1 above 2 T, so the 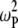 terms cancel). This term is not readily noticeable in the
terms cancel). This term is not readily noticeable in the 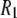 plot, but it is responsible for making the field-squared dependence of the
plot, but it is responsible for making the field-squared dependence of the 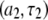 term less noticeable; so the sum of the two terms more nearly appears linear with field.
term less noticeable; so the sum of the two terms more nearly appears linear with field.
In summary, the dispersion in 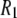 at low field gives a good estimate of the timescale and size of one important motion of the P-HA and P-HB vectors. The rise in
at low field gives a good estimate of the timescale and size of one important motion of the P-HA and P-HB vectors. The rise in 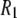 at high field reports on another, probably related, motion but does not give a magnitude and timescale directly, only the product
at high field reports on another, probably related, motion but does not give a magnitude and timescale directly, only the product 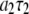 times known constants. Previously a model-free analysis (2) provided a rough picture similar to the above, but lack of the parameters now provided by the simulation prevented drawing many conclusions.
times known constants. Previously a model-free analysis (2) provided a rough picture similar to the above, but lack of the parameters now provided by the simulation prevented drawing many conclusions.
The relatively larger relaxation of the phosphorus by the glycerol proteins, compared to the choline H11 protons, was noticed earlier (3). An explanation was advanced involving possible different distances to the phosphate from these two pairs of protons. However, Table 2 indicates that the distances are almost identical for all four protons and instead the simulation provides a satisfactory explanation for the different relaxation rates: the P-H11 vectors decay much faster than P-HA and P-HB (Table 1). The dipolar and CSA contributions evaluated from the simulation are approximately equal at 3 T, and, as follows from Eq. 5, CSA relaxation dominates at high fields (Table 3).
TABLE 3.
31P 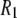 from experiment (318 K) and MD simulation (323 K)
from experiment (318 K) and MD simulation (323 K)
| Dipolar
|
||||||||
|---|---|---|---|---|---|---|---|---|
| H [T] | HA | HB | H11A | H11B | Subtotal | CSA | Total MD | Exp. |
| 0.02 | 0.46 | 0.26 | 0.04 | 0.04 | 0.81 | 0.00 | 0.81 | 1.60 |
| 0.03 | 0.46 | 0.26 | 0.04 | 0.04 | 0.81 | 0.00 | 0.81 | 1.32 |
| 0.03 | 0.46 | 0.26 | 0.04 | 0.04 | 0.81 | 0.00 | 0.81 | 1.44 |
| 0.23 | 0.32 | 0.23 | 0.04 | 0.04 | 0.64 | 0.00 | 0.64 | 1.00 |
| 0.54 | 0.20 | 0.16 | 0.04 | 0.04 | 0.45 | 0.01 | 0.45 | 0.62 |
| 0.67 | 0.17 | 0.15 | 0.04 | 0.04 | 0.40 | 0.01 | 0.41 | 0.65 |
| 1.08 | 0.12 | 0.11 | 0.04 | 0.04 | 0.30 | 0.03 | 0.33 | 0.51 |
| 2.04 | 0.07 | 0.07 | 0.03 | 0.03 | 0.19 | 0.08 | 0.27 | 0.50 |
| 3.00 | 0.05 | 0.05 | 0.02 | 0.02 | 0.15 | 0.14 | 0.28 | 0.41 |
| 4.00 | 0.04 | 0.04 | 0.02 | 0.02 | 0.12 | 0.20 | 0.32 | 0.64 |
| 4.20 | 0.04 | 0.04 | 0.02 | 0.02 | 0.11 | 0.21 | 0.32 | 0.65 |
| 6.74 | 0.02 | 0.02 | 0.01 | 0.01 | 0.08 | 0.39 | 0.47 | 0.73 |
| 8.07 | 0.02 | 0.02 | 0.01 | 0.01 | 0.07 | 0.50 | 0.56 | 0.95 |
| 10.50 | 0.02 | 0.01 | 0.01 | 0.01 | 0.05 | 0.72 | 0.77 | 0.90 |
| 11.74 | 0.01 | 0.01 | 0.01 | 0.01 | 0.05 | 0.84 | 0.88 | 1.00 |
| 14.04 | 0.01 | 0.01 | 0.01 | 0.01 | 0.04 | 1.07 | 1.11 | 1.54 |
| 18.78 | 0.01 | 0.01 | 0.01 | 0.01 | 0.03 | 1.55 | 1.59 | 1.82 |
| 21.13 | 0.01 | 0.01 | 0.01 | 0.01 | 0.03 | 1.79 | 1.82 | 2.13 |
Contributions to the calculated 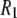 are listed for the four nearest intralipid hydrogens and for the CSA.
are listed for the four nearest intralipid hydrogens and for the CSA.
As explained in Methods, experiments were carried out at 318 K and MD simulations at 323 K. Estimates based on extrapolations of lower temperature data for DPPC and correspondences for dimyristoylphosphatidycholine (DMPC) suggest that 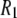 (323 K)/
(323 K)/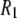 (318 K) = 0.91 and 0.99 at low and high fields, respectively. Consequently,
(318 K) = 0.91 and 0.99 at low and high fields, respectively. Consequently, 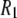 's from the simulation and experiment may be compared directly with experiment at high field, whereas those at low field need to be scaled upward by ∼10% for a more reasonable comparison.
's from the simulation and experiment may be compared directly with experiment at high field, whereas those at low field need to be scaled upward by ∼10% for a more reasonable comparison.
With the preceding considerations in mind, it is clear from Fig. 4 and Table 4 that the overall agreement for simulation and experiment is very good. At high fields (10.5–21.13 T) the average difference is 16%. At lower fields (0.022–8 T) the simulated 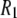 's underestimate experiment by 40% (on average). Applying a 10% correction to account for the temperature difference reduces the lower field differences to 36%. The statistical errors in the
's underestimate experiment by 40% (on average). Applying a 10% correction to account for the temperature difference reduces the lower field differences to 36%. The statistical errors in the 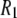 's calculated from the simulation (1–8% at low field and 1–3% at high field) are small compared to the scatter in the experimental
's calculated from the simulation (1–8% at low field and 1–3% at high field) are small compared to the scatter in the experimental  values. Therefore, the differences between simulation and experiment are somewhat, though not substantially, larger than their combined statistical errors.
values. Therefore, the differences between simulation and experiment are somewhat, though not substantially, larger than their combined statistical errors.
Although there are no adjustable parameters in the calculation of 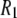 's from simulation, inaccuracies in the potential energy function (or force field) are obviously reflected in the results. Results from C27r compare favorably with a wide variety of lipid data (26). Specifically, the average discrepancies with experimental 13C
's from simulation, inaccuracies in the potential energy function (or force field) are obviously reflected in the results. Results from C27r compare favorably with a wide variety of lipid data (26). Specifically, the average discrepancies with experimental 13C 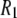 s at 7.04 T and 11.74 T for DPPC multilayers are 15% for resolvable acyl chain carbons, 22% for the choline carbons, and 25% for the glycerol carbons (8). These differences are similar to those reported here for the high field 31P
s at 7.04 T and 11.74 T for DPPC multilayers are 15% for resolvable acyl chain carbons, 22% for the choline carbons, and 25% for the glycerol carbons (8). These differences are similar to those reported here for the high field 31P 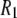 's, indicating an overall consistency in the force field. A likely source of discrepancy at low field is the P-H distance. In contrast to the calculation of 13C relaxation from simulation, where the C-H distance is fixed and well established (27), the P-H distance can fluctuate and is sensitive to small inaccuracies in the dihedral angles in the glycerol and phosphate regions. Specifically, decrease in the average P-H distance of only 0.1 Å increases the low field
's, indicating an overall consistency in the force field. A likely source of discrepancy at low field is the P-H distance. In contrast to the calculation of 13C relaxation from simulation, where the C-H distance is fixed and well established (27), the P-H distance can fluctuate and is sensitive to small inaccuracies in the dihedral angles in the glycerol and phosphate regions. Specifically, decrease in the average P-H distance of only 0.1 Å increases the low field 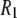 's by 23% and nearly erases all of the difference between simulation and experiment.
's by 23% and nearly erases all of the difference between simulation and experiment. 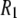 's are also sensitive to the relative contributions of fast and slow motion. For example, small changes in the dihedral potential of the acyl chains lead to a substantial change to both the magnitude and frequency dependencies of the 13C
's are also sensitive to the relative contributions of fast and slow motion. For example, small changes in the dihedral potential of the acyl chains lead to a substantial change to both the magnitude and frequency dependencies of the 13C 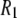 's of acyl chain carbons in DPPC bilayers (26).
's of acyl chain carbons in DPPC bilayers (26).
Lastly, the simulations were carried out for 50 ns in periodic cells of 50 and 100 Å/side. Relaxation times arising from collective motions on longer time and length scales that may contribute to 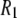 at the lowest low fields are not sampled and are beyond the scope of this study.
at the lowest low fields are not sampled and are beyond the scope of this study.
Motional models
The results so far confirm that the simulations reproduce the dominant timescales observed experimentally and reasonably match the 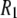 's. This section considers models for the relaxation.
's. This section considers models for the relaxation.
Table 4 lists the fitted parameters for Model I (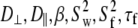 ) and Model II (
) and Model II (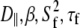 ) for a range of vectors in DPPC. In every case, the fitting error
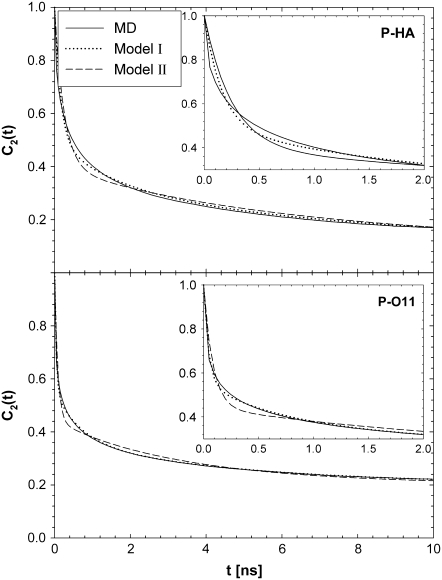
) for a range of vectors in DPPC. In every case, the fitting error 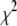 is smaller for Model I (usually by a factor of 2–3). Fig. 5 (top) compares the correlation functions for P-HA. Model I clearly provides a better fit to the simulated data than does Model II, though neither captures the very fast relaxation. This is expected, because librations and isomerizations of several dihedral angles contribute to the subnanosecond relaxation of the PH vector and these have different timescales. To reduce the effects of multiple internal motions, the P-O11 vector was fit to Models I and II. The agreement with the simulated correlation function is now substantially better for Model I (Fig. 5, bottom). Most striking is that
is smaller for Model I (usually by a factor of 2–3). Fig. 5 (top) compares the correlation functions for P-HA. Model I clearly provides a better fit to the simulated data than does Model II, though neither captures the very fast relaxation. This is expected, because librations and isomerizations of several dihedral angles contribute to the subnanosecond relaxation of the PH vector and these have different timescales. To reduce the effects of multiple internal motions, the P-O11 vector was fit to Models I and II. The agreement with the simulated correlation function is now substantially better for Model I (Fig. 5, bottom). Most striking is that 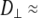 1 × 108 s−1 and
1 × 108 s−1 and 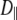 < 0.1 × 108 s−1 for Model I. This implies that slow relaxation times
< 0.1 × 108 s−1 for Model I. This implies that slow relaxation times 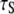 observed in experiment and the slowest decay time
observed in experiment and the slowest decay time 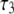 obtained in the simulation (Table 1) arise almost exclusively from wobble. If this is indeed the case, the comparable
obtained in the simulation (Table 1) arise almost exclusively from wobble. If this is indeed the case, the comparable 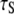 of natural lipids and those tethered at their acyl chains is simple to understand: although tethering effectively eliminates axial rotation, it does not substantially change wobble.
of natural lipids and those tethered at their acyl chains is simple to understand: although tethering effectively eliminates axial rotation, it does not substantially change wobble.
FIGURE 5.
Correlation functions for P-HA and P-O11 from MD simulations and best fits from Models I (Eq. 11a) and II (Eq. 11b). Insets show short time behavior.
Model II, which does not have wobble, yields 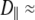 1–2 × 108 s−1, as required to describe a 5−10 ns decay. The fast relaxation time,
1–2 × 108 s−1, as required to describe a 5−10 ns decay. The fast relaxation time, 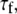 is uniformly smaller for Model I and the order parameter,
is uniformly smaller for Model I and the order parameter, 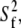 is uniformly higher. This is because Model I, with nine exponentials for overall rotation (Eq. 8), contains the wide range of decays present in the correlation function calculated from the simulation. Model II, which is limited to two exponential decay terms for the overall rotation (Eq. 9), recruits the fast term to describe motions associated with rotation.
is uniformly higher. This is because Model I, with nine exponentials for overall rotation (Eq. 8), contains the wide range of decays present in the correlation function calculated from the simulation. Model II, which is limited to two exponential decay terms for the overall rotation (Eq. 9), recruits the fast term to describe motions associated with rotation.
Both models assume that the lipid is rotating as a single unit. Consequently, 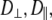 and
and 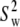 should be similar for different vectors for Model I, and
should be similar for different vectors for Model I, and 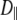 should be similar for Model II; β can be different, as will terms associated with the fast motions,
should be similar for Model II; β can be different, as will terms associated with the fast motions, 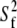 and
and 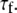 As evident from Table 4, the three overall motion parameters for the glycerol and acyl chain regions for Model I are quite consistent:
As evident from Table 4, the three overall motion parameters for the glycerol and acyl chain regions for Model I are quite consistent: 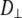 ranges from 1.4 to 3.2 × 108 s−1,
ranges from 1.4 to 3.2 × 108 s−1, 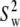 ≈ 0.6, and
≈ 0.6, and 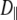 ≤ 1 × 107 s−1. These results support the notion that this portion of DPPC can be modeled as a rigid body to understand rotational relaxation.
≤ 1 × 107 s−1. These results support the notion that this portion of DPPC can be modeled as a rigid body to understand rotational relaxation.
In contrast to the results for the glycerol and acyl chain regions, Model I yields 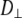 ≈ 4 × 108 s−1 for the P-O12 and P-N vectors; i.e., the same rigid-body parameters cannot describe both the body and the head of the lipid. Other parameter combinations (including constraints) were tested, and similar inconsistencies emerged. Such behavior would be expected, for example, if two parts of an object were connected with a universal joint. A reasonable inference here is that the choline group is rotating relatively independently of the rest of the lipid about the P-O11 bond (Fig. 2). This can be directly tested from the simulation by calculating the potential of mean force (pmf) of selected angles
≈ 4 × 108 s−1 for the P-O12 and P-N vectors; i.e., the same rigid-body parameters cannot describe both the body and the head of the lipid. Other parameter combinations (including constraints) were tested, and similar inconsistencies emerged. Such behavior would be expected, for example, if two parts of an object were connected with a universal joint. A reasonable inference here is that the choline group is rotating relatively independently of the rest of the lipid about the P-O11 bond (Fig. 2). This can be directly tested from the simulation by calculating the potential of mean force (pmf) of selected angles 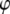 :
:
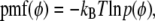 |
(13) |
where 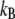 is the Boltzmann constant, T is temperature, and
is the Boltzmann constant, T is temperature, and 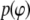 is the (binned) probability of
is the (binned) probability of 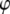 ; the pmf is typically offset so that lowest energy is zero. Fig. 6 plots the pmfs for P-O11-C3g-C2g (α1) and O12-P-O11-C3g (α2). The α1 torsion is primarily in the trans conformation (180°), and rotation is highly hindered by the 7 kcal/mol barrier. This adds to the rigidity of the glycerol group. In contrast, α2 populates gauche− (−60°) and gauche+ (60°) states with nearly equal probability, and the barrier between them is only 1.3 kcal/mol. The population of the trans state for α2 is 20%, and the gauche-trans barrier is only 1.1 kcal/mol. This allows the choline group to rotate 360° without great energetic penalty. Hence, the combination of the stiff glycerol region and the low barriers for rotation of α2 effectively permits DPPC to “swivel” about the P-O11 bond. Headgroup rotation has long been recognized to be important in 31P-NMR (28). The results here from simulation and modeling are consistent with this assertion.
; the pmf is typically offset so that lowest energy is zero. Fig. 6 plots the pmfs for P-O11-C3g-C2g (α1) and O12-P-O11-C3g (α2). The α1 torsion is primarily in the trans conformation (180°), and rotation is highly hindered by the 7 kcal/mol barrier. This adds to the rigidity of the glycerol group. In contrast, α2 populates gauche− (−60°) and gauche+ (60°) states with nearly equal probability, and the barrier between them is only 1.3 kcal/mol. The population of the trans state for α2 is 20%, and the gauche-trans barrier is only 1.1 kcal/mol. This allows the choline group to rotate 360° without great energetic penalty. Hence, the combination of the stiff glycerol region and the low barriers for rotation of α2 effectively permits DPPC to “swivel” about the P-O11 bond. Headgroup rotation has long been recognized to be important in 31P-NMR (28). The results here from simulation and modeling are consistent with this assertion.
FIGURE 6.
pmf for the torsions P-O11-C3g-C2g (α1, top) and O12-P-O11-C3g (α2, bottom). The pmf near α1 = 0 is not smooth because of incomplete sampling.
The preceding discussion of rigid-body motions is not to minimize the effects of internal, or “fast”, motions. From Table 4, 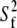 = 0.50 for P-HA. From the cone model, an order parameter, S, can be related to a cone angle,
= 0.50 for P-HA. From the cone model, an order parameter, S, can be related to a cone angle, 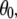 by (29)
by (29)
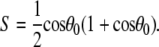 |
(14) |
The resulting value 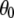 = 38° indicates that fast motions sweep out a substantial solid angle.
= 38° indicates that fast motions sweep out a substantial solid angle. 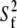 for the acyl carbons is substantially lower, as expected for very flexible chains. The
for the acyl carbons is substantially lower, as expected for very flexible chains. The 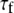 obtained for the acyl chains are in near quantitative agreement with model-free fits (30) to 13C
obtained for the acyl chains are in near quantitative agreement with model-free fits (30) to 13C 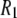 data (31) and our earlier MD simulations (7,32).
data (31) and our earlier MD simulations (7,32).
The fitted values of 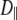 from Model I equaled 0 for many of the vectors. Those with
from Model I equaled 0 for many of the vectors. Those with 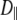 > 0 tended to have higher values of β and
> 0 tended to have higher values of β and 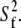 These geometrical features retard axial averaging by wobble and internal motions and thereby allow estimation of
These geometrical features retard axial averaging by wobble and internal motions and thereby allow estimation of 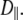 A value of 1 × 107 s−1 appears to be reasonable based on the analysis here but is substantially less certain than the estimate of
A value of 1 × 107 s−1 appears to be reasonable based on the analysis here but is substantially less certain than the estimate of 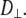 When
When  ≈ 0 for a particular vector, axial rotation will have little or no effect on
≈ 0 for a particular vector, axial rotation will have little or no effect on 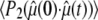 and, consequently, on
and, consequently, on 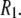 This implies that correlation times on the timescale of
This implies that correlation times on the timescale of 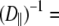 100 ns are unlikely to contribute to 31P relaxation.
100 ns are unlikely to contribute to 31P relaxation.
With 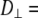 1–2 × 108 s−1 and
1–2 × 108 s−1 and 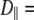 1 × 107 s−1, the axial ratio
1 × 107 s−1, the axial ratio 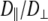 = 0.05–0.1. This is far from the value expected from a simple hydrodynamic treatment for rigid cylinders (33,34). Assuming that DPPC is a cylinder of length 20 Å (half the thickness of the bilayer) and diameter 9 Å (from the surface area of 64 Å2),
= 0.05–0.1. This is far from the value expected from a simple hydrodynamic treatment for rigid cylinders (33,34). Assuming that DPPC is a cylinder of length 20 Å (half the thickness of the bilayer) and diameter 9 Å (from the surface area of 64 Å2), 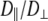 = 2.5. Analysis of internal motions of the lipid chains based on both experiment (31) and simulation (32) indicate that the viscosity of the bilayer interior is similar to neat hexadecane. Setting the viscosity to 1.87 cP (the value for hexadecane at 323 K) yields
= 2.5. Analysis of internal motions of the lipid chains based on both experiment (31) and simulation (32) indicate that the viscosity of the bilayer interior is similar to neat hexadecane. Setting the viscosity to 1.87 cP (the value for hexadecane at 323 K) yields 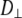 = 1.5 × 108 s−1, a value in the range obtained from the simulations. The 10% temperature correction applied to the simulated
= 1.5 × 108 s−1, a value in the range obtained from the simulations. The 10% temperature correction applied to the simulated 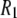 s at low field is also consistent with the 9% viscosity difference of hexadecane at 318 and 323 K. The simulated axial ratio then indicates that
s at low field is also consistent with the 9% viscosity difference of hexadecane at 318 and 323 K. The simulated axial ratio then indicates that 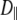 is substantially lower than expected from hydrodynamics of a lipid-sized cylinder. Likewise, the preceding hydrodynamic treatment yields a translational diffusion constant
is substantially lower than expected from hydrodynamics of a lipid-sized cylinder. Likewise, the preceding hydrodynamic treatment yields a translational diffusion constant 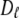 = 1.7 × 10−6 cm2/s, over 10 times larger than the experimental value (35) of 1.5 × 10−7 cm2/s. This result implies that axial rotation and lateral diffusion are retarded by strong interactions (e.g., hydrogen bonds and salt bridges) in the glycerol and headgroup regions compared to wobble.
= 1.7 × 10−6 cm2/s, over 10 times larger than the experimental value (35) of 1.5 × 10−7 cm2/s. This result implies that axial rotation and lateral diffusion are retarded by strong interactions (e.g., hydrogen bonds and salt bridges) in the glycerol and headgroup regions compared to wobble.
Lastly, the results presented here provide a molecular interpretation of the axially averaged lineshape observed for both 31P and deuterium NMR lineshapes in the liquid-crystalline state of bilayers. The lineshapes from acyl chains of lipids in the gel phase bilayers are not axially averaged (36), as would be expected from the greatly reduced range of motion. In contrast, both dielectric relaxation (37) and 31P-NMR (38) studies of DPPC bilayers indicate that the choline group is relatively flexible even in the gel, and, in fact, the lineshape is axially symmetric in excess water and above −10°C (39,40). The simulation results and the model presented here are consistent with this observation. The choline headgroup is relatively uncoupled from the remainder of the lipid, and it is plausible that sufficient averaging can take place by internal motions in the absence of wobble or rotation about the lipid axis. However, substantial differences in 31P-NMR relaxation with the liquid-crystal state are expected because the dipolar interactions with the choline hydrogens are much weaker than those with the glycerol hydrogens.
CONCLUSIONS
31P spin-lattice relaxation rates calculated from MD simulations agree well with experimental values obtained from 1000-Å-diameter DPPC vesicles over the frequency range 0.02–21.13 T. The dominant slow relaxation times are ∼10 ns at low frequency (where dipolar interactions dominate) and 3 ns at higher frequency (where CSA dominates). Both the dipolar and CSA 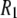 's also contain substantial contributions from other internal motions, leading to relaxation on the 100 ps timescale.
's also contain substantial contributions from other internal motions, leading to relaxation on the 100 ps timescale.
These results place a caution on model-free analysis of 31P-NMR relaxation. In essence, the presence of two “slow” relaxation times (one for the dipolar and one for the CSA) potentially confounds fitting data over a large frequency range. A reasonable approach is to consider very low and very high field regions separately.
Neither NMR relaxation nor simulation studies directly provide models of molecular motion. Based on the very good agreement of simulation and experiment, calculated correlation functions were fit to two motional models. Model I (which combines wobble, axial rotation, and internal motion, as sketched in Fig. 1) provided a better fit than Model II (axial rotational and internal motion only). However, a single set of rigid-body parameters, 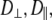 and
and 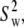 is not applicable to the entire lipid. Rather, two sets, one for the phosphorus, glycerol group, and the acyl chains (denoted here the “body”) and the other for the choline group are necessary. Hence, these two regions of DPPC are partially uncoupled by relatively free rotation about the P-O11 bond.
is not applicable to the entire lipid. Rather, two sets, one for the phosphorus, glycerol group, and the acyl chains (denoted here the “body”) and the other for the choline group are necessary. Hence, these two regions of DPPC are partially uncoupled by relatively free rotation about the P-O11 bond.
With the preceding distinction made, the 10-ns relaxation is associated with wobble of the lipid body, with 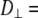 1–2 × 108 s−1. Rotation about lipid long axis (axial rotation) is much slower, with
1–2 × 108 s−1. Rotation about lipid long axis (axial rotation) is much slower, with 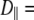 1 × 107 s−1, and does not appear to contribute appreciably to 31P relaxation. Because of extensive averaging by wobble and fast motions, the value of
1 × 107 s−1, and does not appear to contribute appreciably to 31P relaxation. Because of extensive averaging by wobble and fast motions, the value of 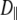 should be considered tentative. As noted above, the 3 ns relaxation indicates that the choline group is partially uncoupled from the rest of the lipid. The
should be considered tentative. As noted above, the 3 ns relaxation indicates that the choline group is partially uncoupled from the rest of the lipid. The 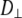 for the P-O12 and P-N vectors ≈ 4 × 108 s−1 and reflects motions of both the lipid body and headgroup.
for the P-O12 and P-N vectors ≈ 4 × 108 s−1 and reflects motions of both the lipid body and headgroup.
The value of 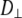 for the lipid body is similar to that of a cylinder of lipid dimensions rotating in a homogeneous fluid with a viscosity of neat hexadecane. The fast relaxation times (14–40 ps for Model I) of the chain CH vectors are almost identical to the torsional dynamics of neat hexadecane. In contrast, the diffusion constants for axial rotation and lateral translation are not consistent with the dynamics of a cylinder in such a low viscosity medium. It is proposed that specific interactions in the water/lipid interface retard this axial rotation and diffusion while leaving wobble relatively unperturbed. The fast rotation of the P-N vector likely plays a minor role in modulating these motions.
for the lipid body is similar to that of a cylinder of lipid dimensions rotating in a homogeneous fluid with a viscosity of neat hexadecane. The fast relaxation times (14–40 ps for Model I) of the chain CH vectors are almost identical to the torsional dynamics of neat hexadecane. In contrast, the diffusion constants for axial rotation and lateral translation are not consistent with the dynamics of a cylinder in such a low viscosity medium. It is proposed that specific interactions in the water/lipid interface retard this axial rotation and diffusion while leaving wobble relatively unperturbed. The fast rotation of the P-N vector likely plays a minor role in modulating these motions.
Although a slight (0.1 Å) reduction in the P-H distances virtually eliminates disagreement of simulation at lower fields, it is also possible that collective motions of the vesicle (31) contribute to the NMR relaxation at these fields. To probe this behavior, simulations of substantially larger systems may be required.
Acknowledgments
We thank Klaus Gawrisch and Attila Szabo for helpful discussions.
This research was supported in part by the Intramural Research Program of the National Institutes of Health, National Heart, Lung and Blood Institute. Support from National Science Foundation MCB-0517381 (to M.F.R.) and National Institutes of Health GM 077974 (to A.G.R.) is also acknowledged.
Jeffery B. Klauda's present address is Dept. of Chemical and Biomolecular Engineering, University of Maryland, College Park, MD 20742.
Editor: Klaus Schulten.
References
- 1.Redfield, A. G. 2003. Shuttling device for high-resolution measurements of relaxation and related phenomena in solution at low field, using a shared commercial 500 MHz NMR instrument. Magn. Reson. Chem. 41:753–768. [Google Scholar]
- 2.Roberts, M. F., and A. G. Redfield. 2004. High-resolution 31P field cycling NMR as a probe of phospholipid dynamics. J. Am. Chem. Soc. 126:13765–13777. [DOI] [PubMed] [Google Scholar]
- 3.Roberts, M. F., and A. G. Redfield. 2004. Phospholipid bilayer surface configuration probed quantitatively by P-31 field-cycling NMR. Proc. Natl. Acad. Sci. USA. 101:17066–17071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chan, S. I., G. W. Feigenson, and C. H. A. Seiter. 1972. Anisotropic and restricted molecular motion in lecithin bilayers. Biochem. Biophys. Res. Commun. 46:1488–1492. [DOI] [PubMed] [Google Scholar]
- 5.Klauda, J. B., B. R. Brooks, and R. W. Pastor. 2006. Dynamical motions of lipids and a finite size effect in simulations of bilayers. J. Chem. Phys. 125:144710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Pastor, R. W., R. M. Venable, M. Karplus, and A. Szabo. 1988. A simulation based model of NMR T1 relaxation in lipid bilayer vesicles. J. Chem. Phys. 89:1128–1140. [Google Scholar]
- 7.Pastor, R. W., R. M. Venable, and S. E. Feller. 2002. Lipid bilayers, NMR relaxation, and computer simulations. Acc. Chem. Res. 35:438–446. [DOI] [PubMed] [Google Scholar]
- 8.Klauda, J. B., N. V. Eldho, K. Gawrisch, B. R. Brooks, and R. W. Pastor. 2008. Collective and noncollective models of NMR relaxation in lipid vesicles and multilayers. J. Phys. Chem. B. In press. [DOI] [PubMed]
- 9.Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM –a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- 10.Phillips, J. C., R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale, and K. Schulten. 2005. Scalable molecular dynamics with NAMD. J. Comput. Chem. 26:1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Klauda, J. B., B. R. Brooks, A. D. MacKerell Jr., R. M. Venable, and R. W. Pastor. 2005. An ab initio study on the torsional surface of alkanes and its effect on molecular simulations of alkanes and a DPPC bilayer. J. Phys. Chem. B. 109:5300–5311. [DOI] [PubMed] [Google Scholar]
- 12.Nosé, S., and M. L. Klein. 1983. A study of solid and liquid carbon tetrafluoride using the constant pressure molecular-dynamics technique. J. Chem. Phys. 78:6928–6939. [Google Scholar]
- 13.Hoover, W. G. 1985. Canonical dynamics—equilibrium phase-space distributions. Phys. Rev. A. 31:1695–1697. [DOI] [PubMed] [Google Scholar]
- 14.Zhang, Y. H., S. E. Feller, B. R. Brooks, and R. W. Pastor. 1995. Computer-simulation of liquid/liquid interfaces. I. Theory and application to octane/water. J. Chem. Phys. 103:10252–10266. [Google Scholar]
- 15.Feller, S. E., Y. H. Zhang, and R. W. Pastor. 1995. Computer-simulation of liquid/liquid interfaces. II. Surface-tension area dependence of a bilayer and monolayer. J. Chem. Phys. 103:10267–10276. [Google Scholar]
- 16.Darden, T., D. York, and L. Pedersen. 1993. Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
- 17.Lagüe, P., R. W. Pastor, and B. R. Brooks. 2004. Pressure-based long-range correction for Lennard-Jones interactions in molecular dynamics simulations: application to alkanes and interfaces. J. Phys. Chem. B. 108:363–368. [Google Scholar]
- 18.Nagle, J. F., and S. Tristram-Nagle. 2000. Structure of lipid bilayers. Biochim. Biophys. Acta. 1469:159–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wallach, D. 1967. Effect of internal rotation on angular correlation functions. J. Chem. Phys. 47:5258–5268. [Google Scholar]
- 20.Lipari, G., and A. Szabo. 1982. Model-free approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 104:4546–4559. [Google Scholar]
- 21.Abragam, A. 1961. The Principles of Nuclear Magnetism. Clarendon Press, Oxford, UK.
- 22.Herzfeld, J., R. G. Griffin, and R. A. Haberkorn. 1978. P-31 chemical-shift tensors in barium diethyl phosphate and urea-phosphoric acid: model compounds for phospholipid head-group studies. Biochemistry. 17:2711–2718. [DOI] [PubMed] [Google Scholar]
- 23.Szabo, A. 1984. Theory of fluorescence depolarization in macromolecules and membranes. J. Chem. Phys. 81:150–167. [Google Scholar]
- 24.Huntress, W. T. 1968. Effects of anisotropic molecular rotational diffusion on nuclear magnetic relaxation in liquids. J. Chem. Phys. 48:3524–3533. [Google Scholar]
- 25.Woessner, D. E. 1962. Nuclear spin relaxation in ellipsoids undergoing rotational Brownian motion. J. Chem. Phys. 37:647–654. [Google Scholar]
- 26.Klauda, J. B., R. M. Venable, A. D. MacKerell, and R. W. Pastor. Considerations for lipid force field development. In Computational Modeling of Membrane Bilayers. S. E. Feller, editor. Current Topics in Membranes 63. Elsevier, San Diego, CA. In press.
- 27.Ottiger, M., and A. Bax. 1998. Determination of relative N-H-N N-C′, C-alpha-C′, and C(alpha)-H-alpha effective bond lengths in a protein by NMR in a dilute liquid crystalline phase. J. Am. Chem. Soc. 120:12334–12341. [Google Scholar]
- 28.Kohler, S. J., and M. P. Klein. 1977. Orientation and dynamics of phospholipid head groups in bilayers and membranes determined from P-31 nuclear magnetic-resonance chemical shielding tensors. Biochemistry. 16:519–526. [DOI] [PubMed] [Google Scholar]
- 29.Lipari, G., and A. Szabo. 1980. Effect of librational motion on fluorescence depolarization and nuclear magnetic-resonance relaxation in macromolecules and membranes. Biophys. J. 30:489–506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Szabo, A. 1986. Nuclear magnetic resonance relaxation and the dynamics of proteins and membranes. Ann. N. Y. Acad. Sci. 482:44–50. [DOI] [PubMed] [Google Scholar]
- 31.Brown, M. F., A. A. Ribeiro, and G. D. Williams. 1983. New view of lipid bilayer dynamics from 2H and 13C NMR relaxation-time measurements. Proc. Natl. Acad. Sci. USA. 80:4325–4329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Venable, R. M., Y. H. Zhang, B. J. Hardy, and R. W. Pastor. 1993. Molecular-dynamics simulations of a lipid bilayer and of hexadecane—an investigation of membrane fluidity. Science. 262:223–226. [DOI] [PubMed] [Google Scholar]
- 33.Tirado, M. M., and J. Garcia de la Torre. 1980. Rotational-dynamics of rigid, symmetric top macromolecules—application to circular-cylinders. J. Chem. Phys. 73:1986–1993. [Google Scholar]
- 34.Tirado, M. M., and J. Garcia de la Torre. 1979. Translational friction coefficients of rigid, symmetric top macromolecules—application to circular-cylinders. J. Chem. Phys. 71:2581–2587. [Google Scholar]
- 35.Scheidt, H. A., D. Huster, and K. Gawrisch. 2005. Diffusion of cholesterol and its precursors in lipid membranes studied by H-1 pulsed field gradient magic angle spinning NMR. Biophys. J. 89:2504–2512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Davis, J. H. 1983. The description of membrane lipid conformation, order and dynamics by H-2-NMR. Biochim. Biophys. Acta. 737:117–171. [DOI] [PubMed] [Google Scholar]
- 37.Shepherd, J. C. W., and G. Buldt. 1978. Zwitterionic dipoles as a dielectric probe for investigating head group mobility in phospholipid membranes. Biochim Biophys Acta. 514:83–94. [DOI] [PubMed] [Google Scholar]
- 38.Seelig, J. 1978. 31P nuclear magnetic resonance and the head group structure of phospholipids in membranes. Biochim Biophys Acta. 515:105–140. [DOI] [PubMed] [Google Scholar]
- 39.Griffin, R. G. 1976. Observation of effect of water on P-31 nuclear magnetic-resonance spectra of dipalmitoyllecithin. J. Am. Chem. Soc. 98:851–853. [DOI] [PubMed] [Google Scholar]
- 40.Griffin, R. G., L. Powers, and P. S. Pershan. 1978. Head-group conformation in phospholipids—P-31 nuclear magnetic-resonance study of oriented monodomain dipalmitoylphosphatidylcholine bilayers. Biochemistry. 17:2718–2722. [DOI] [PubMed] [Google Scholar]