Electrostatic Free Energy Landscapes for DNA Helix Bending

Abstract

Nucleic acids are highly charged polyanionic molecules; thus, the ionic conditions are crucial for nucleic acid structural changes such as bending. We use the tightly bound ion theory, which explicitly accounts for the correlation and ensemble effects for counterions, to calculate the electrostatic free energy landscapes for DNA helix bending. The electrostatic free energy landscapes show that DNA bending energy is strongly dependent on ion concentration, valency, and size. In a Na⁺ solution, DNA bending is electrostatically unfavorable because of the strong charge repulsion on backbone. With the increase of the Na⁺ concentration, the electrostatic bending repulsion is reduced and thus the bending becomes less unfavorable. In contrast, in an Mg²⁺ solution, ion correlation induces a possible attractive force between the different parts of the helical strands, resulting in bending. The electrostatically most favorable and unfavorable bending directions are toward the major and minor grooves, respectively. Decreasing the size of the divalent ions enhances the electrostatic bending attraction, causing an increased bending angle, and shifts the most favorable bending to the direction toward the minor groove. The microscopic analysis on ion-binding distribution reveals that the divalent ion-induced helix bending attraction may come from the correlated distribution of the ions across the grooves in the bending direction.

INTRODUCTION

Nucleic acid (DNA and RNA) helices are highly charged polyanionic molecules. They are usually quite rigid because of the strong Coulombic repulsion between the backbone charges. The presence of the metal ions in solutions, such as Na⁺ and Mg²⁺ ions, can neutralize the negative backbone charges and screen the Coulomb repulsion, which would increase the flexibility of nucleic acids and consequently assist the folding process of nucleic acids (1–11). Therefore, ionic properties, such as ion concentration, ion valency, and ion size, can play a crucial role in the flexibility and the folding of DNAs and RNAs.

The bending flexibility of double-stranded (ds) DNAs is highly relevant to DNA biological functions, such as DNA wrapping around histone protein to form nucleosomes, packaging inside bacteriophage capsids, and binding to proteins (1,12–16). The flexibility of nucleic acids has been investigated extensively through various experimental methods, such as gel electrophoresis, electrooptical technique, and single molecule techniques (17–24). In the past three decades, extensive experiments have been performed to investigate the ion dependence of DNA flexibility (17–24). However, the experiments mainly focused on Na⁺ (or K⁺) effects. For Mg²⁺ and other multivalent ions, quantitative understanding for dsDNA bending remains very limited (17,18,20–24).

Parallel to the experimental studies, several theoretical and computational models have been developed to quantify the ion effects of DNA bending and the persistence length based on the Debye-Hückel (DH) theory (25–27), the counterion condensation (CC) theory (28–31), the (cylindrical) Poisson-Boltzmann (PB) theory (32,33), and the discrete-charge interaction model (34–36). The existing theories, including the DH, CC, and PB theories, have been quite successful in predicting the electrostatics of nucleic acids and proteins (25–44). However, most theories either use simplified models for DNA structure such as the uniform cylinder and the line-charge models or ignore the added salt in the supporting solution. The simplified structural models lack the details of the local bending structure as well as the ion binding distribution. Models neglecting the added salt cannot treat the ion-concentration-dependent properties. Moreover, the DH theory is the linearized analytical form of PB equation, thus is only applicable to weak electrostatic field. The CC theory is based on the assumption of two-state ion distribution and is a double-limit law, i.e., it is developed for dilute salt solution and nucleic acids of infinite length (28). The PB theory is a mean-field theory (37–44). It ignores ion-ion correlations which can be important for multivalent ions, e.g., Mg²⁺ (45–51). Recently, we developed a statistical mechanical (tightly bound ion, TBI) theory (47–51). The primary motivation for developing the TBI theory was to account for the correlations and fluctuations for bound ions. The TBI model can reproduce the experimental results on the thermal stabilities of DNA and RNA helices of finite lengths in Na⁺ and Mg²⁺ solutions (48,51) and the ion-mediated DNA helix assembly (49,50). Here we go beyond the helix structure by considering the different bent shapes of DNA.

An elementary problem in DNA bending is the mechanism of the driving force. Previous theoretical and experimental works suggest that the electrostatic force may play the major role for protein-induced DNA bending and ion-induced DNA bending (10,11,15,29,34). For protein-induced DNA bending, the asymmetric charge neutralization for the phosphate groups can cause the bending (29,31), as suggested by the experiments with phosphate substitutions (52) and with tethered charges (53), and by the all-atom simulations (54). For multivalent ion-induced DNA bending, experiments indicated that the cations localized in the grooves may be critical for DNA bending (10,55,56). Electrostatic modeling by placing a multivalent cation in the major (34) and minor (35) grooves showed that an increased Coulombic attraction between the cation and the bent strands of phosphate charges (34,35) can stabilize a bent structure. However, the a priori placement of a cation in the grooves is an ad hoc procedure. In addition, the previous electrostatic modeling neglects the ion entropy and the (electrostatic and excluded volume) correlation effects for the ions.

Here, we develop a model to predict DNA bending in Na⁺ and Mg²⁺ ionic solutions. The model is based on a newly refined TBI theory. We will first generalize the original TBI model by using the generalized Born (GB) theory to account for the dielectric polarization effect (57–62). We then use the new TBI model to investigate the Na⁺- and Mg²⁺- and ion-size dependences of DNA bending configuration such as the bending angle. Compared to the previous electrostatic (e.g., discrete-charge) models (34–36), this generalized TBI model: 1), is based on the realistic DNA helical structure; 2), can treat the effect of the added salt in the supporting solution; and 3), explicitly treats ion correlations and ensemble of ion distributions (i.e., different ion-binding configurations) (47–51). We calculate the full electrostatic free energy landscape for different bending configurations and consider a wide range of ion concentrations in the supporting solution. Furthermore, we compute the detailed ion distributions, from which we analyze the driving force of the bending.

METHODS

Electrostatic free energy landscape for DNA helix bending

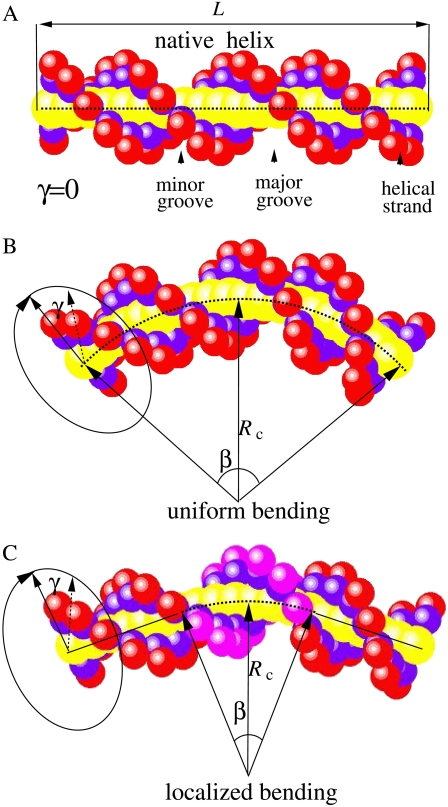
We model DNA helix structure using a reduced atomic model, i.e., the grooved primitive DNA model (47–51,63); see Appendix A for details. We consider two types of DNA helix bending modes: the uniform bending (shown in Fig. 1 B) where the whole DNA helix is assumed to be bent uniformly along the axis, and the localized bending (shown in Fig. 1 C) where only the central helix part (six basepairs) is bent uniformly along the axis. As shown in Fig. 1, a bent structure can be generated through the following procedure: To rotate the original unbent helix around its helix by an angle γ (Fig. 1), then bend the helix axis by angle β, either locally or uniformly. Therefore, a bent helix can be described by two structural parameters: the axial rotation angle γ and the bending angle β (or equivalently the bending curvature radius R_c). The value γ describes the bending direction and β describes the degree of bending in the direction specified by the γ angle. The expression γ ∼ 2π/5 (7π/5) represents bending toward the major (minor) groove for the localized bending and toward the minor- (major-)groove-rich direction for the uniform bending model.

FIGURE 1.

The bending models for a canonical B-form DNA helix with length L. (A) The native DNA helix. (B) The uniform bending mode where the whole helix is bent uniformly along the helical axis. (C) The localized bending mode where only the central six basepairs are bent uniformly along its axis and the two end parts keep straight. The bent DNA helix (bottom) can be characterized by two structural parameters (γ, β). The value γ describes the bending direction and β describes the bending sharpness. The DNA helix is produced from the grooved primitive model, and the red and blue spheres represent the phosphate and the neutral groups, respectively. In the localized bending model, the central bent six basepairs are illustrated in magenta; see Appendix A for the details on the grooved primitive DNA model, the uniform bending model, and the localized bending model (47–51,63).

The electrostatic bending free energy is given by the electrostatic free energy difference ΔG_E between the bent and unbent states,

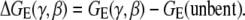(1)

We call the free energy ΔG_E(γ, β) for different configurations; (γ, β) is the electrostatic free energy landscape for the bending. Specifically, we explore the configurational space with 0 ≤ γ ≤ 2π and 0 ≤ β ≤ 40° (for a six-basepair range) involved in the bending (10,34,35,64,65).

A new TBI theory with the generalized Born model

We first generalize the TBI model by including the polarization energy (due to the dielectric discontinuity at the molecule/solvent interface) and ion self-energy using the generalized Born (GB) model. In this section, we will describe the development of the new TBI model briefly and leave the details to Appendices B and C.

In the TBI model for mixed mono/multivalent ions, monovalent ions and multivalent ions are treated separately, to account for the effect of the possible strong correlation for the multivalent ions. Monovalent ions are treated as a diffusive ionic background which can be described by the mean-field PB theory (51). For the multivalent ions, because the ion-correlation can be strong, we classify two types of multivalent ions according to the strength of ion-correlation (47–51): the (strongly correlated) tightly bound ions and the (weakly correlated) diffusive ions. Correspondingly, the whole space is divided into the tightly bound region and the diffusive region, respectively. The motivation to distinguish the two types of multivalent ions (and the two spatial regions for the multivalent ions) is to treat different ions appropriately: for the diffusive multivalent ions, we use PB, and for the tightly bound multivalent ions, we go beyond PB by accounting for the ion-ion correlation (47–51).

For an N-bp DNA helix, the whole tightly bound region is divided into 2N (tightly bound) cells, each around a phosphate. In the calculation, we discretize the space using grids. For each grid point inside the tightly bound region, we find the closest phosphate. In such a way, we can uniquely identify the set of grid points that are in close proximity of each phosphate. These grid points constitute the tightly bound cell for each phosphate. In each cell, e.g., the i^th cell, there can exist m_i = 0, 1, 2.. tightly bound multivalent ions (47–51). Each possible set of the 2N numbers, {m₁, m₂, …, m_2N} defines a binding mode. In practice, we allow at most one multivalent ion in each cell because one multivalent ion would result in charge inversion of the cell. Therefore, for an N-bp (2N-phosphate) DNA, there exist 2^2N binding modes for multivalent ions. The total partition function Z is given by the sum over all the possible binding modes M:

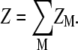(2)

Z_M is the partition function for a given binding mode M (47–51),

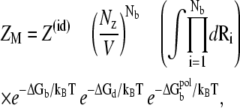(3)

where Z^(id) is the partition function for the uniform ion solution (without the polyelectrolyte). The value N_b is the number of the tightly bound ions, N_z/V is the bulk concentration of the z-valent ion for a 1:z ionic solution (N_z is the total number of the z-valent ions and V is the volume), and R_i denotes the position of the i^th tightly bound ion. The volume integral 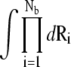over the tightly bound region provides a measure for the free accessible space for the N_b tightly bound ions. ΔG_b is the free energy for the tightly bound ions, being the mean Coulombic interaction energy between the charges in different cells (including the phosphate groups and the tightly bound ions) within the tightly bound region. ΔG_d is the free energy for the diffusive ions, representing the electrostatic interactions between the diffusive ions, between the diffusive ions and the charges in the tightly bound region, and the entropic free energy of the diffusive ions. 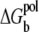is the (Born) self-polarization energy for the charges within the tightly bound region, and is a new term added for this TBI theory.

The free energy of the tightly bound ions

ΔG_b in Eq. 3 can be calculated as the summation of potentials of mean force (47–51),

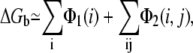(4)

where Φ₁(i) is the potential of mean force for the Coulomb interactions between the different charges within a tightly bound cell i, and Φ₂(i, j) is for the interactions between charges in the cells i and j. In the calculation for the potentials of mean force, we account for the detailed molecular structure (and the associated excluded volume and charge distribution), ion valency, and volume (47–51). In this new TBI model, we account for the polarization effect of the dielectric discontinuity by applying the GB model to the potentials of mean force Φ₁(i) and Φ₂(i, j) (57–62); see Appendix B for details. ΔG_b includes DNA-ion, ion-ion, DNA-solvent, and ion-solvent interactions (through implicit solvent approximation).

The free energy of the diffusive ions

With the mean-field approximation for the diffusive ions (66,67), ΔG_d can be calculated from the following equation (47–51),

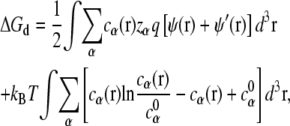(5)

where ψ(r) and ψ′(r) are the electrostatic potentials for the system with and without the diffusive ions, respectively. The values c_α(r) and 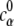are the concentrations of ion species α at position r and in bulk solvent, respectively. The value ψ′(r) is used here because ψ(r) − ψ′(r) gives the contribution to the electrostatic potential from the diffusive ions. The values ψ(r) and ψ′(r) are obtained from the nonlinear PB (with salt) and the Poisson equation (salt free), respectively.

The polarization energy

The new term 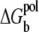in this refined TBI model is the change of the Born (self-)energies for the charges inside the tightly bound region (the 2N phosphate charges and N_b tightly bound ions),

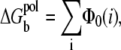(6)

where Φ₀(i) is the Born energy for the charges inside the i^th tightly bound cell. Physically, 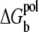is the Born energy change for the charges transferred from the bulk solvent to the tightly bound region; see Appendix B for detailed calculations.

Using the above formulas, we compute the electrostatic free energy as

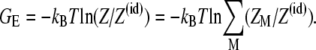(7)

From Eqs. 2–7, G_E accounts for 1), the interactions between phosphate charges, tightly bound ions, and solvent for the tightly bound region; 2), the interactions between diffusive ions (including ion translational entropies) in the diffusive ion region; and 3), the interactions between the diffusive ions and the charges in the tightly bound region. The difference between G_E values for the bent and the unbent DNA helices gives the electrostatic bending free energy through Eq. 1. The detailed procedure for the numerical computations is described in Appendix C.

RESULTS AND DISCUSSIONS

Using the new TBI theory developed here, we have calculated the electrostatic bending free energy landscape for a 20-basepair (bp) DNA helix immersed in a Na⁺ or Mg²⁺ ionic solution. In addition, to test the ion size dependence, we have computed the bending free energy landscape for a small divalent ion (M²⁺). The radii for the three types of ions are 3.5 Å, 4.5 Å (68), and 3.5 Å for Na⁺, Mg²⁺, and M²⁺, respectively. The free energy landscape gives the ion-dependence of the stable bending structure, which can be compared with the experiment.

Ion accessibility to the grooves

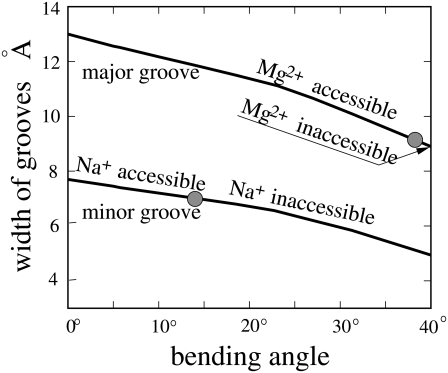
In Fig. 2, we show the width of the minor and major grooves in the bending direction as a function of the bending angle β. This information is important because the width of the groove determines how far an ion with finite size can enter the grooves (1,34,69). For example, the width of the minor groove of an unbent B-DNA helix is ∼8 Å and thus allows ions of radius <4 Å to enter the groove. For a moderate bending (β ∼ 15°), the minor groove, which has a width of ∼7 Å, would allow a hydrated Na⁺ ion (radius ∼3.5 Å) to enter the minor groove and disallow more bulky ligands such as a hydrated Mg²⁺ ion (radius ∼4.5Å) (47–51,68) to deeply enter the groove. By contrast, the major groove (of width ∼13 Å in the unbent state) would allow the binding of the Mg²⁺ ions. Even for sharp bending (β ∼ 27°), the major groove is still sufficiently wide (of width ∼10.7 Å) to allow the bulky ligands such as hydrated Mg²⁺ ions to enter the groove.

FIGURE 2.

The accessible widths of minor and major grooves in the bending direction, as functions of bending angle β (over six basepairs). The shaded circles denote the boundary between accessible/inaccessible widths for Na⁺ and Mg²⁺ ions. Note that the minor groove is always inaccessible for hydrated Mg²⁺, while the major groove is always accessible for Na⁺ over the shown β-range.

Electrostatic bending free energy landscapes

Fig. 3 shows the typical electrostatic bending free energy landscapes ΔG_E(γ, β) for the uniform and the localized bending modes in the solutions of Na⁺, Mg²⁺, and (small) M²⁺ ions, respectively. In the following, we first present the general features for the free energy landscapes. We then discuss the specific features for the different types of ions.

FIGURE 3.

The three-dimensional plot for the electrostatic bending free energy landscapes ΔG_E(γ, β) (in k_BT) for uniformly bent (A–C) and locally bent (E–G) DNA helices with different bending configurations (γ, β) in a solution of 1 M Na⁺ (A and E), 0.1 M Mg²⁺ (B and F), and 0.1 M small divalent ions (M²⁺) with radius 3.5 Å (C and G). The red and blue colors represent the low and high free energies, respectively. The green circles denote the free energy minima at the landscapes, and the red curve (with arrow) denotes the switch between alternative favorable bending modes. (D and H) The illustrations for the bent DNA helix structures in typical bending directions (γ), where β = 25°. Note that γ = 2π/5 (7π/5) is the minor-groove-rich (major-groove-rich) bending direction for the uniform bending mode and is the major (minor)-groove bending direction for the localized bending mode.

General features for electrostatic free energy landscapes

As shown in Fig. 3, the electrostatic bending free energy ΔG_E(γ, β) is strongly dependent on the axial rotation angle γ, bending angle β, ion valency, and ion size. For Na⁺, as shown in Fig. 3 A for the uniform bending and Fig. 3 E for the local bending, ΔG_E is positive, indicating that helix bending is electrostatically unfavorable. The landscape shows that ΔG_E is more/less positive and thus the bending is more/less unfavorable for bending toward the minor/major groove. In contrast, for Mg²⁺, the bending free energies in Fig. 3, B and F, are slightly negative for small bending toward the major groove, suggesting that Mg²⁺ can induce small bending force. For other bending directions, the free energies are positive, especially for the bending toward the minor groove. Therefore, in an Mg²⁺ solution, bending toward the minor (major) groove is unfavorable (favorable). When the size of divalent ion is decreased, the predicted free energy landscape changes dramatically, as shown in Fig. 3, C and G, for M²⁺. M²⁺ ions induce much stronger bending force, and the most favorable bending is toward the minor groove for moderate bending. As for large bending (β ∼ 40°), the most favorable bending is switched to the direction toward the major groove. As will be discussed below, the favorable/unfavorable local bending structure and the bending force are the results of the interplay between the ion valency, ion size, and the groove width.

In Na⁺ solutions

Na⁺ ions have unit positive charges and can only give ionic screening/neutralization for backbone charges, as described by CC and PB theories. For the bending toward minor/major grooves, the approach of two strands would bring stronger/weaker Coulombic repulsions which are partially screened by bound Na⁺. Consequently, in a Na⁺ solution, any bending would be electrostatically unfavorable, and bending toward the minor groove is more unfavorable than toward the major groove because the minor groove is narrower and thus the electrostatic repulsion is stronger; see Fig. 3, A and E, for the uniform and localized bending modes. Furthermore, the energy landscape shows that decreasing [Na⁺] causes weaker ion-binding (due to larger entropy loss upon binding) and thus higher ΔG_E and smaller probability of DNA bending.

In Mg²⁺ solutions

Mg²⁺ ions have higher charges as well as larger size than Na⁺. Mg²⁺ ions can reside between the two opposite backbone stands of the groove to possibly induce an attractive force, in analogy to the Mg²⁺-induced attraction between two DNA helices (49,50,70,71) (and references therein). However, the minor groove is too narrow to accommodate the bulky (hydrated) Mg²⁺ ions (Mg²⁺ radius ∼4.5 Å (47–51,68)) and to induce the attraction between the two backbone strands of the minor groove. Therefore, the two strands of the minor groove repel each other, causing unfavorable bending toward the minor groove. By contrast, the wide major groove would allow Mg²⁺ ions to penetrate into the groove to bridge the two strands of the major groove, inducing an electrostatic attractive force which can drive DNA bending toward the major groove. Therefore, bending toward the major groove is electrostatically favorable.

However, Mg²⁺-induced between the strands is very weak. Unlike the Mg²⁺-induced between two dsDNA helices, the strands of the groove have a much lower charge-density than dsDNA helices and hence have a weaker Mg²⁺-binding and weaker Mg²⁺-mediated attractive force. This is confirmed by our calculated energy landscapes (Fig. 3, B and F), which show a slightly negative ΔG_E for bending toward the major groove as compared to a positive ΔG_E for the minor groove.

Increasing [Mg²⁺] would enhance the Mg²⁺-induced force and thus lower the ΔG_E for bending toward the major groove. This is attributed to the smaller entropic cost for Mg²⁺-binding and hence stronger Mg²⁺-binding at major grooves, causing a stronger bending force (49,50).

In an M²⁺ solution

As shown in Fig. 3, C and G, a decrease in the divalent ion size brings dramatic changes in the free energy landscape. Unlike Mg²⁺ (of radius 4.5 Å), the smaller divalent ion M²⁺ (of radius 3.5 Å) can enter the minor groove (of width 7 Å) and bind to the phosphate strands. The correlation between the ions causes an attractive force between the strands to induce DNA bending toward the minor groove. Such an attractive force is stronger for smaller ions due to the stronger ion-binding (for smaller ions). Therefore, M²⁺ causes a stronger DNA bending than Mg²⁺. Both the major and the minor grooves involve divalent ion-induced attraction, but with different strengths.

The narrow minor groove has a larger phosphate charge density than the wide major groove. Therefore, the minor groove has stronger ion-binding and stronger interstrand attraction. The competition between the interstrand attraction in the major and in the minor grooves leads to a favorable bending toward the minor groove. This is very different in contrast to the favorable bending toward the major groove for Mg²⁺.

For a very sharp bending toward the minor groove (β > 20°), however, the minor groove becomes so narrow that even the small M²⁺ ion will be pushed out from the groove. The situation would be similar to the Mg²⁺ case. Bending toward major groove (e.g., γ = 2π/5) becomes most favorable. However, this favorable bending toward the major groove at sharp bending (β ∼ 40°) is weaker than the favorable bending toward the minor groove at moderate bending angle due to the stronger bending attraction force (for moderate bending toward the minor groove) and the strong intrinsic repulsive force for sharp bending (34–36).

Ion-binding configuration

To provide a physical picture for the driving force for the ion-induced bending attraction, we calculate the ion distribution (ion-binding mode) along unbent and bent DNA helices for both Mg²⁺ and small M²⁺ ions. Here we first present the general features of ion binding configuration responsible for ion-induced attractive force with M²⁺. We use M²⁺ to illustrate the principle because the smaller ions induce a stronger electrostatic bending attractive force and show a more pronounced effect. We then discuss the difference in the ion-binding configuration between M²⁺ and Mg²⁺.

Ion distribution in the bent grooves

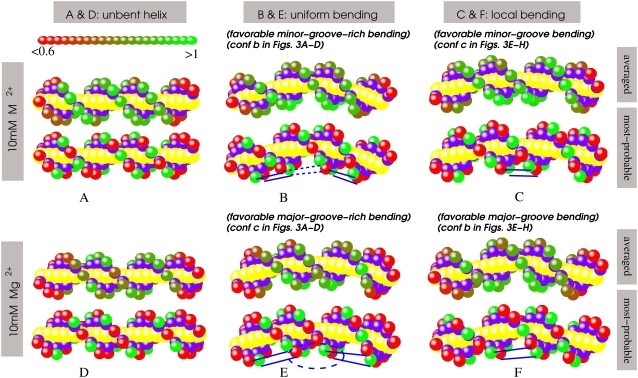
For an unbent helix, ion-binding distribution is nearly uniform except for the 4–6 nucleotides at the two ends (Fig. 4 A) due to the finite length effect. In the most probable distribution, ions are separated by a phosphate to achieve the low energy (Fig. 4 A). It is important to emphasize that an ensemble of low free-energy modes exists for the ion distribution. Here we only show the one with the lowest free energy.

FIGURE 4.

The ion-binding configurations for small divalent ions, M²⁺, radius ∼3.5 Å (A–C) and Mg²⁺ ions (D–F). For each figure panel, the average ion-binding distributions (upper one) and the most probable ion-binding modes (bottom one) are shown, respectively. For the average ion-binding distributions, the green color represents the full neutralization, and the red color describes weak neutralization. For the most probable ion-binding modes, the red spheres represents the unoccupied (bare) phosphates, and the green ones represent the phosphates with tightly bound ions. M²⁺ concentration is 10 mM. The blue lines denote the typical correlated ion configuration across grooves. The shown bending angles β are: (B and C) β = 20°; (E) β = 10°; and (F) β = 25°. Note that γ = 2π/5 (7π/5) is the minor-groove-rich (major-groove-rich) bending direction for the uniform bending mode and is the major (minor)-groove bending direction for the localized bending mode. Panel E shows the correlated ion pattern at the central minor groove. It needs to be noted that the minor groove is too narrow to accommodate (large) hydrated Mg²⁺ and that binding Mg²⁺ should lie outside of the minor groove; however, the present TBI theory can only give the occupied phosphates by binding ions (47).

For a bent helix, the average ion-binding pattern is highly nonsymmetric (29,31,52): More ions are distributed on the side in the bending direction due to the increased charge density of the phosphates (Fig. 4, B and C). The most probable ion-binding pattern (Fig. 4, B and C) shows the correlated ion distribution: If an ion bind to a phosphate, the closest phosphate on the other side of groove would be empty to reduce the Coulomb energy; see, for example, the M²⁺ distribution in the minor groove in a uniformly bent helix (Fig. 4 B) and in a locally bent helix (Fig. 4 C). Such correlated distribution would cause an attractive force between the strands and lead to bending deformation (49,50,72).

Mg²⁺ versus M²⁺

Compared with the M²⁺ ions discussed above, Mg²⁺ ions have a larger size, which leads to two effects: 1), the minor groove is not accessible to Mg²⁺; and 2), the ion-phosphate attraction is weaker, which would cause less tightly bound Mg²⁺ ions and less freedom in ion movement near molecular surface, especially near minor grooves. As shown in Fig. 4, there are fewer tightly bound Mg²⁺ ions, as compared with M²⁺, and for the favorable bending, Mg²⁺ ions also form correlated ion-binding pattern near major grooves, which can cause attractive force between the bent strands. However, due to the bulky size of Mg²⁺, Mg²⁺ ions give a much weaker force than the small M²⁺ ions, and the Mg²⁺-induced attraction occurs only for bending toward major-groove or major-groove-rich directions because minor groove is inaccessible for Mg²⁺.

Bending angle with divalent ions

Following the previous studies (34,35), we estimate the mean bending angle 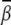based on ΔG_E(γ, β), through

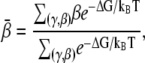(8)

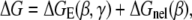(9)

where ΔG is the total bending free energy for a bent helix (γ, β) which includes both electrostatic (ΔG_E(γ, β)) and nonelectrostatic (intrinsic, ΔG_nel(β)) contributions. For simplicity, we estimate ΔG_nel(β) from (34)

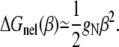(10)

The value g_N is the bending rigidity whose value lies between its hinge value g_hN = k_BT(P₀/2bN) and its isotropic value g_iN = 2g_hN (34), where b (= 3.4 Å) is the rise along axis per basepair and P₀ is the persistence length at high NaCl concentration (34). Experimental measurements show that P₀ of DNA is in the range of 420–500 Å at high NaCl concentration (17–23). In this calculation, we take g_N = g_hN and P₀ = 460 Å (34).

Uniform bending. Fig. 5 A shows the bending angle 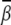induced by Mg²⁺ and the (small) M²⁺ for the uniform bending. At high [Mg²⁺], Mg²⁺ can induce a bending angle of 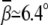(over six bps). As [Mg²⁺] is decreased, 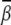decreases too. With the decrease of ion size, the bending angle 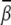increases. Fig. 5 A shows that the small M²⁺ ions can induce sharper bending with 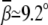at high [M²⁺].

FIGURE 5.

The predicted ion-induced bending angles 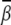of a DNA helix as functions of ion concentrations: Mg²⁺ and small divalent ions (M²⁺) with radius 3.5 Å, for the uniform (A) and localized (B) bending. For the uniform bending, β shown in figures is scaled to the bending over 6 bps, and for the localized bending, β is the bending angle for the central six basepairs.

Localized bending. For the localized bending, the ion-induced bending angle 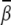is larger than that in the uniform bending case. For example, Fig. 5 B shows that Mg²⁺ can induce a bending angle of 11.4° at high [Mg²⁺]. For the smaller M²⁺ ions, the bending angle 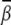can reach ∼14° at 0.1 M M²⁺. Moreover, the bent DNA has higher stability (more negative ΔG(γ, β)) in M²⁺ solution than in Mg²⁺ solution, especially at high ion concentration, as shown in Figs. S7 and S8 in the Supplementary Material.

For a uniform bending, different segments along the helix have different bending modes, namely, bending toward the major or minor groove. As a result, favorable/unfavorable (or less favorable) bending modes are mixed together. As a result, uniform bending usually has a smaller bending angle 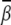than localized bending. For both the uniform and localized bending models, the ion-induced bent DNA helix is dynamic and flexible, especially at low ion concentration. As ion concentration is increased, the bent helix structure is stabilized and more rigid.

Comparisons with previous studies

Mechanisms for DNA bending

The asymmetric charge neutralization has been proposed to be the driving force for protein-induced DNA bending (29), and the mechanisms has been illustrated elegantly by the experiments (52,53) and all-atom simulations (54).

For multivalent ion-induced DNA bending, experiments have suggested that the charged ligands binding into grooves may be responsible for the bending (55,56). Two electrostatic models have been proposed, where a multivalent cation is placed at the center of the major (34) and minor grooves (35). The electrostatic bending (collapse) can be induced by the Coulombic attraction between the placed multivalent cation and the bent strands of phosphates (34,35). However, to place a cation in the groove in this way is rather ad hoc. This TBI model study does not rely on the preset cations and it gives the ion distribution and the driving force for bending. The predicted correlated ion-binding configuration for a bent DNA helix is in qualitative agreement with the mechanism suggested by the experiments (10,55,56).

Local and uniform bending structures

In the previous studies on simplified DNA (cylinder or line-charge) models, the local bending structure is ignored. In the discrete-charge models where helical DNA phosphates are used, the bending is assumed as toward the major groove (34) or the minor groove (35). In this study, which makes no a priori assumption about the bending direction, we calculate the full free energy landscape for the bent conformations, and we find that the local favorable bent structure is determined by the interplay between the ion valency, the ion size, and the width of the bent grooves.

For a uniform bent helix, some segments along the helix bend toward the major groove and some toward the minor groove. Thus, the favorable/unfavorable bending modes are mixed together in the helix. Therefore, the uniform bending mode may be energetically not very favorable. Realistically, bending of a DNA helix may adopt a mode with different favorable localized bending at different local sites, which involves a lower overall energetic barrier for bending. For ion-induced bending, the specific favorable local bending is dependent on ion size and valency, as discussed above. The localized bending can also be induced by the sequence effect, e.g., the localization of A·T (or C·G) sequence can result in the localized bending, which can be further enhanced by the binding of cations (64,65,73–76). This model does not consider such sequence effect. The inclusion of the sequence effect requires the extension of the TBI model to treat the nucleic acid structure at the all-atom level and to assign different partial charges to different groups of the nucleotides. In addition, some nucleotide sequences are more prone to bend toward the major or the minor grooves than other sequences. Such effect would cause sequence-dependent ion-DNA interactions and hence result in sequence-dependent DNA bending.

Ion-induced DNA bending angle

A previous study with multivalent cations placed in the major groove predicted a larger bending angle 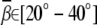for multivalent (valency ≥ 2+) ions (34) than our prediction. The difference may come from the distance-dependent effective dielectric constant, which can enhance the ion-phosphate attraction and thus increase bending angle. However, the dielectric constant near DNA surface is an elusive quantity and has not been quantified directly (35). Moreover, an accurate treatment on the dielectric effects needs to take into account not only the charge-charge interaction energy, but also the ion polarization (Born) energy, which may suppress the ion-binding (47,77) and consequently reduce the bending angle. In another electrostatic model with a cation preset in minor groove, the predicted bending angle induced by divalent ions is ∼9° for a 20-bp DNA helix (35), a value in accordance with our prediction (∼9.2°) for the small divalent ions based on the uniform bending model. As discussed above, in this model, the ion-binding is determined by the overall effects of ion entropy and ion-ion/ion-DNA interactions.

There are no direct experimental data for the bending angles that is comparable to our predictions for the generic (canonical) DNA helix bending. For A-tract DNA bending, a bending angle of 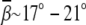for (A·T)₆ has been measured in the presence of Mg²⁺ and kinase (64). To highlight the effect of Mg²⁺, another experiment shows that ∼4 mM Mg²⁺ can promote the bending angle from 7° to 19° (65). Our predictions are in qualitative accordance with the experimental finding that Mg²⁺ can promote DNA bending. It is expected that the experimental bending angles for (A·T)₆ are larger than our prediction because (A·T)₆ DNA helix can be easily curved due to the intrinsic and other ion-binding properties (64,65,73–76).

DNA bending and DNA condensation

The ion-induced DNA bending is directly related to ion-mediated DNA condensation (1,2,10,55). Our predicted free energy landscape clearly shows the different helix bending scenarios for different ion charges and sizes. Na⁺ can only reduce the electrostatic bending repulsion even at high ion concentration. Thus, Na⁺ ions cannot drive helix bending and cannot cause DNA condensation. In contrast, Mg²⁺ can induce electrostatic attractive force to cause bending. However, the Mg²⁺-induced attraction is not strong and thus can only induce weak bending. As a result, Mg²⁺ may only assist the DNA looping (with large curvature radius) (78). The experiments on DNA condensation also show that Mg²⁺ cannot condense DNA in aqueous solution at room temperature (1,2). The decrease of the divalent ion radius can apparently promote the bending. This may partially account for the experimental fact that some divalent ions (e.g., Cu²⁺ and Mn²⁺) can condense DNA while other divalent ions (Mg²⁺) cannot (1,2). Another possible mechanism for the different ability of ions in promoting DNA condensation is the binding specificity (49), which is ignored in the TBI theory presented here.

Effects of modeling parameters

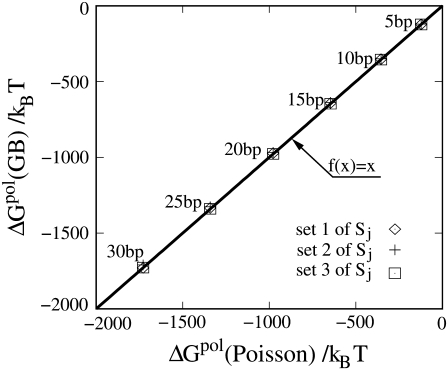
In this section, we discuss the effects of modeling parameters, including the scaling parameters used in the evaluation of the Born radii and the dielectric constant of biomolecule (DNA); see also Fig. 6 and Appendix B.

FIGURE 6.

The polarization energies ΔG^pol calculated from the GB model and the Poisson equation for B-form DNA helices of different lengths. To test the sensitivity of the GB results on the structural scaling parameters S_j (j = p, n, and c for the phosphate sphere, the small neutral sphere, and the central large sphere, shown in red, purple, and yellow, respectively, in Fig. 1), we show three sets of results with (S_p, S_n, S_c) = (0.9, 0.8, 0.55), (1, 0.95, 0.7), and (0.8, 0.65, 0.4) for sets 1, 2, and 3, respectively.

Because the TBI model requires the calculations for the interactions for all the possible charge pairs for different positions of the tightly bound ions, it is impractical to use the Poisson equation, which is computationally expensive. Therefore, we use the GB approximation, which is computationally efficient.

One of the major uncertainties in modeling biomolecular electrostatics with the implicit solvent approximation is the dielectric constant problem. In these calculations, we assume the dielectric constant of the DNA is 20. Such a dielectric constant was suggested in previous studies (79–81). Our control tests show that for the simple structure (helix) studied here, the change of the interior (DNA) dielectric constant only weakly affect the results because of the following two reasons. First, the phosphate charges are exposed to (perpetuate into) the solvent, thus the charge-charge interactions are strongly affected by the dielectric constant of solvent (47,82). Second, changes such as decreasing the interior dielectric constant would slightly strengthen the ion-phosphate attraction that favors the ion-binding. However, in the meantime, the self-energy of the tightly bound ions would increase, resulting in a suppression of the ion-binding. The above two effects would partially cancel each other (47). For example, decreasing the interior dielectric constant from 20 to 10 would cause an increase in the averaged Φ₁(i) + Φ₀(i) (Eqs. 11 and 15) slightly by ∼13%. Such an increase is partially canceled by the enhanced attractions between the bound ion with other phosphates (see Eqs. 4 and 6). Our Poisson equation-based calculation for the interaction between DNA and a test ion shows that the change of an interior dielectric constant only slightly changes the ion-binding pattern. For example, decreasing the DNA dielectric constant would slightly enhance the ion-binding in the minor groove and slightly suppress ion-binding in the major groove (47). Such effects do not alter our conclusions about DNA bending, especially for the hydrated ions used here (47). For the complex molecule structures and dehydrated ions, we expect that the change of molecular dielectric constant can result in larger effects.

CONCLUSIONS AND DISCUSSIONS

In this article, the TBI theory is extended with the implementation of the generalized Born model, and is used to calculate the electrostatic free-energy landscapes for DNA helix bending based on the uniform and localized bending structural models. The electrostatic free energy landscapes are shown to be strongly dependent on ionic conditions, including ion concentration, ion valency, and ion size. The model leads to the following predictions.

1. For Na⁺, DNA bending is electrostatically unfavorable because of the charge repulsion. Bending toward the (narrow) minor groove, which has a higher charge density, is more unfavorable than toward the major groove. Increasing Na⁺ concentration would reduce the repulsive force that opposes bending and consequently enhance bending flexibility.

2. The large size of the hydrated Mg²⁺ does not allow it to enter the narrow minor groove. However, Mg²⁺-binding in the major groove causes a negative electrostatic bending free energy, i.e., the bent state can be more stable than the unbent state. Bendings toward the major groove and the minor groove are the favorable and unfavorable modes, respectively. At high Mg²⁺ concentration, Mg²⁺ can induce a bending angle ∼11° for the localized bending and an angle ∼6° for the uniform bending (greater than six bps).

3. Smaller divalent ions (1 Å smaller than Mg²⁺ in radius) can enter the narrow minor groove, which has a higher charge density. The correlated ion distribution leads to an interstrand attraction in the minor groove region, which would significantly enhance the stability of the bent state. There are two favorable bending directions for different bending angles: (a), For a moderate bending angle, the most favorable bending is toward the minor groove; and (b), for a sharp bending, the minor groove becomes so narrow that it cannot accommodate the ions, so the most favorable bending is toward the major grooves. The bending angle can reach ∼14° (greater than six bps) at high ion concentration.

4. Detailed analysis for ion distribution for different bent states indicates that the ion-induced DNA helix bending can be driven by the interstrand attraction mediated by the correlated ion distribution across the bent grooves.

Our results reply on several approximations. First, we model the bent DNA helix as a uniformly bent helix either over the whole helix, or over the central six basepairs; thus, we ignore other distorted structures and possible unfolded structures at low salt. It has been known that other distorted structures caused by, for instance, the disruption of basepairs and bulge in duplex, can promote DNA and RNA bending. Second, we have ignored the possible specific interactions between the cation and specific groups. These specific interactions may enhance ion-binding affinity and further stabilize the bent state. Third, we have used the hydrated ions and ignored the ion dehydration effect (though ion dehydration can be energetically costly). In addition, the model presented here is a pure electrostatic model, it ignores the sequence-dependence of ion binding and sequence-directed DNA bending which has been known to be important for A-tract and G-tract DNA bending (73,74). Nevertheless, the predicted electrostatic bending free energy landscapes and the mechanism for multivalent ion-induced DNA bending, can be helpful for understanding the ion-mediated DNA bending, looping, and condensation.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

APPENDIX A: STRUCTURAL MODEL FOR BENT DNA HELIX

We use the grooved primitive model to describe a B-DNA helix (47–51,63). The grooved primitive model has been shown to be able to predict the same detailed ion distributions as all-atom computation (63). In the grooved primitive model, each helical basepair is represented by five spheres (47–51): one central large central sphere with radius 4 Å, two small phosphate spheres with radius 2.1 Å, and two small neutral spheres with radius 2.1 Å (63). The centers of the central large spheres are on the axis of DNA helix with equal spacing; the phosphate spheres are placed at the centers of the phosphate groups; and the neutral spheres lie between phosphate spheres and central large one. The coordinates of phosphate spheres 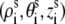are given by the canonical coordinates of B-DNA from x-ray measurements (83): 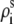= 8.9 (Å); 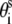= 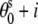36°; and 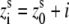3.4 (Å), where s = 1, 2 denotes the two strands and i = 1, 2, …N denotes the nucleotides on each strand. The parameters 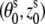for the initial position are (0°, 0 Å) for the first strand and (154.4°, 0.78 Å) for the second strand, respectively. The neutral spheres have the same angular coordinates except they have the smaller radial coordinates 5.9 Å (47–51,63). Every phosphate sphere carries a negative elementary charge −q at its center (see Fig. 1 A for a B-DNA helix produced from the grooved primitive model).

For the uniform bending model, the whole DNA helix is assumed to be uniformly bent along the axis. To produce a uniformly bent DNA helix, we first bend the axis uniformly like a circular arc with a curvature radius R_c (or bending angle β), i.e., the central large spheres lie on the uniformly bent axis with equal spacing. Correspondingly, the coordinates of phosphate/small neutral spheres can be produced by keeping the radial distances, radial angles, and perpendicular angles to the axis; see Fig. 1 B for a bent DNA helix. We also rotate the DNA helix around the axis (by changing axial rotation angle γ) to produce uniformly bent DNA helices with different bending direction, as shown in Fig. 1 B.

For the localized bending model, only the central six basepairs are bent uniformly along the helical axis. The coordinates of the (phosphate, neutral, and central large) spheres for the bent central six basepairs are produced like the uniform bending model. The two end helix parts keep straight (unbent), and are rotated according to the central bent axis, keeping the helical axis continuous. In this way, a locally bent DNA helix can be produced based on the grooved primitive model, as seen in Fig. 1 C.

APPENDIX B: CALCULATING Φ₁(I), Φ₂(I, J), AND Φ₀(I) WITH THE GENERALIZED BORN MODEL

As described in main text, we apply the GB model to account for the DNA/solvent dielectric effects for the tightly bound ions. In this Appendix, we show how to compute the potential of mean forces Φ₁(i), Φ₂(i, j) and the polarization energy ΔG^pol with the GB model (57–62); see Eqs. 4 and 6 in Methods.

The values Φ₁(i) and Φ₂(i, j) are calculated as the average over all the possible positions R of the tightly bound ions in the respective tightly bound cells (47–51),

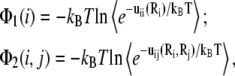(11)

where u_ii is the electrostatic interactions for the charges in cell i, and u_ij-values are the electrostatic interactions between the charges in two different cells i and j. In the calculations for Φ₁(i) and Φ₂(i, j), as shown below, we use the GB model to account for the polarization energy (due to dielectric discontinuity at the DNA/solvent interface) (57–62).

In the GB model, the electrostatic interaction u_ij between two (i ≠ j) charges q_i and q_j is given by

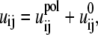(12)

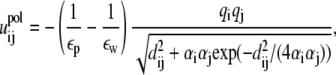(13)

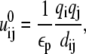(14)

where ε_p (= 20) and ε_w (= 78) are the dielectric constants of DNA helix interior and solvent, respectively; 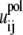is the polarization energy; and 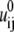is the Coulombic interaction energy in the uniform medium of dielectric constant ε_p. The value d_ij is the distance between the two charges. The values α_i and α_j are the Born radii for the two charges q_i and q_j.

The value Φ₀(i) in Eq. 6 is the Born energy for charges inside the i^th tightly bound cell. For illustrative purposes, we assume there is one tightly bound ion in the i^th cell. The value Φ₀(i) is calculated from an averaging over all the possible positions R_i of the ion,

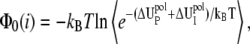(15)

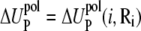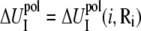where and are the self-energies of the phosphate i and of the ion (at position R_i), respectively. The notation 〈…〉 designates the averaging over all the possible ion positions R_i within the cell. With the GB approximation, we compute 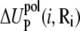and 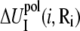using the formulae

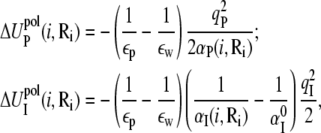(16)

where α_P(i, R_i) and α_I(i, R_i) are the Born radii for the phosphate i and the ion at R_i, respectively. The value 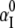is the Born radius for an isolated ion.

In the TBI model, we use a pairwise method to calculate the Born radius α_i (59–62) for a charge i in the tightly bound region,

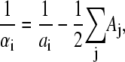(17)

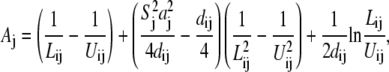(18)

where

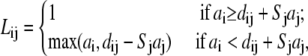(19)

and

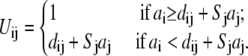(20)

Here, Σ_j denotes the sum over all the groups, d_ij is the distance between charge i and group j, and a_i and a_j are the radii for the charge i and group j. S_j is the structural scaling factor and is equal to unity if there is no overlap between (atomic) spheres. Generally, S_j < 1 for a realistic molecule.

For the grooved primitive DNA model used in this work, we find the calculated polarization energy from the GB model is not sensitive to the scaling factor S_j, as compared with the prediction from Poisson equation; see Fig. 6 for the polarization energy for different sets of S_j, which are listed in the caption of Fig. 6. In these calculations, we use set 1 of S_j: S_p = 0.9, S_n = 0.8, and S_c = 0.55. Here, S_p, S_n, and S_c are the parameters for the phosphate spheres, small neutral spheres, and central large spheres in the grooved primitive model for DNA helix (Fig. 1 and Appendix A). For ions, the scaling parameter S is taken as 1 because there is no overlap between ions and DNA molecule.

APPENDIX C: COMPUTATION OF THE TBI THEORY

The computation with the TBI theory involves the following steps (47–51):

Step one

For a nucleic acid helix in salt solution, we solve the nonlinear PB to obtain the ion distributions around a DNA helix, from which we determine the tightly bound region according to the criteria for the Coulombic and excluded volume correlation (47–51).

Step two

Using Eqs. 11 and 15 in Appendix B, we compute the pairwise potentials of mean force Φ₁(i), Φ₂(i, j), and Born energy Φ₀(i). The Born radii for the charges (including phosphates and tightly bound ions) inside the tightly bound region are calculated with the method (Eq. 17) indicated here:

1. For the Born radius of bare phosphates (without tightly bound ions), the summation in Eq. 17 is over all the groups in DNA model.

2. For the Born radius of phosphates with tightly bound ions, the contribution of the bound ion is accounted for by including an additional term (A_j) in the summation (Eq. 17).

3. For the tightly bound ions, we calculate the Born radii on the grids. The Born radius for an ion at an arbitrary position in the tightly bound region can be approximated as that on the closest grid point.

During the averaging (integration) process for Φ₁(i), Φ₂(i, j), and Φ₀(i), the excluded volume effects between ions and between ions and the molecule (DNA) are accounted for by using a truncated Lennard-Jones potential (49–51). The calculated potentials of mean force are then tabulated and stored for the calculations of partition function.

Step three

We enumerate all the possible binding modes. For each mode, we calculate G_b, ΔG_d, and 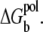Summation over the binding modes gives the total partition function Z (Eq. 2), from which we can calculate the electrostatic free energy.

The computational efficiency of the TBI model is limited by the enumeration of the binding modes, which scales with the number (N) of basepairs as ∼2^2N (for multivalent ions). Therefore, an exhaustive enumeration for all modes is extremely computationally expensive. In our previous study (49), we developed an efficient algorithm by treating the low-energy modes and high-energy modes separately. However, even with the improved efficient algorithm, the TBI model is still computationally much more complex than the standard nonlinear PB calculations, especially for large molecules.

APPENDIX D: PARAMETER SETS AND NUMERICAL DETAILS

In this study, the Na⁺ and Mg²⁺ ions are assumed to be hydrated (47–51), and have radii of 3.5 Å and 4.5 Å (47–51,68), respectively. We also use a smaller divalent ion (with radius ∼3.5 Å) to investigate the ion size effect on DNA bending. In the work, the dielectric constant ε_p of the DNA interior is set to be ε_p ∼ 20 (47,79,80), and ε_w of the solvent is set as the value of bulk water (ε_w ∼ 78 at 25°C).

The TBI calculation requires numerical solution of the nonlinear PB. We have developed a three-dimensional finite-difference algorithm to numerically solve nonlinear PB equation for multispecies ions (47–51). A thin charge-free layer of thickness of one cation radius is added to the molecular surface to account for the excluded volume layer of the cations (47–51). In addition, we use the three-step focusing process to obtain the detailed ion distribution near the molecules (37,47–50). For each run, the electrostatic potentials are iterated to a convergence of <10⁻⁴ k_BT/q. The grid size of the first run depends on the salt concentration used. Generally, we keep it larger than six-times Debye length to include all the ion effects in solutions, and the resolution of the first run varies with the grid size to make the iterative process doable within a reasonable computational time (47–51). The grid size (L_x, L_y, L_z) for the second and the third runs are kept at 204 Å, 204 Å, and 238 Å, and 102 Å, 102 Å, and 136 Å, respectively. The corresponding resolutions are 1.36 Å per grid and 0.68 Å per grid, respectively. As a result, the number of the grid points is 151 × 151 × 176 in the second and 151 × 151 × 201 in the third run. Our results are tested against different grid sizes, and the results are stable.