Multifactor Dimensionality Reduction–Phenomics: A Novel Method to Capture Genetic Heterogeneity with Use of Phenotypic Variables

Abstract

Complex human diseases do not have a clear inheritance pattern, and it is expected that risk involves multiple genes with modest effects acting independently or interacting. Major challenges for the identification of genetic effects are genetic heterogeneity and difficulty in analyzing high-order interactions. To address these challenges, we present MDR-Phenomics, a novel approach based on the multifactor dimensionality reduction (MDR) method, to detect genetic effects in pedigree data by integration of phenotypic covariates (PCs) that may reflect genetic heterogeneity. The P value of the test is calculated using a permutation test adjusted for multiple tests. To validate MDR-Phenomics, we compared it with two MDR-based methods: (1) traditional MDR pedigree disequilibrium test (PDT) without consideration of PCs (MDR-PDT) and (2) stratified phenotype (SP) analysis based on PCs, with use of MDR-PDT with a Bonferroni adjustment (SP-MDR). Using computer simulations, we examined the statistical power and type I error of the different approaches under several genetic models and sampling scenarios. We conclude that MDR-Phenomics is more powerful than MDR-PDT and SP-MDR when there is genetic heterogeneity, and the statistical power is affected by sample size and the number of PC levels. We further compared MDR-Phenomics with conditional logistic regression (CLR) for testing interactions across single or multiple loci with consideration of PC. The results show that CLR with PC has only slightly smaller power than does MDR-Phenomics for single-locus analysis but has considerably smaller power for multiple loci. Finally, by applying MDR-Phenomics to autism, a complex disease in which multiple genes are believed to confer risk, we attempted to identify multiple gene effects in two candidate genes of interest—the serotonin transporter gene (SLC6A4) and the integrin beta 3 gene (ITGB3) on chromosome 17. Analyzing four markers in SLC6A4 and four markers in ITGB3 in 117 white family triads with autism and using sex of the proband as a PC, we found significant interaction between two markers—rs1042173 in SLC6A4 and rs3809865 in ITGB3.

Mendelian genetics explains the relationship between phenotype and genotype in many single-gene disorders, and these genes can be efficiently detected by linkage and association analyses.¹ However, the majority of human diseases, including diabetes, ischemic heart disease, and autism (MIM 209850), are complex with ambiguous inheritance patterns, generally accounted for by many loci of multiple genes, at each of which common alleles typically have only small or modest individual effects.² Complex diseases are well known for genetic heterogeneity,³ in which a single disease phenotype is caused by several different variants within a gene or in multiple genes. In addition, gene-gene and gene-environment interactions are believed to play a role in common complex disease. These complicating factors have made the identification of disease genes in complex diseases challenging. Successful analysis methods must attack the problem of genetic heterogeneity and must evaluate interactions involving multiple genes simultaneously.

Many statistical methods can be used to test for interactions. Standard parametric methods are limited when testing interactions between many factors (e.g., genetic markers) because of the large number of parameters to be estimated; therefore, nonparametric methods, which do not require specific statistical and genetic models (i.e., estimates of parameters or assumption of inheritance pattern), are better suited than are parametric methods to searching for gene effects in high-dimensional data sets of complex diseases.⁴ However, nonparametric methods and parametric methods still face the challenge of separating the signal of a gene effect in high-dimensional data from increased noise. A common technique applied in high-dimensional data is dimension reduction. Multifactor dimensionality reduction (MDR), a nonparametric approach based on this technique, was developed to search for gene-gene and gene-environment interactions by identification of a multilocus model for association, with the use of dichotomous disease status.^5–8 Compared with classic logistic-regression analysis, MDR has greater power for testing interaction among high-dimensional and correlated predicators.⁹ Previous studies of sporadic breast cancer with 10 polymorphisms showed that MDR successfully identified significant interaction in the absence of a detectable main effect by logistic regression.⁵ In an analysis of myocardial infarction,¹⁰ MDR gave interaction models consistent with those identified by logistic regression.

MDR reduces dimensionality of multilocus genotype information to a one-dimensional factor with two levels—“high-risk” and “low-risk” genotypes. The model for the effect of high-risk and low-risk genotypes is trained and validated by cross-validation, and the P value is obtained using a permutation test. MDR has successfully identified gene-gene interactions in sporadic breast cancer,⁵ essential hypertension,¹¹ atrial fibrillation,¹² and type 2 diabetes.¹³ Further, MDR has been extended to include alternative statistics and permutation tests (extended MDR [EMDR])¹⁴ and the analysis of family data (MDR pedigree disequilibrium test [MDR-PDT]).¹⁵

Genetic heterogeneity is often expressed as clinical heterogeneity. Although the effects may be subtle, variation in particular clinical phenotypic covariates (PCs) may reflect differences in the underlying genetic causes of disease. One common approach to attacking genetic heterogeneity is to stratify a sample on the basis of PCs and conduct genetic analyses within strata. This approach poses two challenges. First, definitions of strata may be ad hoc and based on clinical intuition. Second, such a stratified analysis requires adjustment for multiple tests (e.g., Bonferroni correction); however, if there are many PC levels (resulting in many strata), this correction can lead to a loss in power.

In this article, we describe MDR-Phenomics, a novel method for the identification of genetic effects within triad families (an affected offspring and parents) by integration of PCs into MDR. MDR-Phenomics integrates dimensionality reduction with the extended features of MDR-PDT and EMDR. We conducted simulation studies to compare the power of MDR-Phenomics with that of MDR-PDT and stratified phenotype MDR-PDT (SP-MDR). SP-MDR identifies genetic effects within each PC level by MDR-PDT and adjusts for multiple tests with the use of a Bonferroni correction.

To further test MDR-Phenomics, we analyzed candidate genes in autism, a complex disease characterized by social impairments, language difficulties, and unusual or repetitive behaviors.^16,17 Clinical symptoms of autism vary dramatically within these domains. Although many candidate genes have been identified by different methods (i.e., molecular genetic experiments and linkage and association studies), there have been problems with replication. A major difficulty in identifying disease genes in autism is genetic heterogeneity, which may be reflected in variable clinical symptoms. We applied MDR-Phenomics to identify multiple gene effects in autism candidate genes—the serotonin transporter gene (SLC6A4) and the integrin beta 3 gene (ITGB3) on chromosome 17.

Material and Methods

MDR-Phenomics

Beginning with the assumption that there are N loci genotyped in a triad-family data set, MDR-Phenomics identifies genetic effects by testing whether a significant K-locus model exists. A K-locus model (where K is an integer, K=1,2,3,…) refers to a combination of genotypes at a subset of K loci of the N total loci. The null hypothesis of MDR-Phenomics is that combinations of genotypes in a K-locus model are randomly transmitted to affected individuals. A significant K-locus model is identified by extensively searching all K-locus models and applying a permutation method to estimate the P value. For a triad family with an affected child, we can generate a matched pair of transmitted (T) and nontransmitted (U) observations that represent the genotypes transmitted and not transmitted to the affected child. For example, with the assumption of parental genotypes AaBb and Aabb, if the genotype of the affected child is aaBb, then the matched pair of observations is T=aaBb and U=AAbb. If a combination of genotypes of the K loci either directly affect disease risk or are in linkage disequilibrium (LD) with true disease loci, then the transmission will be associated with a K-locus model. MDR-Phenomics includes two procedures, MDR and phenomic analysis, to assess association of a K-locus model with transmission and the “effect” of PCs on the association—that is, the different (or heterogeneous) strength of association across PC levels.

Multilocus analysis considers a subset of K diallelic loci (K⩽N). There will be 3^K genotypes for K loci, and, even if K is small, there may still be few observations for each genotype category (i.e., sparse data). To address this problem, traditional MDR pools multilocus genotypes into high-risk and low-risk groups, reducing the genotype predictors from N dimensions to one dimension.⁵ In traditional MDR, a genotype is labeled “high risk” if the case:control ratio meets or exceeds some threshold or is labeled “low risk” otherwise. In the MDR procedure implemented in MDR-Phenomics, we define the case:control ratio as the ratio of the number of times that a genotype is transmitted to an affected child to the number of times that a genotype is not transmitted to an affected child. Application of the Bayes classifier¹⁸ gives a threshold of 1.0 for a data set composed entirely of triad families; thus, a genotype is classified as “high risk” if its classification ratio exceeds 1.0 or as “low risk” otherwise.

By the Bayes classifier, the K-dimensional variable X representing genotypes from K loci can be transformed to one-dimensional variable G, where G=h codes for high-risk genotype and G=l for low-risk genotype. We define variable Y as an indicator for transmission status of a high-risk or low-risk genotype, where Y=1 codes for transmission and Y=0 for nontransmission; then, the sum of Y is assumed to follow a binomial distribution for both high-risk and low-risk genotypes. To measure the strength of association between Y and G, the C statistic is calculated using a form of the goodness-of-fit test statistic, which tests whether the conditional distribution of Y given G=h (i.e., P(Y|G=h)) is equivalent to the marginal distribution of Y (i.e., P(Y)). For a triad family, transmitted and nontransmitted status can always be generated (P(Y=1)=P(Y=0)=.5). If G is associated with Y, P(Y=1|G=h)>.5 and P(Y=1|G=l)<.5 are expected. Since stronger association between allelic transmission and disease generally results in a larger C statistic, the C statistic can be used to measure allelic association. However, the C statistic may not follow a χ² distribution under the null hypothesis of no allelic association.

In the phenomics procedure, an analysis of variance (ANOVA) model is applied to test whether the strength of association between Y and G is the same within PC levels—in other words, the “effect” of PCs on association between Y and G. With the assumption that L is the number of PC levels and n_i is the number of families in the ith PC level (i=1,2,…,L), the ANOVA model is

where i=1,2,…,L, j=1,2,…,n_i, and E_ij∼iid n(0, σ²), where “iid” means “identically and independently distributed.”

The response variable D_ij (as a function of Y|G=h in the ith PC level and the jth family) is calculated as the number of times a high-risk genotype is transmitted minus the number of times a high-risk genotype is not transmitted. D_ij is a measure of association, since stronger association between Y and G leads to a larger expected value of D_ij. The parameters μ and P_i are unknown, where μ is the expected value of D_ij when no PC “effect” exists and P_i is the “effect” of the ith PC level on D_ij. The standard F statistic for the ANOVA model tests the null hypothesis that P_H0=(P₁,P₂,…,P_L)=(0,0,…,0) (i.e., E(D_ij)=μ, and the mean of D_ij is μ for all P levels). It measures the effect of PC on association between Y and G (i.e., D_ij). The F statistic is calculated as the ratio of the estimated mean squared error (MSE) between the PC levels to that within PC levels:

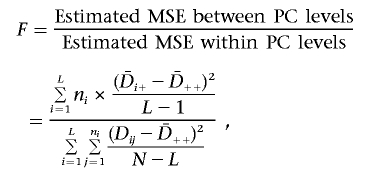where

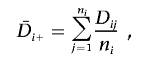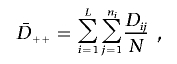and

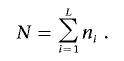A larger F value indicates a bigger difference of mean D_ij across PC levels. The traditional ANOVA test assumes that the random errors, E_ij, are identically and independently distributed normal random variables, under which the F statistic follows the F distribution. In MDR-Phenomics, this assumption is not necessary, since a permutation test is used to estimate the empirical distribution of the F statistic.

Finally, we calculate the MDR-Phenomics statistic as the product of the statistics C and F; M=C×F. The M statistic integrates two types of information: (1) the association between transmission status (Y) and genotype (G), as measured by the C statistic, and (2) the effect of the PC on association, as measured by the F statistic.

To test whether there is a significant genetic effect from a K-locus model, MDR-Phenomics uses a permutation procedure. This procedure calculates the observed M statistic for each K-locus model in the observed triad family data. By comparing the observed M statistic of every K-locus model to an empirical distribution of the M statistic based on permuting the data to simulate the null hypothesis, MDR-Phenomics can identify those K-locus models with significant P values. The empirical distribution is generated using the nonfixed permutation test implemented in EMDR¹⁴ and MDR-PDT.¹⁵ The nonfixed permutation test randomly shuffles the transmission status in every triad family, with genotypes and PCs fixed, to generate a large number of permuted data sets (e.g., 1,000). To adjust for multiple tests, the nonfixed permutation test selects the largest M statistic among all K-locus models in every permuted data set as the permuted statistic, to simulate the empirical distribution of M. The P value of a K-locus model is the percentage of permuted statistics equal to or larger than the observed M statistic. A small P value (e.g., P⩽.05) indicates significant genetic association between the K-locus model and transmission status within at least one PC level.

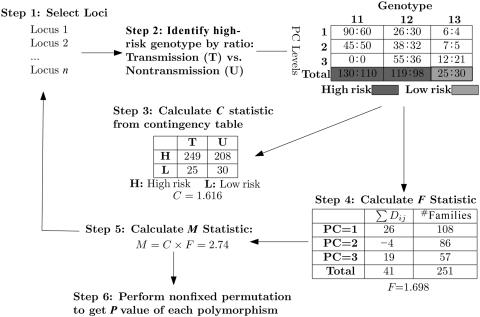
Figure 1 summarizes the MDR-Phenomics algorithm applied in searching for genetic effects from all one-locus models. The data set contains N loci and, therefore, N possible one-locus models. The algorithm begins at step 1, with the selection of a one-locus model. This is followed by step 2, dimension reduction to classify high-risk and low-risk genotypes for the selected one-locus model. As shown in figure 1, genotypes 11 and 12 are classified as “high risk,” since their classification ratios (130:110 and 119:98, respectively) are >1.0. Genotype 22 is classified as “low risk,” since the estimated ratio (25:30) is <1.0. In step 3, a contingency table is created, and a C statistic is calculated (1.616). This statistic indicates the strength of association between genotypes at the locus and their transmissions. In step 4, a PC with three levels is integrated into the analysis with use of an ANOVA model, with a resulting F statistic (1.698). This step estimates the effect of PCs on association in step 3. Step 5 involves calculation of the M statistic by multiplying the C and F statistics. Through repetition of steps 1–5, M statistics were calculated for all one-locus models. The nonfixed permutation test in step 6 generates the empirical distribution of M for a one-locus model while adjusting for N multiple tests, thus providing an adjusted P value for each of the one-locus models.

Figure 1. .

Step 1, The first locus is selected from N loci for testing. Step 2, Three genotypes—11, 12, and 13—have case:control ratios for transmission (T) versus nontransmission (U) of 130:110, 119:98, and 25:30, respectively. Therefore, genotypes 11 and 12 were “high-risk,” with the ratio >1.0, and genotype 22 was “low-risk,” with the ratio⩽1.0. Classification ratios of genotypes are calculated in each PC level too. Step 3, The C statistic is calculated in a two-by-two table, to evaluate the association of that one-locus model with transmission. Step 4, The number of families with high-risk genotypes and the sum of the D statistics are listed for each PC level. F is calculated to estimate the PC “effect” on D. Step 5, The M statistic is calculated by the weighting process. Step 6, The nonfixed permutation test generates the empirical distribution of the M statistic and the P value of each one-locus model.

Analysis of Power and Type I Error for One-Locus Models

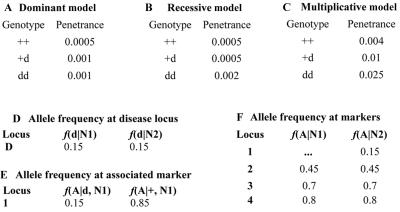
Type I error and power were estimated using the SIMLA software program¹⁹ to generate simulated data sets. Type I error and power were estimated as the percentage of simulated data sets with P⩽.05 under the null (H0) and alternative (H1) hypotheses, respectively. We used SIMLA to generate data sets, assuming one of three disease models—dominant (fig. 2A), recessive (fig. 2B), or multiplicative (fig. 2C). Each data set contained four loci and consisted of two groups of triads, N1 and N2. Genetic heterogeneity in the data sets was simulated by mixing triads from group N1 and group N2. The frequencies of alleles (wild-type [+] and disease [d]) at locus D in group N1 and group N2 are given in fig. 2D. In the triads from group N1, locus 1 was simulated with a genetic effect, and loci 2–4 without any effect (fig. 2E and 2F). In the triads from group N2, all four loci were simulated without a genetic effect (fig. 2F). Groups N1 and N2 were differentiated with different PC values, and every PC level had an exactly equal number of nuclear families.

Figure 2. .

Disease models and allele frequencies

Sixteen data sets (table 1), each containing 1,000 replicates, were generated with different disease models, sample sizes, and numbers of PC levels. We analyzed every data set with MDR-PDT, SP-MDR, and MDR-Phenomics. MDR-PDT is the extension of MDR for the analysis of pedigree genotype data with use of the PDT statistic,²⁰ and it does not consider PCs. The SP-MDR method applies MDR-PDT to analyze the data set stratified by PCs and applies a Bonferroni adjustment to correct for the number of PC levels. The power and type I error are Pr(P⩽α|alternativehypothesis) and Pr(P⩽α|nullhypothesis), respectively. Suppose a PC has L levels. To keep the experimentwise type I error <0.05, we select α=0.05 for MDR-PDT and MDR-Phenomics and α=0.05/L for SP-MDR within each PC level corresponding to Bonferroni adjustment. Since locus 1 was simulated with a genetic effect, the percentage of data sets with P⩽α for this locus estimates power. Similarly, loci 2, 3, and 4 were simulated as unassociated with disease, and the percentage of data sets with P⩽α estimates type I error.

Table 1. .

Disease Model, Sample Size, and PC of Simulated Data^[Note]

		No. of Families in		Possible PC Values of Proband in
Data Set	Disease Modela	N1	N2	N1	N2
1	1	500	500	1, 2, 3, 4	5, 6, 7, 8
2	1	500	1,000	1, 2, 3, 4	5, 6, 7, 8
3	1	500	2,000	1, 2, 3, 4	5, 6, 7, 8
4	1	500	500	1, 2	3, 4
5	1	500	1,000	1, 2	3, 4
6	1	500	2,000	1, 2	3, 4
7	1	1,000	500	1, 2, 3, 4	5, 6, 7, 8
8	1	2,000	500	1, 2, 3, 4	5, 6, 7, 8
9	1	1,000	500	1, 2	3, 4
10	1	2,000	500	1, 2	3, 4
11	2	500	500	1	2
12	2	1,000	500	1	2
13	2	1,000	1,000	1	2
14	3	500	500	1	2
15	3	500	500	1, 2	3, 4
16	3	500	500	1, 2, 3, 4	5, 6, 7, 8

Note.— Each data set contained 1,000 replicates.

^a1 = dominant; 2 = recessive; 3 = multiplicative.

Analysis of Multilocus Effect

To test high-order interaction, 100 replicates of data set 1 were used, and an additional four loci (loci 5–8) were added to generate two two-locus interactions. The interaction models, interaction model 1²¹ and interaction model 2¹³ described by Ritchie,⁷ were modified to give weak two-locus interaction in the absence of main effects, by setting the penetrances of genotypes as shown in table 2. The interaction between loci 5 and 6 and the interaction between loci 7 and 8 were simulated in the same data set with use of the modified interaction models 1 and 2, respectively (table 2); thus, disease risk in the data set is determined by two interactions involving loci [5 6] and [7 8] and one main effect at locus 1. To generate heterogeneity, these genetic effects are simulated in group N1 but not in group N2. Power and type I error based on 100 replicate data sets were calculated as above.

Table 2. .

Interaction Models^[Note]

	Penetrance for Genotypes
Model andGenotype	BB	Bb	bb
1:
AA	.05	.10	.05
Aa	.10	.05	.10
aa	.05	.10	.05
2:
AA	.03	.03	.1
Aa	.03	.05	.03
aa	.1	.03	.03

Note.— Multilocus penetrance functions and allele frequencies are defined to simulate two-locus interaction in the absence of main effects. p and q are the allelic frequencies of A and B, respectively, where p=.5 and q=.5.

Conditional Logistic-Regression (CLR) Analysis of Interaction

CLR can assess the interaction among multiple loci and risk factors (e.g., an environmental factor or other covariate) by testing the rate of allelic transmission to exposed probands versus unexposed probands. This classic approach was first proposed by Harley et al.²² It was then successfully applied to extend the transmission/disequilibrium test (TDT) for testing gene-environment interactions.²³ For each parent in a parent-proband triad, a matched pair of “case” and “pseudocontrol” is generated. Since a matched pair has an identical environmental risk factor (i.e., equal covariate effect), interaction between a biallelic locus and a risk factor (RF) can be modeled as

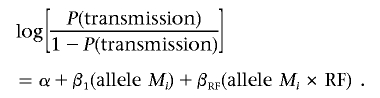Consistent with Maestri’s notation,²³ allele M_i and RF are coded as 1 if allele M_i of the locus and risk factor are present, respectively. Otherwise, they are coded as 0. The coefficients in the CLR model are estimated by maximizing the likelihood, and rejection of β_RF=0 indicates a significant interaction between the tested locus and risk factor.

To test interaction among K loci depending on a PC with L levels, the CLR model above can be extended to include the highest-order interaction among them, all lower-order interaction terms, and K covariates:

Allele M_ji is 1 if allele M_i is present in the jth locus and is 0 otherwise. I(PC=t) is 1 if the proband is “exposed” to the tth level of the PC. A significant interaction among K loci and the PC can be tested by comparing the likelihoods with H0:β_K+1=β_K+2=…=β_K+L=0 versus H1:at least one B_t is not 0, where t=K+1,K+2,…,K+L.

To evaluate the power of CLR for testing interaction under heterogeneity, we simulated 100 replicates of data set 1 (table 1), including a main effect of locus 1, interaction between loci 5 and 6, and interaction between loci 7 and 8 in particular levels of the PC. The power of CLR is the percentage that have the P value of an interaction ⩽.05.

Analysis of Autism Data

A number of candidate genes have been implicated in autism. Two interesting candidates, both on chromosome 17 and related to serotonin function, are the serotonin transporter (SLC6A4) and integrin beta 3 (ITGB3) genes. The serotonin transporter encoded by SLC6A4 mediates the accumulation of the neurotransmitter serotonin in neurons, platelets, and other cells, which in turn regulates emotions and responsiveness.^24,25 Polymorphisms in SLC6A4 have been reported to be associated with autism, although these findings have not been consistently replicated.²⁶ ITGB3 encodes glycoprotein IIIa (ITGB3 [MIM 173470]), the beta subunit of the platelet membrane–adhesive protein receptor complex GPIIb/IIIa. ITGB3 and SLC6A4 were both identified as QTLs for serotonin levels in male subjects.²⁷ To identify potential genetic effects of these genes on autism, we analyzed 117 white family triads ascertained by the Duke Center for Human Genetics and previously genotyped for four markers in SLC6A4 and four markers in ITGB3 (table 3). We used MDR-Phenomics, with the sex of the proband as a PC, as well as MDR-PDT and SP-MDR. Tests of Hardy-Weinberg equilibrium (HWE) and LD were conducted using the GDA²⁸ and GOLD²⁹ software.

Table 3. .

Genes and Markers in Autism Data^[Note]

Gene and Marker	Locus
SLC6A4:
rs1042173	1
rs140700	2
17P6713SLC6A4	3
5HTTLPR	4
ITGB3:
hcv1709582	5
rs5918	6
rs5919	7
rs3809865	8

Note.— All markers are on chromosome 17.

In the analysis of autism data, we followed a conditional searching strategy, in which a higher-dimensional locus model is tested only when no significant lower-dimensional locus model exists. With this strategy, a significant high-dimensional model suggests the existence of interaction not from the main effects of the low-dimensional model. For MDR-Phenomics and MDR-PDT, we set the threshold of α=0.05 as the significance level. With a Bonferroni adjustment applied, the threshold is α=0.025 for SP-MDR, since sex as the PC has two levels.

Results

Power and Type I Error of the One-Locus Model

The results of studies of type I error and power are listed in table 4. Power is defined as the percentage of locus 1 detected to be significant (P<α) among 1,000 replicates, whereas elementwise type I errors Ele-α2, Ele-α3, and Ele-α4 are the percentages of loci 2, 3, and 4, respectively, determined to be significant among 1,000 replicates. Type I error of locus 1, Ele-α1*, was calculated in group N2 too. The experimentwise type I error, Exp-α, is the percentage of any of locus 2, 3, or 4 detected to be significant among 1,000 replicates. We first analyzed data sets 1–10 (table 4), simulated under a dominant disease model. The results were further validated in the remaining six data sets simulated under different disease models (table 4). We see that the elementwise type I errors (Ele-α1, Ele-α2, Ele-α3, and Ele-α4) for all 16 data sets are much smaller than 0.05 because of the adjustment for multiple tests by nonfixed permutation. The experimentwise type I errors are, on average, <0.05. The reason is that the nonfixed permutation test adjusts for tests of four loci (loci 1–4), but only loci 2–4 are simulated without association, and experimentwise type I error (table 4) is calculated as the percentage of any locus (loci 2–4) that has P⩽.05. Since loci are simulated as independent, we expected an elementwise type I error ∼0.0125 (0.05/4) and an experimentwise type I error ∼0.0375 (0.0125×3); the results are consistent with these expectations.

Table 4. .

Type I Error and Power of Data Sets^[Note]

Disease Model, Data Set, and Method	Power	Ele-α1*	Ele-α2	Ele-α3	Ele-α4	Exp-α
Dominant:
1:
SP-MDR	.13	.001	.006	.016	.02	.041
MDR-PDT	.41	.013	.006	.024	.009	.039
MDR-Phenomics	.508	.012	.009	.025	.014	.048
2:
SP-MDR	.118	.009	.01	.018	.025	.052
MDR-PDT	.26	.011	.012	.02	.01	.041
MDR-Phenomics	.451	.005	.009	.02	.007	.036
3:
SP-MDR	.12	.013	.012	.015	.02	.046
MDR-PDT	.151	.010	.015	.013	.018	.046
MDR-Phenomics	.361	.014	.01	.019	.012	.041
4:
SP-MDR	.312	.009	.008	.015	.01	.033
MDR-PDT	.408	.014	.007	.025	.009	.041
MDR-Phenomics	.595	.012	.01	.029	.016	.052
5:
SP-MDR	.301	.015	.003	.012	.006	.021
MDR-PDT	.257	.012	.015	.02	.01	.044
MDR-Phenomics	.551	.016	.009	.02	.009	.038
6:
SP-MDR	.306	.012	.006	.008	.001	.015
MDR-PDT	.147	.012	.015	.014	.018	.046
MDR-Phenomics	.461	.012	.007	.017	.008	.032
7:
SP-MDR	.513	.023	.01	.014	.014	.038
MDR-PDT	.891	.014	.012	.017	.009	.038
MDR-Phenomics	.900	.012	.009	.014	.013	.036
8:
SP-MDR	.943	.023	.011	.018	.011	.040
MDR-PDT	.999	.008	.021	.022	.013	.055
MDR-Phenomics	.996	.012	.013	.027	.014	.053
9:
SP-MDR	.726	.009	.008	.015	.013	.036
MDR-PDT	.889	.014	.014	.019	.011	.044
MDR-Phenomics	.902	.012	.009	.027	.018	.053
10:
SP-MDR	.991	.009	.004	.012	.007	.023
MDR-PDT	.999	.014	.016	.025	.012	.052
MDR-Phenomics	.994	.012	.016	.025	.012	.052
Recessive:
11:
SP-MDR	.198	.012	.021	.013	.016	.049
MDR-PDT	.178	.012	.017	.012	.009	.038
MDR-Phenomics	.273	…	.002	.012	.009	.023
12:
SP-MDR	.492	.012	.015	.013	.012	.040
MDR-PDT	.492	.012	.016	.011	.009	.036
MDR-Phenomics	.543	…	.014	.014	.014	.042
13:
SP-MDR	.447	.017	.021	.014	.013	.047
MDR-PDT	.393	.017	.012	.02	.014	.046
MDR-Phenomics	.521	…	.019	.014	.014	.046
Multiplicative:
14:
SP-MDR	.973	.009	.018	.015	.013	.046
MDR-PDT	.798	.009	.01	.011	.016	.037
MDR-Phenomics	.975	…	.013	.013	.01	.036
15:
SP-MDR	.84	.024	.018	.013	.013	.043
MDR-PDT	.793	.009	.011	.009	.016	.036
MDR-Phenomics	.947	.023	.012	.017	.01	.039
16:
SP-MDR	.507	.030	.007	.007	.019	.033
MDR-PDT	.794	.010	.009	.01	.015	.034
MDR-Phenomics	.915	.016	.004	.018	.012	.034

Note.— Power, Ele-α2, Ele-α3, Ele-α4, and Exp-α are calculated from combined data from groups N1 and N2, whereas Ele-α1* is calculated from group N2 only. Power is the number of times locus 1 is detected to be significant, divided by 1,000. Ele-α1 *, Ele-α2, Ele-α3, and Ele-α4 are elementwise type I errors calculated by the number of times locus 1, 2, 3, or 4, respectively, is detected to be significant, divided by 1,000. Exp-α is the experimentwise type I error calculated by the number of times any of loci 1, 2, or 3 is detected to be significant, divided by 1,000.

The power analysis indicates that MDR-Phenomics has greater power than both SP-MDR and MDR-PDT in the majority of the 16 data sets. The only exceptions were data sets 8 and 10, in which each of the three methods has power close to 1.0. Data sets 1–3 and 4–6 have unchanged sample size in group N1 but varying sample size in group N2. We see that power decreases for all three methods (SP-MDR, MDR-PDT, and MDR-Phenomics) with increasing size of group N2. Power decreases more precipitously for the MDR-PDT analysis that does not use PC information to help distinguish groups N1 and N2. Data sets 1, 7, and 8 and data sets 4, 9, and 10 have increasing sample size in group N1, whereas sample size is unchanged in group N2. These results show that power increases as the size of group N1 increases for each of the three methods, with the power of MDR-PDT and SP-MDR getting closer to the power of MDR-Phenomics as group N1 begins to dominate the sample. We verified these conclusions in data sets 11, 12, and 13 simulated with the recessive disease model, where data set 12 has double the sample size of data set 11 in group N1 and equal sample size in group N2 and where data set 13 has double the sample size of data set 12 in group N2 and equal sample size in group N1.

For MDR-Phenomics and SP-MDR, the number of PC levels affects power too. Since MDR-PDT does not consider phenotypic information, its power is not affected by changes in levels of PC. In five pairs of data sets (data sets 1 vs. 4, 2 vs. 5, 3 vs. 6, 7 vs. 9, and 8 vs. 10), both MDR-Phenomics and SP-MDR had less power when the number of PC levels was larger; the power of MDR-PDT was generally unaffected by PC. The effects of PC levels on the power of MDR-Phenomics were validated again in data sets 14, 15, and 16 simulated in a multiplicative disease model.

When the number of PC levels is large (e.g., eight), MDR-Phenomics has much better power than that of SP-MDR, which uses Bonferroni adjustment for multiple tests. In the examples here, MDR-Phenomics shows power increases over SP-MDR of 80%–400% for those data sets that have eight PC levels and ⩽1,000 triad families in N1 (data sets 1–4, 7, and 16). When the sample size in group N2 is much larger than that in group N1, MDR-Phenomics shows a substantial increase in power over MDR-PDT. For data sets 3 and 6, which have 500 triad families in group N1 and 2,000 triad families in group N2, MDR-Phenomics increases the power of MDR-PDT by 139% and 214%, respectively.

Power and Type I Error of Multilocus Effects

On the basis of our simulation strategies, there are seven kinds of locus effects that can be detected in the data sets from the multilocus disease models, those involving loci [1], [5 6], [7 8] and their combinations. The power of the successful detection of these effects is listed in table 5. The results show that, as in the one-locus models, MDR-Phenomics is better than MDR-PDT and SP-MDR with or without Bonferroni adjustment for all locus models. The effects of loci [1], [5 6], and [7 8] were simulated independently. However, the power of detecting a combined effect from them is intermediate to the power of detecting individual effects. For example, power estimates from [1 5 6], [1 7 8], and [1 5 6 7 8] are all larger than power from locus 1 but smaller than power from [5 6], [7 8], and [5 6 7 8], respectively. These results indicate that a larger model from combined effects washes out an effect in some cases and enhances it in others.

Table 5. .

Power of Multilocus Effects^[Note]

	Power
Locus Model	MDR-Phenomics	MDR-PDT	SP-MDR	SP-MDR*	CLR
[1]	.52	.31	.12	.46	.49
[5 6]	.79	.51	.29	.57	.22
[7 8]	.98	.85	.58	.86	.20
[1 5 6]	.56	.26	.13	.35	.12
[1 7 8]	.88	.75	.33	.62	.12
[5 6 7 8]	.64	.59	.20	.49	NA
[1 5 6 7 8]	.57	.14	.13	.31	NA

Note.— Power is calculated as the percentage of a locus model with P<α among 100 replicates. The α for MDR-Phenomics, MDR-PDT, and CLR is .05. The α for SP-MDR with Bonferroni adjustment is .05/8. SP-MDR* does not adjust for multiple tests among eight phenotypic levels and uses elementwise α=.05. NA = not available due to failure of the algorithm to converge.

If the sample is genetically homogeneous or if the correct PC is not known, the power of MDR-Phenomics will be affected. To evaluate the power under genetic homogeneity, we analyzed group N1 from the first 100 replicates of data set 1 (table 1) including interactions from loci [5 6] and [7 8] in group N1. We found that MDR-PDT had generally larger power than MDR-Phenomics (ranging from a 2% decrease to a 20% increase in power) when there is homogeneity (details not shown). This shows that MDR-PDT is still preferable if heterogeneity cannot be well captured by a PC.

Power of CLR

The results of testing interaction between PC and the loci with use of CLR are listed in the last column of table 5. The test of locus 1 shows that the power of CLR (0.49) is close to the power of MDR-Phenomics (0.52). However, the power of CLR is much smaller than the power of MDR-Phenomics for the analysis of interaction from locus pairs [5 6] and [7 8]. In tests of three-locus effects among [1 5 6] and [1 7 8], the power of CLR is decreased further. Because of sparseness, the maximum-likelihood estimates of coefficients fail to converge for testing effects from [5 6 7 8] and [1 5 6 7 8] (indicated by “NA” in table 5). CLR has less power than all the MDR-based methods considered (table 5), illustrating a clear advantage of using data reduction methods.

Analysis of Autism Data

Analysis of allelic frequencies showed that all markers match HWE expectations except locus 5 (data not shown). The correlation coefficients (r²) from GOLD output (table 6) indicate that loci 5 and 6 had moderate correlation in both affected (r²=0.441) and unaffected (r²=0.51) individuals.

Table 6. .

LD Analysis of Autism Data^[Note]

	r2
Locus	1	2	3	4	5	6	7	8
1		.086	.299	.074	.002	0	0	0
2	.07		.058	.025	.011	.005	.002	.001
3	.22	.065		.101	.002	0	.002	.001
4	.071	.031	.104		0	0	0	.001
5	0	0	.012	.011		.441	.022	.033
6	.001	.015	.001	.001	.51		.014	.235
7	.007	.002	0	0	.026	.009		.037
8	.006	.007	.004	.004	.046	.259	.035

Note.— Values highlighted in bold indicate moderate correlation. r² values in the upper triangle are from affected individuals, and r² values in the lower triangle are from unaffected individuals.

Starting with the test of one-locus models, MDR-Phenomics, MDR-PDT, and SP-MDR all identified locus 6 as the best one-locus model (table 7). Neither this model nor any of the other one-locus models were statistically significant. In the two-locus analysis, MDR-Phenomics found that the model containing locus pair [1 8] is the best one, with a statistically significant P value of .033. SP-MDR detected the model as marginally significant (P=.025), with a threshold of α=0.025 with use of a Bonferroni adjustment, whereas MDR-PDT failed to detect a significant two-locus model. The significant result from MDR-Phenomics and the marginal result from SP-MDR suggest a joint genetic effect involving SLC6A4 (rs1042173) and ITGB3 (rs3809865) when sex is taken into account. Analysis of higher-order interactions by all methods did not give significant results (results not listed).

Table 7. .

Models of Autism Data, with Sex as PC^[Note]

Model and Loci	Statistic	P Value
One-locus:
MDR-Phenomics:
[6]	7.008	.332
[5]	2.014	.822
[3]	1.293	.91
[7]	1.279	.911
[8]	.763	.969
[1]	.708	.973
[4]	.246	.996
[2]	0	1
MDR-PDT:
[6]	1.618	.813
[8]	1.568	.825
[1]	1.122	.986
[5]	1.083	.99
[3]	.907	.999
[4]	.771	.999
[7]	.750	1
[2]	.665	1
SP-MDR:
[6]	2.179	.413
[7]	1.674	.635
[5]	1.558	.838
[8]	1.439	.755
[3]	1.304	.94
[1]	1.062	.9
[4]	.975	.985
[2]	.579	1
Two-locus:
MDR-Phenomics:
[1 8]	58.03	.033
[3 6]	24	.323
[4 8]	11.09	.798
[5 6]	9.278	.851
MDR-PDT:
[4 8]	3.755	.139
[1 8]	2.951	.664
[4 6]	2.445	.943
[3 6]	2.241	.983
SP-MDR:
[1 8]	5.095	.025
[3 6]	3.41	.32
[4 8]	2.888	.631
[4 6]	2.555	.865

Note.— P values for locus pair [1 8] are highlighted in bold.

Discussion

We have presented a novel approach to test for genetic effects in triad families while incorporating information from PCs. This approach integrates dimension reduction from MDR (i.e., handling high-dimensional data) and new features from MDR-PDT for processing pedigree data, as well as the nonfixed permutation test for multiple tests from EMDR. The M statistic developed in MDR-Phenomics measures genetic effects from a multilocus model, with the goal of using PCs to control for genetic heterogeneity. Although we have focused on PCs, the covariate could be any categorical covariate that might capture heterogeneity, such as ascertainment site or environmental exposure. Even though detection of a genetic effect is weakened because of the mixture of data with genetic heterogeneity, MDR-Phenomics appears capable of detecting a genetic effect if genetic heterogeneity is expressed as distinct PC values, as shown in the analysis of autism data.

To evaluate the power of MDR-Phenomics, we compared it with MDR-PDT without consideration of heterogeneity and with SP-MDR with Bonferroni adjustment. Our goal for power comparison was to illustrate differences in power between methods that researchers might commonly use in practice. The Bonferroni correction is usually used to avoid permutation testing. However, as the number of PC levels increases, the power of SP-MDR with the use of Bonferroni correction decreases drastically. This can be seen in the analysis of simulation data sets 14, 15, and 16, which have two, four, and eight PC levels, respectively. Results in table 4 show that the power of SP-MDR decreases nearly 50%, whereas the power of MDR-Phenomics has no obvious change. When MDR-Phenomics was compared with MDR-PDT without analysis of PCs, the results showed that integration of PCs can capture genetic heterogeneity and increase the power of detecting a gene effect under heterogeneity. This conclusion was shown again in the analysis of multiple loci (table 5).

Standard case-triad approaches with use of the logistic model can be used to detect high-order interaction with incorporation of PCs. However, the required number of parameters increases exponentially with the number of loci. Too many parameters relative to the sample size can result in an increase of type I and type II errors.^30,31 Under moderate sample size, it is even impossible to detect a two-way interaction for 10 loci because as many as 180 parameters need to estimated.⁵ Our simulation studies showed that maximum-likelihood estimates of parameters cannot be obtained in the model that includes interaction between eight levels of PCs and loci [5 6 7 8] and [1 5 6 7 8] for a sample with 1,000 triad families. In contrast to classic logistic regression, MDR-Phenomics is nonparametric and assumes no particular genetic model. As shown by our simulation studies, MDR-Phenomics has greater power for testing interactions in heterogeneous genetic data. For testing the main effects of a locus depending on PC, MDR-Phenomics and CLR have similar power.

In the analysis of SLC6A4 and ITGB3 in the autism data, we used sex as a PC because autism has a striking sex bias, which may reflect genetic heterogeneity. MDR-Phenomics detected a statistically significant two-locus model including one marker from each gene. Both loci match HWE expectations, and no LD exists between the two loci (table 7). In addition, neither loci shows a significant main effect, as demonstrated by nonsignificant one-locus tests. Therefore, the result indicates a possible interaction between locus 1 of SLC6A4 and locus 8 of ITGB3. In addition, we see that the interaction appears stronger in one sex but disappears or is weaker in the other sex (i.e., genetic heterogeneity). This was shown by stratified analysis, in which the P value for model [1 8] in female probands is .025, whereas the P value in male probands is 1.0 by MDR-PDT. Heterogeneity of locus effects in the different sexes could explain such patterns and could cause the result to weaken when sex is ignored, as in the MDR-PDT analysis, which fails to find the genetic effect. SP-MDR analysis gives marginally significant results. However, as the number of PC levels increase, we would expect the Bonferroni adjustment to be increasingly conservative.

The P value for the MDR-Phenomics test is estimated using a permutation test to obtain the empirical distribution of the M statistic. The permutation method randomly shuffles only transmission status with genotypes, and PC is unchanged among all families. To adjust for multiple tests, the nonfixed permutation method selects the largest M statistic among all K-locus models in the permuted data as the permuted statistic. The number of K-locus models increases as the number of loci (N) in the data set increases, which causes an increase in the average permuted statistic and a decrease in power as more unassociated loci are added. This represents a potential limitation in the application of MDR-Phenomics to genomewide and candidate-gene analysis with an excessive number of loci to be tested. To restrict the number of loci, we have considered two basic strategies. First, LD analysis can help us pick independent loci or tag SNPs, to reduce the number of loci. The tag SNPs in haplotype blocks can be identified by searching genomic or chromosomal regions in data with heuristic methods, such as the dynamic programming algorithm,³² or by association analysis with the use of HapMap data.^33–35 Second, we can use the design-based two-stage approach,^36,37 where all markers are genotyped in stage 1 and the promising markers are selected for analysis by MDR-Phenomics in stage 2. Instead of reducing the number of loci, we have made efforts to prevent overly conservative results due to traditional adjustments for multiple testing (e.g., the false-discovery rate [FDR]).^38–40 Applied widely in microarray analysis,^40,41 the FDR may have applicability to MDR-Phenomics. To apply FDR, the P value, without adjustment for multiple tests, from the fixed permutation method¹⁴ provided by MDR-Phenomics is used. However, power and type I error based on the adjusted P value with FDR are still under investigation.

For consideration of a PC, a common strategy is to stratify analysis at every phenotypic level. However, multiple tests at every level should be controlled; otherwise, experimentwise type I error (the probability of getting a randomly significant result at any level) will be high. The trade-off in controlling for multiple testing is a decrease in power to detect a particular effect. The optimal method for controlling for multiple testing is debated. It is well known that the Bonferroni adjustment, a popular method applied by SP-MDR, is conservative, which was observed in our simulation studies. This fact should be considered when thinking about the power comparisons between SP-MDR and the other methods. Nevertheless, even when there is no adjustment for multiple testing, the power of stratified analysis could be decreased because of small sample size within a stratum. Such an example was observed in the test of multilocus effect that exists in the four strata, where SP-MDR without adjustment for multiple testing at every stratum has smaller power than that of MDR-Phenomics (table 5). In contrast to stratified analysis, MDR-Phenomics uses the whole data set for testing gene effects, and integrated PC analysis does not require additional adjustment for multiple testing.

MDR-Phenomics uses a C statistic to measure association. Under genetic heterogeneity, the C statistic may underestimate the signal of association. To magnify the signal, MDR-Phenomics derives the M statistic by multiplying the C statistic with a multiplicative factor. The multiplicative factor takes the form of an F statistic from an ANOVA model. This multiplicative factor was chosen for three reasons. First, the F statistic measuring different means of D among phenotypic levels can indicate the level of heterogeneity; a larger F statistic indicates larger heterogeneity. Second, if there is no heterogeneity, it is expected that homogeneous association exists and that the sample mean of D in every stratified level of PC should be the same. The F statistic from the ANOVA model will be ∼1. Therefore, the M statistic will approximate C under homogeneity. Last, the F statistic is calculated in every permuted data set. The empirical distribution of the M statistic is acquired by integrating the empirical distribution of the F statistic under the null hypothesis of no association. By magnifying the statistic for association under heterogeneity, it is expected that MDR-Phenomics will be more powerful than MDR-PDT, which ignores heterogeneity. This was observed in our simulation studies (tables 4 and 5). Notably, we also found that, despite the advantages of MDR-Phenomics in a heterogeneous data set, MDR-PDT is generally more powerful if the data set is genetically homogeneous or if heterogeneity is not captured by a measured PC.

Under uncommon cases, the C statistic may approximate zero even in a heterogeneous sample when genotypes from associated loci are overtransmitted to the proband in one PC level (i.e., positive association from these genotypes) but are undertransmitted to the proband in another PC level (i.e., positive association from complementary genotypes). For an extremely small C value, a large F value may still result in an M value close to zero. To solve this problem, a different method to calculate C could be used. For example, instead of directly calculating C in a sample, we can calculate C in the ith level of the PC (denoted as C_i) and get C in the whole data as the sum of all C_i from different levels. This calculation of C has the properties that stronger association tends to have a larger C value and that genetic heterogeneity will not result in a zero value of C. However, C_i from a small subset generally has a large variance. When the M statistic comes mainly from the sum of C_i, the larger variance can result in a decrease in power of MDR-Phenomics too.

A difficulty with MDR-Phenomics, like all high-order analysis methods, is interpretation of results; determining biological or clinical relevance on the basis of the analysis can be challenging. In MDR-Phenomics, it is difficult to know the biological meaningfulness of what we measure or define as a PC in complex disease (e.g., repetitive behaviors in autism). Additionally, a K-locus model with a large K may be difficult to dissect. To aid interpretation, a standard statistical model (e.g., logistic regression) can be used to describe the effect of individual loci and their interactions. Although this provides a statistical interpretation, statistical significance of a multilocus model does not necessarily translate to biological significance. Biological significance often requires biochemical experiments of molecular pathways. However, molecular investigations of multiple loci acting simultaneously may be difficult to implement.

Currently, MDR-Phenomics analyzes only discrete PCs. For continuous PCs, data-mining methods can be used to cluster and transform a continuous PC to a discrete variable. Alternately, we can consider other models (e.g., a general linear model) to evaluate the effect of a continuous PC on the association of a K-locus model with transmission. MDR-Phenomics analysis may, in fact, give guidance regarding relevant phenotypic classifications based on the underlying genetic associations. In summary, MDR-Phenomics represents a novel method incorporating phenotype information and genetic information, which complements traditional linkage and association analysis to detect genetic effects in heterogeneous complex disease.