Pathway-Based Approaches for Analysis of Genomewide Association Studies

Abstract

Published genomewide association (GWA) studies typically analyze and report single-nucleotide polymorphisms (SNPs) and their neighboring genes with the strongest evidence of association (the “most-significant SNPs/genes” approach), while paying little attention to the rest. Borrowing ideas from microarray data analysis, we demonstrate that pathway-based approaches, which jointly consider multiple contributing factors in the same pathway, might complement the most-significant SNPs/genes approach and provide additional insights into interpretation of GWA data on complex diseases.

Genomewide association (GWA) studies have greater power to detect genetic variants that confer modest disease risks than linkage analysis does, even when a large number of markers is tested across the genome.¹ GWA aims to identify the genetic architecture of complex diseases, which often result from the interplay of multiple genetic and environmental risk factors.² However, in stark contrast to the notion of “multiple factor–complex diseases,” currently, all published GWA studies list only the 20–50 most-significant SNPs and their neighboring genes (the “most-significant SNPs/genes” approach), while paying little attention to the rest. Although such a simple approach has led to the discovery of novel genes for several complex diseases, there are certain limitations. First, genetic variants that confer small disease risks are likely to be missed in the most-significant SNPs/genes approach after adjustment for multiple testing. Second, even those variants that confer a larger effect might not always rank among the top 20–50 among hundreds of thousands of markers tested, especially when the sample size is small.³ Although it is common to report the most-significant results, in many situations, researchers might formally assign weights to the SNPs according to their biological plausibility. For example, it has been proposed to incorporate information on genomewide linkage,⁴ prior belief of the plausibility of positive findings,⁵ or prior probability of disease association⁶ to assign weights to SNPs in GWA studies. Simulations demonstrated that such weighted analyses can improve the power of detecting association when the weights are assigned appropriately. However, in many cases, prior linkage information is not available or does not replicate for complex diseases, and the assignment of a priori probability of association is often arbitrary. Here, we demonstrate that pathway-based approaches, which jointly consider multiple variants in interacting or related genes, might complement the most-significant SNPs/genes approach for interpreting GWA data on complex diseases.

Our proposed approach to the analysis of GWA data is motivated by pathway-based methods of microarray data analysis. When expression profiles of different physiological states are compared, tens or hundreds of genes may have subtle differences in expression levels. Rather than focusing on individual genes that have the strongest evidence of differential expression, these pathway-based approaches typically rank all genes by their significance of differential expression and then look for whether a particular group of genes is enriched at one end of the ranked list more than would be expected by chance.⁷ Application of pathway-based approaches in microarray data analysis often yields biological insights that are otherwise undetectable by focusing only on genes with the strongest evidence of differential expression. For example, when expression levels of 22,000 genes were compared in a microarray study of diabetes, no single gene showed a statistically significant expression difference after adjustment for multiple testing; however, a pathway-based approach was capable of identifying a set of PGC-1α–responsive genes that showed a modest but consistent change in expression levels in muscle samples from subjects with diabetes.⁸ We propose that pathway-based approaches can also be applied to GWA studies of complex diseases, where multiple genes in the same pathway contribute to disease etiology but where common variations in each of these genes make modest contributions to disease risk. Rather than focusing on a few SNPs and/or genes with the strongest evidence of disease association, by considering multiple contributing factors together, we potentially can improve the power to detect causal pathways and disease mechanisms.

There are marked differences between microarray experiments that examine expression levels of transcripts and GWA studies that examine population frequencies of genetic variants. A typical gene has only a few transcripts, and their expression levels are generally correlated, subject to regulation by alternative splicing and alternative promoters. Therefore, it is generally acceptable practice to represent the expression value of a gene by the maximum or median value of all its transcripts and/or probe sets. However, a typical gene may be represented on a chip with either a few or several hundred common SNPs, yet only one or a few of them contribute to disease risk or are in linkage disequilibrium (LD) with causal variants. Therefore, it is not immediately clear what the best strategy is to condense statistics for multiple SNPs within a gene into a single value for the gene. To apply pathway-based approaches to GWA data, we take the maximum statistic for all SNPs near a gene to represent the significance of the gene and use a permutation-based approach that shuffles the phenotype labels of cases and controls to adjust for multiple testing.

To perform pathway-based analysis of GWA data, we modified a preexisting algorithm, the gene-set enrichment analysis (GSEA) algorithm.⁹ The GSEA algorithm was developed originally for microarray data analysis, and it performs especially well for situations where subtle effects of many genes contribute to changes in overall gene-expression patterns. In our modified algorithm, for each SNP V_i (i=1,…,L, where L is the total number of SNPs in a GWA study), we calculated its test statistic value, r_i (e.g., a χ² statistic for a case-control association test or a χ² statistic for the transmission/disequilibrium test). We next associated SNP V_i with gene G_j (j=1,…,N, where N is the total number of genes represented by all SNPs) if the SNP is located within the gene or if the gene is the closest gene to the SNP. SNPs that are 500 kb away from any gene are not considered, since most enhancers and repressors are <500 kb away from genes, and most LD blocks are <500 kb. (In very rare cases where one SNP is located within shared regions of two overlapping genes, we map the SNP to both genes.) For each gene, we assigned the highest statistic value among all SNPs mapped to the gene as the statistic value of the gene. For all N genes that are represented by SNPs in the GWA study, we sorted their statistic values from largest to smallest, denoted by r₍₁₎,…,r_(N). For any given gene set S, composed of N_H genes, we then calculated a weighted Kolmogorov-Smirnov–like running-sum statistic¹⁰ that reflects the overrepresentation of genes within the set S at the top of the entire ranked list of genes in the genome:

where 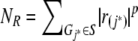and p is a parameter that gives higher weight to genes with extreme statistic values. When p=0, this test statistic reduces to a regular Kolmogorov-Smirnov statistic, which identifies groups of genes whose r_j distribution differs from that of a random gene set.¹⁰ The authors of the original GSEA algorithm recommend using p=1, and we followed this convention here. The enrichment score, ES(S), measures the maximum deviation of concentration of the statistic values in gene set S from a set of randomly picked genes in the genome. Therefore, if the association signal in S is concentrated at the top of the list, then ES(S) will be high.

The calculation of ES(S) relies on the maximum statistic within each gene. For genes with a larger number of SNPs, the maximum statistic will be bigger than for genes with a smaller number of SNPs. To adjust for gene size, we conducted a two-step correction procedure. In the first step, we permuted the disease labels of all samples, ensuring the same number of individuals in each phenotype group for case-control studies; alternatively, the transmitted and untransmitted alleles can be shuffled. During each permutation (denoted by π), we repeated the calculation of enrichment score as described above, except that the disease phenotypes were obtained from permutation. We denote the corresponding enrichment score by ES(S,π). The purpose of this step is to calculate ES(S,π) values for all gene sets S and all permutations π. In the second step, we calculated a normalized enrichment score (NES), defined as

so that different gene sets are directly comparable with each other. The original GSEA algorithm uses a simple approach by dividing a given ES score for a gene set S by the mean value of ES(S,π), which does not consider the different variances of permutated ES scores in gene sets with varying sizes. Our simple two-step correction procedure effectively adjusts for different sizes of genes and preserves correlations of SNPs in the same gene.

Statistical significance and adjustment for multiple hypothesis testing were done by the permutation-based procedure. In the GSEA algorithm, two measures are used to adjust for multiple-hypothesis testing. A false-discovery rate (FDR) procedure can be used to control the fraction of expected false-positive findings to stay below a certain threshold.¹¹ For a gene set, let NES^* denote the normalized enrichment score in the observed data. The FDR¹¹ is calculated as

Alternatively, a familywise error rate (FWER) procedure can be used to adjust for multiple-hypothesis testing. The FWER is a highly conservative correction procedure that seeks to ensure that the list of reported results does not include even a single false-positive gene set. The FWER P value can be calculated as the fraction of all permutations whose highest NES score in all gene sets is higher than the NES^* for a given gene set.

We applied the pathway-based approach to a published GWA study of Parkinson disease (PD [MIM 168600]), for which the raw genotype data are publicly accessible from the Coriell Institute for Medical Research. This study by Fung et al.¹² genotyped 408K SNPs in 267 patients with PD and 270 neurologically normal controls in their stage 1 design and identified the 26 most-significantly associated SNPs. We note that the findings from this study are highly discordant with another GWA study of PD,¹³ in that none of the most-significant genes or even their cytogenetic positions overlap with each other. The apparent discordance between two similar GWA studies underscores the importance of looking beyond the most-significant SNPs/genes and searching for additional risk factors with moderate statistical significance. Our analysis of their data set used 390K SNPs that pass the initial quality-control threshold (defined as minor-allele frequency >0.05 and Hardy-Weinberg equilibrium [HWE] P value¹⁴ >.001). Using a recent human genome assembly (National Center for Biotechnology Information build 36, October 2005) and gene-structure annotation from the Ensembl database (version 42, December 2006),¹⁵ we associated SNPs with their closest protein-coding genes within 500 kb. We used several different resources to construct a database of gene sets and pathways. We first retrieved 260 annotated pathways from the BioCarta database and 190 annotated pathways from the KEGG Pathway Database.¹⁶ Next, we downloaded Gene Ontology (GO) annotation files for human genes from the ^GO Web site.¹⁷ We processed the GO annotation file and constructed 2,077 gene sets on the basis of GO level 4 annotations in Biological Process and Molecular Function. In the GO hierarchy, one node may descend from several ancestral nodes by different paths, and we excluded from our constructed gene sets those GO level 4 nodes that also occur in levels 2 and 3. Genes whose GO annotations are in level 5 or lower in the hierarchy are assigned to their ancestral GO annotations in level 4. To reduce the multiple-testing issue and to avoid testing overly narrow or broad functional categories, in our analysis, we tested only gene sets and pathways that contain at least 20 but at most 200 genes represented by markers in a given GWA data set.

Because of the extreme computational complexity of both permutation-based association tests and the modified GSEA algorithm, we used only 1,000 permutation cycles to adjust for multiple-hypothesis testing. After application of our algorithm to the Fung et al. data set,¹² we identified two significantly enriched gene sets or pathways, including the uridine-5′-diphosphate (UDP)–glycotransferase pathway and the O-glycan biosynthesis pathway (table 1). These two pathways are compiled from the GO database and KEGG database, respectively; they are functionally related and contain 19 overlapping genes. The finding that two glycan-related gene sets or pathways rank high in our pathway-based analysis is quite interesting; the relationship between glycobiology and neurodegenerative diseases has been postulated and recognized only in the past few years.^18–21 We note that the GALNT3 (MIM 601756) gene shared in these two pathways was reported to be one of the most-significant genes in another GWA study of PD,¹³ although the most-significant SNPs around GALNT3 in the study by Fung et al.¹² have a P value of .22. These results suggest that our approach identified a potential disease-susceptibility mechanism for PD and generated a new hypothesis for future replication studies and functional studies of genes that rank high in the most-significant pathways.

Table 1. .

The Most-Significant Gene Sets or Pathways in the Fung et al.¹² GWA Study of PD Identified by a Modified GSEA Algorithm^[Note]

		Rank of Most Significant
Gene Set or Pathway	Set Size	SNP	Gene	Nominal P	FDR	FWER P
UDP-glycotransferase activity	89	59	41	<.001	.006	.006
O-glycan biosynthesis	23	69	49	<.001	.011	.018

Note.— Two pathways (database identifiers: GO accession number 0008194 and KEGG accession number hsa00512) demonstrate statistical significance after adjustment for multiple testing, but the SNPs and genes within these pathways cannot be detected by the most-significant SNPs/genes approach.

We next examined whether the need for permuting the phenotype labels (disease status) can be eliminated by a modified gene-based approach. Unlike microarray data analysis that operates on only tens of thousands of transcripts and dozens of samples, the permutation of phenotypes and recalculation of statistic values for half a million SNPs and hundreds or thousands of samples in the GWA analysis is a very computationally expensive process. We therefore tested the utility of the “preranked” module in the GSEA algorithm on P values for all SNPs. After test statistic values from SNPs are assigned to genes, this gene-based approach shuffles the test statistic values for all genes, instead of shuffling the phenotype labels, and then calculates ES(S,π) and NES(S,π) to adjust for multiple testing. Compared with the approach that we proposed above, this preranked module of GSEA eliminates the need for phenotype shuffling and the requirement of the use of raw genotype data, making it potentially attractive in many cases.

Since the preranked module of GSEA requires the use of a single P value to represent the significance of each gene, we tested two alternative approaches to achieve this goal. The first approach assigns to the gene the most significant P value from all SNPs surrounding the gene. This approach introduces biases, so that larger genes are likely to have more-significant P values, and enrichment statistics for pathways containing large genes will be inflated. The second approach applies a Simes method^22–24 and computes a P value from multiple SNPs. For L SNPs ranked by their P value, p₍₁₎,…,p_(L), the Simes P value is calculated as min{p_(i)L/i}, where 1⩽i⩽L. The Simes method provides an overall P value for the entire collection of L hypotheses, but it is still an overconservative approach that might lead to loss of power. We applied these two approaches to the Fung et al. data set¹² on PD and to two additional GWA data sets for which only P values for SNPs (but not raw genotypes) are available.

Application of the first approach produced biologically plausible signals on multiple data sets (table 2). When applied to the Fung et al. data set¹² on PD, it identified a few pathways that reach statistical significance. The top gene set or pathway (glutamate receptor) is a well-known PD-susceptibility pathway and has been implicated in PD therapy.^26,27 We next analyzed another GWA study of PD by Maranganore et al.¹³ and found that the glutamate pathway ranks as the third-best pathway. Finally, we also tested the first approach on a GWA data set²⁵ on age-related macular degeneration (AMD [MIM 603075]) from the dbGaP database and found that the most-significant pathways in this study are the pathway related to complement factor H (CFH [MIM 134370]) and the ATP-binding cassette (ABC) transporters pathway. Indeed, the association between CFH and AMD has been consistently replicated after the initial publication, and AMD is one of the most common genetic diseases that have been associated with defects in ABC transporters.²⁸ However, after application of the second approach with the Simes adjustment, the enrichment signals disappeared for all three data sets, indicating a severe loss of power. Therefore, we caution that pathway-based methods that use an unadjusted preranked list of genes are biased, and a more powerful solution for condensing P values from multiple SNPs into a single value is needed.

Table 2. .

The Most-Significant Gene Sets and Pathways Identified by a Preranked Module of the GSEA Algorithm for Two GWA Studies of PD and One GWA Study of AMD

		Rank of Most Significant
Study and Gene Set or Pathways	Set Size	SNP	Gene	Nominal P	FDR	FWER P
Fung et al.12 stage 1 association study of PD:
Glutamate receptor activity	39	109	77	<.0001	.003	.003
O-glycan biosynthesis	23	155	114	<.0001	.002	.003
Ligand-gated ion channel activity	97	207	153	<.0001	.001	.004
Transmembrane receptor protein phosphatase activity	20	147	106	<.0001	.004	.015
GABA receptor activity	23	109	77	<.0001	.010	.048
Maraganore et al.13 tier 1 association study of PD:
Axon guidance	56	44	31	<.0001	.005	.006
CNS development	130	118	86	<.0001	.034	.068
Glutamate receptor activity	35	34	23	.0007	.069	.189
Klein et al.25 association study of AMD:
CFH-related pathway	4	1	1	<.0001	.004	.004
ABC transporters	42	157	111	<.0001	.046	.088
Skeletal muscle fiber development	25	75	51	<.0001	.065	.181

Our results demonstrate that pathway-based approaches may incorporate information from markers with moderate significance levels and may detect novel disease-susceptibility mechanisms in GWA studies. The identified most-significant pathways may help formulate new hypotheses or substantiate existing hypotheses, and genes that rank high in candidate pathways can serve as candidates for further replication and functional studies.

The current understanding of human gene function is incomplete, so the curated gene sets and pathways are not a comprehensive representation of functionally related gene cohorts in the human genome. One advantage of our current approach is that we used annotations from the GO database to supplement our pathway collections. The GO database contains large amounts of electronic annotations based on studies of human orthologs or paralogs in model organisms, so that we can incorporate computationally predicted gene sets and pathways in the gene-enrichment analysis to improve power. Nevertheless, a large number of genes in the human genome are uncharacterized or poorly characterized, so that there may not be any pathway information available. Information on SNPs near these genes will not be incorporated in the pathway-based approaches, so our approach can complement but not replace the single-SNP approach.

The modified GSEA algorithm operates on the maximum statistic among all SNPs both surrounding and within a gene and then combines the effects of genes within the same pathway through the Kolmogorov-Smirnov–like running-sum statistic on the maximum statistic of each gene; therefore, it increases the chance of identifying genetic variants that have a modest contribution to disease risk. This pathway-based approach is inherently different from the “best SNPs/genes” approach, which operates on all SNPs in the entire genome and ignores the “joint effect” for genes in the same pathway. To adjust for the effect of different gene sizes, we employed a two-step permutation-based procedure, which preserves the type I error rate across genes of different sizes. We note that larger genes might suffer from power loss more than smaller genes.

We recognize that the maximum statistic is only one way to summarize association signals in a gene. When multiple distinct variants in the gene contribute to the overall association signal, the maximum statistic may no longer be the best statistic to capture such information. As discussed in our description of methodology, there has not been a widely agreed on and accepted theory for how to combine test statistics on multiple SNPs into one single P value. Genes vary greatly in their sizes and their structures of LD blocks, so any method for combining P values may work effectively only on some genes but not on others. Our own experience shows that, generally, if several SNPs in the same gene have higher significance levels than do other SNPs in the same genomic region, they either are located in the same LD block or are in the same copy-number variation (CNV) region (in many cases, HWE filtering criteria are not able to exclude CNV regions from GWA analysis). Therefore, although there are numerous cases in which rare variants in different parts of the same gene may lead to the same or a similar disease phenotype, generally only one or very few LD blocks in a gene will harbor common causal variants. These observations support our use of maximum statistics together with a permutation procedure to adjust for gene sizes. However, we note that once significant pathways are identified, it is possible to use multimarker methods for testing marker-marker or even gene-gene interactions within the same pathway—for example, by the sum statistics for multiple markers.²⁹

Our current pathway-based approach is dependent on the collection of SNPs selected for a specific genotyping assay. Although some commercially available standardized arrays are constructed using HapMap data to reduce marker-marker correlation, many SNP arrays are custom-made on the basis of prior belief of association (e.g., arrays specifically designed for SNPs that cause coding changes or SNPs in conserved genomic regions or arrays supplemented with dense markers in prior linkage regions). The bias in coverage may influence the prior likelihood of detecting associated variants for different genes and may favor some gene sets and pathways over others. For these reasons, we caution that pathway-based approaches may work better on marker sets selected on the basis of genomewide LD structure than on custom-made genotyping arrays.

Constructed gene sets and pathways may be dependent on each other or may correlate with each other. Cellular components and molecules do not work in isolation; instead, pathways overlap, so that many gene sets and pathways will unavoidably share the same genes. The overlap of genes among gene sets and pathways will not affect their relative ranking of NES values; however, because of the permutation procedure for multiple-hypothesis adjustment, dependent pathways will lead to decreased power (in terms of both FDR and FWER) when the causal genes are shared by multiple pathways.

Our modified GSEA algorithm preserves correlation structures between SNPs when permuting the data and therefore can potentially increase the power for detecting association more than can approaches that ignore such correlation. We note that the pathway-based method does not take gene-gene correlation into account. Although this might be a serious issue in microarray data analysis, it is less of a concern in GWA studies, in which genes in the same pathway may be dependent on each other only if they overlap the same LD block or if there are epistatic interactions between them. In these cases, the contribution of genes to test statistics may be correlated and may lead to overestimation of significance of pathways.

In conclusion, our results demonstrate the applicability of pathway-based approaches to the interpretation and analysis of GWA data. We hope to encourage the community to look beyond the tip of the iceberg (the most-significant SNPs/genes) for GWA analysis of complex diseases. The development of pathway-based approaches that incorporate and weigh prior biological knowledge, including those gleaned from model organisms, will greatly facilitate the interpretation of GWA data and will lead to the identification of novel disease-susceptibility genes and mechanisms.