The in Vivo Rate of Somatic Adenomatous Polyposis Coli Mutation

Abstract

Cancer arises through successive somatic mutations/epimutations of oncogenes and tumor-suppressor genes. Accurate estimates of the rates at which these (epi)mutations occur are a vital but missing link in our emerging quantitative understanding of tumorigenesis. Their absence has hindered arguments concerning the importance of genetic instability in tumorigenesis and the number of mutations that precede malignant conversion of healthy cell lineages. Herein, a novel method for calculating the in vivo mutation rate of the adenomatous polyposis coli (APC) tumor-suppressor gene is presented. The large majority of bowel cancers are thought to be initiated by a partial loss of APC function, with the age-onset pattern dramatically altered for the worse in familial adenomatous polyposis (FAP) because these patients harbor selected germline APC mutations. Colon cancer in the context of FAP can be thought of as occurring “one hit quicker” than in the sporadic setting. We were able to isolate and estimate the rate of the initiating APC mutation in sporadic cases using the age incidence of FAP to approximate the time taken for a cell lineage in a sporadic patient with one APC mutation to present clinically as a cancer. Our result of approximately 10⁻⁵ mutations per allele per year, although higher than previous estimates, appears to be consistent with the mutational spectrum of APC. The quality of fit provided by this method supports the theory that FAP and sporadic bowel cancer follow the same genetic pathway and are separated by only one mutation.

The in vivo rate of somatic tumor suppressor or oncogene mutation cannot be measured directly. Often, it is not possible to isolate the precursor cells of a given cancer or, as a consequence, to probe their DNA for abnormalities. In cases where precursor cells can be isolated, the rarity of any specific mutation makes direct measurements of mutation rate impractical. Even in human cell cultures, determining mutation rate is very difficult1 and has only been possible at a handful of loci. Estimates fall between 10⁻⁸ and 10⁻⁶ mutations per gene per cell generation.2,3,4 Similar rates have been observed in yeast.5,6

These data provide only a blurred picture of the somatic mutation rate in humans. Aside from the 3 orders of magnitude over which they are spread, there is a question mark over how well the mutational characteristics of cultured cells mirror those of cells in vivo. Consequently, it is currently very difficult to ascribe a notional rate to tumor suppressor or oncogene mutation.

This is especially apparent when considering that the rate in a particular case will depend not only on microenvironmental factors that modify replication fidelity but also on the specific spectrum of genetic changes that lead to a selected mutant protein product.

Without resorting to cell lines, what alternative methods are available for measuring mutation rate? In vitro, the standard method is Luria-Delbruck fluctuation analysis. Many parallel clones are grown in culture from small parent populations containing no mutated genes. After a certain number of cell generations or when the clones have grown to a specific size, the prevalence of mutant cells within each population is recorded. The mean prevalence per clone is then used to estimate the underlying mutation rate. A simple in vivo analog of this experiment is to observe many patients (rather than clones) and measure the frequency with which neoplasia (rather than mutant colonies) arise, the neoplasia being markers of mutation. In other words, rather than trying to observe gene mutations at the microscopic level, a practical alternative is to observe malignancies at the population level (Figure 1). Luebeck and Moolgavkar7 inferred a rate of 10⁻⁶ per gene per year for adenomatous polyposis coli (APC) mutation in patients with colorectal cancer via this approach.

Figure 1.

In Luria-Delbruck fluctuation analysis (left), the number of mutant colonies arising in plated clones can be used to estimate in vitro mutation rates. By analogy, in vivo, the number of tumors arising in individuals can be used.

The primary advantage of using population data, in place of cell line data, is that they are indicative of in vivo rather than in vitro gene mutations. A second advantage is that neoplasms are markers of precisely the gene mutations whose rates of occurrence we would like to measure. Unfortunately, it is usually difficult to determine the number of precursor cells per patient at risk for a given cancer—a crucial factor in determining the mutation rate. Furthermore, besides the mutation of interest, there are often unknown additional pathogenic events required to produce a cancer. These confound the estimation procedure. For example, the estimate by Luebeck and Moolgavkar7 of the APC mutation rate depends on an assumed number of progenitor cells per colorectum. It also depends on more difficult assumptions about the etiology of bowel cancer. Although it was reasonable for them to suppose that the initiating events are alterations in the two alleles of APC, assumptions about the events that follow from the second APC hit are more speculative. These compromise the accuracy of their estimate.

In cases where there is a well defined genetic and histological sequence, precursor legions can be used in place of cancers for estimating rates of gene mutation. The advantage of using neoplasia at an earlier stage of tumorigenesis is that they contain fewer genetic alterations in addition to the mutation of interest. Iwama8 treated colonic adenomas as representative of two APC hits. From observed data on the incidence of adenomas in the bowel, he was able to infer a rate between 2 × 10⁻⁶ and 3 × 10⁻⁶ APC mutations per gene per year—similar to the estimate of Moolgavkar et al. Although Iwama’s approach removes some of the uncertainty associated with etiology, it is still dependent on assumptions about the number of cells at risk of cancer per patient. Our approach removes this dependency, while still requiring only a limited knowledge of pathogenesis.

We infer the rate of APC mutation by comparing incidence of sporadic colon cancer with that of colon cancers arising in the context of familial adenomatous polyposis coli (FAP). FAP is a hereditary cancer syndrome caused by germline APC mutation. It is commonly assumed that colon cancers arising sporadically and in FAP patients proceed along similar pathways of somatic evolution with FAP cancers requiring one less mutation at the APC locus. If this is the case and if partial loss of APC function is initiating for the large majority of cancers of either type, then it is reasonable to use the age-onset pattern of FAP to estimate the time lapse between the first APC hit and clinical detection in sporadic bowel cancer (Figure 2). Using FAP incidence data in this manner removes the need for assumptions about the adenoma-carcinoma sequence after the first APC mutation. In addition, the method is insensitive to the assumed number of progenitor cells, because this information is implicit in the FAP data, provided that the number of progenitors is the same in FAP and sporadic patients.

Figure 2.

The pathways of FAP and sporadic bowel cancer are separated by only a single, truncating APC hit. In the case of FAP, the first hit already exists in the germline. In a sporadic patient, a given cell lineage takes T_v years to acquire a truncating APC mutation in one allele and then a further T_FAP^lin years to become malignant. A FAP lineage only takes T_FAP^lin altogether to become malignant.

Materials and Methods

Only one source of FAP data was available for the analysis. This was recorded in the UK over a period of several years ending in 1965.9 To match the FAP data as closely as possible, sporadic data recorded in England and Wales between 1960 and 1962 by Doll et al10 were used to estimate ν, the mutation rate per allele per year. It was assumed that sporadic bowel cancer emerges via the same genetic pathway as FAP but with an extra initiating APC “hit” (Figure 2). A quantitative model, describing the time taken for a sporadic bowel cancer to develop, was derived on the basis of this assumption. The initiating APC hit occurs at a rate of ν per allele per year in the model. The time between this hit and clinical detection was estimated from FAP incidence data. Fitting the model separately to sporadic male and female incidence data then allowed ν, the desired mutation rate, to be inferred in each case.

Time until Sporadic Cancer

It was assumed that the colonic epithelium of each patient is sustained by a population of stem cells. These stem cells form the target population for cancer. Periodically, each divides asymmetrically to give rise to one new stem cell and one non-stem cell daughter. A given stem cell, and its lineal stem cell descendants will be referred to collectively as a “stem cell lineage” (Figure 3). We assumed a fixed number of lineages, N, and each was treated as an independent entity. Before the first APC mutation has occurred, each lineage retains only a single stem cell (undergoes no symmetric divisions). This restriction allows the time taken for the first APC mutation to be modeled with an exponential distribution. After the first APC mutation, however, the lineage can expand through symmetric divisions. A cancer is recorded when the first of the lineages has become malignant and grown to be of a detectable size.

Figure 3.

The epithelial sheet is replenished initially by a fixed number of independent stem cell lineages. These are shown in gray, and their differentiating progeny are shown in white. Black cells represent stem cell descendants that have at least one mutant APC allele.

The age at which any single lineage in a sporadic patient becomes malignant is denoted by 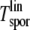. It is the sum of two waiting times (Figure 2): 1) T_v, the time taken for the initial APC hit to occur; and 2) T_FAP^lin, the time taken for the events that comprise the FAP pathway to follow (see Figure 2). So T_spor^lin can be expressed as

1

T_v was assumed to follow an exponential distribution, with rate 2ν (because there are two alleles and ν is the mutation rate per allele per year). Two contrasting methods were then used to derive a distribution for T_FAP^lin from the observed FAP data.

First of all, to avoid forcing a generic shape onto the distribution of T_FAP^lin, it was constructed as a survival curve directly from the FAP data. The construction proceeded in two stages. Initially, the observed FAP data, as summarized by Ashley,11 were used to estimate the distribution of T_FAP, the time at which a patient (rather than a lineage) first develops a malignancy. So, P[T_FAP ≤ t_i] was inferred for t_i = 10, 15, 20, 25,… via the Actuarial method (see for example Parmar and Machin12). Second, we observed that if a patient has N independent lineages at risk of becoming cancerous, then there is a simple relationship between T_FAP and T_FAP^lin:

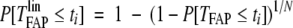Hence, a smooth approximation to P[T_FAP^lin ≤ t] was derived by interpolating the co-ordinates

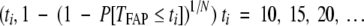Using this approximation to P[T_FAP^lin ≤ t] and equation 1, it follows that:

This gives the age at which cancer arises in a single lineage, T_spor^lin. For the patient, any of the N lineages has the potential to become a cancer. Consequently, the time taken for a patient to present with cancer, T_spor, is much quicker than for a single lineage. The two waiting times are related by

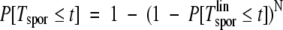2

Fit to Sporadic Data 1

With n fixed and T_FAP^lin defined as above, P[T_spor ≤ t] (equation 2) was used to construct a likelihood function, L(ν), for the sporadic data (for details of this standard construction, see, for example, Ref. 7). In turn, L(ν) was used to calculate a posterior distribution, post(ν). Assuming a uniform prior for ν on 10⁻⁷ to 10⁻³ we took

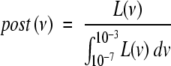3

Equation 3 was evaluated using the Mathematica 5.2 software package by Wolfram Research Inc. (Champaign, IL).

The variance of this posterior is likely to be too narrow because uncertainty over the distribution of T_FAP^lin was ignored in its derivation. To address this issue, in our second method for characterizing T_FAP^lin, we assume its distribution follows a predefined functional form whose parameters are to be inferred. Specifically, we used the formula of Armitage and Doll.13 This gives the probability that a cancer requiring n successive mutations, each occurring at a rate u, has developed from an immortal lineage by time t:

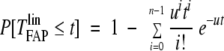4

so that

5

Fit to Sporadic Data 2

Using equations 4 and 5, a likelihood function, L(u, n, ν), was constructed for the FAP and sporadic data together, given the approximated FAP curve (parameterized by u and n) and the model for the sporadic disease. This likelihood was the product of the likelihood for the sporadic data [L(ν), calculated as previously described] and a new likelihood, L_FAP(u, n), for the FAP data.

The FAP data are drawn from a small study involving M patients, where M is ∼100. The patients are observed at 5-year age intervals. During the ith age interval, a total of S_i patients are treated with surgery before being removed from the study, and D_i new cancers occur among the remaining patients. To account for censoring of patients through treatment, Pop_i, the effective number of patients at risk of a primary cancer during the ith interval, is defined by

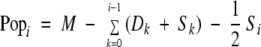ie, the number of healthy patients remaining in the study at the beginning of the interval less one-half those that are treated during the period. The likelihood, L_FAP(u, n), of the FAP data can be expressed as a product of binomial probabilities. If the probability of a cancer arising in a given patient during the ith interval is p_i, then the probability that D_i cancers arise among the effective population Pop_i over the period is

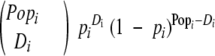L_FAP(u, n) is then equal to the probability of the given distribution of cases {D₁, D₂,… },

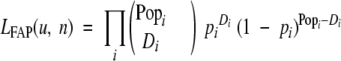If s_i and e_i are the start and end points of the ith age interval, then p_i can be evaluated, using equation 5, as

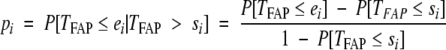6

Ascertainment bias has been neglected in equation 6. Because the penetrance of FAP is 100%, this bias should be minimal. To fit both the sporadic and FAP data simultaneously, the combined likelihood function, L(u, n, ν), was used:

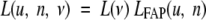The posterior density at ν (Figure 4) was calculated assuming uniform priors for ν, u, and n, respectively, on 10⁻⁷ to 10⁻³, 0 to 10⁻², and 2 to 7:

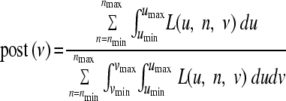Again, Mathematica was used to evaluate this expression.

Figure 4.

Posterior distribution of the APC mutation rate ν, measured in mutations per allele per year, calculated using a three parameter likelihood function. Sporadic colon cancer incidence data on cases diagnosed between 1960 and 1962 taken from Doll et al.10

Results

We assumed that sporadic bowel cancer emerges via the same genetic pathway as FAP but with an extra initiating APC hit (Figure 2). A stochastic model describing the time taken for a sporadic bowel cancer to develop was derived on the basis of this assumption. The intestinal cell lineages of a sporadic patient acquire initiating APC hits at a rate of ν per allele per year in the model. The remaining time taken for any such lineage to become malignant and present clinically was estimated from FAP incidence data. Fitting the resulting model back to the sporadic incidence curve allowed a posterior distribution for ν, the desired mutation rate, to be inferred.

This posterior distribution, post(ν), was derived via two separate methods. In the first, the time taken for an APC^+/− cell lineage to become malignant and present clinically was assumed to be distributed according to a survival curve constructed from the FAP data. The shape of post(ν) (Figure 5) in this case implies that ν, the annual rate of APC mutation per allele, falls between 6 × 10⁻⁵ and 8 × 10⁻⁵ for both males and females. These estimates are insensitive to 2-order of magnitude changes in the assumed number of cell lineages per patient. However, substituting the optimum ν for males or females into the model gives only a rough approximation to the sporadic incidence profiles (Figure 6). The discrepancy is systematic, in that for both males and females, we overestimate the risk before 65 years of age and underestimate it thereafter. It is likely that ascertainment bias in the FAP data is the underlying cause of this error. Ascertainment bias in the FAP data arises because only those patients who present clinically before death from other causes are included in the study. Consequently, risk of cancer at young ages, when mortality is low, is exaggerated whereas risk in older age as mortality increases is downplayed. Another problem is that the FAP data consist of only a small number of observations. By assuming the “real” distribution of FAP cases followed exactly a survival curve constructed from a small sample, the variances of the posterior distributions on ν were underestimated. To quantify the extent of this problem, as an alternative to using the exact survival curve suggested by observed data points, a parameterized class of possible approximations to the FAP curves was used. The posterior densities on ν in this case are only slightly wider (Figure 4). The optimized models naturally give a better fit to the sporadic data (Figure 7) and seem, crudely, to correct for the ascertainment bias described in the FAP data.

Figure 5.

Posterior distribution of the APC mutation rate ν, measured in mutations per allele per year, calculated using a single parameter likelihood function. Sporadic colon cancer incidence data on cases diagnosed between 1960 and 1962 taken from Doll et al.10

Figure 6.

P[T_FAP ≤ t], the cumulative risk of FAP at age t, was calculated separately for males (left column) and females (right column) by interpolating observed FAP data. P[T_spor ≤ t], the cumulative risk of sporadic bowel cancer at age t, was constructed from P[T_FAP ≤ t], according to assumptions about the relationship between FAP and sporadic bowel cancer described in the text. Using the optimum ν, P[T_spor ≤ t] provides an adequate approximation to observed sporadic data.

Figure 7.

P[T_FAP ≤ t], the cumulative risk of FAP at age t, is represented by a smooth function, parametrized by u and n. P[T_spor ≤ t], the cumulative risk of sporadic bowel cancer at age t, was again constructed separately for males and females from P[T_FAP ≤ t], as described in the text. Using the optimum parameter vector (u, ν, n), a good fit to the sporadic data can be made.

Discussion

Our calculations suggest that alleles of the APC tumor suppressor mutate to cause a selected protein change, about 6 × 10⁻⁵ times a year. This is 30 times faster than previous estimates.8,7 A rough consistency check can be done by comparing our estimate against the mutational spectrum of the gene. More than 95% of APC mutations found in bowel cancers are nonsense or frameshift mutations. They take the form of small deletions/insertions or point mutations that result in truncation of the protein.14 Assuming an error rate (insertions/deletions or mismatches) of 10⁻¹⁰ per base per cell generation15 and assuming 100 stem cell divisions per annum, the number, BP, of base pairs through which APC can be truncated (either by insertion/deletion or point mutation) would be

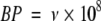Substituting in order 10⁻⁵ for ν gives BP ≃ 1000. This seems a sensible value for BP because more than 700 distinct, somatic APC mutations have been reported in bowel cancers to date.16

Approximations and Assumptions

Confidence in our estimates for ν should be based primarily, on the accuracy of the assumptions/approximations used in their calculation. The most crucial are as follows: 1) FAP and sporadic bowel cancer are both initiated by genetic alterations in the APC gene. 2) A lineage in a sporadic patient, with one APC hit, becomes malignant via the same mechanism as a FAP lineage with the germline genotype. 3) The target lineages for bowel cancer act independently. 4) Loss of the first APC allele in a sporadic patient follows an exponential distribution.

To evaluate the accuracy of these assumptions, a definition of “sporadic” colon cancer is necessary. We take sporadic to mean any case occurring in the general population, excluding those arising in the context of a known, highly penetrant germline mutation. Although initiating APC mutations appear to feature in the large majority of such cases,17 there are alternative avenues available for a progenitor cell in the colonic epithelium.18 Our method is also consistent with a model in which APC mutation appears as an early event, preceding any clonal growth, but is not necessarily initiating. However, cases with no APC mutation are a source of noise in the experiment. Because these cases form a minority of <30% and because their age relatedness is unlikely to be remarkably different from those initiated by APC, the impact should be minimal. A similar, but potentially more serious source of noise arises, because the registry data we use to represent sporadic cases are likely contaminated with FAP and other highly penetrant hereditary bowel cancers. However, these account for only 5% of all colorectal cancers,19 so the effect is negligible. Concerning approximation 2, APC hits can broadly be categorized into two types: 1) truncating mutation and 2) LOH. It is well established that the type and the position of the two hits at APC are not independent in either FAP or sporadic bowel cancer. The first hit in sporadic cases and the germline mutations in FAP are both predominantly truncating mutations, but their spatial distribution is not identical. Consequently, due to nonindependence of the two hits, or otherwise, LOH may occur at a different frequency as a second hit in sporadic cancers. Fortunately, the difference in the spatial distributions is primarily due to certain germline mutations occurring at high frequencies relative to somatic mutations in sporadic cases. Specifically, germline mutations affecting codon 1061 and codon 1309 are relatively frequent in FAP. Because these tend to lead to different second hits, truncating mutation and LOH, respectively, the effect on the overall frequency of LOH as a second hit in FAP is limited. For example, Rowan et al20 and Prall et al21 detected LOH in 23 of 99 (23%) and 20 of 99 (20%) sporadic cancers, respectively, whereas Lamlum et al22 found APC LOH in 42 of 210 (20%) FAP tumors.

Other factors that usually confound estimates taken from incidence data include the assumed number of cell lineages at risk and calendar year effects. Happily, the comparative nature of this study eliminates any sensitivity to the assumed number of lineages. It remains to be shown that the estimate is also robust under age-related changes in cell number. Calendar year effects are mild for bowel cancer before the 1980s7 and are unlikely to have a significant effect. Finally, a difficult problem, when modeling incidence data, is to decide how long it takes for a cancer to be detected once it has come into existence.23 In this study, the FAP data are used to estimate the time taken for an APC^+/− cell lineage to mutate into a cancer and present clinically. Assumptions about how this time is split between tumor formation and tumor progression are not required.

Given a small set of fairly conservative assumptions regarding sporadic colon cancer and its relationship to FAP, incidence data on the two diseases imply that the rate of truncating and disease-causing APC mutation is of order 10⁻⁵ mutations per allele per year. This estimate, although higher than previous estimates, seems to be consistent with the mutational spectrum of APC. Furthermore, the estimate neither requires accurate determination of the number of target cells in the colon nor depends on assumptions about time spans between the appearance of a cancer and its detection clinically. The quality of fit provided by the model supports the theory that FAP and sporadic bowel cancer follow the same genetic pathway and are separated by only one mutation.