Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2009 Mar 1.
Published in final edited form as: Bone. 2007 Dec 4;42(3):591–596. doi: 10.1016/j.bone.2007.11.011

Trabecular Shear Stress Amplification and Variability in Human Vertebral Cancellous Bone: Relationship with Age, Gender, Spine Level and Trabecular Architecture

Yener N Yeni 1, Eric A Zelman 2, George W Divine 3, Do-Gyoon Kim 4, David P Fyhrie 5
PMCID: PMC2276462  NIHMSID: NIHMS42874  PMID: 18180212

Abstract

Trabecular shear stress magnitude and variability have been implicated in damage formation and reduced bone strength associated with bone loss for human vertebral bone. This study addresses the issue of whether these parameters change with age, gender or anatomical location, and if so whether this is independent of bone mass. Additionally, 3D-stereology-based architectural parameters were examined in order to establish the relationship between stress distribution parameters and trabecular architecture. Eighty cancellous bone specimens were cored from the anterior region of thoracic 12 and donor-matched lumbar 1 vertebrae from a randomly selected population of 40 cadavers. The specimens were scanned at 21-μm voxelsize using microcomputed tomography (μCT) and reconstructed at 50 μm. Bone volume fraction (BV/TV), trabecular number (Tb.N), trabecular thickness (Tb.Th), trabecular separation (Tb.Sp), bone surface-to-volume ratio (BS/BV), degree of anisotropy (MIL1/MIL3), and connectivity density (-#Euler/Vol) were calculated directly from micro-CT images. Large-scale finite-element models were constructed and superoinferior compressive loading was simulated. Apparent cancellous modulus (EFEM) was calculated. The average trabecular von Mises stress generated per uniaxial apparent stress (σ̄VM/σapp)and coefficient of variation of trabecular von Mises stresses (COV) were calculated as measures of the magnitude and variability of shear stresses in the trabeculae. Mixed-models and regression were used for analysis. σ̄VM/σapp and COV were not different between genders and vertebrae. Both σ̄VM/σapp and COV increased with age accompanied by a decrease in BV/TV. Strong relationship of σ̄VM/σapp with BV/TV was found whereas COV was strongly related to EFEM/(BV/TV). The results from T12 and L1 were not different and highly correlated with each other. The relationship of σ̄VM/σapp with COV was observed to be different between males and females. This difference could not be explained by architectural parameters considered in this study. Our results support the relevance of trabecular shear stress amplification and variability in age-related vertebral bone fragility. The relationships found are expected to help understand the micro-mechanisms by which cancellous bone mass and mechanical properties are modulated through a collection of local stress parameters.

Keywords: Biomechanics, Stress/Strain, Mechanical Loading, Aging, Osteoporosis

INTRODUCTION

Increase of trabecular stress variability with loss of bone mass has been implicated as a mechanism for increased cancellous bone fragility with age and disease [11, 35]. The underlying notion was that increased variability in trabecular stresses would give rise to stress concentrations resulting in a reduction of bone strength. Consistent with this notion, coefficient of variation of trabecular von Mises stress distributions (COV) as estimated from microcomputed tomography (μCT)-based finite element (FE) calculations has been shown to increase with decreasing bone volume (BV/TV) accompanied by a decrease in strength in human vertebral cancellous bone. It has also been shown that there is a significant positive correlation between COV and the density of in vivo microdamage from the same region in human vertebrae [34].

Average trabecular von Mises stress per apparent uniaxial stress (σ̄VM/σapp) as estimated from finite element (FE) calculations was proposed as a structural index that represents the tendency of the cancellous structure to amplify shear stresses in the tissue [35]. This parameter, too, has been shown to correlate with the density of in vivo microdamage in human vertebral bone [34]. It should be noted that, though only moderately explanatory, COV and σ̄VM/σapp had the strongest correlations ever demonstrated with in vivo microdamage in cancellous bone among mechanical parameters considered thus far. In addition, it was observed that the tissue from the thoracic 12-lumbar 1 junction had the largest σ̄VM/σapp [35] accompanied by the lowest strength [36] suggesting that this parameter may be relevant to the high incidence of vertebral fractures at these spine levels [2, 3, 10, 12, 16, 20, 23, 26].

Together, trabecular shear stress distribution parameters, namely COV and σ̄VM/σapp appear important in understanding the mechanistic consequence of bone loss and trabecular adaptation. However, it is not known whether these parameters change with age and if so, whether these changes are independent of changes in bone volume or gender and type of vertebral bone. Secondly, which microstructural parameters of cancellous bone can explain stress distribution parameters is unknown. Also not known is whether shear stress parameters in tissue from one vertebra can be predicted by those in tissue from another vertebra of the same individual. Our objective was to answer these questions for thoracic 12 (T12) and lumbar 1 (L1) vertebrae from the same individuals.

METHODS

Thoracic 12 and L1 vertebrae were collected fresh from 15 male (66±15 yrs) and 25 female (54±16 yrs) cadavers. Because complete medical history was not available for all donors, all cadavers were included without screening for bone diseases. Eight-mm-diameter and 10-mm-long cylindrical cancellous bone specimens were prepared from the anterior region of vertebral bodies in the superoinferior direction as described previously [15, 30]. Only one specimen from each vertebra was prepared and all donors had both their T12 and L1 represented in the sample population.

The specimens were scanned using an in-house microcomputed tomography system [24] at a voxelsize of 21 μm. Large scale, linear finite element models with uniform isotropic element properties (Young’s modulus = 5 GPa, Poisson’s ratio = 0.3) were constructed and solved using an element size of 50 μm and fixed boundary conditions as described previously [15, 31]. Displacements corresponding to a strain of 0.005 were applied to the models in the superoinferior direction. A six-node Beowulf cluster with 8 GB of main memory was used for solving the FE models.

The mean (σ̄VM) and standard deviation (σ̃VM) of trabecular von Mises stress distribution were calculated from a 3-parameter Weibull cumulative probability function fitted to the stress distribution for each specimen [11, 31, 34, 35]. The variability of trabecular shear stress was expressed as the coefficient of variation: COV=σ̃VM/σ̄VM The magnitude of trabecular shear stress was expressed as the average trabecular shear stress per apparent superoinferior uniaxial stress, σapp, where σ̄VM/σapp is considered a structural index of shear stress amplification in the hard tissue. The apparent uniaxial stress was calculated by summing nodal reaction forces and dividing by the apparent cross-sectional area of specimens. Apparent modulus (EFEM) was calculated from the displacement input and reaction forces at the boundary nodes.

Bone volume fraction (BV/TV), trabecular number (Tb.N), trabecular thickness (Tb.Th), trabecular separation (Tb.Sp), bone surface-to-volume ratio (BS/BV), degree of anisotropy (ratio of mean intercept lengths in principal directions; MIL1/MIL3), and connectivity density (-#Euler/Vol) were calculated directly from micro-CT images using 3D stereological procedures as described previously [9, 13, 19].

PROC MIXED procedures of SAS (Cary, NC) were used to examine the effect of vertebra type, gender, BV/TV and age on COV and σ̄VM/σapp, with vertebra type introduced as a repeated factor with two levels (T12 and L1). Relationships were assessed using regression analysis. Statistical significance was set as p<0.05. p-values corresponding to an μ of 0.05 were indicated for multiple tests, taking into account the correlations between parameters [25].

RESULTS

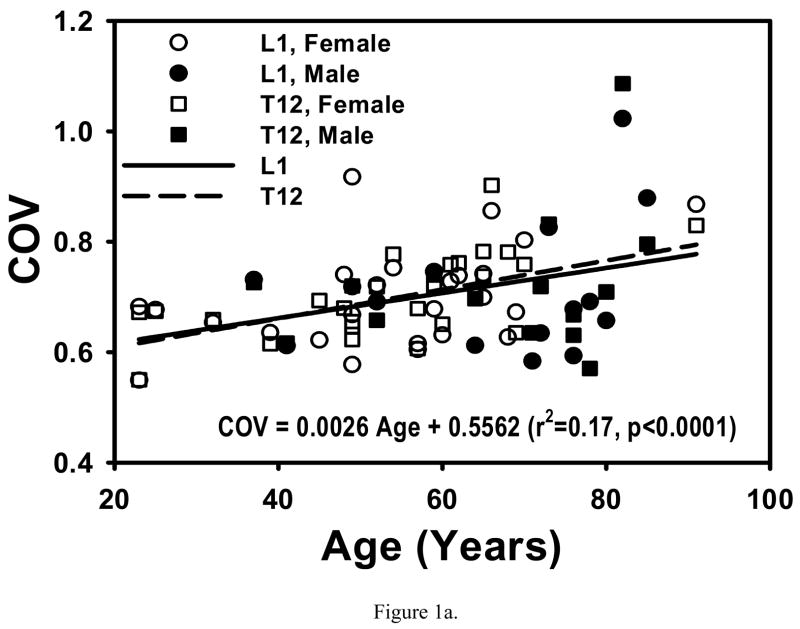
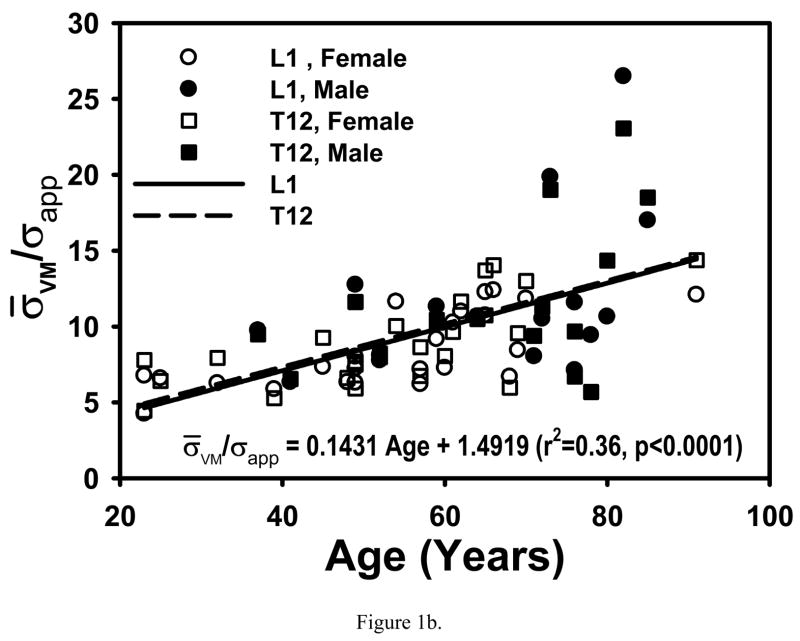
COV and σ̄VM/σapp were not different between T12 and L1 (p>0.76 and p>0.07, respectively) or between males and females (p>0.54 and p>0.18, respectively) after accounting for age. Age was significantly associated with both COV (p<0.0044) and σ̄VM/σapp (p<0.0004) (Fig. 1), however, there was no longer any association between age and the outcomes (p>0.33) with adjustment for BV/TV.

Figure 1.

Figure 1

Figure 1

Open in a new tab

Both COV and σ̄VM/σapp increased with age in T12 and L1 (0.14<r2<0.37, p<0.0001 to p<0.02). These increases with age were not different between T12 and L1 (p>0.58) or between males and females (0.47<p<0.88). Regressions are for pooled data.

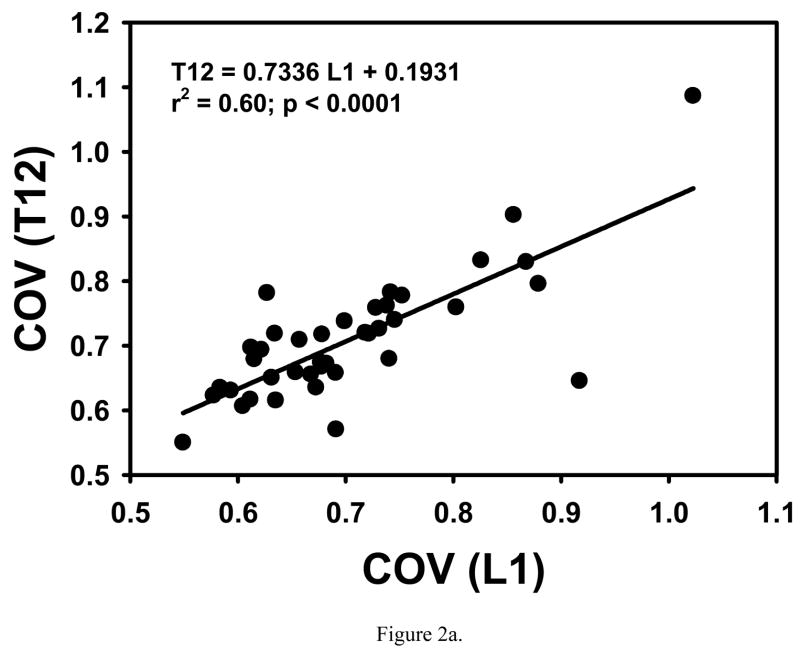
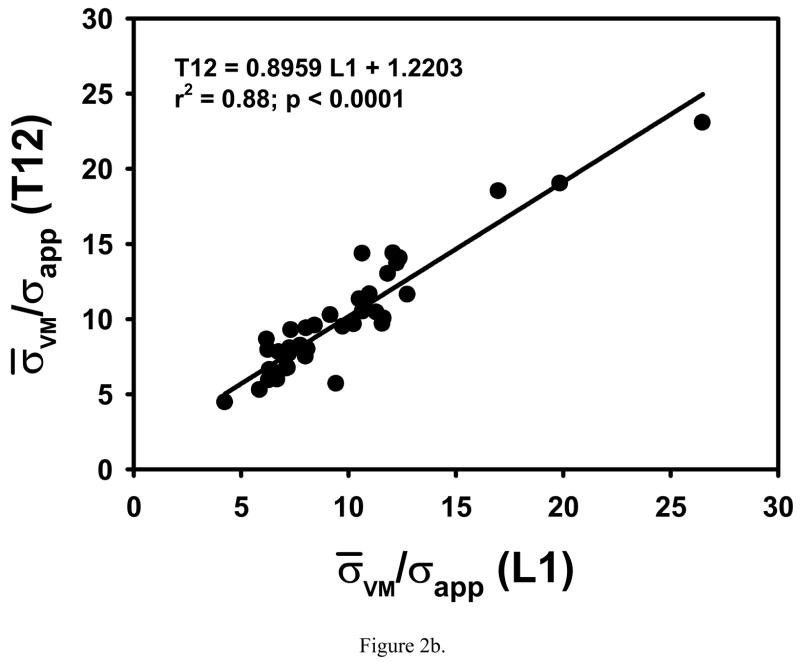
COV, σ̄VM/σapp and microstructural parameters from T12 were significantly correlated to those from L1 in an individual (Table 1, Fig. 2). Significant but small differences in -#Euler/Vol, BS/BV and Tb.Th were found between T12 and L1 (Table 1).

Table 1.

The mean (st. dev) of measured parameters from T12 and L1 vertebrae. Percent difference in means, significance of these differences (as determined from paired t-tests) and correlations between vertebrae are indicated. An adjustment for multiple tests, taking into account the correlations between all parameters, suggested a p-value of 0.018 to be considered as significant for an α of 0.05.

Parameter T12 L1 Difference% Difference (p) Correlation (r)
-#Euler/Vol (mm−3) 0.3884 (0.1662) 0.3673 (0.1498) 5.4 0.047 0.92
BV/TV 0.1445 (0.0447) 0.1477 (0.0439) −2.2 0.277 0.92
BS/BV (mm−1) 8.867 (0.906) 8.645 (0.791) 2.5 0.013 0.81
Tb.Th (mm) 0.2280 (0.0242) 0.2333 (0.0217) −2.3 0.028 0.80
Tb.N (mm−1) 0.6276 (0.1539) 0.6272 (0.1509) 0.1 0.963 0.93
Tb.Sp (mm) 1.473 (0.486) 1.470 (0.494) 0.2 0.899 0.95
MIL1/MIL3 1.641 (0.163) 1.642 (0.191) 0.0 0.976 0.73
EFEM (MPa) 260 (116) 268 (117) −3.3 0.398 0.85
COV 0.7090 (0.0962) 0.7034 (0.1014) 0.8 0.593 0.77
σ̄VM/σapp 9.942 (3.943) 9.736 (4.118) 2.1 0.375 0.94
Open in a new tab

Figure 2.

Figure 2

Figure 2

Open in a new tab

COV and σ̄VM/σapp from T12 are highly correlated with those from L1 in the same individual.

The relationships of mechanical with microstuctural parameters were not different between T12 and L1 (p values between 0.593 and 0.998; ANCOVA). Data were pooled over T12 and L1 for further analyses of relationships between mechanical and microstructural parameters. Significant correlations of COV and σ̄VM/σapp with BV/TV and other microstructural parameters were found (Table 2). Multiple regressions indicated that anisotropy and BV/TV independently contributed to COV and σ̄VM/σapp (Table 3).

Table 2.

Matrix of Pearson’s correlation coefficients (r). An adjustment for multiple tests, taking into account the correlations between parameters, suggested a p-value of 0.005 to be considered as significant for an α of 0.05

Age -#Euler/Vol BV/TV BS/BV Tb.Th Tb.N Tb.Sp MIL1/MIL3 EFEM COV σ̄VM/σapp
Age 1 −0.52 −0.64 0.38 −0.39 −0.63 0.60 0.27 −0.62 0.42 0.60
-#Euler/Vol 1 0.68 0.03 0.00 0.84 −0.77 −0.14 0.56 −0.40 −0.60
BV/TV 1 −0.66 0.68 0.94 −0.88 −0.18 0.95 −0.64 −0.85
BS/BV 1 −0.99 −0.39 0.36 0.15 −0.70 0.43 0.54
Tb.Th 1 0.41 −0.38 −0.15 0.72 −0.43 −0.54
Tb.N 1 −0.95 −0.14 0.87 −0.63 −0.85
Tb.Sp 1 0.10 −0.81 0.66 0.92
MIL1/MIL3 1 −0.05 −0.36 −0.02
EFEM 1 −0.78 −0.86
COV 1 0.80
σ̄VM/σapp 1
Open in a new tab

|r| ≥0.36; p<0.001

|r| ≥0.26; p<0.05

Table 3.

Multiple regression models for COV and σ̄VM/σapp. Models were constructed using a stepwise regression that included BV/TV, Tb.N, -#Euler/Vol and MIL1/MIL3 as explanatory variables. BV/TV was forced to stay in the model in order to determine contributions from other variables that are independent of BV/TV.

COV (r2adj=0.64; p<0.001)
Term Estimate t ratio p<
Intercept 1.400 19.8 0.001
BV/TV −1.629 −10.68 0.001
MIL1/MIL3 −0.278 −7.3 0.001
σ̄VM/σapp (r2adj=0.77; p<0.001)
Term Estimate t ratio p<
Intercept 29.70 12.6 0.001
BV/TV −48.32 −3.2 0.002
Tb.N −9.96 −2.3 0.001
MIL1/MIL3 −3.99 −3.2 0.002
Open in a new tab

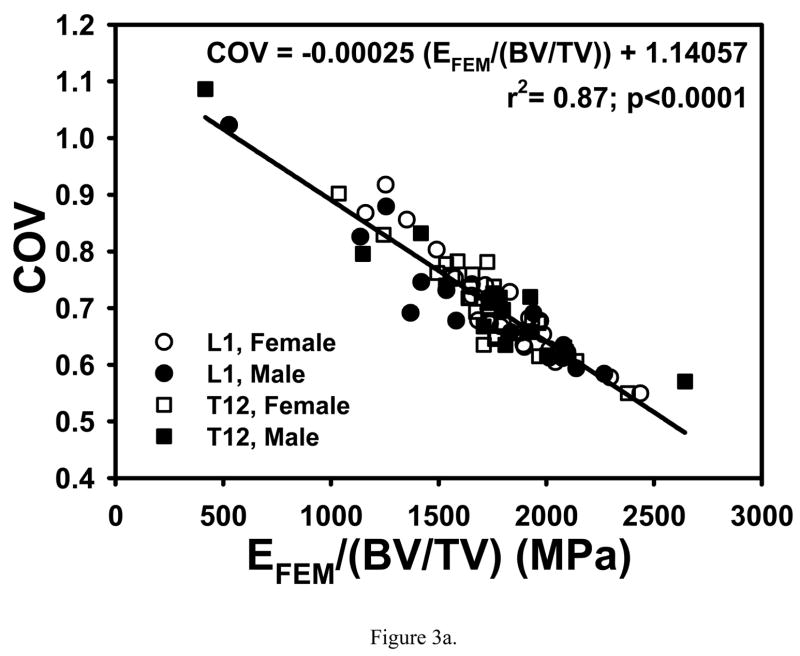
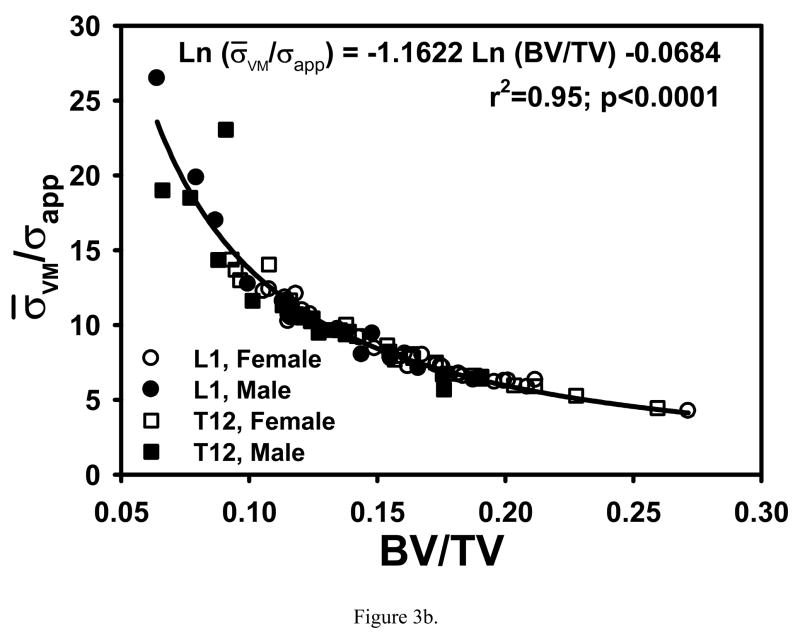
Correlations of COV and σ̄VM/σapp with single variables that were higher than those with multiple variables were found when nonlinear relationships were considered. A strong negative linear relationship was found between COV and finite element calculated apparent modulus normalized with bone volume fraction (EFEM/(BV/TV)) (r2=0.87; p<0.0001, Fig. 3a). The strongest relationship of σ̄VM/σapp was with BV/TV raised to the power −1.1622 (r2=0.96; p<0.0001, Fig. 3b).

Figure 3.

Figure 3

Figure 3

Open in a new tab

(a) COV decreased linearly with increasing EFEM/(BV/TV). (b) Negative log-log relationship between σ̄VM/σappBV/TV showing that σ̄VM/σapp decreased nonlinearly with increasing BV/TV.

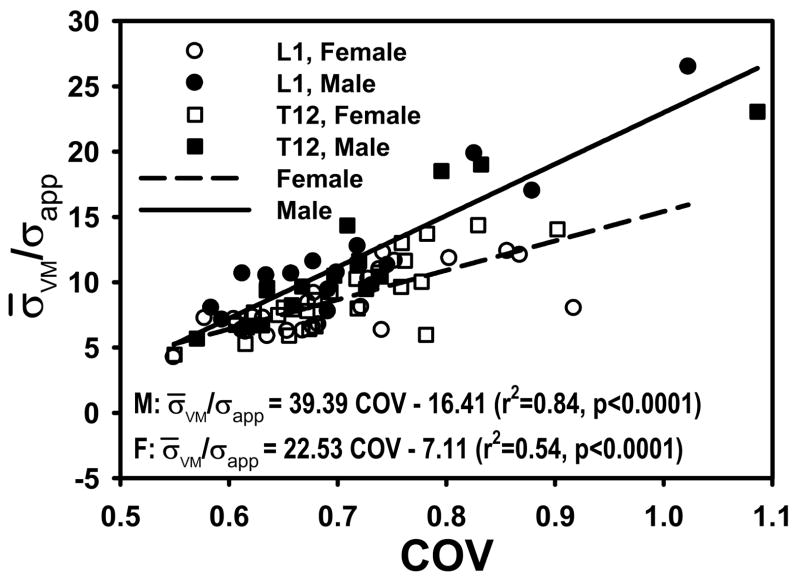
Although COV and σ̄VM/σapp were positively related (r2=0.64, p<0.0001), the relationship was different between males and females (p<0.0001 in age-adjusted models) (Fig. 4). This gender dependence could not be explained by any combination of stereological parameters considered here (the interaction between gender and COV remained significant at p<0.0001 in all models of σ̄VM/σapp).

Figure 4.

Figure 4

Open in a new tab

COV and σ̄VM/σapp are more strongly related in males than in females. The slopes of regressions are statistically different, even after accounting for age (p<0.0001).

DISCUSSION

We demonstrated that the magnitude of trabecular shear stresses relative to the compressive stress applied on the tissue (σ̄VM/σapp) and their nonuniformity (COV) increase with age. These increases were explainable by the negative relationship between bone mass and age. However, this does not mean that the stress parameters are not important once bone mass is taken into account but rather points to a mechanistic consequence of bone loss with aging. These findings are consistent with the idea that a direct consequence of structural changes due to bone loss associated with aging is increased localized stresses at the hard tissue level. Although our analyses are elastic and failure is not explicitly simulated, the decrease in the mean and COV of the shear stress with bone mass suggest that cancellous bone structure is adapted to control stress concentration.

Increasing tissue apparent modulus per available bone mass has been proposed as an optimizing strategy for cancellous structure [29]. Since the amount of material under extreme values of stresses would be reduced in a stiffness-optimized structure, our finding that COV of shear stresses are tightly related to EFEM/(BV/TV) is consistent with this proposal. Thus controlling shear stress variability would provide a mechanism, active at the hard tissue level, for optimization of modulus for a given bone mass. While a composite variable such as EFEM/(BV/TV) was most explanatory for COV, much of the variability in mean von Mises stress amplification (σ̄VM/σapp) could be explained by BV/TV alone, also consistent with the notion that tissue level stresses are being controlled on the average (i.e., the microstructure is designed to control average properties). The strong correlation of COV with EFEM/(BV/TV) and of σ̄VM/σapp with BV/TV indicate that the average and the variability of trabecular stresses are related but they are not entirely equivalent. It should be noted that the relationships (between COV and EFEM/(BV/TV), and between σ̄VM/σapp and BV/TV) found in this study provided much higher r2 values than exist between COV and BV/TV alone [11, 34, 35]. The relationships reported in this study may provide a more refined guide than those in previous reports for further research into how the regulation of apparent level (average) properties can be achieved by sensing and responding to the local (cellular level) mechanical environment.

Current results indicate that the dependence of σ̄VM/σapp on COV of trabecular von Mises stress is statistically different between males and females. This difference suggests that the response of bone to changes in mechanical loading could be different between genders. It is possible that the difference is explained by sexual dimorphism in vertebral cancellous bone osteocyte density [28]. Vertebral osteocyte density is greater in women than in men [28], suggesting that the density of mechanosenory cells and potentially the ability to respond to loading are gender specific. We suggest that the difference in the correlation of σ̄VM/σapp and COV between males and females is caused by the differences in anatomy [28] and pattern of bone loss [22] between genders. The dimorphism in the coupling of these parameters and their potential association with dimorphism in the osteocyte network may be key to understanding the gender-specific differences in the modulation of cancellous bone structure [1, 33].

Note that although both σ̄VM/σapp and COV are correlated to BV/TV and trabecular architecture, the architectural parameters examined here cannot explain the gender dependence of the relationship between the two stress parameters. Also note that, by using homogenous element moduli, we have isolated the effect of structural properties from that of hard tissue material properties. Therefore, the obtained results cannot be attributed to modulus variability within the cancellous bone. The architectural parameters examined in this study are based on stereological principles. Stereology-based calculation of microstructural parameters results in values that are different from those obtained by direct calculation [7, 14] but microstructural parameters calculated using one method are highly correlated to those calculated using the other method [7]. Perhaps more importantly, the microstructural parameters measured in this study represent an average geometry, density or ratio for a given cancellous structure. The results indicate that structural parameters other than those considered in the current study, including parameters that can represent the variability of the microstructure, would be necessary to understand the relationship between stress amplification and variability.

No difference was found in the measured parameters and their relationship with bone mass, age or gender between L1 and T12 levels. In fact, shear stress magnitude and variability in one vertebra was predictable from those in the adjacent vertebra for a given individual. This is consistent with our initial observation that the stress distribution properties of the cancellous tissue from vertebrae at these adjacent locations are similar [35]. The similarity of results from two adjacent but anatomically distinct vertebrae suggests that the stress distribution parameters are related to systemic factors or those that can affect the T12-L1 segment of the spine. It remains to be demonstrated whether the association of stress parameters between vertebrae is maintained for vertebrae that are far apart.

Some limitations should be noted. The FE models were constructed from images coarsened to 50-μm voxelsize and utilized homogeneous and isotropic material properties. Twenty-one μm is the best possible voxelsize that can be achieved for specimens of the current size in our tomography system. We have previously demonstrated that parameters calculated from images scanned at 21 μm and reconstructed at 50 μm were not significantly different and correlated with an r2 value of 0.91 or higher [31]. (The relationships presented in Figures 3a and 3b were confirmed using an independent set of human vertebral cancellous bone specimens (n=31, BV/TV=0.13±0.04, Tb.Th=0.108±0.016 mm) scanned and processed at 27 μm voxel size.) The apparent modulus calculated from FE models is affected by the hard tissue (element) modulus distributions determined by CT-attenuation value distributions [4]. However, there is no established method of converting CT-attenuation values to hard tissue moduli and the variability of tissue moduli depends on the formulae used in the conversion. Our analyses suggest that the change in apparent modulus due to modulus variability only is small in human vertebral cancellous bone when up to a third order relationship is used to convert CT-attenuation values to element moduli [18]. Furthermore, the FE-calculated cancellous modulus from homogenous and isotropic models has been highly predictive of experimentally measured cancellous modulus in previous studies of human vertebral bone indicating that calculation of stresses using the current model is reasonably accurate [15, 32]. The selection of the von Mises stress as a measure of a damaging form of stress and the calculation of the stress parameters were discussed at length in our previous publications [11, 34, 35]. These are the same conditions used in studies where our observations that motivated this study were made [11, 34, 35]. Together, these limitations are expected to have minor effects on our results but not affect our conclusions about cancellous tissue.

This study was also limited to an investigation of the cancellous tissue from the anterior region. Although one would ultimately wish to understand how the strength of a whole vertebra can be affected by stress distribution parameters, the importance of the quality of cancellous tissue in mechanical health of the whole vertebra cannot be denied. Many of the investigations on the contribution of cancellous and cortical tissue to the strength of vertebra used finite element models. These models, all having different levels of structural accuracy, estimated a varying degree of importance (10%–63%) for the cortical shell relative to the cancellous centrum [5, 8, 27]. However, experimental studies reported only a 10% contribution of cortical shell to vertebral strength [21]. Furthermore, the bone density measured in similar regions to ours has been shown to strongly correlate to fracture load for the T12-L1 levels [6]. In our own experience, cancellous bone properties from regions similar to those examined in the current study were highly correlated with the strength of a whole vertebral body [17], consistent with the findings of Cody et al [6]. It is clear that cancellous tissue from the analyzed regions is relevant to whole vertebral strength. As such, this study addresses several questions related to vertebral bone tissue quality and is not focused on predicting vertebral strength.

In summary, we have determined the relationships between trabecular shear stress parameters, apparent mechanical properties, bone architecture, gender and age for human vertebral cancellous bone. The demonstration of these relationships is a step towards better defining the micro-mechanisms by which bone mass and mechanical properties interact and lead to age-related bone fragility.

Acknowledgments

This publication was made possible by Grant Number AR049343 from the National Institutes of Health. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Contributor Information

Yener N. Yeni, Bone and Joint Center, Henry Ford Hospital, Detroit, MI, yeni@bjc.hfh.edu.

Eric A. Zelman, Bone and Joint Center, Henry Ford Hospital, Detroit, MI, eric_zelman@hotmail.com.

George W. Divine, Biostatistics & Research Epidemiology, Henry Ford Hospital, Detroit, MI, gdivine1@hfhs.org.

Do-Gyoon Kim, Bone and Joint Center, Henry Ford Hospital, Detroit, MI, kim@bjc.hfh.edu.

David P. Fyhrie, Department of Orthopaedic Surgery, University of California Davis, Sacramento, CA, dpfyhrie@ucdavis.edu.

References

  • 1.Baiotto S, Zidi M. Theoretical and numerical study of a bone remodeling model: the effect of osteocyte cells distribution. Biomech Model Mechanobiol. 2004;3:6–16. doi: 10.1007/s10237-004-0042-y. [DOI] [PubMed] [Google Scholar]
  • 2.Bick EM, Copel JW. Fractures of the vertebrae in the aged. Geriatrics. 1950;5:74. [Google Scholar]
  • 3.Boukhris R, Becker KL. The inter-relationship between vertebral fractures and osteoporosis. Clin Orthop Relat Res. 1973:209–16. [PubMed] [Google Scholar]
  • 4.Bourne BC, van der Meulen MC. Finite element models predict cancellous apparent modulus when tissue modulus is scaled from specimen CT-attenuation. J Biomech. 2004;37:613–21. doi: 10.1016/j.jbiomech.2003.10.002. [DOI] [PubMed] [Google Scholar]
  • 5.Cao KD, Grimm MJ, Yang KH. Load sharing within a human lumbar vertebral body using the finite element method. Spine. 2001;26:E253–60. doi: 10.1097/00007632-200106150-00011. [DOI] [PubMed] [Google Scholar]
  • 6.Cody DD, Goldstein SA, Flynn MJ, Brown EB. Correlations between vertebral regional bone mineral density (rBMD) and whole bone fracture load. Spine. 1991;16:146–154. [PubMed] [Google Scholar]
  • 7.Day JS, Ding M, Odgaard A, Sumner DR, Hvid I, Weinans H. Parallel plate model for trabecular bone exhibits volume fraction-dependent bias. Bone. 2000;27:715–20. doi: 10.1016/s8756-3282(00)00371-9. [DOI] [PubMed] [Google Scholar]
  • 8.Eswaran SK, Gupta A, Adams MF, Keaveny TM. Cortical and trabecular load sharing in the human vertebral body. J Bone Miner Res. 2006;21:307–14. doi: 10.1359/jbmr.2006.21.2.307. [DOI] [PubMed] [Google Scholar]
  • 9.Feldkamp LA, Goldstein SA, Parfitt AM, Jesion G, Kleerekoper M. The direct examination of three-dimensional bone architecture in vitro by computed tomography. J Bone Miner Res. 1989;4:3–11. doi: 10.1002/jbmr.5650040103. [DOI] [PubMed] [Google Scholar]
  • 10.Fornasier VL, Czitrom AA. Collapsed vertebrae. A review of 659 Autopsies. Clin Orthop Relat Res. 1978:261–5. [PubMed] [Google Scholar]
  • 11.Fyhrie DP, Hoshaw SJ, Hamid MS, Hou FJ. Shear stress distribution in the trabeculae of human vertebral bone. Ann Biomed Eng. 2000;28:1194–1199. doi: 10.1114/1.1318928. [DOI] [PubMed] [Google Scholar]
  • 12.Gershon-Cohen J, Rechtman AM, Schraer H, Blumberg N. Asymptomatic fractures in osteoporotic spines of the aged. J Am Med Assoc. 1953;153:625–7. doi: 10.1001/jama.1953.02940240017005. [DOI] [PubMed] [Google Scholar]
  • 13.Goulet RW, Goldstein SA, Ciarelli MJ, Kuhn JL, Brown MB, Feldkamp LA. The relationship between the structural and orthogonal compressive properties of trabecular bone. Journal of Biomechanics. 1994;27:375–389. doi: 10.1016/0021-9290(94)90014-0. [DOI] [PubMed] [Google Scholar]
  • 14.Hildebrand T, Laib A, Muller R, Dequeker J, Ruegsegger P. Direct three-dimensional morphometric analysis of human cancellous bone: microstructural data from spine, femur, iliac crest, and calcaneus. J Bone Miner Res. 1999;14:1167–74. doi: 10.1359/jbmr.1999.14.7.1167. [DOI] [PubMed] [Google Scholar]
  • 15.Hou FJ, Lang SM, Hoshaw SJ, Reimann DA, Fyhrie DP. Human vertebral body apparent and hard tissue stiffness. J Biomech. 1998;31:1009–15. doi: 10.1016/s0021-9290(98)00110-9. [DOI] [PubMed] [Google Scholar]
  • 16.Johansson C, Mellstrom D, Rosengren K, Rundgren A. A community-based population study of vertebral fractures in 85-year- old men and women. Age Ageing. 1994;23:388–92. doi: 10.1093/ageing/23.5.388. [DOI] [PubMed] [Google Scholar]
  • 17.Kim D-G, Hunt CA, Zauel R, Fyhrie DP, Yeni YN. The Effect Of Regional Variations Of The Trabecular Bone Properties On The Compressive Strength Of Human Vertebral Bodies. 51st Annual Meeting, Orthopaedic Research Society; Washington, DC: 2005. 1271 pp. [DOI] [PubMed] [Google Scholar]
  • 18.Kim D-G, Hunt CA, Zauel R, Fyhrie DP, Yeni YN. Prediction Of Fresh And Embalmed Human Cancellous Bone Strength From Micro-CT Based Finite Element Models Using Inhomogeneous Tissue Modulus. 51st Annual Meeting, Orthopaedic Research Society; Washington, DC: 2005. p. 681. [Google Scholar]
  • 19.Kim DG, Christopherson GT, Dong XN, Fyhrie DP, Yeni YN. The effect of microcomputed tomography scanning and reconstruction voxel size on the accuracy of stereological smeasurements in human cancellous bone. Bone. 2004;35:1375–82. doi: 10.1016/j.bone.2004.09.007. [DOI] [PubMed] [Google Scholar]
  • 20.Kivilaakso R. Fractures of the osteoporotic spinal column. Ann Chir Gynaecol Fenn. 1956;45:1. [PubMed] [Google Scholar]
  • 21.McBroom RJ, Hayes WC, Edwards WT, Goldberg RP, White AA., 3rd Prediction of vertebral body compressive fracture using quantitative computed tomography. J Bone Joint Surg Am. 1985;67:1206–14. [PubMed] [Google Scholar]
  • 22.Mosekilde L. Sex differences in age-related loss of vertebral trabecular bone mass and structure--biomechanical consequences. Bone. 1989;10:425–32. doi: 10.1016/8756-3282(89)90074-4. [DOI] [PubMed] [Google Scholar]
  • 23.Nevitt MC, Ross PD, Palermo L, Musliner T, Genant HK, Thompson DE. Association of prevalent vertebral fractures, bone density, and alendronate treatment with incident vertebral fractures: effect of number and spinal location of fractures. The Fracture Intervention Trial Research Group Bone. 1999;25:613–9. doi: 10.1016/s8756-3282(99)00202-1. [DOI] [PubMed] [Google Scholar]
  • 24.Reimann DA, Hames SM, Flynn MJ, Fyhrie DP. A cone beam computed tomography system for true 3D imaging of specimens. Appl Radiat Isot. 1997;48:1433–1436. doi: 10.1016/s0969-8043(97)00139-5. [DOI] [PubMed] [Google Scholar]
  • 25.Sankoh AJ, Huque MF, Dubey SD. Some comments on frequently used multiple endpoint adjustment methods in clinical trials. Stat Med. 1997;16:2529–42. doi: 10.1002/(sici)1097-0258(19971130)16:22<2529::aid-sim692>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
  • 26.Saville PD. Observations on 80 women with osteoporotic spine fractures. In: Barzel US, editor. Osteoporosis. New York: Grune and Stratton; 1970. p. 38. [Google Scholar]
  • 27.Silva MJ, Keaveny TM, Hayes WC. Load sharing between the shell and centrum in the lumbar vertebral body. Spine. 1997;22:140–150. doi: 10.1097/00007632-199701150-00004. [DOI] [PubMed] [Google Scholar]
  • 28.Vashishth D, Gibson GJ, Fyhrie DP. Sexual dimorphism and age dependence of osteocyte lacunar density for human vertebral cancellous bone. Anat Rec A Discov Mol Cell Evol Biol. 2005;282:157–62. doi: 10.1002/ar.a.20146. [DOI] [PubMed] [Google Scholar]
  • 29.Weinans H. Is osteoporosis a matter of over-adaptation? Technol Health Care. 1998;6:299–306. [PubMed] [Google Scholar]
  • 30.Wenzel TE, Schaffler MB, Fyhrie DP. In vivo microcracks in human vertebral trabecular bone. Bone. 1996;19:89–95. doi: 10.1016/8756-3282(96)88871-5. [DOI] [PubMed] [Google Scholar]
  • 31.Yeni YN, Christopherson GT, Dong XN, Kim DG, Fyhrie DP. Effect of microcomputed tomography voxel size on the finite element model accuracy for human cancellous bone. J Biomech Eng. 2005;127:1–8. doi: 10.1115/1.1835346. [DOI] [PubMed] [Google Scholar]
  • 32.Yeni YN, Fyhrie DP. Finite element calculated uniaxial apparent stiffness is a consistent predictor of uniaxial apparent strength in human vertebral cancellous bone tested with different boundary conditions. J Biomech. 2001;34:1649–54. doi: 10.1016/s0021-9290(01)00155-5. [DOI] [PubMed] [Google Scholar]
  • 33.Yeni YN, Fyhrie DP. Osteocyte Density Correlates With Trabecular Shear Stresses In Human Vertebral Cancellous Bone. 48th Annual Meeting, Orthopaedic Research Society; Dallas, Texas: 2002. p. 0556. [Google Scholar]
  • 34.Yeni YN, Hou FJ, Ciarelli T, Vashishth D, Fyhrie DP. Trabecular shear stresses predict in vivo linear microcrack density but not diffuse damage in human vertebral cancellous bone. Ann Biomed Eng. 2003;31:726–32. doi: 10.1114/1.1569264. [DOI] [PubMed] [Google Scholar]
  • 35.Yeni YN, Hou FJ, Vashishth D, Fyhrie DP. Trabecular shear stress in human vertebral cancellous bone: intra- and inter-individual variations. J Biomech. 2001;34:1341–1346. doi: 10.1016/s0021-9290(01)00089-6. [DOI] [PubMed] [Google Scholar]
  • 36.Yeni YN, Vashishth D, Fyhrie DP. Variations in Apparent Strength and Stiffness of Human Vertebral Cancellous Bone are Consistent with Trabecular Shear Stress Distribution Statistics Along the Spine. Summer bioengineering Conference, the American Society of Mechanical Engineers, Advances in Bioengineering ASME BED; Utah: Snowbird; 2001. pp. 19–20. [Google Scholar]

RESOURCES