Kalman filter control of a model of spatiotemporal cortical dynamics

Abstract

Recent advances in Kalman filtering to estimate system state and parameters in nonlinear systems have offered the potential to apply such approaches to spatiotemporal nonlinear systems. We here adapt the nonlinear method of unscented Kalman filtering to observe the state and estimate parameters in a computational spatiotemporal excitable system that serves as a model for cerebral cortex. We demonstrate the ability to track spiral wave dynamics, and to use an observer system to calculate control signals delivered through applied electrical fields. We demonstrate how this strategy can control the frequency of such a system, or quench the wave patterns, while minimizing the energy required for such results. These findings are readily testable in experimental applications, and have the potential to be applied to the treatment of human disease.

Introduction

In 1809, Carl Frederic Gauss dealt in depth with problem of estimation of planetary and comet orbit parameters when the terrestrial observational data was sparse and imprecise (Gauss 1857). Gauss's problem bears strong resemblance to the problem we face in the estimation of neuronal state through measurement of data from electrical or optical systems.

The introduction of the Kalman filter (Kalman 1960) expanded the work on stationary systems of Gauss, and (for frequency domain) Wiener (1964), to the estimation of dynamical (changing) system states. Although Kalman's original strategy was developed for linear systems, there rapidly emerged extensions of such theory to nonlinear systems (Simon 2006). Nevertheless, the extended (linearized) Kalman filter is beset by difficulties ranging from the bias introduced by truncation of the Taylor series expansion of the governing nonlinear equations of motion of a system, and the need to estimate derivatives from data observations. For nondifferentiable system dynamics, as we will employ here, such an approach is not feasible at all.

The unscented Kalman filter (UKF) was devised by Julier and Uhlmann (1997a, 1997b) to permit the recursive estimation of system state for nonlinear systems. The UKF approximates the a posteriori probability density of the estimated state by a Gaussian distribution, and propagates the estimated system state mean and covariance by specifying an ensemble of points that characterize the state variability—sigma points. This ensemble of sigma points is iterated directly through the nonlinear system dynamics, obviating the need for linearization or derivative estimation. In meteorological applications, this approach has been termed the ensemble Kalman filter (Evensen 1994, Evensen and Van Leeuwen 2000).

Recently, it was demonstrated that UKF could estimate the system state for a reduced model of a neuron (Voss et al 2004). In any neuronal experiment, not all system variables can be observed. By augmenting the observed state variables with unobserved state variables and system parameters, both unobserved variables and system parameters could be estimated and tracked (Voss et al 2004; see also Wan et al (2000)). This is the key to use, for example, the measurements of voltage, through electrodes or optical imaging techniques, to reconstruct the rest of the variables and parameters in any given model (whether neuronal, planetary, or meteorological).

We have recently shown that in the middle layers of mammalian cerebral cortex, a variety of spatiotemporal patterns can self-organize that range from irregular and chaotic waves, to plane, ring and true spiral waves (Huang et al 2004). Further characterization of these patterns reveals a consistent dynamical evolution of such events (Schiff et al 2007). A fundamental model of cortex, consisting of a set of non-local excitable differential equations (Wilson and Cowan 1972, 1973) was found to account well for these qualitative dynamics (Huang et al 2004).

We have also previously explored the feasibility of employing linear (Gluckman et al 2001) and nonlinear (Schiff et al 1994) adaptive control strategies using electrical sensing and stimulation in cerebral tissue. Such strategies were not based on fundamental models of the underlying system, nor did they account for the spatiotemporal structure of brain activity.

We here demonstrate that a UKF strategy is capable of observing system state, including unobserved variables and parameter tracking, in a spatiotemporal model of cortex. The model is constructed such that it simulates our experimental use of voltage sensitive dyes to observe such systems. We simulate the use of electrical field feedback in a manner that can be implemented experimentally (Gluckman et al 2001). We demonstrate that such a system is controllable using an adaptive feedback electrical field, and that employing an observer UKF to generate the control signal can substantially reduce the control energy required to increase or decrease the frequency of spiral oscillations, or to quench such wave activity. The implications for experimental and potential human disease applications are discussed.

Methods

In our model we incorporate the Wilson–Cowan equations (Wilson and Cowan 1972, 1973) to model the excitability of the cortex with excitation, u, and recovery, a, but as in our experiments (Huang et al 2004), no inhibition. Let (x, y) be a grid point from an N × N rectangular grid. The dynamical equations are

$$\begin{array}{ll}\multicolumn{2}{c}{\frac{\text{d}u\hspace{0.17em}(x,y,t)}{\text{d}t}=-\alpha u\hspace{0.17em}(x,y,t)-a\hspace{0.17em}(x,y,t)}\\ & +\text{∑}_{i=1}^N\text{∑}_{j=1}^{N}w\hspace{0.17em}(x,y,p_i,q_j)\hspace{0.17em}f(u\hspace{0.17em}(p_i,q_j,t)-\theta )\\ \multicolumn{2}{c}{\tau \frac{\text{d}a\hspace{0.17em}(x,y,t)}{\text{d}t}=\beta u\hspace{0.17em}(x,y,t)-a\hspace{0.17em}(x,y,t),}\end{array}$$

where w represents the connectivity between neurons as a function of position (x, y):

$$w\hspace{0.17em}(x,y,p,q)=\varphi e^{-\psi ({(x-q)}^2+{(y-p)}^2)}$$

and is a symmetric decreasing Gaussian function. The firing mechanism is represented by f (u − θ), where θ denotes the threshold. In our simulations, f is represented by a Heaviside function (equal to 0 for u < θ, and equal to 1 for u ≥ θ). The a variable represents recovery or adaptation, whose rate of increase is proportional to βu, and τ is the time constant for the rate of change in a relative to change in u. The free model parameters are α, β, τ, φ, ψ and θ. The value of the parameters α = 3, β = 10, τ = 4.85, φ = 1.38, ψ = 0.91, and θ = 0.24 were fixed for all simulations, but because of measurement noise and imprecision, require tracking in an observational paradigm. Although we only will track θ actively in this study, we find that the estimation and tracking of several parameters at once is possible for such systems (to be reported elsewhere).

Each element in the grid represents a collection of neurons that follow the Wilson–Cowan dynamics with input dominated by super-threshold activity of connected neurons. The input from connected neurons is zero unless the variable u at a distant element (p, q) is greater than the threshold θ, in which case the effective synaptic contribution is scaled by the distance between the elements via the Gaussian function w.

In this spatially discrete formulation, each element in the model grid corresponds to the volume of tissue imaged with a photodetector after the tissue was saturated with voltage sensitive dye and illuminated. The signal from each photodetector thus represents the local mean field of transmembrane voltage from the ensemble of cells imaged. In the experiments from Huang et al (2004), inhibition was blocked (with bicuculline), and our modeling reflects the lack of fast synaptic inhibition. Without inhibition, we follow the formulation of Pinto and Ermentrout (2001a), where a is a recovery variable that limits the excitation of the network, representing phenomena lumped together such as potassium membrane repolarization, synaptic depression and spike frequency adaptation. The contrast with the formulation where inhibition is explicitly included is discussed in Pinto and Ermentrout (2001b).

In our simulations of N × N Wilson–Cowan neurons, we implement a fourth-order Runge–Kutta differential equation solver to follow the solutions. Initial conditions are applied (given in Supplementary Material, online at http://www.iop.org/EJ/mmedia/1741-2552/5/1/001) that lead to a sustained spiral wave on the grid, and boundary conditions are free. Nevertheless, we remark that the basin of attraction for initial conditions of our model is quite complex, and that we can observe a wide variety of the qualitative dynamics seen in experiments using this model (data not shown here). Our goal is to use noisy observations of the u variable (voltage signal) only at the N × N grid points as input to the Kalman filter, and to carry out accurate enough tracking of all u and a variables as well as parameters in the Wilson–Cowan neurons to allow control of the spiral wave dynamics. We note that in the Wilson–Cowan formulations, the neurons should be considered to be averaged representations of the real neurons, and just as in our optical measurements the signals represent a volume average of neighboring cells.

To estimate and track the current state of the network, we applied a nonlinear version of the Kalman filter, UKF. The UKF uses known nonlinear dynamical equations and observation functions along with observed data to continuously update a Gaussian approximation for the state and its uncertainty. At each integration step, system states that are consistent with the current state uncertainty, called sigma points, are chosen. The UKF consists of integrating the system from the sigma points, estimating mean state values, and then updating the covariance matrix that approximates the state uncertainty. The Kalman gain matrix updates the new most likely state of the system.

As pointed out in recent literature (Voss et al 2004, Hansen and Penland 2007), the UKF can also be used to fit system parameters from data. The technique consists of introducing the unknown parameters as extra state variables with trivial dynamics. The UKF with random initial conditions for the parameters will converge to the correct parameters, or in the case of varying parameters, can track them along with the state variables.

In general, UKF works as follows. Assume that the one-step dynamics is described by the function F, and the observations by the function W. Assume that the observations are noisy with noise covariance matrix R. For a D-dimensional estimated state x̄, the 2D sigma points X₁,…, X_2D are the D columns of the matrix $\overline{x}+\sqrt{\text{DP}}$ together with the D columns of the matrix $\overline{x}-\sqrt{\text{DP}}$, where P denotes the estimated covariance matrix and the square root sign denotes the matrix square root. Sigma points can be envisioned as sample points at the boundaries of a covariance ellipsoid. Apply one step of the dynamics F to the sigma points and call the results X̃_i = F(X_i). Observations of the new states are denoted by Ỹ_i = W (X̃_i). Then define the means

$$\stackrel{\sim }{x}=\frac{1}{2D}\sum _{i=1}^{2D}{\stackrel{\sim }{X}}_i,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\stackrel{\sim }{y}=\frac{1}{2D}\sum _{i=1}^{2D}{\stackrel{\sim }{Y}}_i$$

which are called the a priori state estimate and a priori measurement estimate, respectively. Define the a priori covariances

$$\begin{array}{c}{\stackrel{\sim }{P}}_{xx}=\frac{1}{2D}\sum _{i=1}^{2D}\hspace{0.17em}({\stackrel{\sim }{X}}_i-\stackrel{\sim }{x}){\hspace{0.17em}({\stackrel{\sim }{X}}_i-\stackrel{\sim }{x})}^T\\ {\stackrel{\sim }{P}}_{xy}=\frac{1}{2D}\sum _{i=1}^{2D}\hspace{0.17em}({\stackrel{\sim }{X}}_i-\stackrel{\sim }{x}){\hspace{0.17em}({\stackrel{\sim }{Y}}_i-\stackrel{\sim }{y})}^T\\ {\stackrel{\sim }{P}}_{yy}=\frac{1}{2D}\sum _{i=1}^{2D}\hspace{0.17em}({\stackrel{\sim }{Y}}_i-\stackrel{\sim }{y}){\hspace{0.17em}({\stackrel{\sim }{Y}}_i-\stackrel{\sim }{y})}^T+R\end{array}$$

of the ensemble members. Then the Kalman estimates of the new state and uncertainty are given by the a posteriori quantities

$$\widehat{x}=\stackrel{\sim }{x}+K(y-\stackrel{\sim }{y})$$

and

$${\widehat{P}}_{xx}={\stackrel{\sim }{P}}_{xx}-K{\stackrel{\sim }{P}}_{xy},$$

where $K={\stackrel{\sim }{P}}_{xy\hspace{0.17em}}{\stackrel{\sim }{P}}_{yy}^{-1}$ is the Kalman gain matrix and y is the actual observation. Thus x̂ and P̂_xx are the updated estimated state x and covariance matrix P for the next step. The a posteriori version of the observation variable ŷ is recovered by ŷ = W (x̂).

In our application, the state x is the 2N² + m dimensional vector consisting of the N × N values of variable u on the grid, the N × N values of variable a on the grid, and the m parameter values to be tracked. The one-step dynamics function F(x) is the time-T map of the Wilson–Cowan system of differential equations in the first 2N² variables for some fixed time step T, and the identity function in the parameters. The observation function W (x) returns the first N² components of the vector x, namely the N × N values of variable u. We treat the second N² components, the N × N values of variable a, as unobserved. For our network N = 8, and m = 1 corresponding to the tracked threshold parameter θ. We customarily used a time step of T = 0.06 ms.

In theory, the unscented Kalman filter matches the nonlinear effects of the dynamics up to second order statistics. In practice, it is common for the UKF to underestimate the uncertainty in the state estimate, due to higher order contributions as well as model error. In this case, the state estimate from the filter can be overweighted in comparison to the observations, causing growing errors in the state estimate from the actual system state. To counteract this tendency, we have followed the recent suggestions in the literature (Hunt et al 2007) to apply covariance inflation. We have applied a small additive constant (typically 10⁻⁴) multiplied by the identity matrix to the covariance matrix P prior to computing the sigma points in each step. This inflation helps stabilize the computation, and we have found that it makes both trajectory following and parameter estimation much more robust.

Our computational code structure builds upon the algorithms of Voss et al (2004). A working set of our Matlab code samples sufficient to replicate our findings is archived in Supplementary Material (online at http://www.iop.org/EJ/mmedia/1741-2552/5/1/001/).

Results

We simulated an experiment conducted in a tangential cortical brain slice as reported in Huang et al (2004) and Schiff et al 2007, using Wilson–Cowan equations representing an 8 × 8 grid of neuronal elements imaged using voltage sensitive dye (figure 1). In the experiments, a blocker of gamma-amino butyric acid type-A (GABA-A) synaptic activity is added to the perfusion solution, and we have accordingly not modeled inhibitory effects. We find that a spatiotemporal network of Wilson–Cowan equations have a complex basin of attraction, and have empirically chosen a set of initial conditions that give spiral wave dynamics as we have frequently seen experimentally.

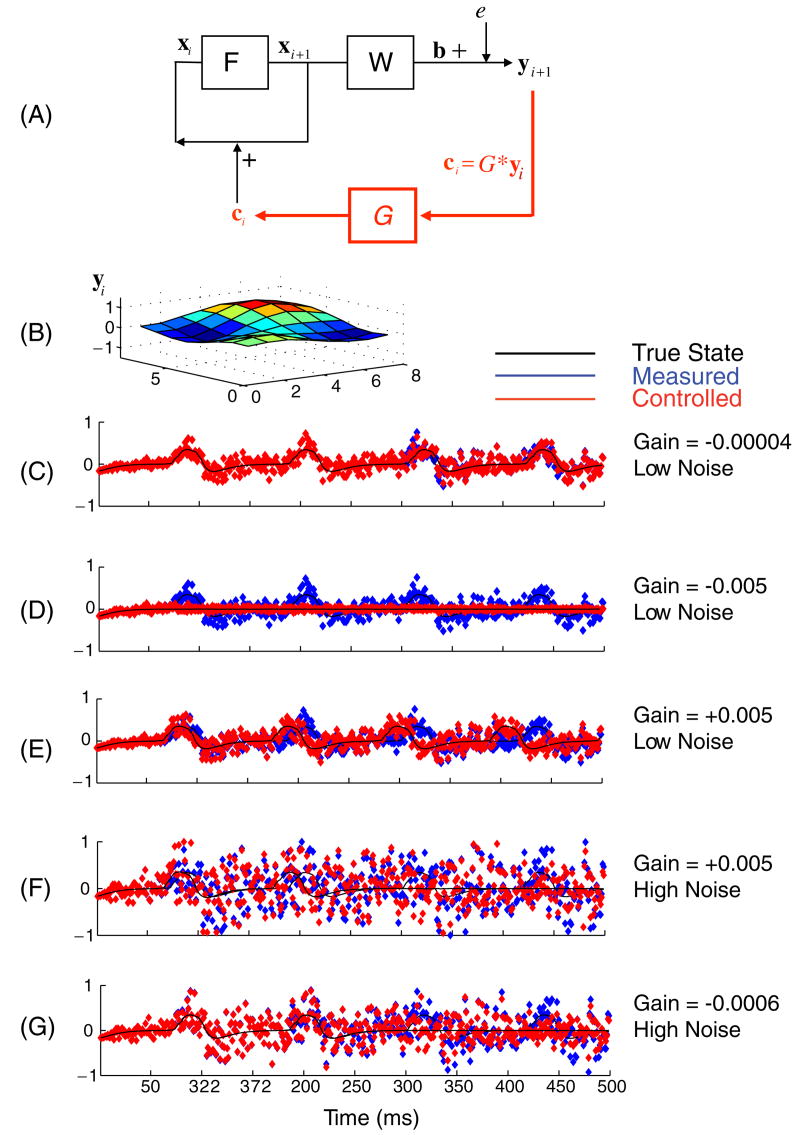
Figure 1.

(A) Schematic of dynamical system F, which acts upon the state variable vector x, and the observation function W which produces the output vector b to which the measurement noise e is added, generating the output observable y. When the direct proportional control is used, the control function G is employed, which generates the control law (c_i = G ∗ y_i). This control vector is directly ‘injected’ into the neuronal elements, adding vector c to the activity variable u (nothing is added to the unobserved variables a or to the parameters of the system). (B) An instantaneous snapshot of the 8 × 8 output y_i during a rotational spiral. (C) The output of the observable y under conditions of small negative gain and low noise, from a single element of the grid in B, shown as a time series without (blue) and with the (red) control applied. The underlying state vector activity element u_i is plotted as a thin black line. In contrast with (C), are shown outputs under conditions of higher negative gain and low noise in (D), positive gain and low noise in (E), and high noise conditions with positive and negative gains shown in (F) and (G), respectively. Low noise corresponds to 1–5, and high noise corresponds to 10–14 on an arbitrary scale. Note that under high noise conditions, the application of direct proportional control as illustrated in the schematic renders the system dynamics unstable and destroys the rotational spiral regardless of positive or negative feedback.

In figure 1(A), we illustrate the schematic of the simulation and a proportional control vector. The dynamics of the Wilson–Cowan equations are represented by block F, applied iteratively, and the observation function by block W. Following the application of the observation function W, random noise e is added to each observation variable to create the noise-contaminated observation vector y. We allow ourselves to only measure the voltage in the simulated photodetector image (variable y, figure 1(B)).

Figures 1(B)–(G) illustrate the wave dynamics with and without the use of a proportional control vector c (c_i = G∗y_i). A snapshot of vector y, plotted in the geometry of the grid, is shown in figure 1(B). This snapshot is of a rotational spiral, and full simulations of such dynamics are illustrated in the Supplementary Material (online at http://www.iop.org/EJ/mmedia/1741-2552/5/1/001/). In figures 1(C)–(G) are shown time series from one of the grid coordinates in figure 1(B). The black traces are the underlying state, x_i, and the traces in blue markers indicate the noise-contaminated observable y_i without control activated. The traces in red markers are for the case where the control feedback loop, shown in red in figure 1(A), is active. For relatively low noise, small negative gains, G, will slow (figure 1(C)), and larger negative gains stop (figure 1(D)) the rotational oscillations. At this level of noise, the slowing with proportional control is relatively small, and the result is brittle—the transition from mild slowing (figure 1(C)) to wave blockade (figure 1(D)) occurs rather abruptly (at gains about twice the negative gain used in figure 1(C)). For positive gains with low noise, the feedback will increase the frequency of the spirals (figure 1(E)). For higher noise levels, the situation is different. In figure 1(F), the loss of stability of the wave activity in the case of positive gain and sufficiently high noise levels is shown and in figure 1(G), the comparable loss of stability with negative gains and high noise is shown. It is the robustness of proportional control that we will next address with model based state estimation.

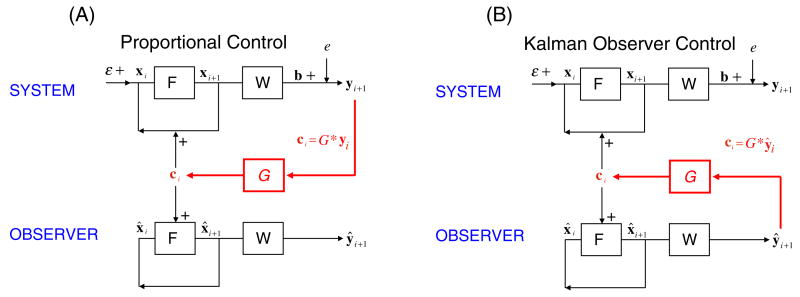
In figure 2 we demonstrate two implementations of the UKF observer. In figure 2(A), the use of proportional feedback control using actual noisy measured data is illustrated, while the Kalman observer system estimates and tracks both the state of the system, x̂, including the observable ŷ while reconstructing the recovery variable a, and the threshold parameter θ (see Methods). The Kalman observer operates without noise, other than the noise introduced through the control vector, c, generated through the use of the noisy observable, y.

Figure 2.

Schematic of the use of a Kalman filter observer. In (A) is illustrated the use of an observer to estimate state variables and parameters while the control is derived from the actual noisy output y. The control vector c is applied to both the system and the observer. In (B) is shown the use of the observer system to calculate proportional control through an estimation of the observable ŷ. Again, the control vector is fed back into both the experimental system and the Kalman observer.

In figure 2(B) is illustrated the case where the Kalman observer is used to generate the control vector c, and in this case it is this control vector which is fed back both to the noisy system and the Kalman observer system. We will demonstrate that using the Kalman observer system to generate the control vector always results in a substantial reduction in control vector energy required during feedback. Furthermore, it is easy to identify ranges of feedback gain and measurement noise for which only through the use of the observer Kalman filter will a stable control vector be generated.

Figure 3 shows comparative details of the high noise positive gain case using the Kalman observer to only track variables and estimate parameters (left column) and to generate the control vector as well (right column). Figure 3(A) is the same simulation parameters as figure 1(F). Figure 3(B) shows the tracking of the unobserved parameter a, both without (blue) and with (red) positive gain proportional control (similar qualitative time series of a are seen in the rest of the grid cells). The rotational spiral is destroyed within two spiral rotations after control is turned on at 40 ms. Figure 3(C) shows that although the Kalman observer tracks the threshold, θ, well without control (blue), that it is unable to track this constant parameter value when the proportional control is on. Figure 3(Da) shows the final snapshot of the 8 × 8 grid of the noisy observed variable y without control, and figure 3(Db) the final snapshot of the estimate of ŷ with control. The full 500 ms of data in figure 3(D) can be viewed as Supplementary Movie 1 in Supplementary Material (online at http://www.iop.org/EJ/mmedia/1741-2552/5/1/001/). The estimate of the observable ŷ is lost in the image in figure 3(Db). The total control energy utilized in the control vector c is plotted in figure 3(E).

Figure 3.

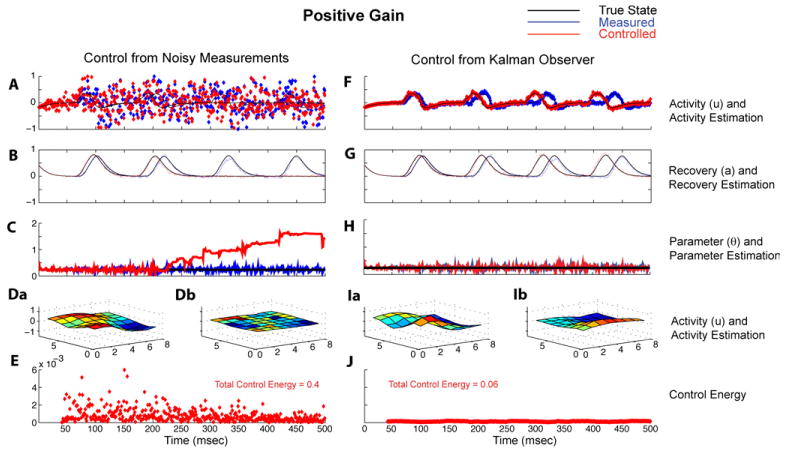
Comparison of the use of positive gain proportional control calculated directly from high noise observations, left column (A)–(E), and from the Kalman observer, right column (F)–(J). (A) Output variable y_i from the single element of grid, same as in figure 1(F). The application of positive feedback gain at this high level of noise results in instability of the rotational oscillation, with loss of both the underlying oscillation u_i (black line) and measured observation y_i (red). (B) Without control being applied, the Kalman observer can accurately estimate (blue) the unobserved variable a (black). With this level of noise, when control is applied, not only is the observable a oscillation lost (red), but the true system state loses stability and the wave is destroyed after two oscillations (black). (C) without control, despite the high noise level, the parameter θ (black) is accurately tracked (blue). When the stability of the dynamics is lost during control, the parameter θ is no longer accurately estimated (red). (Da) shows the underlying activity variable y, and (Db) the estimated ŷ. The snapshots in (Da) and (Db) are taken from the last frame in the 500 ms simulation, and the full simulation can be viewed as Supplementary Movie 1. In (E) is shown the energy (sum of squared voltage) of the control vector c_i, and the total sum of all control vector energy for the 500 ms is 0.4 (arbitrary scale). (F) shows the estimated observable ŷ without (blue) and with (red) control derived from the Kalman observer. (G) With Kalman observer control, the unobserved recovery variable a is now well tracked and the rotational spiral is stably increased in frequency, and in (H), the parameter θ is now well tracked. (Ia) and (Ib) show the underlying experimental variable y and estimated variable ŷ. In (J) is shown that the control energy required is markedly reduced, with total control energy 0.06 (arbitrary scale).

The right column of figure 3 shows the output, ŷ, of the Kalman observer, without (blue) and with (red) it being used to generate the control vector c. Note that in figure 3(F) that by using the Kalman observer to more accurately estimate the underlying system dynamics in the presence of high noise contamination, that positive feedback can both increase the rate of rotation and counterintuitively stabilize the rotating wave. The unobserved variables (in all cells) are now well tracked (a single cell's unobserved variable is shown in figure 3(G)), with and without control, and the threshold parameter, θ, is similarly well tracked in all cells (figure 3(H)). Figures 3(Ia) (observable y) and (Ib) (estimated observable ŷ) show the final snapshots of the 8 × 8 grid after 500 ms of stimulation. The full 500 ms of data in figure 3(I) can be viewed as Supplementary Movie 1 in Supplementary Material (online at http://www.iop.org/EJ/mmedia/1741-2552/5/1/001/). Importantly, note the very substantial reduction (85%) in total proportional control vector energy required over the 500 ms when the Kalman observer is used to estimate the control vector (figure 3(J)).

Figure 4 shows the details of the comparable case of negative gain feedback in the presence of sufficient amounts of noise that render the proportional control case unstable using the directly measured observable y. Figure 4(A) is the same simulation parameters as figure 1(G). We again see that the Kalman observer successfully tracks the unobserved variables a (figure 4(B)) and estimates the parameter θ (figure 4(C)) for the uncontrolled case (shown in blue), but that tracking becomes ineffective when the control renders the system unstable (shown in red). A full simulation of the images (figures 4(Da) (observable y) and (Db) (estimated observable ŷ)) are shown as Supplementary Movie 2 in Supplementary Material (online at http://www.iop.org/EJ/mmedia/1741-2552/5/1/001/). On the right side of figure 4, we show the effectiveness of the use of the Kalman observer to generate control vectors which both effectively slow down the spiral rotational frequency, and stabilize the waves. Unobserved variables (figure 4(G)) and parameters (figure 4(H)) are tracked and estimated. Note again the substantial (77%) reduction in total control energy in this paradigm when the Kalman observer is used to generate the control vector. Below the heavy black line in figure 4, are shown results at increased amplitude of negative gain (10 fold greater than in figures 4(A)–(J)), illustrating that with sufficient negative gain, proportional control calculated directly from high noise observations, K, or from the Kalman observer, L, completely quenches the wave activity.

Figure 4.

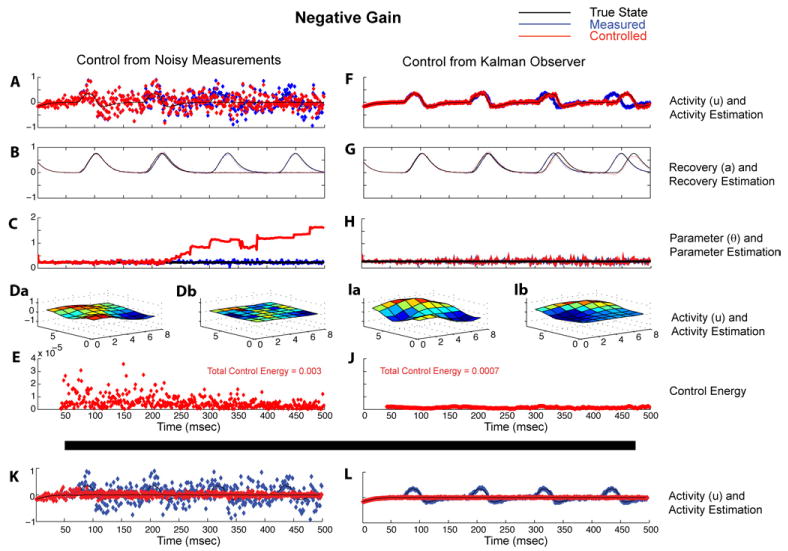
Comparison of the use of negative gain proportional control calculated directly from high noise observations, left column (A)–(E), and from the Kalman observer, right column (F)–(J). (A) Output variable y_i from the single element of grid, same as in figure 1(G). The variables in this figure are similar to the description for figure 3. Note that with control derived from the Kalman observer (right column), that negative gain in high noise conditions stably slows the frequency of the spiral, and requires considerably less control energy, than the unstable case where the direct proportional control is calculated from the noisy observations (left column). Below the heavy black line, are shown results at an increased amplitude of negative gain illustrating that with sufficient negative gain (a 10-fold increase in gain compared with (A)), the proportional control calculated directly from high noise observations, (K), or from the Kalman observer (L), completely quenches the wave activity.

We have used the Kalman observer for the cases in figure 1 where the direct proportional control was effective in slowing down or speeding up the spiral wave (figures 1(C) and (E)). Although in these cases the Kalman filter was not necessary to stably modulate the frequency of this spatiotemporal oscillation, in all such cases, the use of the Kalman-observer-generated control vector resulted in a substantial reduction in control vector energy required in comparison with the direct proportional case (data not shown).

Discussion

We have, to our knowledge, demonstrated the first computational framework to apply nonlinear Kalman filtering to track and control spatiotemporal cortical neuronal activity. We show that the use of a Kalman observer can permit state variable reconstruction and parameter estimation under conditions where the direct proportional control calculated from measured variables would fail.

Kalman filtering and related model-based prediction-corrector methods produced a revolution in control engineering in a wide variety of applications over the past half century. Although Kalman filtering is exact for truly linear systems, the extended Kalman filter linearization of nonlinear systems is well known to generate inaccurate mean and covariance propagation (Julier and Uhlmann 1997a, 1997b). In terms of nonlinear state estimation and forecasting, we find the increasingly compelling role for the UKF in meteorological data assimilation and prediction to share surprising similarities faced by neuroscience experiments. Although the UKF and its variants offered the possibility of applying such model-based state estimation to neuronal systems, it was the work of Voss et al (2004) which demonstrated the first framework of such an application to a reduced model of a single neuron.

In extending the work of Voss et al (2004) to a spatiotemporal neuronal network, there were a variety of numerical strategies that we needed to employ in order to stabilize our implementation (see Methods). Key among these was the control of model error underestimation through covariance inflation (Hunt et al 2007). Although covariance inflation was indirectly discussed by Julier and Uhlmann (1997b), it has found explicit focus in recent meteorological forecasting applications. Our implementation of covariance inflation was empirical, and it is an important area for future work to develop a more systematic implementation to optimize this parameter.

Our use of the Wilson–Cowan equations as our fundamental model is one which although arbitrary, has the advantage of being one of the simplest differential equation systems that models the explicit nonlinearity of neurons, their slower time-scale recovery processes, as well as their network nonlocality of interaction. Indeed, such nonlocal interactions are a problem that distinguishes neuronal networks from convection models of the atmosphere and other diffusive and mechanical processes.

We implemented this fundamental model using homogenous parameters for each spatial location—an unrealistic assumption. For real neuronal systems, it is important to develop a framework to handle the expected errors in variables and parameters. We are presently working on strategies to reach an optimal fit of parameters to such heterogeneous systems.

An alternative to a fundamental model is to use an empirical model, for instance from a principal orthogonal decomposition of the spatiotemporal dynamics of such neuronal systems (Schiff et al 2007). Such an empirical mode decomposition can be utilized to model the dynamics of such a system, and when those dynamics are of sufficiently low dimension, perform short-time prediction of dynamics and the effect of control. A further advantage of such a mode decompositional technique is that it offers the possibility of generating a set of modal equations through a Galerkin projection, a technique which has been of considerable use in fluid dynamics and turbulence studies (Holmes et al 1996, Smith et al 2005). Whether such model reduction might serve use in the state estimation and control of neuronal systems is a subject for future investigation.

Our strategy in this report has been to construct a framework that can be applied in ongoing experimental applications (Huang et al 2004, Schiff et al 2007). We have implemented proportional and proportional-integral control based on single point electrical measurements from neuronal networks and applied through feedback electrical fields (Gluckman et al 2001). The strategy in this present paper would be implemented through the spatiotemporal optical sensing of activity using voltage sensitive dye imaging, either through an in vitro slice preparation, or in an in vivo situation. The in vitro experiment is a straightforward application of electrical field polarization as suggested in our numerical calculations. We recognize that our present calculations employed direct injection of ‘current’ to the elements of the discretized Wilson–Cowan equations, and that the subtleties of true electric field polarization of extended neurons, with the counter-fields generated within each neuron, and the ephaptic electrical cross-talk present between real neurons (Park et al 2005), will complicate the picture during experiments with real neuronal networks. Such complications may dictate that a more detailed model, incorporating the polarization characteristics of neurons as well as the electrically resistive properties of brain tissue within which the neurons are embedded, may be required to provide adequate performance.

There are a variety of applications for which the model-based control strategy discussed here might be applied. The control of single neurons through intracellular electrode impalement would be an interesting if albeit academic exercise and proof of concept. The control of wave mechanics in brain slices would be an interesting prelude to considering such wave control in in vivo applications such as in the motor (Hatsopoulos et al 2006) or visual (Xu et al 2007) systems. The potential to intelligently interact with the oscillatory extrapyramidal system in Parkinson's disease is an attractive possibility. We are also exploring the application of these techniques to the modulation of navigationally associated hippocampal theta rhythm in awake behaving animals, the extraction of features from scalp EEG in brain machine interface applications, and the possibility of the suppression of epileptic seizures.