Pigeons and humans are more sensitive to nonaccidental than to metric changes in visual objects

Abstract

Humans and macaques are more sensitive to differences in nonaccidental image properties, such as straight vs. curved contours, than to differences in metric properties, such as degree of curvature [Biederman, I., Bar, M., 1999. One-shot viewpoint invariance in matching novel objects. Vis. Res. 39, 2885–2899; Kayaert, G., Biederman, I., Vogels, R., 2003. Shape tuning in macaque inferior temporal cortex. J. Neurosci. 23, 3016–3027; Kayaert, G., Biederman, I., Vogels, R., 2005. Representation of regular and irregular shapes in macaque inferotemporal cortex. Cereb. Cortex 15, 1308–1321]. This differential sensitivity allows facile recognition when the object is viewed at an orientation in depth not previously experienced. In Experiment 1, we trained pigeons to discriminate grayscale, shaded images of four shapes. Pigeons made more confusion errors to shapes that shared more nonaccidental properties. Although the images in that experiment were not well controlled for incidental changes in metric properties, the same results were apparent with better controlled stimuli in Experiment 2: pigeons trained to discriminate a target shape from a metrically changed shape and a nonaccidentally changed shape committed more confusion errors to the metrically changed shape, suggesting that they perceived it to be more similar to the target shape. Humans trained with similar stimuli and procedure exhibited the same tendency to make more errors to the metrically changed shape. These results document the greater saliency of nonaccidental differences for shape recognition and discrimination in a non-primate species and suggest that nonaccidental sensitivity may be characteristic of all shape-discriminating species.

Considerable research in visual object recognition has been inspired by the problem of recognizing an object when it is again experienced at different viewpoints, such as when the object is encountered at a different orientation in depth. For example, a straight edge on a three-dimensional object produces a straight line in a two-dimensional projection to the retina; but, so too does a curved edge when the curve is precisely perpendicular to the line of sight. How, then, does the visual system decide whether a three-dimensional object has a straight edge or a curved edge using two-dimensional information?

Lowe (1985) first suggested that certain regularities of two-dimensional images, like curvilinearity, are highly likely to reflect the same regularities in three-dimensional objects. Although it is true that accidental alignment of the eye and a curved edge might result in the projection of a straight line, there are very few accidental viewpoints from which this would be the case. Thus, the visual system simply ignores this possibility and assumes that straight edges in two-dimensional projections correspond to straight edges in three-dimensional objects. Several properties including collinearity (straight edge), curvi-linearity (curved edge), parallelism, and cotermination of edges have been termed nonaccidental (Biederman, 1987; Wagemans, 1992; Witkin and Tenenbaum, 1983). In contrast, metric properties – such as the degree of curvature or the length of a segment – will typically vary with the rotation of an object in depth, and thus are less useful for recognizing objects.

One of the most widely known theories of object recognition – Recognition-By-Components – confers special status to nonaccidental properties of objects (Biederman, 1987). According to this theory, the visual system recognizes objects by decomposing them into two-dimensional or three-dimensional geometric primitives termed “geons.” The geons are a partition of the set of generalized cylinders, or volumes, created by sweeping a cross-section along an axis into shapes that differ in nonaccidental properties. For example, a circle cross-section swept along an axis would produce a cylinder, whereas a square cross-section swept along an axis would produce a brick. Additionally, the cross-section could expand as it is swept along the axis producing a cone or a wedge. The axis could be straight or curved, producing curved cones, bricks, etc. Finally, when the sides of a geon are not parallel, their ending could be truncated, come to a point (or L-vertex), or be rounded.

Note that the differences in cross-section (curved or straight), cross-section size (constant or expanded or expanded and contracted), axis (straight or curved), or ending (truncated, pointed, or rounded) can be described in terms of low-level nonaccidental properties, such as collinearity, curvilinearity, parallelism, and cotermination of edges (Biederman, 1987). For example, cross-sections of constant size have parallel sides, whereas cross-sections that expand or expand and contract do not have parallel sides. Similarly, curved or straight cross-sections or axes can be discriminated by using collinearity and curvature. Finally, the geons can differ from each other in more than one nonaccidental property. For example, a wedge has nonparallel sides and straight edges at its termination, whereas a cylinder has parallel sides and curved edges at its termination. In this way, each geon can be uniquely specified from its two-dimensional image properties, thereby affording accurate recognition from various viewpoints. We describe our stimulus manipulations in terms of geon (or generalized cylinder) properties, namely cross-section, cross-section size, and axis¹ rather than the characteristics of individual edges that they affect.

If the visual system relies on nonaccidental properties for recovering three-dimensional images from two-dimensional retinal inputs, then it should be more sensitive to detecting changes in nonaccidental than metric properties of shapes. Biederman and Bar (1999) had human participants detect whether the sequential presentation of two three-dimensional novel objects, each composed of two parts, e.g., a small cylinder with a curved axis on top of a brick, were the same or different. When the objects did differ, they either differed in a metric property (e.g., an increase in the curvature of the axis of the cylinder) or in a nonaccidental property (e.g., the axis of the cylinder became straight). When the objects were not rotated, the participants were equally good at detecting both types of changes. This equating of performance at 0° was done by making the metric differences physically larger than the nonaccidental differences, as assessed by wavelet and pixel contrast energy differences. But, when the objects were rotated in depth, the participants were much more efficient at detecting changes in nonaccidental than in metric properties: rotation angles of 57° produced only a 2% increase in error rate for changes in nonaccidental properties of the objects, but a substantial 44% increase in error rate for changes in metric properties of the objects. Thus, nonaccidental properties appear to be beneficial for recognizing objects differing in a single part (see also Biederman and Gerhardstein, 1993; Tarr et al., 1997, for similar results).

Additional reports have found a neural basis for the greater sensitivity to nonaccidental than metric properties in the tuning of cells in the inferior temporal cortex of the macaque, an area that is involved in object recognition (Logothetis and Sheinberg, 1996). Despite the smaller physical differences of the nonaccidental changes, the firing of inferior temporal neurons was modulated more strongly by nonaccidental than by metric changes, suggesting that the visual system may indeed be especially receptive to changes in nonaccidental properties (Kayaert et al., 2003, 2005; Vogels et al., 2001).

Is such reliance on nonaccidental properties unique to the mammalian visual system? Evidence suggests that many early visual processes such as odd-item search, texture perception, and figure-ground assignment are analogous in birds and mammals, at least at the behavioral level (Blough, 1989; Cook et al., 1997, 1996; Lazareva et al., 2006). Neurobiological evidence also points to the conclusion that avian and mammalian visual systems process visual information in a similar manner despite notable anatomical disparities (Butler and Hodos, 1996; Jarvis et al., 2005; Medina and Reiner, 2000; Shimizu and Bowers, 1999). So, it seems reasonable to expect that the avian visual system utilizes nonaccidental properties for object recognition, just as the mammalian visual system does.

Our laboratory recently explored which regions of visual objects are critical for pigeons and people to recognize shaded grayscale images of four three-dimensional shapes (Gibson et al., 2007).We used the Bubbles technique (Gosselin and Schyns, 2001) that isolates the features of the object controlling discriminative performance. Both pigeons and people were first trained to discriminate four shapes by selecting one of four response buttons. During subsequent testing, pigeons and people viewed the same images covered by a gray mask which revealed only small portions of the images through multiple randomly located openings or “bubbles”. The position of the bubbles was then correlated with the discriminative response. A correct response indicated that the revealed features were critical for the discrimination, whereas an incorrect response indicated that the revealed features were insufficient for the discrimination.

We found that the cotermination of edges, one of the key nonaccidental properties (Biederman, 1987), was the most salient cue for both pigeons and people. Yet, a performance-matched “ideal” observer which perfectly knew the images of the objects and could use all of the available information in the image relied more heavily on the midsegments of the edges, suggesting that these latter parts of the images were most useful in discriminating the four particular images chosen for the experiment. Although attending to midsegments of the edges may, in some cases, help to determine whether they are straight or curved, the study used two images with curved edges (arch and barrel) and two images with the straight edges (brick and wedge; see Fig. 1). So, in order to discriminate the arch from the barrel using midsegments, the organisms would have to utilize metric properties (e.g., a degree of curvature). Instead, both pigeons and people utilized a nonaccidental property, cotermination, even though it was not the most informative part of the image for the programmed task.

Fig. 1.

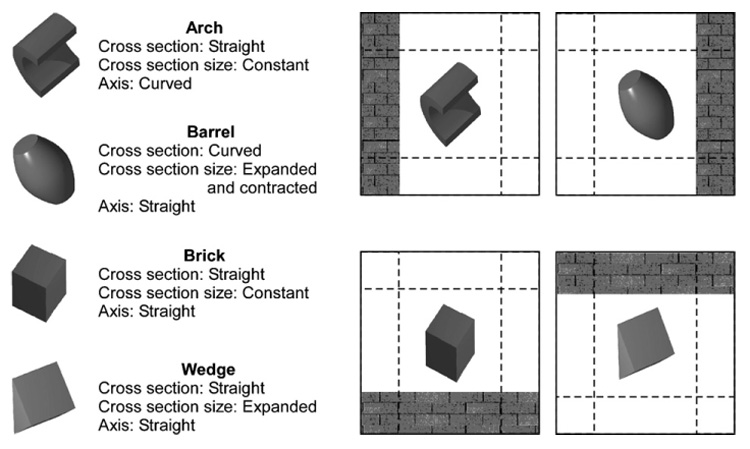
The four shapes used in Experiment 1. The left panel lists the nonaccidental properties for each shape. The dashed lines indicate potential locations of the brick wall, an irrelevant feature of the pictorial stimuli in the present discrimination.

In the present study, we used different methods to obtain converging evidence of pigeons’ reliance on nonaccidental properties. In Experiment 1, we analyzed the errors committed by pigeons trained to discriminate the same shaded grayscale images of four three-dimensional shapes used by Gibson et al. (2007). We expected to find that pigeons would commit most errors to the report key associated with the shape that shared the most nonaccidental properties with the target shape. In Experiment 2, we adapted Blough’s (1982) similarity judgment technique to assess how pigeons and people perceive the similarity of metrically modified shapes and nonaccidentally modified shapes to the original, target shape.

1. Experiment 1

In the first experiment, we trained pigeons to discriminate grayscale images of four three-dimensional shapes – arch, barrel, brick, and wedge (Fig. 1) – by using a four-alternative forced-choice task. Each shape was associated with one of the choice keys; so, when a bird made an error, its choice was associated with one of the other three shapes. Was the pattern of errors affected by how many nonaccidental properties of the generalized-cylinder generating function the shapes shared? As Fig. 1 shows, some of the shapes (e.g., arch and barrel) share no nonaccidental properties; others share one nonaccidental property (e.g., arch and wedge); still others share two nonaccidental properties (e.g., arch and brick). Ignoring any effect of the scale of the differences in the geons, we thus would expect that, when the arch was presented, the birds would commit most errors to the choice key associated with the brick and least errors to the choice key associated with the barrel.

2. Method

2.1. Subjects

The subjects were 12 feral pigeons (Columba livia) maintained at 85% of their free-feeding weights by controlled daily feeding. Grit and water were available ad libitum in their home cages. The pigeons had previously participated in unrelated experiments.

2.2. Apparatus

The experiment used four operant conditioning chambers and four Macintosh computers (detailed by Wasserman et al., 1995). One wall of each chamber contained a large opening with a frame attached to the outside which held a clear touch screen. An aluminum panel in front of the touch screen allowed the pigeons access to a circumscribed portion of a video monitor behind the touch screen. There were five openings or buttons in the panel: a 7 cm × 7 cm square central display area in which the stimuli appeared and four round report areas (1.9-cm diameter) located 2.3 cm from each of the four corners of the central opening. The central area was used to show the stimulus displays, whereas the four report areas were used to show the four report buttons. A food cup was centered on the rear wall level with the floor. A food dispenser delivered 45-mg food pellets through a vinyl tube into a cup. A house light mounted on the rear wall of the chamber provided illumination during sessions.

2.3. Stimuli

Stimulus displays consisted of a single grayscale shape (arch, barrel, brick, and wedge) located in the middle of the display and a red brick wall that could be located at the left, right, top, or bottom of the display. These stimuli had been used in several previous studies (DiPietro et al., 2002; Lazareva et al., 2007). The brick wall was relevant in those prior studies, but it was irrelevant to the present discrimination. The same four grayscale shapes without the brick wall were also used in Gibson et al. (2007). Fig. 1 illustrates the stimuli and provides the list of nonaccidental properties for each shape and Table 1 shows the dimensions of the stimuli. The number of shared nonaccidental properties among the shapes varied from 0 (arch–barrel) to 1 (wedge–barrel, barrel–brick, wedge–arch) to 2 (arch–brick, wedge–brick).

Table 1.

Width, height, and area (in pixels) of the four shapes used in Experiment 1

	Arch	Barrel	Brick	Wedge
Height	88	74	86	67
Width	78	69	65	75
Area	4950	4432	4443	4162

All of the stimuli were created in Canvas™ Standard Edition, Version 7 (Deneba Software Inc.) and were saved as PICT files with 144 dpi resolution.

2.4. Procedure

At the beginning of a training trial, the pigeons were shown a black cross in the center of the white display screen. Following one peck anywhere on the screen, the training stimulus appeared and a series of pecks (observing responses) was required. The observing response requirement varied from bird to bird and ranged from 15 to 53 pecks; this requirement was individually adjusted to the performance of each pigeon. If a bird failed to complete a session due to a high-fixed ratio requirement, then the requirement was decreased. If a bird was pecking but not meeting criterion in a timely fashion, then the requirement was increased to make failures more punishing.

After completing the observing response requirement, the four report buttons were illuminated and the pigeon was required to make a single report response to the button associated with a given shape. If the response was correct, then food was delivered and the intertrial interval (ITI) ensued, randomly ranging from 4 to 6 s. If the response was incorrect, then the house light and the screen darkened and a correction trial was given. On correction trials, the ITI randomly ranged from 5 to 10 s. Correction trials continued to be given until the correct response was made. Only the first report response was scored in the data analysis. Each training session comprised 160 trials (5 blocks of 32 trials). The pigeons were trained until they met an 85/80 criterion (85% correct overall and 80% correct to each shape).

After the pigeons reached the criterion, they were presented with various probe images to explore their ability to recognize occluded objects; these data were previously reported elsewhere (DiPietro et al., 2002; Lazareva et al., 2007). Here, we have reanalyzed the acquisition data from these prior studies concentrating on the pattern of confusion errors.

2.5. Behavioral measures

For all statistical tests, alpha was set at 0.05. We used the percentage of errors committed to the key associated with a specific shape (the number of errors to that shape divided by total number of errors and multiplied by 100) as our dependent measure, termed the percentage of confusion errors. To analyze the effect of changes in the metric properties of the shapes, we computed the absolute difference in pixels for the shapes’ height, width, and area, as well as the mean squared deviation of the pixel values and the absolute difference in pixel energies for each pair of shapes (see Vogels et al., 2001 for further details on computing pixel energies). We then correlated these measures with the percentage of confusion errors.

3. Results and discussion

Discrimination training averaged 18 ± 4.4 sessions (range: 4–51 sessions). Table 2 presents the mean percentage of errors made to the choice keys associated with the four different shapes during discrimination training. When the arch was presented, the birds made most errors to the key associated with the brick (and vice versa); the birds also made least errors to the key associated with the barrel (and vice versa). In other words, the birds treated the arch and the brick (which share two nonaccidental properties) as being most similar and they treated the arch and the barrel (which do not share any nonaccidental properties) as being most dissimilar. The other combinations of shapes generated intermediate confusion errors.

Table 2.

Mean percentage of errors to the choice keys associated with the four different shapes during discrimination training in Experiment 1

Choice key	Presented stimulus
	Arch	Barrel	Brick	Wedge
Arch		24.4!	42.0	21.6!
Barrel	16.2!		22.2	33.7
Brick	57.6*	39.1		44.8*
Wedge	26.1	36.6	35.9

Note: Asterisks and exclamation points signify values that were significantly above and below chance levels, respectively, according to two-tailed t-tests for proportions.

Fig. 2 presents the confusion errors averaged across the various combinations of shapes (e.g., errors to the arch key when the barrel was presented and errors to the barrel key when the arch was presented were averaged together and labeled “Arch–Barrel”) and plotted by the number of shared nonaccidental properties. Clearly, the number of shared nonaccidental properties had a systematic effect on the percentage of confusion errors. The percentage of confusion errors was below chance when the shapes shared no nonaccidental properties, it rose toward chance when the shapes shared one nonaccidental property, and it was above chance when the shapes shared two nonaccidental properties.

Fig. 2.

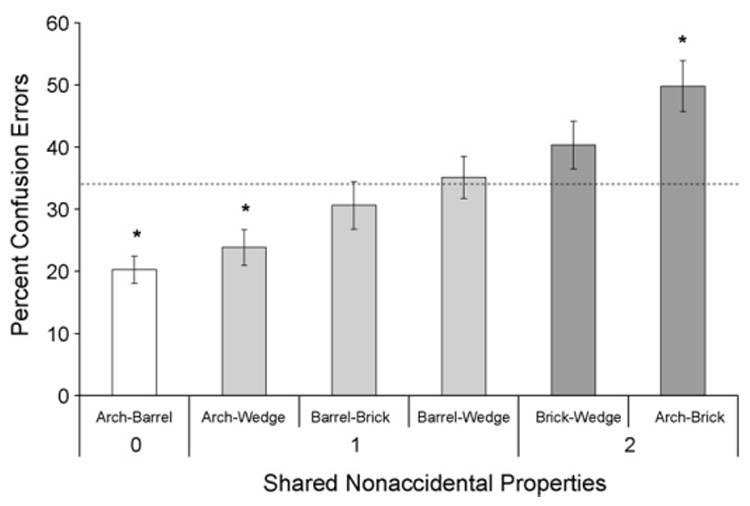
Percentage of confusion errors plotted by the number of shared nonaccidental properties in Experiment 1. The dashed line indicates chance level (33%) and asterisks indicate values significantly different from chance.

An analysis of variance (ANOVA) with Shared Properties (3) as a fixed factor, Bird (12) as a random factor, and the percentage of confusion errors as the dependent variable found a significant main effect of Shared Properties, F(2, 22) = 17.34, p < 0.0001. Planned contrasts indicated that the percentage of confusion errors committed to the shapes sharing one nonaccidental property was significantly higher than to the shapes sharing no nonaccidental properties, F(1, 22) = 4.96, p = 0.037. Likewise, the percentage of confusion errors committed to the shapes sharing two nonaccidental properties was significantly higher than to the shapes sharing one nonaccidental property, F(1, 22) = 19.96, p = 0.0002.

Can we conclude that the birds’ confusion errors were predominantly affected by the nonaccidental properties of the discriminated shapes? To do so, we need to show that the pattern of confusion errors cannot be explained by changes in any metric properties between the contrasted shapes. In this experiment, we simply used the same shapes as we had presented in several prior studies (DiPietro et al., 2002; Gibson et al., 2007; Lazareva et al., 2007). The shapes were not equated for the amount of metric change as were the stimuli used by Biederman and Bar (1999) and Kayaert et al. (2003). Therefore, we computed several measures which reflected the degree of metric change between contrasted shapes: the mean squared deviation of pixel values between shapes, the difference in pixel energy between shapes, as well as differences in the shapes’ height, width, and overall area. The absolute values for the width, height, and area of each shape are presented in Table 1. We then computed Spearman’s rank-order correlation coefficient between percentage of confusion errors and each of these measures as well as the number of shared nonaccidental properties. The values of Spearman’s rank-order correlation coefficient for each measure are shown in Table 3.

Table 3.

Spearman’s rank-order correlation coefficients for the percentage of confusion errors in Experiment 1 (n = 144 for all coefficients)

	Spearman’s r
Shared nonaccidental properties	0.45***
Mean squared deviation of pixel values	−0.40***
Difference in pixel energies	−0.06ns
Difference in shape height	−0.31**
Difference in shape width	0.34***
Difference in shape area	−0.19*

^nsp>0.05

^*p<0.05

^**p<0.01

^***p<0.001.

If the birds had attended to nonaccidental properties, then we expected to find a significant positive correlation between the number of shared nonaccidental properties and the percentage of confusion errors: more shared nonaccidental properties should result in more confusion. However, if the birds had attended to metric properties, then we expected to find a significant negative correlation: small changes in the metric properties should lead to more confusion errors and large changes should lead to fewer confusion errors.

The number of shared nonaccidental properties was indeed positively and reliably correlated with the percentage of confusion errors, indicating that more shared nonaccidental properties produced more confusion errors. One of the metric variables, the difference in shape width, was positively (instead of negatively) and reliably correlated with the percentage of confusion errors. The second metric variable, the absolute difference in pixel energies, was not significantly correlated with the percentage of confusion errors. But, the other three variables, the difference in shape height, the difference in shape area, and the mean squared deviation of pixel values, yielded reliable negative correlations with the percentage of confusion errors: metrically similar shapes produced more confusion errors than metrically dissimilar shapes. Moreover, the proportion of total variance accounted for by the mean squared deviation of pixel values was reasonably close to the proportion of total variance accounted for by the number of shared nonaccidental properties. Because the number of shared nonaccidental properties turned out to be closely associated with the change in at least some of the metric properties, we cannot say to what extent the pattern of confusion errors in Experiment 1 can be exclusively explained by changes in the nonaccidental properties of the shapes.

To directly address this issue, we conducted Experiment 2, which used stimuli that carefully controlled for the overall degree of image change (Kayaert et al., 2003; Vogels et al., 2001). We also modified the experimental task. In Experiment 2, we used a three-alternative forced-choice discrimination procedure which had been successfully deployed for the analysis of similarity judgments by pigeons (Blough, 1982).

4. Experiment 2

In Experiment 2, we trained pigeons to select one out of a trio of simultaneously presented shapes. The choice of the target shape was reinforced with a probability of 1.0 or with a probability of 0.5, whereas the choice of the other two foil shapes was never reinforced. One of the two foil shapes in a trio was obtained by modifying a metric property of the target shape: for example, the metrically modified (MEM) shape could be narrower than the target shape. The second of the two foil shapes in a trio was obtained by modifying a nonaccidental property of the target shape: for example, the nonaccidentally modified (NAM) shape could have curved edges instead of the straight edges of the target shape. Fig. 3 depicts all of the stimuli used in experiment. Importantly, these stimuli had been controlled for physical similarity by using wavelet and pixel measures (see Vogels et al., 2001, for more details).

Fig. 3.

The three trios of stimuli used in Experiment 2. Each trio included a target shape (the choice of which was reinforced) plus metric (MEM) and nonaccidental (NAM) modifications (the choice of which was not reinforced).

As in Experiment 1, we were interested in the pattern of confusion errors. If the birds perceived the MEM shape as being more similar to the target shape, then it should attract more of the confusion errors. We also conducted this experiment with human participants, using the same stimuli and similar experimental procedure as with pigeons, to confirm that our approach was adequate for revealing greater similarity of the MEM shapes to the target shapes, as has been previously reported (Biederman and Bar, 1999; Biederman and Gerhardstein, 1993).

5. Method

5.1. Participants

We studied eight feral pigeons (C. livia) kept at 85% of their free-feeding weights by controlled daily feeding. Grit and water were available ad libitum in their home cages. Before the start of this experiment, four of the eight pigeons had participated in unrelated experiments; the other four birds had participated in a pilot project which sought to assess the degree of sensitivity to metric and nonaccidental changes by using a three-alternative “naming” task. This attempt was unsuccessful and is not reported here. Importantly, the birds participating in the pilot experiment were trained to discriminate the three target shapes from one another (cf. Fig. 3), with the MEM and NAM shapes presented on infrequent and nonreinforced probe trials. Thus, the pilot experiment was unlikely to have introduced any biases into the pigeons’ responding.

A total of 22 undergraduate students at the University of Iowa participated in the experiment for course credit during the academic year. The participants’ data were used only if their accuracy during the entire session was at least 80% overall; otherwise, they were dropped from the study. The final sample included 20 people.

5.2. Apparatus

The pigeons were trained in four operant boxes detailed by Gibson et al. (2004). The boxes were located in a dark room with continuous white noise. The stimuli were presented on a 15-in. LCD monitor located behind an AccuTouch® resistive touchscreen (Elo TouchSystems, Fremont, CA). The pigeons were able to view the entire 15-in. monitor, with the exception of small areas at the top and at the bottom of the screen. A food cup was centered on the rear wall level with the floor. A food dispenser delivered 45-mg Noyes food pellets through a vinyl tube into the cup. A house light on the rear wall provided illumination during the session. Each chamber was controlled by an Apple® iMac® computer. The experimental procedure was programmed in HyperCard (Version 2.4, Apple Computer Inc., Cupertino, CA).

The experiment with human participants used four Apple® iMac® computers with 15-in. LCD screens. The experimental procedure was programmed in HyperCard and was very similar to the procedure used for pigeons.

5.3. Stimuli

Fig. 3 illustrates the three trios of stimuli used in the experiment. Each trio included a target shape, a MEM shape, and a NAM shape. We adapted the stimuli used previously with rhesus macaques (Kayaert et al., 2003; Vogels et al., 2001). These images were constructed so that the dissimilarity in pixel energy between the MEM shape and the target shape was at least as great (or greater) as the dissimilarity in pixel energy between the NAM shape and the target shape. Therefore, any greater sensitivity to nonaccidental changes could not be explained by greater surface dissimilarities.

The location of the stimuli on the screen was identical for both pigeons and people. Three 6.6-cm × 6.6-cm squares, or response buttons, located in the middle of the screen contained the displayed stimuli. The distance between adjacent buttons was 0.8 cm. The distance from the leftmost or rightmost button to the edge of the monitor was 4.5 cm, and the distance to the top of the monitor was 6.0 cm. The rest of the screen was black.

All of the stimuli were originally rendered by 3d Studio MAX, release 2.5, on a black background, and then saved as PICT files with 144 dpi resolution.

5.4. Procedure

5.4.1. Pigeons

Nondifferential training

In order to minimize any response biases, prior to differential training, all of the birds were first given nondifferential training. During nondifferential training, the birds were shown a single stimulus on either the left, the middle, or the right response button, and they had to peck it. Each of the nine stimuli was shown in each of the three locations equally often, to ensure that the birds did not prefer a specific stimulus or location before the experiment began.

Each trial began with the presentation of a black cross in the center of a white square in the center of a black screen. Following one peck at the white square, a single stimulus appeared in one of the three possible locations for 5 s. After 5 s elapsed, the bird had to peck the stimulus once. After that, the stimulus disappeared and food was delivered, followed by an ITI randomly ranging from 6 to 10s.

Each daily session consisted of 6 blocks of 27 trials, for a total of 162 trials. All of the birds had to complete two consecutive nondifferential training sessions to proceed to differential training.

Differential training

During differential training, the birds were shown a trio of simultaneously presented stimuli and they had to select the target shape and to avoid both the MEM shape and the NAM shape. Each trial again began with the presentation of a black cross in the center of a white square in the center of a black screen. Following one peck at the white square, a trio of stimuli appeared for 5 s. The position of the target shape, the MEM shape, and the NAM shape was counterbalanced across trials. After 5 s elapsed, the bird had to respond once to one of the stimuli. After that response, the chosen stimulus stayed on the screen for 2 s while the other two stimuli disappeared; this procedure was designed to improve pigeons’ attention to the chosen stimulus. If the bird selected the target shape, then food reinforcement was delivered followed by an ITI ranging from 13 to 27 s. For four pigeons (Pigeon Consistent Group), every correct response was reinforced. For the other four pigeons (Pigeon Partial Group), the correct responses were reinforced with a probability of 0.5. We introduced a lower probability of reinforcement to reduce the speed of learning and to increase the number of confusion errors. For both groups, if the bird selected the incorrect stimulus, then the house light was turned off for 13–27 s and the trial was repeated until the correct choice was made.

A daily session comprised 10 blocks of 18 randomly presented and reinforced trials in the Pigeon Consistent Group and 5 blocks of 36 trials (18 reinforced and 18 nonreinforced trials, all randomly presented) in the Pigeon Partial Group, for a total of 180 trials. Training continued for 36 complete training sessions. Occasional incomplete sessions were not included in the data analysis.

5.4.2. Humans

Before the experiment, the human research participants were told that they would see three grayscale pictures on the screen and that they had to make a mouse response to the “correct” picture. They were also told that each correct response was awarded 1 point and that their goal was to acquire as many points as possible. These initial instructions did not refer to the comparison of the pictures or to their similarities. Unlike pigeons, people were not exposed to nondifferential training; instead, they proceeded directly to differential training.

A trial started with the presentation of a black cross in the center of the white square located in the center of the black screen. After a single mouse response to the white square, a trio of stimuli appeared for 2 s. The position of the target shape, the MEM shape, and the NAM shape was counterbalanced across trials. After 2 s elapsed, the participants had to respond once to one of the stimuli. After the response, the chosen stimulus stayed on the screen for 2 s while the other two stimuli disappeared.

If the target shape was selected, then the trial was reinforced with a probability of 0.5 (Human Partial Group). The total number of points was displayed at the bottom of the screen. If the response was correct and the trial was reinforced, then 1 point was added; otherwise, the participants proceeded to the next trial and no points were added. If the response was incorrect, then a low-tone sound was played and the trial was repeated until the correct choice was made. Every trial was followed by an ITI ranging from 2 to 6 s. The training session comprised 4 blocks of 36 trials (18 reinforced and 18 nonreinforced trials, all presented randomly), for a total of 144 trials.

The Human Partial Group learned the task quite quickly, averaging 92.2% correct across 144 training trials. Hence, there was no need to include a Human Consistent Group with a 1.0 probability of reinforcement, as their learning would surely have been even faster.

5.5. Behavioral measures

To analyze acquisition, we computed the number of choices of the target, the MEM, and the NAM shapes divided by the total number of choices during the session and multiplied by 100 to obtain the percentage of choices. We also computed the number of errors committed to the MEM shape divided by the total number of errors and multiplied that score by 100 to obtain the percentage of metric errors.

Unlike Experiment 1, Experiment 2 was expressly designed to eliminate alternative explanations by using stimuli that explicitly controlled for the degree of physical change. Specifically, the MEM shapes were just as different (or more different) from the target shape as were the NAM shapes. Under these circumstances, any preference for the MEM shape cannot be explained by higher physical similarity of the MEM shapes to the target shapes. This experimental approach eliminated the need for computing correlations between various metric measures and the percentage of metric errors, as was done in Experiment 1.

6. Results and discussion

6.1. Pigeons

Fig. 4 depicts the percentage of choices for the target shape, the MEM shape, and the NAM shape in the Pigeon Partial Group (top panel) and the Pigeon Consistent Group (bottom panel) throughout the 36 training sessions. In the Pigeon Partial Group, the percentage of choices for all three shapes initially began near chance (33%). As the pigeons began to learn the task, the percentage of choices for the target shapes increased and the percentage of choices for the NAM shapes decreased. Interestingly, pigeons continued selecting the MEM shapes even as the choices of the NAM shapes declined, indicating that they perceived the MEM shapes as being more similar to the target shapes than the NAM shapes.

Fig. 4.

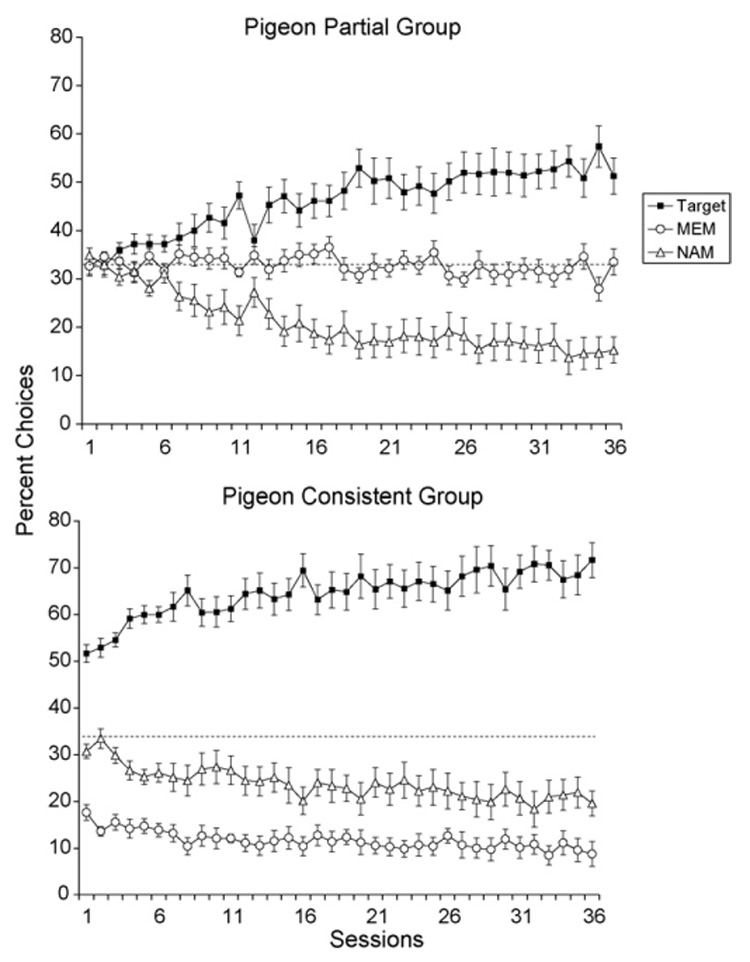
Percentage of choices of the target shape, the MEM shape, and the NAM shape measured over 36 discrimination training sessions. The top panel shows the data for the Pigeon Partial Group and the bottom panel shows the data for the Pigeon Consistent Group. The dashed line indicates chance discrimination performance (33%).

In contrast, the percentage of target shape choices in the Pigeon Consistent Group was well above chance in the very first session and it continued to rise as training proceeded. As well, pigeons in this group always committed more errors to the MEM shapes than to the NAM shapes, even though overall errors decreased to both shapes as training proceeded.

An ANOVA with Session (36), Group (2), and Trio (3) as fixed factors, with Bird (8) as a random factor, and with the percentage of choices for the target shape as the dependent variable confirmed these observations. The main effect of Group was significant, F(1, 6) = 7.45, p = 0.03, showing that the Pigeon Consistent Group chose the target shape more often than the Pigeon Partial Group. The main effect of Trio was significant as well, F(2, 642) = 640.9, p < 0.0001. A follow-up Tukey HSD test indicated that the percentage of target shape choices could be ordered: Trio 1 > Trio 2 > Trio 3. Although the Trio × Group interaction was significant, F(2, 642) = 25.17, p < 0.0001, a follow-up Tukey HSD test found that the above ordering, Trio 1 > Trio 2 > Trio 3, was true for both groups. Finally, the ANOVA found a significant Session × Trio interaction, F(70, 642) = 1.33, p = 0.04, indicating that the speed of learning for the three shapes differed. Specifically, Trio 1 showed the best target shape improvement (30.8% increase from Session 1 to Session 36), followed by Trio 2 (16.6% increase), and by Trio 3 (10.6% increase). No other interactions were significant.

Fig. 5 plots the percentage of metric errors across the 36 sessions for the Pigeon Partial Group and the Pigeon Consistent Group. In the Pigeon Consistent Group, the percentage of metric errors varied very little throughout the sessions (Session 1: 69.8%; Session 36: 66.3%). In contrast, the Pigeon Partial Group exhibited a noticeable increase in the percentage of metric errors as training proceeded. At the beginning of training, these birds showed no preference for the MEM shape (Session 1: 48.3%), but by the end of training they committed more errors to the MEM shape (Session 36: 69.5%). Interestingly, the Pigeon Consistent and Partial Groups responded similarly over the last half of training.

Fig. 5.

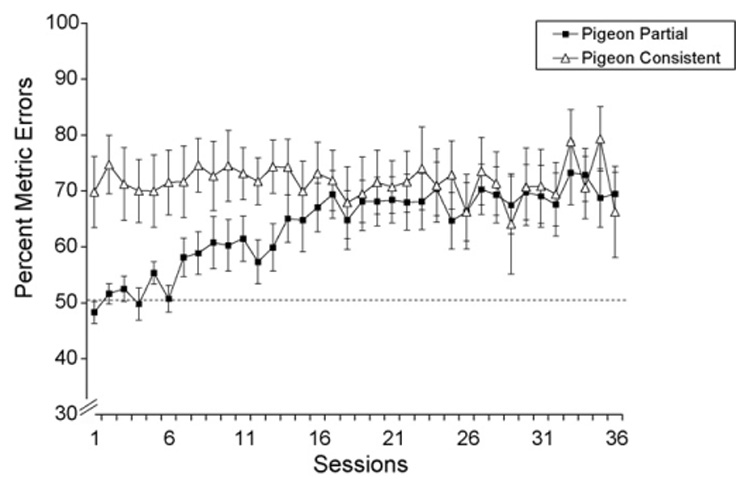
Percentage of metric errors measured over 36 discrimination training sessions for the Pigeon Consistent Group and the Pigeon Partial Group. The dashed line indicates chance discrimination performance (50%).

Table 4 shows the mean percentage of metric errors to each trio in the Pigeon Partial Group and the Pigeon Consistent Group. With only one exception, the birds committed more errors to the MEM shape than expected by chance. Note that Trio 3, with the lowest percentage of responses to the target shape (see above), also exhibited the lowest percentage of metric errors, which did not differ from chance for the Pigeon Partial Group.

Table 4.

Mean percentage of metric errors committed to the MEM shape by pigeons and people in Experiment 2

	Pigeons		Human Partial Group
	Partial group	Consistent group
Trio 1
M ± S.E.	68.8 ± 5.3	77.3 ± 7.4	77.3 ± 5.8
One-tailed t-test	3.56*	3.69*	4.69***
Trio 2
M ± S.E.	70.9 ± 3.7	82.1 ± 7.9	62.8 ± 7.2
One-tailed t-test	5.71**	4.02**	1.8*
Trio 3
M ± S.E.	51.6 ± 1.6	55.6 ± 2.0	65.2 ± 8.0
One-tailed t-test	0.99ns	2.78*	1.89*

^nsp>0.05

^*p<0.05

^**p<0.01

^***p<0.001

An ANOVA with Session, Group, and Trio as fixed factors, with Bird as a random factor, and with the percentage of metric errors as the dependent variable confirmed these observations. The main effect of Session was significant, F(35, 642) = 1.91, p = 0.002, indicating that the percentage of metric errors increased as training proceeded. The main effect of Trio was significant as well, F(2, 642) = 244.00, p < 0.0001. A follow-up Tukey HSD test found that the percentage of metric errors could be ordered: Trio 2 > Trio 1 > Trio 3. The main effect of Group failed to reach significance, F(1, 6) = 2.18, p = 0.19. But, the Trio × Group interaction was significant, F(2, 642) = 5.18, p = 0.006, suggesting a difference in the pattern of metric errors between the groups. Nonetheless, a follow-up Tukey HSD test found that the order of metric errors in two groups was quite similar: Trio 2 = Trio 1 > Trio 3 for the Pigeon Partial Group and Trio 2 > Trio 1 > Trio 3 for the Pigeon Consistent Group. Finally, the Session × Group interaction was significant, F(35, 642) = 1.88, p = 0.002, confirming the difference in the pattern of metric errors throughout sessions in two groups (cf. Fig. 5).

Overall, when trained to select the three target shapes, the pigeons committed more errors to the MEM shapes than to the NAM shapes, indicating that the birds viewed the MEM shapes as being more similar to the target shapes. Additionally, the birds committed more metric errors when they were able to discriminate the target shape more accurately (Trios 1 and 2 vs. Trio 3).

6.2. Humans

Table 4 shows the mean percentage of metric errors for each trio of shapes in the Human Partial Group. For each of the trios, people committed more errors to the MEM shape, suggesting that, just like pigeons, people perceived the MEM shape to be more similar to the target shape than to the NAM shape. Acquisition was so rapid that most of the errors were made in the first block of 36 trials; hence, we could not compare the percentage of metric errors in 4 training blocks. Although people selected the MEM shape more often in Trio 1 than in Trios 2 and 3 (Table 4), a one-way, repeated-measures ANOVA found no significant effect of Trio for the percentage of metric errors, F(1, 18) = 1.4, p = 0.27, or for the percentage of target choices, F(2, 18) = 0.31, p = 0.79.

7. General discussion

In two experiments, we found that pigeons’ confusion errors were more strongly affected by changes in the nonaccidental properties of the target shapes (e.g., change from a straight edge to a curved edge) than by changes in their metric properties (e.g., change in shape width). In Experiment 1, we found that pigeons made more errors to shapes that shared more nonaccidental properties. Because the nonaccidental changes in the images in this experiment were partially confounded with metric variations, it was difficult to distinguish the two types of changes.

Using much better controlled stimuli in Experiment 2, we found that pigeons trained to discriminate a target shape from MEM and NAM shapes committed more errors to the MEM shape, indicating that they perceived it to be more similar to the target shape than to the NAM shape. Human participants trained using similar stimuli and procedures exhibited the same tendency to make more errors to the MEM shapes, although the exact pattern of errors differed from that shown by pigeons.

In Experiment 2, we found that pigeons had the greatest difficulty discriminating the target shape from the foils in Trio 3 (see Fig. 3). At the same time, this trio produced the lowest percentage of metric errors (significantly different from chance only for the Pigeon Consistent Group, Table 4). This result is consistent with our analysis of the metric errors during acquisition of the task. As the birds became more proficient in selecting the target shape, the percentage of metric errors increased (Fig. 4 and Fig. 5). As Trio 3 was the most difficult discrimination to master, the percentage of metric errors for this trio was the lowest.

Why did the pigeons find Trio 3 so difficult? Note that in both Trio 1 and Trio 2, the nonaccidental change entailed a modification in cross-section where two straight edges were changed to two curved concave edges. In contrast, the nonaccidental change in Trio 3 entailed a change from one straight edge to one curved convex edge at the side of the shape; the cross-section was left intact. It is possible that the change in a side edge is less salient for pigeons than is the change in a cross-section edge; or, the change of two edges is more noticeable to pigeons than is the change of one edge; or perhaps a combination of both factors was involved. Because Experiment 2 used a small number of trios, we cannot arrive at a definitive conclusion at this time. Future research is needed to systematically examine the sensitivity of the avian visual system to different types of nonaccidental changes.

Alternatively, one might suggest that pigeons were using local differences in pixel energy to make their similarity judgments. Recall that our stimuli were controlled for the overall change in pixel energy. In order for this approach to be successful, the pigeons ought to attend to the entire object. But, if the pigeons were only attending to some part of the object, then the local differences in pixel energy may still provide a useful clue, at least for some trios. For example, in Trio 1, the NAM shape has a dark top band and a bright bottom band that is absent on both MEM shape and target shape. If the pigeons were selectively attending to these areas, then they might indeed view NAM shape as being more different from both MEM shape and target shape. However, the results of Gibson et al. (2007) suggests that pigeons discriminating three-dimensional, shaded shapes, attend more to the contours of these shapes than to their surface, suggesting that the local differences in pixel energy are unlikely to control pigeons’ behavior in our experiment.

Our data together with those of Gibson et al. (2007) suggest that the avian visual system uses the same working principles for object recognition as does the mammalian visual system despite clear anatomical differences. Both visual systems appear to be particularly attuned to nonaccidental properties of shapes, to detect any changes in these properties, and to utilize these properties for object recognition. We believe that this collective evidence confirms the ubiquitous nature of nonaccidental properties for object recognition by biological systems, regardless of their particular anatomical structure.

7.1. Concluding comments

It is appropriate here to acknowledge that some authors might question the validity of the present study and others like it which use highly controlled, stylized stimuli which our animals would rarely if ever encounter in their natural environment. These critics would insist that comparative behavioral research should focus on how animal perception and cognition function in nature, an approach which entails the use of stimuli and settings which come as close as possible as those found in the pigeon’s natural world (e.g., Shettleworth, 1993; Sturdy et al., 2007).

If this were the only goal of research in comparative cognition, then the criticism would be justified. But, many comparative researchers are also interested in establishing how perceptual and cognitive processes operate at the behavioral and neural levels as well as in the degree to which these perceptual and cognitive processes are similar in humans and animals. The search for general mechanisms of perception and cognition necessarily involves highly controlled and simplified stimuli which afford researchers the means of identifying the specific parts of organic systems that respond to different properties of these stimuli.

With respect to object recognition, extensive research demonstrates that the human visual system interprets some properties of edges in two-dimensional projection to the retina as an indication that the edges of three-dimensional objects in the real world have the same properties, and it does so because such an interpretation works for all but accidental viewpoints. A curved edge will produce a straight line in two-dimensional projection to the retina only when the curve is precisely perpendicular to the line of sight; from all other viewpoints, a curved edge will produce a curved line. The human visual system takes an advantage of these image regularities, and, as suggested by our data, so does the pigeon visual system. To explore the potential effect of these and similar features of visual stimuli on perception, one would need to employ simple visual stimuli that afford precise control over different properties of the edges.

Surely, there are limits to how far the information provided by simple stylized stimuli can be used to predict organisms’ reactions to more complex lifelike stimuli. In these cases, it will be necessary to use more elaborate and realistic stimuli to further our knowledge about the biological mechanisms of perception and cognition. We believe that neither the “naturalistic” approach nor the “laboratory” approach is superior; rather, both must be deployed in order to fully elucidate how animal cognition functions both inside and outside the laboratory.