Impact of temperature on cross-bridge cycling kinetics in rat myocardium

Abstract

The dependence of contractile properties on intracellular calcium in cardiac tissue is a highly cooperative process. Here, the temperature and calcium dependence of contractile and energetical properties in permeabilized cardiac trabeculae from rat were studied to provide novel insights into the underlying kinetic processes. Myofilament Ca²⁺ sensitivity significantly increased with temperature between 15 and 25°C, whereas its steepness was independent of temperature. A direct proportionality between active tension and Ca²⁺-activated rate of ATP hydrolysis was observed; the slope of this relationship (tension cost) was highly temperature dependent. The rate of tension redevelopment following a quick release–restretch manoeuvre (k_tr) depended in a complex manner on the level of contractile activation and on temperature. At saturating calcium levels, the temperature dependence (Q₁₀) of k_tr and Ca²⁺-activated ATP hydrolysis rate were similar (Q₁₀∼3.5), and significantly higher than the Q₁₀ for maximum tension (T_max; Q₁₀∼1.3) or tension cost (Q₁₀∼2.5). In contrast, at a low level of contractile activation (∼5% of T_max), the Q₁₀ of k_tr was similar to that of tension cost, and significantly lower than the Q₁₀ of Ca²⁺-activated ATP hydrolysis at that level of contractile activation. Our results are consistent with the hypothesis that at high levels of contractile activation, the rates of tension redevelopment and Ca²⁺-activated ATP hydrolysis are determined by both apparent cross-bridge attachment and detachment rates, while at low levels, k_tr is limited by cross-bridge detachment rate. Tension cost, on the other hand, is determined solely by cross-bridge detachment kinetics at all temperatures and levels of contractile activation.

The actin-activated myosin ATPase activity in solution has been determined to be highly temperature dependent (Barany, 1967; Siemankowski et al. 1985). In cardiac muscle, a Q₁₀ of 5 has been reported for rat cardiac muscle (Siemankowski et al. 1985) (Q₁₀ is the relative change in kinetics upon a 10°C temperature change). In intact muscle a similar temperature dependence of V_o, the maximal velocity of sarcomere shortening, has been reported (de Tombe & ter Keurs, 1990). This finding is consistent with the hypothesis that the rate-limiting for cross-bridge cycling in solution is identical to that during unloaded shortening in muscle (Barany, 1967; Siemankowski et al. 1985). However, information on the temperature dependence of the actin–myosin ATPase in cardiac muscle, that is, within the intact sarcomere lattice, is scarce. This also applies to the temperature dependence of isometric tension cost, the amount of ATP consumption in relation to isometric force development in cardiac tissue. The range of temperatures that apply to mammalian muscle in situ is narrow and usually well above that employed in isolated muscle studies. Nevertheless, knowledge of the temperature dependence of sarcomere function allows for extrapolation of experimental findings to muscle function at physiological temperatures in vivo.

Muscle contraction is initiated by a rise in cytosolic free calcium concentration, a process that is highly cooperative. The mechanisms that underlie the activation of the thin filament and the subsequent formation of actively cycling cross-bridges are incompletely understood (de Tombe & Solaro, 2000). The impact of temperature on cross-bridge cycling and thin filament dynamics is not expected, a priori, to be identical. Hence, temperature changes in vitro are useful to obtain information about the molecular transitions that take place during muscle contraction and, in particular, which of these steps may be rate limiting (Fujita & Kawai, 2002; Kawai, 2003; Campbell et al. 2004; Moss et al. 2004).

Accordingly, in the present study the impact of a change of temperature on myofilament function and its regulation by activating Ca²⁺ ions was examined. These results suggest that the kinetics of the cross-bridge are highly temperature dependent and are consistent with a model where Ca²⁺ activation of the thin filament regulates only the transition of weakly bound cross-bridges into a strongly attached force-generating state, but not the rate of cross-bridge detachment. Furthermore, our results indicate that at high levels of contractile activation, the rate of tension development and Ca²⁺-dependent ATP hydrolysis are determined by both apparent cross-bridge attachment and detachment rates, while at low levels, cross-bridge detachment is rate limiting for k_tr. Tension cost, on the other hand, is determined solely by cross-bridge detachment kinetics at all temperatures and all levels of contractile activation.

Methods

Preparation

Rats, 250–350 g in weight and of either sex, were administered pentobarbital (50 mg kg⁻¹i.p.) to achieve a deep plane of anaesthesia. Next, the hearts were rapidly excised. All procedures were in accordance with institutional guidelines and approved by the Animal Care and Use Committee. After excision, the heart was immediately perfused according to Langendorff with a Tyrode solution also containing 20 mm 2,3-butanedione monoxime (BDM) and placed in a dissection dish beneath a binocular microscope equipped with an ocular micrometer (∼10 μm resolution). Treatment with BDM has been shown to protect myocardium from cell contracture and muscle damage during dissection (Mulieri et al. 1989). Thin, unbranched and uniform trabeculae were carefully dissected from the free wall of the right ventricle. After dissection, the trabeculae were transferred to a dish containing cold standard relaxing solution to which 1% (v/v) Triton X 100 was added to chemically permeabilize the preparations. The composition of this standard relaxing solution was (mm): Na₂ATP 7.3, MgCl₂ 10.6, EGTA 20, phosphocreatine (PCr) 10, Bes 100; pH = 7.1, adjusted with KOH, ionic strength 200 mm (adjusted with KCI). The preparations were left in this solution for 2 h to allow solubilization of virtually all membranous structures. Next, a skinned trabecula was attached to aluminium T-clips (Goldman & Simmons, 1984) and mounted in the experimental set-up. To suppress any residual mitochondrial ATPase or ATP synthase activity, both sodium azide (5 mm) and oligomycin B (10 μm) were added to all solutions. Furthermore, it has been previously shown that addition of inhibitors of the sarcoplasmic reticulum calcium ATPase (such as cyclopiazonic acid) does not significantly affect the rate of ATP consumption at full contractile activation (Kentish & Stienen, 1994; Wannenburg et al. 1997). Hence, it appears that this potentially confounding enzyme activity is removed by the 2 h skinning procedure.

Experimental apparatus

The skinned preparation was attached to a displacement generator (Ling Dynamic Systems 101, Royston, UK) on one end, and to a force transducer element (AE 801, SensoNor, Norway) on the other end. The bath that was used for the ATPase assay allowed transmission of near-UV light for the measurement of NADH absorbance. The volume of this bath was 30 μl and was continuously stirred by motor-driven vibration of a membrane positioned at the bottom of the bath. The force and displacement generator position (i.e. muscle length) signals were filtered at 1 kHz (corner frequency, slope −12 dB octave⁻¹). The NADH absorbance signal was filtered at 2.5 Hz (corner frequency, slope −12 dB oct⁻¹). The data were recorded on a chart recorder and sampled via an A/D converter on computer disk. Samples were collected at a rate of 5 Hz for 5 min. In addition, force and muscle length signals were also collected at a higher sample rate (1 kHz for 0.5 s) during the rapid release–restretch steps (20% muscle length; 5–20 ms), applied to the muscle at the end of a contraction to measure apparent muscle stiffness and the rate of tension redevelopment (k_tr). Sarcomere length of the preparation was measured in relaxing solution by means of a He–Ne laser (Model 1125, Uniphase, San Jose, CA, USA).

Measurement of the ATPase activity

The ATPase activity of the skinned trabecula was measured on-line by means of an enzyme-coupled assay as previously described (Glyn & Sleep, 1985; de Tombe & Stienen, 1995). Formation of ADP by the muscle was stoichiometrically coupled first to the synthesis of pyruvate and ATP from phosphoenolpyruvate, a reaction that is catalysed by the enzyme pyruvate kinase, and subsequently to synthesis of lactate, a reaction that is catalysed by the enzyme lactate dehydrogenase and during which NADH is oxidized to NAD⁺. The breakdown of NADH was determined photometrically by measuring the absorbance of 340 nm near-UV light obtained from a 75 W xenon lamp that was projected through the bath just beneath the preparation. The first time derivative of this signal, which is proportional to the rate of ATP consumption in the assay bath, was determined off-line by linear regression of the sampled data using custom-designed software. A small decline in the absorbance signal in the absence of the muscle fibre in the bath, caused by an ATPase contamination in the LDH enzyme preparation and by photo bleaching of NADH, was subtracted off-line from the absorbance data throughout the recording period. After each recording in the assay bath, the NADH absorbance signal was calibrated by multiple injections of 0.50 nmol ADP (0.050 μl of 10 mm ADP solution) using a stepper motor controlled calibration pipette. Using this method, the standard error of the first time derivative of the NADH absorbance signal, determined during a period of 20 s, corresponded to about 0.1 pmol s⁻¹. Since the isometric ATPase activity during contractions at saturating calcium concentrations typically amounted to 25 pmol s⁻¹ (20°C), this translates to a signal-to-noise ratio of about 250 under these conditions. During contractions at submaximal activation or at 15°C, where the ATPase activity of the skinned trabecula was lower, a signal-to-noise ratio of at least 25 was achieved by appropriately increasing the time the preparation was activated so as to allow linear regression to be performed over a longer time period. Likewise, contractions that were performed at 25°C were performed over a shorter time period. Ca²⁺-activated ATPase activity was obtained by subtracting the basal ATPase rate (measured in relaxing solution, pCa 9) from the rate measured in activating solution.

Solutions

Three bathing solutions were used: a relaxing, a pre-activating solution with low calcium buffering capacity, and an activating solution. The composition of these solutions is summarized in Table 1. In addition, all solutions contained (mm): 0.9 NADH, 100 Bes, 5 sodium azide, 10 phosphoenolpyruvate (PEP), 0.2 P¹,P⁵-di(adenosine-5) pentaphosphate (A₂P₅), 1 leupeptin, 1 PMSF, as well as 4 mg ml⁻¹ pyruvate kinase (500 U mg⁻¹), 0.24 mg ml⁻¹ lactate dehydrogenase (870 U mg⁻¹), and 10 μm oligomycin B. The ionic strength of the solutions was kept at 200 mm by adding the appropriate amount of potassium propionate. The compositions were calculated using methods previously described (Fabiato & Fabiato, 1979). The free Mg²⁺ and MgATP concentration were calculated at 1 mm and 5 mm, respectively. To achieve a range of free calcium concentrations, one batch of activating and relaxing solutions were appropriately mixed assuming an apparent stability constants of the Ca–EGTA complex of 10^6.56, 10^6.57, and 10^6.59 at 15, 20 and 25°C, respectively. The pH of the solutions was adjusted to 7.1 at each temperature with KOH. All chemicals were of the highest purity available (Sigma Chemical Co., St Louis, MO, USA).

Table 1.

Ionic composition of the solutions

Solution	MgCl2	Na2ATP	EGTA	HDTA	CaEGTA	KProp
Relaxing	8.37	5.80	20	0	0	42.5
Pre-activating	7.78	5.80	0.5	19.5	0	43.6
Activating	7.63	5.87	0	0	20	43.6

Concentrations are shown in mm. Potassium propionate (KProp) was prepared by dissolving equimolar amounts of propionic acid with KOH. CaEGTA was made by dissolving equimolar amounts of CaCO₃ and EGTA followed by boiling of the solution to remove CO₂. At each temperature the pH of the solutions was adjusted to 7.1 with KOH.

Experimental protocol

The protocol consisted of three series of measurements: a first series under control conditions (20°C), followed by a second and third series at 15°C and 25°C, respectively. During each series of measurements, the muscle was incubated in the relaxing solution for 4 min, in the pre-activating solution for 3 min, in the activating solution for about 2 min, and then back into the relaxing solution. Preliminary experiments suggested that prolonged exposure of the skinned muscle to 25°C accelerated tension rundown of the preparation. Therefore, temperature was varied only in the measurement chamber; the relaxing and pre-activating solutions were kept at 20°C (Pate et al. 1995). Before the first activation–relaxation cycle, sarcomere length in the preparation measured in relaxing solution was adjusted to 2.2–2.3 μm. Then, following a first activation at saturating calcium concentration (∼50 μm free [Ca²⁺]; pCa = 4.3) sarcomere length was readjusted to 2.2–2.3 μm, if necessary. It was found that after this readjustment, resting sarcomere length remained stable throughout the experiment. Next, a second activation at the saturating [Ca²⁺] was performed which served as a first tension and ATP consumption rate reference. The next five to six contractures were carried out at a range of intermediate [Ca²⁺] that also included the relaxing solution (pCa = 9). These measurements were then followed by a final control contracture at saturating [Ca²⁺]. In each contracture, after active tension had become stable and after sufficient data were collected to allow reliable calculation of the rate of ATP consumption, k_tr was estimated by a quick (∼1 ms) release of 20% muscle length for 20 ms (15°C), 10 ms (20°C), or 5 ms (25°C) followed by a quick restretch to the starting muscle length. Inbetween the series of contractions at the three temperatures, an activation at the saturating [Ca²⁺] was performed at 20°C to assess rundown of the preparation.

Data processing and statistical analysis

During the course of the experiment steady-state tension deteriorated to same extent in all muscle preparations, as judged by the control contractures at saturating [Ca²⁺] at 20°C that bracketed each series of measurements; this phenomenon has been observed previously (de Tombe & Stienen, 1995; Wannenburg et al. 1997). The amount of this decline was rather small; the average deterioration was 13.1 ± 3.8% for the entire study protocol (i.e. 15, 20 and 25°C). Nevertheless, this phenomenon could obscure the effect of temperature on the calcium sensitivity (EC₅₀) or maximum tension (T_max) parameter. Therefore, the steady-state tension data were corrected in each individual trabecula assuming that the deterioration was a contraction-related phenomenon, i.e. that a similar amount of deterioration occurred with each contraction as previously described (de Tombe & Stienen, 1995). To calculate tension cost (the amount of ATP consumed for a given level of tension development), steady-state tension was not corrected for the slight deterioration during the experiment as described above, since steady-state tension and the rate of ATP consumption decreased proportionally during the course of the experiment (de Tombe & Stienen, 1995). Sigmoidal relationships were fitted to a modified Hill equation (de Tombe & Stienen, 1995; Wannenburg et al. 1997):

(1)

where P(Ca²⁺) represents the Ca²⁺-dependent parameter of interest, P_max is the maximum value of P, EC₅₀ the [Ca²⁺] at which P is 50% of P_max (a compound index of Ca²⁺ sensitivity), and n_H the Hill cooeficient (an index of the level of cooperativity). The fit parameters that resulted from this non-linear fit for the three series were next subjected to one-way ANOVA, i.e. the fit parameters were treated statistically as if they were obtained by direct measurement (Motulsky & Ransnas, 1987). The average impact of temperature on the various parameters was estimated by non-linear regression of the Arrhenius relationship ([parameter = constant × exp(−ΔA/RT)] where T is temperature in K, R is the Boltzman constant; ΔA is the activation energy) in each individual muscle preparation. The Q₁₀ of the parameters was calculated from ΔA over the range from 15°C to 25°C. Commercially available software was used for all statistical analyses (SYSTAT, Evanston, IL, USA); KaleidaGraph (Synergy Software, Reading, PA, USA) was used for non-linear curve fitting. Data are presented as means ±s.e.m.; P < 0.05 was considered significant.

Results

Isometric tension and ATP consumption

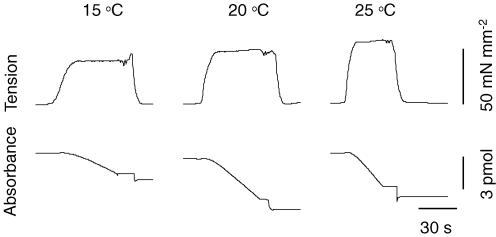
Recordings of isometric tension and the rate of ATP consumption obtained at 15, 20 and 25°C are shown in Fig. 1. This figure illustrates that the maximum isometric tension reached at saturating Ca²⁺ concentration increases slightly (1.4-fold) when temperature was increased from 15 to 25°C, whereas the increase in the maximum rate of ATP consumption was considerably larger (3.4-fold). The basal ATPase rate measured in relaxing solution amounted to 12.6 ± 3.0, 21.4 ± 2.3 and 28.3 ± 2.8 pmol s⁻¹ mm⁻³ at 15, 20 and 25°C, respectively.

Figure 1. Original recordings of isometric tension development (top) and NADH absorbance (bottom) at the experimental temperatures indicated.

Upon incubation of the preparation into activating solution containing a saturating Ca²⁺ concentration, tension started to increase until a steady level was reached. During this phase, NADH absorbance started to decline; its final slope reflects the rate of ATP hydrolysis. During the final period of steady activation, stirring of the solution was stopped to reduce noise in the force signal during the measurement of k_tr. After transfer of the preparation back into the relaxing solution, tension and NADH consumption returned to the baseline levels.

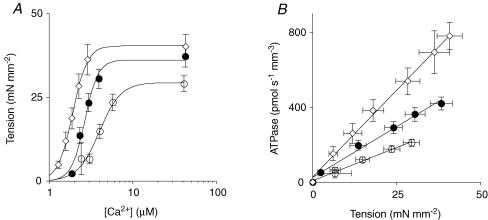
At each of the experimental temperatures the free Ca²⁺ concentrations in the activating solutions were varied in order to study the Ca²⁺ dependences of tension and ATPase. The calcium dependence of isometric tension shown in Fig. 2A indicates that tension at a given Ca²⁺ concentration increases with temperature not only because of the increase in the maximum tension generating capacity but also because of an increase in myofilament Ca²⁺ sensitivity. This increase in Ca²⁺ sensitivity is reflected in the decrease in EC₅₀ from 5.2 ± 0.4 μm at 15°C to 2.7 ± 0.1 μm at 25°C. The Hill coefficient, a measure of the steepness of the tension–Ca²⁺ relationship, was similar at the different temperatures studied.

Figure 2. Temperature dependence of the tension–Ca²⁺ relationship (A) and the ATPase–tension relationship (B).

In A, mean values are shown obtained at the different Ca²⁺ concentrations, while in B, data were averaged in various tension ranges (binned data). The ATPase activity in B was normalized to fibre volume; the slope reflects tension cost. ^, 15°C; •, 20°C; ⋄, 25°C. Averaged fit results are summarized in Table 1.

At each temperature, the Ca²⁺-activated ATPase rate varied in proportion with tension at different free Ca²⁺ concentrations (Fig. 2B). This indicates that the Ca²⁺-activated ATPase rate divided by tension, i.e. tension cost, was independent of the free Ca²⁺ concentration. On average, tension cost increased 2.5-fold when temperature was increased from 15 to 25°C.

k_tr measurements

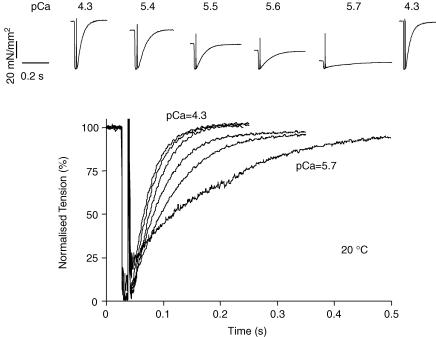
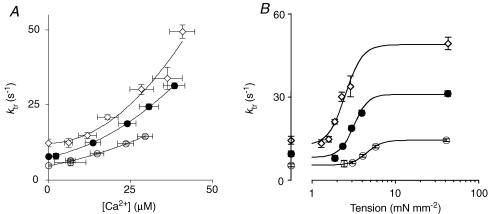
Figure 3 illustrates the k_tr measurements performed at different Ca²⁺ concentrations. Recovery of tension towards the isometric level was fitted to a single exponential, yielding the rate constant k_tr. k_tr depended on free Ca²⁺ concentration in a temperature-dependent manner (Fig. 4). Plotted as a function of the steady-state tension reached at each Ca²⁺ concentration, the relationships obtained were curvilinear, approaching a finite value at very low Ca²⁺ activation levels. The average extrapolated values at zero tension are shown in Fig. 4B on the ordinate. Maximum k_tr increased 3.3-fold when temperature was increased from 15 to 25°C, while minimum k_tr increased 2.4-fold over the same temperature range. In contrast, the temperature dependence of ATPase activity was similar at maximum activation (3.4-fold) and at 5% tension activation (3.3-fold). These results suggest that k_tr at low levels of activation is rate limited by the same processes that control tension cost, most probably the rate of cross-bridge detachment.

Figure 3. Measurement of K_tr.

Top panel: original recordings of tension during a 20% quick release–restretch manoeuvre at different free Ca²⁺ concentrations as indicated by the pCa values (−log[Ca²⁺]). Tension redevelopment after the restretch, 10 ms after the release step, started from values close to the baseline tension level. Bottom panel: data from the top panel is shown as normalized tension; the rate of force redevelopment is significantly reduced at low [Ca²⁺]. The recovery of tension towards the isometric level was fitted to a single exponential, yielding the rate constant k_tr.

Figure 4. Temperature dependence of the k_tr–[Ca²⁺] relationship (A) and the k_tr–tension relationship (B).

In A, the relationship between tension and k_tr was curvilinear at all three temperatures; exponential fits of these data allowed for the determination of an extrapolated value of k_tr at zero tension (k_tr−min); this parameter is indicated on the y-axis in B. ^, 15°C; •, 20°C; ⋄, 25°C.

The average tension, Hill fit parameters, maximum and 5% activation ATPase, as well as maximum and minimum k_tr, values obtained in the eight preparations studied at the three temperatures are summarized in Table 2. In addition, this table also provides an overview of the activation energies and the Q₁₀ values derived from these experiments.

Table 2.

Average impact of temperature on cross-bridge dynamics parameters

Parameter	15°C	20°C	25°C	ΔA	Q10
Tmax (mN·mm−2)	29.1 ± 2.3	37.2 ± 3.1	40.2 ± 3.6	22.8 ± 2.4	1.4 ± 0.1
Hill coefficient	5.4 ± 0.7	5.5 ± 0.4	5.7 ± 0.5	4.8 ± 1.9	1.0 ± 0.1
EC50 (μm)	5.2 ± 0.4	3.8 ± 0.2	2.7 ± 0.1	−55.1 ± 2.3	0.5 ± 0.1
Amax (pmol s−1 mm−3)	207 ± 19	408 ± 33	772 ± 70	87.5 ± 2.3	3.4 ± 0.1
Tension cost (pmol s−1 mm−3)	6.3 ± 0.6	9.9 ± 1.0	17.8 ± 1.4	65.7 ± 4.1	2.5 ± 0.1
ktr−max (s−1)	14.5 ± 0.5	31.4 ± 1.0	49.4 ± 2.2	85.3 ± 3.8	3.3 ± 0.2
ktr−min (s−1)	5.4 ± 0.5	9.5 ± 1.0	14.4 ± 1.4	56.8 ± 5.0	2.4 ± 0.1
ATPase–5% tension (pmol·s−1·mm−3)	10.0 ± 0.9	20.4 ± 1.7	36.9 ± 3.4	84.4 ± 3.1	3.3 ± 0.1

Tension–[Ca²⁺] relationships were fitted to a modified Hill equation that yielded the parameters (mean ±s.e.m.; n= 8): maximum, Ca²⁺ saturated tension development (T_max), Hill coefficient, and calcium sensitivity (EC₅₀). The maximum rates of Ca²⁺-activated ATP hydrolysis (A_max) and k_tr−max were measured at saturating Ca²⁺ concentration. Tension cost was calculated from the slope of the ATPase–tension relationship obtained over a wide range of activator [Ca²⁺]. Rate of tension redevelopment (k_tr) was estimated from a single mono-exponential fit of the tension data following a rapid release–restretch manoeuvre. ATPase–5% tension and k_tr−min were estimated from their relationships as a function of Ca²⁺-activated tension at each temperature. Temperature dependence is indicated as the activation energy (ΔA in kJ mol⁻¹ K⁻¹) obtained by non-linear regression of the Arrhenius plot and as Q₁₀ (the relative increase with a 10°C temperature increase) between 15°C and 25°C. All parameters varied significantly with temperature (P < 0.05), except the Hill coefficient.

Discussion

Our results show that maximum tension and the cooperativity of the activation process are slightly affected by temperature, while myofilament Ca²⁺ sensitivity and cross-bridge cycle kinetics parameters are highly temperature dependent. The main advantage of the current study resides in the simultaneous measurement of a number of different myofilament activation parameters, thereby allowing probing of various rate-limiting steps in the activation and contraction process. The current study revealed that rate of force redevelopment (k_tr) at low levels of Ca²⁺ activation most probably reflects the rate of cross-bridge detachment.

Comparison with previous studies

The activation of contraction in rat cardiac tissue is a highly cooperative process as is reflected in the high value of the Hill coefficient in this study (approximately 5.5 at all temperatures studied) as well as in previous studies (Dobesh et al. 2002). To date, there have been few studies of the temperature dependence of cardiac myofilament function. Our present force–[Ca²⁺] results in the rat (Fig. 2) are consistent with a previous study in rabbit myocardium by Harrison and Bers (Harrison & Bers, 1989), who also showed a significant increase in myofilament calcium sensitivity but a modest impact of temperature on maximum force upon an increase in temperature. Interestingly, the impact of temperature on maximum force development is even further reduced when the regulatory proteins troponin and tropomyosin are removed from the sarcomere by gelsolin treatment (Fujita & Kawai, 2002).

A recent follow-up study by this group has shown that this is caused, in part, by modulation of the number of myosin heads interacting with the thin filament, rather than a direct effect of temperature on the force developed by an attached cross-bridge (Kawai et al. 2006). To our knowledge, this is the first study to investigate the impact of temperature on the rate of ATP hydrolysis and tension cost in cardiac tissue. Our data indicate that these parameters are strongly influenced by temperature, consistent with previous results on proteins in solution (Barany, 1967; Siemankowski et al. 1985). A similar conclusion has also been obtained by others in skinned muscle employing either sinusoidal length perturbation analysis (Kawai, 2003; Kawai et al. 2006; Lu et al. 2006) or quick temperature jumps (Ranatunga & Wylie, 1983). Likewise, there have some reports that indicate a large temperature dependence of the rate of force redevelopment, k_tr, in skinned myocardium, consistent with the present study (Hancock et al. 1996).

Regulation of myofilament contractility

A key finding in our study is that the temperature coefficient (Q₁₀) of k_tr at low levels of activation (2.4 ± 0.1) is very similar to the temperature coefficient of tension cost (2.5 ± 0.1). In addition, it was found that k_tr declined with the level of activation in a temperature-dependent manner and that the Q₁₀ of ATPase activity was quite insensitive to the level of activation. These findings may be interpreted in a two-state cross-bridge model in which f denotes the overall rate constant of the transitions from the non-force-generating state to the force-generating states and g the rate of the reverse transition. In this model, tension is proportional to f/(f + g), ATPase proportional to f · g/(f + g), tension cost proportional to g and k_tr equals f + g. The correspondence between the temperature coefficients of tension cost and k_tr at low levels of activity is consistent with the notion that k_tr at low levels of activation reflects the cross-bridge detachment rate g (Brenner & Eisenberg, 1986; Tesi et al. 2002; Poggesi et al. 2005; de Tombe et al. 2007). The observation that tension cost was independent of the level of Ca²⁺ activation indicates that the cross-bridge detachment rate g is independent of the level of myofilament activation. This notion is consistent with results obtained in single myofibrils where the level of Ca²⁺ activation was varied by rapid solution switching (Tesi et al. 2002; Poggesi et al. 2005).

The curvilinearity of k_tr (equal to f + g) with Ca²⁺ concentration implicates that the apparent cross-bridge attachment rate f increases with the level of activation, as a result of Ca²⁺ binding to the troponin complex. Interestingly, k_tr at saturating Ca²⁺ concentrations had a higher Q₁₀ than the cross-bridge detachment rate g, indicating that the maximum apparent attachment rate (f_max) is more sensitive to temperature than the rate g. This also explains the progressive increase in k_tr as a function of tension with an increase in temperature.

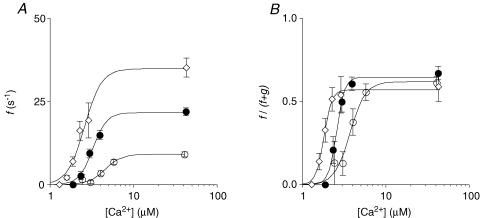
Within this framework, our measurements provide estimates of the apparent cross-bridge detachment rate g (which equals k_tr−min), the maximum rate of apparent cross-bridge attachment (f_max), and the maximum fraction of attached cross-bridges. In addition, the Hill parameter, i.e. the Ca²⁺ sensitivity of force can be predicted from the values of f and g at all levels of Ca²⁺ activation. Using these model parameters, the predicted relationship between [Ca²⁺] and the apparent attachment rate f (Fig. 5A) and fraction of attached cross-bridges (f/(f + g) (Fig. 5B) can be derived. The average calculated parameters, as well as the Hill parameters obtained in all preparations studied, are summarized in Table 3. It follows from the calculations that ∼60% of the participating myosin heads are attached to actin at maximum activation, and that this fraction is rather independent of temperature. This result is further supported by the observation that stiffness, estimated from 1 kHz sinusoidal muscle length oscillations (results not shown) – a measure of the amount of attached cross-bridges – was rather insensitive to temperature.

Figure 5. Two state cross-bridge model prediction of the relationships between activating [Ca²⁺] and the apparent forward rate of cross-bridge attachment f (A) and the fraction of attached cross-bridges f/(f + g) (B).

^, 15°C; •, 20°C; ⋄, 25°C.

Table 3.

Estimated rates of cross-bridge dynamics and predicted Ca²⁺ sensitivity of force

Parameter	15°C	20°C	25°C	ΔA (kJ mol−1 K−1)	Q10
g(s−1) (=ktr−min)*	5.4 ± 0.5	9.5 ± 1.0	14.4 ± 1.4	56.8 ± 5.0	2.4 ± 0.1
fmax (s−1)*	9.1 ± 0.7	21.7 ± 1.2	35.0 ± 2.8	79.8 ± 6.4	3.1 ± 0.3
EC50 of f/f + g (μm)*	4.3 ± 0.4	3.3 ± 0.2	2.7 ± 0.3	−34.8 ± 6.4	0.63 ± 0.06
Hill coefficient of f/(f + g)	7.5 ± 1.2	7.7 ± 1.0	8.0 ± 0.9	2 ± 7	1.1 ± 0.1
Fraction attached cross-bridges (=f/(f + g))	0.61 ± 0.04	0.67 ± 0.04	0.59 ± 0.09	−9 ± 4	1.1 ± 0.1
No(μm)	68 ± 9	69 ± 9	82 ± 12	16 ± 7.8	1.3 ± 0.1
R (=No/150 μm)	0.40 ± 0.08	0.46 ± 0.06	0.55 ± 0.08	16 ± 7.8	1.3 ± 0.1

k_tr at a nominal low level of Ca²⁺ activation is assumed to approximate the Ca²⁺-independent cross-bridge detachment rate g. The rate of cross-bridge attachment was calculated from k_tr and g at each [Ca²⁺]. A simple 2-state cross-bridge model described in the text predicts the fraction of attached cross-bridges f/(f + g) and its apparent Ca²⁺ sensitivity (cf. Fig. 5). The maximum ATPase activity (A_max) allows for the calculation of the concentration of cycling cross-bridges (N_o= (f + g)A_max/(gf)) and the fraction of myosin heads participating in the cross-bridge cycle (R) assuming a total myosin concentration of 150 μm.

^*P < 0.05 impact of temperature.

The ATPase activity and the rates f and g allow calculation of the fraction of the myosin molecules that participate in the cross-bridge cycle, i.e. cross-bridge recruitment (R). Assuming that concentration of myosin heads in the cardiac sarcomere corresponds to 0.15 mm (Barsotti & Ferenczi, 1988), our results indicate that this fraction amounts to approximately 50% at the temperatures studied (Table 3). This fraction was rather insensitive to temperature, and also did not vary significantly with the level of Ca²⁺ activation (results not shown). Cross-bridge recruitment might be less than the available amount because of geometrical constraints such as mismatch of the periodicity of the thin and thick filament. Alternatively, a cross-bridge recruitment of 50% of myosin heads present in the sarcomere could also reflect a limitation of the independent role of each globular domain in the dimeric myosin molecule, such that only one of the myosin heads can attach to actin at a given time.

A wide range of values for the fraction of attached cross-bridges are available in the literature, ranging from values around 50–75% from equatorial X-ray diffraction studies and stiffness measurements (Goldman & Simmons, 1977; Higuchi et al. 1995), ∼26% for stereo-specific binding of myosin to actin (Bershitsky et al. 1997) and values of approximately 12% from cross-bridge orientation studies using fluorescently labelled probes (Hopkins et al. 1998). Our values in rat cardiac muscle range between 40 and 55% and are consistent with the values derived from X-ray diffraction and stiffness measurements in rabbit and frog skeletal muscle. The values of the maximum isometric tension (T_max) and ATPase activity (A_max) and k_tr−min (=g) at each temperature can be used to calculate the force per attached cross-bridge (F_cb) within each half sarcomere (hs; 1.1 μm): F_cb=T_max·g/(A_max· hs ·N_A), where N_A equals Avogadro's number (6.10²³ mol⁻¹). The values for F_cb obtained amount to 1.3 ± 0.2, 1.2 ± 0.2 and 1.1 ± 0.2 pN at 15, 20 and 25°C, respectively, and do not vary significantly with temperature. These values correspond very well with those found using an in vitro motility assay (Kawai et al. 2006). It should be noted that the 2-state model used here does not explicitly include the Ca²⁺ activation of the thin filament and loose coupling to cross-bridge cycling (Landesberg & Sideman, 1994; Rice & de Tombe, 2004). However, such an extensive model is beyond the scope of the present study. Nevertheless, the simple two-state model predicts many features of cardiac muscle activation, including the dependence of k_tr on contractile activation and the apparent rate of cross-bridge activation, as reflected by the lumped kinetic parameter f (Brenner & Eisenberg, 1986; Landesberg & Sideman, 1994; Geerdink & de Tombe, 1996). Finally, the fraction of attached cross-bridges and the recruitment parameter R are calculated at maximum activation, a condition at which Ca²⁺ binding to troponin is saturated.

Implications for the activation process

Our results revealed that Ca²⁺ sensitivity increased with temperature but that the steepness of the tension–Ca²⁺ relationship remained the same. The EC₅₀ values and the Hill coefficient of the Ca²⁺ sensitivity curve predicted on the basis of the estimated rates of cross-bridge attachment and detachment (Table 3; Fig. 5B) were in good agreement with the parameter values derived from the measured Ca²⁺–force relationships. This indicates that the increase in Ca²⁺ sensitivity of force with temperature is largely determined by the temperature dependence of cross-bridge kinetics. Furthermore, the rate of tension redevelopment at low levels of contractile activation is limited by the rate of cross-bridge detachment, as is tension cost.