Mechanical and neural contributions to hysteresis in the cardiac vagal limb of the arterial baroreflex

Abstract

According to conventional wisdom, hysteresis in cardiac vagal baroreflex function exhibits a specific pattern: pressure falls are associated with longer heart periods and a smaller linear gain. A similar pattern occurs in the pressure–diameter relationship of barosensory vessels, and therefore it has been suggested that baroreflex hysteresis derives solely from vascular behaviour. However, we hypothesized that mechanical and neural baroreflex components contribute equally to baroreflex hysteresis. Blood pressure, carotid diameter and the electrocardiogram were recorded continuously during two trials of sequential bolus injections of nitroprusside and phenylephrine in 14 young healthy subjects. Baroreflex gain and its mechanical and neural components were estimated for falls and rises in pressure and diameter. The position or set point of the relations was quantified at the mean pressure and mean diameter. Gains were determined via piecewise linear regression. Set points and gains for falls versus rises in pressure and diameter were compared with the Chow test. Hysteresis was observed in all individuals, but not in every trial. In most, but not all, trials pressure falls were associated with longer heart periods and smaller linear gain, as conventional wisdom would predict. However, the pattern of hysteresis derived from the interaction of both mechanical and neural components. The two components most often acted in opposition to determine differences in set point, but in conjunction to determine differences in baroreflex gain. Therefore, we conclude that hysteresis is not solely determined by barosensory vessel behaviour but by the complex interaction of mechanical and neural aspects of the arterial baroreflex.

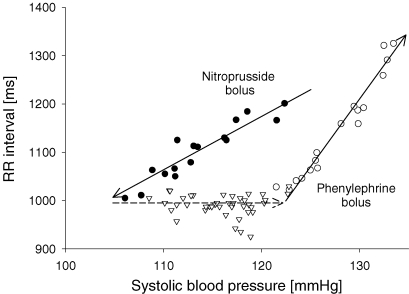
Cardiac vagal baroreflex function is most often characterized by its gain, calculated from the linear portion of the sigmoid relationship between blood pressure and heart period. This simple relation, however, neglects important differences in baroreflex mediated responses that depend upon the direction of blood pressure change. There exists a different relation for falling versus rising pressures that creates an elliptical pattern between blood pressure and heart period that has been termed baroreflex hysteresis (Eckberg & Sleight, 1992). This apparently intrinsic feature of human baroreflex function is a peculiar pattern such that at identical pressures heart period is longer with falling than rising pressure, and across the range of pressures, linear gain is lower with falling than rising pressure (Fig. 1). Thus, according to the conventional wisdom, hysteresis refers to a qualitative difference defined as a change in the position (set point) of the pressure–heart period relation and a quantitative difference defined as a change in baroreflex gain.

Figure 1.

Typical baroreflex hysteresis pattern observed after sequential bolus injections of nitroprusside and phenylephrine Filled circles and continuous arrow pointing downwards represent the linear relation in the pressure–RR interval relationship for pressure fall. Open triangles and dashed arrow represent baroreflex resetting between pressure fall and rise. Open circles and continuous arrow pointing upwards represent the linear relation in the pressure–RR interval relationship for pressure rise.

It has been proposed that the pattern of baroreflex hysteresis derives from the viscoelastic nature of compliant barosensory vessels (Bonyhay et al. 1997; O'Leary et al. 2005). For example, within a pulse interval, carotid artery diameters are larger at any given pressure when pressure is falling than when pressure is rising (Lénárd et al. 2000). If greater barosensory vessel diameters across falling versus rising pressures generate proportional cardiac vagal outflows, this would generate longer RR intervals during falls and hence a higher set point. Moreover, this would indicate that the vagal response is dependent upon both direction of pressure change and absolute level of pressure. In addition, data suggest that the carotid artery pressure–diameter relationship has a less steep slope for pressure falls than for pressure rises, possibly explaining the lower baroreflex gain with falling pressure.

However, barosensory vessel mechanics may not be the sole mechanism for baroreflex hysteresis. Inferential evidence suggests that neural aspects of the arterial baroreflex may contribute to this characteristic pattern of response. For example, in order for set point to be lower when pressure rises, baroreflex hysteresis must encompass a shift to higher pressures without significant RR interval response. If this occurred solely due to vascular behaviour, then it would suggest that in the low pressure range the carotid artery is non-responsive to the pressure increase. Reasons for this non-responsiveness may be that the vessel is either unstressed throughout this low pressure range or behaving as a rigid tube. However, neither explanation is completely reasonable. The carotid artery should not be in an unstressed condition within a range of physiological systolic pressures and carotid artery distensibility is actually greater, not lesser at low pressures (Myers et al. 2002). Therefore, it seems reasonable that at least the change in baroreflex set point between pressure fall and pressure rise may be of neural origin.

In the current study, we characterized baroreflex hysteresis by comparing baroreflex set point and gain with falling versus rising pressures. Our goal was to determine whether mechanical transduction of pressure into carotid diameter can fully explain baroreflex hysteresis. We hypothesized that it could not, that neural transduction of carotid diameter into RR interval contributes to hysteresis, and that neural resetting is at least partially responsible for this pattern of baroreflex response.

Methods

Subjects

Fourteen healthy young (aged 25 ± 3 year, 6 women) volunteers participated in the study. All subjects were non-smokers, non-obese (BMI < 26 kg m⁻²), normotensive (resting blood pressure < 140/90 mmHg), and free of overt autonomic or cardiovascular disease. Women were non-pregnant, not on oral contraceptives and not on hormone replacement therapy. All subjects gave written informed consent prior to participation. The study conformed to the standards set by the Declaration of Helsinki and all procedures were approved by the local ethics committee.

Measurements

Standard three-lead electrocardiogram and arterial blood pressure via finger photoplethysmography (Finapres, Ohmeda, Louisville, CO, USA) were recorded continuously throughout the study. During baroreflex testing, ultrasound images of the common carotid artery ∼1.5 cm proximal to the bifurcation were obtained using a 7.5 MHz linear array transducer (Hewlett-Packard, Andover, MA, USA) and a commercially available data acquisition system (DT-3152 Frame Grabber, Data Translation, Andover, MA, USA; CVI Acquisition, Information Integrity, Maynard, MA, USA).

Protocol

All subjects were studied in the morning after overnight fasting and at least 24 h after refraining from strenuous exercise and consumption of caffeine or alcohol. After instrumentation, resting heart rate and blood pressure were monitored for ∼10 min in the supine position. Subsequently baroreflex function was tested via two trials of the modified Oxford method, using sequential bolus injections of 100 μg sodium nitroprusside followed 60 s later by 150 μg phenylephrine hydrochloride (Hunt et al. 2001). This approach allows the characterization of baroreflex responses to falling and rising pressures in one cycle. At least 10 min of recovery was allowed between the two trials.

Data analysis

Time series of systolic blood pressure and RR interval were derived using signal processing software (WINDAQ, Dataq Instruments, Akron, OH, USA). Systolic blood pressure was derived from the maximum of the pressure waveform and RR intervals were derived from the time difference between peaks of the R waves. Systolic carotid artery diameters were obtained via image analysis software developed in our laboratory (Hunt et al. 2001).

Baroreflex function

Baroreflex function was estimated from the relation of systolic pressure to RR interval. For pressure fall, analysis began at the onset of pressure decrease after the bolus injection of nitroprusside and ended when pressure reached its nadir. For pressure rise, analysis began at the lowest pressure value after the bolus injection of phenylephrine and ended when pressure peaked. This selection of data points often encompasses threshold and saturation regions of the sigmoid relationship. Our aim, however, was to determine linear gain with the exclusion of these regions. Previously, exclusion of data points was performed by subjective visual inspection of data averaged across 2–3 mmHg pressure increments (Rudas et al. 1999; Hunt et al. 2001). To make the analysis objective and therefore independent of investigator bias, we analysed the data via piecewise linear regression (Neter et al. 1989; Draper & Smith, 1998). Our piecewise model required at least five data points to define the presence of threshold and/or saturation (if any). We therefore used raw data points instead of averaged ones. For details on this procedure, see the Appendix.

To gain further insight to baroreflex function, the mechanical and neural components of the baroreflex were calculated. The mechanical transduction of pressure was assessed from the relation of carotid diameter to arterial pressure, and the neural transduction of stretch was assessed from the relation of RR interval to carotid diameter (Hunt et al. 2001). The linear portion of these relationships was extracted with the application of the piecewise test indicated above. Threshold and saturation regions were excluded from a given relation (e.g. RR interval to pressure) without considering where these regions lie in the other two relations (e.g. diameter to pressure and RR interval to diameter). Whenever the model was not a simple linear regression for all relations, and threshold or saturation regions differed in length, the linear gain for the three relations encompassed different, but overlapping, subsets of data. This approach allowed the independent determination of baroreflex gain and its components without the consideration of any a priori mathematical relation between them (Kaushal & Taylor, 2002).

Statistics

The linear portions of the relations encompassing falls and rises were compared using the Chow test. This test is also referred as a test of structural change or as an F-test for comparing regression functions (Chow, 1960; Neter et al. 1989). The test estimates both a restricted and unrestricted model and then compares the residual sums of squares from the two models. This enables the assessment of differences in the set point and gain of two relations. Values represented on the x-axis were centred to the mean to compare set point at the mean × value of the relations. Thus, the presence and nature of hysteresis within a given baroreflex trial was defined as statistically significant differences in set point, gain or both between the falling and rising phases of baroreflex engagement. Differences at P < 0.05 were determined for the integrated baroreflex (ms mmHg⁻¹) and for its mechanical (μm mmHg⁻¹) and neural (ms mm⁻¹) components.

Results

Baroreflex gain averaged 20.3 ± 11.9 ms mmHg⁻¹ (range: 5.6–44.5) for falling pressure and 20.3 ± 7.2 ms mmHg⁻¹ (range: 7.8–34.4) for rising pressure. Despite the lack of significant differences between the group averages, baroreflex hysteresis was observed in every individual; it was present in both trials in eight subjects and in one trial in six subjects. Of the eight subjects with hysteresis in both trials, only five showed the same pattern in both trials with regard to differences in set point and gain.

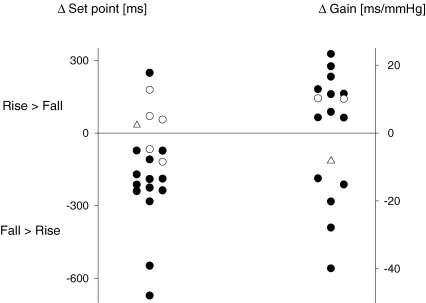
Across the 22 baroreflex trials with hysteresis, both set point and gain differed in 14 trials, only set point differed in five trials, and only gain differed in two trials (Fig. 2). There was a single trial in which neither set point nor gain achieved a significant difference, yet the joint test that considers interaction of variables indicated hysteresis was present. For the trials wherein set point contributed to hysteresis, the majority displayed the pattern consistent with the conventional wisdom: RR interval was longer at similar pressures during the fall than during the rise. However, there were four trials that demonstrated the opposite pattern: RR interval was shorter at similar pressures during the fall for both trials in one subject and for one trial in two other subjects. Similarly, when a difference in gain contributed to hysteresis, the majority showed the expected smaller gain during the pressure fall than during the rise. But again, there were trials showing the opposite pattern: two subjects demonstrated greater gains in both trials and another subject in one trial (Table 1). These observations suggest that baroreflex hysteresis may not always derive from a single mechanism, even within an individual.

Figure 2.

Contribution of differences in baroreflex set point and gain to baroreflex hysteresis •, trials with differences in both set point and gain. ○;, trials with a difference either in set point or in gain. Open triangles represent the trial with no difference in set point and gain, yet exhibiting hysteresis.

Table 1.

Differences in set point and gain regarding baroreflex function and its mechanical and neural components

	Difference in set point		Difference in gain
	Rise > Fall	Fall > Rise	Rise > Fall	Fall > Rise
Integrated baroreflex	4	15	11	5
Mechanical component	22	2	7	5
Neural component	0	22	12	3

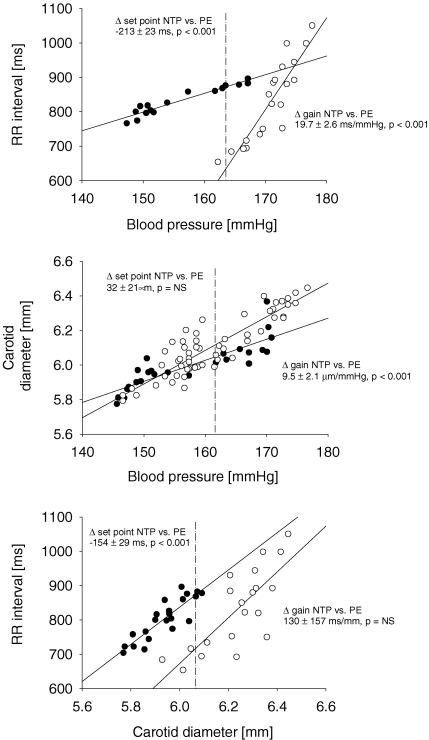
Inconsistency in the pattern of baroreflex hysteresis may be understood by examining the contribution of mechanical and neural components of the baroreflex. For example, Fig. 3 represents a trial in which baroreflex hysteresis appears as a difference in both set point and gain (top panel), with the mechanical component contributing to the difference in gain (middle panel) and the neural component contributing to the difference in set point (lower panel). In fact, differences in set point or gain were more common in the components than in the integrated baroreflex (Table 1); there was not a single baroreflex trial that did not demonstrate differences in at least one component. Thus, the six trials without baroreflex hysteresis demonstrated falling and rising differences in both mechanical and neural components that were actually offsetting.

Figure 3.

Hysteresis in integrated baroreflex function (top panel) and the contribution of mechanical (middle panel) and neural (bottom panel) components of baroreflex in a representative trial •, falls after bolus injection of nitroprusside (NTP); ○, rises after bolus injection of phenylephrine (PE). Dashed lines indicate the position of set point.

The fact that the two components work in concert to determine the nature of baroreflex hysteresis is apparent when examining differences in set point (Table 2). In the majority of trials, the set point differed during falling and rising phases in both components, and in all but one trial the differences were in direct opposition in the mechanical versus the neural component. For the mechanical component, the pressure fall was associated with smaller diameters, whereas for the neural component the diameter fall was associated with larger RR intervals. This opposition resulted in the dominant effector of differences in baroreflex set point being the mechanical component in three trials and the neural component in 11 trials. Thus, in the majority of cases, differences in baroreflex set point were driven by the neural component.

Table 2.

Determinants of baroreflex hysteresis: contribution of mechanical and neural aspects of baroreflex to differences in baroreflex set point and baroreflex gain

	Mechanical component	Neural component	Both, being additive	Both, opposing each other
Baroreflex set point	2	2	1	14
Baroreflex gain	3	6	5	2

The interaction between the two components regarding baroreflex gain followed a less uniform pattern: in nine trials only one of the components determined differences in baroreflex gain and in seven trials both components contributed (Table 2). According to these results neither the mechanical nor the neural component seems to have had a dominant role in determining differences in baroreflex gain that result in hysteresis.

Discussion

We defined cardiac vagal baroreflex hysteresis as differences in set point and/or gain in the pressure–RR interval relation between falling and rising phases of baroreflex engagement. Our characterization in young healthy humans showed that hysteresis was detectable in every subject and that the majority of trials showed higher set point and lower gain with pressure falls. However, the pattern of hysteresis was not uniform across subjects, or even within some subjects. There is a complexity in baroreflex hysteresis that derives from the interaction of mechanical and neural aspects of the baroreflex. For example, differences in barosensory vessel response to pressure changes can be offset by the RR interval responses to stretch such that hysteresis in a given trial may not be observed. In fact, mechanical and neural baroreflex components showed characteristic differences in set point with pressure/diameter fall and rise that most often were offsetting rather than additive. In contrast to set point, differences in gain generally derived from mechanical and neural components acting in the same direction. Thus, although our data broadly support conventional wisdom, they suggest that the baroreflex system can rapidly reset and does not generate the same pattern of response each time it is engaged.

Hysteresis is an intrinsic feature to the cardiac vagal baroreflex, and is observable with both drug-induced changes in blood pressure (Pickering et al. 1972; Bonyhay et al. 1997; Rudas et al. 1999) and direct carotid stimulation (Eckberg & Sleight, 1992). Hysteresis was first explained by the fact that in young healthy people the point at which the baroreflex operates at rest tends to lie close to threshold (Eckberg, 1980), and therefore pressure drops would demonstrate lower gain because they encompass the less steep threshold portion of the sigmoid relation. However, this is insufficient to explain the pattern since it has been reported that lower gain is present during pressure falls even from levels above resting pressure (Rudas et al. 1999).

The typical pattern of hysteresis has been identified as longer RR intervals at identical pressures and lower baroreflex gain with pressure falls (Eckberg & Sleight, 1992; Rudas et al. 1999). It has been proposed that barosensory vessel mechanics may contribute significantly to this phenomenon, since a similar pattern is manifested in the pressure–diameter relationship of large elastic arteries (Bonyhay et al. 1997). For example, within the cardiac cycle, diameters are larger with pressure falls than with pressure rises (Lénárd et al. 2000). It is not known, however, whether this pattern appears with slower changes in pressure across cardiac cycles. Indeed, our results show a different pattern: systolic diameters were actually smaller, not larger during pressure falls. One explanation may be that an increase in carotid artery diameter occurs after the fall and prior to the rise from a direct effect of nitroprusside. Although previous work suggests that carotid artery diameter follows changes in blood pressure passively after vasoactive drug administration (Bonyhay et al. 1997), the only values measured were the peak of the pressor response to phenylephrine and nadir of the depressor responses to nitroglycerin. The time course of the response has not been previously studied, and it is conceivable that after increased vascular sympathetic outflow terminates the rapid decrease in blood pressure, the direct vasodilatory effect of nitroprusside is manifest. One might hypothesize that increased sympathetic outflow would oppose the direct drug effect in the carotid artery, but there is no published evidence of sympathetic innervation of the human carotid artery.

Nonetheless, baroreceptors are coupled in parallel with smooth muscle in the carotid wall (Eckberg & Sleight, 1992) such that increased vessel diameter should stimulate afferent baroreceptor firing regardless of its origin. RR interval, however, did not respond to this increase in diameter, suggesting neural resetting in the baroreflex. This resetting could occur at any site of the neural baroreflex arc; one candidate is the afferent nerves themselves. In animals, diameter changes in the aortic arch by perivascular balloon inflation results in a pattern of aortic nerve activity characteristic of hysteresis with rapid resetting to lesser firing rate with decreasing diameter (Burke et al. 1986). Likewise, carotid baroreceptor firing can demonstrate lesser nervous activity at identical pressures during pressure falls (Chapleau & Abboud, 1987). However, we found that RR intervals did not follow the pattern expected from these animal data. RR interval was found to be longer at identical pressures with the fall, suggesting that baroreflex resetting may not be restricted to the afferent nerves, and that other sites in the reflex arc must contribute to the development of the characteristic pattern. Efferent vagal mechanisms may have a role in generating the pattern of hysteresis we observed; stimulation of the transected vagus nerve with sequential increases and decreases in voltage evokes RR intervals that are longer at a given stimulus intensity with decreasing voltage (Masuda et al. 1984). It is also conceivable that neural hysteresis was due to an interplay between sympathetic and vagal outflows. Increased vascular sympathetic outflow with a pressure fall may not only terminate the rapid decrease in blood pressure, but also interfere with vagal activation, restraining a more rapid response in heart rate to carotid diameter increases. Lastly, the complex extravascular effects of nitric oxide donors (Casadei & Paterson, 2000) may also contribute to baroreflex hysteresis. However, many of these effects develop slowly (Hogan et al. 1999), and it is not known whether they have similar effects in humans with rapid venous administration of nitroprusside.

Difference in baroreflex gain was almost as common as altered set point in producing baroreflex hysteresis. Similar to set point, it has been suggested that differences in gain are primarily driven by differences in the mechanical response of the barosensory vessels. Bonyhay et al. (1997) found that a lower baroreflex gain with pressure falls primarily resulted from a less steep pressure–diameter relationship. We found that differences in gain derived equally from mechanical and neural components of the integrated reflex. Our results may differ because we applied sequential bolus doses of vasoactive drugs whereas Bonyhay et al. increased and decreased pressure in separate trials. This may simply underscore our conclusion that the baroreflex does not generate the same pattern of response each time it is engaged.

In our study, we used only the single drug order of the traditional modified Oxford technique. However, baroreflex mediated responses have been shown to be always greater after bolus phenylephrine than after bolus nitroprusside (Rudas et al. 1999), indicating that hysteresis – due to a difference in gain – may be present with any order of pressure changes. It is not known, however, whether components of the baroreflex behave the same way. Therefore, we performed the same analyses on data obtained during pressure changes induced by the reverse drug order of the modified Oxford technique (data not shown). This analysis showed that hysteresis of similar characteristics exists in the baroreflex components and a similar interaction of mechanical and neural baroreflex components occurs regardless of drug order.

Measuring vessel diameter in the carotid artery instead of the innervated carotid sinus is a clear limitation of our study. It is not known whether different segments of the carotid artery respond to vasoactive drugs or to sympathetic activation in a quantitatively different manner. However, in young healthy subjects, pulsatile distensibility of the carotid artery varies only slightly in its various segments, including the sinus area (Reneman et al. 1985). In addition, vessel wall movement can be more reliably estimated in the common carotid artery due to its easily accessible position and parallel vessel walls, as compared to the variable position and more complex geometry of the carotid sinus. We therefore assumed that the common carotid artery is an adequate representative of barosensory vessel responses.

The significance of hysteresis is that baroreflex mediated autonomic outflow may be least responsive in the face of falling arterial pressure and reduced vital organ perfusion. Baroreflex resetting that allows the increase of carotid diameter without a response in RR interval after reaching the nadir in pressure may indeed protect from prolonged hypotension; carotid diameter, and, to some lesser extent, pressure may increase without any baroreflex inhibition. Increased gain in the later phase of a pressure rise, on the other hand, may protect from excessive increases in pressure. Therefore, changes in set point and gain may represent fine-tuning of the arterial baroreflex to the prevailing conditions so that systemic pressure and perfusion are adequately protected. These changes were thought to be dependent primarily on barosensory vessel function, but in our study we found that the contribution of vascular elasticity and neural resetting are equally relevant, and the two baroreflex components act in concert in the generation of hysteresis. Inconsistency in hysteresis pattern between and within subjects, however, suggests that other factors such as changes in sympathetic activity or stroke volume during the course of vasoactive drug injection may also have some role in generating baroreflex hysteresis.

Appendix

Cardiac vagal baroreflex gain is generally estimated from the linear portion of the pressure–heart period relation. A simple linear model, however, may be insufficient when pressure changes across a large range encompassing threshold and/or saturation regions of the relation. It is common practice, though, that even in these cases a linear gain is calculated after visual estimation and exclusion of threshold and saturation regions (Rudas et al. 1999). Visual estimation is neither objective nor exact, and can result in considerable inter- or intraobserver variability in gain estimates. To resolve these issues, sigmoid models have been applied in the past. For example, the first derivative of the logistic sigmoid function can provide a baroreflex gain at any observed pressure (Potts et al. 1993). A linear gain can also be reconstructed from the second derivative of the sigmoid curve (Hunt & Farquhar, 2005). Neither of these can be considered as a perfect solution. Peak baroreflex gain calculated from a single point of derived logistic function is not a robust estimate of baroreflex function and its physiological relevance is unclear. Moreover, although a sigmoid curve may be fitted to the data, this does not indicate that all model parameters are significant. That is, a sigmoid model may achieve an acceptable level of significance despite the fact that there is no threshold and/or saturation. In these cases, the reconstruction of a linear gain using the second derivative of the logistic function is not feasible. On the other hand, trials that do encompass the entire sigmoid relation may result in a reconstructed linear model encompassing very few data points and therefore having a low regression coefficient (Hunt & Farquhar, 2005).

We sought to overcome the shortcomings of visual inspection and sigmoid modelling so that we might define a more rigorous and reliable approach to estimating linear baroreflex gain in humans, as well as gain objective insight to baroreflex hysteresis. We used piecewise linear regression (Neter et al. 1989; Draper & Smith, 1998) to determine the changes in slope (if any) across the range of observed pressures in the falling and rising phases of drug administration. The essential difference between a linear regression and a piecewise linear regression is that in a linear regression the slope does not change within the range of the data while in a piecewise model the slope does change. In essence, the piecewise model searches for breakpoints that occur at threshold and/or saturation, and will derive one to three slopes for the data. By definition, slopes below threshold and above saturation are not significantly different from zero and contain at least five data points. Threshold is first identified by iteratively regressing the data starting with the first five data points; the regression with the smallest error sum of squares and P-value above 0.05 defines the presence and location of threshold. If the iteration results in a P-value less than 0.05 with only five points, there is no threshold for the data. An identical process is applied to identify saturation starting with the last five data points. The data that do not fall in threshold or saturation are also fitted with a linear regression, but one that has no constraint on number of data points and has a P-value less than 0.05. This provides a piecewise regression with a linear gain, potentially a threshold and potentially a saturation. If neither threshold nor saturation exists, then, of course, we simply apply a linear regression to the entire data set. Finally, Cook's Distance (Cook, 1977) values are produced for each linear model as a check for outliers that are particularly influential; these data points can then be checked for accuracy, and, if desired, a limit can be applied to remove outliers.

A comparison of this approach to the sigmoid and the simple linear model can be made for all trials. Since all models are maximum likelihood estimates, a likelihood ratio test can be computed based on the log-likelihoods. In addition, Akaike's Information Criterion (Akaike, 1969) and Schwartz's Bayesian Information Criterion (Schwartz, 1978) can be computed. In general, even when the statistics show a slight preference for the sigmoid model over the piecewise model, the piecewise model should be chosen as it allows the easy use of other predictors, allows simple tests comparing the results across different trials and across groups of subjects, and allows the use of standard regression diagnostics, including influence statistics such as Cook's Distance. Most importantly, piecewise regression determines threshold and saturation in an objective manner, estimates a gain across a pressure region rather than at a single point, and can be applied successfully in trials that do not encompass all parts of the sigmoid relation.