The interspecific mass–density relationship and plant geometry

Abstract

We present an a priori theoretical framework for the interspecific allometric relationship between stand mass and plant population density. Our model predicts a slope of −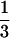 between the logarithm of stand mass and the logarithm of stand density, thus conflicting with a previously assumed slope of −½. Our model rests on a heuristic separation of resource-limited living mass and structural mass in the plant body. We point out that because of similar resource requirements among plants of different sizes, a nonzero plant mass–density slope is primarily defined by structural mass. Specifically, the slope is a result of (i) the physical size-dependent relationship between stem width and height, (ii) foliage-dependent demands of conductance, and (iii) the cumulative nature of structural mass. The data support our model, both when the potential sampling bias of taxonomic relatedness is accounted for and when it is not. Independent contrasts analyses show that observed relationships among variables are not significantly different from the assumptions made to build the model or from its a priori predictions. We note that the dependence of the plant mass–density slope on the functions of structural mass provides a cause for the difference from the zero slope found in the animal population mass–density relationship; for the most part, animals do not have a comparable cumulative tissue type.

The inverse relationship between the logarithm of plant mass and the logarithm of population density has been interpreted most frequently as encompassing both a within-population time trend through stand development and as a static interspecific pattern (1–5). More recently, it has been suggested that the intra- and interspecific relationships are the consequence of different processes, and thus deserve different explanations. That is, the intraspecific relationship is a reflection of the dynamics of competition through time; differences among stands of a particular species are the result of differences in developmental stage and/or environmental conditions (6, 7). On the other hand, differences among species have other origins (8, 9). When compared at the same point in development, their position in the mass–density relationship reflects basic functional differences among species (10, 11).

Previously, speculations on the factors behind possible relationships between plant mass and plant density have been a posteriori, that is, drawn from perceptions of patterns resulting from statistical analyses of data collected from many individual studies. However, empirical patterns are highly subject to the vagaries of data choice, data quality, and methods of analysis used (5, 8, 9, 12–15). Specifically important to previous analyses, the confidence interval around a log–log relationship is such that any number of slopes could be represented; to decide on causative factors based on only one of those many possible slopes (e.g., see refs. 5, 16, 17) makes an argument from what may be false premises.

Thus the interspecific relationship between mass and number can be best understood by building an a priori expectation of the relationship from basic principles. Once such an expectation is constructed, data can be used to examine the value of the explanation. Being a priori, the model presented herein builds an expectation of a relationship that allows us to speculate on possible causes for deviations from the predicted relationship, and to suggest focal areas for data collection. We construct this model on the proposition that any relationship that may exist between plant population density and above-ground mass of a stand is the result of the multiple roles played by above-ground plant tissue. These roles are light interception, conduction of resources along the plant body, and physical support. Whereas the first function is fulfilled exclusively by live tissues (leaves), the second and third functions are carried out by a combination of live and dead tissues in stem and branches. Given these considerations, our model explains the interspecific mass–density relationship in terms of regulation on the live component and allometric relationships that enable plants of different sizes to perform the other two functions properly.

REGULATION IN PLANT POPULATIONS

We differentiate between the functions of living and nonliving tissue as a heuristic tool. We realize that some nonliving tissue is involved in vascular function (dead cells in sapwood; refs. 18–21) and that cell walls of living tissue contribute to the structure of the stem. Nonetheless, in contrast to previous explanations, we consider the similarity of physical variables used to describe and marry the differing functions, in order to arrive at an allometric relationship that we test with existing data.

The amount of living tissue in a stand of either woody or herbaceous species appears to be regulated by resource availability. Documented evidence of the regulatory power of resource availability underpins the so-called “law of constant final yield” (22), which springs from the observation that (in annual crops) maximal yield per unit area is independent of population density. That is, a plot of the amount of living tissue per unit area vs. population density shows a zero slope, the intercept of which is determined by the amount of resources available and the efficiency of the metabolic apparatus as affected by such processes as photosynthetic pathway (e.g., ref. 23) or shade tolerance (24). However, living tissue requires continuous resource input to maintain itself regardless of life form, and it is reasonable to expect that the amount of live material in woody as well as herbaceous plants will be determined by the resources available. This expectation is supported by the observation of a similar range of variation among herbaceous and woody species in the maximum amount of leaf area per unit of ground (leaf area index, or LAI; refs. 25–29), indicating a similarity of regulatory processes.

On the other hand, stand mass is not regulated by the same processes in herbaceous versus woody plants. In herbs, any equilibrium in stand mass is primarily a result of sloughing off and replacement of living tissues. In contrast, in woody species, structural tissue (S) accumulates as a stand ages, eventually becoming the dominant component of total mass per unit area (M; figure 2 in ref. 30), to the extent that differences among species in the amount of living tissue are likely to be small relative to the differences in total mass; equilibrium in stand mass occurs when accumulation of structural tissue is offset by its decomposition. Thus, apparent equilibrium in stand mass of herbaceous species is achieved by the processes of cell death, whereas that of woody species is through the differing processes of cellulose degradation.

We therefore use maximal LAI of a species to indicate the living component of the plant body regulated by resource availability. Although maximal LAI does not directly measure total live tissue, respiration rates in sapwood can be measured and used to estimate the proportion of live cells embedded in the dead tissue matrix (18–21). Overall, total living tissue (B) is proportional to LAI, and it can be reasonably assumed to be similarly proportional in herbaceous and woody species.

SCALING MASS AND DENSITY IN PLANTS

If n represents population density and f represents foliage area of an average plant in a population with the maximal amount of living tissue (B_max)

1

and therefore

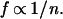2

Additionally, f is related to the plant’s stem cross-sectional area (the “pipe model”; refs. 31–34); thus

3

(where d is stem diameter).

Next, once LAI_max is reached, any increase in total mass (M) is due to the accumulation of support tissue (S). S (but also M because M = B + S and B = B_max = constant) will increase in proportion to the height of the canopy (h), i.e.,

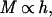4

which is supported both theoretically and empirically (see next section and Table 1).

Table 1.

Results of analyses of log₁₀ values of assumed and predicted relationships between h, d, M, and n

Relationship			SE	r	N1/N2*	95% CI†	Slope
	Slope						Major axis model	Cross-species, major axis model (N = N1)
	Theoretical expectation	Least-squares regression
log(h) vs. log(d)	0.667	0.790	0.128	0.935	45/18	±0.274	0.779	0.892
log(M) vs. log(h)	1.0	1.032	0.141	0.792	58/25	±0.297	0.897	0.959
log(M) vs. log(n)
Complete data	−0.333	−0.291	0.080	0.662	75/31	±0.164	−0.375	−0.350
Angiosperms only	−0.333	−0.312	0.071	0.694	43/22	±0.148	−0.337	−0.285
Dicots only	−0.333	−0.349	0.078	0.745	36/17	±0.166	−0.369	−0.293
Dicots without Asteridae	−0.333	−0.350	0.081	0.745	34/16	±0.733	−0.340	−0.283

Major axis regression is often called for in calculating slopes of allometric relationships (9), and this has been noted for the plant mass–density relationship in particular (6). However, major axis regression apportions error between the x- and y-axes according to the assumption that all error is measurement error. In fact, deviation from the postulated relationship may also be due to other factors such as unknown or unaccounted for variables that may affect x and y differently. In such a case, assignment of error according to an assumption that it arises from measurement only would not be correct. Hence, model II regression is as likely to be incorrect in its distribution of the error as model I for the plant mass–density relationship. Therefore, we have performed both least-squares and major axis analyses on the independent contrasts data, forcing the intercept through the origins for both models (44). The predicted slope was tested against the observed least-squares slope by using the standard error of the regression coefficient to calculate the 95% confidence interval for the derived slope. Cross-species analyses were not forced through the origin. 

^*N₁ = number of species used in the analysis; N₂ = number of independent contrasts used in the analysis. 

^†Note that in all cases, predicted slopes fall within the 95% confidence interval of the observed slope. 

An additional assumption is made, that to stay upright, longer stems need to be proportionally thicker than short ones. The assumption of increasing stem thickness with height is derived from the physical principle of elastic similarity (35)

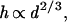5

which also enjoys theoretical and empirical support (see next section and Table 1).

From the preceding, we are able to substitute M for h, and 1/n for d² and arrive at

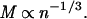6

That is, under the conditions defined by this model the mass–density relationship will follow a line (in a log–log plot) with slope equal to −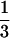. Because one or more of these conditions are likely to change with individual age and/or size, we do not expect the above relationship to hold true as a time trend through the life of a cohort. We contend that, given the similar architectural restrictions among vascular plants, the relationship will be observed when comparing individual species that have been measured at a standard point in the development of the stand. That is, a single point must be chosen to represent a species, the rationale for which is discussed below.

Further Explanation of the Model

We note that the assumptions of this model are valid for interspecific comparisons and are not always applicable to other levels of study. Although this caveat has been clear for some time to students of allometry (36, 37), overlooking the possible nontransference of assumptions between intra- and intraspecific levels has caused great confusion among researchers working in what has been termed generically “self-thinning.” For our purposes it is irrelevant whether populations have undergone density-dependent mortality (self-thinning) or not. One may conceive situations where populations are at LAI_max and yet self-thinning may not occur—e.g., in bamboo or palm populations that may reach a constant crown size and, with little or no mortality, simply grow vertically until individuals begin to senesce.

Our initial proportionality formulates our intention to substitute LAI for living tissue, and it presents the logical outcome of the substitution in terms of foliage area and population density. Not incidentally, this proportionality also represents a solution to a recurring problem of both intra- and interspecific studies by presenting an independent definition of “space filling.” Previous studies have depended on a “working definition” of the point at which resources become limiting, and intraspecific competition should begin to have an effect (e.g., refs. 4 and 5; but see criticism in ref. 13). However, this definition becomes dissatisfying when it is realized that the process that is being used as a criterion for data collection, particularly in intraspecific studies, mortality rate, is also that which purportedly is being demonstrated independently by the slope. LAI_max, which by definition is the point at which there is no available space to fill, offers a reasonable solution to this problem. Our second proportionality merely reflects the fact that under LAI_max, the average amount of foliage per plant must be inversely related to the number of individuals that are present.

Our third proportionality draws upon the recognition that the stem area of a plant determines the quantity of vascular material present, the vascular material determines the vascular flow, and the amount of leaves depends upon the water delivered to the canopy. Notice that although the proportion of xylem involved in water conduction decreases with the size of the plant as heartwood develops at the core of stem and branches, a substantial amount of dead tissue (sapwood; see ref. 21) participates in this function. If plants are described by a branching fractal tree that fills space—i.e., a tree with a fractal dimension of 3—different species, which characteristically attain different sizes, can be represented by different portions of that tree. Small herbs behave as branch tips while massive trees contain more branch orders of this fractal tree. Notice that even though in real life the individual plant is not self-similar (the ratio of sapwood area to foliage mass, known as the Huber value after ref. 38, changes along the tree), different species will be fractally similar at the base of their corresponding basal stems. That is, Huber values will show the same range of variation among species of different maximal sizes and regardless of whether whole sectional area or just sapwood area is measured. This relationship is well supported by empirical observations (32–34, 38–42). Furthermore, the facts that (i) the relationship between foliage and total stem cross-sectional area runs parallel to that of foliage and sapwood area (42), and (ii) the variation in Huber values between xeric and mesic (or even aquatic) environments is higher than the variation among species and plant forms (38–42) mean that the proportionality holds regardless of which measure (sapwood or sapwood plus heartwood) d² represents. Thus, our use of d² makes it compatible with its use in other parts of the model.

We further assume that, when comparing stands (species) at their maximal height, mass per unit area has a linear relationship with height of the stand. In an intraspecific version of the model, M ∝ h implies that once LAI_max is reached, further production of foliage and its corresponding supporting/conducting tissue occur by addition of further layers of foliage to the upper parts of the canopy, while lower layers die. That is, leaf production would be isometrically related to both the production of supporting/conducting tissues and the lifting of the canopy as the stand develops (i.e., the canopy “sweeps” the vertical space through time). A word-picture may further illustrate this assumption. First, it is necessary to keep in mind that we are referring to the relationship between a stand of plants and its canopy, not between an individual plant and its crown, and that the canopy sits on top of a stand like frosting on top of a cake. As time goes by, stems grow taller and the canopy “floats” up in space. Although initially increasing, canopy thickness (depth) is determined externally by the amount of incident sunlight and internally by the physiological requirements of the photosynthetic apparatus, and is not related to the number of individuals in the stand. Once LAI_max is reached, the thickness of the canopy stays the same over time, and indeed as h increases. Thus, if a stand increases in mass over time, that can be only through accumulation of wood in stems and branches and this increase will be proportional to the increase in stand height. The interspecific version of this dynamic process simply states that because “packing” of plant material is similar among species (43) this isometry is also valid across species at LAI_max. That is, average density of the plant material (“packing”) is not correlated with total mass per unit area (11). This isometry is also supported by the independence (lack of correlation) between the ratio of wood to foliage net primary production and tree height in a sample of 477 forest stands (30). As in the previous relationships, this does not mean there is no variation among species in this attribute, but rather that packing (like LAI_max) is similarly distributed at all plant sizes (i.e., among species).

Although other studies have assigned other values to this relationship (M^1.28 ∝ h from data in ref. 3, analyzed in ref. 11; M^0.95 ∝ h, in ref. 11) these values have been derived from empirical estimations of the very relationship we are trying to define by a priori means, and do not account for the potential effect of taxonomic relatedness (9). Thus, it is especially satisfying that we find the relationship M ∝ h^1.032 (in data drawn from refs. 44 and 45) by using an analysis of independent contrasts to minimize effects of taxonomic relatedness (46). In this analysis, variation in stand height explains 63% of the variation in stand mass, and the observed value of the exponent of h is not statistically different from its assumed value (1.0; Table 1).

The assumption that h is also proportional to d^2/3 (elastic similarity: see ref. 35) is based on the idea that plants under the conditions described above maintain a similar margin of safety (when measured on a logarithmic scale) with regard to the “buckling limit” of their stems, an assumption also made for the dynamics of self-thinning (47). That buckling limit can function in determining plant geometry has been shown experimentally in that, when given external support, individuals of Liquidambar styraciflua (sweet gum) have a significantly higher length-to-width ratio than individuals grown under the same conditions but without support (48). To further determine the validity of this assumption, we investigated the relationship between log(h) and log(d) for the dataset we used to test the overall model. Once again, applying the independent contrasts method to account for any potential taxonomic bias, we found h ∝ d^0.790, which is not significantly different from our assumed relationship (0.667; Table 1).

We assumed elastic similarity to hold true among crowded stands. This includes plants without secondary thickening, such as grasses and palms, which nevertheless are limited to a maximum height, in the absence of external support, by the same relationship (49–51). Again, we are not using this relationship as a description of stand development, but as a limit expected in stands at LAI_max (see next section).

Data Analysis

Our model describes an allometric, not a boundary, relationship that is a function of the amount of living and total mass that can be fitted into a unit area depending on such ecological variables as shape, shade tolerance, metabolic efficiency, etc. of individual species. There has been considerable controversy about the choice of data points appropriate for demonstration of a mass–density relationship in plants (5–7, 10, 13), and recognition that we are describing an allometric, not a self-thinning or a boundary, function can clarify some of the issues that have been raised.

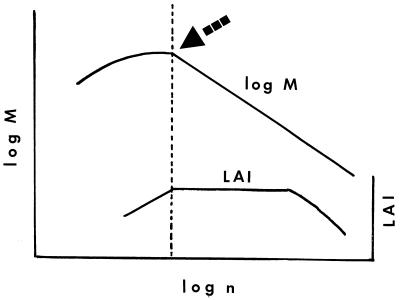
To establish an interspecific mass–density slope free of sampling bias, only one point for each species may be included in the analysis; inclusion of unequal numbers of a group with one solution vs. a group with another solution can lead to biases in the determination of the relationship(s). This point is that of maximal total mass (which incorporates LAI_max) achieved with the maximal number of individuals. At this point, we expect LAI to decrease from a constant, leading to an abrupt change of slope in the intraspecific mass–density relationship (Fig. 1). We speculate that, in plants with secondary growth, this is also the point at which the primary cause of mortality switches from density-dependent to density-independent effects, signaling that space is no longer totally filled. Although in the past data have not been collected that makes this point easily discernible, for our purposes we have chosen for each species in the dataset the point of greatest combined values of mass and density. In the presence of more than one stand with a maximum value of mass, the latter guarantees that canopy space is as full as possible.

Figure 1.

Representation of the logic behind the data choice rationale. Only one point per species, that of highest mass and maximal number of individuals (arrow) is used for the estimation of the interspecific relationship. The point corresponds to maximal LAI as well as maximal mean tree height and diameter. Support for the shape of the representative distribution is provided by data presented by Osawa and Sugita (53) and Osawa and Allen (54).

We also take into consideration the problem that data points are not independent. Thus, we performed an analysis of independent contrasts to take into account potential taxonomic biases, as we did in all tests of our assumptions (46, 52). Independent contrasts compare differences in the value of a trait within and among taxonomic groups, thus statistically accounting for similarities due to shared ancestry. Our single-point/species criterion allowed inclusion of 75 stands from which we calculated 31 independent contrasts to estimate the fit of the data against the predicted slope (data drawn from refs. 44 and 45).

RESULTS AND DISCUSSION

Despite all the discussion about the mass–density relationship, and although Weller (11, 13) has constructed an empirical slope of −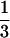 through using different criteria for data inclusion, there seems to be a general acceptance that a −½ slope describes at least the interspecific association (e.g., refs. 4, 5, 16, 17, 55). However, plotting our predicted slope onto a figure often used as support for a higher slope shows that either slope could explain equally well the empirical evidence (Fig. 2). Of central interest is that our model provides a priori theoretical support for a shallower slope, theoretical support that is singularly lacking for the originally posited slope. More detailed analyses of slopes among taxonomic groups could serve to reveal any contribution to the mass–density slope of particular variables such as taxonomically based architectural ground plans (e.g., degree of branching) or metabolic processes such as photosynthesis. Although the data available at this time do not allow rigorous testing of any such hypothesis, successive restriction of the taxonomic breadth of the data entered into an analysis of the mass–density relationship shows noticeable changes in slope depending on the taxonomic groups included (Table 1; Fig. 3).

Figure 2.

Position of the predicted interspecific mass–density relationship according to the model presented in this paper (continuous line) and the previously assumed relationship based on empirical, cross-species analyses (broken line). The cross-species relationship has been redrawn from White (55), and mass is represented on an individual basis (m = average individual mass), thus the respective slopes are − and −.

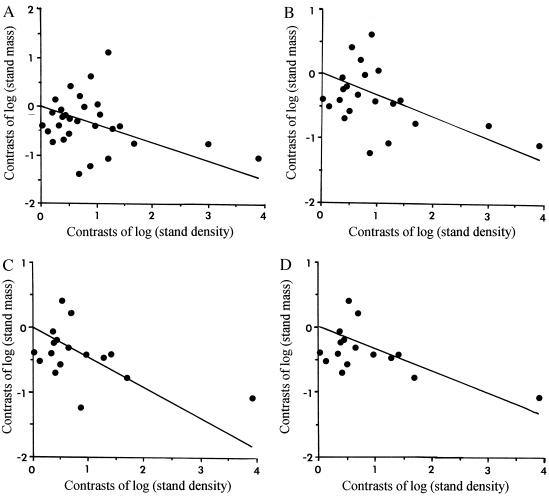
Figure 3.

Major axis regressions of the independent contrasts of log(stand mass) vs. the independent contrasts of log(stand density). The relatively small sample sizes for the majority of clades made calculation of contrasts for individual subgroups impracticable. However, to visualize how different groups may affect the slope, analyses have been performed with various subsets of the dataset. (A) Complete dataset. (B) Restricted to Angiospermae. (C) Restricted to Dicotyledonae. (D) Restricted to Dicotyledonae minus Asteridae. See Table 1 for slopes and sample sizes.

We wish to draw attention to some of the biological implications of the terms we have used in relating our four assumptions, to offer some explanation for differences among groups in intercepts and slopes for the mass–density relationship. Because we assumed factors such as maximal living tissue and architecture to vary to the same degree among species with different maximal sizes, it is possible to use deviation from the slope predicted by the model to identify the effects of differences in such factors in the relationship between mass and density for a particular species or group of species. Referring to our proportionalities, in Eq. 1 the term relating foliage area to number of individuals at LAI_max, f⋅n, represents the total amount of foliage per unit area, but may also be seen to represent a measure of shade tolerance: LAI_max will be higher with more shade-tolerant species (56). Similarly, d²/f, referring to Eq. 3, is proportional to the Huber value, the amount of cross-sectional area per unit amount of foliage, or a measure of “pipe” (stem) thickness relative to foliage. From Eq. 4 we obtain M/h, which is a scaled equivalent of Weller’s “packing constant” (11). He asserts that the volume occupied by an average plant, v, is equal to the surface area it covers, s, multiplied by its height (h), or s⋅h. Because average mass per individual, m, equals volume times the density (“packing”) of plant material (p), and total mass M = m⋅n, then M/h = psn, or “packing” multiplied by total population surface area. Or, because M is measured on the same unit area, just “packing.” Finally, h³/d², from our terms in Eq. 5, can be envisaged as an expression of the strength of the supporting tissue. In the model M = k⋅n^−1/3, the intercept k is the scaled product of all of the above expressions, and thus is a combination of both physical and biological effects. Thus, the intercept (but also the slope as the intercept rotates the relationship) for any particular group will depend on the extent to which any one of several effects dominates for the group.

A cross-species comparison, in which potential taxonomic effects were not accounted for, produced a major axis slope of −0.350 for the overall data set. This empirical slope is highly consistent with the −0.333 predicted by our model. It may be worth noting that, in the cross-species analysis, the relationship is largely a function of the relationship between two clouds of points, that representing herbs and that representing trees, a problem that has also plagued earlier studies (e.g., ref. 11). In such a situation, where there are few or no intermediate values, the slope is especially sensitive to sampling intensity of points within a cloud, through altering the average value for the cloud on which the slope depends.

In the same vein, planned sampling would allow greater inference from the analyses using independent contrasts. Of the dicotyledon species available with the appropriate information, only three are herbs, and all three are in the same family (the Leguminosae); shrubs are similarly undersampled. In Fig. 3 A–D, the point farthest to the right is the comparison between trees and herbs in the Leguminosae; when monocots are excluded from the analysis, this point appears isolated (Fig. 3 C and D). A wider, more even distribution of data among life forms, as well as among taxonomic groups, would allow investigation of models regarding variation among them, which is not possible with the existing data. Alternatively, a greater selection of any one life form may permit a better determination of the effects of metabolic differences apart from larger architectural ones; herbs would be an especially good candidate for this type of analysis, presenting an instance where effects of metabolism on living tissue would be largely unconfounded by effects of dead tissue. Similarly, intensive sampling within a metabolically similar taxonomic group may best reveal the effects of differences in architecture on dead tissue accumulation.

For animals, the slope of a relationship between individual size and number appears to be determined by energetic requirements of the population; overall population mass (at maximum density) is approximately equivalent across species (9, 57), and a graph of log(population mass) vs. log(population number) would have a zero slope. The observation of an LAI_max that is similarly distributed across species describes essentially the same situation: living tissue per unit area has a maximum across species that is independent of size. However, in plants, unlike animals, total mass also encompasses dead, nonliving support tissue, and it is this attribute that gives the population mass–density relationship a nonzero slope. Thus, unlike Westoby (58), we cannot use this relationship to assert any innate difference between animals and plants in the regulation of living tissue, but rather that the additional functions of dead tissue that are particular to plants produce the observed differences.

We find it interesting that Weller (11), after empirically finding a −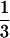 slope (such as we have predicted), used this result to derive a posteriori an explanation based on slenderness of the space occupied by individual plants and “packing” of plant material in this space. His explanation, however, differs from ours in that it is not derived from the basic a priori principles we have used here.

In summary, the primary value of our model is that it can give meaning to individual deviations about a predicted relationship. Because these deviations are not used to define the relationship, it is possible to speculate as to the causes behind particular points or groups of points not falling exactly within the relationship predicted by the model. For example, plants with weaker stem tissue, as a result of either cell or wood characteristics, need to have thicker stems to support the same weight as plants with stronger tissue. Similarly, stands subject to stresses such as high winds or heavy fruit crops may develop a thicker stem than might be expected from the height of the plant alone. Also falling into this category would be architectural differences in canopy structure, e.g., plagiotropic vs. orthotropic branching systems, which would affect load and hydraulic conductivity. We do not restrict the possibilities to our examples here; just to name two more, shade tolerance and metabolic specializations are also likely to affect the placement of particular species relative to the predicted relationship. Overall, our a priori model creates an opportunity for investigation into a plant mass–density relationship not heretofore possible with empirical a posteriori formulations.

In conclusion, we demonstrate here a different approach to a plant mass–density relationship than has previously been attempted. We outline new and different criteria for data selection, while our a priori model represents a logically different and more rigorous method of deriving the causation behind a plant mass–density relationship, thus expanding our ability to use data to better understand the physical and biological properties governing the relationship between plant shape and size.