Abstract
Both 5-year-old children and adults determine the quantity of a number by the use of a similar parietal lobe mechanism. Event related potentials indicate that input from Arabic digits and from dot patterns reach areas involved in determining quantity about 200 ms after input. However, voluntary key presses indicating the relation of the input to the quantity five take almost three times as long in children. The ability to trace the networks of brain areas involved in the learning of school subjects should aid in the design and testing of educational methods.
How does the brain execute high level skills taught in school, such as reading and arithmetic (1)? By isolating the critical operations involved when skilled performers execute such tasks it is possible to relate their anatomy, from studies using neuroimaging methods that trace cerebral blood flow, to the time course of their activation from electrical activity recorded from scalp electrodes (1, 2). This approach makes it possible to examine changes in brain circuitry involved in adult learning (3, 4) or in initial acquisition of the skill (5). We have examined aspects of number processing from this perspective and our results suggest that the basic brain areas involved in comparing the quantity of numbers do not change from the age of 5 to adults, whereas the reaction time (RT) to respond to the task drops 3-fold over this period.
Recently the basic anatomy (6) and circuitry (4) for determining the quantity of Arabic and spelled digits in normal adults has been determined. The task used is to compare an input digit (e.g., 4, four) to determine whether it is above or below the number five. Reaction times for inputs far from 5 (e.g., 2 or 9) are about 40 ms faster (distance effect) than those close to 5 (e.g., 4 or 6) (7). Studies of scalp electrical activity (4, 6) show that this distance effect is localized to the left and right parietal regions (right greater than left) at about 200 ms after input. Variables involved in input processing, such as whether the input is an Arabic or spelled digit influence more posterior electrodes at earlier times than those areas showing the distance effect. Variables influencing output, such as whether the right or left hand is used, influence more anterior structures at later times than was found for the distance effect. Moreover, the increase in RT with distance from 5 does not interact with either the input or output variable. These findings suggest that the parietal lobe is related to determining the quantity of the input independent of its form and of the output needed to express the decision (4, 8).
To understand the development of the circuitry involved in number processing we sought to determine whether 5-year-old subjects showed the same localization of function as adults. We used a 128-channel geodesic sensor net (9) to record scalp electrical activity from 5-year-olds and adults as they performed number comparisons and examined differences in the event related potentials (ERPs) associated with the distance effect. Both dot patterns and Arabic digits were used to determine whether perceptual and symbolic representations of magnitude effect the localization or timing of the distance effect. We found that the distance effect was similar for both forms of representation and that the localization and timing in 5-year-old subjects was remarkably similar to those seen in adults. These findings suggest that the system involved in rapid estimation of quantity develops before formal schooling in the same brain areas as found in adults.
MATERIALS AND METHODS
Subjects.
Thirty-two subjects from two age groups (adults and 5-year-olds) participated. The adult group consisted of 16 subjects. One subject was rejected after having less than 50% artifact-free trials after editing. The remaining 15 subjects (6 female and 9 male) were between 19 and 38 years old (average age: 23). Sixteen children between 5 years and 2 months of age and 6 years of age participated. Two were rejected after abandoning the experiment following the first block. One was excluded from ERP analysis because of excessive eye movement. Reaction time analysis included 14 children (7 females and 7 males) at an average age of 5 years, 5.28 months. ERP analysis included 13 children (7 females and 6 males) with an average age of 5 years, 5.4 months.
Procedure.
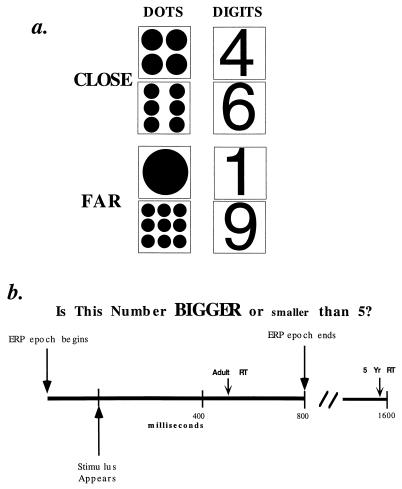
All subjects were paid $5 per hour. Informed consent was obtained from the subject and the parent if the subject was a minor. To begin each trial the subject fixated on the center of a computer monitor. In each trial a stimulus was presented consisting of either one of the digits, 1, 4, 6, and 9 or an arrays of dots corresponding to those digits (Fig. 1a). Stimuli were presented on a Radius 20e computer monitor, and were presented in random order. Digits were presented in Helvetica font 5 cm high. The dots varied in size such that all arrays fit into a 5-cm square.
Figure 1.
(a) One of these eight stimuli was presented to subjects as indicated in b. (b) Stimulus presentation occurred 200 ms after the ERP recording epoch had begun and remained present until response. Subject classified stimulus as bigger or smaller than 5. ERP epoch ended after 1,000 ms (800 ms after stimulus onset). The average adult RT was 500 ms; the average 5-year-old RT was 1,600 ms.
Subjects pressed a key as rapidly as possible to indicate whether the stimulus was larger or smaller than 5 (Fig. 1b). The assignment of larger or smaller to keys was balanced over subjects. The stimulus remained on the screen until the button was pressed (up to 7 s). If the subject’s response was correct, a “smiley face” was presented. Response keys were connected to the millisecond timer of a National Instruments NB-DMA-8 card to measure reaction time. A session consisted of a practice set with 24 trials and 4 blocks of 40 recorded trials, for a total of 160 recorded trials per subject and 20 presentations of each stimulus.
Procedure varied slightly between age groups in that children were given more time to become comfortable with the experimental set up and the net for recording electrophysiological data. In addition, children were given a number knowledge test modeled after Griffin et al. (10) to ascertain their mathematical age. This pretest concluded with a description and practice of the number comparison task.
All subjects performed the task in a sound-attenuated booth with their chins placed in a chin rest. To minimize movement, 5-year-old children stood rather than sat, and one researcher was present during the entire experiment. To minimize eye movement in this group, stickers shaped as stars, one large and one small, were stuck on the upper portion of the computer screen. The size and location of the star (on the left or right side of the monitor) corresponded to the size and location of the response key, i.e., the large star was in the upper left when the “larger” response key was assigned to the left. This allowed the children to look at the stars to remember which key was which. All children were assured throughout the task that they could stop or take rests at any time. In addition, all children were given small prizes during the planned breaks in the task. Adults simply rested during breaks and continued when ready.
Scalp Electrical Recording.
Electrical recordings from a 128-channel geodesic sensor net (9) (Electrical Geodesics, Eugene, OR.) (Fig. 2) were taken during each trial (Fig. 1b). The net consists of 128 Ag/AgCl electrodes embedded in electrolytic sponge, plus reference and isolated common electrodes. The sensors are housed in injection-molded plastic housing and interconnected by polyurethane elastomer threads that form the tension lines of an icosahedron. Intersensor spacing is approximately 2.8 cm with impedances typically in the 10–20 kΩ range. Recording was amplified with NetAmp by using a 0.01–50-Hz bandpass (3 dB attenuation) and a 60-Hz notch filter. The signals were sampled at 256 samples per second beginning 200 ms before stimulus onset.
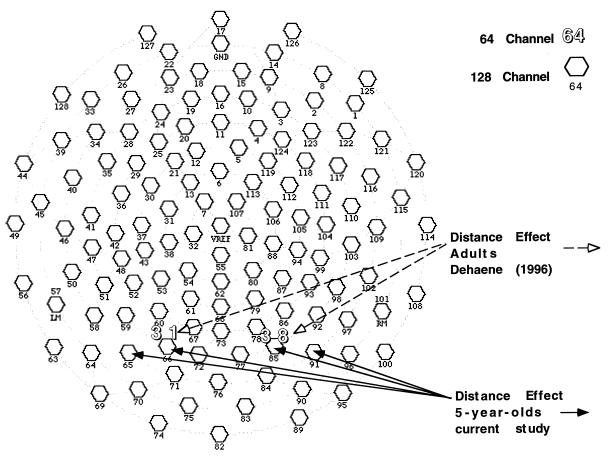
Figure 2.
A 128-channel geodesic sensor net map of recording sites. Channels 38 and 31 on the 64-channel map are where Dehaene (4) found voltage differences associated with distance. Preliminary analysis showed distance effect at electrode pairs 67 and 78, 66 and 85, 60 and 86, 65 and 91, 71 and 84, and 70 and 90. Results from representative electrode sites 66 and 85 and 65 and 91 are shown here.
Electroencephalography (EEG) Analysis.
Time-locked average reference ERPs were computed separately for each subject for close to 5 vs. far from 5 (distance) and for dot vs. digit (notation) stimuli. Editing of EEG data was performed by computer algorithm. Trials were rejected for eye blinks, movement, eye movement, and incorrect responses. The artifact-free trials were then baseline corrected for the 200 ms before stimulus onset, low-pass filtered at 40 Hz, and averaged for each subject. A grand average was created for all subjects in the same age group, consisting of 129 epochs of 256 samples for each experimental condition (4 numbers × 2 notations). The data were averaged separately for both notations (digit or dot) and for both distances (close to 5 or far from 5) within each notation. This averaged data were visualized by using a computer algorithm, graphical rendering of averaged data (GRAD).
Statistical Analysis.
EEG. These data were averaged across subjects and analyzed by nonparametric sign tests to isolate locations (electrode sites) and time spans of consistent differences between experimental conditions. Sample-by-sample nonparametric statistics were performed by using the Wilcoxon matched pairs signed-rank test to isolate the location and time window of consistent differences between experimental conditions. This information led to the selection of time windows of between 30–50 ms and electrodes of interest for each age group for which average voltages were obtained. These averages were analyzed by using an ANOVA with factors of laterality (left hemisphere vs. right hemisphere), notation (digit vs. dot), and distance (close to 5 vs. far from 5).
Behavioral.
Reaction times were rejected for incorrect responses and for responses more than 5 s. Reaction times and error rates for each age group were subjected to an ANOVA with notation (digit vs. dot), distance (close to 5 vs. far from 5), and magnitude (smaller than 5 vs. larger than 5) as within-subjects factors and target hand (left vs. right) as a between-subjects factor.
RESULTS
Behavioral.
Reaction times of both groups, shown in Table 1, were significantly longer for stimuli close to 5 (average RT was 519 ms for adults and 1,665 ms for children) than those far from 5 (average RT was 480 ms for adults and 1,495 ms for children). Analysis of the adult data showed main effects for notation [digits 22 ms faster than dots; F(1,13) = 31.344, P < 0.0001] and distance [far 39 ms faster than close; F(1,13) = 124.473, P < 0.0001]. Both notations showed a significant effect independently [digits; F(1,13) = 60.589, P < 0.0001 and dots; F(1,13) = 45.974, P < 0.0001]. No interaction between notation and distance was observed [F(1,13) < 1, P > 0.1]. The independence between notation and distance effect confirmed the previous results from adults (4).
Table 1.
Mean reaction time and error rates
| Adults
|
5-year-olds
|
|||
|---|---|---|---|---|
| RT (ms) | Errors (%) | RT (ms) | Errors (%) | |
| Overall | 498 | 2 | 1,576 | 6.3 |
| Digits | 488 | 1.75 | 1,565 | 7.3 |
| Close | 508 | 3 | 1,606 | 8.9 |
| Far | 469 | 0.5 | 1,524 | 5.8 |
| Dots | 510 | 2.2 | 1,594 | 5.3 |
| Close | 529 | 4.2 | 1,723 | 7.1 |
| Far | 490 | 0.2 | 1,466 | 3.5 |
Analysis of the data from 5-year-olds showed a main effect for distance [far 170 ms faster than close; F(1,12) = 21.246, P = 0.0006]. Far digits were 82 ms faster [F(1,13) = 5.107, P = 0.0416]. Far dots were 257 ms faster [F(1,13) = 14.9481, P = 0.0019]. Notation and distance did not significantly interact [F(1,13) = 4.357, P = 0.06], but there was a trend toward interaction reflecting the larger distance effect for the dots than for digits.
The interaction between the size of the distance effect and notation was shown to be true only for numbers larger than 5. When only the numbers smaller than 5 were analyzed, far digits were 166 ms faster than close, far dots were 143 ms faster than close, and no interaction between distance and notation was observed (F < 1, P > 0.1). Upon closer analysis it was observed that the trend toward an interaction was due primarily to increased RT for the digit 9.
Error rates showed this same discrepancy only to a greater degree. The error rates of 5-year-olds showed an effect for distance [F(1,12) = 4.984, P = 0.0454 (average error close to 5 = 8%, far from 5 = 4.7%)], but it was only significant with dots [F(1,13) = 5.2, P = 0.04]. This lack of significance in digits was because of an excess in errors for the digit 9 (9%). Smaller digits, 1 and 4, followed the expected distance effect. The error rates of adults showed an effect for distance [F(1,13) = 27.393, P = 0.0002 (average error close to 5 = 3.6%, far from 5 = 0.3%)]. The distance effect was significant for both notations [digits; F(1,14) = 7.5, P = 0.016 and dots; F(1,13) = 19.478, P = 0.0006]. The deterioration in the children’s performance for larger digits may reflect the approach of an upper limit of their abstract concept of numbers.
Electrophysiology.
We examined the brain areas associated with the behavioral distance effect for each age group. All electrode sites were analyzed and electrode pairs and time windows were chosen for further analysis based on proximity to electrodes reported by Dehaene, as well as the results of exploratory nonparametric statistics. Fig. 2 indicates electrodes showing a significant distance effect were located in an area very similar to those previously reported by Dehaene. Time windows used for the adult group were 124–174 ms and 184–234 ms after stimulus onset. Time windows for the children were 154–194 ms, 194–224 ms, and 356–396 ms after stimulus onset. Electrode pairs 67 and 78, 66 and 85, 60 and 86, 65 and 91, 71 and 84, and 70 and 90 (left hemisphere listed first) were analyzed with ANOVA (Fig. 2). There were significant effects for distance in each of the six chosen electrode pairs. Two of the electrode pairs (66 and 85 and 65 and 91) that were close to those reported previously and that were typical of the others were used for the comparison described below and one of them (91) is shown in Fig. 3 to illustrate the main effect of notation and the effect of distance for each notion for both adults and children.
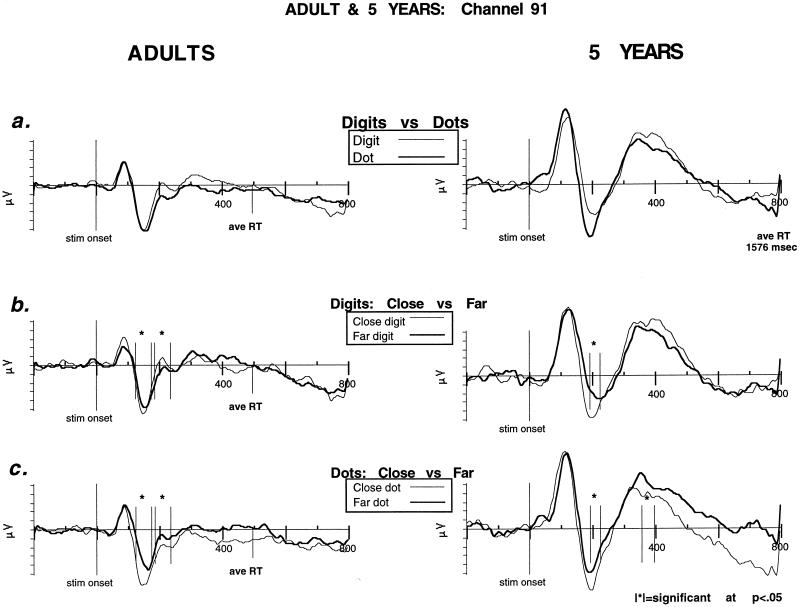
Figure 3.
Representative posterior channel (91) comparing ERPs in adults and 5-year-olds for a number comparison task. The x-axis is in milliseconds and corresponds to a 1-s epic of recorded EEG (200 ms baseline, 800 ms poststimulus). The y-axis is in microvolts. |∗|, significance at P < 0.5. (a) Notation effects (digits vs. dots). The two age groups show qualitatively similar initial components (P1, N1, and P2p) with only slightly delayed peaks in the 5-year-olds. (b) Digits (close vs. far). ERP distance effect for digits in both age groups. (c) Dots (close vs. far). ERP distance effect for dots in both age groups. Significant differences associated with distance began in children 50 ms after adults despite RTs > 1,000 ms longer.
Adults.
The waveforms showed at the selected sites had similar components to those reported previously by Dehaene (4). An initial positivity (P1) peaked at 98 ms (96 ms for digits and 100 ms for dots) after stimulus onset, and was followed by a negativity (N1) at about 170 ms (168 ms for digits and 172 ms for dots) after stimulus onset. As in Dehaene’s results, a second posterior positivity followed the N1, which Dehaene labeled as a P2p. The P2p culminated at 228 ms after stimulus onset. The time windows used in the ANOVA to identify ERP differences associated with distance were 124–174 ms and 184–234 ms, focusing on the N1 and the transition to the P2p.
The adult EEG data showed significant differences associated with distance for both notations in those time windows, close more negative than far in the first time window [digits 65 and 91: F(1,13) = 10.995, P = 0.0056; dots 66 and 85: F(1,13) = 35.305, P < 0.0001 and 91 and 65: F(1,13) = 20.244, P = 0.0006]. As the N1–P2p transition occurred, the close digits became more positive and were significantly more positive during the second time window [digits 61 and 95: F(1,13) = 7.109, P = 0.019 and 66 and 85: F(1,13) = 5.845, P = 0.031]. Dots remained significantly more negative [66 and 85; F(1,13) = 5.845, P = 0.031 and 65 and 91; F(1,13) = 7.109, P = 0.019]. No effect of laterality was seen for any of the electrode sites analyzed.
Children.
Initial effects of distance were seen for both digits and dots centered on the N1, 194–224 ms after stimulus, close more negative than far [digits 66 and 85: F(1,12) = 6.016, P = 0.03 and 65 and 91: F(1,12) = 7.247, P = 0.02; dots 65 and 91: F(1,12) = 6.761, P = 0.02]. The overall size of the ERPs for children were larger than for adults (11). However, the overall organization of brain activations seen in 5-year-olds was remarkably similar to those seen in adults, both in terms of brain area localization and components of waveform affected by distance (N1 and P2p). Furthermore, despite RTs three times as long (about 1,600 ms in children vs. 500 ms in adults), the major components of the waveform and the time at which a distance effect was observed were only slightly delayed in 5-year-olds when compared with adults. The first effects of distance in 5-year-olds were delayed approximately 50 ms when compared with adults. These subjects’ P1 culminated 124 ms after stimulus onset and 26 ms after adult P1, and the N1 culminated at 212 ms after stimulus and 42 ms after adult N1; the P2p was more delayed (412 ms poststimulus) 128–184 ms after adult P2p and quite broad (84 ms).
DISCUSSION
Both adults and children showed a behavioral distance effect for both notations, replicating reaction time studies done previously with 6-year-old children and adults (12, 13). Dehaene (4), recording scalp voltage with a 64-channel recording net, reported voltage differences associated with the distance effect for both Arabic digits and written number words at electrodes at the parieto-occipito-temporal junction (slightly right lateralized) from 174–230 ms after stimulus onset. These results led Dehaene to suggest that the distance effect represents a separate magnitude comparison step in processing carried out in localized brain areas involved in the abstract representation of magnitude, a “number comparison” area. The results from our adult subjects replicated Dehaene’s results with respect to comparison of digits, both in terms of the localization of the voltage difference and the approximate time after stimulus presentation those differences were observed, and we extended his results by identifying another number form, arrays of dots, in which this brain area is implicated. EEG data in adults showed significant differences associated with distance for digits in two time windows spanning 124–234 ms after stimulus onset (Fig. 3), centering on the first posterior negativity, N1, and a second positivity termed the P2p.
The processing of arrays of dots showed a voltage difference associated with distance in the same electrodes and in the same time windows as seen with the processing of digits both in this study and in Dehaene’s previous study. This voltage difference was large, significant, and slightly earlier than that seen for digits. (All channels analyzed showed differences beginning at 124 ms and continuing through 234 ms after stimulus.) The ERP distance effect seen with dots differed somewhat in its characteristics; rather than reversing polarity during the transition to the P2p, the far condition remained more negative than the close. This difference may be related to differences in the perceptual components of the far vs. the close stimuli or something more fundamental to the evaluation of quantity from these perceptual representations. However, considering only four easily discriminable dot patterns were used in our study, it is of interest that adults and children both seem to refer these patterns to the same comparison process as found with digits. This suggests that the analysis of quantity is highly similar irrespective of the input mode and lends further support to the identity of a localized inferior parietal brain area involved in abstract magnitude comparison. Contrary to previous EEG results, our results suggest that the area is bilateral rather than right-lateralized. More recent work by Dehaene using positron emission tomography (6), has suggested that bilateral brain areas may be associated with number comparison.
EEG analysis of 5-year-old subjects showed voltage differences associated with distance for both notations in the same regions as adults and only slightly delayed. The overall organization of brain activations seen in 5-year-olds was remarkably similar to those seen in adults. The ERP distance effect in children was centered around the same electrodes as the effect in adults. This scalp voltage signature has previously been shown to be modeled by dipoles (4) located within the parieto-temporo-occipital junction and this effect has been related to changes in blood flow in similar tasks (6). The components of the waveform affected by distance in the 5-year-olds was similar to those affected in the adults as well. The main effect of distance was observed in the N1 and P2p. This was highly similar to the adult results presented here and somewhat similar to previously reported adult results (4).
This study found somewhat earlier effects of distance than Dehaene’s in both children and adults. We see effects of distance in the first negativity as well as in the transition to the second positivity, whereas Dehaene reported only affects of notation on the N1. Dehaene’s subjects were more practiced with faster reaction times than our subjects. The differences we see when the distance effect begins may be because of this difference in procedural methods. The ERP effect we see in the N1 may reflect the strong attention when the task is less practiced. Also, it is possible that the larger number of electrodes used in our study has increased the sensitivity to these effects.
Regardless of these differences, the scalp voltage signature associated with the distance effect was strikingly similar for both groups. Both groups showed the same scalp differences when making decisions about magnitude. These differences occurred early in the processing and were centered at the same components of the waveform. In addition to the similarities seen in brain areas and components of the waveform affected by distance and despite RTs three times as long (about 1,600 ms in children vs. 500 ms in adults), the major components of the waveform and the time at which a distance effect was observed were only slightly delayed in 5-year-olds as compared with adults.
What might account for the long RTs of the 5-year-olds? One reason was clear in the behavior of the 5-year-olds who systematically looked down at about 1 s to verify the correct key to press. The association of the quantity computation with an arbitrary key press seemed to be much more difficult for the children than for the adults. We suspect that this overt behavior, signifying difficulty with associating a behavior with the internal computation of quantity, may reflect a more profound difficulty of children of this age in organizing appropriate voluntary actions to reflect internal thoughts (14), particularly those computed by posterior structures (15). This idea is consistent with the slow maturation of frontal areas (16) and clearly requires further study.
The ERP results coupled with the results of the RT analysis lead to a number of significant conclusions. These results suggest that a localized area of the brain, the “number comparison” area, is involved in response to questions of magnitude comparison independent of the notation. This brain region has shown differences when making quantitative judgments of three different notations, a perceptual form of number in an array of dots (•), a digit form (1), and a written form (one) (4). This suggests that the processing of any of these forms of numbers involves the abstraction of magnitude, and the brain areas responsible for that abstract representation are located in the inferior parietal areas of the brain. These results suggest that this area develops and is responsive to number comparison before the age of 5 and formal mathematical training.
Although Piaget concluded in the 1950s that preschoolers lack a basic concept of numbers (17), more recent research has discovered that children possess an elementary concept of numbers that is much richer than previously thought (18). This concept of numbers may be present from birth (19, 20) and is present in many animals species (21). Recently there have been empirical efforts to train number comparison in low socioeconomic status children at risk for failure in elementary school arithmetic (22). The results of our study suggest that the success of these methods may lie in their ability to develop connections between input and a preexisting number comparison area. Our studies indicate that because normal children develop brain areas involved in understanding quantity before the age of 5, intervention for at-risk children may be more successful when begun before the first grade.
More generally, our studies identify tools that may be used to understand further how the brain is reorganized through learning and to examine educational strategies in school instruction. The importance of detailed analysis of brain circuitry during the performance of these tasks is reinforced by striking differences between the acquisition of the visual word form in reading (3) and the number comparison area. Our studies of reading suggest that the visual word form undergoes a very lengthy developmental process and is still quite different from what is found in adults even at the age of 10, when children read well (5). On the other hand, this study suggests that the number comparison area is similar to adults even by the age of 5. The ability to study brain circuitry during reading and arithmetic provides the possibility of observing changes in circuitry during the acquisition of many forms of learning and could help to indicate which teaching strategies are most effective, not only in mathematics, but also in listening, reading, and other skills.
Acknowledgments
This research was supported by Office of Naval Research Grant N00014-96-0273 and by the James S. McDonnell, Pew Memorial Trusts, and W. M. Keck Foundations through a grant to the Center for the Cognitive Neuroscience of Attention. Elise Temple was supported, in part, by a grant from the Howard Hughes Medical Institute.
ABBREVIATIONS
- RT
reaction time
- EEG
electroencephalography
- ERP
event related potentials
References
- 1.Posner M I, DiGirolamo G J, Fernandez-Duque D. J Consciousness Cognition. 1997;6:267–290. [PubMed] [Google Scholar]
- 2.Abdullaev Y, Posner M I. Neuroimage. 1998;7:1–13. doi: 10.1006/nimg.1997.0309. [DOI] [PubMed] [Google Scholar]
- 3.McCandliss B D, Posner M I, Givón T. Cognit Psychol. 1997;33:88–110. [Google Scholar]
- 4.Dehaene S. J Cognit Neurosci. 1996;8:47–68. doi: 10.1162/jocn.1996.8.1.47. [DOI] [PubMed] [Google Scholar]
- 5.McCandliss B. Ph.D. thesis. Eugene, OR: Univ. of Oregon; 1997. [Google Scholar]
- 6.Dehaene S, Tzurio N, Frak V, Raynaud L, Cohen L, Mehler J, Mazoyer B. Neuropsychology. 1996;34:1097–1106. doi: 10.1016/0028-3932(96)00027-9. [DOI] [PubMed] [Google Scholar]
- 7.Moyer R S, Landauer T K. Nature (London) 1967;215:1519–1520. doi: 10.1038/2151519a0. [DOI] [PubMed] [Google Scholar]
- 8.Sternberg S. Acta Psychologia. 1969;30:276–315. [Google Scholar]
- 9.Tucker D M, Liotti M, Potts G, Russell G, Posner M I. Hum Brain Mapp. 1994;1:134–152. [Google Scholar]
- 10.Griffin S, Case R, Seigler R S. In: Classroom Lessons: Integrating Cognitive Theory and Classroom Practice. McGilly K, editor. Cambridge, MA: MIT Press; 1995. pp. 25–49. [Google Scholar]
- 11.Dustman R E, Schenkenberg T, Lewis E G, Beck E C. In: Visual Evoked Potentials in Man. Desmedt J E, editor. Oxford: Clarendon; 1977. pp. 363–377. [Google Scholar]
- 12.Dehaene S, Alkhavein R. J Exp Psychol. 1995;21:314–326. doi: 10.1037//0278-7393.21.2.314. [DOI] [PubMed] [Google Scholar]
- 13.Sekuler R, Mierkiewicz D. Child Dev. 1977;48:630–633. [Google Scholar]
- 14.Diamond A. Dev Psychobiol. 1989;22:271–294. doi: 10.1002/dev.420220307. [DOI] [PubMed] [Google Scholar]
- 15.Diamond A. In: Brain Maturation and Cognitive Development: Comparative and Cross-Cultural Perspectives–Foundations of Human Behavior. Gibson K R, Petersen A C, editors. New York: de Gruyter; 1991. pp. 127–180. [Google Scholar]
- 16.Thatcher, R. W. Dev. Neuropsych. 7, 397–419.
- 17.Piaget J. The Child’s Conception of Number. New York: Norton; 1952. [Google Scholar]
- 18.Gelman R, Gallistel C R. The Child’s Understanding of Number. Cambridge, MA: Harvard Univ. Press; 1986. [Google Scholar]
- 19.Starkey P, Spelke E S, Gelman R. Cognition. 1990;36:97–127. doi: 10.1016/0010-0277(90)90001-z. [DOI] [PubMed] [Google Scholar]
- 20.Wynn K. Nature (London) 1992;358:749–750. doi: 10.1038/358749a0. [DOI] [PubMed] [Google Scholar]
- 21.Dehaene S, Changeaux J. J Cognit Neurosci. 1993;5:390–406. doi: 10.1162/jocn.1993.5.4.390. [DOI] [PubMed] [Google Scholar]
- 22.Griffin S, Case R, Capodilupo A. In: Teaching for Transfer: Fostering Generalization in Learning. McKeough A, Lupart J, Marini A, editors. Mahwah, NJ: Erlbaum; 1995. pp. 123–151. [Google Scholar]