Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2008 Apr 1.
Published in final edited form as: J Acoust Soc Am. 2007 Oct;122(4):EL107–EL114. doi: 10.1121/1.2771369

A comparison of vocal tract perturbation patterns based on statistical and acoustic considerations

Brad H Story 1
PMCID: PMC2278006  NIHMSID: NIHMS43051  PMID: 17902738

Abstract

The purpose of this study was to investigate the relation between vocal tract deformation patterns obtained from statistical analyses of a set of area functions representative of a vowel repertoire, and the acoustic properties of a neutral vocal tract shape. Acoustic sensitivity functions were calculated for a mean area function based on seven different speakers. Specific linear combinations of the sensitivity functions corresponding to the first two formant frequencies were shown to possess essentially the amplitude variation along the vocal tract length as the statistically-derived deformation patterns reported in previous studies.

1. Introduction

Statistical analyses of collections of tongue configurations or complete vocal tract shapes (i.e., area functions) have revealed that a small number of canonical deformation patterns (variously referred to as factors, components, basis functions, or modes) can explain most of the variation in vocal tract shape during vowel production (Harshman et al. 1977; Shirai and Honda, 1977; Jackson, 1988; Johnson et al. 1993; Nix et al. 1996; Story and Titze, 1998; Hoole, 1999; Zheng et al. 2003; Iskarous, 2005; Story, 2005; Mokhtari et al. 2007). These deformation patterns tend to exhibit similarities in shape across speakers and are related to specific formant frequency patterns when superimposed on a mean or neutral vocal tract shape.

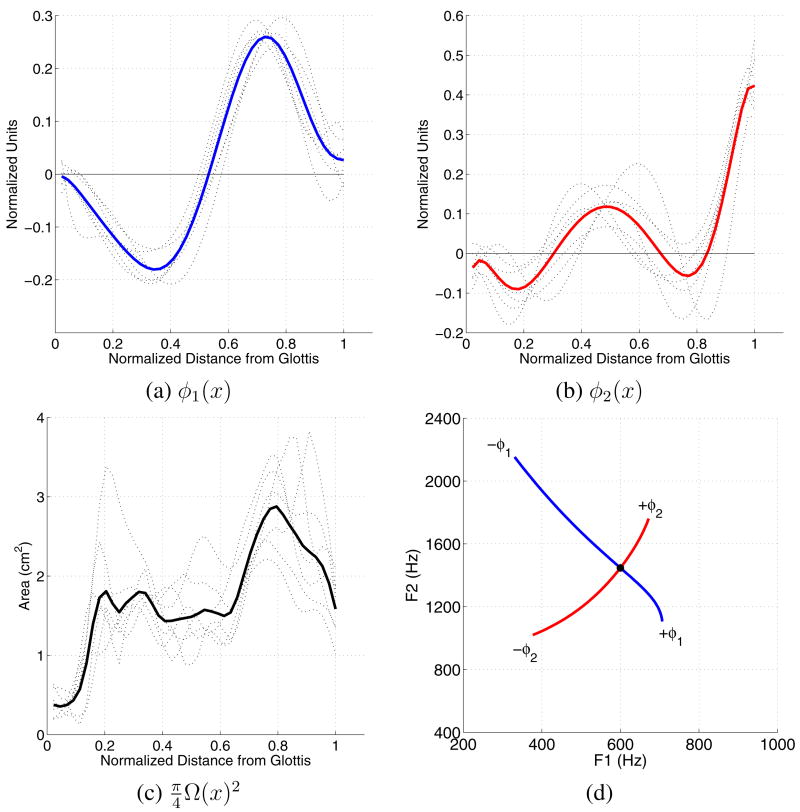
As an example, mode shapes (deformation patterns) and mean area functions determined with principal component analysis are shown by the dotted lines in Figure 1 for the one speaker of Story and Titze (1998) and the six speakers of Story (2005). The vocal tract length has been normalized so they can be easily compared. The thick line in each plot indicates the mean shape calculated across the seven speakers and is shown to summarize the general shape. The two modes shown accounted for at least 85 percent of the total variance in each speaker’s collection vowel area functions. Mathematically, an arbitrary area function for a particular speaker can be represented as,

Figure 1.

Figure 1

Open in a new tab

(Color online) Mode shapes and mean area functions for seven speakers (dotted lines) from Story and Titze (1998) and Story (2005), along with the [F1, F2] plot produced by each mode isolation. The vocal tract lengths have been normalized to 1.0 so they can be overlaid for comparison purposes. The thick lines indicate the mean of the given function in each plot. (a) first mode φ1, (b) second mode φ2, (c) mean area function (MAF) π4Ω2, and (d) [F1, F2] trajectories produced by independently superimposing φ1 and φ2 on the MAF.

V(x)=π4[Ω(x)+q1φ1(x)+q2φ2(x)]2 (1)

where x is the distance from the glottis, Ω(x) is the mean diameter function, φ1(x) and φ2(x) are the modes, and q1 and q2 are the weighting coefficients1. When used in Eqn. (1) with a positive weighting coefficient, the first mode φ1 for any of the speakers would have the spatial effect of expanding the front portion of the vocal tract while constricting the back, whereas, a negative coefficient would have the opposite effect. Although there is variation among the speakers, in any of the cases a positively weighted second mode φ2 would impose expansions in the lip and mid-tract regions, and constrictions posterior to the lips (between 0.6–0.85 in Fig. 1b) and just above the glottis. A negative coefficient would again create the opposite spatial effect.

To demonstrate the effects of each mode on the first two formant frequencies (F1 and F2), the mean φ1 and φ2 shown in Figs. 1a and 1b were superimposed on the mean vocal tract shape (Fig. 1c) according to Eqn. (1). The scaling coefficients were incrementally varied as q1 = [−4.5, 4.0] while q2 = 0 and again as q2 = [−2.5, 2.5] while q1 = 0. Formant frequencies calculated for each of the series of area functions generated along the respective coefficient continua are plotted in the [F1,F2] space shown in Figure 1d. Relative to the neutral position denoted by the solid dot at [600,1450] Hz, a negatively scaled −φ1 decreases F1 while increasing F2, whereas a positive scaling increases F1 and decreases F2. For φ2, a negative scaling coefficient will cause both F1 and F2 to decrease, whereas a positive scaling will have the opposite effect. The endpoints of each [F1,F2] trajectory roughly correspond to the vowels [i æ ɑ u] in respective clockwise order, beginning in the upper left hand corner of the plot. Although this demonstration is somewhat artificial because it is based on average modes across speakers, similar effects for F1 and F2 have been previously reported for all seven speakers. Various other studies have also reported prinicipal component analyses of area functions that resulted in modes shapes similar to those in Figs. 1a and 1b (Meyer et al. 1989; Yehia et al. 1996; Mokhtari et al. 2007).

Although the modes are statistical constructs that describe a specific set of vocal tract data, their similarity across speakers suggests that they could represent some kind of generalized vocal tract shaping patterns that are produced and scaled by the speech motor system during vowel production. But why is it that these particular mode shapes emerge from the analyses of vocal tract data? It is possible that they are an artifact of the type of analysis performed. For instance, if a covariance matrix generated from a set of vocal tract shapes takes on Toeplitz form, the eigenvectors (e.g., modes, components, basis functions) of that matrix will be sinusoidal (cf. Jolliffe, 2004) and could perhaps resemble the modes shown in Fig. 1. In such a case, the modes could be expected to reconstruct the original data with small error, but may not be related to anything specifically articulatory or acoustic. The systematic relation of the modes to the first two formant frequencies, however, suggests that their shapes emerge in order to exploit the acoustic properties of the vocal tract itself. In this view, the particular variation of each mode along the length of the vocal tract should reflect some representation of the pressure and volume velocity distribution that exists within the vocal tract at the resonance (formant) frequencies, and would predict how those frequencies should change when each mode is superimposed on a given vocal tract shape.

The concept that global changes in vocal tract shape during speech could be explained by the acoustic properties of a uniform tube was established by Schroeder (1967) and Mermelstein (1967). Using considerations of potential and kinetic energy densities, both showed that a uniform tube (i.e., an area function with constant area), of length comparable to a human vocal tract, could be systematically perturbed with a superposition of a series of sinusoids to produce area functions that supported a particular set of formant frequencies. Similar acoustic theory was later used by Fant and Pauli (1975) to predict the direction of formant frequency change when small perturbations were applied to a specific area function. They calculated acoustic “sensitivity functions” which quantify the difference between potential and kinetic energy at each formant frequency as a function of the distance along the vocal tract. Thus, these functions can be used to indicate which parts of the area function should be expanded or contracted in order to move a formant frequency toward a desired value. Mrayati, Carré, & Guérin (1988) made extensive use of sensitivity functions to develop a model, called the Distinctive Region Model (DRM), in which a uniform tube representation of the vocal tract could be divided into a small number of regions (4–8 depending the number of formants to be controlled), each of which could impose a “distinctive” change in the formant frequencies when expanded or contracted. Although the DRM was criticized for being too simplistic as a comprehensive model of speech production (cf. Boe & Perrier, 1990), it clearly demonstrated that formant frequencies could be efficiently moved when tube shape changes were roughly aligned with the distinctive regions. More recently, Carré (2004) has reported similar results when the vocal tract tube shape is perturbed with scaled versions of the sensitivity functions themselves, rather than the discrete regions of the DRM. Carré (2004) emphasizes that the shape changes imposed on a uniform tube that produce speech-like formant patterns are based purely on the acoustic properties of that tube; i.e. other than approximate length, no a priori knowledge of the human vocal tract was assumed. If such theoretically-based shape changes are truly indicative of those produced during speech, then they should be well correlated with vocal tract shaping patterns derived from human articulatory data.

Using the factors derived from tongue configuration data reported by Harshman et al. (1977), Fitch et al. (2003) developed a sinusoidal model of vocal tract shape. That is, two sinusoids were used to approximate the effect of the factors on the vocal tract area function. They noted a correspondence between the shapes of linear combinations of the sinusoidal components in the model and the variation of the sensitivity functions for F1 and F2. The implication was this particular representation of articulatory patterns did indeed exploit the acoustic sensitivity of the vocal tract. At nearly the same time, Ru et al. (2003) reported a similar sinusoidal model of the area function that was also based on the Harshman et al. factors. Whereas the goals of this study were different than Fitch et al., an equivalence between the acoustic characteristics of the vocal tract and the sinusoidal components was noted.

Although the area function-based modes share some similarities with the factors reported by Harshman et al. (1977) and others, they are not identical, and hence their relation to sensitivity functions is expected to be somewhat different. The purpose of this letter is to demonstrate that each of the two modes derived from principal component analyses of area functions (e.g., Fig. 1) corresponds to specific linear combinations of acoustic sensitivity functions. It will be shown that such a correspondence provides some explanation as to why these common mode shapes are observed across speakers for vowel production.

2. Sensitivity functions

As a demonstration case, sensitivity functions were calculated for the “mean of the mean area functions” shown by the dark line in Fig. 1c. This idealized vocal tract shape, henceforth referred to as “MAF,” contains features typical of the mean area functions that have been calculated for various speakers. For example, the initial 10 percent (0.1) of the normalized tract length tends to coincide with small cross-sectional areas (approx. 0.4 cm2 in Fig. 1c) and is sometimes referred to as the epilaryngeal space. The pharyngeal portion extending from about 0.2 to 0.6 (of normalized length) is fairly constant with an area of about 1.5 cm2, whereas, in the oral cavity there is a moderate expansion.

For computational purposes MAF was represented by two vectors, a(i) and l(i), which are the cross-sectional areas and lengths, respectively, of each of 44 sections (i = [1 … 44]) extending along the vocal tract from glottis to lips. Because the sensitivity function calculation requires an actual vocal tract length (rather than a normalized length), the 44 sections of the length vector were each assigned a value of l(i) = 0.4 cm. This choice generates a total tract length of 17.6 cm which is typical of an adult male speaker. Although it may seem inappropriate to impose a male tract length on an area function that is based on both male and female speakers, the amplitude variation of the sensitivity functions along the tract length is unaffected by uniform length scaling. Hence, the choice of section length is arbitrary and the normalized length axis will be maintained for subsequent plots.

The method for calculation of sensitivity functions for this study was identical to that described in Story (2006) in which pressures, flows, frequency response functions, kinetic and potential energies were determined with a transmission-line type model of the vocal tract [e.g., Sondhi and Schroeter, 1987; Story, et al. 2000] that included energy losses due to yielding walls, viscosity, heat conduction, and acoustic radiation at the lips. The sensitivity of a specific formant frequency to a change in cross–sectional area can be defined as the difference between the kinetic energy (KE) and potential energy (P E) as a function of distance from the glottis, divided by the total energy in the system (Fant & Pauli, 1975). A set of sensitivity functions Sn(i) can be determined for the resonance frequencies (formants), Fn, of any given area function a(i), where n is the formant number. In theory, sensitivity functions, Sn(i) can be used to compute the change in a particular formant frequency (Fn) due to perturbation of the area function (Δa) with the relation,

ΔFnFn=∑i=1NsSn(i)Δa(i)a(i). (2)

where Ns is the number of sections comprising the area function. When the sensitivity function Sn(i) is positively valued and an area perturbation is also positive (i.e., area is increased), the change in formant frequency will be upward. If the area change is negative (area decreased) the formant frequency will decrease. When the sensitivity function is negatively valued, the opposite effect occurs for positive or negative area perturbations, respectively.

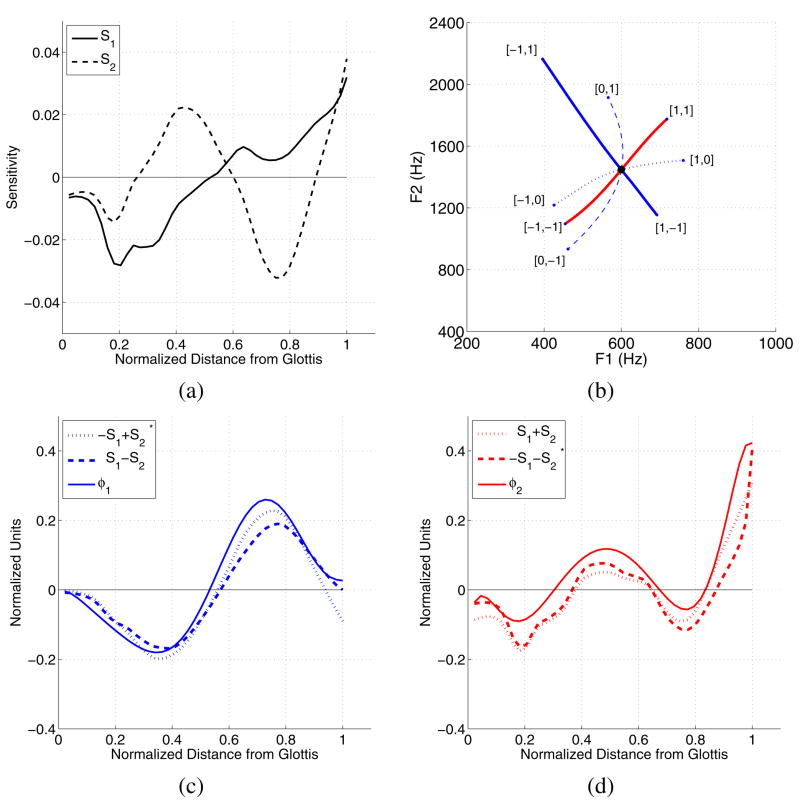
The sensitivity functions, S1 and S2, calculated for MAF are shown in Fig. 2a. Each line extends along the distance from the glottis to lips and indicates the relative sensitivity of the first and second formants (F1 and F2) to a small perturbation of the area function (Δa(i)). Using S1 in Fig. 2a and Eqn. 2 as a guide, it is observed that F1 could be increased by expanding the area in the front half (0.5–1.0 of the normalized tract length) of the vocal tract. F1 could also be increased by constricting the regions between the glottis and halfway to the lip termination. Lowering F1 would require the opposite changes in area within the same regions. For S2, an increase in F2 could be produced by expanding the regions between 0.25–0.6 and 0.9–1.0 of the normalized length, and constricting the regions of the area function that extend from 0–0.25 and 0.6–0.9; lowering F2 would require the opposite changes in area.

Figure 2.

Figure 2

Open in a new tab

(Color online) (a) Sensitivity functions calculated for the first two resonances of MAF (dark line in Fig. 1c), (b) [F1,F2] trajectories produced by Eqn. 4 with eight different settings of the z1 and z2 coefficients, (c) comparison of φ1 (solid) to the mean (−S1 + S2) (dotted) and mean (S1 −S2) (dashed), and (d) comparison of φ2 (solid) to the mean (S1 + S2) (dotted) and mean (−S1 − S2) (dashed). In (c) and (d), the sensitivity function combinations have been linearly scaled so that they have roughly the same amplitude as the modes and those with an * have been flipped in polarity purely for visual comparison purposes.

3. Comparison of sensitivity function perturbations and vocal tract modes

The predictions afforded by the shapes of the sensitivity functions in Fig. 2 suggest that formant frequencies could be controlled and positioned (in the acoustic domain) by perturbing the original vocal tract shape with replicas of the sensitivity functions themselves (Carré, 2004; Story, 2006). For example, direct superposition of S1 on MAF would raise F1, whereas its opposite, −S1, would lower it. Similarly F2 could be controlled with a superposition of a scaled S 2 replica, where +S2 would increase F2 and −S2 would decrease it.

It follows that simultaneous modification of F1 and F2 could be realized with a superposition of both S1 and S2. For example, when appropriately scaled to affect cross-sectional area and superimposed on the original area function, the combination (S1 − S2) would be expected to alter the vocal tract shape such that F1 increases and F2 decreases. An arbitrary area function can be described mathematically as,

anew(i)=a0(i)+[z1S1(i)+z2S2(i)]         i=[1,Nareas] (3)

where a0(i) is the area function on which S1(i) and S2(i) are based, and anew (i) is a new area function generated by the superposition of the linear combination. The z1 and z2 are scaling coefficients that, for the example above, would be equal to 1 and −1, respectively. Because the sensitivity functions are dependent on a particular vocal tract shape, the prediction of formant frequency change is limited to small area changes. Thus, generating vocal tract deformations comparable to those during vowel production requires an iterative perturbation process in which anew(i) in Eqn. 3 replaces a0(i) in subsequent iterations. Eqn. 2 can be recast as,

ak+1(i)=ak(i)+[z1S1k(i)+z2S2k(i)]         i=[1,Nareas],         k=[0,Niter] (4)

where the ak (i)’s and S nk ‘s are area vectors and sensitivity functions, respectively, at successive iterations, and k is the iteration index which ranges from 0 (to denote the initial area function) to the number of desired iterations (Niter ).

Using Eqn. 4 with MAF as the initial vocal tract shape a0(i), a series of area vectors was generated for each of eight different settings of the z1 and z2 coefficients. These consisted of all combinations of z1 = [−1, 0, 1] and z2 = [−1, 0, 1] (except for [0,0]) where, in each case, area vectors were generated for a maximum of 50 iterations or until the minimum area was equal to 0.2cm2. The [F1,F2] formant trajectories corresponding to each coefficient setting are shown in Fig. 2b as projecting outward from a central point determined by the formant frequencies of MAF. The dotted and dashed lines indicate the effect of a perturbation based on only the positive and negative polarities S1 or S2, respectively; i.e. either z1 or z2 was zero. The S1 trajectory (dotted) primarily traverses the F1 dimension but does curve upward in F2 on the [1,0] side and downward on the [−1,0] side. In contrast, the S2 trajectory (dashed) moves mostly along the F2 dimension, but curves downward (in frequency) in the F1 dimension at both ends. The other two trajectories, shown as solid lines in Fig. 2b, are the result of the four linear combinations of both S 1 and S2 in which z1 and z2 were equal to either 1 or −1. The trajectory corresponding to [−1,1] and [1,−1] is nearly linear and extends from a region of low F1 and high F2 to a region of high F1 and low F2, the endpoints of which would roughly correspond to the vowels /i/ and /ɑ/ or /ɔ/. A nearly opposite change in formant frequencies is traced out by the trajectory corresponding to [−1,−1] where F1 and F2 are both low, and [1,1] where both F1 and F2 are high. This trajectory is also fairly linear and the endpoints would approximately correspond to the vowels /u/ or /o/ at the lower left hand corner and /ae/ at the upper right.

These latter two trajectories nearly replicate the paths through the [F1,F2] space produced by the φ1 and φ2 modes presented previously in Fig. 1d. Since the initial area function (MAF) was the same for both the mode-based and sensitivity-based perturbations, it should follow that the perturbation shapes of either method should be similar. Shown in Fig. 2c are the means of the linear combinations (S1 − S2) and (−S1 + S2) plotted along with the φ1 mode from Fig. 1a. For ease of visual comparison, the amplitudes of each function have been similarly scaled and the polarity of the (−S1 + S2) perturbation has been intentionally flipped. With the exception of a zero crossing offset near the middle of the vocal tract and a slight difference in amplitude at the lips, the two sensitivity-based perturbation appear to be nearly identical to φ1. To quantify the similarity, a correlation coefficient (R) was calculated for each sensitivity-based perturbation relative to φ1, and resulted in both being equal to R = 0.97. A similar plot is shown in Fig. 2d where the φ 2 mode is compared to the means of the linear combinations (−S1 − S2) and (S1 + S2). Although the similarity is perhaps not as visually distinct as in the previous case, the correlation coefficients for the two sensitivity-based perturbations relative to φ2 are 0.92 and 0.97, respectively. It can also be observed that each of the three perturbation functions would generate expansions and constrictions in nearly the same locations along the tract length. The main differences consist of slight offsets of the zero crossing locations and a greater amplitude of the negative portions of (−S1 − S2) and (S1 + S2).

4. Discussion

The results of this study suggest that the shape of the statistically-based area function modes can be approximately related to acoustic sensitivity functions with the following equivalences,

+φ1≡(+S1−S2),         [F1↑F2↓]−φ1≡(−S1+S2),         [F1↓F2↑]+φ2≡(+S1+S2),         [F1↑F2↑]−φ2≡(−S1−S2),         [F1↓F2↓] (5)

where the directions of formant frequency changes due to a superposition of either a mode or sensitivity function combination are shown in the right column. The implication is that the vocal tract shaping patterns (i.e., φ1 and φ2) determined through statistical analyses of sets of area functions represent essentially the same spatial variation along the length of the vocal tract as do these linear combinations of the sensitivity functions. In either case, it is noteworthy that the perturbations move F1 and F2 from a neutral location toward the corners of the vowel space that approximately correspond to [i æ ɑ u]. Carré (2004) reported similar trajectories and noted that shape changes based on sensitivity function combinations could achieve a given acoustic contrast more effectively than those based on a single sensitivity function. That is, vocal tract perturbation patterns that create simultaneous changes to both F1 and F2 provide an efficient means by which to navigate the vowel space. Thus, the equivalence of the φ1 and φ2 modes with particular combinations of S1 and S2 would seem to emerge because these shapes allow for efficient traversal to the extreme regions of the acoustic vowel space.

Acknowledgments

This research was supported by NIH grant number R01-DC04789.

Footnotes

1

Since the principal components analysis was performed on the equivalent diameters of each cross-sectional area within the area function sets, the squaring operation and scaling by π/4 are needed to convert diameter to area (see Story, 2005 for details).

References

  1. Boë LJ, Perrier P. Comments on “Distinctive regions and modes: A new theory of speech production” by M. Mrayati, R. Carré and B. Guérin. Speech Comm. 1990;9:217–230. [Google Scholar]
  2. Carré R. From an acoustic tube to speech production. Speech Comm. 2004;42:227–240. [Google Scholar]
  3. Fant G, Pauli S. Spatial characteristics of vocal tract resonance modes. Proc. Speech Comm. Sem. 74.; Stockholm, Sweden. Aug 1–3; 1974. pp. 121–132. [Google Scholar]
  4. Fitch HL, Kupin JJ, Kessler IJ, Delucia J. Relating articulation and acoustics through a sinusoidal description of vocal tract shape. Speech Comm. 2003;39:243–268. [Google Scholar]
  5. Harshman R, Ladefoged P, Goldstein L. Factor analysis of tongue shapes. J Acoust Soc Am. 1977;62(3):693–707. doi: 10.1121/1.381581. [DOI] [PubMed] [Google Scholar]
  6. Hoole P. On the lingual organization of the German vowel system. J Acoust Soc Am. 1999;106:1020–1032. doi: 10.1121/1.428053. [DOI] [PubMed] [Google Scholar]
  7. Iskarous K. Patterns of tongue movement, J. Phonetics. 2005;33:363–381. [Google Scholar]
  8. Jackson MTT. Analysis of tongue positions: Language-specific and cross-linguistic models. J Acoust Soc Am. 1988;84(1):124–143. doi: 10.1121/1.396979. [DOI] [PubMed] [Google Scholar]
  9. Johnson K, Ladefoged P, Lindau M. Individual differences in vowel production. J Acoust Soc Am. 1993;94:701–714. doi: 10.1121/1.406887. [DOI] [PubMed] [Google Scholar]
  10. Jolliffe IT. Principal Component Analysis. 2. Springer; 2004. [Google Scholar]
  11. Mermelstein P. Determination of the vocal-tract shape from measured formant frequencies. J Acoust Soc Am. 1967;41(5):1283–1294. doi: 10.1121/1.1910470. [DOI] [PubMed] [Google Scholar]
  12. Meyer P, Wilhelms R, Strube HW. A quasiarticulatory speech synthesizer for German language running in real time. J Acoust Soc Am. 1989;86(2):523–539. [Google Scholar]
  13. Mokhtari P, Kitamura T, Takemoto H, Honda K. Principal components of vocal tract area functions and inversion of vowels by linear regression of cepstrum coefficients, J. Phonetics. 2007;35:20–39. [Google Scholar]
  14. Mrayati M, Carre R, Guerin B. Distinctive regions and modes: A new theory of speech production. Speech Comm. 1988;7:257–286. [Google Scholar]
  15. Nix DA, Papcun G, Hogden J, Zlokarnik I. Two cross-linguistic factors underlying tongue shapes for vowels. J Acoust Soc Am. 1996;99(6):3707–3717. doi: 10.1121/1.414968. [DOI] [PubMed] [Google Scholar]
  16. Ru P, Chi T, Shamma S. The synergy between speech production and perception. J Acoust Soc Am. 2003;113(1):498–515. doi: 10.1121/1.1525288. [DOI] [PubMed] [Google Scholar]
  17. Schroeder MR. Determination of the geometry of the human vocal tract by acoustic measurements. J Acoust Soc Am. 1967;41(4):1002–1010. doi: 10.1121/1.1910429. [DOI] [PubMed] [Google Scholar]
  18. Shirai K, Honda M. In: Estimation of articulatory motion, in Dynamic Aspects of Speech Production. Sawashima M, Cooper F, editors. Univ. of Tokyo Press; 1977. pp. 279–302. [Google Scholar]
  19. Sondhi MM, Schroeter J. A hybrid time-frequency domain articulatory speech synthesizer. IEEE Trans ASSP. 1987;ASSP-35(7):955–967. [Google Scholar]
  20. Story BH. A technique for “tuning” vocal tract area functions based on acoustic sensitivity functions. J Acoust Soc Am. 2006;119(2):715–718. doi: 10.1121/1.2151802. [DOI] [PubMed] [Google Scholar]
  21. Story BH. Synergistic modes of vocal tract articulation for American English vowels. J Acoust Soc Am. 2005;118(6):3834–3859. doi: 10.1121/1.2118367. [DOI] [PubMed] [Google Scholar]
  22. Story BH, Laukkanen AM, Titze IR. Acoustic impedance of an artificially lengthened and constricted vocal tract, J. Voice. 2000;14(4):455–469. doi: 10.1016/s0892-1997(00)80003-x. [DOI] [PubMed] [Google Scholar]
  23. Story BH, Titze IR. Parameterization of vocal tract area functions by empirical orthogonal modes. Journal of Phonetics. 1998;26(3):223–260. [Google Scholar]
  24. Yehia HC, Takeda K, Itakura F. An acoustically oriented vocal-tract model. IEICE Trans Inf & Syst. 1996;E79-D(8):1198–1208. [Google Scholar]
  25. Zheng Y, Hasegawa-Johnson M, Pizza S. Analysis of the three-dimesional tongue shape using a three-factor analysis model. J Acoust Soc Am. 2003;113(1):478–486. doi: 10.1121/1.1520538. [DOI] [PubMed] [Google Scholar]

RESOURCES