Statistical Methodology for Classifying Units on the Basis of Multiple Related Measures

SUMMARY

Both the private and public sectors have begun giving financial incentives to health care providers, such as hospitals, delivering superior ”quality of care”. Quality of care is assessed through a set of disease specific measures that characterize the performance of health care providers. These measure are then combined into an unidimensional composite score. Most of the programs that reward superior performance use raw averages of the measures as the composite score. The scores based on raw averages fail to take into account typical characteristics of data used for performance evaluation, such as within-patient and within-hospital correlation, variable number of measures available in different hospitals, and missing data. In this article we contrast two different versions of composites based on raw average scores with a model-based score constructed using a latent variable model. We also present two methods to identify hospitals with superior performance. The methods are illustrated using national data collected to evaluate quality of care delivered by US acute care hospitals.

1. Introduction

Recently there has been a national debate about using financial incentives to improve quality of care delivered by US health providers [1]. Several programs have been implemented that reward hospitals based on their quality of care as measured by quality indicators. For example, the Centers for Medicare and Medicaid Services (CMS) initiated in 2005 the Premier Hospital Quality Incentive Demonstration project that paid bonuses totaling $8.85 million to 123 superior (those in the upper decile) performing institutions that voluntarily participated in the project [2]. Several concerns have been raised regarding how to construct a composite measure of quality, however. Most of the issues raised about the adoption of such initiatives do not necessarily reflect statistical concerns, rather they reflect social, ethical, medical, political and economical issues. However, the implementation of such financial incentives rely on the use of statistical methods for the analysis of the performance data reported by each hospital. Therefore there is the need to investigate the various approaches, and propose a valid and appropriate methodology to be used for such problems.

Quality of care is an abstract and multidimensional construct that cannot be measured directly. Instead, several measurable indicators are used to characterize a certain dimension of ”quality of care”. To read more about the concept of quality of care see, for example, the series of articles on this topic published in the New England Journal of Medicine [3; 4; 5; 6; 7; 8]. Several authors identify three dimensions of quality of care: structure, process, and outcome. Structural measures are characteristics of the health provider (e.g., nursing ratios and presence of residency programs). Process measure are the components of the encounter between a physician or another health care professional and a patient (e.g., appropriate use of peri-operative beta blockade). Outcome measures refer to the patient's subsequent health status (e.g., mortality). In this article we use data on hospital quality of care, evaluated by several process-based measures.

Statistical methods for comparing health care providers based on one single outcome have been described before [9; 10]. The major statistical challenge when the performance is based on multiple measures is to summarize all the measures into an unidimensional composite score. This composite score should be a valid and reliable overall measure of quality of care for a hospital, and should provide an objective procedure to compare quality of care delivered by different institutions. Several financial reward programs use a raw average of the measures weighted by the number of patients as the composite score for hospital performance [2; 11; 12]. Despite the simplicity of this method, composite scores based in raw averages have some pitfalls and may not be a reliable measure of quality. The raw average is a sufficient statistic for the underlying construct of interest - quality of care - if all measures have equal contribution for the construct and if the number of measures per hospital is the same [13; 14]. Another problem with raw average scores is that they fail to take into account the correlation structure of the data. Typically, the same patient will contribute to some or all measures (within-patient correlation) and patients are treated and thus clustered within hospitals (within-hospital correlation). Ignoring these correlations will lead to difficulties in adopting inferential procedures because the computation of the variance of the score variance may be biased. Finally, other issues such as missing data, adjustment for covariates and handling mixed type of measures, as for example binary and continuous measures, cannot be addressed with raw average scores.

In this paper we contrast two different versions of raw average scores with a model based score constructed using a latent variable model. The model-based score weights each process-based measure by its ability to discriminate performance among hospitals. We also present two methods to identify hospitals with superior performance. The methods are illustrated using national data collected to evaluate quality of care delivered by US acute care hospitals in the context of the Hospital Compare initiative promoted by the CMS.

2. Data and Measures

We focus on two clinical conditions: acute myocardial infarction (AMI) and heart failure (HF). These conditions are common causes of hospital admission and they rank in top 5 most expensive conditions treated in US hospitals. During 2004, AMI resulted in $31 billion of hospital charges for 695,000 hospital admission. The 1.1 million hospitalizations for HF amounted to nearly $29 billion in hospital charges during the same period [15; 16].

Hospital quality of care is based on the condition specific measures currently reported as part of CMS' Hospital Compare program. There is substantial scientific evidence that these measures represent the best practices for the treatment of AMI and HF [17; 18]. The goal for each hospital is to achieve more than 90% on all measures. For AMI, eight binary measures are currently reported by hospitals, namely:

• Aspirin at arrival - AMI patients without aspirin contraindications who received aspirin within 24 hours before or after hospital arrival.

• Aspirin at discharge - AMI patients without aspirin contraindications who were prescribed aspirin at hospital discharge.

• ACE inhibitor or ARB for left ventricular systolic dysfunction - AMI patients with left ventricular systolic dysfunction (LVSD) and without angiotensin converting enzyme inhibitor (ACE inhibitor) contraindications or angiotensin receptor blocker (ARB) contraindications who are prescribed an ACE inhibitor or an ARB at hospital discharge.

• Beta blocker at arrival - AMI patients without beta - blocker contraindications who received a beta-blocker within 24 hours after hospital arrival.

• Beta blocker at discharge - AMI patients without beta-blocker contraindications who were prescribed a beta-blocker at hospital discharge.

• Thrombolytic agent received within 30 minutes of hospital arrival - AMI patients receiving thrombolytic therapy during the hospital stay and having a time from hospital arrival to thrombolysis of 30 minutes or less.

• PCI Received Within 120 Minutes Of Hospital Arrival - AMI patients receiving Percutaneous Coronary Intervention (PCI) during the hospital stay with a time from hospital arrival to PCI of 120 minutes or less.

• Smoking cessation advice/counseling - AMI patients with a history of smoking cigarettes who are given smoking cessation advice or counseling during a hospital stay.

For HF, four binary measures are currently reported by hospitals, namely:

• Assessment of left ventricular function (LVF) - Heart failure patients with documentation in the hospital record that left ventricular function (LVF) was assessed before arrival, during hospitalization or is planned for after discharge.

• ACE inhibitor or ARB for left ventricular systolic dysfunction - Heart failure patients with left ventricular systolic dysfunction (LVSD) and without angiotensin converting enzyme inhibitor (ACE inhibitor) contraindications or angiotensin receptor blocker (ARB) contraindications who are prescribed an ACE inhibitor or an ARB at hospital discharge.

• Discharge instructions - Heart failure patients discharged home with written instructions or educational material given to patient or care giver at discharge or during the hospital stay addressing all of the following: activity level, diet, discharge medications, follow-up appointment, weight monitoring, and what to do if symptoms worsen.

• Smoking cessation advice/counseling - Heart failure patients with a history of smoking cigarettes who are given smoking cessation advice or counseling during a hospital stay.

The data were collected from hospitals that volunteered to participate in the Hospital Compare program sponsored by the CMS. The participating hospitals submitted their data for the measures described above on patients admitted with AMI or HF between July 2004 and June 2005. The data submission included auditing procedures and edit checks, that assess whether data submitted are consistent with defined parameters for sample size, outliers, and missing data.

Data were available for 4238 US acute care hospitals (hospitals that provide inpatient medical care and other related services for surgery, acute medical conditions or injuries) and critical access hospitals (small and generally geographically remote facilities that provide outpatient and inpatient hospital services to people in rural areas).

The Hospital Compare data contains patient data aggregated to the hospital-level but not patient-level data, i.e., for each measure, each hospital submitted the total number of patients that were admitted and were eligible for the measure as well as the percentage of eligible patients that received the therapies. The eligibility of a patient for each therapy is defined according to the CMS and Joint commission on Accreditation of Healthcare Organizations specifications [19]. For example, a patient is eligible for smoking cessation advice/counseling if he has a history of smoking cigarettes anytime during the year prior to hospital arrival. An important characteristic of the data is that some hospitals may not have patients eligible for some measures. This can happen because none of the patients admitted met the eligibility criterion for a certain therapy.

Hospitals with more than 30 eligible patients in at least one of the eight measures for AMI were included in the analysis of AMI quality of care and hospitals with more than 30 eligible patients in at least one of the four measures for HF were included in the analysis of HF quality of care. This restriction is adopted by CMS in their reports.

3. Statistical Methods

3.1. Composite scores for hospital quality of care

We consider three estimators of hospital quality of care for AMI and for HF. Each estimator of quality of care is obtained by using a different method to summarize the measures associated with AMI (eight measures) and HF (four measures) into hospital composite scores for each condition.

We compute the condition specific raw average score (RAS) for each hospital as the sum of the proportions of eligible patients who received the therapies divided by the number of therapies with eligible patients at each hospital. Let y_ij denote the number of eligible patients at the i^th-hospital who receive therapy j and let n_ij denote the number of eligible patients for the j^th-therapy at the i^th-hospital. The number of therapies measured at the i^th-hospital is denoted by J_i and varies from 1 to 8 for AMI patients and 1 to 4 for HF patients. If there are no eligible patients in a hospital for a specific measure, then that measure is not considered in the composite score for the hospital. The expression for the RAS is given by,

$${\text{RAS}}_i=\frac{{\sum }_j\frac{y_{ij}}{n_{ij}}}{J_i}$$ (1)

The RAS is an non-weighted average of the proportions of patients who received the therapy for which they were eligible, across all measures for each condition. This score can be interpreted as an average of the measures. Despite the computational simplicity of this estimator, the assessment of its variance is far from trivial (see for example reference [20]). If patient-level data were available one could use an approximation to the normal distribution to obtain an estimate of the variance. However, in the Hospital Compare dataset there is only information at hospital level and it does not allow us take into account both the within-patient and withing-hospital correlations. An approximation to the variance of RAS could be obtain by ignoring these correlations and computing the variance of the sum of independent binomials.

Another estimator is given by the average of the proportions of patients who received the therapies, weighted by the number of eligible patients for each measure. We denote this estimator as the raw weighted average score (RWAS). Measures with higher number of eligible patients have more weight in the final RWAS. Although the contribution of each measure to the final scores is proportional to the number of eligible patients, the RWAS does not differentiate between measures in the sense that if two measures have the same number of eligible patients, they both have the same weight in the final score. This is the estimator adopted by the CMS. Using the same notation as above, the RWAS is expressed as

$${\text{RWAS}}_i=\frac{{\sum }_j{y}_{ij}}{{\sum }_j{n}_{ij}}$$ (2)

Similar to the RAS estimator, the computation of the variance of the RWAS depends on the within-patient and within-hospital correlations. Without individual information at the patients level we can only approximate its variance ignoring these correlations.

Both the RAS and RWAS can give paradoxical results. Consider the following hypothetical and extreme situation. Two hospitals, A and B, have only one of the measures with eligible patients, therapies A* and B*, respectively. Both RAS and RWAS will coincide with the performance for measure A* in the case of hospital A* and B* for Hospital B. Hospital A had 60% of the eligible patients receiving the therapy A* and hospital B also had 60% of patients receiving therapy B*. Both hospital have the same RAS and RWAS equal to 0.6. However, suppose measure A* is much harder to achieve (for example, primary percutaneous coronary intervention which is an invasive proceadure) and its mean across all hospitals is 40% while for measure B*, the average performance is 80%. One could argue that hospital A is performing above the average and hospital B below the average. Nevertheless both hospital will have the same score of performance.

Another disadvantage of the the RWAS arises from its definition. By weighting each measure by the number of eligible patients, the RWAS is influenced by the performance in measures where there is more information and therefore where there is more certainty about the hospital performance. Although this is a valid point, it happens in our data, and most likely in data of the same nature, that measures that discriminate better between hospitals, i.e, measures that have more variability, also have less eligible patients. Therefore, the RWAS penalizes measures that could make a better distinction between hospitals.

A third estimator for quality of care is obtained from positing a latent variable model for the observed individual measure. Landrum et al. [21] proposed this class of models, designated as as 2-parameter Normal-Ogive model [22] or the multivariate probit model [23], to construct profiles of health care providers. The condition specific latent variable θ_i represents the quality of care for the i^th-hospital. A large value of θ_i corresponds to better hospital quality. This approach is identical to item response theory (IRT) models used extensively in educational and psychological testing [24; 25]. These models assume that the observed measures reflect one single underlying construct (quality of care) but each measure may have a different weight in the final score, depending on the measure's ability to discriminate subjects (hospitals). Conditional on the latent variable, the measures are assumed to be independent. Let y_ij and n_ij be defined as above; p_ij is the probability that a patient receives therapy j at the i^th-hospital given that the patient is eligible to the therapy; β_j is a measure specific discrimination weight. Finally, α_j represents a baseline for each measure and it is associated with performance of an average hospital for the j^th-therapy.

$$\begin{array}{r}\hfill y_{\text{ij}}\sim \text{Binomial}(p_{\text{ij}},n_{\text{ij}})\\ \hfill \text{probit}(p_{\text{ij}})={\alpha }_j+{\beta }_j{\theta }_i\\ \hfill {\beta }_j>0\\ \hfill {\theta }_i\sim N\left(0,1\right)\end{array}$$ (3)

The sign of β_j is not identifiable so the constraint that β_j > 0 is added to the model. Given the model in (3), it can be shown that the average performance for the j^th-therapy, $E(y_{ij}/n_{ij})=E(E(y_{ij}/n_{ij}|{\theta }_i))=\Phi \left(\frac{{\alpha }_j}{\sqrt{1+{\beta }_j^2}}\right)$, where Φ(·) represents the cdf of the standard normal distribution. If the hospital performance, θ_i, was observed, the model would indicate that the probability, in the probit scale, that a patient receives therapy j at the i^th-hospital is the sum of a baseline that is associated with the performance of all the hospitals at measure j (α_j), and a quantity specific to hospital i that is proportional the overall performance of hospital i (β_jθ_i).

A process measure that is less homogeneous among hospitals should have a higher value for β_j because it can discriminate better between hospitals. Estimates for the latent scores (LS) are given by the posterior means of θ_i. The values for the LS range from −∞ to +∞ and are assumed to be normally distributed around zero with standard deviation fixed to be 1. Fixing the mean and the standard deviation of the LS is not a restriction but just a standardization. Low values for the LS indicate poor quality of care and a hospital with LS equals zero indicates that the hospital has an average performance in terms of quality of care.

Although the LS solves some of the problems of the RAS and RWAS discussed above by weighting and taking into account the correlation between measures, it is not free of criticism. The normality assumption of the latent variable might be too restrictive and it is not verifiable. Other disadvantages include the misspecification of the link function and covariance structure imposed by the model. Because patient-level data are not available we are not able to take into account the within-patient correlation but only within-hospital correlation. This can result in a underestimation of the variance for the latent score.

3.2. Model estimation and fit

We adopt a fully parametric Bayesian approach and used the generic Bayesian package WINBUGS [26]. Other software is available and specific specialized in IRT analysis as for example, Winsteps [27], Multilog [28] and Bi-log [29] among others. Another option to fit these models would be to use maximum likelihood theory within the frequentist framework [30].

The prior distributions for α_j was chosen to be N(0, 100) and for β_j was chosen to be N(0, 100) truncated below zero. We used the posterior means of θ_i's as the estimates for the quality of care score and the variances of the posterior distributions as the variances for θ_i's. The parameter estimates were based on a chain of 3000 iterations after a burn-in chain of 2000 iterations. We examined convergence of the MCMC by running two parallel chains starting at different initial values and checking the trace plots.

We fitted other models for AMI and HF: one imposing the constraint that all the β_j's are equal, similar to the one parameter Rash model [31]; and for AMI we fitted an additional model where β₇ = 0. The constraint that all β_j's are equal implies that all measures contribute equally to the final scores. The justification for the last model is the poor correlation of ’fibrinolytic therapy’ (measure 7) with the other AMI measures, suggesting that this measure is associated with a different underlying construct.

The deviance information criterion (DIC) [32] was computed to compare and select the final models for AMI and HF. For each condition, models with lower DIC were chosen as the final models. Goodness of fit was assessed using posterior predictive checks [33]. The main idea of this method is to compare the observed data with replicated data under the model. Let $y_i^{\text{rep}}=(y_{i1}^{\text{rep}},\dots y_{i{J}_i}^{\text{rep}})$ represent the vector of replicated data for the i^th-hospital. The distribution of $y_i^{\text{rep}}$ given the observed data is:

$$p(y_i^{\text{rep}}|(y_{i1},\dots ,y_{i{J}_i}))=\int p(y_i^{\text{rep}}|\omega )p(\omega |y_i)d\omega$$ (4)

where ω is the vector of the model parameters in (3). Sampling from (4), we replicated 1000 datasets given the model in (3). We calculated the empirical distribution of several summary statistics, T_v(y_i) for each replicated dataset and compared them with the statistics in the observed dataset. We report Bayes p-values, estimated as the proportion of times the statistics in the replicated data were more extreme than the observed one, i.e, $\text{Bayes p-values}=\mathrm{Pr}(T_v(y_i^{\text{rep}})\ge T_v(y_i)|\omega )$. T_v was chosen as v^th percentile of the distribution of RWAS^rep with v = 5, 10, …, 95. The choice of the percentiles of the RWAS was motivated by the main interest in the 90^th percentile of the performance scores in order to identify hospitals with superior performance. This way it seemed reasonable to use the percentiles of one of the scores to evaluate model fit. Bayes p-values were computed for each T_v(RWAS^rep). P-values that are close to 0 or 1 are indicative of poor model fit.

Additionally we used posterior predictive checking to analyse hospital fit and measure fit, by computing the empirical distributions of $p_{ij}^{\text{rep}}$ for each hospital and each measure. The empirical distributions for $p_{ij}^{\text{rep}}$ were obtained using the same 1000 replicated datasets. We then compared the observed values for each hospital with the empirical distributions by computing the Bayes p-values. We report for each measure the number of hospitals that had a p-value<0.01 and for each hospital the number of measures with p-values less than 0.01.

3.3. Hospital classification based on the quality of care scores

There is considerable research proposing different methods to rank institutional performance. Laird and Louis [34] and Lockwood et al. [35] show that if the objective is to estimate the rank of the institution, the posterior means of the ranks perform better than the ranks of the posterior means. Shen and Louis [36] discuss several estimators and present a new estimator that optimize on estimation of the empirical distribution function of the unit-specific parameters and the ranks. More recently, Austin et al. [37; 38] compare some of these methods and show that they can differ in their results. In this paper we are not interested in ranking hospitals, but rather classifying hospitals based on the posterior distributions of θ_i.

The CMS uses the upper decile (above 90^th percentile) of the quality of care score to characterize superior performance. We use this classification rule by determining the 90^th percentile of the distribution of the posterior means of each score and classifying each hospital accordingly. Agreement of the classification using the RAS, RWAS and LS is measured by Cohen's Kappa statistics (agreement above that expected by chance) and proportions of agreement.

A hospital with smaller volume of patients is more likely be classified in the superior performance category by chance, due to higher variability of the score estimate. Therefore, the classification should take into account the amount of certainty that a hospital belongs to the category of superior performance. This can be achieved by classifying a hospital as superior only if the probability of being above the 90^th percentile is larger than a predefined threshold, i.e.

$$P(Sc\widehat{o}r{e}_i>{\zeta }_{90\mathrm{th}})>\gamma ,$$ (5)

Where ζ_90th is defined has the score's 90^th-percentile, γ is the predefined threshold and Scôre_i is the estimator of quality of care. This ensures that a hospital is classified as having superior quality of care only when there is some degree of certainty that the true score is above ζ_90th. By construction the number of hospitals classified as having superior performance is now less than 10%. Therefore, if we want to classify exactly 10% of the hospitals as having superior performance we have to consider a lower percentile as the cutoff for superior performance.

Choosing the percentile that classifies exactly 10% of the hospitals with proabability higher than γ is equivalent to finding the threshold above which 10% of the credible intervals for the hospital performance lie entirely above it. The 90^th percentile of the lower bounds of the credible intervals satisfies this condition because by definition 10% of the credible intervals will lie above it. To chose the credible intervals, we use the fact that they are simmetric around Scôre_i. Then, with some simple algebra, we get that the ((2γ − 1) × 100)% credible intervals for the scores have a lower bound above which the Score_i's will lie with a probability of γ. For example, if γ = 0.8, the probability that the score is above the lower bound of its ((2 × 0.8 − 1) × 100)% = 60% credible interval is 0.8 because the probability of being in the credible interval is, by definition, 0.6 and we have to sum the probability of being above the upper bound of the interval which is 0.2. So, by determining the 90^th-percentile of the lower bounds of the ((2γ − 1) × 100)% credible intervals, we are able to classify exactly 10% of hospitals as having superior performance taking into account the uncertanty of the scores estimates. We applied this classification rule to the LS only. The results were then compared with the classification based on the point estimates of RAS and RWAS. We use the non-weighted Cohen's Kappa statistics and proportions of agreement to measure agreement of the classifications.

The uncertainty about the LS score for a hospital depends on the number of eligible patients for each therapy. Therefore, using the last criterion of classification, it is harder for a hospital with a smaller volume of patients to be classified in the upper category of hospital performance because their credible intervals are wider. For this reason we also report the proportion of low volume hospitals classified under both rules. For each condition, AMI and HF, we define low volume hospitals as those in the first decile of the distribution of number of patient-measures for all hospitals (128 patient-measures for condition AMI and 94 patient-measures for HF). We use patient-measures units instead of patients because the same patient will contribute to the number of eligible patients for several measures.

4. Results

4.1. Summary statistics

The total numbers of hospitals that had more than 30 eligible patients in at least one of the measures for each condition and were included in the analysis were 2449 (58%) and 3376(80% of original hospitals) for AMI and CHF, respectively. The number of eligible patients varied substantially for each measure (Table I). For AMI, there were 9 hospitals with only 4 measures included in the final scores (no eligible patients for the remaining 4 measures), 229 (9%) hospitals with 5 measures, 330 (13%) with 6 measures, 1148 (47%) with 7 measures and 733 (30%) with all the 8 measures. For HF most of the hospitals (3016 (89 %) hospitals) had eligible patients in all the 4 measures, 39 (1%) hospitals had 3 measures available, 320 (9%) had two measures and only one hospital contributed with a single measure for the final scores.

Table I.

Summary statistics for the number of eligible patients per measure and percentage of patients that received the therapy. Results for 2449 and 3376 hospitals for acute myocardial infarction and heart failure, respectively. *If a hospital has a missing value for the number of eligible patients for a specific therapy, the number of eligible patients is zero for the calculation of the median and percentiles.

	Number of eligible patients*	Percentage of eligible patients that received therapy
	median (percentile 10; percentile 90)	median (percentile 10; percentile 90)
Acute Myocardial Infarction
Aspirin at Arrival	122 (42; 305)	96 (88; 99)
Aspirin at Discharge	88 (17; 431)	94 (78; 99)
ACEI or ARB for LVSD	12 (2; 55)	86 (60; 100)
Adult Smoking Cessation Advice	20 (0; 156)	90 (50; 100)
Beta blocker at Discharge	92 (19; 444)	94 (78; 100)
Beta blocker at Arrival	101 (36; 257)	92 (79; 99)
Fibrinolytic Therapy	1 (0; 14)	45 (20; 87)
Primary PCI Received	1 (0; 58)	65 (38; 87)
Heart Failure
Discharge Instructions	135(0; 469)	55 (15; 87)
Evaluation of LVS Function	200(51; 580)	89 (64; 98)
ACEI or ARB for LVSD	34(5; 120)	83 (60; 100)
Adult Smoking Cessation Advice	25(1; 98)	79 (40; 100)

ACEI - angiotensin converting enzyme inhibitor; ARB - angiotensin receptor blocker; LVSD - left ventricular systolic dysfunction; PCI - percutaneous coronary intervention

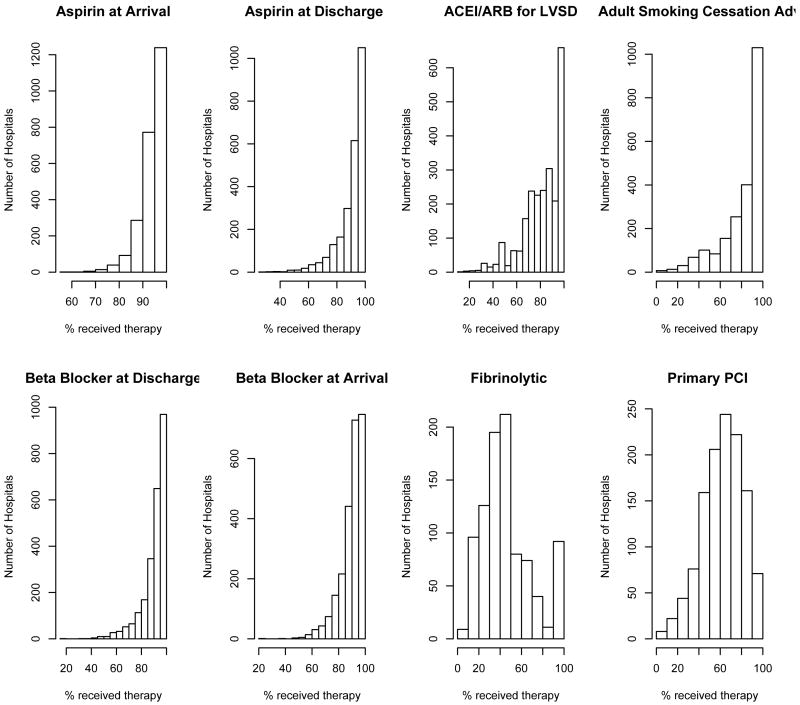
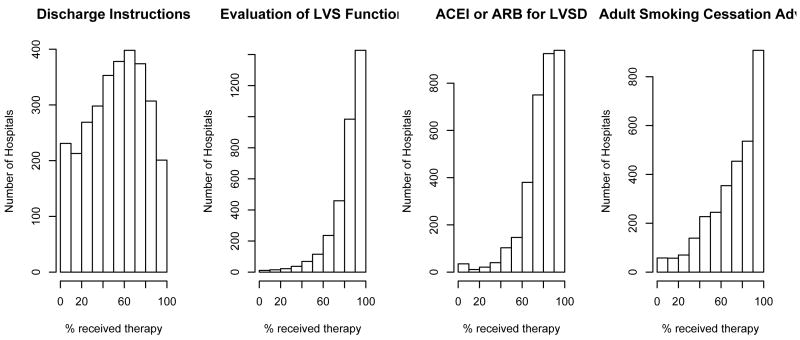
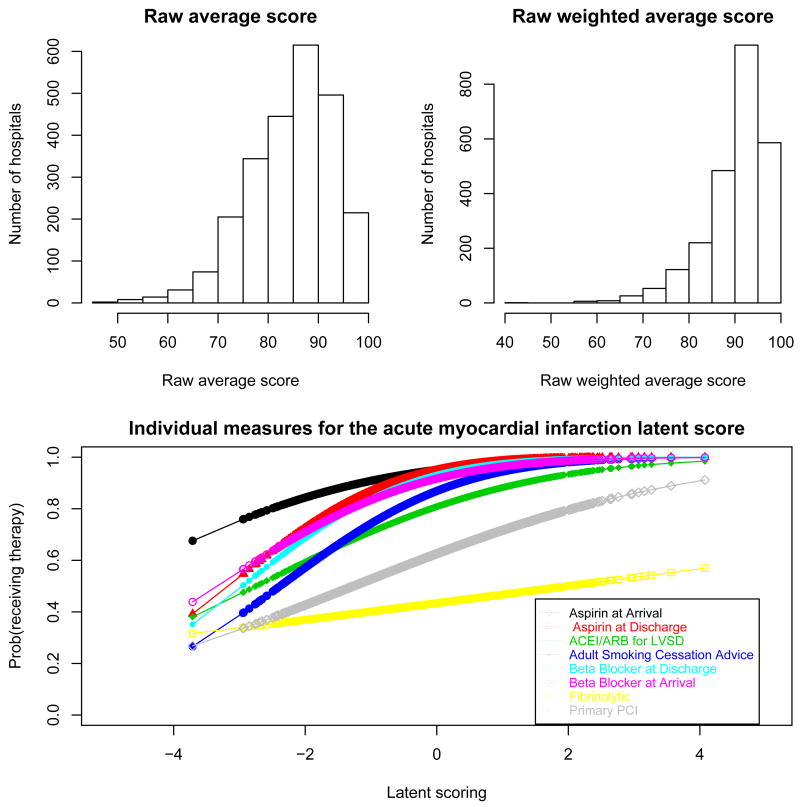
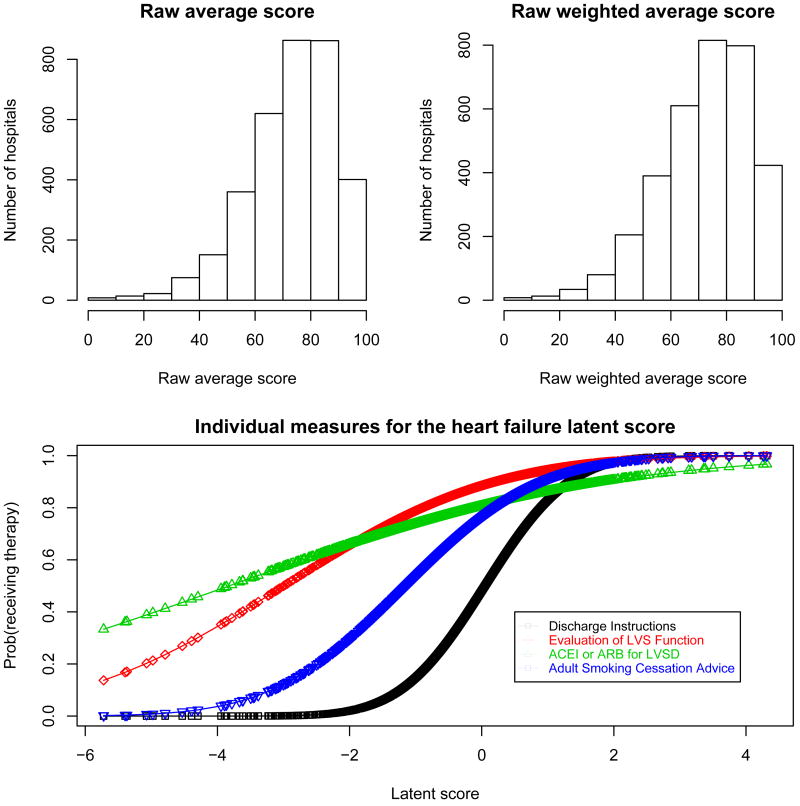
Several measures for both conditions, AMI and HF, had ceiling effects with little variability across hospitals. This effect is most dramatic for ”‘aspirin prescribed at arrival”’ and ”aspirin prescribed at discharge”, for AMI. Typically, therapies with fewer patients have more variability across hospitals and potentially might have more discriminative power for hospital performance. See for example ’fibrinolytic therapy’ and ’primary PCI’ for patients hospitalized with AMI (Figure 1 and Figure 2). Tables II and III display the Spearman pairwise correlation coefficients for measures for each condition. Fibrinolytic therapy for AMI patients is poorly correlated with the other measures, suggesting that it is not measuring the same underlying construct as the other measures.

Figure 1.

Hospital-Specific distribution for eight measures collected to evaluate quality of care for patients hospitalized with acute myocardial infarction. Data on 2449 hospitals.

Figure 2.

Hospital-Specific distribution for four measures collected to evaluate quality of care for patients hospitalized with heart failure. Data on 3376 hospitals.

Table II.

Spearman pairwise correlation coefficients for measures and composite scores associated with acute myocardial infarction

	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(RAS)	(RAWS)	(LS)
(1) Aspirin at Arrival	1.00
(2) Aspirin Prescribed at Discharge	0.58	1.00
(3) ACEI or ARB for LVSD	0.29	0.27	1.00
(4) Adult Smoking Cessation Advice	0.23	0.25	0.19	1.00
(5) Beta blocker Prescribed at Discharge	0.52	0.67	0.34	0.27	1.00
(6) Beta blocker at Arrival	0.64	0.56	0.32	0.25	0.69	1.00
(7) Fibrinolytic Therapy	0.09	0.05	0.14	0.11	0.10	0.09	1.00
(8) Primary PCI Received	0.23	0.24	0.19	0.27	0.28	0.24	0.24	1.00
(RAS)Raw average scoring	0.53	0.57	0.55	0.55	0.63	0.60	0.54	0.64	1.00
(RWAS)Raw weighted average scoring	0.73	0.77	0.41	0.43	0.81	0.82	0.22	0.46	0.82	1.00
(LS)Latent score	0.74	0.82	0.39	0.43	0.85	0.83	0.14	0.40	0.75	0.97	1.00

ACEI - angiotensin converting enzyme inhibitor; ARB - angiotensin receptor blocker; LVSD - left ventricular systolic dysfunction; PCI - percutaneous coronary intervention

Table III.

Spearman pairwise correlation coefficients for measures and composite scores associated with heart failure

	(1)	(2)	(3)	(4)	(RAS)	(RAWS)	(LS)
(1) Discharge Instructions	1.00
(2) Evaluation of LVS Function	0.39	1.00
(3) ACEI or ARB for LVSD	0.28	0.34	1.00
(4) Adult Smoking Cessation Advice/Counseling	0.55	0.38	0.21	1.00
(RAS) Raw average scoring	0.84	0.64	0.54	0.77	1.00
(RWAS) Raw weighted average scoring	0.90	0.70	0.39	0.63	0.94	1.00
(LS) Latent scoring	0.96	0.64	0.34	0.62	0.88	0.93	1.00

ACEI - angiotensin converting enzyme inhibitor; ARB - angiotensin receptor blocker; LVSD - left ventricular systolic dysfunction; PCI - percutaneous coronary intervention

4.2. Model fit

The DIC for the fitted latent score models are shown in table IV. Models A and D permitted different discrimination parameters across the measures for AMI and HF, respectively. Models B and E assume that all the discrimination parameters are equal for AMI and HF, respectively. Model C assumes that ”Fibrinolytic therapy” does not contribute to the LS.

Table IV.

Deviance information criterion (DIC), posterior mean of the deviance (D-bar) and effective number of parameters (pD) for model (3) with different restrictions on the parameters β_j

	DIC	D-bar	pD
Acute Myocardial Infarction
Model A - with βj > 0, j = 1, …, 8	96890	94584	2306
Model B - with β1 = β2 = … = β8 > 0	99279	96981	2299
Model C - with βj > 0, j = 1, …, 6, 8 and β7 = 0	96929	94619	2310
Heart Failure
Model D - with βj > 0, j = 1, …, 4	145774	142486	3288
Model E - with β1 = β2 = β3 = β4 > 0	170485	167196	3289

Models A and D had the lowest DIC values for AMI and HF, respectively, and they were chosen as the final models. The weight estimate for the ’fibrinolytic therapy’ in the final model for AMI is 0.08 (Std. Error=0.015). This result is in agreement with the poor correlation of this measure with the other ones. However, the model with ’fibrinolytic therapy’ removed from the latent score (Model C) had a higher DIC and for this reason we chose to maintain it in the final model.

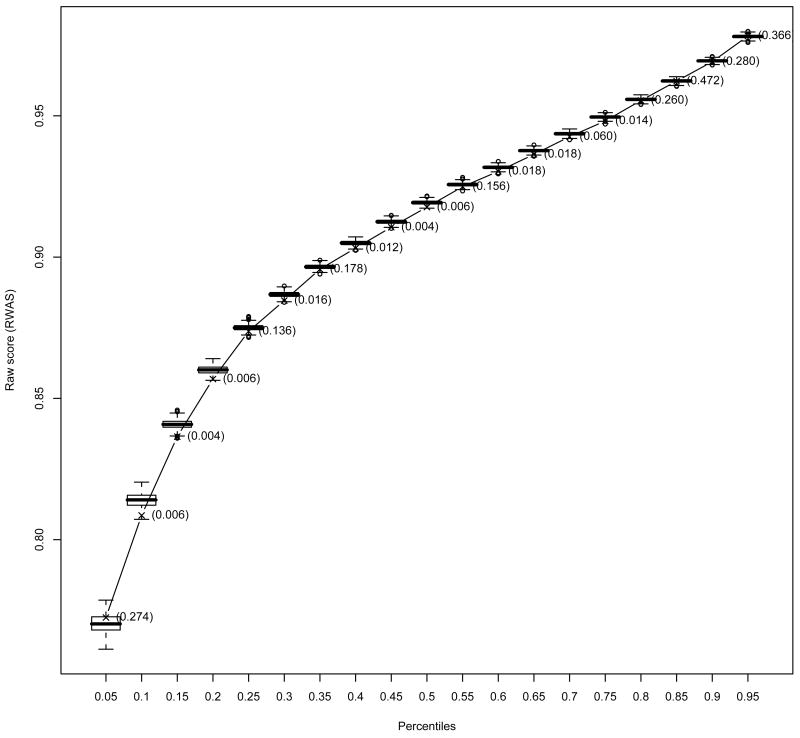
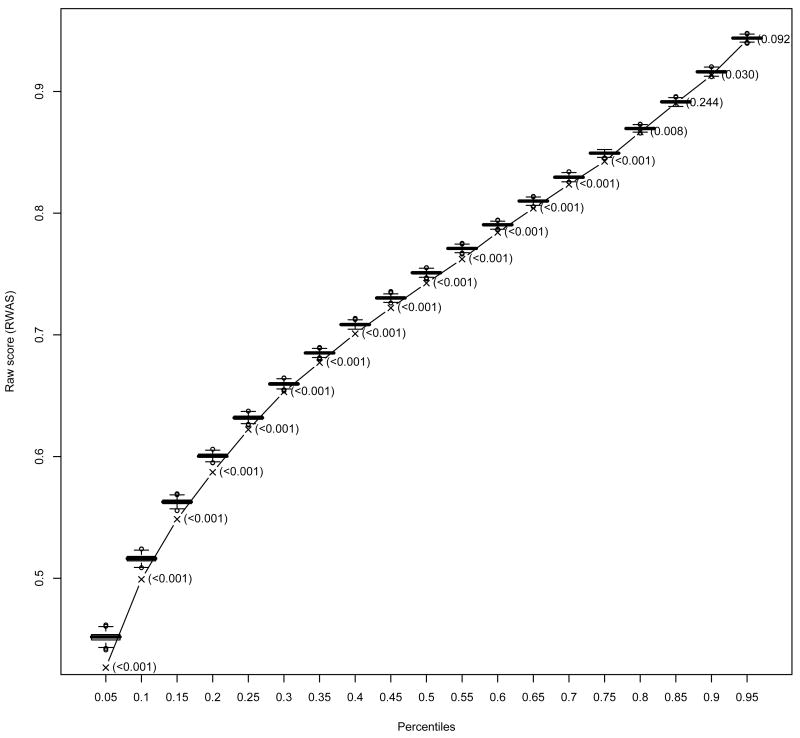
Posterior predictive checks indicated good fit of the model for the upper percentiles but poor fit for most of the low percentiles of the RWAS for both AMI and HF (Figures 3 and 4). Table V presents the relative number of hospitals at each measure having a p-value less than 0.01 as an indication of measure fit. Regarding hospital fit for AMI, 82% of the hospitals had at most one of the eigth measures with a p-value less than 0.01, and only 2% of the hospital had more than three measures with p-values less than 0.01. For HF, 74% of the hospitals had at most one measure (out of four) with a p-value less than 0.01 and 1% of the hospitals presented p-values less the 0.01 for all measures.

Figure 3.

The boxplots represent the predictive distributions for the percentiles of the raw weighted average score (RWAS) for acute myocardial infarction. The predictive distributions were computed by drawing from the posterior, 1000 vectors of parameter estimates and for each vector generating a predictive sample. The line represents the observed value for the correspondent percentile and the values in parentheses next to it are the Bayes p-values.

Figure 4.

The boxplots represent the predictive distributions for the percentiles of the raw weighted average score (RWAS) for heart failure. The predictive distributions were computed by drawing from the posterior, 1000 vectors of parameter estimates and for each vector generating a predictive sample. The line represents the observed value for the correspondent percentile and the values in parentheses next to it are the Bayes p-values.

Table V.

Percentage of hospitals with Bayes p-values below 0.01 at each measure. The p-values were obtained for each hospital and each measure using the predictive distributions of the number of patients receiving the therapy (measure) they were eligible to. Predictive distributions were computed by drawing from the posterior, 1000 vectors of parameter estimates and for each vector generating a predictive sample.

Acute Myocardial Infarction		Heart Failure
Aspirin at Arrival	8%	Discharge Instructions	10%
Aspirin Prescribed at Discharge	8%	Evaluation of LVS Function	45%
ACEI or ARB for LVSD	6%	ACEI or ARB for LVSD	21%
Adult Smoking Cessation Advice	24%	Adult Smoking Cessation Advice	25%
Beta blocker Prescribed at Discharge	4%
Beta blocker at Arrival	9%
Fibrinolytic Therapy	7%
Primary PCI Received	24%

ACEI - angiotensin converting enzyme inhibitor; ARB - angiotensin receptor blocker; LVSD - left ventricular systolic dysfunction; PCI - percutaneous coronary intervention

The estimates for the final model parameters are presented in Table VI. A lower value for the intercepts α_j indicates that, on average across all hospitals, a patient has a lower probability of receiving therapy j. Measures with higher intercepts correspond to those with stronger ”celling effects” (Figure 1 and Figure 2). The weight coefficients β_j indicates how much the measure contributes to the final LS. Higher values for these coefficients indicate a ”steeper slope” for the corresponding probit and therefore a higher ability to discriminate among hospitals (Figures 5 and 6). Aspirin and beta blocker prescribed at discharge were the two measures with higher discrimination for AMI. For HF, ”discharge instructions” had the measure with highest ability to discriminate among hospitals (Table VI).

Table VI.

Posterior means and standard deviations for the coefficients from the latent variable models for acute myocardial infarction and heart failure.

	αj	(SD)	βj	(SD)
Acute Myocardial Infarction
Aspirin at Arrival	1.65	(0.007)	0.32	(0.006)
Aspirin Prescribed at Discharge	1.62	(0.010)	0.51	(0.009)
ACEI or ARB for LVSD	0.87	(0.008)	0.32	(0.010)
Adult Smoking Cessation Advice	1.12	(0.010)	0.47	(0.010)
Beta blocker Prescribed at Discharge	1.49	(0.009)	0.51	(0.008)
Beta blocker at Arrival	1.38	(0.008)	0.41	(0.007)
Fibrinolytic Therapy	-.17	(0.013)	0.08	(0.015)
Primary PCI Received	0.32	(0.008)	0.25	(0.009)
Heart Failure
Discharge Instructions	-0.05	(0.013)	1.00	(0.013)
Evaluation of LVS Function	1.20	(0.005)	0.40	(0.005)
ACEI or ARB for LVSD	0.87	(0.005)	0.23	(0.005)
Adult Smoking Cessation Advice	0.72	(0.010)	0.63	(0.010)

ACEI - angiotensin converting enzyme inhibitor; ARB - angiotensin receptor blocker; LVSD - left ventricular systolic dysfunction; PCI - percutaneous coronary intervention

Figure 5.

Distribution of the raw average score and raw weighted average score; and estimated probability of receiving each therapy as a function of the latent score for patients hospitalized with acute myocardial infarction

Figure 6.

Distribution of the raw average score and raw weighted average score; and estimated probability of receiving each therapy as a function of the latent score for patients hospitalized with heart failure

4.3. Comparison of performance scores

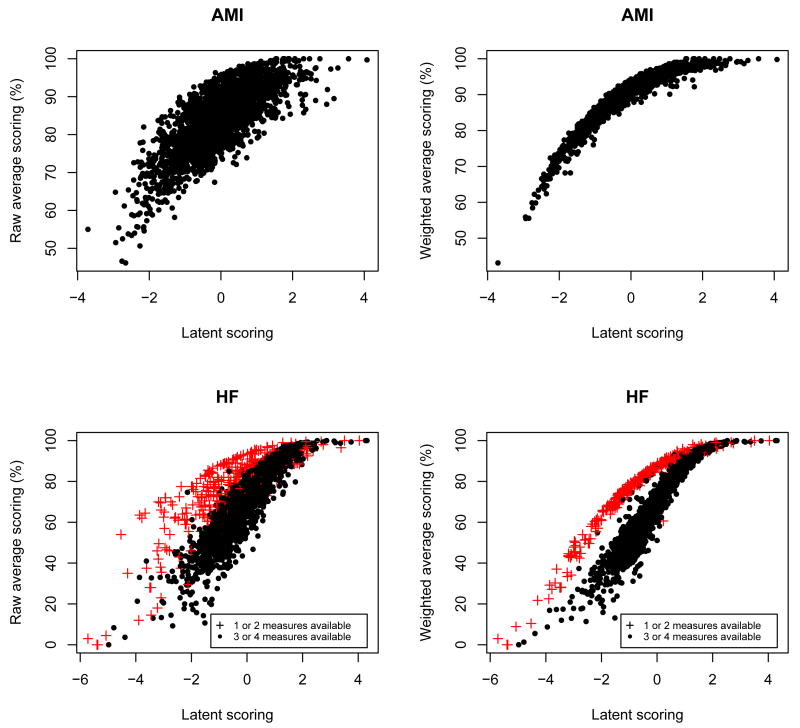
The RAS, RAWS and LS were strongly correlated for both conditions (Figure 7). However, the scatterplot for LS and RWAS suggests two different groups of hospitals. Although not as clear, the same pattern occurs in the scatterplot for LS and RAS. The group with higher values for the RWAS and RAS is formed mostly by hospitals that only had eligible patients for two measures: ”Evaluation of LVS function” and ”ACEI/ARB for LVSD”. ”Evaluation of LVS function” and ”ACEI/ARB for LVSD” have the highest values for α_j (Table VI), implying that they have highest averages of proportion of eligible patients that receive the therapy. This situation corresponds to the paradoxical effect described earlier. For this reason, the RAS and RWAS will overestimate the performance of these hospitals. The LS, on the other hand takes into account the relative performance of the hospital in each measure and it is not affected as much by the fact that there is no information in some of the measures.

Figure 7.

Comparison of the three scoring methods - raw average score, raw weighted average score and latent score - by AMI and HF. For HF, the number of measures available at each hospital (’1 or 2 measures’ and ’3 or 4 measures’) is represented in the plot.

Table VII describes the agreement between the classification of hospitals with superior performance using the point estimates of the scores. The LS and RWAS had a good agreement (kappa = 0.76(SE_kappa = 0.02) and kappa = 0.84(SE_kappa = 0.02) for AMI and HF, respectively) by agreeing in the classification of 192 hospitals out of 245 as having superior performance for AMI and 290 hospitals out of 338 for HF. The classification using the RAS agreed on 117 of the 245 hospitals classified as having superior performance by the LS for AMI (kappa = 0.42(SE_kappa = 0.03)) and 253 of the 338 for HF (kappa = 0.73(SE_kappa = 0.02)).

Table VII.

Agreement between classification methods for hospitals performance for treatment of acute myocardial infarction and heart failure patients. Hospitals with scores above the 90^th percentile are classified as having superior performance.

	Latent score (LS)		Agreement with LS(%)	Kappa statistic (Std. Error)
	Superior	Not superior
Acute Myocardial Infarction
Raw average score
Superior performance	117	128	48%
Not superior performance	128	2079	94%	0.42 (0.03)
Raw weighted average score
Superior performance	192	53	78%
Not superior performance	53	2151	98%	0.76 (0.02)
Heart Failure
Raw weighted score
Superior performance	253	80	76%
Not superior performance	85	2958	97%	0.73 (0.02)
Raw weighted average score
Superior performance	290	48	86%
Not superior performance	48	2990	98%	0.84 (0.02)

Adding the uncertainty of the point estimates of the LS and classifying hospitals as superior if there is probability higher than 80% that the LS score will be above cut-off for the superior perfomance category lowers the agreement between the scores (Table VIII). The cut-off for the superior perfomance category is chosen so 10% of the hospitals are classified as having superior performance. The comparison between the classification based on the RAS and RWAS point estimate, and the LS credible interval is obviously not fair because they are based on different classification rules. However, it serves the purpose of illustrating how the classification changes depending on the methodology used. For AMI only 103 out of 245 hospital (42%) are classified in the superior performance category both by the RAS point estimate and the LS credible interval procedure. For this condition, the classification of superior performance based on the RWAS and LS coincided in 169 out of 245 (69%) hospitals. For HF, 247 out 333 hospitals (74%) are classified in the superior performance category both by the RAS point estimate and the LS credible interval procedure. The classification of superior performance based on the RWAS and LS coincided in 280 out of 338 (83%) hospitals for HF.

Table VIII.

Agreement between classification methods for hospitals performance for treatment of acute myocardial infarction and heart failure patients. Hospitals with raw average score and raw weighted average score above the 90th percentile are classified as having superior performance. Hospitals above a certain threshold for the latent score are classified as having superior performance. The threshold is chosen so 10% of the hospitals fall in superior category.

	Latent score (LS)		Agreement with LS(%)	Kappa statistic (Std. Error)
	Superior	Not superior
Acute Myocardial Infarction
Raw average score
Superior performance	103	142	42%
Not superior performance	142	2062	94%	0.36 (0.03)
Raw weighted average score
Superior performance	169	76	69%
Not superior performance	76	2128	97%	0.66 (0.03)
Heart Failure
Raw weighted score
Superior performance	247	86	74%
Not superior performance	91	2952	97%	0.71 (0.02)
Raw weighted average score
Superior performance	280	58	83%
Not superior performance	58	2980	98%	0.81 (0.02)

Regarding small hospitals, the approach based on the credible intervals for the LS is more restrictive than the one based on the point estimate. For the classification using the point estimate alone of the LS, the proportion of small volume hospitals in the higher category of performance was 6.5% for AMI and 4.1% for HF. For the LS credible interval approach the proportion was 3.2% and 2.0% for AMI and HF, repectevely.

5. Discussion

We compared a model based score for quality of care with two scores based on the raw average of the outcomes using a national data collected to assess the quality of hospital care for two common diseases. We have shown that there is an overall good agreement between the scores. However, a significant number of hospitals was classified differently as having superior performance according to the methodology used.

We discussed the sensitivity of the RAS and RWAS in situations where hospitals have no eligible patients for some measures. This aspect was illustrated in assessing hospital care following HF, where the RAS and RWAS overestimated the performance of hospitals that had eligible patients for some measures. This is an important because some authors justify the use of raw averages by arguing that the weights obtained in a factor analysis are identical for all measures [12]. However, this argument is only valid if the number of measures is the same for all hospitals. Also, the simplicity of the calculation of scores based on raw averages contrasts with the difficulty of computing their standard errors because of the correlation structure of the data. Unless we are willing to assume independence of the observations, this limits the analysis to descriptive methods. Having data at the patient-level, a bootstrapping approach could be an alternative to estimate the standard errors of the raw average scores taking into account the correlation structure by bootstrapping patients within each hospital.

We described two procedures to classify hospitals as having superior performance, one based on the point estimates of the scores and another taking into account the uncertainty about the point estimates of the scores. The last criterion is more restrictive for hospitals with smaller volume of patients and we observed that fewer hospitals with small volume of patients were classified as having superior performance. This can be explained by two facts. First, there is a positive association between quality of care score and volume of patients, i.e., ’practice makes perfect’ phenomenon. A similar effect has been reported by other authors [39] in the context of medical procedures. Therefore it is no surprise that a fewer number of small volume hospitals appeared in the superior performance category. Second, the scores' credible intervals for small volume hospitals are wider due to a smaller number of patient-measures, resulting in a more restrictive criterion for low volume hospitals. However, this criterion reduces the possibility of a hospital being classified on the upper category of performance by chance. Although the agreement between the LS and RWAS was good for both methods, there was a significant proportion of hospitals that are classified differently depending on the score we use.

The model-based score overcomes some of the disadvantages of the raw average scores. Hospitals with different number of measures are handled properly and the standard errors for the estimates are obtained directly from the model estimation. While the model cannot compensate for the unavailable of patient-level data it did accommodate the repeated measures within-hospital. The model based approach also allows extensions to more generic settings such as missing data, inclusion of additional covariates for adjustment purposes and outcomes measured in different scales (e.g., binary and continuous outcomes). The last topic on mixed type of outcomes has been subject of recent methodological research [40; 41; 42; 43] and application to the evaluation of the performance of health care institutions [44; 45]. A possible extension of this method could be the prediction of the latent variable value for a new observation (hospital), but this requires further investigation.

The model-based scores are not as easily computed and understood by non-statisticians as the average scores. There are other concerns that one has to take into account when adopting the model based procedure such as the adequacy of the model to the data (model fit). In our analysis the proposed model had a poor fit for some features of the data. One explanation is the possibility of some overdispersion in some measures or that the measures are measuring different underlying constructs. One possible solution would be to fit a model with more latent variables but the number of measures available (8 for AMI and 4 for HF) could lead to identifiability problems. Nevertheless, the model showed a good fit for features of interest, such as the upper percentiles of hospital performance.

Appendix

Sample of acute myocardial infarction (AMI) data and Winbugs code to fit the latent variable model (equation 3). The complete data include 2449 hospitals and 8 measures for AMI. The variable npat refers to the number of patients that correctly received the therapy associated with each measure, the meas identifies the measure and hosp the hospital. The variable denom refers to the total number of patients in a hospital that are eligible for a given measure.

Data:

npat	hosp	meas	denom
250	1	1	258
29	2	1	38
244	3	1	246
296	4	1	312
44	5	1	47
⋮	⋮	⋮	⋮
22	2443	8	34
33	2448	8	48
34	2449	8	56

Winbugs code:

model{

for ( j in 1:16428 ){

npat[j]∼dbin(p[hosp[j], meas[j]],denom[j])

p[hosp[j], meas[j]] <- phi(a[meas[j]] + b[meas[j]]*theta[hosp[j]])

}

for ( k in 1:2449 ){

theta[k]∼dnorm(0,1)

}

for ( h in 1:8 ){

a[h]∼dnorm(0,.0001)

b[h]∼dnorm(0,.0001)I(0,)

}

}