Abstract
There is growing evidence that in a variety of organisms the majority of meiotic recombination events occur at a relatively small fraction of loci, known as recombination hotspots. If hotspot activity results from the DNA sequence at or near the hotspot itself (in cis), these hotspots are expected to be rapidly lost due to biased gene conversion, unless there is strong selection in favor of the hotspot itself. This phenomenon makes it very difficult to maintain existing hotspots and even more difficult for new hotspots to evolve; it has therefore come to be known as the “hotspot conversion paradox.” I develop an analytical framework for exploring the evolution of recombination hotspots under the forces of selection, mutation, and conversion. I derive the general conditions under which cis- and trans-controlled hotspots can be maintained, as well as those under which new hotspots controlled by both a cis and a trans locus can invade a population. I show that the conditions for maintenance of and invasion by trans- or cis-plus-trans-controlled hotspots are broader than for those controlled entirely in cis. Finally, I show that a combination of cis and trans control may allow for long-lived polymorphisms in hotspot activity, the patterns of which may explain some recently observed features of recombination hotspots.
THERE is growing evidence from several model systems across the eukaryotic phylogeny that meiotic recombination events, rather than being distributed uniformly across the genome, are largely concentrated into relatively small regions known as “recombination hotspots.” Hotspots in yeast (Malone et al. 1994; Wu and Lichten 1995; Petes 2001; Cromie et al. 2005), mice (Guillon and De Massy 2002; Kelmenson et al. 2005; Shifman et al. 2006; Baudat and De Massy 2007), and humans (Jeffreys et al. 1998, 2000, 2001, 2005; Crawford et al. 2004; McVean et al. 2004; Myers et al. 2005; Conrad et al. 2006; International HapMap Consortium 2007) have now been well characterized, and evidence suggests that hotspots also exist in chimpanzees (Ptak et al. 2005) and several plants (Dooner and Martinez-Ferez 1997; Okagaki and Weil 1997; Yao et al. 2002; Drouaud et al. 2006). While some other well-studied eukaryotes (e.g., Drosophila melanogaster and Caenorhabditis elegans) show no evidence of hotspots (Hey 2004), the phenomenon is widespread enough across the tree of life to merit substantial study.
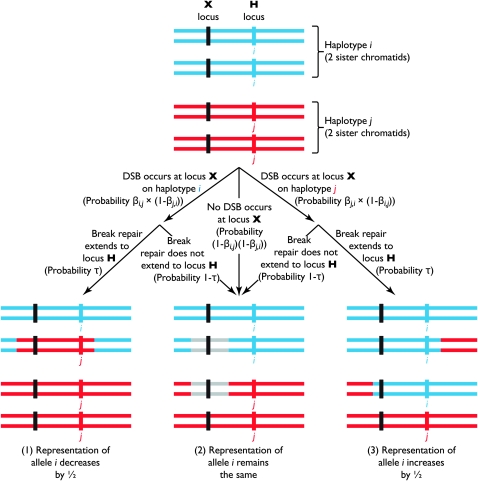
These hotspots pose a variety of interesting questions for population geneticists, not the least of which is that of their continued existence. One striking characteristic of hotspots is that they are subject to a form of meiotic drive: when a DSB occurs at a hotspot heterozygous for an active (“hot”) and an inactive (“cold”) hotspot allele, the cold allele tends to appear in a higher proportion of the offspring than does the hot allele (often in an ∼3:1 ratio rather than the expected 2:2) (Catcheside 1975; Nicolas et al. 1989; Grimm et al. 1991; Malone et al. 1994; Guillon and De Massy 2002; Jeffreys and Neumann 2002; Jeffreys and May 2004; Cromie et al. 2005). This is likely the result of the mechanism by which recombination is thought to be initiated: a double-strand break (DSB) forms on one chromatid; this break extends a variable distance in the 5′ direction on each strand; and the sequence of the nonsister chromatid is used as a template to repair the gap. The physical connections (Holliday junctions) between the two chromatids that form as a result of this repair often (but not always) result in a crossover event (Szostak et al. 1983); however, a more direct consequence is that a stretch of DNA sequence on the chromatid that experiences the initial DSB is replaced (“converted”) by homologous sequence from the nonsister chromatid: while the converted sequence was originally present on two of four chromatids (a 2:2 ratio), after DSB repair it is present on only one of four (a 3:1 ratio). Figure 1 shows a diagram of this process. Since DSBs occur at hot alleles more frequently than at cold alleles, they are converted in this manner more frequently as well and are therefore expected to rapidly decrease in frequency when there is a cold allele present in the population. The continued existence of recombination hotspots in the face of this biased gene conversion has been termed the “hotspot conversion paradox” (Boulton et al. 1997).
Figure 1.—
Schematic of double-strand breaks (DSBs) and gene conversion. Shown are homologous regions of two pairs of sister chromatids (each pair is referred to here as a haplotype), coded by color/shading, lined up as for metaphase I of meiosis. This region carries two loci of interest: the H locus controls the rate of DSBs, which occur at the X locus. We are interested in the rate at which allele i (carried by the blue/lightly shaded haplotype) at the H locus changes as a result of gene conversion. On this measure, there are three possible outcomes: (1) one copy of allele i can be converted to allele j, which decreases the representation of allele i by a factor of  ; (2) no conversion, which causes no change to the representation of allele i; and (3) one copy of allele j on one chromatid can be converted to allele i, which increases the representation of allele i by
; (2) no conversion, which causes no change to the representation of allele i; and (3) one copy of allele j on one chromatid can be converted to allele i, which increases the representation of allele i by  . The schematic details the paths by which these outcomes can occur and the associated probabilities. The diagram also shows that some, but not all, conversion events can be accompanied by crossover (recombination) events; in this case, a crossover occurs in the rightmost set of chromosomes (3) but not in the left two (1 and 2). The gray regions in the middle set of chromosomes (2) may come from either original chromatid, depending on the path followed to yield this outcome. Note that the probability that DSBs occur in both haplotypes is ignored in this figure but not in the models presented in the text.
. The schematic details the paths by which these outcomes can occur and the associated probabilities. The diagram also shows that some, but not all, conversion events can be accompanied by crossover (recombination) events; in this case, a crossover occurs in the rightmost set of chromosomes (3) but not in the left two (1 and 2). The gray regions in the middle set of chromosomes (2) may come from either original chromatid, depending on the path followed to yield this outcome. Note that the probability that DSBs occur in both haplotypes is ignored in this figure but not in the models presented in the text.
This paradox has been addressed in several recent theoretical studies (Boulton et al. 1997; Pineda-Krch and Redfield 2005; Calabrese 2007; Coop and Myers 2007), but a general solution to the problem remains elusive. Simulation studies show that selection favoring DSBs can counteract the process of biased gene conversion and slow or stop the loss of a hotspot, but only if there is a strong fitness benefit directly associated with activity at the hotspot itself (Boulton et al. 1997; Pineda-Krch and Redfield 2005). This appears to largely preclude the classical evolutionary explanation for recombination, which appeals to the ability of recombination to break down associations between alleles at multiple loci (linkage disequilibrium) and therefore potentially increase the ability of a population to respond to natural selection (Barton 1995). Since this classical explanation works through indirect fitness effects, in which alleles that increase recombination become associated with high-fitness genotypes at other loci, it is unlikely to provide strong enough selection on the recombination alleles (i.e., hostpots) themselves to overcome the force of biased gene conversion (Boulton et al. 1997).
There is some reason to think that DSBs (and therefore hotspots) may provide direct fitness benefits. In species with recombination hotspots (but not those without), DSBs serve as a trigger for the formation of the synaptonemal complex and therefore guarantee the correct segregation of chromosomes in meiosis (Hey 2004). This potentially provides a source of selection directly on hotspots; unfortunately, previous models have suggested that this selection is unlikely to provide strong enough selection to overcome biased gene conversion (Boulton et al. 1997; Pineda-Krch and Redfield 2005; Coop and Myers 2007).
Because selection must be unrealistically strong to provide a way around the conversion paradox by itself, recent theoretical work has concentrated on other potential escapes. One appealing approach is to allow hotspot activity to be controlled not by the sequence at the hotspot itself (in cis), but by the sequence at a site some distance away (in trans). Under such circumstances, DSB repair at the hotspot may only infrequently (or never) extend to the controlling locus; biased gene conversion at the hotspot itself would then not necessarily translate to biased gene conversion of hotspot activity.
But is trans control of hotspots likely? The mode of control of hotspots remains poorly understood. It is clear that cis control is important in many cases: several specific sequences (often, 6- to 10-bp motifs) have been shown to be associated with hotspot activity (Petes 2001; Jeffreys and Neumann 2002; Myers et al. 2005), although importantly these motifs appear to be neither necessary nor sufficient to form hotspots (Petes 2001; Myers et al. 2005). More direct evidence for cis control comes from several examples in which polymorphisms in hotspot activity have been shown to be associated with sequence polymorphisms at the hotspots themselves (Jeffreys and Neumann 2002, 2005; Baudat and De Massy 2007). However, there is also substantial scope for trans control: in yeast, many hotspots require the action of sequence-specific transcription factors (Petes 2001); changes in the specificity or activity of these or any other DSB-repair-specific proteins would be expected to have remote-acting effects on hotspot activity. Similarly, the details of chromatin structure and modification in a region appear to affect hotspot activity in some cases; in particular, regions with a relatively open chromatin structure provide better access for the recombination machinery (Petes 2001). Mutations at remote loci that change the patterns of histone modification, for example, might open up entirely new regions as potential hotspots. More specifically, recent evidence suggests that some polymorphisms in hotspot activity map only partially or not at all to local sequence variation (Neumann and Jeffreys 2006; Baudat and De Massy 2007), suggesting that variation in trans or epigenetic variation is responsible for some variation in hotspot activity. A combination of cis and trans control is therefore likely to be a fruitful direction for theoretical exploration.
Recent comparisons of hotspot distributions in humans and chimpanzees have highlighted further mysteries about recombination hotspots. Many hotspots are identified by the “chunks” of linkage disequilibrium—“haplotype blocks”—they cause in the genome. The fact that hotspots cause these signatures implies that they are maintained for thousands of generations. However, a large fraction of hotspots that are present in humans are absent in chimpanzees (Ptak et al. 2004, 2005; Winckler et al. 2005), suggesting that hotspots have been gained (and/or lost) over the scale of hundreds of thousands of generations. Combined with evidence, based on the comparison of historical rates of recombination (the strength of signal from haplotype blocks) with current rates (from sperm-typing studies), that the “heat” of at least some hotspots is decreasing in humans (Jeffreys et al. 2005), this suggests a picture in which hotspots arise and are then slowly lost over thousands of generations, causing turnover of hotspots at larger timescales.
But what can explain this pattern? Biased gene conversion can easily explain the loss of hotspots, but what can explain the appearance of new ones? Given that the conversion paradox is likely to be at its strongest when a hot allele is rare (so that the hot allele is always found in heterozygotes and is therefore constantly being lost to conversion), explaining the spread of a new hotspot is more difficult than explaining the existence of an old one. Recent theoretical studies exploring the action of genetic drift on modifiers undergoing biased gene conversion suggest that only when the force of conversion (that is, the product of the DSB rate and the probability that the control allele is converted when a DSB occurs) is weak can a hotspot spread or be maintained at high frequency (Calabrese 2007; Coop and Myers 2007). That is, very-hot cis-controlled hotspots act essentially as strongly deleterious mutations, which almost never fix due to drift. One possible mechanism by which very hot hotspots may arise is if biased gene conversion does not act against them on their initial spread through the population (Coop and Myers 2007): again, this might be achieved if the hotspot is, at least initially, controlled from a locus located in trans.
Theoretical approaches to the hotspot conversion paradox to date have consisted of simulations of finite populations (Boulton et al. 1997; Pineda-Krch and Redfield 2005) and diffusion approximations focusing on the stochastic fate of hotspots (Calabrese 2007; Coop and Myers 2007). Here, I present an analytical model of the deterministic processes underlying the evolution of a single recombination hotspot, to clearly define the conditions under which selection can overcome the effects of biased gene conversion and allow the maintenance of an existing hotspot and/or the spread of a new one. I focus on the evolution of hotspots under cis control, trans control, or a combination of the two, with emphasis on those conditions under which a hotspot under complete or partial trans control can spread but one under pure cis control cannot.
ONE-LOCUS MODEL
I begin by examining the fate of two alleles—H (the hot allele) and h (the cold allele)—at locus H (for the hotspot-control or simply the “control” locus), under the forces of mutation, selection, and biased gene conversion. The genotype at the H locus determines the DSB rate at the potential hotspot, which I refer to as locus X (as in, X marks the spot); the DSB rate in turn determines fitness and the rate of gene conversion. There is no allelic variation at the X locus per se; X is simply the physical location at which DSBs occur, although the H locus and the X locus may be one and the same, in which case the control of the hotspot is in cis. Alternatively, the H locus may be located some arbitrary distance from the X locus (it may, in fact, be located on a different chromosome, although to minimize confusion in the text I refer to the X and H loci as being on the same chromosome), in which case the control locus is in trans to the hotspot. In the following I describe in more detail the workings of the model. A summary of all important notation in this article can be found in Table 1, and a diagram of key features of gene conversion can be seen in Figure 1. All analyses described below were performed using Mathematica 6.0 (Wolfram Research 2007).
TABLE 1.
Notation used in the text and the model
| Notation | Definition |
|---|---|
| X | Hotspot locus |
| H, H, h | One-locus model: control locus, cold allele, hot allele |
| Modifier model: cis locus, cold allele, hot allele | |
| M, M, m | Modifier locus, active allele, inactive allele |
| hi | Dominance of i allele over alternative allele (at H locus in one-locus model and at M locus in modifier model) |
| βH, βh | “Hot” double-strand break rate, “cold” double-strand break rate |
| βi,j | Per-haplotype double-strand break rate of chromosome i in diploid genotype ij |
| pi, pij | Frequency of allele i, frequency of chromosome ij |
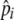 , , 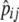
|
Equilibrium frequencies |
| σ | Selection gradient: slope of relationship between fitness and DSB rate |
| μ, ν | Mutation rates at H locus (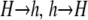 ) ) |
| τ | One-locus model: probability that locus H is converted when a DSB occurs at locus X |
| Modifier model: probability that locus M is converted when locus H is converted | |
| r | Rate of recombination between H and M loci (modifier model only) |
Double-strand break rate:
The per-chromatid DSB rate at the hotspot locus X of a given homolog in a diploid genotype is determined by the allele carried at the control locus, H, on the same homolog, possibly with some dominance effect arising from the allele carried at locus H on the other homolog. This requires two DSB rates for each diploid genotype ij: βi,j, which describes the DSB rate on the homolog carrying allele i when the other homolog carries allele j; and βj,i, which describes the DSB rate on the homolog carrying allele j when the other homolog carries allele i. Individuals homozygous for allele H have a per-chromatid DSB rate of βH ≡ βH,H, while those homozygous for allele h have a per-chromatid DSB rate of βh ≡ βh,h (βH > βh). DSB rates in heterozygotes are determined by a pair of “dominance coefficients”: hH, which denotes the extent to which the presence of allele H on the homologous chromosome increases the DSB rate associated with the h allele, and hh, which denotes the extent to which the presence of allele h on the homologous chromosome decreases the DSB rate associated with the H allele (in this article, one or both of the dominance coefficients are always set to zero, and 0 ≤ hi ≤ 1). All in all, in heterozygotes the DSB rate associated with allele H is 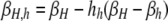 , and that associated with allele h is
, and that associated with allele h is 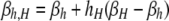 . Table 2 summarizes the values of βi,j for each diploid one-locus genotype.
. Table 2 summarizes the values of βi,j for each diploid one-locus genotype.
TABLE 2.
Double-strand break rates in one-locus models
| i = h (βh,j) | i = H (βH,j) | |
|---|---|---|
| j = h (βi,h) | βh | 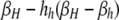 |
| j = H (βi,H) | 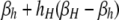 |
βH |
βi,j gives the per-haplotype DSB rate of haplotypes carrying the i allele when the other haplotype in a diploid genotype carries the j allele. In the H-dominant model, hh is set to zero; in the h-dominant model, hH is set to zero; in the no-dominance model, both hH and hh are set to zero.
Gene conversion at the H locus:
The probability that the control locus, H, undergoes conversion when a DSB occurs at locus X is given by τ. This parameter can be thought of as the trans parameter: the greater the physical distance is between loci X and H, the lower the probability that a DSB at locus X causes a conversion at H. τ = 1 therefore implies that control of the hotspot is completely in cis, while τ = 0 implies that control is completely in trans. Note that this yields a very broad definition of “trans” (and a correspondingly narrow definition of “cis”): the H locus may be only a few kilobases away from the X locus and still have τ = 0. Given these assumptions, the differential equation describing the rate of change of the frequency of allele H (pH) due to conversion is
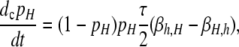 |
(1) |
where dc denotes change due to conversion; similar subscripts are used for selection and mutation below.
Selection:
In reality, selection on overall DSB rate within a chromosomal region likely results from some combination of the direct benefits (e.g., proper chromosome segregation) and the indirect benefits [which arise in turn from linkage disequilibria between loci flanking the DSB site and require models explicitly including selection on two or more viability loci to evaluate completely (Barton 1995)] of crossovers. These overall rates seem likely to be under stabilizing selection; however, as with any quantitative trait under stabilizing selection, any single allele causing a small difference in DSB rates relative to the total DSB rate in the region may be under directional selection (Falconer and Mackay 1996). Because I am interested in evaluating the strength of selection required for hotspots to be maintained or increase in frequency, I assume that there is directional selection on DSB rate at the X locus. In particular, I assume that fitness increases as a linear function of the probability that a DSB occurs at the X locus; that is, the fitness of diploid genotype ij is 1 + sij, where the selection coefficient is sij = (1 − (1 − βi,j)(1 − βj,i))σ and σ is the selection gradient for DSB rate at locus X (i.e., the slope of the relationship between DSB rate and fitness). Under these conditions, the differential equation for the change in pH due to selection is
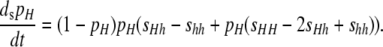 |
(2) |
Mutation:
Finally, I assume that mutation from 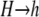 occurs at rate μ, and mutation from
occurs at rate μ, and mutation from 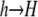 occurs at rate ν, yielding the differential equation
occurs at rate ν, yielding the differential equation
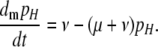 |
(3) |
Mutation–selection–conversion equilibria:
The overall equation describing the rate of change of the frequency of allele H is 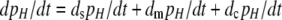 . I used Taylor series to approximate this and all further equations under the assumption that the DSB rate induced by the cold allele and mutation are both weak forces [i.e., that βh, μ, and ν are
. I used Taylor series to approximate this and all further equations under the assumption that the DSB rate induced by the cold allele and mutation are both weak forces [i.e., that βh, μ, and ν are 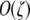 , where
, where 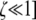 . Numerical analysis suggested that there is an equilibrium near pH = 1 and one near pH = 0 (i.e., near-fixation and near-loss of the hot allele). To express these equilibria analytically, I approximated the differential equation under further assumptions: to find the equilibrium when pH ≈ 1 (near-fixation, i.e., maintenance of the hotspot), I approximated around the point pH ≈ 1 [i.e., assuming that 1 − pH is
. Numerical analysis suggested that there is an equilibrium near pH = 1 and one near pH = 0 (i.e., near-fixation and near-loss of the hot allele). To express these equilibria analytically, I approximated the differential equation under further assumptions: to find the equilibrium when pH ≈ 1 (near-fixation, i.e., maintenance of the hotspot), I approximated around the point pH ≈ 1 [i.e., assuming that 1 − pH is 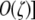 ; to find the equilibrium when pH ≈ 0 (loss of the hotspot), I approximated around the point pH ≈ 0 [i.e., assuming that pH is
; to find the equilibrium when pH ≈ 0 (loss of the hotspot), I approximated around the point pH ≈ 0 [i.e., assuming that pH is 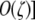 . Under these assumptions, the first-order approximation of the equilibrium near pH = 0 is
. Under these assumptions, the first-order approximation of the equilibrium near pH = 0 is
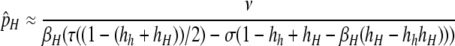 |
(4) |
and that of the equilibrium near pH = 1 is
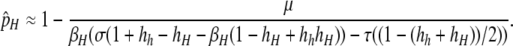 |
(5) |
Recall that for this analysis hH = 0 (h partially dominant), hh = 0 (H partially dominant), or hH = hh = 0 (no dominance); these substitutions simplify these expressions considerably.
These equilibria are similar in form to the classic diploid mutation–selection balance, in which the disfavored allele is held at a frequency of 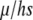 , where μ is the mutation rate to the disfavored allele and hs is the strength of selection against the heterozygote. Here, which allele is “disfavored” is determined by the relative strengths of conversion (the τ-terms in Equations 4 and 5) and selection (the σ-terms).
, where μ is the mutation rate to the disfavored allele and hs is the strength of selection against the heterozygote. Here, which allele is “disfavored” is determined by the relative strengths of conversion (the τ-terms in Equations 4 and 5) and selection (the σ-terms).
Of more interest than the expressions describing the precise frequencies at equilibrium are the conditions under which equilibrium (5) is stable (i.e., the hotspot can be maintained at high frequency) and those under which equilibrium (4) is unstable (i.e., the hotspot can increase in frequency when rare). These conditions are summarized in Table 3A. Also included in Table 3A is a further approximation of the conditions under which Equation 4 is unstable; this approximation assumes that the difference in DSB rate between the H and h alleles is small [i.e., βH − βh is 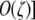 and therefore βH itself is small (but still greater than βh). This approximation is included to facilitate comparison with the modifier analysis below, which makes the same assumption.
and therefore βH itself is small (but still greater than βh). This approximation is included to facilitate comparison with the modifier analysis below, which makes the same assumption.
TABLE 3.
Stability conditions
| No dominance | H partially dominant | h partially dominant | |
|---|---|---|---|
| (hH = hh = 0) | (hh = 0; 0 < hH < 1) | (hH = 0; 0 < hh < 1) | |
| A. One-locus model | |||
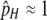 stable (hotspot maintained) stable (hotspot maintained) |
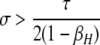 |
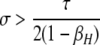 |
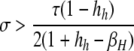 |
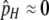 unstable (hotspot increases in frequency) unstable (hotspot increases in frequency) |
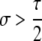 |
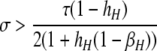 |
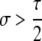 |
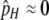 unstable (assuming βH and βH − βh are small) unstable (assuming βH and βH − βh are small) |
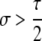 |
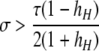 |
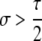 |
| B. Modifier model | |||
| pM = 0 unstable (hotspot-activating modifier increases in frequency) | 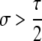 |
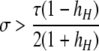 |
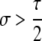 |
A detailed examination of the stability conditions in Table 3A leads to several conclusions. First, as shown by simulation studies (Boulton et al. 1997; Pineda-Krch and Redfield 2005), selection must be strong to maintain a hotspot whose activity is controlled by cis sequence (τ = 1). If we assume that cis-acting sequences experience no dominance effects (hH = hh = 0), to maintain a cis hotspot selection must be strong enough that 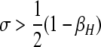 (that is,
(that is, 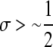 ). Recall that σ represents the rate of increase of fitness with DSB rate; similarly, under cis control,
). Recall that σ represents the rate of increase of fitness with DSB rate; similarly, under cis control,  represents the rate of increase of conversions with DSB rate (Figure 1). Thus, near-fixation is stable (and hotspots are maintained) whenever fitness increases more rapidly than conversion with increases in DSB rate. Put more concretely, this can be visualized as requiring that individuals that experience a DSB at the X locus have 50% higher fitness than those that do not (although note that formally the increase in fitness could be due to effects of the H allele other than DSBs per se). In other words, the fitness advantage must exceed the 3:1 transmission disadvantage of the hot allele in heterozygotes undergoing a DSB.
represents the rate of increase of conversions with DSB rate (Figure 1). Thus, near-fixation is stable (and hotspots are maintained) whenever fitness increases more rapidly than conversion with increases in DSB rate. Put more concretely, this can be visualized as requiring that individuals that experience a DSB at the X locus have 50% higher fitness than those that do not (although note that formally the increase in fitness could be due to effects of the H allele other than DSBs per se). In other words, the fitness advantage must exceed the 3:1 transmission disadvantage of the hot allele in heterozygotes undergoing a DSB.
Another important conclusion from Table 3A is that the conditions for maintenance (pH ≈ 1 stable) or invasion (pH ≈ 0 unstable) of the hotspot are more stringent for cis control than for trans control. As the probability that the control (H) locus is converted alongside the hotspot (τ) decreases, the strength of selection required for maintenance or invasion decreases proportionally: for fully trans loci (τ = 0), any σ > 0 suffices. In general, dominance (hH > 0 or hh > 0) also decreases the strength of selection required for invasion or maintenance of a hotspot, largely because dominance decreases the difference in DSB (and therefore conversion) rate of the hot and cold alleles in heterozygotes, which is where biased gene conversion occurs.
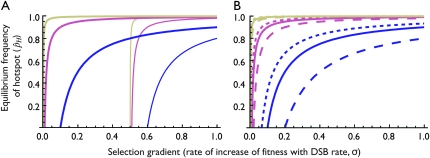
Figure 2 shows the “near-fixation” equilibrium frequency of allele H as a function of σ for the range over which it is stable for a variety of parameter values. As seen in Table 3A, trans control allows the maintenance of hotspots over a broader range of selection strengths than does cis control; Figure 2A demonstrates in addition that trans-controlled hotspots are held at higher frequencies at equilibrium than are cis-controlled hotspots. In addition, Figure 2B demonstrates that partial dominance at the H locus affects the equilibrium frequency of the H allele under trans control. In particular, if the H allele is partially dominant (hh = 0; 0 < hH < 1), the frequency of H at equilibrium is higher than under no dominance; if the h allele is partially dominant (hH = 0; 0 < hh < 1), the frequency of H is lower than under no dominance. This is due to the fact that when allele H is at high frequency, its fitness advantage is slightly elevated when it is dominant and slightly decreased when it is recessive.
Figure 2.—
Stable “near-fixation” equilibria in the one-locus model. Lines show the values of the 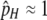 equilibrium over the range for which it is valid and stable for a variety of parameter values. (A) cis vs. trans control with no dominance (hH = hh = 0). Thin lines represent cis control (τ = 1); thick lines represent trans control (τ = 0). (B) The effects of dominance under trans control (τ = 0). Solid lines represent no dominance (hH = hh = 0; the same as seen in A); short dashes represent H partially dominant (hh = 0,
equilibrium over the range for which it is valid and stable for a variety of parameter values. (A) cis vs. trans control with no dominance (hH = hh = 0). Thin lines represent cis control (τ = 1); thick lines represent trans control (τ = 0). (B) The effects of dominance under trans control (τ = 0). Solid lines represent no dominance (hH = hh = 0; the same as seen in A); short dashes represent H partially dominant (hh = 0, 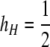 ); long dashes represent h partially dominant (hH = 0,
); long dashes represent h partially dominant (hH = 0, 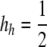 ). (A and B) Color/shading represents the DSB rate of the hot allele (βH): blue/dark lines, βH = 10−6; magenta/medium lines, βH = 10−5; gold/light lines, βH = 10−4. Higher DSB rates (βH > 10−4) closely resemble the pattern for βH = 10−4. Other parameter values: μ = ν = 10−7. The drop to zero at low values of σ in the trans case is a side effect of the approximation; see supplemental material for exact results.
). (A and B) Color/shading represents the DSB rate of the hot allele (βH): blue/dark lines, βH = 10−6; magenta/medium lines, βH = 10−5; gold/light lines, βH = 10−4. Higher DSB rates (βH > 10−4) closely resemble the pattern for βH = 10−4. Other parameter values: μ = ν = 10−7. The drop to zero at low values of σ in the trans case is a side effect of the approximation; see supplemental material for exact results.
Finally, it is worth noting that, although these equilibria are determined under the assumption that the equilibrium frequency of the hotspot is very close to one (pH ≈ 1), the actual equilibrium values can be substantially less than one, particularly for trans-controlled hotspots when the fitness advantage of increasing DSB rate (σ) and/or the DSB rate of the hot allele (βH) are low (Figure 2). This is because under these conditions the standard mutation–selection balance assumption that selection is a much stronger force than mutation is violated: the total strength of selection in this model is on the order of 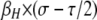 , which may be quite small under reasonable parameter values. One consequence of this is that it potentially allows for hotspot polymorphisms to be maintained deterministically; however, because this tends to occur when selection is weak, drift may be more important than selection under these parameter values (Calabrese 2007; Coop and Myers 2007). A comparison of these approximate results to the exact solutions, along with confirmation through numerical results, can be found in the supplemental material.
, which may be quite small under reasonable parameter values. One consequence of this is that it potentially allows for hotspot polymorphisms to be maintained deterministically; however, because this tends to occur when selection is weak, drift may be more important than selection under these parameter values (Calabrese 2007; Coop and Myers 2007). A comparison of these approximate results to the exact solutions, along with confirmation through numerical results, can be found in the supplemental material.
TWO-LOCUS (CIS HOTSPOT AND TRANS MODIFIER) MODEL
The one-locus model described above confirms that strong selection is required if a cis-controlled hotspot is to be maintained at an appreciable frequency, while trans-controlled hotspots can be maintained over a much broader range of selection strengths. Thus, in this purely deterministic model, there are two solutions to the hotspot conversion paradox: (1) allow strong selection on modifiers or (2) allow hotspot activity to be controlled in trans. Unfortunately, neither of these solutions offers a complete escape from the paradox: selection on individual hotspots is not expected to be particularly strong (Coop and Myers 2007) (but see discussion below), and there is convincing evidence that many hotspots are at least partially under cis control (Petes 2001; Jeffreys and Neumann 2002, 2005; Myers et al. 2005; Baudat and De Massy 2007). Thus, the hotspot paradox remains for cis-controlled modifiers where selection is weak 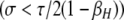 .
.
One possible explanation for the existence of hotspots under such circumstances may be that hotspots are under some combination of cis and trans control; that is, there must be a specific sequence at the hotspot locus itself to induce an increased frequency of DSBs, but that frequency increase occurs only when a particular allele is carried at another (trans) locus. This might be the case if, for example, a trans-acting regulating protein induces DSBs at a specific cis sequence or if the trans-acting protein affects histone modifications in a chromosomal region, which in turn control the accessibility of cis trigger sequences in that region to the DSB machinery.
To explore hotspot dynamics under such circumstances, I extend the one-locus model described above. First, I assume that the H locus is completely cis to the X locus (that is, that DSBs occur at the H locus—H is now both the control locus and the hotspot itself, so we ignore locus X) and that the effects of the two alleles at this locus (h and H) are determined by the genotype at “modifer” locus M, which has two alleles—an “active” allele (M) and an “inactive” allele (m). I am particularly interested in the extent to which the trans modifier can lead to the formation of new hotspots under circumstances where individual hotspots under purely cis control are expected to be lost.
Extensions of the one-locus model:
To build the modifier model, I generalize the one-locus model in several ways. First, I define separate DSB rates for every possible chromosome (the “inactive-cold” chromosome, hm; the “inactive-hot” chromosome, Hm; the “active-cold” chromosome, Hm; and the “active-hot” chromosome, HM) for every possible diploid genotype in which it might be found (note that, as for the X and H loci in the one-locus model, while I refer to the H and M loci as being on the same chromosome for clarity, the mathematical machinery does not require them to be on the same chromosome; it applies as well to any pair of alleles at the H and M loci that are inherited from the same parent). In this article, all of these DSB rates are defined as functions of βH and βh, the hot and cold DSB rates as seen in the one-locus model: individuals homozygous for the inactive modifier allele (m) experience the cold DSB rate no matter what alleles they carry at the H locus, while individuals homozygous for the active modifier allele (M) undergo DSB rates depending on their genotypes at the H locus as in the one-locus, no-dominance model above. DSB rates in Mm heterozygotes depend on the genotype at the H locus, as well as on dominance at the M locus, as given by dominance coefficients hM and hm in a manner analogous to hH and hh in the one-locus model. There is assumed to be no dominance at the H locus (i.e., hH = hh = 0). Table 4 shows the specific values of these DSB rates for all chromosomes in all genotypes. While the H locus is assumed to be in cis, the M locus may be in cis or trans; similar to the one-locus model, the probability that the M locus undergoes conversion when a DSB occurs at the H locus is described by the parameter τ. The differential equation describing the rate of change of the frequency of haplotype xy due to conversion is
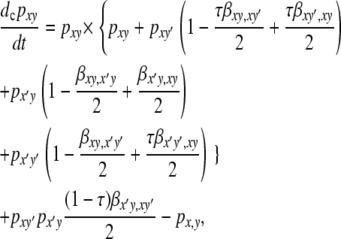 |
(6) |
where x′ and y′ represent the alternative alleles at loci H and M, respectively.
TABLE 4.
DSB rates in cis-plus-trans modifier models
| i = hm | i = hM | i = Hm | i = HM | |
|---|---|---|---|---|
| (βhm,j) | (βhM,j) | (βHm,j) | (βHM,j) | |
| j = hm | βh | βh | βh | 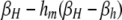 |
| (βi,hm) | ||||
| j = hm | βh | βh | 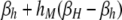 |
βH |
| (βi,hM) | ||||
| j = HM | βh | βh | βh | 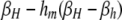 |
| (βi,Hm) | ||||
| j = HM | βh | βh | 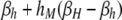 |
βH |
| (βi,HM) |
βi,j gives the per-haplotype DSB rate at the H locus of chromosome i when in a diploid genotype with chromosome j. For example, in a diploid genotype made up of chromosomes HM and hm, to determine the DSB rate of the HM chromosome, i = HM and j = hm, yielding 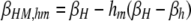 ; to determine the DSB rate of the hm chromosome, i = hm and j = HM, yielding βhm,HM = βh. In the M-dominant model, hm is set to zero; in the m-dominant model, hM is set to zero; in the no-dominance model, both hM and hm are set to zero.
; to determine the DSB rate of the hm chromosome, i = hm and j = HM, yielding βhm,HM = βh. In the M-dominant model, hm is set to zero; in the m-dominant model, hM is set to zero; in the no-dominance model, both hM and hm are set to zero.
The fitnesses of diploid genotypes are then defined as a linear function of the probability that a DSB occurs in that genotype, as defined in the one-locus model: wij = 1 + sij, where sij = (1 − (1 − βi,j)(1 − βj,i))σ; i and j now refer to haplotypes (e.g., hM), and βi,j and βj,i refer to the DSB rates at the H locus of haplotypes i and j, respectively, when found in genotype ij (Table 4). The differential equation describing the change in frequency of haplotype xy due to selection is therefore
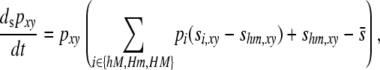 |
(7) |
where 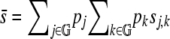 is the mean selection coefficient, and G is the set of all chromosomes
is the mean selection coefficient, and G is the set of all chromosomes 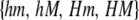 .
.
Mutation is assumed not to occur at the M locus, but occurs at the H locus at rates μ and ν as defined in the one-locus model; that is, mutation will convert only between haplotypes hm 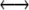 Hm or hM
Hm or hM 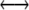 HM. The differential equation describing the change of the frequency of haplotypes HM and Hm due to mutation is
HM. The differential equation describing the change of the frequency of haplotypes HM and Hm due to mutation is
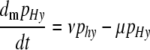 |
(8) |
and that describing the change of frequency of haplotypes hM and hm is
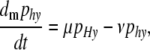 |
(9) |
where y indicates the allele carried at the M locus.
Finally, I assume that the rate of recombination between the H and M loci is r. Note that, while DSB activity at the H locus is expected to affect the rate of recombination between loci on opposite sides of the H locus, it is not necessarily expected to affect the rate of recombination between H itself and other loci; hence, for this model, I treat r as independent of βi,j. In addition, because I concentrate primarily on fully trans modifiers, which I imagine to be on the order of kilobases or more away from the hotspot and therefore well outside the range of repair of DSBs originating at that hotspot (τ = 0) but still potentially linked (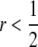 ), I treat r as independent of τ. The differential equation describing the rate of change of the frequency of haplotype xy due to recombination is
), I treat r as independent of τ. The differential equation describing the rate of change of the frequency of haplotype xy due to recombination is
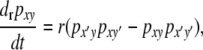 |
(10) |
where x′ and y′ represent the alternative alleles at loci H and M, respectively.
The modifier analysis proceeds by determining under what conditions a rare mutant at the M locus can increase in frequency in (invade) a population at equilibrium at the H locus (the “resident population”). This requires a set of three equations that describe the changes in frequency of four chromosome types (as opposed to the one-locus model, which required one equation to describe the changes in frequency of two alleles). Complete details of this analysis can be found in the supplemental material.
Since I am interested here in the origin of new hotspots, I assume that the resident population is fixed for the inactive (m) allele at the M locus, which causes both the H and the h alleles at the H locus (and therefore all diploid genotypes) to have the same DSB rate (βH). Under these circumstances there is no biased gene conversion and no selection, so the equilibrium frequency of allele H is determined by mutation alone: 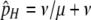 . To examine the ability of a modifier to spread when an allele at the H locus is at an arbitrary frequency (e.g., fixed), I also consider populations with no mutation (in which any allele frequency is an equilibrium in the absence of gene conversion/selection).
. To examine the ability of a modifier to spread when an allele at the H locus is at an arbitrary frequency (e.g., fixed), I also consider populations with no mutation (in which any allele frequency is an equilibrium in the absence of gene conversion/selection).
This process involves showing that the resident population is in equilibrium under the full system of three equations when the frequency of the M allele (pM) is set to zero and then determining under what conditions the M allele will increase in frequency, and at what rate (Otto and Day 2007). To yield rates that are amenable to interpretation, in addition to the approximations described for the one-locus model, I approximate under the assumption that the modifier is weak; that is, βH − βh is small (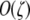 ), and therefore βH itself is small (but still greater than βh). In a manner similar to the one-locus model, I separately consider the cases in which the M allele is partially dominant to the m allele (hm = 0 and 0 < hM < 1 in Table 4), the m allele is partially dominant to the M allele (hM = 0 and 0 < hm < 1 in Table 4), or neither modifier allele is dominant (hM = hm = 0 in Table 4).
), and therefore βH itself is small (but still greater than βh). In a manner similar to the one-locus model, I separately consider the cases in which the M allele is partially dominant to the m allele (hm = 0 and 0 < hM < 1 in Table 4), the m allele is partially dominant to the M allele (hM = 0 and 0 < hm < 1 in Table 4), or neither modifier allele is dominant (hM = hm = 0 in Table 4).
Under these assumptions, over the vast majority of the parameter space the first-order approximation of the rate of change of the frequency of allele M (the active modifier allele) when the resident population is fixed for allele m is
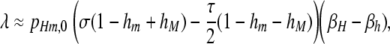 |
(11) |
where pHm,0 is the initial frequency of allele H (and therefore of chromosome Hm). This equation describes the rate of change of the M allele both when the resident population is at its mutational equilibrium (in which case 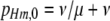 ) and when we ignore mutation (i.e., μ = ν = 0, in which case pHm,0 can be any frequency). The active modifier M will increase in frequency when λ > 0; the conditions under which this requirement is met (assuming that βH > βh; i.e., the hot allele increases DSB rate when found with the active modifier) are given in Table 3B.
) and when we ignore mutation (i.e., μ = ν = 0, in which case pHm,0 can be any frequency). The active modifier M will increase in frequency when λ > 0; the conditions under which this requirement is met (assuming that βH > βh; i.e., the hot allele increases DSB rate when found with the active modifier) are given in Table 3B.
A comparison of Table 3B with Table 3A shows that the conditions allowing for the spread of a trans modifier that affects the DSB rate of cis allele H are identical to those allowing for the spread of the hot allele in the one-locus model, when both are subject to the same approximation (i.e., comparing the third row of Table 3A with Table 3B). As with the one-locus model, a modifier located completely in trans of the hotspot (τ = 0) can spread under any selective conditions as long as there is some fitness benefit to DSB formation (σ > 0). This allows a new, cis-controlled hotspot to initially increase in frequency even when an increase in DSB rate causes only a slight increase in fitness: that is, it may offer a way around the hotspot conversion paradox even for cis-controlled hotspots under weak selection. Whether this initial frequency increase translates into measurable frequencies of such hotspots in real populations requires exploration of longer-term processes, as discussed below.
Overall, Equation 11 and the associated invasion conditions show that, as with Equations 4 and 5 and their stability conditions, the fate of the system is largely determined by the difference between a selection (σ) term and a conversion (τ) term. One potentially surprising aspect to this result is the fact that the rate of recombination between the H and M loci (r) does not affect the rate of spread in the first-order approximation (but note that, when r is very low, a more permissive invasion condition takes effect under the no-mutation model; see supplemental material. This condition is not discussed in detail here, because the parameter range under which it is relevant is quite restrictive). In “traditional” modifier models of the evolution of recombination, the rate of recombination between the modifier locus and viability loci is often an important parameter in determining whether or not the modifier can spread (Barton 1995). The fact that r is not important in this case is almost certainly due to the fact that the modifier has a direct effect on fitness in this model (i.e., the fitness of individuals with the HM chromosome is by definition higher than those without it), whereas in standard recombination modifier models any fitness benefit to the modifier must arise through associations with high-fitness genotypes (which are broken down more rapidly when r is high). Because my primary goal in the current study is to determine the strength of selection on the hotspot itself that is required for it to spread, and because there is reason to think that there may be direct selection on hotspot activity due to its importance in proper chromosome segregation, these effects are beyond the scope of the current model.
Long-term fate of hotspots:
It is important to note that this modifier analysis predicts only the short-term behavior of the system: the ability of a modifier to invade does not necessarily imply that it will go to fixation. In fact, even if the active modifier does fix (or nearly so), the system then reduces to the one-locus case: a cis-controlled hotspot established by the spread of a trans modifier will be lost to biased gene conversion except under strong selection, as shown in Table 3A. Thus, the rise of a new hotspot through the spread of a trans modifier is at best a temporary escape from the hotspot conversion paradox. But can an active hotspot—that is, active-hot chromosome HM—remain at high frequency for long enough to be observed in natural populations?
To address this question, I examined the numerical solutions to the exact differential equations approximated above for a range of parameter values. In particular, I considered the case in which the population is fixed or nearly fixed for the hot allele at the H locus (pH = 1 or pH = 0.99) and the active modifier allele (M) is introduced at a low frequency (pHM = 0.001 × pH). This is relevant to situations in which a “potentially hot” sequence has fixed, or nearly so (e.g., due to drift), in a chromosomal region in which it does not act as a hotspot; the modifier then “activates” this hotspot.
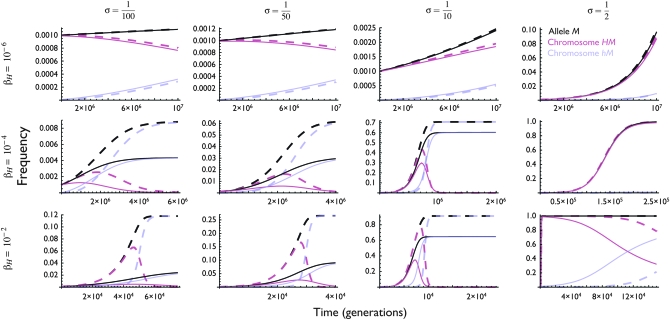
Figure 3 shows a representative set of frequency changes for the range of selection strengths under which hotspots are predicted to be unstable in the cis case, but a trans modifier is expected to spread ( ). In all cases, active modifier M increases in frequency initially, as predicted by the analytical results: because initially all (or nearly all) copies of the active modifier (M) allele are found with hot cis (H) alleles, the active-hot chromosome HM increases in frequency, displacing the inactive resident chromosomes. Eventually, however, as mutation produces cold allele h, active-cold chromosome hM begins to displace active-hot chromosome HM due to biased gene conversion (that is, the hotspot conversion paradox takes effect); once hot allele H is lost due to gene conversion, the spread of the active modifier M stops, often at an intermediate frequency.
). In all cases, active modifier M increases in frequency initially, as predicted by the analytical results: because initially all (or nearly all) copies of the active modifier (M) allele are found with hot cis (H) alleles, the active-hot chromosome HM increases in frequency, displacing the inactive resident chromosomes. Eventually, however, as mutation produces cold allele h, active-cold chromosome hM begins to displace active-hot chromosome HM due to biased gene conversion (that is, the hotspot conversion paradox takes effect); once hot allele H is lost due to gene conversion, the spread of the active modifier M stops, often at an intermediate frequency.
Figure 3.—
Dynamics of an active trans (τ = 0) modifier allele M (black/dark lines) and the two chromosomes carrying it: the “active-hot” chromosome (HM, magenta/medium lines) and the “active-cold” chromosome (hM, blue/light lines) under a variety of selection regimes. Note that the scales of both the x- and the y-axes change from section to section. Exact (nonapproximated) differential equations were solved numerically, starting from fixation (thick dashed lines) or near-fixation (pH = 0.99, thin solid lines) of the H allele and near-fixation of the m allele (pHM = 10−3; pHm = 1 − 10−3). Other parameter values are μ = 10−6, ν = 10−7, βh = 10−8, hM = hm = 0, and 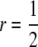 ; varying these parameters varies the rates of these processes but not the range of outcomes.
; varying these parameters varies the rates of these processes but not the range of outcomes.
The final frequency of active modifier M, and more importantly the length of time during which active-hot chromosome HM exists at high frequency in the population, is determined largely by the relative strengths of mutation, selection, and biased gene conversion: if selection is strong relative to the rate of mutation, the M allele may spread to near-fixation before the h allele appears at high enough frequency to cause substantial amounts of biased gene conversion. This allows chromosome HM to exist at relatively high frequency for hundreds or even thousands of generations if selection is strong enough (σ > 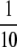 and βH > 10−4). If selection is weak, however (σ ≤
and βH > 10−4). If selection is weak, however (σ ≤ 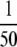 and β < 10−4), chromosome HM never reaches high frequencies. In addition, even small deviations from fixation of the H allele at time zero (e.g., pH = 0.99; solid lines in Figure 3) can magnify the effects of weaker selection, substantially limiting the spread of chromosome HM. As such, this mechanism is likely to be effective only on hotspot loci at which the (inactive) hot allele is truly at fixation.
and β < 10−4), chromosome HM never reaches high frequencies. In addition, even small deviations from fixation of the H allele at time zero (e.g., pH = 0.99; solid lines in Figure 3) can magnify the effects of weaker selection, substantially limiting the spread of chromosome HM. As such, this mechanism is likely to be effective only on hotspot loci at which the (inactive) hot allele is truly at fixation.
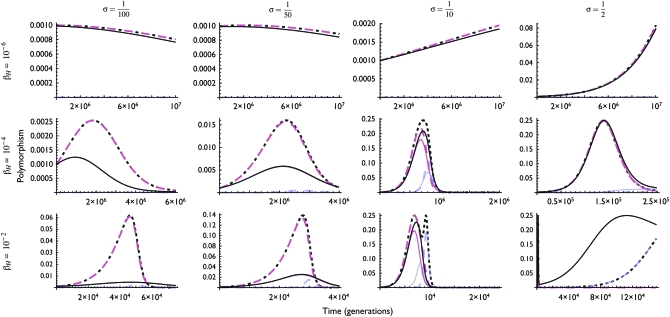
These patterns of allele and chromosome frequencies can lead to complicated patterns of hotspot activity polymorphism, particularly when selection is strong (Figure 4). Polymorphism in hotspot activity can result from polymorphism at the M locus (trans polymorphism) when the frequency of hot allele H is high or from polymorphism at the H locus (cis polymorphism) when the frequency of the active modifier, M, is high. Because the active modifier, M, spreads when the frequency of the hot allele, H, is high, after which the cold allele, h, spreads through the population, this can lead to two periods during which there is polymorphism for hotspot activity: a period of trans polymorphism followed by a period of cis polymorphism. Under most parameter values considered here, these two periods largely overlap, although if selection is strong and the hotspot is very hot (e.g., 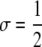 , βH = 10−2), there can be two very distinct peaks of polymorphism separated by thousands of generations.
, βH = 10−2), there can be two very distinct peaks of polymorphism separated by thousands of generations.
Figure 4.—
Dynamics of polymorphism over the lifespan of a hotspot under the cis-plus-trans modifier model. Panels and parameter values correspond to those in Figure 3. Black/dark line shows total polymorphism for the hotspot phenotype, measured as 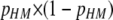 ; magenta/medium line shows polymorphism due to variation at the trans (modifier) locus, measured as
; magenta/medium line shows polymorphism due to variation at the trans (modifier) locus, measured as 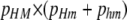 ; blue/light line shows polymorphism due to variation at the cis (hotspot) locus, measured as pHM × phM. Note that the scales of both the x- and the y-axes change from section to section.
; blue/light line shows polymorphism due to variation at the cis (hotspot) locus, measured as pHM × phM. Note that the scales of both the x- and the y-axes change from section to section.
As with the analytical results, these patterns depend largely on the relationship between selection (σ) and conversion (τ) and the magnitude of the modifier effect (βH). The other parameters of the model (cold DSB rate βh, mutation rates μ and ν, dominance parameters hM and hm, recombination rate r) affect the rates of change and therefore the duration of polymorphism and the maximum frequency of the active-hot chromosome (HM). In addition, the initial frequencies at the H locus have a strong effect on these results: for example, if the resident population is at its mutational equilibrium (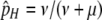 ), the frequency of cold allele h likely begins at a high enough frequency that biased gene conversion takes effect immediately, preventing active-hot chromosome HM from reaching high frequencies. Thus, this process is most likely to be important when populations are finite, such that there is an appreciable rate of turnover of neutral alleles (in particular, leading to some likelihood of fixation of the H allele when on the inactive-hot chromosome), but large enough that selection on the order of
), the frequency of cold allele h likely begins at a high enough frequency that biased gene conversion takes effect immediately, preventing active-hot chromosome HM from reaching high frequencies. Thus, this process is most likely to be important when populations are finite, such that there is an appreciable rate of turnover of neutral alleles (in particular, leading to some likelihood of fixation of the H allele when on the inactive-hot chromosome), but large enough that selection on the order of 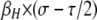 can act.
can act.
DISCUSSION
These results demonstrate the ability of trans control, on its own or in combination with cis control, to expand the conditions under which recombination hotspots can persist or increase under the influence of purely deterministic forces. When fitness increases rapidly enough with DSB rate (σ ≈ 0.1) and hotspot activity is under a combination of cis and trans control, these processes can explain both the appearance and the loss of hotspots, even (in fact, particularly) “very-hot” hotspots (βH ≥ 10−2; see Figure 3). This suggests a process of constant turnover of hotspots, in which individual hotspots are constantly disappearing due to biased gene conversion, and trans modifiers spread infrequently, allowing new hotspots to arise. Weaker selection (0 < σ < ∼0.1), while it is still able to explain the existence of hotspots controlled purely in trans (Table 3A; Figure 2), is unlikely to cause the appearance of new hotspots under both cis and trans control: although alleles in trans that activate such hotspots can spread initially (Table 3B), cold cis alleles arise and spread too quickly for active hotspots to reach any appreciable frequency (Figure 3).
The obvious question arising from these results is, “How strong is selection likely to be?” Since there are no direct estimates of the fitness effects of single hotspot alleles, there is no clear answer to this question. However, we may be able to get some indication of whether the results presented here fall within a range that is ever likely to be relevant. To begin with, it may be helpful to make the required σ-values above as concrete as possible. Recall that σ represents the slope of the relationship between fitness increase and DSB rate—that is, it is a selection gradient. Put simply, if fitness differences arise strictly from differences in DSB rate, σ represents the increase in fitness accruing to an individual that does undergo a DSB at locus X, relative to one that does not. σ = 0.1, therefore, implies that the fitness of individuals experiencing a DSB at locus X is 1.1 relative to those that do not, σ = 0.5 implies that this relative fitness is 1.5, etc.
Now we must consider the various mechanisms by which selection might favor a hotspot. In the broadest and most general sense, there are two: indirect benefits deriving from the breakdown of linkage disequilibrium and direct benefits, largely deriving from the association of DSBs and crossovers with the correct segregation of chromosomes. The degree of effective selection from the former depends strongly on assumptions about how linkage disequilibrium forms among loci flanking the hotspot. As an example, however, one recent model providing a relatively strong advantage to recombination finds that the effective selection on a recombination modifier under reasonable parameter values is se = 0.008 times the amount by which the modifier increases recombination (Barton and Otto 2005). Assuming that a DSB has a 50% chance of resolving as a crossover, this translates to σ = 0.004. This number decreases as the recombination rate between the modifier and the selected loci (or, in the present model, between the H and the M loci) increases.
It seems clear that indirect fitness effects of recombination alone are unlikely to cause selection strong enough to allow the evolution of new, cis-plus-trans-controlled modifiers as seen above. This leaves us with direct effects. Here, although there are no formal models to guide us, some rough calculations may be enough to determine whether such selection is ever likely to be strong enough to yield these patterns. I begin with the assumption that at least one crossover per chromosome arm is required to yield correct chromosome segregation (Hassold and Hunt 2001) and that individuals that segregate correctly have a fitness of one, while those that do not have fitness w0. The probability that a crossover occurs in the chromosome arm carrying locus X is dictated not only by the probability of a DSB at X, but also by the number of other hotspots on that chromosome arm, their DSB rates, the probability that a DSB resolves as a crossover, and the background (nonhotspot) crossover rate. The probability that a crossover occurs at a hotspot other than locus X is r* = 1 − (1 − β*ρ)2L, where β* is the per-haplotype-per-locus probability of a DSB at these hotspots (i.e., the probability that a DSB occurs at a given copy of a given hotspot), ρ is the probability that a DSB at a hotspot resolves as a crossover, and L is the number of hotspot loci (not including X). Finally, I assume that the probability of a crossover event somewhere other than a hotspot is a fraction b of the probability that a crossover occurs in a hotspot. The selection gradient can now be calculated as 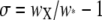 , where
, where
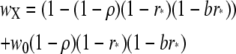 |
is the fitness of individuals experiencing a DSB at locus X, and
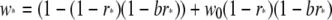 |
is the fitness of individuals with no DSB at locus X.
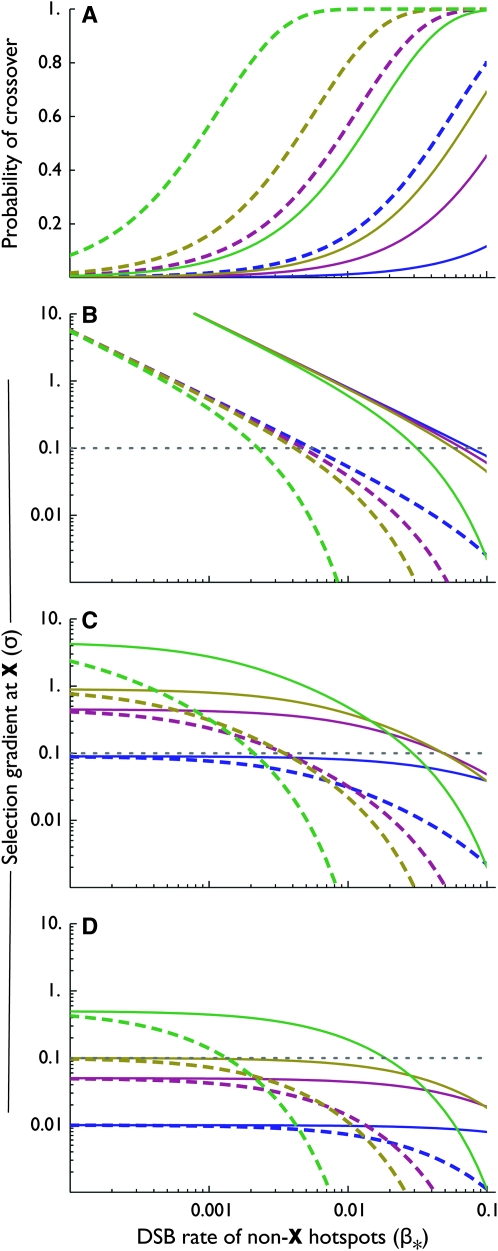
To place values on these numbers, we can turn to recent data from humans. In particular, recent studies suggest that there are 25,000–33,000 hotspots in the human genome (Myers et al. 2005; International HapMap Consortium 2007), translating to several hundred per chromosome arm (L ≤ ∼700), and that 60–80% of recombination occurs in hotspots (and therefore 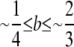 ). Although the DSB rates (β*) of all of these hotspots are not clear, well-characterized hotspots in humans range from β* ≈ 5 × 10−6 to β* ≈ 5 × 10−3 (Coop and Myers 2007). Finally, the probability that a DSB resolves as a crossover may be as low as ρ ≈ 0.1 (Jeffreys and May 2004); the maximum possible probability is ρ =
). Although the DSB rates (β*) of all of these hotspots are not clear, well-characterized hotspots in humans range from β* ≈ 5 × 10−6 to β* ≈ 5 × 10−3 (Coop and Myers 2007). Finally, the probability that a DSB resolves as a crossover may be as low as ρ ≈ 0.1 (Jeffreys and May 2004); the maximum possible probability is ρ =  . Figure 5 shows the value of σ over parameter values in these ranges. When the fitness of individuals with no crossover (w0) is zero, as the number of hotspots, or their heat (measured either as DSB rate, β*, or the probability that a DSB resolves as a crossover, ρ) decreases, the probability of correct segregation without a DSB at X decreases as well; this causes the strength of selection on DSB rate at locus X (σ) to increase. The primary effect of increasing the fitness of individuals with no crossover is to flatten out the relationship between non-X DSB rate (β*) and the selection gradient σ at low values of β*; this effect is stronger when the probability that a DSB resolves as a crossover (ρ) is low (hence the crossing of the lines when w0 > 0). Perhaps surprisingly, σ falls within the range under which rapid turnover of cis-plus-trans-controlled hotspots is expected under deterministic processes alone (σ ≥ 0.1, assuming allele H is fixed prior to the introduction of the modifier) over a variety of reasonable parameter values (β* ≤ ∼10−2 with 500 hotspots/chromosome arm; β* ≤ 10−1 with 50 hotspots/chromosome arm).
. Figure 5 shows the value of σ over parameter values in these ranges. When the fitness of individuals with no crossover (w0) is zero, as the number of hotspots, or their heat (measured either as DSB rate, β*, or the probability that a DSB resolves as a crossover, ρ) decreases, the probability of correct segregation without a DSB at X decreases as well; this causes the strength of selection on DSB rate at locus X (σ) to increase. The primary effect of increasing the fitness of individuals with no crossover is to flatten out the relationship between non-X DSB rate (β*) and the selection gradient σ at low values of β*; this effect is stronger when the probability that a DSB resolves as a crossover (ρ) is low (hence the crossing of the lines when w0 > 0). Perhaps surprisingly, σ falls within the range under which rapid turnover of cis-plus-trans-controlled hotspots is expected under deterministic processes alone (σ ≥ 0.1, assuming allele H is fixed prior to the introduction of the modifier) over a variety of reasonable parameter values (β* ≤ ∼10−2 with 500 hotspots/chromosome arm; β* ≤ 10−1 with 50 hotspots/chromosome arm).
Figure 5.—
Effects of DSBs other than at locus X on the probability of crossover occurrence and on the selection gradient (σ) at locus X. (A) Probability that a crossover occurs on the chromosome arm carrying locus X, assuming no DSB occurs at locus X, as a function of DSB rate at other hotspots on the same chromosome arm. (B–D) Log–log plots of selection gradient (σ) of DSB rate at locus X under direct selection for crossovers (e.g., due to a requirement for proper segregation) as a function of DSB rate at other hotspots on the same chromosome arm. B–D correspond to different fitnesses when there is no crossover (w0): (B) w0 = 0; (C) w0 = 0.1; (D) w0 = 0.5. The gray dotted line at σ = 0.1 indicates the approximate cutoff for the cis-plus-trans model to allow the spread of new hotspots to appreciable frequencies starting from fixation of the H allele. In all sections, line dashing corresponds to number of other hotspots (L): dashed, 50; solid, 700. Color/shading corresponds to the probability that a DSB resolves as a crossover (ρ): blue/dark lines, 0.01; magenta/semidark lines, 0.05; gold/semilight lines, 0.1; green/light lines, 0.5. In all cases, the ratio of the frequency of crossovers outside of hotspots to that inside them (b) is 2/3.
These rough calculations point out an important pattern: as the heat (β*) and/or number (L) of hotspots on a chromosomal arm decreases due to biased gene conversion, conditions become increasingly favorable for the spread of a new hotspot under any control scenario (cis, trans, or cis-plus-trans). In fact, these parameters (number and heat of hotspots) may not have to decrease particularly far, if at all, from their current levels for these conditions to be achieved.
In addition, the cis-plus-trans model provides another avenue by which the effective strength of selection might be increased: a trans modifier is likely to affect more than one hotspot locus. For example, such a modifier might affect an entire chromosomal region or globally change the specificity of a protein involved in the DSB or histone modification machinery. Selection on a trans modifier might therefore be stronger than that on any individual hotspot, allowing the modifier to spread to higher frequencies before individual hotspots begin to be lost to gene conversion and decreasing the per-hotspot selection gradient (σ) required for new hotspots to arise. This may be particularly important in cases where the H allele at one or more hotspots is not initially fixed. A full analysis of this process requires an explicit model of multiple hotspots, which is beyond the scope of this article.
Overall, it appears that a new, active hotspot under a combination of cis and trans control can spread to high frequencies under the deterministic forces of drift and gene conversion under reasonable parameter values, particularly as old hotspots become colder and are ultimately lost to biased gene conversion. In circumstances under which selection is weaker, of course, there is the potential for drift to contribute to the appearance of new hotspots; however, rather than requiring the fixation of effectively deleterious mutations (Coop and Myers 2007), the cis-plus-trans model allows the hotspot initially to be a mildly beneficial mutation, which may occasionally spread faster than expected due to drift. That is, a trans modifier that might spread only to low frequencies under purely deterministic processes may occasionally spread to higher frequencies under drift, yielding a high frequency of the active-hot modifier before biased gene conversion causes the hot allele to be lost. Again, an explicitly stochastic model of the cis-plus-trans case will be required to analyze this possibility fully.
Interestingly, the predictions of the cis-plus-trans model converge with a pair of recent observations regarding hotspot polymorphisms in mammals. One clear requirement of this model is that hotspots be under some combination of cis and trans control. Recent data from mice suggest just that: activity at recombination hotspot Psmb9 appears to be under control of a trans-acting enhancer that increases crossover rate ∼2000-fold, specifically at the Psmb9 locus. In addition, variation at the hotspot locus itself (in cis) can change the crossover rate by a factor of 10 (Baudat and De Massy 2007).
A more subtle prediction of the cis-plus-trans model involves the relationship between polymorphism and hotspot age. If an active hotspot originally arises through the spread of a trans modifier and then is lost to biased gene conversion in cis, two (possibly discrete) periods of polymorphism arise: initially, as the active trans modifier spreads, there is a period of polymorphism due to the fact that the modifier has not fixed; later, as the hot cis allele is lost to biased gene conversion, a second period of polymorphism occurs due to the cis allele being at intermediate frequencies (Figure 4). In other words, relatively young hotspots are more likely to show polymorphisms due to variation in trans, while older hotspots are more likely to show polymorphisms due to variation in cis (and possibly also in trans, depending on the maximum frequency reached by the modifier).
In a tantalizing recent analysis of two closely spaced hotspots in humans (Neumann and Jeffreys 2006)—a putatively young hotspot (MSTM1a) and an older hotspot (MSTM1b)—both show evidence of trans control (more precisely, non-cis control, which could also include purely epigenetic control), in that there is significant variation in crossover frequency among individuals with identical DNA sequences in a large interval around the hotspot. In addition, for neither hotspot is there a significant relationship between cis sequence and hotspot activity. However, this evidence appears stronger for the young hotspot, which shows a strictly “on-off” polymorphism in which individuals with active hotspots have no unique sequence difference that distinguishes them from those with inactive hotspots. The older hotspot shows much more continuous variation in hotspot activity, and only individuals classified as having “high” and “low” activity were examined for diagnostic sequence differences; this would appear to leave open the possibility that some variation in hotspot activity is due to DNA sequence variation in cis. It is possible, therefore, that the younger hotspot shows a polymorphism in trans while the older hotspot shows polymorphisms both in cis and in trans. It is also possible that these two hotspots are under joint control by the same trans element [the authors discount this possibility, but this is based on a marginally nonsignificant (P = 0.08) rank correlation on 26 individuals; it is therefore possible that this conclusion was based on a statistical test with marginal power]. This admittedly optimistic interpretation is precisely the prediction of a cis-plus-trans model in which the trans- and cis-polymorphism phases overlap. Further experiments explicitly comparing the nature of polymorphisms in young vs. old hotspots are likely to be a fruitful (if challenging) direction for exploring the realism of these models.
Another consequence of the prediction that older hotspots are more likely to show cis polymorphisms is that the majority of identified hotspots may provide a nonrandom sample for testing the mechanisms of hotspot control. Most hotspots are identified due to the blocks of linkage disequilibrium they cause over thousands of generations; however, new hotspots have not had the time to cause such blocks to form and are therefore unlikely to be detected by even the most sensitive linkage disequilibrium mapping techniques; only relatively intensive approaches such as sperm typing are likely to find these newer hotspots (Jeffreys et al. 2005). Any failure to find trans polymorphisms for hotspots identified by linkage-disequilibrium mapping cannot necessarily be taken as evidence that trans control has not been important to the evolution of these hotspots: the cis-plus-trans model specifically predicts that cis polymorphisms will become more prominent in older hotpots.
These models, particularly the cis-plus-trans control model, demonstrate that there is scope for the rise of new recombination hotspots under purely deterministic forces, given reasonable parameter values. Unlike recent stochastic models (Calabrese 2007; Coop and Myers 2007), it allows for the fixation of very-hot hotspots, assuming selection is strong enough (in fact, very-hot modifiers are more likely to fix under a given selection strength than less-hot modifiers; see Figure 3). Of course, this model requires several simplifying assumptions. As mentioned above, it models the benefits to hotspots as direct fitness effects rather than the indirect effects traditional in recombination modifier models; however, given that the effective selection coefficients in such models are so weak relative to the force of conversion (Barton 1995; Barton and Otto 2005), ignoring these effects is probably appropriate to a first approximation. Also as discussed above, the explicit consideration of multiple hotspot loci under the control of a single modifier seems likely to expand the conditions under which the cis-plus-trans model can bring a new hotspot to high frequencies; this is therefore likely to be a useful direction for future modeling efforts. Another dimension that may be of importance is the possibility that there are more than two levels of activity possible at a hotspot. As one example, if there are more than two alleles in cis, each with its own level of heat, then the secondary hotspot decline seen as biased gene conversion removes the hot allele in cis may not lead, at least immediately, to a complete reversion of a hotspot to its historical (premodifier) levels of recombination.
Finally, of course, the importance of stochastic processes cannot be denied: full understanding of the expected distribution of outcomes of any evolutionary process requires a formal inclusion of genetic drift. However, it is important to have a full understanding of the underlying deterministic processes to build a complete stochastic model. In this article, I have provided the first analytical approach to the deterministic processes behind the evolution of recombination hotspots and have shown that the inclusion of trans control can substantially broaden the circumstances under which hotspots are expected to be present in populations. Further, I have shown that cis-plus-trans control can explain the turnover of hotspots observed at the species level, even without the inclusion of stochastic processes. Further expansions of this model seem likely to expand these conditions.
Acknowledgments
I thank B. Payseur for invaluable discussions leading up to the preparation of this model and helpful comments throughout; B. Dumont, A. R. Ives, and R. T. Gilman for discussion; and S. P. Otto, Aneil Agrawal, J. Crow, R. Redfield, and an anonymous reviewer for comments on earlier versions of this manuscript. This work was supported by funds from the Department of Zoology and the Graduate School at the University of Wisconsin, Madison.
References
- Barton, N. H., 1995. A general model for the evolution of recombination. Genet. Res. 65 123–144. [DOI] [PubMed] [Google Scholar]
- Barton, N. H., and S. P. Otto, 2005. Evolution of recombination due to random dirift. Genetics 169 2353–2370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baudat, F., and B. de Massy, 2007. Cis- and trans-acting elements regulate the mouse Psmb9 meiotic recombination hotspot. PLoS Genet. 3 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boulton, A., R. S. Myers and R. J. Redfield, 1997. The hotspot conversion paradox and the evolution of meiotic recombination. Proc. Natl. Acad. Sci. USA 94 8058–8063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calabrese, P., 2007. A population genetics model with recombination hotspots that are heterogeneous across the population. Proc. Natl. Acad. Sci. USA 104 4748–4752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catcheside, D. G., 1975. Occurrence in wild strains of Neurospora crassa of genes controlling genetic recombination. Aust. J. Biol. Sci. 28 213–225. [DOI] [PubMed] [Google Scholar]
- Conrad, D. F., M. Jakobsson, G. Coop, X. Wen, J. D. Wall et al., 2006. A worldwide survey of haplotype variation and linkage disequilibrium in the human genome. Nat. Genet. 38 1251–1260. [DOI] [PubMed] [Google Scholar]
- Coop, G., and S. Myers, 2007. Live hot, die young: transmission distortion in recombination hotspots. PLoS Genet. 3 377–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crawford, D. C., T. Bhangale, N. Li, G. Hellenthal, M. J. Rieder et al., 2004. Evidence for substantial fine-scale variation in recombination rates across the human genome. Nat. Genet. 36 700–706. [DOI] [PubMed] [Google Scholar]
- Cromie, G. A., C. A. Rubio, R. W. Hyppa and G. R. Smith, 2005. A natural meiotic DNA break site in Schizosaccharomyces pombe is a hotspot of gene conversion, highly associated with crossing over. Genetics 169 595–605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dooner, H. K., and I. M. Martinez-Ferez, 1997. Recombination occurs uniformly within the bronze gene, a meiotic recombination hotspot in the maize genome. Plant Cell 9(9): 1633–1646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drouaud, J., C. Camilleri, P.-Y. Bourguignon, A. Canaguier, A. Berard et al., 2006. Variation in crossing-over rates across chromosome 4 of Arabidopsis thaliana reveals the presence of meiotic recombination “hot spots”. Genome Res. 16(1): 106–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falconer, D. S., and T. F. C. Mackay, 1996. Introduction to Quantitative Genetics, Ed. 4. Pearson, Harlow, UK.
- Grimm, C., P. Schaer, P. Munz and J. Kohli, 1991. The strong ADH1 promoter stimulates mitotic and meiotic recombination at the ADE6 gene of Schizosaccharomyces pombe. Mol. Cell. Biol. 11 289–298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guillon, H., and B. de Massy, 2002. An initiation site for meiotic crossing-over and gene conversion in the mouse. Nat. Genet. 32 296–299. [DOI] [PubMed] [Google Scholar]
- Hassold, T., and P. Hunt, 2001. To err (meiotically) is human: the genesis of human aneuploidy. Nat. Rev. Genet. 2 280–291. [DOI] [PubMed] [Google Scholar]
- Hey, J., 2004. What's so hot about recombination hotspots? PLoS Biol. 2 730–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- International HapMap Consortium, 2007. A second generation human haplotype map of over 3.1 million SNPs. Nature 449 851–862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffreys, A. J., and C. A. May, 2004. Intense and highly localized gene conversion activity in human meiotic crossover hotspots. Nat. Genet. 36 151–156. [DOI] [PubMed] [Google Scholar]
- Jeffreys, A. J., and R. Neumann, 2002. Reciprocal crossover asymmetry and meiotic drive in a human recombination hotspot. Nat. Genet. 31 267–271. [DOI] [PubMed] [Google Scholar]
- Jeffreys, A. J., and R. Neumann, 2005. Factors influencing recombination frequency and distribution in a human meiotic crossover hotspot. Hum. Mol. Genet. 14 2277–2287. [DOI] [PubMed] [Google Scholar]
- Jeffreys, A. J., J. Murray and R. Neumann, 1998. High-resolution mapping of crossovers in human sperm defines a minisatellite-associated recombination hotspot. Mol. Cell 2 267–273. [DOI] [PubMed] [Google Scholar]
- Jeffreys, A. J., A. Ritchie and R. Neumann, 2000. High resolution analysis of haplotype diversity and meiotic crossover in the human TAP2 recombination hotspot. Hum. Mol. Genet. 5 725–733. [DOI] [PubMed] [Google Scholar]
- Jeffreys, A. J., L. Kauppi and R. Neumann, 2001. Intensely punctate meiotic recombination in the class II region of the major histocompatibility complex. Nat. Genet. 29 217–222. [DOI] [PubMed] [Google Scholar]
- Jeffreys, A. J., R. Neumann, M. Panayi, S. Myers and P. Donnelly, 2005. Human recombination hot spots hidden in regions of strong marker association. Nat. Genet. 37 601–606. [DOI] [PubMed] [Google Scholar]
- Kelmenson, P. M., P. Petkov, X. Wang, D. C. Higgins, B. J. Paigen et al., 2005. A torrid zone on mouse chromosome 1 containing a cluster of recombinational hotspots. Genetics 169 833–841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malone, R. E., S. Kim, S. A. Bullard, S. Lundquist, L. Hutchings-Crow et al., 1994. Analysis of a recombination hotspot for gene conversion occurring at the HIS2 gene of Saccharomyces cerevisiae. Genetics 137 5–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVean, G. A. T., S. R. Myers, S. Hunt, P. Deloukas, D. R. Bently et al., 2004. The fine-scale structure of recombination rate variation in the human genome. Science 304 581–584. [DOI] [PubMed] [Google Scholar]
- Myers, S., L. Bottolo, C. Freeman, G. McVean and P. Donnelly, 2005. A fine-scale map of recombination hotspots across the human genome. Science 310 321–324. [DOI] [PubMed] [Google Scholar]
- Neumann, R., and A. J. Jeffreys, 2006. Polymorphism in the activity of human crossover hotspots independent of local DNA sequence variation. Hum. Mol. Genet. 15 1401–1411. [DOI] [PubMed] [Google Scholar]
- Nicolas, A., D. Treco, N. P. Schultes and J. W. Szostak, 1989. An initiation site for meiotic gene conversion in the yeast Saccharomyces cerevisiae. Nature 338 35–39. [DOI] [PubMed] [Google Scholar]
- Okagaki, R. J., and C. F. Weil, 1997. Analysis of recombination sites within the maize waxy locus. Genetics 147(2): 815–821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otto, S. P., and T. Day, 2007. A Biologist's Guide to Mathematical Modeling in Ecology and Evolution. Princeton University Press, Princeton, NJ.
- Petes, T. D., 2001. Meiotic recombination hot spots and cold spots. Nat. Rev. Genet. 2 360–369. [DOI] [PubMed] [Google Scholar]
- Pineda-Krch, M., and R. J. Redfield, 2005. Persistence and loss of meiotic recombination hotspots. Genetics 169 2319–2333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ptak, S. E., A. D. Roeder, M. Stephens, Y. Gilad, S. Pääbo et al., 2004. Absence of the TAP2 human recombination hotspot in chimpanzees. PLoS Biol. 2 849–855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ptak, S. E., D. A. Hinds, K. Koehler, B. Nickel, N. Patil et al., 2005. Fine-scale recombination patterns differ between chimpanzees and humans. Nat. Genet. 37 429–434. [DOI] [PubMed] [Google Scholar]
- Shifman, S., J. T. Bell, R. R. Copley, M. S. Taylor, R. W. Williams et al., 2006. A high-resolution single nucleotide polymorphism genetic map of the mouse chromosome. PLoS Biol. 4 2227–2237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szostak, J. W., T. L. Orr-Weaver and R. J. Rothstein, 1983. The double-strand-break repair model for recombination. Cell 33 25–35. [DOI] [PubMed] [Google Scholar]
- Winckler, W., S. R. Myers, D. J. Richter, R. C. Onofrio, G. J. McDonald et al., 2005. Comparison of fine-scale recombination rates in humans and chimpanzees. Science 308 107–111. [DOI] [PubMed] [Google Scholar]
- Wolfram Research, 2007. Mathematica, Version 6.0. Wolfram Research, Champaign, IL.
- Wu, T.-C., and M. Lichten, 1995. Factors that affect the location and frequency of meiosis-induced double-strand breaks in Saccharomyces cerevisiae. Genetics 140 55–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao, H., Q. Zhou, J. Li, H. Smith, M. Yandeau et al., 2002. Molecular characterization of meiotic recombination across the 140-kb multigenic a1-sh2 interval of maize. Proc. Natl. Acad. Sci. USA 99(9): 6157–6162. [DOI] [PMC free article] [PubMed] [Google Scholar]