The Impact of Dissociation on Transposon-Mediated Disease Control Strategies

Abstract

Vector-borne diseases such as malaria and dengue fever continue to be a major health concern through much of the world. The emergence of chloroquine-resistant strains of malaria and insecticide-resistant mosquitoes emphasize the need for novel methods of disease control. Recently, there has been much interest in the use of transposable elements to drive resistance genes into vector populations as a means of disease control. One concern that must be addressed before a release is performed is the potential loss of linkage between a transposable element and a resistance gene. Transposable elements such as P and hobo have been shown to produce internal deletion derivatives at a significant rate, and there is concern that a similar process could lead to loss of the resistance gene from the drive system following a transgenic release. Additionally, transposable elements such as Himar1 have been shown to transpose significantly more frequently when free of exogenous DNA. Here, we show that any transposon-mediated gene drive strategy must have an exceptionally low rate of dissociation if it is to be effective. Additionally, the resistance gene must confer a large selective advantage to the vector to surmount the effects of a moderate dissociation rate and transpositional handicap.

THE creation of transgenic mosquitoes that have a fitness advantage when feeding on Plasmodium-infected blood (Marrelli et al. 2007) has greatly renewed interest in the use of genetically modified vectors as a means of disease control. Resistance genes are unlikely to reach fixation in a wild-vector population on their own, partly because disease prevalence tends to be relatively low in vector populations (Beier et al. 1999) and partly because the selective advantage of a resistance gene diminishes as the disease becomes less prevalent (Boëte and Koella 2003). Consequently, a series of gene drive systems have been proposed to bias the disease-resistance gene in favor of fixation (Craig 1963; Curtis 1968). One such drive system is a transposable element (TE), which is able to spread through a population by virtue of its ability to replicate within a genome (Charlesworth et al. 1994).

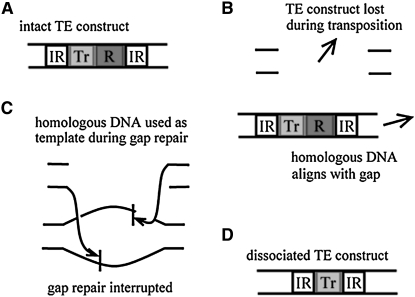
Any successful gene drive strategy requires tight linkage between the drive system and effector gene (James 2005). A general concern of drive systems is that rare recombination events can lead to loss of linkage between the drive system and effector gene (Curtis 2003; Knols and Scott 2003; Riehle et al. 2003). For TEs, there is an additional concern that internal deletion of DNA sequences within elements can occur during transposition. In the class of transposons being considered for genetic modification, this is thought to occur by an abortive gap-repair mechanism (Rubin and Levy 1997). Following excision or transposition, a double-stranded gap is introduced into the host chromosomal DNA. This gap is sometimes filled by copying information from a homologous chromosome, sister chromatid, or ectopic chromosomal site still containing the TE. If this process is interrupted, then the central portions of the element will not be copied, leading to an internal deletion event (Figure 1).

Figure 1.—

Abortive gap-repair mechanism of internal deletion. (A) An intact TE construct consists, at the very least, of a transposase gene (Tr), a disease-resistance gene (R), and a pair of inverted repeats (IR) marking its boundaries. (B) Following transposition or deletion, a double-stranded gap is introduced into the host chromosome DNA. (C) This gap is sometimes filled by copying information from a homologous chromosome, sister chromatid, or ectopic chromosomal site containing the intact construct. (D) If this process is interrupted, then the central portions of the TE will not be copied. In some cases, this produces a dissociated construct not containing the resistance gene.

The rate of internal deletion is largely dependent on the TE and host species being considered. In Drosophila melanogaster, P (Engels 1989) and hobo (Gelbart and Blackman 1989) elements produce deletion derivatives at a significant frequency due to abortive gap repair. The same mechanism is primarily responsible for the formation of nonautonomous Ds elements in maize (Rubin and Levy 1997) and the prevalence of nonautonomous mariner elements in many natural populations (Lohe et al. 2000). Despite this, there are other TEs, such as the Herves element in Anopheles gambiae, that remain in an almost exclusively intact form throughout evolutionary history (Subramanian et al. 2007).

Variability in the rate of internal deletion poses the question: What dissociation rate can be tolerated by an effective disease control strategy? If the dissociation rate is exceptionally slow, then the TE will drive the resistance gene into the vector population before the resistance gene has a chance to become detached. However, if the dissociation rate is exceptionally fast, then the resistance gene will be lost from the construct as the transposon spreads through the population, preventing the resistance trait from reaching a sufficiently high prevalence for effective disease control.

The situation is complicated by the tendency of TEs to transpose less frequently as their size is increased. Experiments in which Himar1 mariner elements were increased in size by adding various fragments of exogenous DNA (Lampe et al. 1998) found that the mobility of these elements is inversely proportional to their size. A similar relationship was observed for P elements in Drosophila melanogaster (Spradling 1986). These results are particularly relevant to the use of genetically modified vectors since it is projected that any useful gene drive system will carry at least two effector genes, a marker gene, and regulatory elements (M. Jacobs-Lorena, personal communication). Of concern is the possibility that elements no longer carrying their transgenic load will spread more quickly than their intact counterparts.

Another complicating factor is the impact of disease-resistance genes on host fitness. Mounting an immune response is generally associated with an evolutionary cost in insects (Kraaijeveld and Godfray 1997) and hence any resistance gene is likely to be associated with a selective disadvantage. Despite this, transgenic mosquitoes have been created that have no notable fitness cost when fed on Plasmodium-free blood (Moreira et al. 2004) and are in fact more fit when fed on Plasmodium-infected blood (Marrelli et al. 2007). Whether the resistance gene confers a fitness benefit or cost to the host will significantly influence the fate of the resistance gene in the vector population.

Successful disease control requires that the disease-resistance trait reaches a high prevalence in the vector population within a reasonable time frame. Throughout our modeling, we make recommendations regarding the dissociation rates, transpositional handicaps, and fitness costs or benefits required to achieve this goal.

METHODS

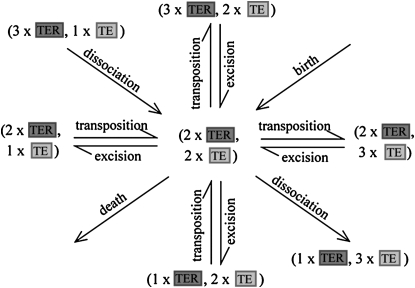
We use a system of ordinary differential equations to describe element spread through a randomly mating population incorporating dissociation (Figure 2). To simulate a transgenic release, we initiate the model with a proportion of the vector population having one copy of the intact TE construct and the rest having none. Element spread occurs as long as replicative transposition exerts a greater influence on element copy number than element deletion and host fitness costs. Dissociation leads to the number of intact constructs decreasing by one and the number of elements free of their transgenic load increasing by one. This reduces the number of TEs having a copy of the disease-resistance gene.

Figure 2.—

Schematic for the spread of an element construct incorporating dissociation of the resistance gene. An individual having two copies of the intact construct (TER) and two copies of the dissociated construct (TE) can gain a copy of either through transposition and lose a copy of either through deletion. The proportion of individuals having this genotype can also increase or decrease as a result of transposition or deletion. Dissociation is a one-way process leading to a TER becoming a TE. Analogous schematics can be drawn for every other genotype.

Mathematical model:

Particles in the model may have between 0 and T copies of the TE, where T is the maximum element copy number attainable during the period of spread. Of these copies, m are attached to the resistance gene and n are dissociated from their transgenic load. We keep track of the proportion of vectors having each genotype, 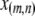, using a separate differential equation for each one. The process of element spread can then be modeled by a system of 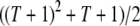simultaneous ordinary differential equations,

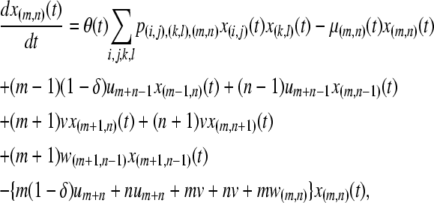(1)

where 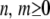and .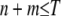

The first two terms in Equation 1 describe the birth and death rates of a vector having the genotype 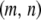. The death rate of a type- 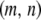vector, 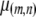, is given by the equation

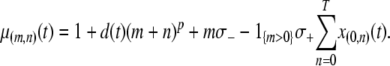(2)

The first term represents the death rate of a type-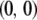 vector, the second term represents the fitness cost of 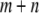TEs, the third term represents the fitness cost of m resistance genes, and the fourth term represents the selective advantage of the resistance trait. The fitness cost of a single TE, 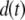, is assumed to decrease over time according to the equation

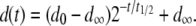(3)

Here, 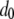represents the mean fitness cost of a new TE insert, 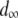represents the mean fitness cost of a TE segregating in the population, and 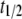represents the number of vector generations after which the mean fitness cost of a TE is 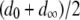. Following Charlesworth and Charlesworth (1983), we assume that the fitness cost of the TE is a log-concave function of element copy number. The power 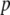determines the rate at which this fitness cost increases with total TE copy number (Charlesworth and Charlesworth 1983). The fitness cost of the resistance gene, 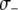, is assumed to increase linearly with dosage, m, while the fitness benefit of the resistance trait, 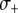, is conditional upon the presence of one or more resistance genes and is proportional to the fraction of the vector population that is susceptible to the disease at time .

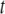The total birth rate of disease vectors, 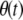, is equal to the total death rate, normalizing for the sum of 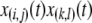terms in the birth rate term. This leads to the equation

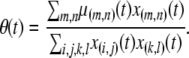(4)

The birth rate of a type-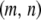 vector is then given by summing over every pair of genotypes in the population and weighting each pair by the probability that, when a type- 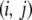vector mates with a type- 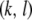vector, the offspring will be of type-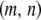. Assuming that all TEs are fairly well-spaced and hence segregate independently, this probability is given by

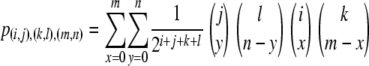(5)

The tendency of some elements to transpose locally (Tower et al. 1993; Zhang and Spradling 1993; Guimond et al. 2003) and display homing behavior (Guimond et al. 2003), although important, is beyond the scope of this study.

The third and fourth terms in Equation 1 describe the rate at which replicative transposition increases the proportion of type-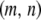 vectors in the population. This rate is proportional to the rate of replicative transposition and, due to the presence of repression of transposition (Charlesworth and Charlesworth 1983; Townsend and Hartl 2000; Le Rouzic and Capy 2005), is also a function of total element copy number. In a genome having a total of 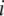element copies, the replicative transposition rate can be described as

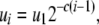(6)

where c determines the rate at which the replicative transposition rate falls off with additional element copies, and 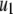is the replicative transposition rate when there is only a single element in the genome. Transposition is slowed down by the presence of a resistance gene, and so the replicative transposition rate of an intact TE construct is given by 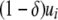, where 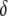represents the fractional decrease in transposition rate due to the effector gene.

The fifth and sixth terms in Equation 1 describe the rate at which element deletion increases the proportion of type-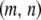 vectors in the population. The rate of element deletion, v, is very small and we assume this to be constant, independent of the total TE copy number or transgenic load. The seventh term describes the rate at which dissociation increases the proportion of type- 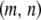vectors in the population. Internal deletion is hypothesized to occur during the act of transposition, and hence its rate is modeled as proportional to the rate of replicative transposition:

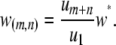(7)

Here, 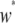is the dissociation rate when there is only a single intact construct in the genome. Finally, the eighth term describes the rate at which replicative transposition, element deletion, and dissociation decrease the proportion of type- 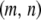vectors in the host population.

Parameter values:

Table 1 contains the parameter values and ranges used in the implementation of our model. At present there is little or no data regarding the postintegration behavior of the candidate elements in human disease vectors such as An. gambiae and Aedes aegypti, so most of these values were taken from measurements in other species, in particular D. melanogaster (Nuzhdin et al. 1997; Maside et al. 2000; Guimond et al. 2003; Pasyukova et al. 2004).

TABLE 1.

Parameter values, ranges, and source references

Parameter	Definition	Estimated value	Range	References
	Replicative transposition rate	0.1 TE−1 gen−1	—	Seleme et al. (1999); Vasilyeva et al. (1999)
c	Transpositional regulation parameter	2.866 TE−1	—	Townsend and Hartl (2000); Subramanian et al. (2007)
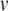	Element-deletion rate	4 × 10−6 TE−1 gen−1	—	Nuzhdin et al. (1997); Maside et al. (2000)
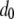	Initial TE fitness cost	0.02 TE−1	[0.01, 0.1] TE−1	Crow and Simmons (1983); Mackay et al. (1992)
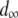	Asymptotic TE fitness cost	10−3 TE−1	—	Nuzhdin et al. (1997); Pasyukova et al. (2004)
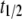	Half-time of TE fitness cost decline	5 gen	[2, 20] gen	Charlesworth (1991)
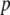	Rate of decrease in vector fitness	1.5	—	Charlesworth and Charlesworth (1983)
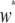	Dissociation rate	0.05 TE−1 gen−1	[0, 0.1] TE−1 gen−1	Levis et al. (1985); Robertson et al. (1988)
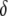	Transpositional handicap	0.95	[0, 0.99]	Spradling (1986); Lampe et al. (1998)
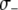	Fitness cost of resistance gene	—	[0, 0.05] TE−1	Beier et al. (1999); Ahmed et al. (2002)
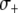	Fitness benefit of resistance gene	—	[0, 0.05]	Appawu et al. (2003); Marrelli et al. (2007)
x(1,0)	Initial proportion of transgenic vectors	0.025	[0.01. 0.1]	Taylor et al. (2001)

We consider a baseline replicative transposition rate of 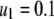per element per generation (TE⁻¹ gen⁻¹). Although this is a fairly high transposition rate, it is realistic (Seleme et al. 1999; Vasilyeva et al. 1999) and several modeling approaches have recommended it as a minimum requirement for gene drive to occur in a time frame acceptable to public health goals (Rasgon and Gould 2005; Le Rouzic and Capy 2006). We chose the transpositional regulation parameter to be 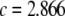per element (TE⁻¹) to achieve an average equilibrium element copy number of four. This was motivated by the observation that Herves, a functional class II TE in An. gambiae, is present across many geographical locations at an average copy number of four (Subramanian et al. 2007). Herves is of particular interest to transposon-mediated gene drive strategies since it rarely undergoes internal deletion and maintains its structural integrity over long periods of time (Subramanian et al. 2007).

Element-deletion events are so rare that they are often not observed in laboratory line experiments (Nuzhdin and Mackay 1994). We consider a deletion rate of 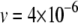TE⁻¹ gen⁻¹ as suggested by pooled estimates from several laboratory line experiments (Nuzhdin et al. 1997; Maside et al. 2000).

Following Mackay et al. (1992), we estimate the mean fitness cost of a new TE insertion by the average fitness cost of a spontaneous mutation. This has been estimated as 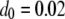TE⁻¹ (Mukai et al. 1972; Ohnishi 1977; Crow and Simmons 1983) and is a reasonable estimate in the early stages of TE spread when insertional mutagenesis is the dominant fitness cost and selection has not yet eliminated TEs with higher fitness costs (Charlesworth 1991). For TEs already segregating in the population, the mean fitness cost has been estimated from simple models of population dynamics by sampling chromosomes from natural populations and assuming that selection and transposition have an equal and opposite influence on TE copy number at equilibrium (Nuzhdin et al. 1997; Nuzhdin 2000). This has led to an estimate of fitness cost per element between 10⁻⁵ and 10⁻³ (Nuzhdin et al. 1997). We consider a fitness cost of 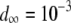TE⁻¹ since studies on laboratory lines of D. melanogaster suggest a fitness cost toward the upper end of this range (Pasyukova et al. 2004).

Charlesworth (1991) has proposed models to understand the abundance of TEs in nature when chromosomal sites vary with respect to the effect of element insertions on host fitness. These models predict that TEs will become more highly represented at neutral or weakly selected sites, and that the mean fitness cost of a TE will decline over a timescale “roughly equal to the reciprocal of the rate of transposition.” For a transposition rate of 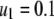TE⁻¹ gen⁻¹, this corresponds to a fitness decline over a scale of 10 generations. We therefore consider a half-time of 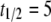mosquito generations for the mean fitness cost of the TE to fall from 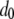to 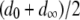. Following Charlesworth and Charlesworth (1983), we also consider a power of 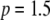to account for additional fitness costs at higher copy numbers, such as ectopic recombination (Langley et al. 1988).

A realistic range for the rate at which exogenous DNA becomes dissociated from an engineered TE construct can be deduced from experiments in which P elements were screened for loss of a visible marker gene (Daniels et al. 1985; Levis et al. 1985; Robertson et al. 1988). Here, expression of the rosy and white marker genes is disrupted at a rate of 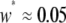TE⁻¹ gen⁻¹. Data on the fractional decrease in replicative transposition rate due to the presence of exogenous DNA (Spradling 1986; Lampe et al. 1998), the fitness cost of mounting an immune response (Kraaijeveld and Godfray 1997; Moreira et al. 2004), and the selective advantage of being disease resistant (Beier et al. 1999; Marrelli et al. 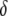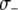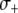2007) can be used to form realistic ranges for the parameters , , and , respectively.

Limiting our considerations to a single village where a disease vector is present, we estimate the initial proportion of disease vectors having one copy of the intact TE construct. The village of Banambani in Mali, West Africa, serves as a well-studied example for the malaria vector An. gambiae (Taylor et al. 2001). Here, there is an estimated abundance of 2000 mosquitoes of any given chromosomal form at the peak of the dry season (Taylor et al. 2001). Considering a release of 50 transgenic mosquitoes, each having a single copy of the intact TE construct, leads to an initial release proportion of .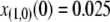

Numerical analysis:

As a measure of the spread of disease resistance, we calculate the proportion of vectors having one or more copies of the intact construct over time. This quantity can be calculated numerically using the fourth order Runge–Kutta method. For the parameterization described above, the maximum number of TEs in the genome is 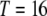. This can be used to reduce the number of equations being solved simultaneously.

RESULTS

Dissociation rate:

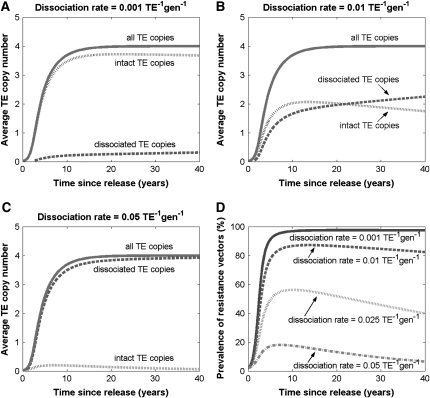
Using this system of differential equations, we consider the impact of varying the dissociation rate on the spread of the disease-resistance gene through a randomly mating vector population. In the simplest case (Figure 3), the resistance gene has no fitness consequences for the host and confers no transpositional handicap on the TE. The total genomic copy number reaches an equilibrium of four within 20 years and is very close to equilibrium after 10 years (Figure 3, A–C). Dissociation is hypothesized to occur during the act of transposition, and hence the proportion of dissociated TEs increases most rapidly during the early stages of element spread. Once equilibrium has been reached, transposition still occurs at a slower rate to counteract the forces of selection, deletion, and the random effects of gamete sampling. Consequently, the proportion of intact constructs decreases slowly until the resistance gene is lost from the population.

Figure 3.—

Element spread with dissociation. The resistance gene has no impact on host fitness or transposition rate. (A–C) Total element copy number reaches an equilibrium of four within 20 years, while the proportion of intact element copies decreases monotonically over time. Lines correspond to numerical solutions of the differential equation model for three different dissociation rates. (D) The prevalence of the disease-resistant vectors reaches a maximum within 10 years and then decreases gradually. The maximum prevalence and duration of presence depend largely on dissociation rate.

The proportion of element copies that have an intact copy of the disease-resistance gene is largely dependent on the dissociation rate. For a dissociation rate of 0.001 TE⁻¹ gen⁻¹, almost all element copies contain an intact resistance gene, and the average number of intact gene copies per individual is significantly greater than three, even after 40 years of spread (Figure 3A). This suggests that, for default parameters, a dissociation rate of 0.001 TE⁻¹ gen⁻¹ is acceptable for public health goals. A dissociation rate of 0.01 TE⁻¹ gen⁻¹ may also be tolerable since, in this case, intact and dissociated TE constructs are present at fairly equal numbers up to 40 years following release (Figure 3B). However, for a dissociation rate of 0.05 TE⁻¹ gen⁻¹, the vast majority of elements are devoid of an intact resistance gene well before the element construct has had a chance to reach equilibrium in the vector population (Figure 3C).

One indicator of an effective disease control strategy is the presence of a high number of disease-resistant vectors over a significant time span. Assuming that only a single copy of the resistance gene is necessary for its expression, the prevalence of disease-resistant vectors is equal to the proportion of vectors having at least one copy of the resistance gene. This quantity is plotted over time in Figure 3D for four different dissociation rates. For default parameters, disease-resistant vectors reach a maximum prevalence >80% for dissociation rates <0.013 TE⁻¹ gen⁻¹ and always reach a maximum prevalence within the first decade of spread.

To put this into perspective, dissociation rates have been measured for P elements by screening for the loss of a visible marker gene within the element (Daniels et al. 1985; Levis et al. 1985; Robertson et al. 1988) and are typically on the order of 0.05 TE⁻¹ gen⁻¹. According to our model, disease-resistant vectors reach a maximum prevalence of 18% at this rate, again suggesting that a dissociation rate of 0.05 TE⁻¹ gen⁻¹ is unacceptable for public health goals. On the other hand, for a dissociation rate of 0.01 TE⁻¹ gen⁻¹, disease-resistant vectors reach a maximum prevalence close to 87% and remain at a high prevalence for several decades following release. This confirms that a dissociation rate of 0.01 TE⁻¹ gen⁻¹ is potentially acceptable for public health goals.

An interesting conclusion that follows from Figure 3D is that, if the prevalence of disease-resistant vectors reaches a significantly high proportion in the vector population, then this prevalence will remain high for several decades following release. This implies that a high maximum prevalence of disease-resistant vectors will also tend to satisfy the requirement of a long duration of prevalence. For the remainder of this article, we use the maximum prevalence of disease-resistant vectors as an indicator of an effective disease control strategy.

The qualitative predictions of this model are relatively insensitive to changes in lesser-known parameters such as the fitness cost of a new TE insert, 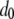, the half-time for TE fitness cost to fall, 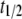, and the proportion of transgenic mosquitoes released, 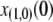. The release proportion of 2.5%, although motivated by the use of 50 transgenic mosquitoes in a small village, also applies, for example, to the release of 5000 transgenic mosquitoes in an endemic region with 200,000 wild-type mosquitoes. Increasing the release proportion to 10% decreases the time taken for the resistance trait to reach near-fixation and moderately increases the maximum prevalence that the resistance trait reaches in the population. Decreasing the release proportion to 1% has the converse effect (results not shown).

Transpositional handicap:

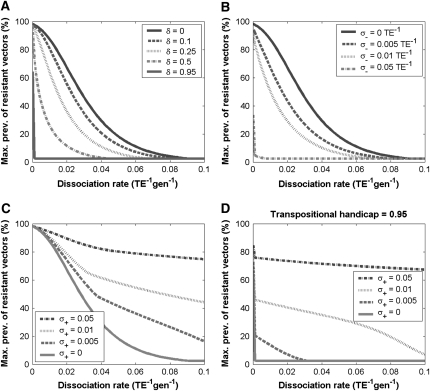
We extend this simple model of dissociation to the case where the effector gene compromises the rate of replicative transposition (Figure 4A). Using a parameter, 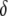, to account for the fractional reduction in transposition rate due to the presence of an effector gene, we model the impact of a transpositional handicap on the prevalence of disease-resistant vectors. Even a modest transpositional handicap can significantly reduce the maximum prevalence of disease resistance. As seen in Figure 4A for a transpositional handicap of , the dissociation rate must be <0.005 TE⁻¹ gen⁻¹ for the maximum prevalence of disease-resistant vectors to exceed 80%. When the transpositional handicap is 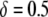then the dissociation rate must be <0.001 TE⁻¹ gen⁻¹ to achieve the same maximum prevalence; and when the transpositional handicap is 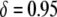then dissociation essentially cannot be tolerated.

Figure 4.—

Maximum prevalence of disease-resistant vectors. The resistance gene influences both transposition rate and host fitness. (A) The replicative transposition rate of an intact element construct is reduced by a fraction, 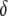. Increasing the value of 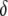decreases the maximum prevalence of resistant vectors and makes dissociation requirements more demanding. (B) The fitness cost conferred by the resistance gene, 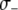, has a large impact on its maximum prevalence. (C) Dissociation requirements are considerably relaxed when the resistance gene confers a fitness benefit, 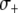. (D) A highly advantageous resistance gene is able to spread irrespective of a daunting dissociation rate or transpositional handicap.

To put these results into perspective, the RNAi-based strategy for resistance to multiple dengue serotypes currently consists of an effector gene, marker gene, and regulatory elements amounting to ∼6.5 kb (K. Olson, personal communication). A Himar1 mariner element containing a construct of this size would suffer a reduction in transposition rate of 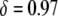(Lampe et al. 1998). Typical constructs now used in laboratory experiments are on the order of ∼5–6 kb (M. Jacobs-Lorena, personal communication) and would suffer a transpositional handicap of 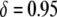if attached to a Himar1 mariner transposase gene (Lampe et al. 1998). Any construct acceptable for release in the field will need to have at least two or three effector genes to counteract evolution of the disease agent and to increase effectiveness of the intervention (M. Jacobs-Lorena, personal communication). These field-release constructs will be on the order of ∼8–12 kb and, contained within a Himar1 mariner transposon, would cause a transpositional handicap of 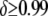(Lampe et al. 1998).

Although these transposition rate calculations specifically apply to the Himar1 mariner element, they clearly make the point that the transpositional handicap of an effector gene is of great concern to any transposon-mediated control strategy. The transpositional properties of any candidate element must be measured in both the presence and absence of a transgene construct, and the size of the construct should be minimized wherever possible, while still satisfying the requirements for effective intervention. As seen in Figure 4A, a transpositional handicap of 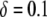is tolerable for dissociation rates <0.01 TE⁻¹ gen⁻¹, and higher transpositional handicaps are tolerable for smaller dissociation rates. An additional concern, however, is that gap repair becomes significantly less efficient for segments >11 kb (Johnson-Schlitz and Engels 2006). This provides an additional incentive for minimizing the size of the transgene construct.

Fitness consequences:

We consider the impact of a fitness cost associated with the effector gene using a parameter, 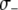, to account for the increase in vector death rate due to the effector gene. As with the case of a transpositional handicap, even a small fitness cost to the host can significantly reduce the maximum prevalence of disease-resistant vectors. As seen in Figure 4B, when the fitness cost of the effector gene is 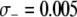TE⁻¹, then the dissociation rate must be <0.005 TE⁻¹ gen⁻¹ for the maximum prevalence of disease-resistant vectors to exceed 80%. When the fitness cost of the effector gene is 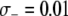TE⁻¹, the maximum tolerable dissociation rate to reach the same prevalence is 0.001 TE⁻¹ gen⁻¹, and when the fitness cost is 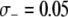TE⁻¹, then effective disease control is virtually impossible.

To account for a selective advantage associated with the effector gene, we introduce a parameter, 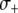, to model the mean increase in mosquito longevity due to the resistance trait. According to our model results (Figure 4C), when the fitness benefit of the effector gene is small (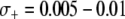) then the dissociation rate required for effective disease control is moderately relaxed. However, when the fitness benefit is large (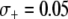) then disease control becomes feasible for a large range of dissociation rates—the maximum prevalence of disease-resistant vectors exceeds 80% for dissociation rates <0.05 TE⁻¹ gen⁻¹ and exceeds 75% for dissociation rates <0.1 TE⁻¹ gen⁻¹.

It is difficult to put these results into perspective due to the lack of reliable comparative fitness measurements in vector populations; however fitness costs have been documented in several insect species due to both mounting an immune response (Moret and Schmid-Hempel 2000; Ahmed et al. 2002) and maintaining the physiological machinery necessary to do so (Kraaijeveld and Godfray 1997; Koella and Boëte 2002). Ahmed et al. (2002) found that egg production was reduced by 18.6% in An. gambiae mosquitoes whose immune system was artificially stimulated with lipopolysaccharides. Given that the proportion of mosquitoes infected with malaria parasites varies between 1 and 20% in Africa (Beier et al. 1999), this corresponds to a mean fitness cost of 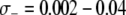TE⁻¹, depending on the region of Africa. Measurements of the fitness cost of immune surveillance are not as well-documented as they are for immune deployment.

These considerations are meaningless if the corresponding selective advantage of the resistance trait is not also considered. Indeed, Hurd et al. (2005) found that the fitness cost of resistance to malaria is equal to the selective advantage of avoiding infection, and hence the two factors effectively cancel each other out. If this were the case, then fitness effects could be completely ignored.

A recent encouraging result is that transgenic mosquitoes have been engineered that exhibit no measurable fitness cost when fed on Plasmodium-free blood (Moreira et al. 2004) and exhibit a fitness benefit when fed on Plasmodium-infected blood (Marrelli et al. 2007). Although these results were obtained from cage experiments using the rodent malaria parasite Plasmodium berghei, it is conceivable that similar results could be obtained for the human malaria parasite P. falciparum and vector An. gambiae. Marrelli et al. (2007) measured a 50% fitness benefit of being transgenic and a 35% fitness cost of being homozygous for the transgene; however this fitness measurement was on a population of mosquitoes that were all exposed to Plasmodium. In western Kenya, ∼6.3% of An. gambiae mosquitoes are infected with Plasmodium (Shililu et al. 1998), while in northern Ghana, ∼11% of An. gambiae mosquitoes are infected (Appawu et al. 2003). 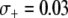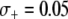Assuming that a 50% fitness benefit is possible without overdominance, then these mosquito infection rates correspond to a mean selective advantage of and , respectively.

Thus far, the effects of transpositional handicaps and fitness costs and benefits have been considered in isolation. However, of considerable interest is whether the selective advantage of resistance could counteract the detrimental effects of a transpositional handicap. In Figure 4D, we consider the impact of a fitness benefit on the spread of refractoriness when there is a transpositional handicap of 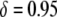. Interestingly, the maximum prevalence of disease-resistant vectors depends more on the fitness benefit than on the dissociation rate. For a fitness benefit of 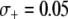, the maximum prevalence of disease-resistant vectors varies between 76% for a dissociation rate of 0.001 TE⁻¹ gen⁻¹ and 67% for a dissociation rate of 0.1 TE⁻¹ gen⁻¹. For fitness benefits of 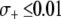, disease control is not feasible. The implication of this result is that a highly advantageous resistance gene (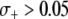) can spread to a high prevalence in the vector population irrespective of a daunting dissociation rate or transpositional handicap.

DISCUSSION

Several commentaries on the use of TEs to drive resistance genes into vector populations have expressed concern that dissociation will ultimately lead to the resistance gene being lost from the population (Curtis 2003; Hahn and Nuzhdin 2004). One of the key conclusions of this modeling effort is that the epidemiological outcome of the gene drive strategy critically depends on the rate at which the resistance gene dissociates from the drive system. For slow rates of dissociation (0.01 TE⁻¹ gen⁻¹) disease control is expected to occur within decades, while for intermediate rates of dissociation (0.05 TE⁻¹ gen⁻¹) disease-resistant vectors are predicted to reach a much smaller maximum prevalence (<20%) and to be lost within decades. These contrasting scenarios highlight the importance of having good estimates of dissociation rates for the TEs and host species being considered for transgenic release. They also lead to the interesting prediction that, if dissociation inhibits the success of the project, then the resistance gene could be lost from the vector population within a human time frame.

Another recommendation of the model is that the size of the effector gene and associated regulatory elements should be restricted to limit the transpositional handicap of a TE attached to its transgenic load. While small transpositional handicaps may be tolerable, experiments on the Himar1 mariner element indicate that the effector gene constructs currently being developed in the laboratory would suffer a reduction in transposition rate of at least 95% if attached to this element. It is therefore important that, in addition to measuring the dissociation rate of the candidate elements, we also measure their transposition rates both in the presence and absence of the transgene construct. It is not sufficient that a transposable element replicates quickly within a genome—its transposition rate must also be relatively unaffected by exogenous DNA.

The fitness impact of the refractory gene is also of great importance in determining its fate in the vector population. Although a selective advantage may not be sufficient on its own to achieve fixation (Boëte and Koella 2003), when combined with a drive system it greatly improves the chances of success. A large selective advantage of refractoriness is a crucial factor in outweighing the daunting effects of dissociation and reduction in transposition rate. It is therefore essential to have comparative measurements of the fitness of both transgenic and wild-type mosquitoes both exposed and unexposed to the disease agent. If a transgenic release becomes more feasible, it will also be essential to make these measurements under taxing field conditions using the human vector and disease agent and to develop innovative ways for differentiating these effects from inbreeding depression and the process of transgenesis. Such measurements are not currently available.

Model limitations:

Symptomatic of any mathematical analysis, simplifications have been made in this model that may compromise its predictions. First, the choice of Herves as a model element that has an average copy number of four (Subramanian et al. 2007) is not representative of the vast number of TEs that are present at much higher copy numbers (Charlesworth et al. 1992). This choice was motivated in part by the fact that Herves rarely undergoes internal deletion and also by the fact that model complexity greatly increases with element copy number. To assess the dynamics of TEs with higher copy numbers, another modeling framework should be proposed.

Second, in the model formulation all genomic elements are assumed to act independently during gamete formation, implying that all element copies are at least 50 cM apart. This contradicts the tendency for TEs to jump locally rather than distally (Tower et al. 1993; Zhang and Spradling 1993; Guimond et al. 2003) and to home in on certain genomic regions (Guimond et al. 2003). This is an important consideration since clustering of element copies can reduce the rate of element spread (Rasgon and Gould 2005); however to focus on the impact of dissociation, this consideration is beyond the scope of the present study.

Future directions:

The model presented here is of special relevance to diseases such as malaria and dengue fever, which are currently being considered for transposon-mediated control strategies (Scott et al. 2002). The present study could be supplemented by imbedding the spread of the resistance gene within a model of the epidemiology of malaria or dengue fever (Boëte and Koella 2002). This would give us a better idea of the exposure rate of vectors to the malaria parasite or dengue virus. It would also allow us to better predict the maximum prevalence of disease-resistant vectors and hence the rate of dissociation that is required for effective disease control.