Abstract
Under a hypothesis that the host–parasite interaction system is governed by genome-for-genome interaction, we propose a genetic model that integrates genetic information from both the host and parasite genomes. The model can be used for mapping quantitative trait loci (QTL) conferring the interaction between host and parasite and detecting interactions among these QTL. A one-dimensional genome-scan strategy is used to map QTL in both the host and parasite genomes simultaneously conditioned on selected pairs of markers controlling the background genetic variation; a two-dimensional genome-scan procedure is conducted to search for epistasis within the host and parasite genomes and interspecific QTL-by-QTL interactions between the host and parasite genomes. A permutation test is adopted to calculate the empirical threshold to control the experimentwise false-positive rate of detected QTL and QTL interactions. Monte Carlo simulations were conducted to examine the reliability and the efficiency of the proposed models and methods. Simulation results illustrated that our methods could provide reasonable estimates of the parameters and adequate powers for detecting QTL and QTL-by-QTL interactions.
THE interaction between a host and a parasite is a ubiquitous biological phenomenon, which has a significant impact on ecology, evolution, and agriculture. Host–parasite interaction drives the coevolution of both the interacting species (Hamilton 1980; Thompson 1994). It is believed that host–parasite coevolution has generated much of the biological diversity on the earth (Rausher 2001). Processes analogous to the host–parasite coevolution also occur in agricultural systems. When breeders release disease-resistant crop varieties, new virulent pathogen strains will rapidly emerge to overcome the resistance of the crop.
Host–parasite interaction is genetically controlled by both the host and the parasite genomes. Most studies on the genetic mechanisms of host–parasite interaction and coevolution have focused on related major genes of both the host (termed resistance genes) and the parasite (termed infection or virulence genes). Several models have been proposed to describe the relationship between the host resistance gene and the parasite infection gene. In plants, the most prevalent model is the gene-for-gene (GFG) model, in which the disease resistance of a host occurs only when its resistance (R) gene is matched by the parasite avirulence (AVR) gene (Flor 1971; Thompson and Burdon 1992). In animals, the most prevalent model is the matching-alleles model, in which a host can defend against any parasite whose genotype does not match the host's genotype (Peters and Lively 1999; Agrawal and Lively 2001). These two models represent two ends of a continuum (Agrawal and Lively 2001).
The GFG model has become the theoretical basis for plant disease-resistance breeding and has substantial molecular evidence. It has been known that R and AVR genes are responsible for the mutual recognition between plants and pathogens. During the past decade, >40 plant R genes have been cloned (Martin et al. 2003), all of which follow the GFG model. In addition, two pairs of R and AVR genes (Pto/AVR-Pto and Pita/AVR-Pita) have been proved to interact directly via their encoded proteins (Scofield et al. 1996; Tang et al. 1996; Jia et al. 2000). Although the resistance and infection genes play the most important roles in the host–parasite interaction, they are not the only genes involved. In fact, host–parasite interaction is a complicated biological process, in which many genes apart from the resistance/infection genes in either the host or the parasite genome are involved. In addition, many host–parasite interactions do not rely on the resistance/infection genes, but are presumably controlled by many genes with minor effects. Therefore, host–parasite interaction is actually a complex system controlled by many genes of both species. To completely understand the genetic basis of host–parasite interaction, it is necessary to study not only the resistance/infection genes, but also many related minor genes.
With the advent of molecular marker technology, mapping of quantitative trait loci (QTL) has become a powerful tool for dissecting the genetic architectures of complex traits. Systematic statistical methods for QTL mapping have been well established (Lander and Botstein 1989; Haley and Knott 1992; Zeng 1994; Kao et al. 1999; Ljungberg et al. 2004). However, all the genetic models for QTL mapping proposed to date are limited to single species. Consequently, QTL mapping for host–parasite interaction can be performed only either in the host or in the parasite. In fact, most QTL mapping studies on the plant–pathogen interaction reported have been focused on the plant (host) side. Since the host–parasite interaction involves the genetic control of both the host and the parasite genomes, a comprehensive understanding of the genetic basis of host–parasite interaction requires knowing not only the genes involved in host and parasite, but also the interaction between host genes and parasite genes. Hence, current genetic models of QTL mapping are not adequate for the full dissection of the genetic architecture of host–parasite interaction.
By considering host and parasite as an integrated biological system and assuming a genome-by-genome interaction mechanism in the system, we propose a general quantitative genetic model for the host–parasite interaction. The genetic model fits our current knowledge on the genetic basis of host–parasite interaction and enables us to simultaneously detect QTL and their interactions related to host and parasite. Monte Carlo simulations are conducted to demonstrate the application of the host–parasite model to mapping QTL under a special experimental design.
GENETIC MODELS
In quantitative genetics, there is a basic formula for describing a quantitative trait,
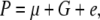 |
(1) |
where P is the phenotypic value, μ is the mean of the population, G is the genotypic effect, and e is the environmental deviation. Although the original formula is limited to a single species, it can be extended to describe the interaction between a host and a parasite. Suppose PHP is the phenotypic value of a trait (e.g., disease index) reflecting the host–parasite interaction. Obviously, the trait is genetically controlled by both the host genome and the parasite genome. Therefore, the genotypic effect (G) can be partitioned into components due to host genotypic effect (GH), parasite genotypic effect (GP), and genotypic interaction between host and parasite (GGHP), so that the basic formula can be rewritten as
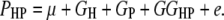 |
(2) |
This extended formula provides us with a general genetic model for the analysis of host–parasite interaction.
A detailed genetic model of host–parasite interaction depends on the genetic structures of both the host and the parasite in a specific experimental design. Without loss of generality, we can use the plant–fungus interaction as a model to address the basic principle of our methodology. An obvious feature of this system is that the sporophyte generation is generally dominant in the host (plant) life cycle, while the gametophyte generation is generally dominant in the parasite (fungus) life cycle. Therefore, the host is generally diploid and the parasite is generally haploid. For simplicity, we consider the situation of using a population of doubled haploid lines (DHLs) of the host derived from a cross between two pure lines (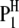 and
and 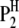 ) and a population of haploid strains (HSs) of the parasite derived from a cross between two strains (
) and a population of haploid strains (HSs) of the parasite derived from a cross between two strains (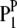 and
and 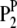 ). Suppose the number of DHLs is nH and that of HSs is nP. Both the host population and the parasite population have been genotyped with molecular markers, and their corresponding genetic maps have been constructed. The host DHLs are randomly inoculated by the parasite HSs and the symptom of each inoculation combination is measured as an index of interaction between the host DHL and the parasite HS. There is a constraint that each host line or parasite strain is involved in at least one inoculation.
). Suppose the number of DHLs is nH and that of HSs is nP. Both the host population and the parasite population have been genotyped with molecular markers, and their corresponding genetic maps have been constructed. The host DHLs are randomly inoculated by the parasite HSs and the symptom of each inoculation combination is measured as an index of interaction between the host DHL and the parasite HS. There is a constraint that each host line or parasite strain is involved in at least one inoculation.
On the basis of the above experimental design, we can set up a genetic model of the plant–fungus interaction. Suppose that there are 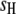 QTL in the host genome (
QTL in the host genome (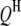 ),
), 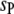 QTL in the parasite genome (
QTL in the parasite genome (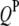 ),
),  epistatic QTL pairs in the host genome (
epistatic QTL pairs in the host genome (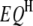 ),
), 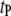 epistatic QTL pairs in the parasite genome (
epistatic QTL pairs in the parasite genome ( ), and
), and 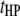 pairs of interspecific QTL interactions between the host genome and the parasite genome (
pairs of interspecific QTL interactions between the host genome and the parasite genome (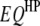 ). When trilocus or higher-order interactions are ignored, the host–parasite (plant–fungus) interaction can be expressed with the genetic model
). When trilocus or higher-order interactions are ignored, the host–parasite (plant–fungus) interaction can be expressed with the genetic model
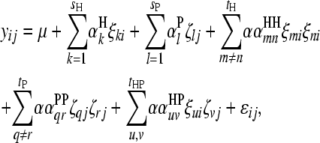 |
(3) |
where 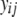 is the trait value (symptom) of the ith host (plant) DHL and the jth parasite (fungus) HS;
is the trait value (symptom) of the ith host (plant) DHL and the jth parasite (fungus) HS; 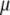 is the model mean;
is the model mean; 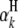 is the additive effect of the kth
is the additive effect of the kth 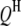 ;
; 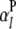 is the additive effect of the lth
is the additive effect of the lth 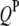 ;
; 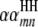 is the
is the 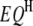 effect between the mth and the nth
effect between the mth and the nth 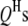 ;
; 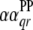 is the
is the  effect between the qth and the rth
effect between the qth and the rth 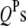 ;
; 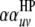 is the
is the 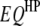 effect between the uth
effect between the uth 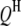 and the vth
and the vth 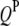 ;
; 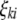 (
(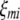 ,
, 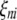 , or
, or  ) is a dummy variable taking a value of 1 or −1 when the genotype of the kth (mth, nth, or uth)
) is a dummy variable taking a value of 1 or −1 when the genotype of the kth (mth, nth, or uth) 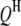 in the ith DHL is like that of
in the ith DHL is like that of 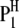 or
or 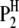 ;
; 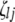 (
(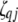 ,
, 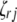 , or
, or 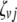 ) is also a dummy variable taking a value of 1 or −1 when the genotype of the lth (qth, rth, or vth)
) is also a dummy variable taking a value of 1 or −1 when the genotype of the lth (qth, rth, or vth) 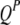 in the jth HS is like that of
in the jth HS is like that of 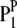 or
or 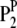 ; and
; and 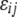 is the residual error, which is generally assumed to follow a normal distribution with zero mean.
is the residual error, which is generally assumed to follow a normal distribution with zero mean.
METHODOLOGY OF QTL MAPPING
Model (3) provides a theoretical basis for simultaneously mapping host (plant) and parasite (fungus) QTL underlying the host–parasite interaction and for estimating the intragenomic and intergenomic QTL interactions. When fitting (3), it involves a problem of a multidimensional search of multiple loci in two genomes. We adopt a two-step mapping strategy, by which QTL are first searched for individual effects using a one-dimensional (1D) scan throughout the host and parasite genomes and then for intra- and intergenomic QTL interactions using a two-dimensional (2D) scan with the previously mapped individual QTL fixed in the model. After the mapping procedure is finished, all the detected QTL and QTL interactions are integrated into (3) to estimate their effects.
Scanning for QTL in the host and parasite genomes:
The 1D scan is performed following the principle of composite-interval mapping (Zeng 1994). But we select marker intervals (pairs of adjacent markers) instead of individual markers as cofactors in the model. This would enable more efficient control of the effects of background QTL presumably located in the selected marker intervals, because the effect of a QTL could be completely absorbed by its flanking markers (Zeng 1993). Suppose 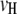 marker intervals in the host and
marker intervals in the host and 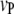 marker intervals in the parasite are selected as cofactors, respectively. Define two dummy variables,
marker intervals in the parasite are selected as cofactors, respectively. Define two dummy variables, 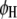 and
and 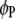 , which take values of 1 and 0 when the test is performed on a putative QTL in the host genome or 0 and 1 when in the parasite genome. Thus, according to (3), the model for testing a putative QTL in either the host genome or the parasite genome can be written as
, which take values of 1 and 0 when the test is performed on a putative QTL in the host genome or 0 and 1 when in the parasite genome. Thus, according to (3), the model for testing a putative QTL in either the host genome or the parasite genome can be written as
 |
(4) |
where  (or
(or  ) is the additive effect of the putative QTL in the host (or parasite) genome;
) is the additive effect of the putative QTL in the host (or parasite) genome;  (or
(or 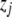 ) is the expected value of the indicator variable of the putative QTL in the ith host DHL (or jth parasite HS), conditioned on the genotypes of its flanking markers (Jiang and Zeng 1997);
) is the expected value of the indicator variable of the putative QTL in the ith host DHL (or jth parasite HS), conditioned on the genotypes of its flanking markers (Jiang and Zeng 1997); 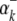 and
and 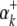 (or
(or 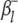 and
and 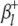 ) are the additive effects of the left and the right markers of the kth (or lth) marker interval in the host (or parasite) genome; and
) are the additive effects of the left and the right markers of the kth (or lth) marker interval in the host (or parasite) genome; and 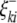 and
and 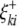 (or
(or 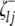 and
and 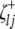 ) are indicator variables for the genotypes of the left and the right markers of the kth (or lth) marker interval in the ith host DHL (or jth parasite HS) following the similar definitions of
) are indicator variables for the genotypes of the left and the right markers of the kth (or lth) marker interval in the ith host DHL (or jth parasite HS) following the similar definitions of 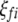 (or
(or 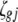 ) in (3).
) in (3).
Model (4) can be expressed in matrix form as
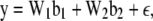 |
(5) |
where y is an n × 1 vector of trait values; 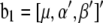 and
and 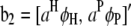 ; W1 and W2 are the design matrices corresponding to b1 and b2, respectively; and ɛ is an n × 1 vector of residual errors. A general equation for the expected reduction sum of squares of b2 can be obtained,
; W1 and W2 are the design matrices corresponding to b1 and b2, respectively; and ɛ is an n × 1 vector of residual errors. A general equation for the expected reduction sum of squares of b2 can be obtained,
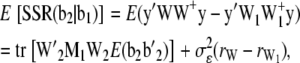 |
(6) |
where 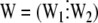 ,
, 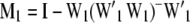 ,
, 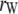 is the rank of W, and
is the rank of W, and 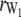 is the rank of W1. Accordingly, under the null hypothesis H0: b2 = 0, an F-test can be performed on the basis of Henderson's method III:
is the rank of W1. Accordingly, under the null hypothesis H0: b2 = 0, an F-test can be performed on the basis of Henderson's method III:
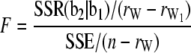 |
(7) |
(Searle et al. 1992). The F-test can be performed across the host genome (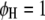 and
and 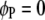 , for
, for 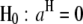 ) and the parasite genome (
) and the parasite genome (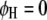 and
and 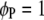 , for
, for 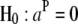 ) with a step length of 1 cM. When the F-values in a region exceed a predefined critical threshold, a QTL is indicated at the position of the maximum F-value.
) with a step length of 1 cM. When the F-values in a region exceed a predefined critical threshold, a QTL is indicated at the position of the maximum F-value.
In regard to the selection of cofactor marker intervals, we adopt a method similar to that of marker pair selection (MPS) (Piepho and Gauch 2001) to select cofactor marker intervals. The MPS approach has the advantage that markers enter the model in adjacent pairs, which reduces the number of models to be considered, thus alleviating the problem of overfitting and increasing the chances of detecting QTL. For the kth marker interval of the host (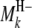 ,
, 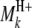 ) or the lth marker interval of the parasite (
) or the lth marker interval of the parasite (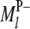 ,
, 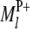 ), a single-marker interval model can be written as
), a single-marker interval model can be written as
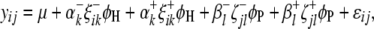 |
(8) |
where all the parameters and variables have the same definitions as in (4). With Equation 8, F-tests are used for testing all marker intervals on the basis of Henderson's method III. Marker intervals showing F-values greater than the given critical threshold are taken as candidate marker intervals.
Detecting intra- and intergenomic interactions between QTL:
Suppose 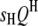 's and
's and 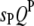 's have been mapped in the 1D scan. Obviously, interaction between these QTL can be tested easily by a model selection technique analogous to the strategy of multiple-interval mapping (Kao et al. 1999). However, there may be interactions involving some QTL not detected by the 1D scan due to small or even no individual effects. To find all possible QTL interactions, we adopt a 2D scan procedure, which tests any possible pair of loci within and between the host and parasite genomes, conditioned on the effects of the
's have been mapped in the 1D scan. Obviously, interaction between these QTL can be tested easily by a model selection technique analogous to the strategy of multiple-interval mapping (Kao et al. 1999). However, there may be interactions involving some QTL not detected by the 1D scan due to small or even no individual effects. To find all possible QTL interactions, we adopt a 2D scan procedure, which tests any possible pair of loci within and between the host and parasite genomes, conditioned on the effects of the 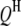 's and
's and 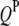 's mapped by the 1D scan. In addition, we select marker-interval pairs that show significant interactions between them and put them into the model as cofactors to control background variance. Suppose we select
's mapped by the 1D scan. In addition, we select marker-interval pairs that show significant interactions between them and put them into the model as cofactors to control background variance. Suppose we select 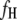 and
and  pairs of marker intervals within the host and parasite genomes and
pairs of marker intervals within the host and parasite genomes and 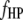 pairs of marker intervals between the host and parasite genomes. For simplicity, the interaction between two marker intervals (A and B) is approximately represented by the interactions between the left markers (
pairs of marker intervals between the host and parasite genomes. For simplicity, the interaction between two marker intervals (A and B) is approximately represented by the interactions between the left markers (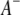 and
and 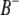 ) and between the right markers (
) and between the right markers (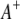 and
and 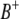 ) of the two intervals. Thus, the significance of
) of the two intervals. Thus, the significance of 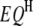 ,
, 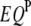 , or
, or 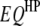 of any pair of loci (denoted by f and h) can be tested with an F-statistic based on Henderson's method III, using the model
of any pair of loci (denoted by f and h) can be tested with an F-statistic based on Henderson's method III, using the model
 |
(9) |
where 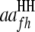 and
and  are QTL interactions within the host and parasite genomes, respectively;
are QTL interactions within the host and parasite genomes, respectively; 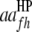 is QTL interaction between the host and parasite genomes;
is QTL interaction between the host and parasite genomes; 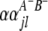 and
and 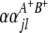 (
(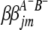 and
and 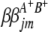 ) are interactions between the left and between the right markers of the lth (mth) pair of marker intervals in the host (parasite) genome;
) are interactions between the left and between the right markers of the lth (mth) pair of marker intervals in the host (parasite) genome; 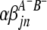 and
and 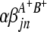 are interactions between the left and between the right markers of the nth pair of marker intervals between the host and parasite genomes; and the remaining parameters and variables have the same definitions as above. The 2D genome scan can be performed within the host (
are interactions between the left and between the right markers of the nth pair of marker intervals between the host and parasite genomes; and the remaining parameters and variables have the same definitions as above. The 2D genome scan can be performed within the host (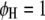 and
and 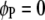 , for
, for 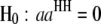 ) or the parasite (
) or the parasite (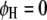 and
and  , for
, for  ) genome for intragenomic QTL interactions and between these two genomes (
) genome for intragenomic QTL interactions and between these two genomes (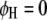 and
and 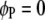 , for
, for 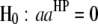 ) for intergenomic QTL interactions.
) for intergenomic QTL interactions.
Selection of significant interactive marker-interval pairs used as cofactors in (9) is performed with the following model using an F-statistic based on Henderson's method III:
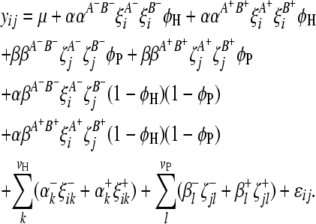 |
(10) |
All the parameters and variables in (10) have been defined above. The cofactor marker intervals used in (4) are also fixed in (10) to reduce residual variance and increase the power of detecting marker-interval interactions. We can perform this test on all possible pairs of marker intervals in the integrated host–parasite genetic system and consequently get a 2D F-statistic profile, according to which marker-interval pairs corresponding to the peaks of F-values that exceed the predefined significance threshold value can be selected.
Threshold determination and model selection:
Every step of the analysis discussed above (marker-interval selection, 1D scanning for QTL, marker-interval pair selection, or 2D scanning for QTL pairs) involves the problem of testing multiple null hypotheses. Therefore, multiple-test correction is needed. We can adopt the method of permutation tests (Churchill and Doerge 1994; Doerge and Churchill 1996) to control the experimentwise false-positive rate. For each of the steps, we shuffle only the relationship between the trait and the effect(s) to be tested but leave the relationships between the trait and the other effects unchanged because if the relationships between the trait and the nontested effects are destroyed, an artificially low empirical threshold could be obtained from the permutation tests and thus an enormously high false-positive rate would be obtained (Churchill and Doerge 1994). This is done by shuffling the row order of the design matrix of the testing effects (e.g., W2 in Equation 5).
Furthermore, in each of the steps, the F-statistic profile is plotted and the peaks that exceed the critical F-value calculated by permutation tests are identified as significant marker intervals, QTL, marker-interval pairs, or QTL pairs. However, some of the peaks could be ghost peaks due to the correlation of closely linked markers and random noise, etc. So, we perform a stepwise model selection with also the aforementioned F-statistic as criteria to remove possible ghost peaks (marker intervals, QTL, marker-interval pairs, or QTL pairs). The threshold of the F-value at a significance level of  is used to control the type I error rate in the model selection, where K is the number of tests in each forward or backward selection process in the stepwise selection procedure.
is used to control the type I error rate in the model selection, where K is the number of tests in each forward or backward selection process in the stepwise selection procedure.
MONTE CARLO SIMULATIONS
Real data sets necessary to validate the concept and method presented in this study are not yet available in the public domain. To examine the feasibility, reliability, and robustness of the proposed models and analysis methods, we performed simulation studies. The genetic maps of host and parasite were assumed to have five and three chromosomes, respectively. Eleven markers were evenly spread over each of the host and parasite chromosomes with spacing of 10 cM. Assuming that there were five 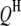 's and three
's and three 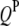 's (Table 1), one
's (Table 1), one 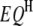 , one
, one 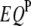 , and two
, and two 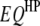 's (Table 2), 60% of the trait variation was attributed to the assumed interspecific genetic architecture. The relative contribution (RC) of individual QTL (additive effects) and QTL pairs (interaction effects) ranged from 3.22 to ∼9.46% and from 3.45 to ∼6.57%, respectively; the population size of host DHLs and parasite HSs was 200, respectively. The number of host–parasite inoculation combinations was set at three cases, namely 400 (case I), 600 (case II), and 800 (case III). Every case was simulated for 200 replicates. For every analysis step in every case, an empirical threshold of F-statistic at the experimentwise significance level of 0.05 was estimated with 1000 permutation tests.
's (Table 2), 60% of the trait variation was attributed to the assumed interspecific genetic architecture. The relative contribution (RC) of individual QTL (additive effects) and QTL pairs (interaction effects) ranged from 3.22 to ∼9.46% and from 3.45 to ∼6.57%, respectively; the population size of host DHLs and parasite HSs was 200, respectively. The number of host–parasite inoculation combinations was set at three cases, namely 400 (case I), 600 (case II), and 800 (case III). Every case was simulated for 200 replicates. For every analysis step in every case, an empirical threshold of F-statistic at the experimentwise significance level of 0.05 was estimated with 1000 permutation tests.
TABLE 1.
Estimation of individual QTL for positions, additive effects, and statistical powers
| True value
|
Estimate of positiona
|
Estimate of effecta
|
Power (%)
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| QTL | Chrom. | Pos. (cM) | Effect | RC (%) | Case I | Case II | Case III | Case I | Case II | Case III | Case I | Case II | Case III |
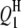 |
1 | 41.0 | 3.0 | 3.69 | 40.48 (4.00) | 41.01 (3.43) | 40.79 (2.81) | 3.12 (0.57) | 3.08 (0.51) | 3.04 (0.44) | 77.5 | 94.0 | 96.0 |
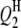 |
2 | 18.0 | 0.0 | 0.00 | — | — | — | — | — | — | 0.0 | 0.0 | 0.0 |
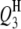 |
3 | 87.0 | −3.4 | 4.75 | 86.70 (3.85) | 86.45 (3.66) | 86.91 (3.47) | −3.45 (0.59) | −3.36 (0.53) | −3.35 (0.47) | 84.0 | 96.0 | 98.5 |
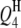 |
4 | 20.0 | 4.0 | 6.57 | 20.61 (2.76) | 20.08 (2.12) | 20.29 (1.88) | 4.19 (0.66) | 4.07 (0.56) | 4.11 (0.52) | 97.5 | 98.5 | 99.0 |
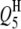 |
5 | 48.0 | −4.8 | 9.46 | 47.97 (3.13) | 47.73 (2.27) | 47.54 (2.44) | −4.79 (0.68) | −4.76 (0.54) | −4.73 (0.45) | 98.0 | 100.0 | 100.0 |
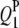 |
1 | 24.0 | 3.7 | 5.62 | 23.74 (4.24) | 24.35 (3.55) | 24.13 (3.04) | 3.73 (0.65) | 3.74 (0.52) | 3.67 (0.50) | 90.0 | 99.0 | 97.5 |
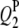 |
2 | 65.0 | −2.8 | 3.22 | 65.66 (5.26) | 66.06 (4.76) | 64.94 (4.12) | −3.01 (0.54) | −2.80 (0.48) | −2.82 (0.46) | 62.0 | 86.5 | 93.5 |
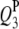 |
3 | 73.0 | −4.4 | 7.95 | 73.24 (3.24) | 73.44 (3.00) | 73.19 (2.44) | −4.40 (0.62) | −4.34 (0.52) | −4.29 (0.52) | 96.0 | 99.0 | 100.0 |
Chrom., chromosome; Pos., position.
Mean and standard error (in parentheses) of 200 simulation replicates.
TABLE 2.
Estimation of pairwise QTL for epistasis effects, and statistical powers
| True value
|
Estimate of effecta
|
Power (%)
|
|||||||
|---|---|---|---|---|---|---|---|---|---|
| QTLi | QTLj | Effect | RC (%) | Case I | Case II | Case III | Case I | Case II | Case III |
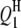 |
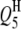 |
−2.9 | 3.45 | −2.85 (0.53) | −2.74 (0.58) | −2.73 (0.54) | 60.5 | 92.0 | 99.5 |
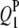 |
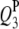 |
3.0 | 3.69 | 2.93 (0.55) | 2.79 (0.59) | 2.68 (0.62) | 61.0 | 94.5 | 97.5 |
 |
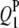 |
4.0 | 6.57 | 3.83 (0.59) | 3.81 (0.57) | 3.77 (0.53) | 74.5 | 96.0 | 98.5 |
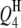 |
 |
−3.5 | 5.03 | −3.36 (0.68) | −3.42 (0.50) | −3.43 (0.48) | 95.0 | 98.5 | 100.0 |
Mean and standard error (in parentheses) of 200 simulation replicates.
Simulation results are shown in Tables 1 and 2. In general, our method could provide reasonably accurate estimates of the parameters (positions, additive effects, and interaction effects). The precisions of parameter estimates and the statistical powers of QTL detection increased with the increase of sample size. The increase was considerable for those QTL or QTL pairs with small RCs, indicating that a large sample is desirable for detecting QTL and QTL interactions with minor RCs. The powers of detecting QTL with RCs >5.0% were >90.0% in all three cases. The simulation results demonstrated the feasibility of our method for mapping QTL underlying the host–parasite interaction.
DISCUSSION
Host–parasite interaction is a complex system controlled by many genes from the host and parasite genomes. For understanding the genetic basis of host–parasite interaction, it is necessary to study the underlying gene effects and their interactions from both the host genome and the parasite genome. The method proposed in this article integrates the host genome and the parasite genome into a genetic model so that host QTL and parasite QTL as well as their interactions can be simultaneously detected.
In the past, because of no suitable QTL mapping method, studies of QTL mapping for host–parasite interaction were limited to single species especially of the host side (Kover and Caicedo 2001). Such a single-species-analysis approach cannot comprehensively dissect the interspecific genetic architecture underlying the host–parasite interaction system, because it cannot detect the interactions between host and parasite QTL. In addition, the separated analysis approach would possibly decrease the statistical powers of detecting QTL and epistasis but increase the standard errors of the estimates of QTL positions and effects in comparison with the method proposed in this article. This was demonstrated by analyzing the aforementioned simulated data on the basis of the host genome and the parasite genome separately (results not presented). Take case I, for example. The powers of detecting 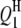 ,
, 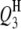 ,
, 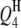 , and
, and 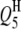 decreased to 73.0, 82.0, 97.0, and 97.0%, and the powers of detecting
decreased to 73.0, 82.0, 97.0, and 97.0%, and the powers of detecting  ,
, 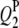 , and
, and  decreased to 86.5, 55.5, and 97.0%.
decreased to 86.5, 55.5, and 97.0%.
Sample size is an important factor determining the statistical power in QTL mapping. With the objective of mapping QTL in both the host and the parasite genomes and detecting their QTL interactions, relatively large population sizes are required for both the host and the parasite. We conducted a simulation study with a sample size of 400 generated from 200 host DHLs and 20 parasite HSs. In that case, each host DHL was inoculated by 2 different parasite HLs and each parasite HS was inoculated to 20 different host DHLs. As compared with the result of case I, the powers of detecting parasite QTL decreased by about half and the precision of effect estimation of these QTL remarkably decreased. It was not only because of the small size of the parasite population, but also because many data points were dependent, resulting from the multiple inoculations of each parasite HS. In our opinion, an ideal design for our method is using two large populations (at least >200) of host and parasite with the same size and inoculating each host line by each different parasite strain for only one time. However, in practice, it might be quite difficult to conduct such a balanced design. Our simulation study demonstrated that if one host line (or parasite strain) was involved in inoculation no more than four times, it would not generate much independent data but still result in reasonable mapping results. In addition, the accuracy of estimated QTL effects is another important issue in QTL mapping. It was shown in the simulation study that the biases of all of the QTL-effect estimates were <5%. However, the genomewide scan approach tended to overestimate the QTL effects (Goring et al. 2001). Any conclusion based on QTL-effect estimates should take into consideration the estimation bias.
In principle, the general genetic model proposed in this article could be applicable to all sorts of host–parasite interactions and the corresponding QTL mapping methodology would be suitable for all sorts of interactions between eukaryotic hosts and parasites. The detailed QTL mapping method presented could be directly applied to researching the genetic architecture of plant diseases caused by fungal pathogens. A suitable example would be rice blast, the most devastating fungal disease of rice, because the genomes of both rice and the fungal pathogen (Magnaporthe grisea) have been sequenced.
Every species interacts with other species in the ecosystem. There are various interactions between species such as competition and symbiosis. The host–parasite interaction is only one case of them. The method of QTL mapping for host–parasite interaction could be applied to other types of between-species interaction in principle, as long as a suitable trait could be found to quantitatively reveal the between-species interaction. Sometimes there might be several traits reflecting the between-species interaction from either or both of these species. For example, in an interaction system of food competition between two species, the growth rate of either species could be taken as a trait representing the interaction between the two species. In this case, it would be recommended to analyze the traits jointly for QTL mapping. Several methods of joint analysis of multiple traits for QTL mapping have been proposed (Jiang and Zeng 1995; Wu et al. 1999). Following similar principles, the genetic model of between-species interaction could also be extended for QTL mapping on the basis of multiple traits. This would probably increase the statistical power of QTL mapping.
Genotype-by-environment interaction could also be considered in the between-species interaction analysis. The interaction between two species might be different under various environments. It has been revealed that the geographical separation may cause unique ecological and evolutionary dynamics of host and parasites at different locations (Benkman 1999; Burdon and Thrall 1999). The reciprocal selection between plants and parasite usually occurs in a subset of locations or coevolutionary hotspots (Thompson 1999). Therefore, as a prospect, a more general genetic model of between-species interaction should not only integrate the genetic information of both species, but also consider the influence of the macro- and microenvironmental factors on the expression of the genes and gene interaction to fit the interacted traits from both species.
Acknowledgments
We thank William Hill at Edinburgh University for insightful comments. We also thank two anonymous reviewers for useful comments and suggestions on an earlier version of the manuscript. This research was supported in part by the National Basic Research Program (973 Program) of China (2004CB117306) and the National Natural Science Foundation of China (30671123).
References
- Agrawal, A. F., and C. M. Lively, 2001. Parasites and the evolution of self-fertilization. Evol. Int. J. Org. Evol. 55 869–879. [DOI] [PubMed] [Google Scholar]
- Benkman, C. W., 1999. The selection mosaic and diversifying coevolution between crossbills and lodgepole pine. Am. Nat. 153 75–91. [DOI] [PubMed] [Google Scholar]
- Burdon, J. J., and P. H. Thrall, 1999. Spatial and temporal patterns in coevolving plant and pathogen association. Am. Nat. 153 15–33. [DOI] [PubMed] [Google Scholar]
- Churchill, G. A., and R. W. Doerge, 1994. Empirical threshold values for quantitative trait mapping. Genetics 138 963–971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doerge, R. W., and G. A. Churchill, 1996. Permutation tests for multiple loci affecting a quantitative character. Genetics 142 285–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flor, H. H., 1971. The current status of the gene for gene concept. Annu. Rev. Phytopathol. 9 275–296. [Google Scholar]
- Goring, H. H., J. D. Terwilliger and J. Blangero, 2001. Large upward bias in estimation of locus-specific effects from genomewide scans. Am. J. Hum. Genet. 69 1357–1369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haley, C. S., and S. A. Knott, 1992. A simple regression method for mapping quantitative trait loci in line crosses using flanking markers. Heredity 69 315–324. [DOI] [PubMed] [Google Scholar]
- Hamilton, W. D., 1980. Sex versus no-sex versus parasite. Oikos 35 282–290. [Google Scholar]
- Jia, Y., S. A. McAdams, G. T. Bryan, H. P. Hershey and B. Valent, 2000. Direct interaction of resistance gene and avirulence gene products confers rice blast resistance. EMBO J. 19 4004–4014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang, C., and Z. B. Zeng, 1995. Multiple trait analysis of genetic mapping for quantitative trait loci. Genetics 140 1111–1127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang, C., and Z. B. Zeng, 1997. Mapping quantitative trait loci with dominant and missing markers in various crosses from two inbred lines. Genetica 101 47–58. [DOI] [PubMed] [Google Scholar]
- Kao, C. H., Z. B. Zeng and R. D. Teasdale, 1999. Multiple interval mapping for quantitative trait loci. Genetics 152 1203–1216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kover, P. X., and A. L. Caicedo, 2001. The genetic architecture of disease resistance in plants and the maintenance of recombination by parasites. Mol. Ecol. 10 1–16. [DOI] [PubMed] [Google Scholar]
- Lander, E. S., and D. Botstein, 1989. Mapping Mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics 121 185–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ljungberg, K., S. Holmgren and O. Carlborg, 2004. Simultaneous search for multiple QTL using the global optimization algorithm DIRECT. Bioinformatics 20 1887–1895. [DOI] [PubMed] [Google Scholar]
- Martin, G. B., A. J. Bogdanove and G. Sessa, 2003. Understanding the functions of plant disease resistance proteins. Annu. Rev. Plant Biol. 54 23–61. [DOI] [PubMed] [Google Scholar]
- Peters, A. D., and C. M. Lively, 1999. The Red Queen and fluctuating epistasis: a population genetic analysis of antagonistic coevolution. Am. Nat. 154 393–405. [DOI] [PubMed] [Google Scholar]
- Piepho, H. P., and H. G. Gauch, Jr., 2001. Marker pair selection for mapping quantitative trait loci. Genetics 157 433–444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rausher, M. D., 2001. Co-evolution and plant resistance to natural enemies. Nature 411 857–864. [DOI] [PubMed] [Google Scholar]
- Scofield, S. R., C. M. Tobias, J. P. Rathjen, J. H. Chang, D. T. Lavelle et al., 1996. Molecular basis of gene-for-gene specificity in bacterial speck disease of tomato. Science 274 2063–2065. [DOI] [PubMed] [Google Scholar]
- Searle, S. R., G. Casella and C. E. McCulloch, 1992. Variance Components. John Wiley & Sons, New York.
- Tang, X., R. D. Frederick, J. Zhou, D. A. Halterman, Y. Jia et al., 1996. Initiation of plant disease resistance by physical interaction of AvrPto and Pto kinase. Science 274 2060–2063. [DOI] [PubMed] [Google Scholar]
- Thompson, J. N., 1994. The Coevolutionary Process. University of Chicago Press, Chicago.
- Thompson, J. N., 1999. Specific hypotheses on the geographic mosaic of coevolution. Am. Nat. 153 1–14. [Google Scholar]
- Thompson, J. N., and J. J. Burdon, 1992. Gene-for-gene coevolution between plants and parasites. Nature 360 121–125. [Google Scholar]
- Wu, W. R., W. M. Li, D. Z. Tang, H. R. Lu and A. J. Worland, 1999. Time-related mapping of quantitative trait loci underlying tiller number in rice. Genetics 151 297–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng, Z. B., 1993. Theoretical basis for separation of multiple linked gene effects in mapping quantitative trait loci. Proc. Natl. Acad. Sci. USA 90 10972–10976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng, Z. B., 1994. Precision mapping of quantitative trait loci. Genetics 136 1457–1468. [DOI] [PMC free article] [PubMed] [Google Scholar]


