Neofunctionalization of Duplicated Genes Under the Pressure of Gene Conversion

Abstract

Neofunctionalization occurs when a neofunctionalized allele is fixed in one of duplicated genes. This is a simple fixation process if duplicated genes accumulate mutations independently. However, the process is very complicated when duplicated genes undergo concerted evolution by gene conversion. Our simulations demonstrate that the process could be described with three distinct stages. First, a newly arisen neofunctionalized allele increases in frequency by selection, but gene conversion prevents its complete fixation. These two factors (selection and gene conversion) that work in opposite directions create an equilibrium, and the time during which the frequency of the neofunctionalized allele drifts around the equilibrium value is called the temporal equilibrium stage. During this temporal equilibrium stage, it is possible that gene conversion is inactivated by mutations, which allow the complete fixation of the neofunctionalized allele. And then, permanent neofunctionalization is achieved. This article develops basic population genetics theories on the process to permanent neofunctionalization under the pressure of gene conversion. We obtain the probability and time that the frequency of a newly arisen neofunctionalized allele reaches the equilibrium value. It is also found that during the temporal equilibrium stage, selection exhibits strong signature in the divergence in the DNA sequences between the duplicated genes. The spatial distribution of the divergence likely has a peak around the site targeted by selection. We provide an analytical expression of the pattern of divergence and apply it to the human red- and green-opsin genes. The theoretical prediction well fits the data when we assume that selection is operating for the two amino acid differences in exon 5, which are believed to account for the major part of the functional difference between the red and green opsins.

ONE of the most important questions in genome evolution is how new genes accumulate in a genome. Gene duplication is believed to be a source for a novel functional gene because one of the duplicates has an opportunity to accumulate mutations that might create a new function while the other retains the original function, i.e., neofunctionalization (Ohno 1970). This is an attractive process for adaptive genome evolution of novelty, but how often it occurs still remains unclear. Our current knowledge is limited to the fact that neofunctionalization is a very rare event in comparison with the alternative and most likely fate, pseudogenization, where one of the duplicated copies is silenced (Walsh 2003).

The neofunctionalization process has been of theoretical interest in population genetics (Ohta 1987; Walsh 1995). In a two-locus model assuming the two duplicated genes accumulate mutations independently, Walsh (1995) derived the relative probability of neofunctionalization to pseudogenization, which is given by . ρ is the ratio of the advantageous mutation rate to the null mutation rate, and S is the population selection parameter, 4N_es, where N_e is the effective population size and s is the selection intensity. This equation means that the relative probability of neofunctionalization is determined by the selective advantage and the relative rate of advantageous mutations. However, this equation does not hold when the assumption of the independent evolution of the duplicated genes is violated. Concerted evolution should be the most likely cause of the violation. When the duplicated genes undergo concerted evolution via gene conversion, the two duplicated copies coevolve by exchanging DNA fragments. In such a case, the relative probability of neofunctionalization is greatly decreased because homogenization would potentially prevent neofunctionalization (Innan 2003b).

Recent genomic data analysis revealed that gene conversion between duplicated genes could be a quite common phenomenon in various species (Semple and Wolfe 1999; Rozen et al. 2003; Gao and Innan 2004; Ezawa et al. 2006). This indicates the need to develop models of neofunctionalization under the pressure of gene conversion. However, population genetic models of duplicated genes with gene conversion are still limited, especially when selection is involved (Walsh 1985, 1986; Ohta 1987, 1988, 1991; Innan 2003b). Walsh (1985) investigated the process in which a beneficial mutation spreads in a multigene family by gene conversion, while Ohta (1991) emphasized the effect of gene conversion to create a novel combination of DNA sequences, which would be advantageous in genes under diversifying selection such as the MHC genes. Innan (2003b) pointed out that gene conversion works as a mechanism to retard neofunctionalization. The purpose of this article is to investigate the theoretical behavior of a neofunctioned allele through the process from its appearance to the event that neofunctionalization is completely achieved.

This article considers the neofunctionalization process in a simple two-locus model, where only two alleles, A and B, are allowed. Therefore there are four haplotypes (gametes), A-A, A-B, B-A, and B-B (the former and latter characters represent the allelic states at the first and second loci, respectively). The model incorporates selection such that haplotypes having both alleles (A-B and B-A) are more favored than those with only one kind (A-A and B-B). This is because A and B are assumed to have slightly different functions so that having both A and B is advantageous. As the initial state, we consider a random-mating population with N diploids, in which A-A is fixed. A mutation is then introduced at one locus, say the second locus. In this system, A and B are considered the original and neofunctionalized alleles, respectively. Our focus through this article is on the behavior of the neofunctionalized allele B, which is determined by the joint effect of selection, gene conversion, recombination, and genetic drift. We are particularly interested in the conditions under which the neofunctionalized allele increases in frequency and becomes stably maintained in the population.

The behavior of the neofunctionalized allele is quite complicated. Suppose a mutation occurs at time T = 0, introducing a new haplotype A-B at frequency 1/2N. Subsequently, there should be several possible behaviors of the four haplotypes as illustrated in Figure 1. The most likely fate is that A-B becomes extinct by genetic drift in a relatively short time (Figure 1A). Alternatively, A-B can be maintained for a reasonably long time when selection is sufficiently strong. This process can be divided into two phases (Figure 1, B and C). First, the frequency of A-B quickly increases by positive selection and then reaches an equilibrium. We call the former and the latter “preequilibrium stage” and “temporal equilibrium stage,” respectively. In the temporal equilibrium stage, the frequency of A-B fluctuates around its equilibrium value, which is determined by two mechanisms that work in opposite directions, namely, selection and gene conversion. This is because selection acts to increase the frequency of A-B, while gene conversion changes A-B to deleterious haplotypes, A-A and B-B. Random genetic drift is another important factor to determine the behavior of A-B in the temporal equilibrium stage. In a small population, A-B could fix in the population, especially when selection is strong (Figure 1C), while in a large population, the frequency of A-B might fluctuate around equilibrium without fixation (Figure 1B).

Figure 1.—

Illustration of the behavior of the haplotype frequencies. Typical patterns in a relatively short period after the mutation when selection is weak (A), strong (B), and very strong (C) are shown. If the neofunctionalized allele is lost, the system automatically returns to the initial state (D and E). Permanent neofunctionalization can be achieved when one of the advantageous haplotypes (A-B) is completely fixed (F).

Once the state gets to the temporal equilibrium stage, it is likely that the two alleles are stably maintained in the population for a reasonably long time. However, it is very important to note that this stage is not a terminal state in terms of neofunctionalization. That is, as long as gene conversion keeps creating A-A and B-B, the neofunctionalized allele may become extinct as illustrated in Figure 1E, although the rate might be low. This means that complete (permanent) neofunctionalization can be achieved only when gene conversion is somehow inactivated so that the two alleles are permanently preserved in the population. Several mutational mechanisms can terminate gene conversion given that gene conversion is a kind of recombination event in meiosis. One is those causing drastic changes in the DNA sequences, including transposon insertions and large indels (Teshima and Innan 2004). Those changes could prevent chromosomal pairing between duplicated regions in meiosis. The accumulations of point mutations would have a similar effect because gene conversion requires sequence homology between duplicated regions (Walsh 1987).

Thus, the temporal equilibrium stage should be a necessary step for permanent neofunctionalization, and the inactivation of gene conversion is also required during the temporal equilibrium stage, so that the neofunctionalized allele can be stably maintained forever. In this article, we investigate this process to permanent neofunctionalization since the birth of the neofunctionalized allele by theory and simulations.

MODELS

The sequence model:

To incorporate all factors described above, we consider a two-locus model called the sequence model. The model consists of a pair of duplicated sequences, each of which is L bp long. We assume that there is a target site of selection for neofunctionalization at the center of the L-bp region and that the rest is essentially neutral. Using this model, we simulate DNA sequence evolution in a random-mating diploid population with size N. The standard Wright–Fisher model is assumed, in which the fitness is determined by the allelic states at the two selected sites, as described below.

At the selected site, two allelic states, A and B, are allowed, so that there are four haplotypes (gametes), A-A, A-B, B-A, and B-B. As we are interested in the fate of this single mutation, no recurrent mutation is allowed between the two alleles, so that there are two initial fates. This assumption will not affect the results because gene conversion has essentially the same effect as back mutation, which should occur at a much higher rate than point mutations. We first assume that selection symmetrically works at the haploid level. That is, the haplotypes A-B and B-A are equally advantageous (the fitness is 1 + s) over A-A and B-B (the fitness is 1). It is assumed that the selection effect is additive, so that the situation is identical to that in a haploid population model with size 2N. This assumption is relaxed later by considering other modes of selection.

Except for the target site of selection, the allelic states at nucleotide sites are essentially neutral. At each site, there are two allelic states, “0” or “1,” between which recurrent neutral mutations are allowed at rate μ. The target site of selection is likely within a protein-coding region, in which purifying selection is operating as a background. To incorporate this effect, codons (triplets of nucleotides) are assigned in the nucleotide sequences, and the neutral mutation rate is determined depending on the position of the codons. For simplicity, we assume that mutations on the first and second positions cause nonsynonymous changes, while at the third positions, nonsynonymous and synonymous mutations occur at the relative rates, a and 1 − a, respectively. Because some nonsynonymous mutations are deleterious and do not contribute to long-term molecular evolution, we automatically remove a certain proportion, b, of nonsynonymous mutations. Through our simulations, we set a = 0.3 and b = 0.8, such that the relative evolutionary rate at nonsynonymous sites compared to synonymous sites (called the K_a/K_s ratio) is ∼0.2.

The model involves homologous recombination and interlocus gene conversion. The former occurs only between the duplicated regions at rate r, and no intragenic recombination is allowed. Gene conversion transfers a certain length of a tract from one locus to the corresponding position of the other, and the gene conversion model follows that of Teshima and Innan (2004). In brief, gene conversion occurs at rate g per region per generation. A conversion event can be initiated at a certain site in the region, and the elongation of a tract occurs in either the 5′ or the 3′ direction. The length of a conversion tract, z, follows a geometric distribution with parameter q, q(1 − q)^z−1 (Wiuf and Hein 2000). q determines the tract length, and the average length is 1/q bp. If a gene conversion occurs on an advantageous haplotype and a conversion tract covers the selection target site, the haplotype turns into a deleterious haplotype. In this setting, the rate that a particular site is involved in a gene conversion event per generation is given by c = g/Q, where Q = qL. This rate, c, corresponds to the gene conversion rate per site defined in Innan (2002, 2003b).

According to Teshima and Innan (2004), we assume that the success of gene conversion depends on the divergence (see also Walsh 1987). Here, a simple model is employed in which gene conversion can occur only when the divergence in a tract is lower than a threshold value. Throughout this article, this threshold is set to be 10%.

In addition to the divergence, gene conversion might also be suppressed by mutations that block further conversion such as large insertions/deletions and transposable elements. Such mutations are called terminator mutations in Teshima and Innan (2004). We assume that if a terminator mutation occurs, it completely suppresses further gene conversion. Through our simulations, we introduce a terminator mutation arbitrarily, rather than setting its rate.

Using this model, the patterns of the evolution of DNA sequences in duplicated genes after a neofunctionalized allele is introduced were investigated by computer simulations. We set the population size 2N = 1000. At the beginning of each replication, the population consists of 2N sets of duplicated regions with identical sequences, where the allelic status at each of the L nucleotides is given by 0. At the selected sites, the allele A is given in both of the two duplicated regions. In other words, the A-A haplotype is fixed in the population. A prerun of simulation is performed so that neutral mutations are accumulated. In this prerun, there is no positive selection because the selected site is monomorphic. Then, at time T = 0, a mutation is introduced, creating the A-B haplotype. After this event, selection works on the target site.

The single-site model:

The sequence model might be too complicated to allow analytical treatments. However, the behavior of the allelic frequencies in the initial phase (pre- and temporal equilibrium stages) may be analytically studied when the model is simplified. In this simplified model called the single-site model, we consider only the target site of selection and the gene conversion process is simplified. We assume that gene conversion rate is given by a constant, c. This means that the haplotypes A-B and B-A change to A-A at rate c per generation and to B-B at the same rate. The model is identical to that of Innan (2003b) except that recurrent mutation between A and B is not allowed here. This model enables us to investigate the behavior of allelic frequencies under the framework of diffusion theory. This simplification should be reasonable because we are interested in a relatively short-term process.

THE INITIAL PHASE IN THE SINGLE-SITE MODEL

To understand how often the neofunctionalized allele successfully increases in frequency and is stably maintained for a significantly long time, we use the single-site model. In this section, we use theoretical approaches to obtain general insights, but some simulations are also used. We are particularly interested in the process from the introduction of allele B at one locus, say the second locus. The initial state is given such that a single A-B haplotype arises in the population where A-A was fixed. If we let the frequencies of the four haplotypes, A-A, A-B, B-A, and B-B be x₁, x₂, x₃, and x₄, respectively, the initial state is given by . Since this initial state, the joint behavior of the frequencies of the four haplotypes is well described in a three-dimensional diffusion process with x₁, x₂, and x₃, because x₄ is automatically determined when the other three are given. However, such a three-dimensional diffusion process is extremely difficult to handle analytically. Therefore, we consider the behavior of p, the sum of the frequencies of the two advantageous haplotyes (i.e., p = x₂ + x₃), so that we can use a one-dimensional diffusion method (Innan and Stephan 2001).

The Kolmogorov backward equation is commonly used to handle the behavior of allelic frequencies (Crow and Kimura 1970). The diffusion operator requires two terms, the mean and the variance of the change in frequency, p, per generation, denoted by M_δp and V_δp, respectively. In the following derivation, we assume no recombination (r = 0), and the effect of recombination is later investigated by simulations. In our simple additive selection model, the frequency of the haplotype increases by sp(1 − p) by the effect of selection, while p decreases at rate 2c by gene conversion because it changes the advantageous haplotypes into deleterious ones. Therefore, M_δp and V_δp are given by

(1)

and

(2)

Thus, the behavior of p is specified by the two factors: the systematic pressure due to selection and gene conversion as represented by Equation 1 and the effect of random genetic drift (Equation 2). It is very important to note that Equation 1 is not always positive for 0 ≤ p ≤ 1: M_δp is positive for 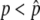while negative for 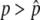, where . In other words, p has an equilibrium value, 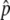, which is given when M_δp = 0. This makes the behavior of p quite complicated, which is demonstrated by simulations. A single run of the simulations starts at time T = 0, when an advantageous haplotype arises so that the initial value of p is . Then, at T = 0.01N, 0.1N, N, 10N, and 100N generations, p is scored. With 10⁶ replications of the simulations, the probability density distributions of p are obtained and shown in Figure 2, A–D. Values of 4Ns = 40 and 2N = 10⁴ are assumed, and we investigate four different gene conversion rates, 4Nc = 0.1, 1, 4, and 10.

Figure 2.—

(A–D) Probability density distributions of the frequency of the advantageous haplotypes at T = 0.01N, 0.1N, N, 10N, and 100N generations (red, magenta, purple, blue, and green lines, respectively) for a wide range of the gene conversion rate (4Nc = 0.1, 1, 4, and 10 from left to right). The three distributions for T = N, 10N, and 100N are almost identical in A, B, and C and are therefore represented by N ∼ 100N. (E–H) The probability that p hits p′. Gray lines are those obtained by simulations and dashed lines are from Equation 3. The triangle on each horizontal axis is 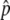, the equilibrium frequency of p. Values of 4Ns = 40 and 2N = 10⁴ are fixed.

For all four gene conversion rates, the distributions of p at T = 0.01N are L-shaped around p = 0, indicating that the advantageous haplotype is quickly removed or still drifting in low frequencies. The distribution moves toward larger p when T = 0.1N. This means that if the advantageous haplotype escaped from immediate loss, it increases in frequency to the equilibrium value, 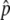, which is shown by a triangle in Figure 2. Then, once p hits 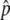, p fluctuates around 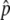for a long time. This fluctuation is quite stable when 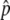is relatively large. In Figure 2A, 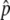is close to 1, and p stays at 1 most of the time. That is, the situation is similar to that illustrated in Figure 1C. As the gene conversion rate (4Nc) increases, decreases and the pattern is getting close to that illustrated in Figure 1B, where p fluctuates around 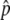without hitting p = 1 (e.g., Figure 2C). This fluctuation continues for a quite long time in Figure 2, A–C, in which the distributions for T = 1N, 10N, and 100N are almost identical.

If the gene conversion rate is too high in comparison to the selection intensity (therefore, 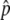is relatively low), it is possible that p happens to hit p = 0 during the fluctuation, and then the state returns to the original, where there is no neofunctionalized allele in the population. An example is seen in Figure 2D, where 4Nc = 10 and 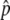∼ 0.5. The density distribution around 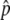decreases as time increases from T = N to 100N due to the loss of one of the two alleles by random genetic drift. Considering this important role of random genetic drift, the process is population-size dependent. However, we expect that the pattern would be similar as long as the time is measured in units of N generations, which is confirmed with additional simulations by a wide range of N (not shown).

These simulation results indicate that the process to permanent neofunctionalization requires two steps. First, the advantageous haplotype with the neofunctionalized allele escapes from immediate loss by drift and gets in the temporal equilibrium stage. Then, while the neofunctionalized allele is maintained in high frequencies in the temporal equilibrium stage, additional mutations occur to inactivate gene conversion and permanent neofunctionalization is achieved (i.e., p = 1 forever), as mentioned in the Introduction (see also Figure 1). In the following, we provide theoretical understandings of these two processes.

For the first process, we are interested in how often the system enters the temporal equilibrium stage. In the standard population genetics theory of directional selection, it is known that an advantageous allele could be lost by genetic drift when its frequency is low, but once the frequency exceeds a certain level, it almost automatically goes to fixation. The process of the advantageous haplotype in our model should be similar to this. Figure 2, E–H, shows the probability that p hits a certain value, p′, which is denoted by u(p′). This probability is obtained by simulations and shown by the gray solid line in Figure 2, E–H. All four distributions are almost flat for 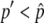except for the region with very low frequency, say, p′ < 0.1. This means that p almost always hits once it becomes >0.1. Therefore, it is possible to consider that the probability that the system enters the temporal equilibrium stage is approximately given by u(x), where x could be any value between 0.1 and . Here, we use as this probability.

From Equations 1 and 2, u(p′) is easily obtained analytically. Following Kimura (1962), the probability is given by

(3)

where G(x) is given by

p₀ is the initial frequency of the haplotype, which is 1/(2N) in our model. Figure 2, E–H, also shows u(p′) computed by Equation 3 by dashed lines, which are in excellent agreement with the simulation results. In a similar way, the time required to get into the temporal equilibrium stage may be obtained by modifying the method of Kimura and Ohta (1969),

(4)

where

These theoretical results for and are checked by simulations. Figure 3 shows that and are in very good agreement with the simulation results for a wide range of the parameter set. It should be noted that the equilibrium frequency, 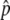, which plays a crucial role to determine 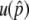and , is given by a function of the selection intensity and gene conversion rate (i.e., 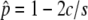). Equations 3 and 4 work for any selection intensity and gene conversion rate, but may be meaningless when 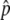is so low that the temporal equilibrium stage does not last long. In such a situation (e.g., 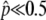), the probability that p hits 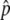is very high even without selection, and is very small. 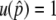In the extreme case of , it is obvious that and 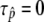, where selection does not mean anything. This is the reason why when . Therefore, in Figure 3, we show the results for with solid lines. Within this range, as the selection intensity increases, increases (Figure 3A). There is a negative correlation between the gene conversion rate and . The effect of gene conversion is minor on because the solid parts of all lines for the five values of gene conversion rate are very similar.

Figure 3.—

(A) The probability to get into the temporal equilibrium stage or the probability that p hits 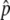. (B) The first arrival time for p to reach 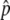. Time is in units of N generations. The initial frequency of the haplotype (= 1/2N) is 0.001. Values of 4Nc = 0, 5, 10, 15, and 20 are used. The theoretical results for s < 4c are presented by dashed lines and those for s ≥ 4c by solid lines.

Next, we consider the second step to permanent neofunctionalization, that is, the temporal equilibrium stage. As discussed above, if this stage continues for a significantly long time, other mutations might occur and lead the state to permanent neofunctionalization. In other words, the rate to achieve permanent neofunctionalization depends on how long this stage lasts. This is quantitatively investigated by simulations. A large number of simulation replications (10⁶) were performed as described above. For replications in which p hits 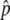, we investigated the probabilities that the neofunctionalized allele is still maintained in the population after 20N and 200N generations (Figure 4). It is found that this probability is primarily determined by the ratio of 4Nc to 4Ns (or c to s). The blue line represents s = 4c, which gives 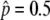. This line roughly fits to the boundary of 99%. For the parameter sets below this line, it is very likely that the state is still in the temporal equilibrium stage even after 200N generations. However, the probability quickly decreases as c/s increases over the blue line. Again, this argument holds for any population size as long as it is measured in units of N generations.

Figure 4.—

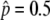The probability that the advantageous haplotype is still maintained (p > 0) at T = 20N and 200N generations, conditional on the event that p hits . s = 4c () is shown by the blue lines; 2N = 10⁴ is assumed.

It can be concluded that the process to complete neofunctionalization requires two initial steps: (i) the system gets in the temporal equilibrium stage, and (ii) this stage continues for a sufficiently long time. The probability for the former event is given by Equation 3, and 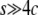would be a sufficient condition for the latter. We thus far assumed no recombination between the two loci. Additional simulations with recombination show that this conclusion generally holds, but recombination has some quantitative effects on 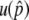and the probability of the preservation of the neofunctionalized allele (Figure A1 in the appendix). As the recombination rate increases, 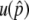increases when the gene conversion rate is relatively large (Figure A1A). The 99% boundary of the probabilities that B is preserved at T = 20N and 200N are roughly given by s = 2c (Figure A1B). It seems that the effect of selection is enhanced by recombination; therefore, the chance that neofunctionalization occurs is larger with recombination. This joint effect of gene conversion and recombination can be explained as follows. With no gene conversion, there are only two haplotypes, A-A and A-B, between which recombination is ineffective; therefore, the recombination rate has no effect on (Figure A1A). Gene conversion increases the frequencies of the deleterious haplotypes, A-A and B-B, and thereby decreases 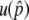. On the other hand, recombination has an effect to cancel it out: recombination between A-A and B-B creates advantageous haplotypes; therefore, recombination has a positive effect on 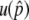. 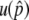is primarily determined by the population frequency of the B allele when it is small, and this is when the positive effect of recombination can be emphasized because the frequency of B-B can be ignored.

Figure A1.—

The effect of recombination on and the preservation probability of the neofunctionalized allele. (A) The probability that p hits . The initial frequency of the haplotype (= 1/2N) is 0.001. (B) The probability that the advantageous haplotype is still maintained (p > 0) at T = 20N and 200N generations, conditional on the event that p hits 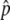. A value of 4Nr = 100 is assumed. s = 4c and s = 2c are shown by the blue solid and dashed lines, respectively. Note that these simulations are based on the haploid-based selection model.

We also performed the same simulations under a different selection model, in which diploids that have both A and B (i.e., genotyopes AAAB, AABB, and ABBB) are more advantageous than those with only one type (i.e., genotyopes AAAA and BBBB). Let the fitness of the former and the latter be 1 + s and 1, respectively. Figure A2 in the appendix shows that the overall patterns are similar to those in the additive selection model in Figures 3, 4, and A1 when there is no recombination (although there are quantitative differences), whereas the preservation probability is enhanced when the recombination rate is large.

Figure A2.—

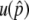and the preservation probability of the neofunctionalized allele in the diploid-based selection model. (A) The probability that p hits 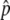. (B) The probability that the advantageous haplotype is still maintained (p > 0) at T = 20N and 200N generations, conditional on the event that p hits 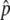. The results for 4Nr = 0 and 100 are shown. s = 4c is shown by the blue lines.

THE ENTIRE PROCESS TO PERMANENT NEOFUNCTIONALIZATION IN THE SEQUENCE MODEL

Simulation:

To consider the whole process to the terminal phase (see Figure 1), we use the sequence model, which can incorporate mutations (point mutations and terminator mutations) in the flanking regions of the target site. Using this model, the patterns of the evolution of DNA sequences in duplicated genes after the introduction of a neofunctionalized allele are investigated by computer simulations. We consider the duplicated region with L = 6000 and the population size 2N = 1000 throughout this section. See models for details.

Figure 5 shows typical trajectories of the divergence in the entire simulated region for c/μ = 1 (blue), c/μ = 10 (green), and c/μ = 100 (red). Note that the simulation ends when one of the alleles at the selected site (A or B) is lost, and such an event is shown by an x. We present results for two population mutation rates, 4Nμ = 0.001 (A and C) and 0.01 (B and D), which show very similar patterns when c/μ is the same. It is indicated that the ratio of c to μ should be the crucial parameter to determine the pattern. Although only one realization is shown for each parameter set in Figure 5, our simulations with multiple replications (at least 20 replications for each parameter set) showed that almost all replications exhibited very similar patterns, indicating that one can capture quite good intuitive understanding of the behavior of the divergence from Figure 5.

Figure 5.—

Typical trajectories of the divergence obtained by simulations. Results are shown only for cases where the initial fixation occurred. The average tract length is assumed to be 1/q = 200 bp, and 4Nr = 20 is used. The length of prerun of the simulations is 4N generations.

It is found that there might be two major patterns for the fate of a neofunctionalized allele when selection is strong (Figure 5, A and B). When the gene conversion rate is low, after entering the temporal equilibrium stage, further divergence occurs relatively quickly without staying in this stage for a long time. This is the case when c/μ = 1 (blue) and c/μ = 10 (green). On the other hand, if the gene conversion rate is high (c/μ = 100), the divergence fluctuates around its equilibrium value for a very long time, indicating that the duplicated genes experience a long-term temporal equilibrium stage (i.e., concerted evolution). In Figure 5, A and B, the divergences for c/μ = 100 are ∼0.5 and 1.0%, respectively. Note that these values are very similar to those expected under neutrality (Equation 9 in Innan 2002). This result can be understood when the effect of selection is very minor on the average divergence over the whole region, probably restricted only around the target site of selection (see below).

These results can be summarized together with those from Figure 4. First of all, when gene conversion is active, relatively strong selection intensity is needed for neofunctionalization to occur (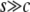). Given this condition, the gene conversion rate is the key factor to determine the behavior of the nucleotide divergence. When c is small, the divergence on the whole region automatically increases. When c is sufficiently large, the duplicated genes experience a long-term temporal equilibrium stage, and Figure 4 quantitatively demonstrates how long the temporal equilibrium stage continues. During the temporal equilibrium stage, we find that selection may not have a strong effect on the average divergence over the whole duplicated region; rather, the effect should be limited to a narrow region around the target site of selection. This creates an interesting pattern in the spatial distribution. In the next section, we present some analytical results for this distribution.

Spatial distribution of the divergence in the temporal equilibrium stage:

The simulation results indicate that the divergence is governed by the joint effect of selection and gene conversion, primarily in the temporal equilibrium stage, which continues for a considerably long time when 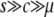. In this phase, however, we do not see a strong effect of selection on the average divergence over the whole region, probably because selection affects only a restricted region around the target site. This is demonstrated in Figure 6. It is assumed that 4Ns = 40, 4Nc = 1, and 4Nμ = 0.01 and no recombination. The mean gene conversion tract length is assumed to be 200 bp. The spatial distribution of the divergence across the region through the process to neofunctionalization is shown to investigate the local effect of selection along the sequence. In the simulations here, at a certain time point, we introduced a terminator mutation, which immediately terminates concerted evolution (see Teshima and Innan 2004). A terminator mutation is involved because the gene conversion rate for this simulation is so high that it takes an extremely long time to wait for the termination of concerted evolution by the accumulation of point mutations. Note that this treatment is only to demonstrate the point and a similar pattern is expected even when the termination of concerted evolution is caused by the accumulation of point mutations alone (data not shown).

Figure 6.—

Spatial distributions of the divergence across the region in the process to neofunctionalization. (A) Distribution before the neofunctionalized allele arises. (B and C) Distributions during the temporal equilibrium stage. (D) Distribution after the termination of concerted evolution. (E) Trajectories of the divergences in the 200-bp region centered at the target site of selection (red) and in the whole region (blue). Values of 4Nμ = 0.01, 4Nc = 1, and Ns = 10 are assumed. The expected divergence under neutrality is shown by the gray dashed lines. A long prerun (200N generations) was performed to compare the patterns before and after the appearance of the neofunctionalized allele.

Although Figure 6 shows the result of only a single run of the simulations, we confirmed that similar patterns to Figure 6 are observed in almost all of 20 replications. It is also found that we observe similar patterns for a wide range of parameters as long as a long temporal equilibrium stage is involved, although there are some quantitative variations in the duration of the stage and the level of divergence. The overall picture is also robust to the mode of selection and recombination between duplicated regions (data not shown). The simulations assumed a simple model of gene conversion cutoff, in which no gene conversion occurs when the divergence exceeds a threshold value of 10%. We found that the general pattern holds with more complicated models of gene conversion such as those in Teshima and Innan (2004), unless we set the model such that gene conversion is suppressed with very low divergence.

Under this setting, we compare the spatial distribution of the divergence before the introduction of the neofunctionalized allele, during the temporal equilibrium stage, and after the termination of concerted evolution in Figure 6, A–D. It is found that the distribution is roughly flat before the neofunctionalized allele arises, while there is a high peak around the target site of selection in the temporal equilibrium stage. Except for this small region, the divergence is around its expected value under neutrality (i.e., 1.0%). This is also clearly seen in Figure 6E, where the behaviors of the average divergences in the 200-bp region centered at the target site (red) and in the whole region (blue) are presented. When the system gets in the temporal equilibrium stage, the divergence in the 200-bp region immediately increases to 4–6%, while that in the other region still fluctuates around 1%.

It seems that the local peak of the divergence is so narrow that this selection does not have power to terminate concerted evolution. In such a case, permanent neofunctionalization should largely depend on a terminator mutation. As shown in Figure 6E, when a terminator mutation is introduced, concerted evolution ends automatically. After this event, the divergence in the whole region begins to increase (Figure 6D).

It should be noted that the width of the peak is ∼200 bp, which is roughly the mean length of gene conversion tracts. This may indicate that the region under the effect of selection depends on the lengths of gene conversion tracts. This can be demonstrated by the theoretical expectation of the spatial distribution of the divergence obtained as follows.

The derivation basically follows the sequence model, except that we assume that selection is so strong that disadvantageous haplotypes (A-A and B-B) created by gene conversion are eliminated from the population immediately. Only gene conversion events that involve the target site can create deleterious haplotypes. Suppose that the target site of selection is located at position y_s. First, we consider the probability that a conversion tract that includes a neutral site at position y also covers the target site of selection, which is given by

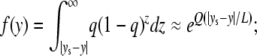(5)

therefore,

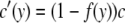(6)

can be considered the effective gene conversion rate at position y. Therefore, the expected divergence at position y may be simply expressed by the formula of Innan (2002), in which the gene conversion rate is given by Equation 6. That is,

(7)

where

and

We performed simulations to check this equation. After 10N generations of prerun, the neofunctionalized mutation is introduced. Every N generations, the spatial distribution of the divergence was investigated by a window analysis, in which a 100-bp window was moved with a 25-bp increment. Figure 7 shows that this formula fits reasonably well the simulation results. It is indicated that the average tract length of gene conversion is an important factor to determine the spatial distribution of the divergence. The height and the width of the peak of the distribution are positively correlated with the average tract length. The distribution is quite robust to the selection intensity under the assumption of strong selection (). As discussed above, the major effect of the intensity of selection is to determine the probability to get into the temporal equilibrium stage, but once it happens, the effect of selection on the pattern of divergence may be minor. This is expected from Equation 7, which is independent of the selection intensity.

Figure 7.—

Spatial distribution of the divergence between the duplicated genes obtained by Equation 7 (solid lines) and simulation (dashed lines). The parameters are the same as those used in Figure 6, except for the gene conversion tract length.

DISCUSSION

The process to neofunctionalization of a pair of duplicated genes under the pressure of gene conversion is investigated theoretically. In practice, this article considers the fate of a neofunctionalized allele that arises in duplicated genes undergoing concerted evolution by gene conversion. As illustrated in Figure 1, the process to permanent neofunctionalization is quite complicated. First, the neofunctionalized allele increases in frequency by selection (preequilibrium stage). However, gene conversion prevents its complete fixation, thereby creating an equilibrium (temporal equilibrium stage). During the temporal equilibrium stage, gene conversion can be inactivated by the accumulation of point mutations or by a terminator mutation in the flanking regions of the target site of selection, and then complete neofunctionalization is achieved.

We first theoretically investigate the process that the system gets in a stable temporal equilibrium stage. By using the diffusion theory, we obtained the probability to get into the temporal equilibrium stage, 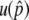, which is given by a function of N, s, and c under the single-site model. By simulations, it is found that the temporal equilibrium stage could last sufficiently long when the selection intensity is much larger than the gene conversion rate. Then, additional mutations during this temporal equilibrium stage result in permanent neofunctionalization.

Our results would revise a part of Walsh's (1995) formula for the relative probability of neofunctionalization to pseudogenization. It is reasonable to go back to Ohta's (1987) more general formula, which is given by

(8)

where u₊ (u₋) is the fixation probability of a neofunctionalized (silencing) allele and v₊ (v₋) is the mutation rate of neofunctionalized (silencing) alleles. With gene conversion, u₊ can be given by the probability to get into the temporal equilibrium stage, conditional on so that the temporal equilibrium stage continues sufficiently long to lead to permanent neofunctionalization. Therefore, when the additive effect of selection and no recombination is assumed, 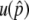given by Equation 3 gives the upper bound of u₊. With recombination, the probability to get into the temporal equilibrium stage is increased as demonstrated in Figure A1. Modifications should also be needed for the denominator, but the fixation process of a null mutation under the pressure of gene conversion is not well understood theoretically. Although it may be easy to imagine that gene conversion also retards the fixation process of a null mutation, its quantitative effect is an open question for further investigations.

Thus, our simulations demonstrate that the most significant effect of gene conversion in the process to neofunctionalization is that it adds the temporal equilibrium stage when the gene conversion rate is much higher than the point mutation rate so that duplicated genes undergo concerted evolution. Our previous study (Teshima and Innan 2004) demonstrated that duplicated genes would undergo long-term concerted evolution when 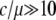under neutrality, although it depends on other parameters. This ratio (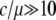) should be within a typical range of observations in various species (Drosophila, humans, and yeast; Innan 2003a,b; Gao and Innan 2004). This quantitative argument should hold in our selection model as long as selection affects a narrow region encompassing the target site of selection.

The difference in the pattern of the divergence between the neutral and selection models is seen around the target site. Here, we demonstrate that the spatial distribution of the nucleotide divergence between duplicated genes has a local peak in the temporal equilibrium stage, which was theoretically predicted by Innan (2003b). With analytical results, we show that the extent to which selection affects (i.e., the width of the divergence peak) is mainly determined by the lengths of gene conversion tracts, while the c/μ ratio has some effect on the height of the peak (Equation 7). It is also found that the behavior of the divergence roughly follows the neutral expectation in most regions except for this peak. It is suggested that if the mean length of gene conversion tracts is much smaller than the region under concerted evolution, the effect of selection is limited in a narrow region around the target site; therefore, selection may not have much power to cause a large change in the divergence in the overall region. Consequently, this temporal equilibrium stage with a peak in the divergence would last for a long time.

The divergence pattern is quite similar to that in a single-locus biallelic balancing selection (Hudson and Kaplan 1988; Nordborg and Innan 2003), in which the divergence between sequences with different alleles has a local peak around the target site of selection. The peak created by balancing selection is usually limited to a narrow region surrounding the target site because recombination between the two alleles shuffles polymorphism in regions apart from the target site. In our two-locus model, gene conversion works to shuffle the variation between the two regions.

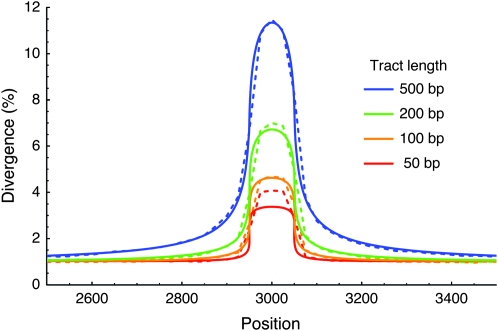
One of the most important implications in this article is that we might be able to find signatures of selection for neofunctionalization on the basis of our finding. That is, a signature for selection can be a peak of the divergence between duplicated regions, especially when the peak is in a region of functional importance, although the signature might be missed if one looked only at the average divergence. Our theoretical results fit well the observation of the human RHCE/RHD duplicated genes. Innan (2003b) reported that the divergence is very much elevated in exon 7, which specifies the Rh antigen types (Avent and Reid 2000). Another example is the human red- and green-opsin genes, which are arranged in a head-to-tail tandem array on the X chromosome (Nathans et al. 1986). The two genes are considered to have arisen by gene duplication after the split of New and Old World primates, i.e., 30–40 MYA. The sequences of the red and green genes are very similar to each other, indicating that the two genes are undergoing concerted evolution. There are a very limited number of fixed differences between the two genes (Nathans et al. 1986; Winderickx et al. 1993; Hayashi et al. 2001), at least three of which are known to be responsible for the difference in color sensitivity. Particularly, two of the three are closely located in exon 5 (amino acids 277 and 283), and these two account for >80% of the functional difference (measure by λ_max, a peak value of the light absorption spectrum) between the red and green pigments (Neitz et al. 1991). Because these two sites are very closely located, we suppose that these sites can be treated as a single selected site. Then, our theory predicts that a peak of the divergence should be observed around the two amino acids in exon 5, and the observation is in good agreement with our theory.

In Figure 8, we fit Equation 7 to the observed distribution of the divergence. We first estimated that the c/μ ratio may be ∼300 because the average divergence in the surrounding region is ∼0.003 (from Equation 17 in Innan 2002). Using this estimate, it is found that the expected distribution is roughly consistent with the observation when the mean tract length is 200 bp, which is within the range reported by Jeffreys and May (2004) (the average is 55–290 bp).

Figure 8.—

Distribution of the divergence between the human red- and green-opsin genes. The data are from GenBank, accession nos. Z68193 and Z46936. The observed distribution is shown by the black line. The theoretical expectations when the mean gene conversion tract lengths = 100, 200, and 300 bp are shown. Values of 4Nr = 6.75 and c/μ = 300 are assumed. The arrows represent the locations of amino acids 277 and 285.

Thus, this article demonstrates that a pair of duplicated genes exhibit strong signatures of selection for neofunctionalization when they undergo a long-term concerted evolution, that is, a peak of the divergence in a region of functional importance. This encourages the use of this idea for scanning a genome for signatures of selection. A successful result was obtained when applied to the Drosophila melanogaster and D. simulans genomes, which will be published elsewhere (N. Osada and H. Innan, unpublished results).