Gene Network Inference via Structural Equation Modeling in Genetical Genomics Experiments

Abstract

Our goal is gene network inference in genetical genomics or systems genetics experiments. For species where sequence information is available, we first perform expression quantitative trait locus (eQTL) mapping by jointly utilizing cis-, cis–trans-, and trans-regulation. After using local structural models to identify regulator–target pairs for each eQTL, we construct an encompassing directed network (EDN) by assembling all retained regulator–target relationships. The EDN has nodes corresponding to expressed genes and eQTL and directed edges from eQTL to cis-regulated target genes, from cis-regulated genes to cis–trans-regulated target genes, from trans-regulator genes to target genes, and from trans-eQTL to target genes. For network inference within the strongly constrained search space defined by the EDN, we propose structural equation modeling (SEM), because it can model cyclic networks and the EDN indeed contains feedback relationships. On the basis of a factorization of the likelihood and the constrained search space, our SEM algorithm infers networks involving several hundred genes and eQTL. Structure inference is based on a penalized likelihood ratio and an adaptation of Occam's window model selection. The SEM algorithm was evaluated using data simulated with nonlinear ordinary differential equations and known cyclic network topologies and was applied to a real yeast data set.

SYSTEM biologists are interested in understanding how DNA, RNA, proteins, and metabolites work together as a complex functional network. Projecting this network onto the gene space (Brazhnik et al. 2002) yields a gene network, where only the relationships between genes are modeled, although the physical interactions between genes are mediated through other components. While networks including genes, RNA, proteins, and metabolites would be more informative, gene networks are system-level descriptions of cellular physiology and provide an understanding of the genetic architecture of complex traits and diseases.

Bayesian networks are currently a popular tool for gene network inference (Friedman et al. 2000; Pe'er et al. 2001; Hartemink et al. 2002; Imoto et al. 2002; Yoo et al. 2002). Bayesian networks use partially directed graphical models to represent conditional independence relationships among variables of interest and are suitable for learning from noisy data (e.g., microarray data) (Friedman et al. 2000). Bayesian networks are directed acyclic graphical (DAG) models, which cannot represent structures with cyclic relationships. However, gene networks reconstructed on the basis of genetical genomics (or other perturbation) experiments are expected and have been found to be cyclic. Gene networks are phenomenological networks whose edges represent causal influences. These can be physical binding of a transcriptional regulator to the target promoter or more complicated biochemical mechanisms (involving signal transduction and metabolism), as there is much genetic regulation beyond transcription factors (Brazhnik et al. 2002). Recent articles point to the need for methods that can infer cyclic networks, note the limitation of the Bayesian network approach (Lum et al. 2006), and show better performance of a linear regression method over a Bayesian network algorithm most likely due to the presence of cycles (Faith et al. 2007). An alternative approach to the reconstruction of directed cyclic networks (directed cyclic graphs, DCGs) is based on the assumption that a cyclic graph represents a dynamic system at equilibrium (Fisher 1970) and includes a time dimension to produce a causal graph without cycles (DAG), which then can be studied using Bayesian networks, an approach called dynamic Bayesian networks (Murphy and Mian 1999; Hartemink et al. 2002). However, this approach requires the collection of time series data, which is difficult to accomplish, as it requires synchronization of cells and close time intervals not allowing for feedback (Spirtes et al. 2000).

Xiong et al. (2004) were the first to apply structural equation modeling (SEM) to gene network reconstruction using gene expression data. However, their application was limited to gene networks without cyclic relationships by using a recursive SEM, which has an acyclic structure and uncorrelated errors and is equivalent to a Gaussian Bayesian network. These authors reconstructed only small networks with <20 genes. Here, we apply SEM in the context of genetical genomics experiments.

In genetical genomics (Jansen and Nap 2001, 2004; Jansen 2003), a segregating population of hundreds of individuals is expression profiled and genotyped. With expression quantitative trait locus (eQTL) mapping and selection of regulator–target pairs, an encompassing directed network (EDN) of causal regulatory relationships among gene expression levels (expression traits, “e-traits”) and eQTL can be constructed. The network is called “encompassing” because it contains regulators with both direct and indirect effects on the same targets, which are actually only indirect regulations, and multiple candidate regulator genes for a given eQTL and target.

We present an SEM implementation to search for a set of sparser structures within the EDN that are well supported by the data. The method is evaluated on simulated data with known underlying network structures and on a real yeast data set. Typically, SEM analyses have included at most tens of variables, but our implementation is capable of reconstructing networks of several hundred genes and eQTL on the basis of a factorization of the likelihood and a strongly constrained network topology search space.

The genetic variation in a segregating population has been utilized to construct interaction networks among component traits or subphenotypes of complex diseases. Nadeau et al. (2002) reconstructed a network of component traits of the cardiovascular system using phenotypic data on a segregating population and Bayesian network analysis, while Li et al. (2006) analyzed both phenotypic and DNA marker data on a segregating population to construct networks including subphenotypes and QTL related to obesity and bone geometry, using SEM. While in this article we focus on using SEM to infer a gene regulatory network using e-traits only, it would not be too difficult to extend the method to the combined network inference including all of the above: genes, eQTL, disease (sub)phenotypes, and other phenotypes such as metabolomic data.

METHODS

The methodology we discuss here can be applied to any organism where a segregating population is extensively marker genotyped and expression profiled and where DNA sequence information is available. We perform gene (regulatory) network inference by a three-step approach: (1) eQTL mapping, (2) regulator–target pair identification to obtain the EDN, and (3) a search for a set of sparser optimal networks within the search space defined by the EDN. For the evaluation of this three-step approach, we analyzed the yeast genetical genomics data set (Brem and Kruglyak 2005). After removing the 20% of genes with the lowest e-trait variability from the original data, our data set contained e-traits for 4589 genes and genotypes for 2956 genetic markers on 112 haploid offspring from a cross between a laboratory and a wild strain (see supplemental material at http://www.genetics.org/supplemental/ for data preprocessing). We performed a small simulation study to evaluate the regulator–target pair selection. For evaluation of the SEM in step 3, we developed a method to simulate genetical genomics data with known underlying network topologies, and we assessed the SEM on the basis of its ability to infer these networks.

Expression QTL analysis:

We used three different eQTL mapping strategies, and we applied false discovery rate (FDR) control using the Benjamini–Hochberg procedure (Benjamini and Hochberg 1995). To identify chromosomal regions affecting multiple e-traits, the eQTL regions of two different e-traits were combined into a single region if the two eQTL were located at the same marker or their confidence intervals (C.I.'s) overlapped by >80%. The first strategy was cis-eQTL mapping, where only the marker(s) closest to the location of an e-trait's gene are tested (e.g., Doss et al. 2005), and subsequently the secondary targets of the cis-eQTL, the so-called cis–trans-regulated e-traits, are found by testing the effects of the identified cis-eQTL regions on other e-traits.

Multiple-trait analysis can provide more power to detect pleiotropic QTL. It is therefore desirable to utilize, in some way, the information from multiple correlated expression profiles in the search for eQTL. Therefore, we used two approaches that utilize information from correlated e-traits: QTL mapping of principal components (PC) and trans-eQTL mapping. It has been shown that using a small number of PC traits for QTL mapping, when a (large) number of original traits are (highly) correlated (in groups of traits), is very effective for QTL identification; i.e., essentially the same QTL are identified by analyzing PC and original traits (Mähler et al. 2002; see also Jiang and Zeng 1995 and Mangin et al. 1998). We used k-means with absolute correlation as the distance measure to cluster genes into 100 subsets with on average 46 genes per cluster. We then performed PC analysis separately for each cluster, followed by eQTL mapping of each retained PC. We chose 100 clusters because we found considerably more eQTL with 100 than with fewer clusters and because with >100 clusters many small clusters had only one or two genes. An eigenvalue cutoff of 1.5 was used to retain PCs within each cluster, so that the PCs from different clusters contained a similar amount of information. An eQTL affecting a PC was assumed to be a common regulator of all e-traits with high loadings, but there was no clear cutoff for “high.” Therefore, all e-traits were individually tested only for the identified PC–eQTL regions. For cis and PC mapping, we performed single-marker analysis using the Kruskal–Wallis test (Lehmann 1975).

Trans-regulated e-traits are affected by an eQTL genotype and the e-trait of the corresponding candidate regulator gene simultaneously. Therefore, Kulp and Jagalur (2006) proposed to include candidate regulatory e-traits in the QTL model. While these authors performed interval mapping, we used a regression model and the intersection-union test (IUT) (Casella and Berger 1990) to test whether the eQTL genotype and the e-trait of the candidate regulator gene r both significantly affect the e-trait of target gene t

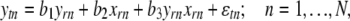(1)

where y_tn and y_rn are deviations of e-trait values in observation n from their means, x_rn is the deviation of the genotype value (0 or 1) from its mean for the marker closest to the physical location of candidate regulator gene r, and 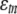is a residual. Coefficients b₁ and b₂ (b₃) represent main effects (interaction) of gene and eQTL regulators, and both must be significantly different from zero for gene r to be declared as a trans-regulator of gene t as determined by the IUT. There are two reasons why the trans-analysis might give false positives: the presence of a cis-eQTL affecting the target and multicollinearity between y_r and x_r. We therefore did not consider any candidate regulator whose closest marker had a recombination rate of ≤0.25 with the marker closest to the target e-trait. We performed multicollinearity tests (see supplemental material), which indicated that our trans-mapping results should essentially be unaffected by multicollinearity.

Regulator–target pair identification and encompassing directed network:

In contrast with previous work (e.g., Doss et al. 2005; Kulp and Jagalur 2006), in this article we consider cis-, cis–trans-, and trans-regulations jointly with the goal of reconstructing an EDN that defines the network search space for network inference by SEM. While the SEM represents a global structural model evaluating regulator–target relationships in the context of an entire network, for regulator–target pair identification we use single equations (similar to trans-mapping) expressing the e-trait of a target gene as a linear combination of the expression levels of some of its regulator genes and eQTL. We therefore refer to these single equations as local structural models or equations.

Regulator–target pair identification for cis and PC mapping:

For the eQTL identified by cis- and PC mapping, the regulator–target pair selection was performed in three steps separately for each eQTL: (1) identification of those of the detected cis-linked e-traits that were most likely truly cis-linked and those that were probably cis–trans-effects, (2) identification of those of the detected trans-affected e-traits that were probably cis–trans-affected rather than likely trans-affected, and (3) a search for the candidate regulator among all genes physically located in the eQTL C.I. for each of the likely trans-affected e-traits.

1. Distinguishing cis from cis–trans: We tested whether a cis-affected gene t was likely truly cis-affected using model (1) but omitting the interaction term, with r denoting any other gene found to be cis-affected by the same eQTL and with x_rn denotingthe genotype of the marker at which the peak test statistic of the eQTL occurred. If y_t is actually cis–trans-affected through y_r, then b₂ should not be significantly different from zero with y_r included in the regression equation. If for an e-trait t, b₂ remained significant (at the P < 0.05 level) for all e-traits r, then it was identified as a “true” cis-affected e-trait.

2. Distinguishing trans from cis–trans: Using model (1) again, y_t is now a trans-affected e-trait, and y_r is a cis-affected e-trait identified in step 1. Cis–trans regulation is indicated by b₂ not being significantly different from zero. If b₂ remains significant for all cis-affected e-traits r, then gene t is identified as a likely trans-affected e-trait.

3. Selecting regulator–target pairs in the same eQTL region: To find the candidate regulator(s) for a likely trans-affected e-trait t among all genes physically located in the eQTL region, for target e-trait t we fitted model (1) with any candidate regulator e-trait r located in the eQTL region and the eQTL marker (without the interaction term) and any additional candidate regulator e-trait r′. The additional candidate e-trait was included to examine whether the regulator–target correlation was due to some indirect mechanism. We retained the maximum P-value of the b₁ coefficients for y_r across all r′ and if it was significant, then we retained the regulator–target pair (r, t) [we used a P-value cutoff of (0.05/number of candidate regulators) for all tests performed for each eQTL–target pair].

Identification of regulator–target pairs for trans-mapping:

For each target e-trait t with at least two identified regulators, for each identified regulator r of e-trait t, we included another identified regulator e-trait (r′) of t and its nearest marker in model (1) to obtain

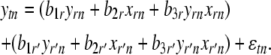(2)

The marker for regulator r′ was not included in the model when its recombination rate with the marker for regulator r was <0.25. We retained the maximum P-value of the IUT test for b_1r and b_2r across all r′ and if it was significant (at the P < 0.05 level), only then we retained the regulator–target pair (r, t). Otherwise we discarded gene r as a regulator of t and assumed that its effect was due to an indirect mechanism.

Simulation study on regulator–target pair identification:

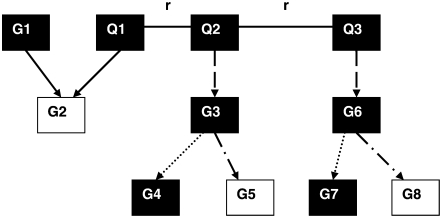
We evaluated our regulator–target pair selection in a small simulation study. For a population of 112 individuals (as in the yeast data), we simulated an eQTL region containing three eQTL causal polymorphisms and several candidate regulator and target genes. This local network is depicted in Figure 1, with G (Q) representing a gene (eQTL). The target list for the eQTL region is T = [G2, G3, G4, G5, G6, G7, G8]. Gene G1 is the only candidate trans-regulator, while genes G3, G4, G6, and G7 are candidate cis-regulators. There are four types of regulations: one true trans-regulation (from G1 and Q1 to G2), two true cis-regulations (Q2 to G3 and Q3 to G6), two true cis–trans-regulations of targets located in the eQTL region (Q2 to G3 to G4 and Q3 to G6 to G7), and two true cis–trans-regulations of targets not located in the eQTL region (Q2 to G3 to G5 and Q3 to G6 to G8).

Figure 1.—

The network model used in the simulation study for regulator–target pair identification. Solid squares with letter Q, causal polymorphisms in the same eQTL region; solid squares with letter G, genes located in the eQTL region; open squares with letter G, genes not located in the eQTL region but affected by it; solid arrows, true trans-regulations; dashed arrows, true cis-regulations; dotted arrows, true cis–trans-regulations of target genes located in the eQTL region; dashed-dotted arrows, true cis–trans-regulations of target genes not located in the eQTL region. Solid lines among the Q polymorphisms represent direct genetic linkage (recombination rate = 0 or 0.09).

Data were simulated with linear regression models with regression coefficients fixed at the value of 1 and residual standard deviations (SD) set to 0.125, 0.25, or 0.5 (one value for all genes, or for genes with odd numbers SD = 0.5 or 0.25, and for genes with even numbers SD = 0.25 or 0.125). For a gene directly regulated by an eQTL, the model was y = bx + e = x + e, where x is QTL genotype (0/1), variance due to the eQTL was 0.25, and heritability was 0.25/(0.25 + SD²) = 0.941, 0.80, or 0.50 for the three SD values, respectively. For a gene indirectly regulated by an eQTL (Q2 → G3 → G4), the model was y₂ = b(bx + e₁) + e₂ = x + e₁ + e₂, and heritability was 0.25/(0.25 + 2 SD²) = 0.889, 0.667, and 0.333. The three causal polymorphisms in the eQTL region had order Q1–Q2–Q3 (see Figure 1) with recombination rate r = 0.0 or r = 0.09 between adjacent polymorphisms. A total of 1000 data replicates were simulated and analyzed for each of several combinations of SD and r values.

EDN construction:

The eQTL mapping and regulator–target pair selection steps resulted in three lists of causal regulatory relationships: (1) a list containing all identified cis-regulations (eQTL A affects gene A located in its confidence region), (2) a list containing all cis–trans-regulations (cis-regulated gene A regulating gene B), and (3) a list containing all trans-regulations [gene A regulating gene B and eQTL A affecting gene B (but not gene A)]. To construct an EDN, we assembled all the identified and retained regulator–target relationships, which consisted of directed edges (representing causal influences) from eQTL to cis-regulated target genes, from cis-regulated genes to cis–trans-regulated target genes, from trans-regulator genes to target genes, and from trans-eQTL to target genes. The EDN consisted of two types of nodes: continuous nodes for the genes (e-traits) and discrete nodes for the eQTL (genotypes).

Structural equation modeling:

A structural equation model:

SEM has been widely used in econometrics, sociology, and psychology, usually as a confirmatory procedure instead of an exploratory analysis for causal inference (e.g., Johnston 1972; Judge et al. 1985; Bollen 1989). Shipley (2002) discusses the use of SEM in biology with an emphasis on causal inference. SEM has been used for association and linkage mapping of QTL (e.g., Neale 2000; Stein et al. 2003). In contrast, we treat the eQTL as known in the SEM, as the high-dimensional nature of the e-traits forces us to perform a three-step analysis (eQTL mapping, EDN construction, and SEM network sparsification).

In general, an SEM consists of a structural model describing (causal) relationships among latent variables and a measurement model describing the relationships between the observed measurements and the underlying latent variables. Any SEM can be represented both algebraically through a system of equations and graphically. A special case is the SEM with observed variables only, where all variables in the structural model are observed, and therefore there is no measurement model. Our model is a SEM with observed variables, which can be represented as

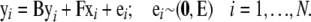(3)

In this model, for sample i (i = 1, … , N), y_i = (y_i1, … , y_ip)^T is the vector of expression values of all (p) genes in the network, and x_i = (x_i1, … , x_iq)^T denotes the vector of marker or eQTL genotype codes. The y_i and the x_i are deviations from means, e_i is a vector of error terms, and E is its covariance matrix.

Matrix B contains coefficients for the direct causal effects of the genes on each other: Element b_km represents the effect of e-trait m on e-trait k. Matrix F contains coefficients for the direct causal effects of the eQTL on the genes: Element f_km represents the effect of eQTL m on e-trait k. The structure of matrices B and F corresponds to the path diagram or directed graph representing the structural model, in which vertices or nodes represent genes and eQTL and edges correspond to the nonzero elements in B and F. Matrices B and F are sparse when the model represents a sparse network. When the elements in e_i are uncorrelated and matrix B can be rearranged as a lower triangular matrix, the model is recursive, there are no cyclic relationships, and the graph is a DAG. If the error terms are correlated (E is nondiagonal), or matrix B cannot be rearranged into a triangular matrix (indicating the presence of cycles), the model is nonrecursive. The graph corresponding to a nontriangular matrix B is a DCG.

The x_i may be fixed or random. In genetical genomics experiments, the eQTL x_i are random because individuals are sampled from a segregating population. However, the joint likelihood of the y_i and x_i can be factored into the conditional likelihood of the y_i given the x_i times the likelihood of the x_i, and the latter does not depend on any of the network parameters in B, F, and E and can therefore be ignored. Thus, we need only to assume multivariate normality for the residual vectors.

An important issue in nonrecursive SEM or DCG is equivalence. Models are equivalent when they cannot be distinguished in terms of overall fit. For DAGs, algorithms for checking the equivalence of two models or for finding the equivalence class of a given model in polynomial time are available (Verma and Pearl 1991; Andersson et al. 1997). Therefore, model search is performed among equivalence classes rather than among individual DAGs (Chickering 2002a). An equivalence class discovery algorithm for DCGs, which is polynomial time on sparse graphs (Richardson 1996; Richardson and Spirtes 1999), is available but there is no algorithm for model search among equivalence classes. Two DAG models are equivalent if they have the same undirected edges but differ in the direction of some edges (edge reversal) (Pearl 2000). Two DCG models can be equivalent even if they differ in their undirected edges (Richardson 1996; Richardson and Spirtes 1999). In our case, two models cannot be equivalent under edge reversal, because the directions of the edges are determined by the eQTL. By using an information criterion for model selection with a penalty for the number of parameters, we prefer the sparser model of two equivalent models that differ in the number of edges. Therefore, equivalence is of less concern in our case. Instead of selection among equivalence classes, we use a model search algorithm that selects multiple models (described below).

A main concern about using SEM for gene network inference is the severe constraint on the network size when using existing SEM software [e.g., LISREL (Jöreskog and Sörbom 1989) and Mx (Neale et al. 2003)]. Typical applications of SEM include models with at most tens of variables. No existing software program can analyze models with a size relevant to genomics (hundreds or even thousands of variables). Even the SEM implementation of Xiong et al. (2004), which employed a genetic algorithm, was applied only to small networks of <20 genes. Here, we implement SEM analysis in the context of genetical genomics experiments, where the EDN provides a strongly constrained topology search space, allowing us to reconstruct networks with up to several hundred genes and eQTL.

Algorithms for likelihood maximization:

The most commonly used estimation method for SEM is the maximum-likelihood (ML) method. Assuming a multivariate normal distribution of the residual vectors, or e_i ∼ N(0, E), the logarithm of the conditional likelihood of the y_i's given the x_i's and given a particular structure is

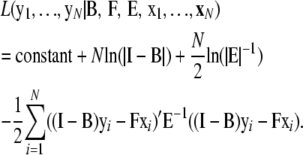(4)

This log likelihood is maximized with respect to the parameters in B, F, and E.

A nonrecursive SEM model can be underidentified, while a recursive SEM is always identified. A model is “identified” if all parameters are independent functions of the data covariance matrix. Under regularity assumptions, an underidentified model can be equivalent to an identified model nested within it (Bekker et al. 1994). Since we prefer the sparser model, our model selection based on an information criterion should arrive at identified models (an SEM can be checked numerically for underidentification by computing the rank of the information matrix or by repeated model fitting).

The likelihood function is nonlinear in the parameters, and therefore an iterative optimization procedure is required for its maximization. The likelihood can be factored into a product of local likelihoods that all depend on different sets of parameters and that are maximized individually in analogy with Bayesian network analysis. For directed acyclic graphs, the global directed Markov property permits the joint probability distribution of the variables to be factored according to the DAG (Pearl 2000). Let V be the random variable associated with a particular node (vertex). The factorization can be represented as p(V₁, V₂, … , V_n) = 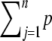(V_j | V(parents of j), θ_j), where V(parents of j) is a vector of V's of the parent vertices of vertex j, and θ_j is the parameter vector of the local likelihood p(V_j | .). A network with cyclic components (systems of connected cycles, in which any gene can find a path back to itself through any other genes) becomes acyclic when a set of genes pertaining to the same cyclic component is collapsed into a single node; i.e., V_j represents either an individual gene or the set of genes involved in the same cyclic component. If the error terms are also uncorrelated (diagonal E), then p(V₁, V₂, … , V_n) can be factored as above, thereby turning the optimization problem from one of thousands of dimensions into many of much smaller dimensions. For genes that are not involved in a cyclic component, the univariate conditional likelihood of a gene is maximized efficiently using linear regression. For the genes involved in a cyclic component, their joint multivariate conditional likelihood is maximized. We note that in our case the factorization is applied to the likelihood in Equation 2, so that the V variables correspond to the genes with observed e-traits (y), which are the endogenous variables (they are determined by the system), while the eQTL genotypes (x) are exogenous variables. Consequently, cyclic components are composed of gene nodes, not eQTL nodes, with the latter appearing as parents of genes only in a cyclic component.

For a cyclic component c, p(V_c | V(parents of c), θ_c) involves the equations for all genes in cyclic component c from (4),

(5)

where 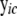is a vector of expression values in sample i for all genes in cyclic component c and their parent genes, which can be partitioned into subvectors 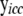and 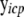pertaining to the genes in cyclic component c and to their parent genes not in cyclic component c, respectively; 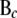(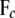) is a submatrix obtained from the original B (F) matrix by extracting all rows corresponding to the genes in c and all columns pertaining to these genes and their parents; 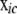contains the genotype codes of all eQTL parents of genes in c; and 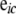is the residual vector for all genes in c. Matrix 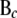can be further partitioned into 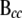and 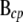, corresponding to columns pertaining to genes in c and parent genes not in c, respectively. Then

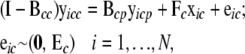(6)

where 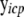is a vector of exogenous variables (variables that do not receive any inputs) just like x_ic. The likelihood function for this model is then

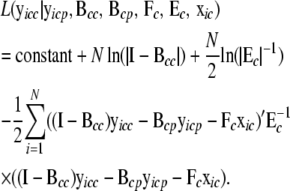(7)

The likelihood function (7) of the genes in a cyclic component is maximized using a genetic algorithm (GA)-based global optimization procedure. During the model search, the local likelihood of cycle c needs to be remaximized with respect to θ_c only if the set of parents of genes involved in the cyclic component has changed.

GA is a stochastic iterative optimization tool (Holland 1975, 1992; Goldberg 1989). Although GA is computationally more expensive than the gradient-based methods, it has been shown that GA is more successful for problems with very complex parameter spaces (Mendes 2001; Moles et al. 2003). The GA C++ library GAlib (http://lancet.mit.edu/ga/) was used in our implementation. GA evaluates the fit of a chromosome using the objective function, which in our case is the log-likelihood function for genes in a cyclic component. With a diagonal E matrix, the most computationally demanding part for evaluating the objective functions is the computation of the determinants of matrices (I − B)_c. These matrices are sparse, and determinants are calculated using sparse LU decomposition as implemented in the C library UMFPACK, which applies the unsymmetric multifrontal method for sparse LU factorization (Davis and Duff 1997, 1999; Davis 2004a,b). Since the patterns of the matrices remain the same for a given structure, symbolic factorization is performed only once, and the result is used by all numerical factorizations for objective functions of that structure.

In our model search algorithm, for remaximization of the local likelihood of a cyclic component, we use four types of starting values simultaneously in the initial GA population: random starting points, starting values obtained from two-stage least squares (2SLS) (described below), starting values equal to the current parameter estimates, and starting values from the current parameter values for all genes except 2SLS estimates for the genes directly affected by the deletion or addition of an edge. We use current parameter values as starting values because we search the model space by removing and adding single or a few edges at a time, and therefore most parameter estimates do not change or do not change much. However, the parameter values associated with the gene directly affected by the deletion or addition of an edge can change considerably and we hence initiated them by 2SLS. Using these starting values greatly increased the efficiency of the GA optimization.

2SLS (e.g, Judge et al. 1985; Goldberger 1991) is a computationally efficient parameter estimation method for SEM. The 2SLS estimates are computed on the basis of one portion of the model at a time, while ML estimation takes the entire model into account. Therefore, ML is called a “full information” method, while 2SLS is a “partial information” method, and ML estimates are generally better than 2SLS estimates. However, 2SLS is a noniterative approach and computationally very efficient. In 2SLS, the first step is to obtain predicted values of y using all of the exogenous variables in the system on the basis of the following reduced-form equations and their ordinary least-squares (OLS) fits,

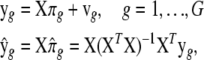(8)

where

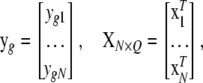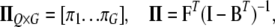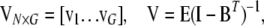where N is sample size, G is the number of endogenous variables, and Q is the number of exogenous variables in X. The reduced-form equations are derived from (3) (details are given in our supplemental material). Predictions 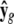are then used in the original model to obtain OLS estimates of the nonzero elements in each row of B (b_g) and each row of F (f_g), or

(9)

where

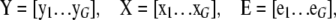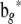and 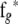are obtained from 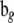and 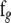by deleting all elements fixed at zero (in a given network structure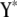), and and 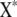have the corresponding columns deleted from Y and X. 2SLS may not work well for some genes with no suitable instrumental variables. An instrumental variable for prediction of an endogenous variable exists only under certain conditions in cyclic networks (e.g., Heise 1975). These conditions are likely not met for all genes in a network. Only if each gene had a cis-linked eQTL, would the conditions then always be met.

Network topology search:

Alternative models or structures (topologies) were compared using information criteria. Information criteria (IC) combine the maximized likelihood with a penalty term to adjust for the number of free parameters, and some also adjust for sample size. The information criteria we used include the Bayesian information criterion (BIC) (Schwartz 1978) and a modification, BIC(δ) (Broman and Speed 2002).

The EDN contains 2^d submodels, where d is the number of edges. It is impossible to exhaustively search this space even for EDNs of moderate size. Therefore, we adapted a heuristic search strategy based on the principle of Occam's window model selection (Madigan and Raftery 1994) that potentially selects multiple acceptable models. Let A denote a set of acceptable models; C, the set of candidate models; and K, the set of models with minimum IC (the model selection criterion). The search algorithm includes a down and an up component. The down algorithm consists of the following steps:

• 0. Initialize A and K as empty sets and C as a set containing only the EDN.

• 1. Select a model M₁ in C and move it to A. Set IC_min = 0.

• 2. Select a submodel M₂ of M₁ by removing an edge from M₁ and compute the model selection criterion for these two models, IC₁₂.

• 3.

  1. If IC₁₂ < T (i.e., model M₂ is strongly better than M₁), then remove M₁ from A if M₁ A, add M₂ to C if M₂ C, set K to the empty set, and set IC_min = −∞.
  2. Else if T < IC₁₂ < IC_min (i.e., M₂ is the best among all submodels of M₁ considered so far), then set IC_min = IC₁₂, replace the model in set K with M₂, and remove M₁ from A if M₁ A.
  3. Else if IC_min < IC₁₂ < 0 (i.e., model M₂ improves M₁ but is not strongly better and is not the best among all submodels of M₁ considered so far), then (i) with probability w (e.g., w = 0.20 or 0.10) this model is chosen as a candidate model by removing M₁ from A if M₁ A and adding M₂ to C if M₂ C, or (ii) otherwise take no action.
  4. Else take no action.
• 4.

  1. If there are more submodels of M₁, then go to step 2.
  2. Else move the model in K to C if it is not already in C.

• 5. If C is not empty, go to step 1.

Starting from all models accepted in the down algorithm, the up algorithm follows the same steps as in the down algorithm, except each time an edge that was removed from the EDN is added back into the model. Once the up algorithm is completed, the set A contains the set of potentially acceptable models.

For large networks with many removable edges, the original Occam's window model-selection (Madigan and Raftery 1994) approach may search a very large model space. In the worst case, it is equivalent to an exhaustive search. Therefore, we imposed a threshold T on the IC (step 3a). Only if the IC of the submodel strongly improves over the model it is nested in (IC < T), is the sub-model then kept as a candidate model. Otherwise, if no submodel passes T and the minimum IC is less than zero, then the model with minimum IC is kept as a candidate model. The size of the search space depends on the value of T. If T = −∞ and probability w is zero, the algorithm is similar to the greedy hill search (Chickering 2002a,b). If −∞ < T < 0, then the algorithm searches a larger network space and possibly accepts multiple models. Because T requires the submodel to strongly improve over the model it is nested in, it is likely that the search will accept only one final model. Therefore, probability w in step 3ci can be set to a positive value to introduce multiple search paths to be followed.

The model or structure search space is constrained to models nested within the EDN, and additionally, certain edges cannot be removed from the EDN, because their removal would contradict the results from the eQTL analysis. If a gene's expression profile is found to be influenced by an eQTL, then there must remain a direct or indirect path from the eQTL to that target gene in the network. For example, an edge for cis-regulation of a gene by an eQTL cannot be removed unless the eQTL has multiple cis-candidates, in which case one of the cis-edges needs to remain.

Data simulation for evaluation of SEM and network topology search:

To evaluate the performance of the linear SEM for gene network inference, we simulated data with nonlinear kinetic functions and cyclic network topology in the context of a genetical genomics experiment with 300 recombinant inbred lines. We simulated QTL genotypes using the QTL cartographer software (Basten et al. 1996) and steady-state (equal synthesis and degradation rates and constant gene expression levels in time) gene expression profiles according to the simulated genotypes with the Gepasi software (Mendes 1993, 1997; Mendes et al. 2003), using nonlinear ordinary differential equations

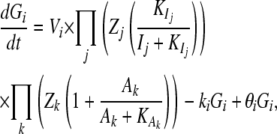(10)

where G_i is the mRNA concentration of gene i, V_i is its basal transcription rate, 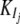and 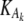are inhibition and activation rate constants, respectively, I_j and A_k are inhibitor and activator concentrations, respectively (the expression levels of genes in the network affecting the expression of gene i), and k_i is a degradation rate constant. Each gene has two genotypes, and the polymorphism is located either in its promoter region affecting its transcription rate (cis-linkage with V = 1 for one genotype and V = 0.75 for the other) or in the coding region of a regulatory gene changing the basal transcription rates of the target genes by multiplying V by a factor Z (Z = 1 for one genotype and Z = 0.75 for the other). Each gene has a 50% probability of having a promoter (cis-) or coding region (trans-) polymorphism. The error parameter 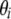represents “biological” variance and was sampled from a normal distribution with a mean 0 and a standard deviation of 0.1 each time before the calculation of a steady state. All other parameters were set to 1. Finally, we also added “experimental noise” to the generated data at 10% proportional to the variance of each gene's expression values.

The parameters were chosen so that the estimated heritabilities were close to those found in real data. For a simulated data set, we calculated the heritability of an e-trait by dividing the steady-state variances simulated without biological and technical noise by the variance simulated with biological and technical errors. The simulated e-traits had an average heritability of 56% with 60% of the e-traits having heritabilities >57%. The simulated e-traits had somewhat lower heritabilities than the actual e-traits in the yeast data set where 60% of the genes had estimated heritabilities >69% (Brem and Kruglyak 2005), which were calculated as (e-trait variance in the segregants − pooled e-trait variance among parental measurements)/e-trait variance in the segregants.

Random network topologies were generated as described by Mendes et al. (2003). For each generated network we created an EDN by adding links from any node i to node j, if node j was no more than two edges separated from node i in the true network.

RESULTS

The regulator–target pair identification and the SEM method were tested on simulated data, and the entire three-step analysis was applied to the real data set from a yeast segregating population (Brem and Kruglyak 2005).

Simulation results on regulator–target pair identification:

The results of our regulator–target pair identification from simulated data for the single eQTL network in Figure 1 are summarized in Table 1 in terms of power and FDR (see Table 1 for definition of power and FDR) for four types of simulated regulatory effects (see Figure 1 and methods), which demonstrate that the procedure works well, with the exception of a case where some genes have extremely high and other genes low heritability (column 5 in Table 1). This problem was actually due to one of the cis-linked genes (G3) having very small residual variance and being assigned as a regulator for other genes incorrectly.

TABLE 1.

Results from a simulation study on regulator–target pair identification in a single-eQTL region with three causal polymorphisms and with multiple candidate regulator and target genes (true network structure is in Figure 1)

Methods	SD = 0.5	SD = 0.25	SD = 0.125	SD = 0.5/0.125	SD = 0.5/0.25	SD = 0.25/0.125
Cis-link, power (%)	100, 100	100, 100	100, 100	55.3, 59.85	89.4, 98.65	97.8, 98.5
Cis-link, FDR (%)	0.6, 0.9	0.7, 0.67	0.67, 0.57	0.48, 0.53	0.6, 0.72	0.62, 0.57
Cis-reg cis, power (%)	99, 99	99, 99	99, 99	54.8, 59.4	88.6, 97.8	97.2, 97.8
Cis-reg cis, FDR (%)	0.35, 0.13	0, 0	0, 0	38.6, 0.25	3.27, 0.15	1.8, 0.1
Cis-reg, power (%)	99, 98.8	99, 98.9	98, 98.5	54.9, 59.2	88.2, 97.4	96.9, 97.5
Cis-reg, FDR (%)	0.93, 0.4	0, 0	0, 0	45, 25.82	4.82, 1.33	2.85, 1.3
Trans-reg, power (%)	99, 99.2	100, 100	100, 100	41.8, 45.1	92.9, 96.1	96.3, 96.5
Trans-reg, FDR (%)	0.85, 1.1	1.1, 1.15	1.57, 1.52	26.95, 62.52	10.92, 2.52	2.3, 2.77

Power, percentage of replicate data sets in which the regulation type was found; FDR, percentage of replicate data sets in which a regulation of a certain type was found that did not exist in the underlying network; Cis-link, cis-regulation of target in eQTL region; Cis-reg, cis–trans-regulation of target not in eQTL region; Cis-reg cis, cis–trans-regulation of target in eQTL region; Trans-reg, trans-regulation. For the last three columns, even-numbered gene nodes (Figure 1) received the left amount of error variance and odd-numbered nodes the right amount. The two numbers in each cell correspond to 0% recombination and 9% recombination among the three causal polymorphisms in the single-eQTL region, respectively. A P-value cutoff of 0.01 was used.

SEM analysis of simulated data:

Ten data sets of 300 observations each, with different random network topologies, were analyzed. These networks had 100 genes, 100 eQTL, and on average 148 gene → gene and 123 eQTL → gene edges. Their EDN contained on average 360 gene → gene and 301 eQTL → gene edges. On average 42 genes were involved in one to three cyclic components in each data set, with the biggest cyclic component involving on average 37 genes. The algorithm was run on a multiprocessor SGI Origin2000 and took between 2 and 8 hr (total time) per data set with an average of 4 hr. We report the results in terms of FDR and power. The FDR is expressed as the number of wrongly identified edges divided by the total number of identified edges. Power is defined as the number of edges correctly inferred as a fraction of the total number of edges in the true network. In Table 2, we compared results obtained using BIC and BIC(δ). The results showed that for the simulated data sets, BIC was not sufficiently stringent for the eQTL → gene edges, with an average power of 99% and an average FDR of 22%. For the gene → gene edges, the average FDR was 8%, with average power of 88%. For the eQTL → gene edges, the average FDR with BIC(δ) was 9%, while the average power was 99%. For the gene → gene edges, with BIC(δ) the average FDR was only 1%, while the power was reduced to on average 78%. Overall, the algorithm performed well, and the results show that the linear SEM appears to be robust under violation of the linearity assumptions.

TABLE 2.

Results of the SEM analysis on the simulated data

	Edge type		Model
IC			Measure	1	2	3	4	5	6	7	8	9	10
BIC	F	FDR	18.4	24.3	27.4	17.9	19.5	21.6	20.7	19.0	23.9	22.2
		Power	100.0	100.0	100.0	100.0	100.0	99.2	99.2	100.0	97.5	100.0
	B	FDR	6.6	7.1	7.6	7.6	5.7	8.5	3.8	15.3	9.5	11.0
		Power	87.6	89.7	89.9	89.3	89.3	88.4	85.9	85.8	88.7	87.2
BIC(δ)	F	FDR	7.5	7.9	7.7	5.1	8.1	7.1	6.3	14.8	11.9	14.5
		Power	100.0	100.0	99.2	99.2	100.0	96.7	100.0	98.4	100.0	100.0
	B	FDR	0.8	0.0	1.7	0.0	1.6	3.4	0.0	3.4	1.8	0.9
		Power	80.7	82.2	79.9	78.5	81.2	76.2	77.9	77.7	72.7	71.8

False discovery rate and (percentage) power of edge detection are given for 10 artificial data sets using BIC and BIC(δ) criteria and separately for the eQTL → gene and gene → gene edges.

While the above results were based on retaining a single, final SEM model, for some of the 10 data sets we allowed the topology search algorithm to follow 20 different, random search paths. This was done to determine whether there were different models (topologies) with the same likelihood (equivalent models) and to identify multiple models with the same or nearly the same BIC [or BIC(δ)]. These additional networks contain important information that would be missed when searching only for a single network, and they reflect the uncertainty about the true network structure after observing the data. On average 16 very similar final models were obtained per data set. Of an average of 134 detected eQTL → gene edges, the average number of edges different from the best model was 4.4. Of an average of 153 detected gene → gene edges, the average number of edges different from the best model was 7.9. The average BIC difference to the best model was 26. The average likelihood difference was 12, while the mean likelihood was 26,969. Two models had the exact same likelihood (and hence were equivalent), while having six different eQTL → gene edges and seven different gene → gene edges. Another four pairs of models had likelihood differences <1, with on average four different eQTL → gene edges and 7.3 different gene → gene edges.

Yeast data analysis:

eQTL mapping:

When analyzing PCs computed from separate PC analysis of the 100 gene clusters, a total of 250 combined eQTL regions (median size 37 kb) were identified. When testing these 250 eQTL on all individual e-traits, a total of 10,316 eQTL–target pairs were detected. For cis-mapping, a total of 578 combined cis–eQTL regions (median size 36 kb) were identified. We then searched for cis–trans-affected e-traits and found a total of 7481 eQTL–target pairs.

Trans-mapping appeared to greatly increase the power to detect eQTL. A total of 41,309 significant candidate regulator–target pairs were identified. The interaction between eQTL and candidate regulator (b₃ in Equation 1) gene did not appear to be important. Of all tests performed, only 0.08% had a significant eQTL-by-regulator gene interaction with FDR control at the 5% level for this term. Of the tests with a significant IUT, 4.94% had P-values for b₃ < 0.01, and 0.43% had P-values smaller than the FDR cutoff from all tests. More details on the eQTL analysis and results can be found in our supplemental material.

Regulator–target pair identification and EDN construction:

For the 10,316 eQTL-target pairs identified by PC mapping, 9843 regulator-target pairs were retained, involving 3581 genes, with 1103 regulators and 3262 targets. For the 7481 eQTL–target pairs identified by cis-mapping, 6090 regulator–target pairs involving 3034 genes were found, with 1099 regulators and 2562 targets. After local sparsification of the trans-mapping results, the 41,309 candidate regulator–target pairs were reduced to 15,835 pairs involving 3858 genes with 1433 regulators and 3682 targets. We combined these results into an EDN, which included 28,609 regulator–target pairs. This EDN can be found online in several file formats at http://www.bioinformatica.crs4.org/Members/alf/genetics/.

The network consisted of 4274 gene nodes. The remaining 315 genes did not receive any inputs nor were they affecting any other genes. A total of 2118 genes were regulators of at least one target, among which 158 did not receive any inputs. A total of 4116 genes were targets having at least one regulator, among which 2156 did not affect any other genes in the network. A total of 1960 genes occurred both as regulators and as targets. There were 135 instances of reciprocal regulation present (gene A directly affects gene B and vice versa). Gene PHM7 had the most targets, 468; gene YLR152C had the most regulators, 32.

The confirmed regulators and the strong candidate regulator genes for the 13 eQTL with widespread transcriptional effects identified in Yvert et al. (2003) were investigated in this EDN. Amn1, a confirmed regulator gene with widespread influence, was found to be a top cis–trans-regulator with 408 cis–trans-targets. The strong candidate regulator MAK5 with five coding region polymorphisms between the two parental strains had 110 trans-targets. Another confirmed regulator gene GPA1 had 60 targets, about half of which are trans-targets. The genes LEU2 and URA3 had 98 (most were cis–trans) and 32 (most were cis–trans) targets, respectively. The heme-dependent transcription factor HAP1 had 141 targets (100 cis–trans, the others trans).

SEM analysis:

We performed SEM analysis on a subnetwork of the EDN, which was obtained by starting out with 168 genes involved in a cycle and including all genes connected to the cycle genes by up to 3 edges and all the eQTL associated with these genes. The sub-EDN had 265 genes, 241 QTL, 832 gene → gene edges, and 640 eQTL → gene edges. After sparsification using our SEM implementation, the resulting network contained 475 gene → gene edges and 468 eQTL → gene edges. The SEM analysis took ∼110 hr or 4.5 days (total time) on the multiprocessor SGI Origin2000. The network topology is available in our supplemental material, and the yeast subnetwork can be found online in several file formats at http://www.bioinformatica.crs4.org/Members/alf/genetics/.

Table 3 shows the significant biological function groups of the genes in this network. About 41.6% of these genes are involved in catalytic activity, and another 18% are involved in hydrolase activity. All biological functions in Table 3 are significantly enriched in this network.

TABLE 3.

Significant biological function groups of genes in the yeast subnetwork

GO_term	Frequency (%)	Genome frequency (%)	Probability	Genes
Catalytic activity	41.6	26.8	1.50E-07	AAD14 AAD6 ACO1 AKL1 ALD6 AMD2 APN2 ARA1 ARD1 ARP5 AYR1 BDS1 CIT2 COQ5 COX5B DCP2 DIA4 DLD3 DUS3 ECM40 ERF2 EXG1 FET3 FET5 FRE2 GAB1 GCV3 GPA1 GRX5 HIS4 HIS5 HMG1 HMG2 HO HOS4 ICL2 ILV6 KCC4 KTR1 KTR6 LAT1 LEU2 LSC1 LYS2 LYS4 MAP1 MCM6 MET22 MKT1 MSH2 MSK1 MTQ2 MTR3 NFS1 NOP2 NUC1 NUG1 OST2 OST6 PDE1 PDR12 PHO8 PHO85 PLB2 PMA2 POL1 PPZ1 RAD16 RAD52 RAS1 RCK2 RFC4 RFC5 RHO2 RIB3 RPE1 RPM2 RPO41 SAP4 SCO1 SEN1 SHR5 SKM1 PAH1/SMP2 SPO11 SSA4 SUR1 THR4 TIP1 TOP2 TPS1 TRM7 TRP3 TYR1 TYS1 UBP14 UBP16 UGA2 URA3 WRS1 YAL061W RXT2 YEL077C YER138C YER160C YNL045W NMA111 YOL155C YPT53 YPT6
Hydrolase activity	17.8	10.5	0.00026	AMD2 APN2 ARP5 BDS1 DCP2 EXG1 GAB1 GPA1 HIS4 HO HOS4 MAP1 MCM6 MET22 MKT1 MSH2 MTR3 NUC1 NUG1 PDE1 PDR12 PHO8 PLB2 PMA2 PPZ1 RAD16 RAS1 RFC4 RFC5 RHO2 RPM2 SAP4 SEN1 PAH1/SMP2 SPO11 SSA4 TIP1 UBP14 UBP16 RXT2 YER138C YER160C YNL045W NMA111 YOL155C YPT53 YPT6
Transporter activity	9.0	5.6	0.01485	AAC1 AGP2 ALR1 AQR1 ATO2 ATR1 COX5B CRC1 DIC1 HXT2 ITR1 KAP114 LPE10 MCH4 MRS11 PDR12 PHO91 PMA2 POR1 SAL1 TAT1 UGA4 YFL054C YMC2
Oxidoreductase activity	7.9	3.5	0.00066	AAD14 AAD6 ALD6 ARA1 AYR1 COX5B DLD3 FET3 FET5 FRE2 GCV3 GRX5 HIS4 HMG1 HMG2 LEU2 LYS2 SCO1 TYR1 UGA2 YAL061W
Pyrophosphatase activity	6.8	3.5	0.00615	ARP5 DCP2 GPA1 HIS4 MCM6 MSH2 NUG1 PDR12 PMA2 RAD16 RAS1 RFC4 RFC5 RHO2 SEN1 SSA4 YPT53 YPT6
Nucleoside- triphosphatase activity	6.0	3.2	0.01405	ARP5 GPA1 MCM6 MSH2 NUG1 PDR12 PMA2 RAD16 RAS1 RFC4 RFC5 RHO2 SEN1 SSA4 YPT53 YPT6

Data were obtained from the Saccharomyces genome database at http://www.yeastgenome.org/. Column headings from left to right: GO terms, significant GO terms; Frequency (%), frequency of the terms in genes submitted; Genome frequency (%), frequency of the terms in the whole genome; Probability, a score of significance of the terms in the genes submitted; Genes, genes involved in the biological process.

DISCUSSION

We are interested in gene network inference in genetical genomics or systems genetics experiments or more generally in inferring a causal network among DNA markers, expressed genes, disease (sub)phenotypes, and other phenotypes. Due to the very high-dimensional nature of the data we propose a three-step approach: First we perform eQTL analysis that produces a list of cis-regulations, a list of cis–trans-regulations, and a list of trans-regulations. These can be combined into an EDN, or prior to forming the EDN one can perform regulator–target pair selection using local structural models as described here to reduce the number of edges in the EDN and hence the search space for subsequent network inference. Finally, we identify a set of sparser networks within the EDN using SEM analysis.

Our EDN construction and network inference methodology requires the availability of DNA sequence information and it explicitly considers cis-, cis–trans-, and trans-regulation. This approach is most powerful, but it is possible to construct a causal gene network from a genetical genomics data set even in the absence of sequence data, although such an approach should have (much) reduced power. It is of course possible to map eQTL without specifically considering the different forms of regulation, and the power of such an approach can potentially be increased by including e-trait covariates as suggested by Perez-Enciso et al. (2007). Moreover, eQTL mapping permits (some degree of) causal inference even without knowing the candidate regulator genes in an eQTL region (for any two genes G1 and G2 found to interact directly, if eQTL1 affects G1 and G2 but eQTL1 affects G2 only indirectly through G1 and eQTL2 affects only G2, then regulation of G2 by G1 would be indicated).

Our SEM implementation for gene network inference advances current methodology in at least two respects: Current, general purpose SEM software and SEM software for gene network inference (Xiong et al. 2004) can analyze only small numbers of e-traits (∼ <20), and current network inference in genetical genomics has relied on Bayesian network analysis limited to acyclic networks (e.g., Zhu et al. 2004; Li et al. 2005; Lum et al. 2006). Because cycles or feedback loops are expected to be common in genetic networks, it is imperative to investigate alternative methods such as the SEM. Our current implementation of SEM permits inference about cyclic networks with several hundred gene and eQTL nodes.

One possible way to verify the results of our network inference approach would be to check whether the interactions we find also are present in “transcriptional regulatory networks” (e.g., Lee et al. 2002). However, there is (a lot of) genetic regulation beyond transcription factors (Brazhnik et al. 2002) and therefore such comparison may not be very insightful. For example, a recent study (Faith et al. 2007) using gene expression data recovered only 10% of the transcription factor (TF)-to-target relationships known in Escherichia coli, while it found about three times as many interactions that cannot be explained simply through TF-to-regulatory motif sequence binding. The yeast subnetwork studied in this article contains cases of genetic regulation that are beyond transcription factors; these are genes coding mostly for metabolic enzymes (Table 2) and communicating with each other probably through metabolic changes and metabolic effects on gene expression. Interactions in gene networks thus may correspond to causal effects mediated through signal transduction and metabolism, which are hidden variables when studying gene expression alone. Due to the “phenomenological” nature (Brazhnik et al. 2002) (rather than “mechanistic,” such as physical binding of transcription factors to regulatory sequences) of gene networks it is not trivial to compare our findings to currently existing knowledge.

Maximum likelihood is the predominant full-information method for parameter inference in SEM. It is therefore natural to perform a model (structure) search on the basis of an information criterion that is a function of the maximized likelihoods of two competing models. While BIC and BIC(δ) performed satisfactorily in this study, further research into appropriate model selection criteria for large, very sparse networks is required. There is also concern about the validity of BIC for Bayesian network (and hence SEM) inference (Rusakov and Geiger 2005). In our current method, the BIC criterion could be modified to incorporate structure priors that prefer sparse structures and allow dependencies among edges to further reduce the search space (e.g., for a trans-regulation, the regulator gene → target gene edge and the eQTL → target gene edge must both be present or both be absent). The feasibility of a full Bayesian analysis via Markov chain Monte Carlo algorithms must be explored and this work is ongoing. A major advantage of the Bayesian analysis is its ability to incorporate prior knowledge, which we believe to be essential for reliable network inference. For at least some of the edges (regulator–target pairs) in the EDN, there may be prior biological knowledge from various sources, for example, transcription-factor-binding location data, information on pathway relationships (Franke et al. 2006), SNP presence in candidate regulators (Li et al. 2005), and information on protein–protein interactions (Tu et al. 2006). A principled incorporation of such prior knowledge into methods for gene network reconstruction from microarray data has been considered by a few authors (e.g., Imoto et al. 2003; Bernard and Hartemink 2005; Werhli and Husmeier 2007) via prior distributions in Bayesian analysis, which is quite straightforward at least when prior evidence from a given external biological source is available in the form of P-values.

Our SEM model can be generalized to include certain types of interactions: those between an eQTL and a regulator gene jointly trans-regulating a target gene and epistatic interactions between eQTL found in the eQTL analysis and hence included in the EDN. With this model, we can still solve for y_i and assume a normal distribution for the residuals as in Equation 4. Furthermore, we have considered networks with only causal, directed interactions or regulations. However, two genes may be correlated, but there may be no eQTL information available to determine causation. Although such associations could be incorporated via correlations in the residual covariance matrix E in Equation 3, this approach would pose a computational problem, as a nondiagonal E would hinder the likelihood factorization.

Trans-mapping, regulator–target pair identification, encompassing directed network construction, and SEM network sparsification were implemented in C++ programs that we intend to make available after additional modifications and testing on a large real data set.