Soft glassy rheology of supercooled molecular liquids

Abstract

We probe the mechanical response of two supercooled liquids, glycerol and ortho-terphenyl, by conducting rheological experiments at very weak stresses. We find a complex fluid behavior suggesting the gradual emergence of an extended, delicate solid-like network in both materials in the supercooled state—i.e., above the glass transition. This network stiffens as it ages, and very early in this process it already extends over macroscopic distances, conferring all well known features of soft glassy rheology (yield-stress, shear thinning, aging) to the supercooled liquids. Such viscoelastic behavior of supercooled molecular glass formers is difficult to observe because the large stresses in conventional rheology can easily shear-melt the solid-like structure. The work presented here, combined with evidence for long-lived heterogeneity from previous single-molecule studies [Zondervan R, Kulzer F, Berkhout GCG, Orrit M (2007) Local viscosity of supercooled glycerol near T_g probed by rotational diffusion of ensembles and single dye molecules. Proc Natl Acad Sci USA 104:12628–12633], has a profound impact on the understanding of the glass transition because it casts doubt on the widely accepted assumption of the preservation of ergodicity in the supercooled state.

Many liquids fail to crystallize when they are cooled below their thermodynamic solidification temperature (the melting point of the crystal). Instead, these supercooled liquids become enormously viscous, eventually turning into solid glasses when their glass transition temperature T_g is reached. After more than half a century of research, the structural glass transition remains mysterious (1). It has long been clear that glass formation requires cooperation beyond the molecular scale (2) and is intimately connected with inhomogeneities. The nature, length-scale, and time-scale of these inhomogeneities are unknown. One may envision them as frozen-in density fluctuations. They cause deviations from pure liquid behavior and tend to relax by processes known as environmental exchanges. The exchange time scales must be significantly longer than those of the pure liquid. If they exceed experimental times, ergodicity is broken in practice, and the system appears heterogeneous.

Heterogeneity is readily observed in optical experiments on supercooled liquids, notably in light and x-ray scattering (3, 4), polarized hole-burning (5, 6), and single-molecule spectroscopy (7, 8), and it appears to relax slowly. Tracking of individual particles in colloidal glasses (9, 10), as well as computer simulations (11–13), provides further evidence for heterogeneity and confirms that relaxation is driven by collective rearrangements. In parallel, a large body of experimental data (2) from molecular-scale techniques—most importantly NMR (14, 15) and dielectric relaxation (16, 17) spectroscopy—also suggests dynamical heterogeneity, with a length scale that increases upon approaching the glass transition temperature (18). The latter experiments, however, invariably find relaxation time scales comparable with molecular reorientation times (α-relaxation), and length scales of a few nanometers only.

Our group has recently studied the local relaxation of supercooled glycerol, up to 30 K above its glass transition, using single-molecule polarization microscopy (19). The rotational dynamics of individual chromophores provide a nanometer-scale probe of the material in which they are embedded. These experiments showed that different single dye molecules tumble at different rates in the supercooled glycerol in which they are dissolved, with the spread of tumbling times spanning almost one decade. Our most surprising observation was that environmental exchanges were very rare, even over the several hours of a typical measurement. This period is up to approximately one million times longer than the α-relaxation time; i.e., the average tumbling time of a glycerol molecule (19). It is very difficult to reconcile such long exchange times with the picture of a pure liquid, in which all molecules should be equivalent on average. It was therefore suggested (19) that the long memory arises from nearly static structures, which form a fragile solid-like network dividing the supercooled liquid into heterogeneous “liquid pockets.” Such a scenario naturally explains our previous single-molecule experiments, as well as similar studies in another molecular glass former, ortho-terphenyl (OTP) (7). However, the existence of such static structures is completely at odds with the commonly held view of supercooled liquids above the rheological glass transition, in which fast environmental exchanges are thought to quickly erase memory effects, and to restore ergodicity. We therefore performed the rheological experiments reported here to test our hypothesis of the presence of an extended solid-like network in supercooled molecular liquids. As it turned out, we indeed found surprising behavior for both supercooled glycerol and OTP.

An embedded solid network can be expected to lead to non-Newtonian rheology, a behavior that is actually the rule in heterogeneous fluid mixtures, gels, suspensions, emulsions, foams, slurries, pastes, and quicksand, and surprisingly even in simple fluids close to the critical point (20). All of these systems display distinctly non-liquid-like characteristics such as viscoelasticity, yield stress, shear-thinning, and aging—a combination of features known as “soft glassy rheology” (21). Similar properties have furthermore been reported in simulations of Lennard–Jones glasses (22). For the present investigation we chose two archetypal molecular glass formers that were previously studied by single-molecule microscopy (7, 19): glycerol (T_g = 190 K), which is a comparatively strong glass former because of its extended network of hydrogen bonds, and ortho-terphenyl (OTP) (T_g = 244 K), whose structure is governed by weaker van der Waals interactions. We indeed find pronounced non-Newtonian behavior, which manifests itself significantly above the glass transition temperature for both of these materials, and we thus demonstrate that supercooled molecular liquids can exhibit all of the hallmarks of soft glassy rheology. The history-dependent behavior shows that such molecular glass formers already exhibit clear signatures of nonergodic behavior in a significant temperature range above the glass transition temperature.

Results

Viscoelastic Behavior and Yield Stress.

Previous studies of the viscosity of glycerol (23) and OTP (24) throughout the supercooled region down to their respective glass transition temperatures failed to find deviations from Newtonian behavior (apart from the expected observation of viscoelasticity at high frequencies). However, the putative solid-like network is thought to be formed only very slowly, and by limited inhomogeneous compaction of the liquid—not by extended homogeneous crystallization. Therefore, we can expect this network to break or shear-melt at the comparatively large stresses [>1 MPa (23)] that are used in conventional viscosity measurements. Accordingly, we have built a temperature-variable Couette cell that allowed us to apply weak stresses. Furthermore, because the rheological response in yield-stress materials can be highly nonlinear, we did not follow the usual approach of recording the harmonic response with sinusoidal excitation. Instead, to discriminate easily between liquid and yield-stress behavior, we applied constant torques (see Experimental Procedures and SI Appendix for details).

We found that both glycerol and OTP continued to behave as seemingly perfect Newtonian liquids during the initial cooldown—even for the smallest stress we could apply (≈100 Pa), and all of the way down to a few kelvin above their respective glass transition temperatures. The measured viscosities were in agreement with those previously reported (as can be seen in SI Fig. 5 in SI Appendix). However, the emergence of solid-like behavior could be observed in both materials when the temperature was raised again after a significant waiting period, as shown in Fig. 1.

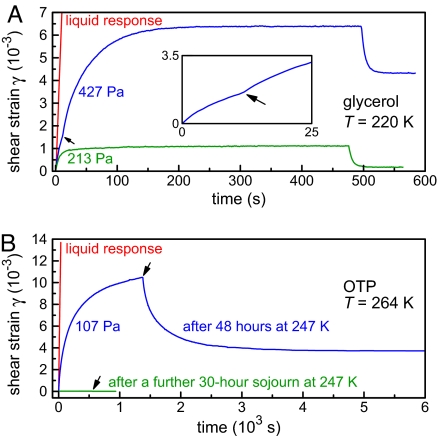
Fig. 1.

Viscoelastic behavior of supercooled glycerol and OTP. (A) Shear strain response of supercooled glycerol at 220 K, induced by the application of a constant shear stress at time 0. The plot shows the liquid-like reaction during the initial cooldown (red line, at 213 Pa shear stress) and the viscoelastic behavior that could be observed after an excursion to 197 K = T_g + 7 K (green curve at 213 Pa; blue curve at 427 Pa). In the case of the latter two curves, the torque was released at ≈470 s, giving rise to a backward spring motion toward the initial position. The data for 427 Pa exhibit a yielding event (marked by an arrow; see also the enlarged view in the Inset), and the initial position is not recovered. (B) Shear strain response of supercooled OTP, measured at 264 K for an applied shear stress of 107 Pa, at three different stages of aging. The red line shows the liquid-like response observed during initial cooldown. After 48 h at 247 K (T_g + 3 K), a clear solid-like response appeared (blue curve). The system sprang back toward its initial position after removal of the applied shear stress (denoted by the arrow). The associated shear modulus was ≈10 kPa, 100,000 times smaller than the shear modulus of crystalline OTP. After the next excursion to 247 K (30 h), the system had become so hard that no response could be measured at 264 K, even at the largest stress we could apply (3 kPa). The associated shear modulus was >10 MPa.

In the case of glycerol, we allowed for aging periods of ≈1 h at 197 K (T_g + 7 K) and then the material was brought to 220 K. We chose this probing temperature for practical reasons; testing flow properties took only a few minutes at 220 K, whereas reaching the same deformation at a given applied torque would have required 130 times longer at 205 K and 4,000 times longer at 197 K. We then repeated this cooling/warming cycle a few times (see SI Fig. 6 and text in SI Appendix), until a clear solid-like behavior appeared: Upon application of the shearing torque, the angle of the inner cylinder reached a quasi-stationary value (see Fig. 1A), which then continued to drift slowly. This observation is the signature of a solid-like connection between the inner Couette cylinder and the outer cup. For larger torques, breaking events occurred at a shear deformation of ≈0.1–0.2%, as Fig. 1A Inset shows, and the rotation angle did not return to its initial value when the stress was released. This points to the expected yield-stress and confirms the considerable nonlinearity of the mechanical properties of the supercooled liquid in this regime, already for low stresses (200 Pa) and small deformations (≈0.1%). Breaking events may arise from shear localization, as found earlier in numerical simulations of glasses (22).

We used the same experimental protocol for OTP, adjusting the parameters to allow for the higher glass transition temperature of OTP (T_g = 244 K) and for the differences in viscosity, which affect the kinetics of the formation of the solid network. Consequently, we cooled the OTP sample down to 247 K, 3 K above the glass transition temperature. After 48 h at 247 K, the temperature was raised to 264 K within ≈1 h and the mechanical properties were tested. Already after <1 h of waiting time at 264 K, the material exhibited a very clear solid-like response, as shown in Fig. 1B. As was the case with glycerol, we found that once the solid response had appeared, the system continued aging and became increasingly stiff, at a rate that strongly depended on temperature. This behavior is very similar to that reported for OTP by Patkowski et al. (3, 4), who detected the scattering signature of a “supercooled liquid with clusters.”

Phenomenological Model.

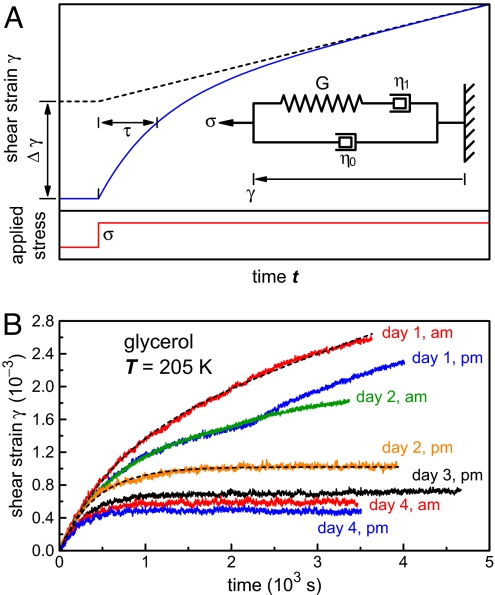
To evaluate the angular traces quantitatively, we fitted them with a simple phenomenological model (see Fig. 2A). We think of the aged supercooled liquid as a solid-like network that responds elastically for small deformations, and that is embedded in a viscous fluid. A movement of the inner cylinder in the Couette cell gives rise to two torques: a viscous one from the surrounding fluid, and an (initially) elastic one from the solid network. The solid network will soon undergo microscopic rearrangements and will yield for large enough deformation. We represent this plastic deformation as another viscous response. As a first-order approximation, we neglect a possible strong dependence of this effective viscosity on the applied stress (see next section, Fig. 4). We therefore represent the solid network as a spring and a dashpot in series (adding deformations), and this viscoelastic system itself is placed in parallel (adding torques) with a dashpot representing the liquid, as shown in Fig. 2A. In the spirit of a mean-field approximation, we consider the whole system as a collection of identical cells, all of them with the same elastic modulus and effective viscosities. This oversimplified model obviously fails to represent individual breaking events. The shear strain response γ(t) of the model to a constant stress σ applied at time 0 is easily found to be a superposition of a linear drift in a fluid with a total effective viscosity η = η₀ + η₁ (the sum of the viscosity η₀ of the liquid and of the effective viscosity η₁ of the network), and of an exponential transient:

The latter term corresponds to stretching the springs of the solid-like network, represented by the shear rigidity modulus G, in the surrounding liquid; this process has a characteristic response time τ:

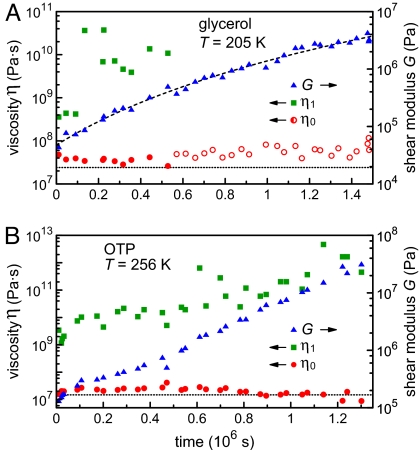
Fitting the experimental trajectories with this model gave us the three rheological parameters of the material, η₀, η₁, and G, at every temperature and any stage of the aging process. Some examples of fitted traces are shown for glycerol in Fig. 2B. We then followed the aging of glycerol at the constant temperature of 205 K for >2 weeks. The evolution of the three parameters G, η₀, and η₁ during this period is presented in Fig. 3A. The effective viscosity η₁ was often difficult to determine at later stages of the aging process because experimental drifts overwhelmed the weak creep signal. Moreover, η₁ strongly depended on the applied torque. We nevertheless indicate several values of η₁ in Fig. 3A to give a feeling for the large increase of effective viscosity correlated with the increase in stiffness of the network. In contrast, the viscosity η₀ was found to be constant within experimental error and consistent with the viscosity of supercooled glycerol obtained in previous rheological measurements (23). This result suggests that the solid network remained a minor component of the fluid throughout our study of Fig. 3A. The most remarkable feature is the large increase of the shear rigidity modulus G, by two orders of magnitude over 2 weeks at 205 K. At the end of this measurement run, the shear modulus had reached ≈1 MPa, a value that is, however, still more than three orders of magnitude lower than the modulus of crystalline glycerol (25).

Fig. 2.

Rheological response of a solid-like network that is embedded in a liquid. (A) Phenomenological model for the quantitative evaluation of rotation traces, from which three parameters are deduced: the shear modulus G of the solid network, the viscosity η₀ of the embedding liquid, and the effective viscosity η₁ representing plastic deformation of the solid network. The constant shear stress σ is suddenly applied at time 0. The expression of the characteristic time τ is given in the text, and the strain amplitude Δγ is the prefactor of the exponential term in Eq. 1. (B) Examples of strain traces acquired during the aging and hardening of glycerol, induced by the application of a constant shear stress σ = 107 Pa at time t = 0. The plot shows data taken during the first 4 days of an observation period of 2 weeks. The traces were fitted with Eq. 1 resulting from the model described in A, except when breaking events occurred (e.g., day 1, p.m.). The dashed lines give two examples of these fits to the data.

Fig. 4.

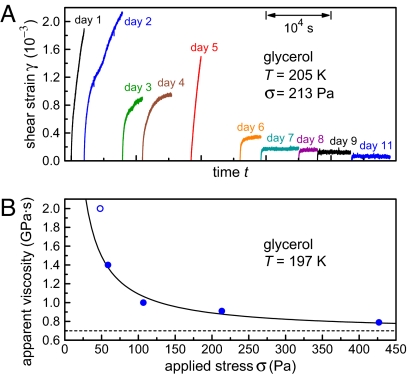
Shear thinning and rejuvenation of supercooled glycerol. (A) Hardening of glycerol at 205 K, which is interrupted by temporary rejuvenation due to the application of a large shear stress (day 5). (B) Shear thinning at 197 K due to the application of increasingly larger torques. The dashed line represents the literature value.

Fig. 3.

Aging of glycerol and OTP. (A) Aging of the shear modulus G (right y-axis) and of the viscosity parameters η₀ and η₁ (left y-axis) of glycerol at 205 K as functions of time over a period of 2 weeks. Note that the system already presented a weak shear modulus at the beginning of the measurements. The values of the effective viscosity η₁ (squares) depend on the applied stress (see Fig. 4). The measurements up to 5 × 10⁵ s were done at a shear stress of 107 Pa (filled circles representing η₀), and later measurements at 213 Pa and 427 Pa (open circles). The dotted line corresponds to the viscosity derived from the liquid response at large stress, which is close to the literature value. The dashed curve, drawn through the shear modulus data points (triangles) as a guide to the eye, is a fit by a power law of time, G(Pa) = 10^−18.5 × [t(s) + 750,000]^3.9. (B) Aging of OTP over a period of 2 weeks at 256 K. The plot shows the evolution of the viscosities η₀ (circles, left y-axis) and η₁ (squares, left y-axis), as well as of the shear modulus G (triangles, right y-axis). The dotted line denotes the viscosity value derived from the liquid response during initial cooldown, which is in agreement with previous measurements.

Similarly, we followed the rheological response of the OTP sample as it aged over a period of >2 weeks at a temperature of 256 K. The three parameters G, η₀, and η₁ were again fitted using the model described in Fig. 2; these data are shown in Fig. 3B. As with glycerol, the liquid viscosity η₀ of OTP was comparable with the literature value and with our measurement of the viscosity of the non-aged sample at that temperature (≈10 MPa·s). We again found a pronounced stiffening: The shear modulus increased by more than two orders of magnitude in ≈14 days and did not yet seem to saturate at the end of the measurement. However, the maximum value of ≈10 MPa is still two orders of magnitude smaller than the shear modulus of crystalline OTP. The measurements were stopped at that point because, at the maximal torque we could apply, the accuracy of our rheometer was not sufficient to measure smaller deformations.

Shear Thinning and Rejuvenation.

We have seen that, when left undisturbed, supercooled glycerol hardens over time, but it shows shear-thinning when strongly perturbed. Fig. 4A presents a different run of aging experiments, again indicating hardening at 205 K for days 1–4. On day 5, we applied large shears to the sample (>10 times the shear previously used for probing) for several minutes. After this strong perturbation, the material presented a liquid-like response with a large amplitude, indicating that the solid connection had been disrupted, possibly by shear banding. This trace was very similar to that of day 1, illustrating the phenomenon of rejuvenation by a strong strain [such shear rejuvenation phenomena are currently attracting interest in other complex fluids as well (26, 27)]. Nevertheless, if the system is left unperturbed, the solid connection can heal quickly; in our case, the hardening process had resumed already during the night between days 5 and 6. Because of experimental limitations in the applied torques, we could not test whether the memory of previous aging can be erased permanently by sufficiently energetic stirring.

Fig. 4B documents another manifestation of shear thinning. The apparent (total) viscosity of the material during the first waiting period at 197 K after the first cooldown is measured by the long-time drift of the inner cylinder under an applied torque. If the torque is increased, the apparent viscosity decreases. We can provide a first-order description of this effect with the following mean-field model: Consider a typical hydrogen bond in the solid network, and suppose that this bond can break under stress or under thermal fluctuations and can also reform with rate k_r, possibly at a different place. According to Kramers theory of passage of an activation barrier (28), the rate of bond opening k_o is modified by the application of an external force F according to

where a is a characteristic bond length, k_B is the Boltzmann constant, and K is the rate in the limit of F → 0. Upon deformation of the solid network, an average force develops from stretching of the network's springs represented by the shear-modulus G. This force acts only during the periods when the bond is closed. The average force, proportional to the deformation rate γ̇, can be represented by an effective viscosity η₁:

which decreases exponentially with the applied force. However, we have to realize that the force F that acts on the solid network (see the model described in Fig. 2A) is not exactly the applied total force F_t. The difference arises because the network is yielding and there is an additional viscous force from the liquid component. According to the model, F and F_t are indeed related by

In this expression, the viscosity η₁ itself depends on the force F according to Eq. 4. Together, Eqs. 4 and 5 lead to an implicit equation for the effective viscosity. The exact solution of these equations for forces much larger than k_BT/a shows that the effective viscosity varies approximately as 1/F_t; i.e., much slower than the exponential decay of Eq. 3. This approximation has been used to fit the experimental data in Fig. 4B (filled circles). It correctly predicts an asymptotic approach to the viscosity of the liquid for a large applied force (dashed line; value taken from ref. 23) and a slow algebraic decay of the effective viscosity. (The data point for the lowest torque—i.e., the open circle in Fig. 4B—is less reliable, being close to our instrumental limit. This point has therefore been disregarded in the fit.)

Discussion

The crucial feature of our experiments is that, once supercooled glycerol and OTP have been kept for some time at temperatures slightly above the glass transition, they show a combination of liquid- and solid-like behaviors: Our force response measurements reveal that, in addition to the expected viscous response, there is a small elastic component whose strength increases steadily with time. The typical shear rigidities that we found were considerably smaller than those of the crystalline materials: the shear rigidity modulus always stayed at least three orders of magnitude below that of the crystal for glycerol, and at least two orders of magnitude for OTP. We could measure such weak shear rigidities because we allowed the systems to age and then perturbed them only weakly and rarely. Presumably, in typical viscosity measurements with conventional oscillatory rheometers, a delicate solid-like network is either shear-melted or prevented from forming altogether. We have been able to shear-melt the network by subjecting it to sufficiently large torques. Their initial fragility explains why such solid-like structures have not been reported earlier.

Observation of these signatures of a solid-like network in the macroscopic properties of these glass formers is in agreement with the evidence for long-lived structural heterogeneity on the microscopic scale. Previous studies of single molecules embedded in supercooled OTP (7) and glycerol (19) reported that the probe chromophores locally experience a liquid environment but that they display a large spread of rotational correlation times. The environment of each individual molecule appeared static over time scales that are long compared with both the rotational correlation time of the probe and the α-relaxation time of the host. This effect was most dramatic for glycerol, with the memory time being at least five orders of magnitude greater than the rotational correlation time of the dye and more than a million times longer than the α-relaxation time of glycerol. The combined experimental evidence on microscopic and macroscopic scales inevitably leads one to conclude that, after a temperature quench to a few degrees above T_g, supercooled molecular liquids can develop a fragile solid-like elastic matrix that encloses liquid pockets. This scenario was proposed earlier to explain the aforementioned single-molecule results (19); it is completely consistent with the rheological measurements presented here. The picture that thus emerges is that a supercooled molecular liquid can phase-separate into locally liquid and solid-like regions, leading to the emergence of solid-like yield stresses and elastic moduli, which build up over temperature-dependent time scales. As conjectured earlier (29), we find that a supercooled liquid can exhibit soft glassy rheology well above T_g, and that the onset of this rheological behavior coincides with the appearance of structural heterogeneity, reminiscent of that found in computer simulations (30) and colloids (9), but associated here with such an extreme separation of scales that ergodicity is effectively broken tens of degrees above the glass transition temperature.

Although phase separation is normally characterized by ever-increasing length scales as the domains of each phase coarsen, this apparently is not the case in the systems we investigated. A natural interpretation of this observation is in terms of frustration—a geometric frustration as proposed by Tarjus et al. (31), a dynamic frustration, or both. Such frustration limits the size that domains can attain and, in an equilibrium system, can indeed lead to an “avoided critical point.” In practice, dynamical arrest will most likely be important: It is natural to assume, and consistent with light scattering, that the two phases will have different densities. Therefore, any mass transport required for phase separation will be prohibitively slowed down because of the high viscosity and reduced pore size. This scenario indeed agrees with our observation that the aging of the network (which we infer from its increasing shear modulus) proceeds slower at lower temperatures. In this picture, the previously reported broad distribution of single-molecule rotational diffusion times (7, 19) reflects the differences in densities in the various liquid pockets, as well as, possibly, the pocket size.^¶ The ratio Dη/T should be constant if the Stokes–Einstein relation holds, but is found to increase sharply as one approaches the glass point (32). This increase is naturally explained by the large dispersion of local viscosities. The average mobility determination of D is biased toward the fastest molecules in the low-viscosity liquid lakes, whereas the average viscosity favors the slowest molecules in the high-viscosity lakes (32). With solid-like parts, this difference between the two averages becomes extreme. This description is similar to Bouchaud's concept of self-inhibitory dynamics in glasses and granular materials (33), in which an important ingredient is the postulated local conservation of free volume. Free volume conservation would naturally follow from an effective sealing of local areas by a solid-like structure. A related picture is provided by the defect-diffusion model of Shlesinger and colleagues (34), according to which different amounts of free volume can be trapped in different mobility islands. In first approximation, we can relate the concentration of free volume in each island to a local pressure. From the change of the average viscosity with pressure (35) and the spread in local viscosity uncovered in the single-molecule measurements (19), we can estimate the variation of the local pressure to be ≈1–2 bar for glycerol.

Neither the typical scale nor the short-range structure of the solid-like network can be determined directly from our present experimental results. However, the above picture implies long-lived density fluctuations, which should be visible in light-scattering experiments. Indeed, a large excess of Rayleigh-scattered light compared with Brillouin-scattered light has been observed in the spectra of OTP (4, 36) and other molecular glass formers. Ultrasmall-angle x-ray scattering (3) indicates the presence of slowly relaxing density fluctuations on even smaller scales. The combined evidence from all of these experiments points to a broad range of scales for the density inhomogeneities, from ≈10 to at least a few hundred nanometers, with extremely slow relaxation—up to a million times slower than α-relaxation processes. Furthermore, the excess light scattering depends on the thermal history of the sample, similar to what we observe for the viscoelastic response. [Careful sample preparation and handling can produce specimens in which the excess light scattering is absent or in which its occurrence is significantly delayed (4).] Although these light scattering results are thus largely consistent with our measurements (which probe both smaller and larger length scales), their interpretation in terms of isolated clusters in a liquid phase (1, 3, 4, 36) is not supported by the gradual build-up of a finite shear rigidity that we observe. Instead, our results imply the existence of a continuous, system-spanning network (37) that ages over time, as was discussed above. Future study of more supercooled liquids will show whether this feature is generic for molecular glass-formers, or even for glasses in general.

It is noteworthy that extrapolation of the spread in tumbling times of our single-molecule data to higher temperatures suggests that the heterogeneity of the liquid pockets disappears at a temperature somewhat below 1.2 T_g (19). In other words, this type of behavior is found approximately in the same temperature range T_g < T < 1.2 T_g in which fragile glasses are known to show strong non-Arrhenius behavior. One has to wonder whether this is just a coincidence or the signature of a characteristic property of the supercooled state. In addition to exploring this behavior systematically as a function of temperature and aging for various materials, an important issue for future research is therefore whether the rheological anomalies studied would fail to appear or to grow above some temperature around 1.2 T_g. Furthermore, these findings may also clarify a puzzling feature of mode-coupling theory (MCT), its prediction of a sharp transition to a nonergodic kinetically arrested phase at a critical temperature T_c significantly larger than T_g, sometimes called the “best-known failure” of MCT (38). Our experiments suggest that this supposed failure may only reflect the inadequacy of the widely assumed ergodicity and uniqueness of the metastable supercooled liquid above T_g. They suggest that the main problem may lie in the association of T_c with T_g. Our results show that both supercooled glycerol and supercooled OTP can exhibit all of the features commonly found in the soft glassy rheology of a complex fluid: flow, rigidity, yield stress, aging, rejuvenation, and shear melting. Rather than either flowing or breaking, these supercooled liquids actually flow and break at the same time, and they do so already at temperatures significantly above their respective glass transition temperatures.

Experimental Procedures

Sample Preparation.

Anhydrous glycerol (specified to contain <0.1% water) was used as obtained from Sigma–Aldrich, transferred from the newly opened bottle into the Couette cell as quickly as possible, and then purged repeatedly with dry helium gas. Ortho-terphenyl purissimum (Fluka; purity >99%) was distilled twice before usage. All rheological samples were kept under a dry helium atmosphere for the duration of the experiments.

Design of the Couette Cell.

The rheology experiments were conducted with a variable-temperature Couette cell, in which a sample film filled the gap between an inner cylinder and an outer cup. Torque was applied to the cylinder by means of a torsional spring, and the viscoelastic response of the sample was deduced from the subsequent movement of the cylinder, which was recorded via the deflection of a laser beam. Additional experimental details can be found in SI Appendix.