Absence of equilibrium cluster phase in concentrated lysozyme solutions

Abstract

In colloidal systems, the interplay between the short range attraction and long-range repulsion can lead to a low density associated state consisting of clusters of individual particles. Recently, such an equilibrium cluster phase was also reported for concentrated solutions of lysozyme at low ionic strength and close to the physiological pH. Stradner et al. [(2004) Equilibrium cluster formation in concentrated protein solutions and colloids. Nature 432:492–495] found that the position of the low-angle interference peak in small-angle x-ray and neutron scattering (SAXS and SANS) patterns from lysozyme solutions was essentially independent of the protein concentration and attributed these unexpected results to the presence of equilibrium clusters. This work prompted a series of experimental and theoretical investigations, but also revealed some inconsistencies. We have repeated these experiments following the protein preparation protocols of Stradner et al. using several batches of lysozyme and exploring a broad range of concentrations, temperature and other conditions. Our measurements were done in multiple experimental sessions at three different high-resolution SAXS and SANS instruments. The low-ionic-strength lysozyme solutions displayed a clear shift in peak positions with concentration, incompatible with the presence of the cluster phase but consistent with the system of repulsively interacting individual lysozyme molecules. Within the decoupling approximation, the experimental data can be fitted using an effective interparticle interaction potential involving short-range attraction and long-range repulsion.

The arrested dynamics of colloidal systems and protein solutions interacting via short-range interactions have been actively studied both theoretically and experimentally in recent years (1–4). The mode coupling theory and molecular dynamics (MD) simulations have successfully unified seemingly dissimilar dynamical arrest scenarios in colloidal systems (4, 5). In addition to the conventional glassy state induced by the packing constraints, the presence of short-range attraction leads to a different glassy behavior. The apparently diverse type of dynamical arrest, such as gelation, jamming, glassification or non-ergodicity transition, etc., found in attractive systems can be unified in terms of this attractive glass transition (3). As competing short-range attraction and long-range repulsion are introduced, additional features are observed (5). In particular, at intermediate volume fractions, the colloidal particles can form an equilibrium cluster phase, which in turn stabilizes a low-density arrested state (6). This type of particle clustering process at low volume fractions has been observed for various colloidal systems (7–9).

Although the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory successfully describes the microstructure and equilibrium phase behavior of charged colloidal systems over a wide parameter space (10), concentrated protein solutions present a more complicated case. First of all, the distinct separation between electrostatic and dispersion forces is questionable (12), and the matter is further complicated by the asymmetric distribution of surface charges and patchy hydrophobic regions on a globular protein molecule (11). The electrostatic repulsive interactions can be treated approximately by a screened Coulomb potential, but the short-range attraction is modified by the presence of other effects such as hydration forces (10). The relative strength of these interactions can be tuned by varying the salt concentration or pH or temperature (13). In addition, the interaction potential between the globular proteins is softer than the hard-sphere type interactions assumed in model colloidal systems (10). As a result, protein solutions offer a rich variety of conditions to test the predictions of computer simulations (5), and, in particular, specific ion effects cannot be explained by DLVO theory (11).

Small-angle scattering of X-rays and neutrons (SAXS and SANS) is an effective method to study the structure and interactions of macromolecular solutions (14). The scattering intensity from an interacting suspension of globular particles measured as a function of momentum transfer [q = (4π/λ) sin(θ), where 2θ is the scattering angle and λ is the wavelength] can be written as (15, 16)

Here, N is the number density of particles, Δρ and V are their average scattering contrast and volume, respectively. The form-factor, 〈P(q)〉, the averaged particle scattering over the ensemble of sizes and orientations, is related to the particle structure. The effective structure factor, S_M(q), provides information about the interparticle interactions in solution and for very dilute solutions of noninteracting particles, S_M(q) ≈ 1. For a concentrated system, S_M(q = 0) is proportional to the osmotic compressibility and it decreases with the concentration (c). In addition, S_M(q) displays a peak at small angles, and the position of the peak q_M is related to the average distance between the neighboring particles, d ≈ 2π/q_m. In contrast, when particles attract each other, they could form clusters or aggregates, which are manifested by an increase of S_M (0), being proportional to the mean cluster mass and number density (17). For a nonaggregating system, q_m increases with c and the low angle peak in S_M(q) moves to higher q values. SAXS and SANS are widely used to study interactions in protein solutions, e.g., at the onset of crystallization (18–21).

Recent SAXS and SANS studies pointed to the presence of an equilibrium cluster phase in salt-free concentrated solutions of lysozyme at moderate pH (1). These solutions expectedly revealed largely repulsive interactions showing an interaction peak in S_M(q) but, unexpectedly, the position of this peak did not appear to move with concentration. This result was interpreted as aggregation of lysozyme molecules into small clusters with the aggregation number (up to 10) increasing with concentration such that the peak revealed the distance between the clusters, and not individual molecules. This publication prompted a series of related studies yielding interesting albeit sometimes conflicting results (2, 16, 22, 23). SANS investigations of cytochrome c and lysozyme solutions suggested not only cluster peak but also indicated an intensity upturn near q = 0 attributed to weak long-range attraction (2). The corresponding static structure factor was modeled by an effective potential involving two Yukawa terms pertaining to intermediate range repulsion and a long-range weak attraction (2, 16). The upturn near q = 0 was subsequently shown to be caused by impurities in the sample (22), and this issue was further discussed in ref. 23. Indications of equilibrium clusters were also recently reported in insulin solutions, even at low protein concentrations (24). The cluster formation in lysozyme solutions was subsequently analyzed by MD simulations using a Lennard–Jones (LJ) potential for short-range attraction and Yukawa long-range repulsion, and the results were correlated with the effective structure factor obtained by the scattering experiments (25).

The experimental proof for the cluster phase relies on the original SAXS/SANS finding (1) that the interference peak does not shift with concentration. A thorough inspection of the original data (1) reveals some inconsistencies. Most notably, the I(0) values of the lysozyme solutions appear to significantly decrease with increasing protein concentration. Given that I(0) is proportional to the coherently scattering volume, clustering should have led to the opposite effect, namely an increase of I(0) (see also above discussion after Eq. 1). Although the observed decrease might, in principle, be explained by repulsive interactions between the clusters, such repulsion would have to be unexpectedly strong, especially given the dynamic nature of the clusters and the limited surface charge density of lysozyme near physiological pH (26). Furthermore, for a system with clusters and interactions between them, the structure factor in Eq. 1 should have been determined after appropriately taking into account the form factor of these clusters and not just of the individual lysozyme molecules, as has been done in refs. 1, 2, and 16. Also, the theoretical fits computed in ref. 27 reported the volume fraction of the clusters in solution coinciding with that of the protein itself. However, if proteins had aggregated into (even densely packed) clusters, the latter should inevitably contain significant amounts of solvent, and the apparent volume fraction of the clusters should have been significantly different from that of the protein. To resolve these controversial issues, we have repeated the scattering experiments on lysozyme following the procedures described in ref. 1. The measurements were performed on state-of-the-art high brilliance and high-resolution SAXS and SANS instruments to ensure reliable detection of the peak position. A broad range of concentrations, temperatures, and solvent conditions were explored, and several lysozyme samples were prepared independently from material of different suppliers. All SAXS and SANS experiments on low-salt lysozyme solutions reproducibly yielded interference peaks shifting to larger q with increasing protein concentrations. The experimental data thus display no evidence of equilibrium clusters and, instead, the scattering patterns are fitted by considering a system of individual lysozyme particles with an effective interaction potential consisting of short-range attraction and long-range repulsion terms.

Results

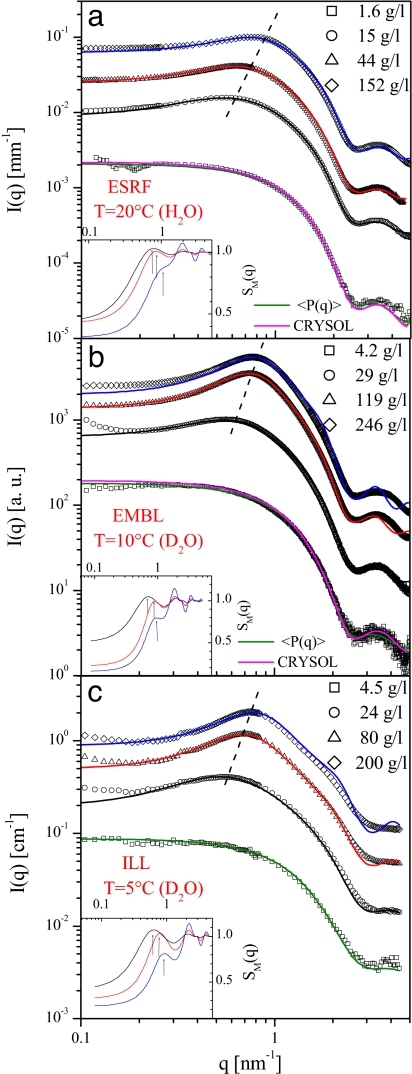
Multiple series of SAXS and SANS measurements were performed at various conditions and Fig. 1 summarizes typical and representative results for the salt-free solutions at pH 7.8. The three concentration series were collected on different instruments at different temperatures, in H₂O (ESRF) and D₂O (EMBL, ILL) solutions. The scattering patterns at the lowest concentrations exhibit negligible interference effects and are adequately described by the computed scattering from the atomic model of lysozyme (28), confirming that the protein is monomeric at low concentrations. At elevated concentrations (>15 mg/ml), interference peaks are observed close to q = 0.8 nm⁻¹, which become more pronounced with decreasing temperature. In all cases, the peak clearly and systematically moves toward higher q values with increasing concentration. This, of course, is also evident in the effective structure factors S_M(q) obtained after division of the experimental data by the computed form factor from the fits to the low concentration data. We deliberately present here the raw experimental data to demonstrate that the peak shift is observed without any additional operations. The data and the structure factors for the sets in Fig. 1 are also shown in double logarithmic scale in supporting information (SI) Fig. 5.

Fig. 1.

Scattering intensities from salt-free lysozyme solutions at pH 7.8 for different concentrations recorded on three SAXS/SANS instruments. Symbols, experimental data; continuous lines, computed fits. Green lines, the form factor; pink lines, crystallographic model, blue, red, and magenta lines, fits to higher concentration data using Eq. 1 with parameters listed in Table 1. The dashed line indicates the evolution of the interference peak. (Insets) The computed structure factors indicating the position of the first low q peak.

The experimental data can be fitted within the decoupling approximation by using an effective interaction potential between the individual lysozyme molecules consisting of short-range attraction and long-range repulsion terms (see Materials and Methods). The fits are displayed in Fig. 1, and the parameters are given in Table 1. As expected, the effective attraction increases with decreasing temperature, whereas the repulsive parts remain nearly temperature-independent and the system stays repulsive above 5°C. Over the concentration range studied, lysozyme exhibits a liquid–liquid phase separation at lower temperatures (13). This phase behavior could lead to a more complicated scattering dependence than that described by Eq. 1. The data sets taken at 20°C, well above the liquid–liquid coexistence region, are thus adequately fitted. Close to the critical concentration (≈240 g/liter), additional contributions to I(q) arise from the critical fluctuations for the temperatures approaching the liquid–liquid phase separation. The higher concentration fits at 10°C and especially at 5°C display therefore some systematic deviations at higher angles (but, notably, not in the range of the first maximum corresponding to the average nearest neighbor distance). The computed structure factors of the best fits displayed as insets in Fig. 1 and also in SI Fig. 5 unambiguously reveal a pronounced shift of the first maximum toward higher q with increasing concentration.

Table 1.

Fit parameters for the scattering data from salt-free lysozyme solutions at pH 7.8

c, mg/ml	φ	T, °C	K1, kBT	K2, kBT	σ/Z1, nm	σ/Z2, nm	κ−1,* nm
ESRF
1.6	0.001	20
15	0.012	20	8.00	3.20	0.260	2.94	2.98
44	0.033	20	8.20	2.60	0.24	1.74	2.24
152	0.12	20	9.80	2.30	0.16	1.04	1.40
EMBL
4.2	0.003	10
29	0.022	10	13.00	4.00	0.36	1.92	2.49
119	0.090	10	14.00	3.50	0.16	1.42	1.50
246	0.186	10	16.00	3.10	0.15	1.14	1.09
ILL
4.5	0.0034	5
24	0.018	5	8.48	2.00	0.43	3.23	2.61
80	0.060	5	10.28	2.45	0.28	1.73	1.75
200	0.151	5	9.90	2.22	0.23	1.24	1.19

c and φ, protein concentration and volume fraction, respectively; T, specimen temperature; K₁, K₂, σ/Z₁, σ/Z₂, κ⁻¹, and Z are parameters describing the interaction potentials (see Methods).

*Net charge Z = +8e.

All of the fitted parameters in Table 1 describing the behavior of the system have physically reasonable values. Thus, the interaction peak is described by the known volume fraction of the proteins in solution. The apparent range of repulsive interaction decreases with concentration, which can be attributed to the elongated shape of the protein molecule (higher probability of side-by-side type interactions at elevated concentrations). The value of the screening length corresponds to the net buffer ionic strength of 6 mM, is in agreement with the net charge of the protein known from titration experiments to be about +8e (26) at the pH used.

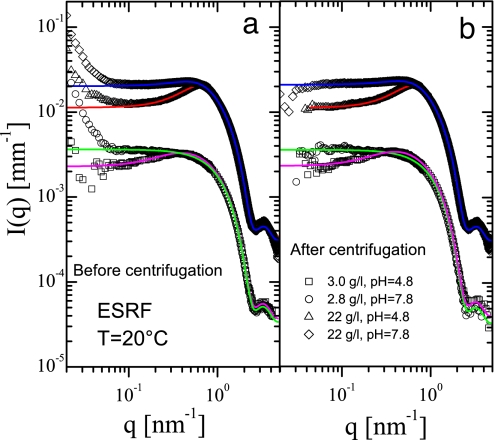
Some scattering patterns in Fig. 1 display an intensity upturn at low q region pointing to the presence of large aggregates, as also been observed in earlier SANS studies (2, 23). In agreement with ref. 22, these aggregates were removed by centrifugation (9,500 × g for 30 min), without noticeable alterations of the scattering at high q values, and, accordingly, without significant change in the fit parameters (Fig. 2 and SI Table 2). The intensity upturn is less pronounced at lower pH when the system becomes more repulsive (Fig. 2), further confirming that this excess intensity arises due to permanent aggregates. The main interaction peak at pH 7.8 is less pronounced as compared at pH 4.8 due to decreasing protein surface charge weakening the electrostatic potential (SI Table 2).

Fig. 2.

Effect of centrifugation on the low q excess intensity for two different lysozyme concentrations and pH values. The continuous lines display the calculated fits using Eq. 1 (parameters are listed in SI Table 2). (a) Before centrifugation. (b) After centrifugation.

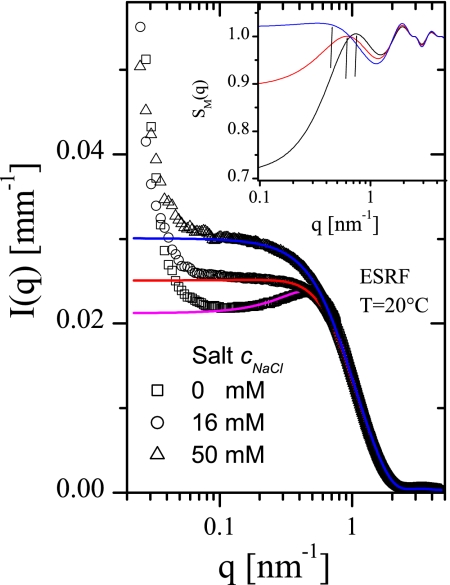
Further SAXS and SANS measurements were performed to study the influence of the ionic strength of the buffer and temperature on the interaction peak. Addition of NaCl, as expected for an electrostatically stabilized system, diminishes the magnitude of the interaction peak (Fig. 3). The computed fit parameters display decreased repulsive interactions, whereas the attractive interactions show a small increase, which can be attributed to a specific counterion effect (SI Table 3). For the given protein concentration in a salt-free buffer, the interaction peak moves to lower q values with decreasing temperature (SI Fig. 6). The main cause of the shift is an increase in the attraction while the repulsive part remains nearly unchanged (SI Table 4). At sufficiently strong attraction, the system would show phase separation (13, 29).

Fig. 3.

Effect of the NaCl addition on the scattered intensities at pH 7.8 and c = 22 g/liter. (Inset) The fitted structure factors indicating the position of the interference peak. Continuous lines indicate calculated fits using Eq. 1 (parameters in SI Table 3).

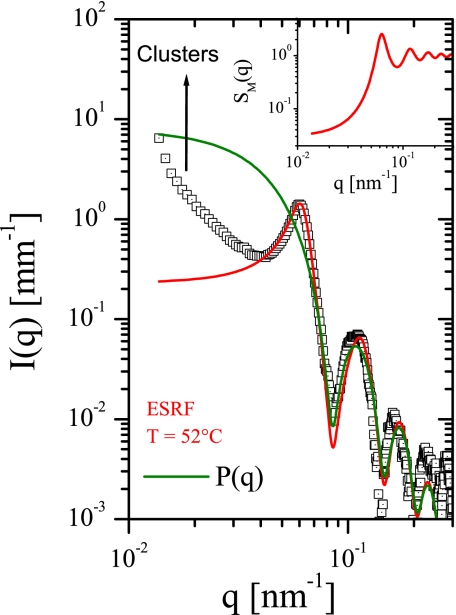
To illustrate a typical scattering signature of a system containing clusters of colloidal particles, Fig. 4 presents the scattering from a suspension of polystyrene latex particles (volume fraction φ ≈ 0.009) in a quasi-binary mixture of 3-methyl pyridine (3MP), H₂O and D₂O above its aggregation temperature. This system is known to exhibit a thermally reversible aggregation near the phase separation temperature of the solvent mixture (7), which, in this case, is >52°C. The evolution of the interparticle attraction near this aggregation temperature can be modeled in terms of a short-range attractive potential alone (30). Interestingly, the obtained value of φ = 0.46 corresponds to an effective volume fraction of the latex particles within the clusters, which is much higher than the bulk value of φ (≈0.009). In addition, the low q region shows the power law scattering, a typical feature of scattering by these aggregates (30). In contrast, the interaction peak in lysozyme samples (Fig. 1) is fully described by the bulk volume fraction of protein and the data do not display any power-law scattering signature of the clusters. The excess scattering at low q region, as demonstrated in Fig. 2, is due to the permanent aggregates, which are not directly related to the interaction peak (the latter stays unchanged also after the removal of these aggregates).

Fig. 4.

SAXS intensity from a suspension of polystyrene latex particles in the binary mixture of 3-methyl pyridine with H₂O/D₂O revealing the fingerprint of equilibrium clusters. The form factor 〈P(q)〉 is the scattering from a system of spheres with radius 52.6 nm and polydispersity 4% (green line). Red line, the computed fit using Eq. 1 with parameters σ = 109 nm, φ = 0.46, Z₁ = 8, and K₁ = 1.2 k_BT. The structure factor S_M(q) is displayed in the Inset.

Discussion

The presence of an equilibrium cluster phase in concentrated protein solutions would have had important biological significance, especially in protein stability and aggregation, as well as related diseases. Indeed, controllable short-range attraction and long-range repulsion is central to self-assembly processes in biological systems, in particular, protein crystallization occurring in the attractive regime of interparticle interactions (31–33). Aggregation-prone proteins seem to exhibit a similar very deep attractive potential (≈50 k_BT) as opposed to stable globular proteins (24). A recent SAXS study on amyloidogenic insulin (24) suggests that an equilibrium cluster phase may exist in such proteins, though the concentration and angular range of the experimental data are limited.

A natural question arises: why was the shift of the interference peak not observed in the publications reporting the equilibrium cluster phase in lysozyme? First, we must state that the differences cannot be attributed to the sample preparation procedures. We have precisely followed the protocols described in the original publications (1, 22) and used a total of six different lysozyme batches from four commercial product codes, including the same one (Sigma/Fluka lysozyme code L7651) used in refs. 1 and 22. The solutions were repeatedly washed and filtered to remove ionic impurities, and control measurements on other purchased proteins and differently prepared samples reproducibly yielded very similar results. Multiple series of experiments were performed specifically to compare the samples prepared with and without pH adjustment after the sample preparation, with and without repeated washing and/or dialysis of the protein solutions, and conductivity was measured to independently monitor the ionic strength. All these measurements displayed the same peak shifts with concentration (see examples in SI Figs. 7 and 8). Secondly, one might ask whether the resolution of the SAXS/SANS instruments played a role. The previous studies (1, 2, 22) were done either on x-ray sources or neutron instruments with relatively low flux and resolution, whereas we present the x-ray and neutron data from high resolution experimental stations. The smearing of the data in the previous work might have made the shift in peak position less detectable. In our opinion, however, this shift should have been observed also on low resolution instruments. In fact, visual inspection of the x-ray data from lysozyme at 30°C given in figure 2b of ref. 22 reveals a noticeable peak shift toward higher q values with increasing concentration, similar to that presented in Fig. 1, which was not commented in ref. 22.

It should also be noted that most of the measurements in refs. 1 and 22 were apparently performed at conditions close to the liquid–liquid phase separation. Although these conditions (low temperature and high concentration) lead to most pronounced interference peaks, the scattering from the critical fluctuations may complicate the interpretation, because Eq. 1 is not fully adequate in these cases. However, our results demonstrate that clear peak shifts are observed both far from and close to the liquid–liquid phase separation conditions.

Conclusion

We have repeated the SAXS and SANS experiments on concentrated lysozyme solutions at exactly the same conditions as those reported in recent publications (1, 22). In contrast to the latter results, the interference peak due to the repulsive interactions displayed a clear trend toward higher q values with increasing protein concentration. Several experimental sessions were performed in H₂O and D₂O buffers using different protein batches, different high resolution instruments and under varying experimental conditions (temperature, concentration, ionic strength, pH). In all cases, the appearance and behavior of the interference peak is adequately and consistently described by the form and structure factors of individual lysozyme particles using an interaction potential involving short-range attraction and long-range repulsion. Therefore, our data did not reveal any equilibrium clusters, but instead are fully compatible with a system of largely repulsive individual lysozyme molecules in solution. We are far from making a claim that the equilibrium cluster phase does not exist in concentrated protein solutions, but this phase has been absent in lysozyme solutions under the experimental conditions used in the present study. Based on these results, we believe that some of the recent work on lysozyme and other proteins related to the equilibrium cluster phase behavior needs to be revisited, perhaps requiring further experimental evidence.

Materials and Methods

Sample Preparation.

For the measurements at EMBL Hamburg and ILL Grenoble, three commercial hen egg white lysozyme powders were used (product codes 62970 and 62971 from Fluka and L7651 from Sigma) and the solutions were prepared following the procedure described in refs. 1 and 22. Approximately 40 mg of protein were dissolved per 1 ml of a 20 mM Hepes buffer in D₂O (Sigma product code 613444) or deionized H₂O. The pH value (as read by a pH meter) was adjusted to 7.8 by adding NaOH both for H₂O and D₂O solutions. Control measurements performed with and without adjusting the pH of the final protein solution, and also with adjusting the pD value of the D₂O samples to 7.4 (which would correspond to pD 7.8) yielded practically no differences in the scattering patterns of the resulting samples. The solution was washed several times with excess buffer using a Sartorius Vivaspin centrifugal concentrator with 5-kDa cutoff, which was further used to concentrate the protein solution. At different steps of the concentration process, aliquots were removed, giving a range of concentrations from ≈4 to 300 mg/ml (as determined by the absorption at 280 nm). The samples with 50 mM NaCl were also prepared by diluting a concentrated sample with buffer containing the appropriate amount of NaCl at the same pH.

For the ESRF measurements, the lysozyme from Sigma (L-6867, Lot 57H7045, three times recrystallized and dialyzed) was dissolved in Hepes (pH 7.8) and acetate buffer (pH 4.8). Control experiments performed on the samples with further dialysis yielded similar scattering curves to those presented. Lower protein concentrations were prepared by diluting the stock solution with the corresponding buffer. Samples with different salt contents (10, 25, and 50 mM NaCl) were obtained by dissolving the concentrated protein sample with buffer containing the appropriate amount of NaCl at pH 7.8. The effective concentration of the protein was also validated by using absolute scattered intensity and the reported density of lysozyme (21).

For the colloidal sample, polystyrene latex spheres (radius, ≈53 nm; polydispersity, ≈4%) were suspended in a density-matched quasi-binary mixture solvent composed of 25 wt % of 3MP with 1:1 H₂O to D₂O by volume. This system exhibits a thermally reversible aggregation of colloids near the binary mixture liquid–liquid phase separation (7). The bulk colloid volume fraction was 0.009, and the sample was kept in sealed flat capillaries.

SAXS and SANS Experiments.

Synchrotron x-ray scattering data at the EMBL were collected on the X33 beamline (storage ring DORIS-III, Hamburg, Germany) (14) using a MAR345 image plate detector and a Pilatus 500K pixel detector. The scattering patterns were obtained with 2-min exposure time for all concentrations at temperatures ranging from 10°C to 25°C. To monitor for radiation damage, two successive protein exposures were compared, and no changes were found. The measurements were performed using vacuum and in-air mica sample cells at the x-ray wavelength of 0.15 nm and at sample-detector distance of 2.7 m, covering the range 0.09 < q < 5 nm ⁻¹. The data were normalized by the intensity of the transmitted beam, azimuthally averaged and the solvent scattering was subtracted using PRIMUS (34).

The SAXS measurements at the ESRF (Grenoble, France) were performed on the beamline ID02 (17) at two sample-detector distances (1 and 5 m) to cover the q range from 0.02 to 6 nm⁻¹. The x-ray wavelength was 0.1 nm and the data were collected by a high sensitivity fiber-optic coupled CCD (FReLoN) detector placed in an evacuated flight tube. The solutions were loaded in a flow-through quartz capillary cell (diameter, ≈2 mm; wall thickness, ≈10 μm) temperature controlled at 20°C. The radiation damage was checked with 10 successive exposures of 0.1 s. The incident and transmitted beam intensities were simultaneously recorded with each SAXS pattern with exposure of 0.3 s. The patterns were normalized to an absolute scale and azimuthally averaged to obtain the intensity profiles, and the solvent background was subtracted.

The SANS data were collected on the D22 instrument (14) at the ILL (Grenoble, France) at sample-detector distances of 8.0 and 1.4 m and the neutron wavelength of 0.8 nm (with a wavelength spread of 10% FWHM) to cover the q range from 0.07 to 4.4 nm⁻¹. Samples were thermostated at 5°C in 1 mm path-length quartz cuvettes (Hellma, France). The scattering patterns were averaged about the incident beam, normalized by the water scattering, contributions from buffer and empty cell were subtracted, and the difference curves were appropriately scaled using standard routines.

Modeling.

The scattering from the models was computed based on Eq. 1 and the orientation-averaged form factor 〈P(q)〉 = 〈|F(q)|²〉, where F(q) is the scattering amplitude of an isolated particle and the averaging is performed over different orientations. Experimentally, the form factor is provided by the lowest concentrations for each series in Fig. 1, which agree with the calculated curves from the atomic coordinates of lysozyme (28). However, for the combined form and structure factor analysis, lysozyme scattering was approximated by the radially averaged scattering function of a prolate ellipsoid (16) with the major semi-axis of r_a = 2.39 nm and the axial ratio r_a/r_b = 1.5. From the volume of the ellipsoid, V = 4/3π(r_ar_b²) = 25 nm³, the electron density of lysozyme (426 e/nm³) and its partial specific volume (0.756 cm³/g) (21), Δρ in water is calculated to be ≈2.6 × 10⁻⁴ nm⁻². The analytic 〈P(q)〉 calculated by this method is in good agreement with that calculated from CRYSOL (27), except that a small additive constant background (0.011 × 〈P(q)〉_{q = 0}) was necessary to describe the high q data.

Because of the asymmetric shape of the lysozyme molecules, their form and structure factors are coupled (16). For the concentration range investigated here, the effective structure factor, S_M(q), can be related to individual structure factor, S(q), and 〈P(q)〉 by the decoupling approximation (15, 16),

The coupling factor, β, is given by β(q) = |〈F(q)〉|²/〈|F(q)|²〉.

S(q) is related to the effective interparticle potential U(r) through the direct correlation function, C(r) (15). S(q) = 1/(1 − N C(q)), where C(q) is the Fourier transform of C(r) and N is related to φ =πNσ³/6, with σ an effective hard-sphere diameter. In terms of the ellipsoid parameters, σ = 2(r_ar_b²)^1/3.

The effective interprotein potential used in the analysis has the following general form,

The short-range attraction and long-range repulsion can be simulated by two Yukawa terms in U_TY (16),

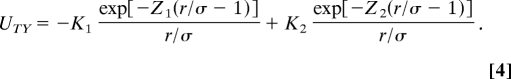The solution for C(r) using the above potential is available within the mean spherical approximation (16). In the modeling of interactions, parameters K₁, Z₁, K₂, and Z₂ are made free and the remaining shape parameters have already been obtained from the form factor analysis. The range of repulsive interaction Z₂ = σκ, is compared with the Debye–Hüeckel screening length, κ⁻¹ (10). The parameters of the best fits to the experimental data obtained by nonlinear minimization are presented in Table 1 and SI Tables 2–4. Slight improvements in the fits can be obtained by increasing the axial ratio of the approximating ellipsoid ra/rb up to 1.8 for higher lysozyme concentrations.

Note Added in Proof.

After receiving a number of comments from the authors of ref. 1, we added SI Fig. 9 displayinig a SAXS series measured in salt-free D₂O buffer at 10°C at six concentrations ranging from 20 to 250 mg/ml. The series does diplay a systematic peak shift with concentration, but also reveals that the shift at higher concentrations is much less pronounced than that at lower concentrations. The trend in the interaction parameters points to gelation effects at higher concentrations (above 200 mg/ml) leading to a reduced peak movement, which could have been difficult to detect with low-resolution instruments.