Eye Orientation During Static Tilts and Its Relationship to Spontaneous Head Pitch in the Laboratory Mouse

Abstract

Both eye position and head orientation are influenced by the macular (otolith) organs, via the tilt maculo-ocular reflex (tiltMOR) and the vestibulo-collic reflexes, respectively. The mechanisms that control head position also influence the rest position of the eye, because head orientation influences eye position through the tiltMOR. Despite the increasing popularity of mice for studies of vestibular and ocular motor functions, relatively little is known in this species about tiltMOR, spontaneous orientation of the head, and their interrelationship. We used 2D video oculography to determine in C57BL/6 mice the absolute horizontal and vertical positions of the eyes over body orientations spanning 360° about the pitch and roll axes. We also determined head pitch during ambulation in the same animals. Eye elevation varied approximately sinusoidally as functions of pitch or roll angle. Over the central ±30° of pitch, sensitivity and gain in the light were 31.7°/g and 0.53, respectively. The corresponding values for roll were 31.5°/g and 0.52. Absolute positions adopted in light and darkness differed only slightly. During ambulation, mice carried the lambda-bregma plane at a downward pitch of 29°, corresponding to a horizontal eye position of 64° and a vertical eye position of 22°. The vertical position is near the center of the range of eye movements produced by the pitch tiltMOR. The results indicate the tiltMOR is robust in this species, and favor standardizing pitch orientation across laboratories. The robust tiltMOR also has significant methodological implications for the practice of pupil-tracking video oculography in this species.

1. Introduction

The use of the laboratory mouse in ocular motor research is growing rapidly, due to widespread interest in applying the tools of molecular genetics to the study of ocular motor circuits, and to the recent adaptation of accurate eye movement recording techniques for use in these tiny animals (Stahl, 2004b; Stahl, 2008). To date, most studies of murine ocular motility have focused on the eye movements induced by dynamic stimulation of the semicircular canals (the angular vestibulo-ocular reflex, aVOR), retina (the optokinetic reflex, OKR), or macular (otolith) organs (Andreescu, et al., 2005; Killian and Baker, 2002). In contrast, eye movements induced by static stimulation of the macular organs have received less attention. The macular organs induce the compensatory maculo-ocular reflexes (MOR) in response to either maintained tilts (tiltMOR) or linear translations (transMOR) (Paige and Tomko, 1991). While transMORs are weak in mammals lacking a fovea (or homologous retinal structure) such as rabbits and rats (Baarsma and Collewijn, 1975; Hess and Dieringer, 1991), their tiltMORs are strong (Maruta, et al., 2001; Van der Hoeve and De Kleijn, 1917). Descriptions of the mouse response to sustained tilts published to date indicate that the mouse tiltMOR is similarly robust, but these descriptions were either semi-quantitative (Harrod and Baker, 2003) or limited to assessments of eye position relative to an arbitrary zero position and for rotation about one axis (roll) over a relatively restricted range (Andreescu, et al., 2005). It is possible using video-oculography, however, to determine eye positions in more absolute terms, i.e., as deviations with respect to the earth-horizontal and to the mid-sagittal plane of the animal (Stahl, 2004a).

The control of head pitch and the MOR are interrelated. Both eye position and head orientation are influenced by the macular organs, via the tiltMOR and the vestibulo-collic reflexes, respectively. At the same time, the mechanisms that control head position determine the rest position of the eye, because head orientation determines the orientation of the macular organs, and thus the output of the tiltMOR. This effect of head position on eye position has a very practical significance for ocular motor research in which eye movements are recorded with the head fixed in place; the selection of the pitch in which the head is fixed determines, in any animal with a robust tiltMOR, the rest position of the eyes, and this may in turn influence the geometry of compensatory eye movements. To date, there has been only limited data available regarding the natural pitch orientation of the mouse head. Vidal and colleagues (Vidal, et al., 2004) x-rayed mice as they trotted on a treadmill and concluded that the horizontal semicircular canals are carried at an angle pitched up from the earth-horizontal by 15.4°. However, the study does not frame its results in terms of the lambda-bregma axis, the bony reference point more commonly used to determine pitch angle where stereotactic apparatus are involved. Moreover, it is unclear to what extent these data – obtained from vestibular-deficient mutants and C3H controls – are applicable to the C57BL/6 mouse – the strain more commonly used for studies of “normal” mice or as the genetic background for many mutant strains.

The purpose of this study was to characterize the tiltMOR during pitch and roll over the entire 360° range, determining the eye angles relative to the mid-sagittal and earth horizontal planes, rather than as angles relative to an arbitrary zero. Additionally we determined the pitch of the head during forward ambulation, expressing this pitch in terms of the orientation of the lambda-bregma axis with respect to the earth-horizontal. By obtaining the tiltMOR and head orientation data from the same animals we were able to determine where the animals “place themselves” on the relationship between eye position and pitch angle, and so to approximate the vertical position of the eyes during ambulation. A preliminary report has been published (Oommen and Stahl, 2007).

2. Results

Pitch tilts

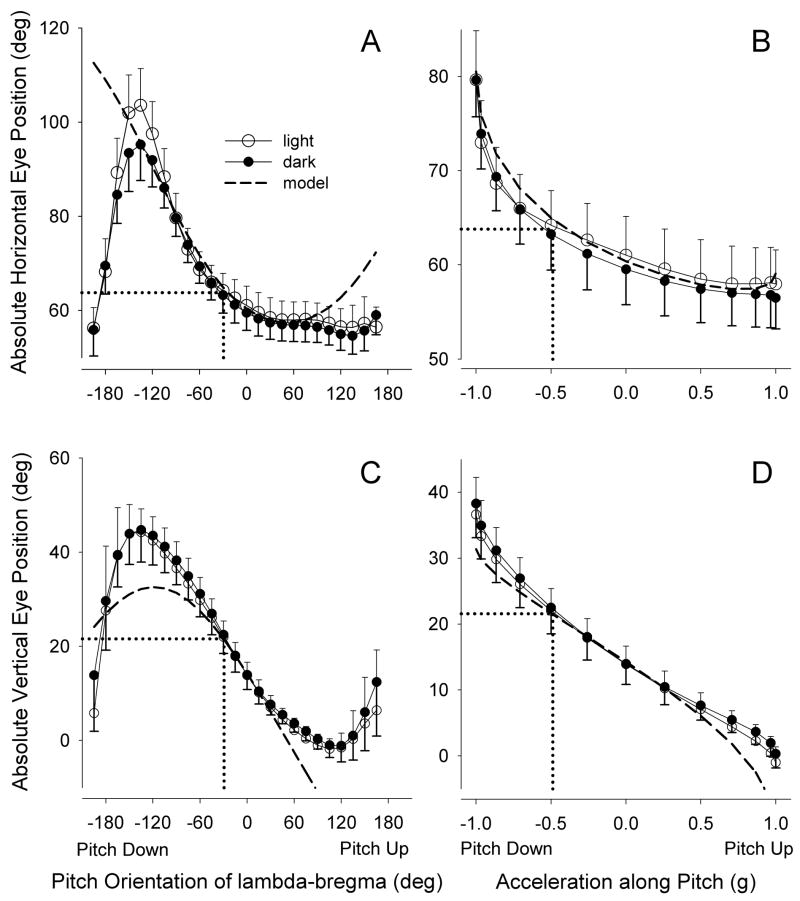
Figures 1a,c plot the horizontal eye position (relative to the mid-sagittal plane) and vertical eye position (relative to the earth-horizontal plane) versus the angle of the lambda-bregma axis with respect to earth-horizontal (∠L-B) in response to tilts about the pitch axis. (See Experimental Procedure for definitions of all angles abbreviated in Results.) Separate curves are shown for eye positions measured in the light and dark. The dashed line indicates the predicted horizontal and vertical positions, based on the assumption that the eye counter-rotated about an axis parallel to the pitch gimbal axis (Model described in Experimental Procedure). As in the modeled response, the eye moved vertically and temporally as the head was pitched downward. (Note that the model makes the simplifying assumption that the utricle is able to uniquely transduce tilt angles over the entire range of pitch and roll; since otolithic afferents modulate as a sinusoidal function of tilt angle (Fernandez, et al., 1972; Loe, et al., 1973), this assumption does not hold once pitch or roll exceeds approximately ±90° from some central position, and the data is not expected to fit the model beyond this range.) Eye elevation varied approximately sinusoidally with pitch angle in the range of 90° nose-up to 90° nose-down. Beyond this range, eye elevation tended to return toward the position assumed in the neutral gimbal position. Previous tilt studies have described eye position as a linear function of the component of the gravity vector lying in the plane of the utricle (Andreescu, et al., 2005; Maruta, et al., 2001). Figures 1b,d show actual and predicted eye positions re-plotted versus this component of the gravitational acceleration (in units of g) for the central −90° to 90° of tilt. The sensitivities (slopes) of the eye response in light and dark over the central ±30° of these plots averaged 5.8°/g and 14.9°/g for horizontal and vertical eye movements, respectively. After adjusting for the fact that the observed vertical eye movement should only be 0.47 times the actual response of the pitch tiltMOR (see Experimental Procedure), the true sensitivity for vertical eye movements was 31.7°/g, which equates to a gain of 0.53. While the curves were similar for tilts in the light and dark, examination of the plots in figure 1 suggests systematic differences. The eye deviated more temporally in the light, especially as downward pitch exceeded 90°. In the vertical direction, the eye was slightly more elevated in darkness at most pitch orientations. The eye positions in light and dark were compared by 2-way ANOVA, with one factor being illumination (light or dark) and the second factor being pitch orientation. The effect of illumination on absolute position was significant for both horizontal (p = 0.0001) and vertical (p = 0.008) eye positions. On the other hand, the sensitivities in the light and dark were not statistically different (paired t-test, horizontal: p=0.99; vertical: p=0.92).

Figure 1.

Effect of pitch tilts on absolute horizontal and vertical positions of the eye. 1a,c: eye positions plotted versus tilt angle of L-B axis. 1b,d: eye positions for the central ±90° of tilt replotted versus the fraction of the gravity vector projecting into the horizontal plane (the approximate plane of the utricle). On all panels, dashed lines indicate the predicted eye positions, based on the assumption that the eye counter-rotated about an axis parallel to the gimbal pitch axis. Dotted drop lines indicate eye position at a pitch of 29°, the average pitch assumed by the animals during ambulation. Error bars are 1 SD, plotted asymmetrically for graphical clarity.

Roll tilts

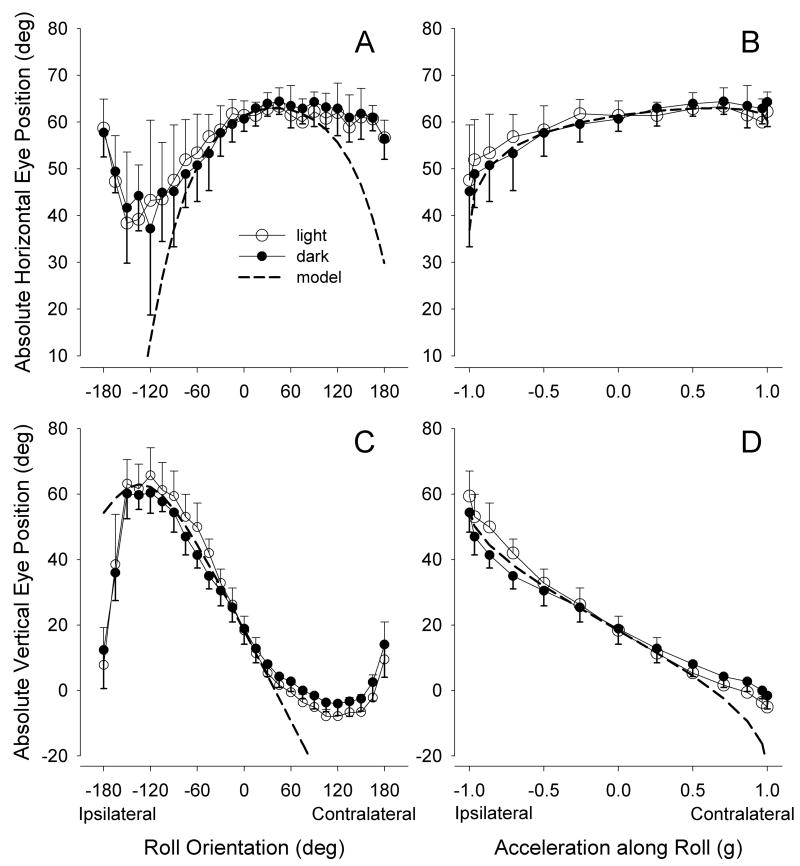
Figures 2a,c plot horizontal and vertical eye position versus roll angle in the light and dark in response to static roll tilts. Again, the dashed lines indicate the predicted positions based on the model described in Experimental Procedure. As predicted, over the central ±90° of roll, the eye moved upward and nasally as the head rolled ipsilaterally. Vertical eye position varied approximately sinusoidally with tilt in the range of ±90°, returning toward the position assumed at the neutral gimbal position as tilt exceeded this range. The eye deviated nasally with ipsilateral tilt, but, as predicted for much of the range, changed minimally during contralateral tilt. Figures 2b,d show the horizontal and vertical eye positions re-plotted versus the fraction of the gravity vector projecting into the horizontal plane of the head. The vertical sensitivities measured over the central ±30° range were 27.7°/g in the light and 22.8°/g in the dark. These sensitivities were significantly different (p = 0.004, t-test). After adjusting for the fact that the observed vertical eye movement should only be 0.88 times the actual output of the roll tiltMOR (see Experimental Procedure), the true sensitivity for vertical eye movements was 31.5°/g in light and 25.9°/g in darkness, equating to gains of 0.52 and 0.43, respectively. The horizontal response to roll was less linear, with sensitivities over the ±30° region measuring 3.4°/g in the light and 6.3°/g in the dark. These values were not significantly different by t-test. Absolute horizontal and vertical eye positions in the light and dark were compared over the entire ±180° tilt range by a 2-way ANOVA, and were found not to differ significantly (p=0.94). However, inspection of the plot of vertical eye position versus roll angle suggested that the non-significance may have arisen from eye elevation being greater in the light than in the dark for ipsilateral roll, but lesser for contralateral roll. Indeed, when separate ANOVAs were performed for ipsilateral and contralateral roll, the light and dark values differed significantly (ipsilateral: p=0.0007; contralateral: p<0.0001).

Figure 2.

Effect of roll tilts on absolute horizontal and vertical positions of the eye. 2a,c: eye positions plotted versus tilt angle of interocular axis. 2b,d: eye positions for the central ±90° of tilt replotted versus the fraction of the gravity vector projecting into the horizontal plane. Dashed lines indicate the eye position predicted from the simple geometrical model. Directions of roll are reported with respect to the recorded eye.

Head pitch during ambulation

During ambulation, the lambda-bregma pitch angle with respect to earth-horizontal (∠L-B) measured −29.3 ± 4.6°. This pitch angle is marked on the pitch ocular response curves in figure 1, corresponding to an absolute horizontal eye position of 64° and a vertical eye position of 22° in the light. The natural head pitch fell near the midpoint of the linear range of the vertical eye position versus head pitch curve (figure 1c).

To assess whether the weight of the head fixation pedestal and marker plate (see Experimental Procedure) affected head pitch, measurements were performed in four animals with and without the marker plate. In the latter case the plane of the pedestal was identified manually in each video frame. In the two conditions the plane of the pedestal with respect to earth-horizontal was virtually identical (with plate: 34.5±3.1°; without plate: 35.1±2.2°, paired t-test p=0.77). Given that the 1.6 gm marker plate had no effect on head orientation, it is unlikely that the acrylic pedestal and skull screws (which together weigh only about 0.8 gm, half of the weight of the marker plate) affected head pitch.

3. Discussion

The experiments demonstrated that the tiltMOR in the mouse is robust, producing sustained deviations of the eye of approximately 50% of the pitch or roll tilt angle (i.e., gains of approximately 0.5) over the central ±30° of tilt. The 0.5 gain values take into account the fact that the optic axes of the mouse (and thus the reference frame for our 2D video oculography) are significantly deviated with respect to both the pitch and roll stimulus axes. The uncorrected sensitivity and gain to roll tilts in the dark (22.8°/g and 0.38, respectively) are similar to the uncorrected values of 26°/g and 0.45 previously reported for C57BL/6 mice rolled over ±20° in darkness (Andreescu et al., 2005), as well as to the uncorrected value of 0.41 in a pigmented rat undergoing 0.02 Hz sinusoidal roll tilts (Brettler, et al., 2000). The tiltMOR responses in darkness have also been reported for the rabbit, a species that, like the mouse, lacks a circumscribed retinal structure adapted for high-acuity vision (e.g., a fovea or area centralis). The rabbit exhibited somewhat weaker responses than the mouse, measuring 17°/g (gain of 0.28) for pitch and 16°/g (gain of 0.26) for roll over the central ±30° (Maruta, et al., 2001). These rabbit gain and sensitivity values should be compared to our corrected values for the mouse; as the rabbit responses were obtained using 3D coil oculography and an eye movement reference frame aligned with the stimulus reference frame, there is no need to correct, as in our case, for the deviation between the stimulus axes (pitch and roll) and the animals’ optic axes. It should be noted that a higher value for the rabbit’s roll tiltMOR, roughly equivalent to the value in the mouse, has also been reported (Baarsma and Collewijn, 1975). This higher value (0.5–0.6) was obtained using prolonged transverse linear accelerations with the eyes covered to prevent vision.

The tiltMOR of the rabbit has been argued to assist that species in maintaining its retinal visual streak aligned with the projection of the horizon (Collewijn, et al., 1985). The observation that most animals with visual streaks do align them with the horizon has, in turn, been cited as support for the idea that the purpose of a visual streak is to enhance visual discrimination in the vicinity of the horizon, a useful goal because the retinal projections of most terrestrial objects fall in this vicinity (Hughes, 1977). The results of the current study, however, would argue against the conclusion that the principal purpose of a robust tiltMOR is to orient the visual streak. The mouse retina lacks a visual streak or, for that matter, much of any variation of ganglion cell or photoreceptor density along its dorsal/ventral axis (Hughes, 1977; Jeon, et al., 1998). The mouse retina does exhibit some differences in the spectral sensitivities of cone populations of its dorsal and ventral halves (Szel, et al., 1996), so there may still be some advantage to orienting its eyes, for instance, so that the majority of the projection of the sky falls on the ventral half of the retina. However, such a task would seem less exacting than that of aligning a visual streak with the horizon, and yet the current results suggest that the mouse tiltMOR could be stronger than that of the rabbit. Thus our demonstration that the mouse has a particularly robust tiltMOR raises the possibility that the purposes of this orienting reflex have yet to be fully understood.

Much of the variation in eye position as a function of roll and pitch was explained, at least qualitatively, by a simple model in which the eye counter-rotates about an axis passing through the eye and parallel to the stimulus (tilt) axis, and horizontal and vertical motions are defined with respect to a viewpoint roughly aligned with the optic axis (see dashed lines in figures 1,2). The model captures how the mismatch between the stimulus (pitch or roll) axis and the optic axis causes the optic axis to sweep the shape of a cone during pitch and roll, creating the appearance of horizontal eye motion, even in the absence of actual rotation of the eye about the animal’s vertical axis. The model, however, is obviously incomplete. It makes the non-physiological assumption that the otolith organs encode a linear function of tilt angle over all orientations. In fact, individual otolith primary afferents modulate as a sinusoidal function of tilt angle (Fernandez, et al., 1972; Loe, et al., 1973), and thus our model is only expected, at best, to fit the behavior over a 180° midrange within which otolith output is a monotonic function of tilt. The exact positioning of this midrange within a ±180° range of tilt angles should depend on the precise orientation of the average planes of the two utricular maculae with respect to the head (assuming the tiltMOR for each eye is influenced equally by the otolith organs of the two sides), an anatomical detail that has not been determined in mice. An upward angulation of that plane, for instance, would result in the midrange shifting leftward in figures 1a and 1c, toward more pitch-down positions. Indeed, the region over which horizontal and vertical eye positions most closely follow the model in figure 1 does appear to be shifted to the left with respect to the 0° L-B orientation. On the other hand, the midrange of the response to roll might be expected to be centered on zero degree roll, since any roll inclination of one utricular plane should be offset by the symmetrical inclination of the contralateral utricle. Unfortunately for this simple scheme, while the region of coincidence of the model and the response to roll tilt is centered on 0° roll for the horizontal response (figure 2a), it is prominently left-shifted for the vertical response (figure 2c). Thus additional factors must contribute to the disparities between model and actual behavior, limiting the degree to which the region of best correspondence can be used to predict utricular geometry. One of these additional complexities is the appearance of a saturation in vertical eye position during both rightward roll and nose-up pitch, suggesting that depression of the eye reaches some soft limitation around 0° elevation. An effect of this flattening is to shift the region of model/behavior correspondence to the left, i.e., away from the nose-up and contralateral roll positions.

Another simplification of our model is that it assumes a concordance between the tilt axis and the counter-motion of the eyes. However, in the rabbit the eyes do make true horizontal movements (i.e., movements about the animal’s vertical axis and consequently orthogonal to a pitch or roll stimulus) such that the eyes diverge during downward and converge during upward pitch, or rotate contralaterally during ipsilateral roll and ipsilaterally during contralateral roll (Maruta, et al., 2001). Similar movements have been observed in the rat in response to equivalent forces produced by linear translation (Hess and Dieringer, 1991). Maruta and colleagues (Maruta, et al., 2001) observed that these horizontal movements during static tilts produce advantageous repositionings of the visual fields of the two eyes with respect to the entire surround. For instance, when the animal’s eyes diverge as it pitches its head down to feed, the animal maximizes its ability to detect predators approaching from overhead or behind. Our 2D recording is incapable of determining the extent to which pitch and roll induced rotations about the animal’s vertical axis, although the fact that horizontal eye movements in the midrange were so well explained by our simple geometrical model suggests that any movements about the vertical axis account for only a small portion of the horizontal variations we recorded. Nevertheless, it should be recognized that the horizontal movements predicted by our model (e.g. temporal movement during pitch down, nasal movement of the recorded eye during ipsilateral roll) are in the same directions as the ones generated by movements about the vertical axis in the rabbit. Thus the idea that horizontal eye movements during tilt work to optimize the positioning of the visual fields may be applicable to the mouse, irrespective of the origin of the horizontal deflection.

Natural position of the head and the “rest” position of the eyes

We found that during ambulation, mice hold the head with the lambda-bregma (L-B) axis inclined 29° down. The angle of the horizontal semicircular canal is 23° upwards from L-B (Calabrese and Hullar, 2006), placing the canal during ambulation at 6° downwards from earth-horizontal. This value accords with the observation that most species position their heads so as to hold the plane of the horizontal semicircular canal horizontal. A previous study of posture in mice concluded that they carry their horizontal canals oriented 15° upwards during rest and locomotion (Vidal, et al., 2004), while a study of Long-Evans rats yielded a value of 14° (Rabbath, et al., 2001), and a comparative study of several mammalian and non-mammalian species found an average upwards pitch of about 5°, although there was a large degree of moment-to-moment variation (Vidal, et al., 1986).

A number of factors other than sampling variation may have contributed to the 21° difference between the canal inclination values obtained in the current study and that reported by Vidal and colleagues. The results were arrived at quite differently. Our figure of 6° was arrived at in a four-step process: First we measured the inclination of the top of the pedestal as an animal ambulated along a raised walkway, second we used postmortem measurements of angle ∠Ped/AOJ-I from the same animal to convert the pedestal inclination to the inclination of the AOJ-I plane, third we used post-mortem measurements of angle ∠L-B/AOJ-I from a separate set of animals to convert the AOJ-I inclination to inclination of the L-B axis, and fourth and finally, we used Calabrese and Hullar’s micro-CT measurements of the angle between the horizontal canal and the L-B axis in C57BL/6 mice (Calabrese and Hullar, 2006) to convert the inclination of L-B to inclination of the horizontal canal. In contrast, Vidal and colleagues used cineradiography to measure directly the inclination of AOJ-I as mice trotted in place on a treadmill, and then converted it to inclination of the canal based on a measurement of the angle between AOJ-I and the canal obtained from dissection of a single skull. The effects on head pitch of any differences in ambulation speed in the two experiments are unknown. Additionally, although the pitch measurement of Vidal and colleagues involved fewer steps and a lesser potential for compounded errors, it introduced a larger potential for error due to the smaller number of animals studied. Furthermore, the canal dissection procedure (which was not described in detail) almost certainly provided a less accurate measure of the horizontal canal plane than did the micro-CT procedure. It is also possible that the difference in horizontal canal inclination reflects the different mouse strains used in the two studies. The micro-CT study demonstrated significant inter-strain variation in the anatomic orientations of the semicircular canals (Calabrese and Hullar, 2006). Of particular significance, Vidal and colleagues studied the C3H strain. Although the breeding history of their animals was not detailed, the reference for this strain maintained by The Jackson Laboratory harbors a retinal degeneration gene (variously termed rd, rd-1, or Pde6b^rd1), which causes complete rod degeneration and consequent near-blindness by weaning age. If the animals they studied were in fact blind, that could have affected the self-adjustment of the animals’ vestibular systems and with it, head posture during ambulation.

Combining the data on eye position versus pitch angle with the data on the spontaneous pitch of the head during ambulation would suggest that during ambulation, each eye is deviated 64° lateral to the mid-sagittal plane and 22° superior to the horizon. These positions may be thought of as the spontaneous, “rest” positions of the eyes. This conclusion rests on the assumption that the eye position vs. pitch angle functions established by passively tilting the head-fixed mouse apply to the situation in which the animal is ambulating and free to establish its head pitch spontaneously. It also assumes, reasonably, that the animal maintains on average a 0° roll angle, the roll angle at which we determined the effect of pitch tilts on eye position.

The validity of our rest positions is supported by previous reports. The horizontal angle is essentially identical to the value of 62° tabulated for rats and mice by Walls (Walls, 1942), who was in turn summarizing the older ophthalmoscopic measurements of Johnson (Johnson, 1901). The elevation accords well with our own vertical measurements from different group of C57BL/6 animals recorded as controls for calcium channel mutants (Stahl, et al., 2006). In that study the average elevation was 18°, obtained with the head restrained at a bregma-lambda pitch angle of 18° downward. By comparison, in the current study, the elevation angle for an 18° head pitch (obtained by interpolating between the 15° and 30° pitch values in figure 1a) would have been 18.7°. It may be significant that the eye elevation of 29° falls close to the midpoint of the range of vertical eye positions achieved over the entire range of pitch orientations (figure 1a), suggesting that the animal normally adjusts its head to place the eyes at the center of the range of the tiltMOR. Alternatively, the tiltMOR may have been optimized by an evolutionary process so that the midpoint of the variation of eye elevation coincides with the average head orientation during ambulation, which in turn may be dictated by the constraints of skeletal geometry (Vidal, et al., 2004; Vidal, et al., 1986). It is also interesting that the horizontal resting angle of 64° occupies something of a special position in the plots of horizontal eye orientation versus tilt angle, coinciding, as it does, with the approximate temporal limit in response to roll and the nasal limit in response to pitch tilts.

Practical implications of results for studies of eye movements in head-fixed mice

To date, there has been no consistency across laboratories in the pitch orientation at which the mouse head is fixed during eye movement recording. In studies of the rabbit, the head is usually placed in the approximate pitch of the “freeze” position, the position this species adopts spontaneously when startled (Hughes, 1971). No equivalent standard orientation has been promulgated in the mouse. In our own work (Stahl, 2004a; Stahl, et al., 2006), the pitch of the lambda-bregma plane was placed at 18° down, a position arrived at empirically in early experiments by angling the pedestal fixation armature until we found a position at which the armature and pedestal could be screwed together without requiring a forced change in head pitch. Some of the positions used in other studies have included placing the nasal plane at a 35° angle (Goossens, et al., 2004)(equating to an ∠L-B of approximately 8° down, based on measurement of the angle between the nasal bone and L-B in our figure 3b), 60° (De Zeeuw, et al., 1998), or 30° (Faulstich, et al., 2004), or by placing ∠L-B at 45° (Killian and Baker, 2002). Most studies do not supply this information, or provide an angle but are ambiguous as to how the angle was defined (e.g., (Iwashita, et al., 2001)). The effect of head pitch on the eye movement response of rodents to rotation about an earth-vertical axis is unknown, but in the absence of a demonstration that the response is independent of pitch, it would seem prudent for different laboratories to use the same orientation. A reasonable choice of orientation would be that assumed by the animal spontaneously during ambulation, which the current results indicate to coincide with an L-B pitch of 29° degrees. Certain applications of course, may warrant a different head orientation. For instance, in studies of neuronal activity within the horizontal aVOR circuit, it is customary to place the head so that the vertical semicircular canals are orthogonal to the stimulation axis, thereby minimizing the chance that a neuron belonging to a vertical canal circuit will be misidentified as a low-sensitivity horizontal canal neuron.

Figure 3.

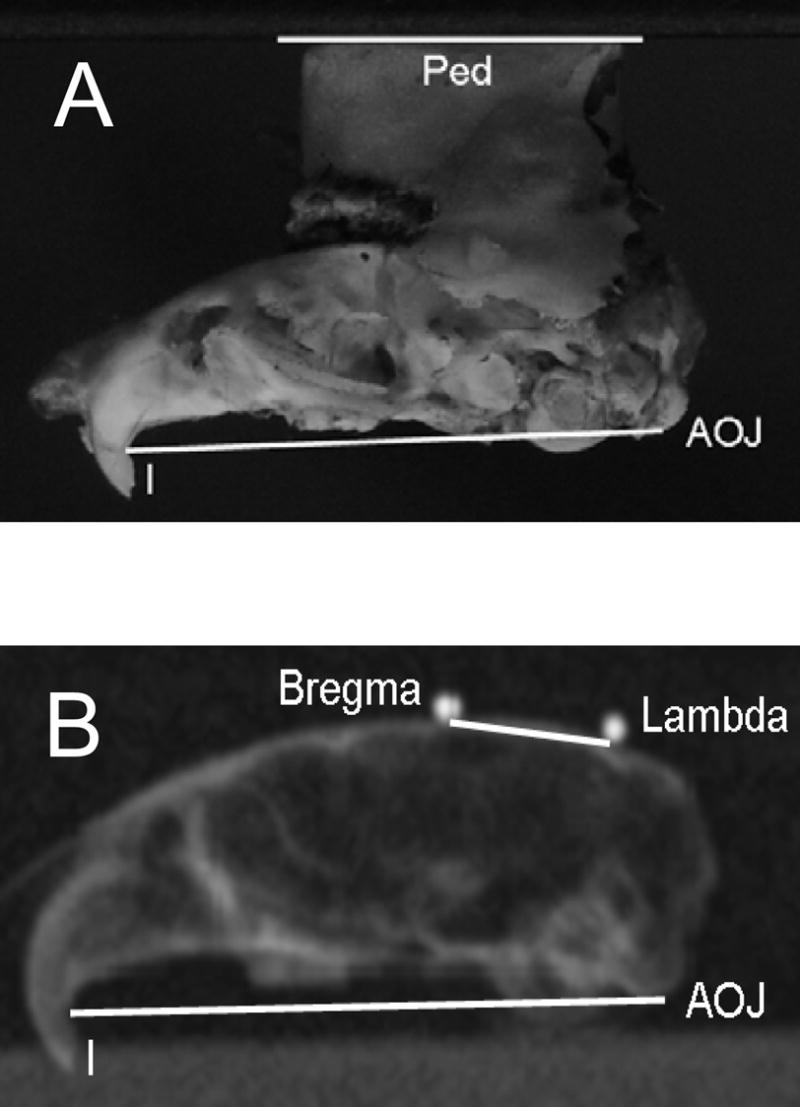
Demonstration of photographic and radiographic measurement of bony landmarks. 3a: Lateral photograph used to measure angle between the plane of the pedestal and the line joining the root of the maxillary incisors and the atlanto-occipital joint (∠Ped/AOJ-I). 3b: Lateral radiograph used to measure angle between lambda-bregma axis and the AOJ-I line (∠L-B/AOJ-I).

Beyond the hypothetical concern that pitch orientation could affect the response to rotation about an earth-vertical axis, the robust tiltMOR of the mouse has a practical significance for all studies in which the eye movements are recorded using pupil-tracking video oculography. Pupil tracking initially yields a measurement of the linear position of the pupil, which must then be converted to eye rotation. Mice cannot be trained to fixate small targets at known angular deviations (the usual calibration procedure when working with humans), but the conversion can be accomplished by a trigonometric transformation incorporating R_P, the shortest distance from the centroid of the pupil to the vertical line passing through the center of corneal curvature (Stahl, et al., 2000). This distance varies according to the elevation of the pupil (Stahl, 2004a), which the current study demonstrates depends strongly on head pitch. Where pupil elevation is likely to be roughly constant throughout the experiment, the effect can be ignored, so long as R_P is determined under conditions that produce the same degree of pupil elevation (Stahl, et al., 2000). Alternatively, one can follow the procedure of the current study, making use of R_P0, the distance of the pupil centroid to the actual center of corneal curvature (Stahl, 2004a). In studies that do neither (e.g., (Shutoh, et al., 2002)) gain values could be over-or underestimated, depending on the selected R_P and the elevation of the eye determined by the pitch of the head. For example, if one were to estimate R_P from a post-mortem cross section through the equator of the eye (e.g., (Remtulla and Hallett, 1985)), R_P would equal R_P0. This R_P would be 1.08 times (1/cos22°) the correct value at a head pitch of 29° where eye elevation is 22°, and 1.12 times too large at a head pitch of 45°. If, while investigating the effects of orientation on VOR gain, one were to record the animal at a pitch 45° down from the spontaneous orientation (i.e., at an ∠L-B of 74°), the anatomically defined R_P would be 1.19 times too large and recorded eye movement amplitudes would be significantly underestimated. This effect would also lead to a small, but systematic artifactual reduction in VOR gain in cerebellar mutants as compared to control strains, due to the higher mean eye positions in the mutants (Stahl, 2002; Stahl, et al., 2006). In sum, a practical implication of the current results is that studies using pupil-tracking video oculography should exert explicit control over head orientation during recording. Since the measurement of the mouse nasal bone is imprecise and its animal-to-animal consistency has never been demonstrated quantitatively, it seems preferable to implant pedestals using stereotactic methods to assure a known and consistent relationship between the pedestal surface and bony reference points, and then to report the inclination of the pedestal during recording. Furthermore, one should determine R_P for each animal under the conditions of the experiment, or, alternatively, calculate R_P from R_P0 and a measurement of eye elevation.

Limitation of current study

Since this study employed 2D oculography, it did not characterize some aspects of the mouse tiltMOR, such as the degree of correspondence between the response and stimulus axes. Such issues must await the development of an accurate 3D oculography technique applicable to the mouse and the large-amplitude eye rotations engendered by tilts. On the other hand, an important aspect of our 2D oculography is that it measures absolute vertical and horizontal eye positions. Absolute 3D positions cannot be defined in the mouse, since this species lacks any sort of a retinal structure that could be used to define an absolute torsional reference position. Absolute horizontal and vertical positions are of particular importance, since they are the strongest determinants of an animal’s total visual field, the regulation of which may be one goal of the tiltMOR (Maruta, et al., 2001). Finally, a useful aspect of absolute eye positions is that they should be fully comparable across different laboratories.

4. Experimental Procedure

The animal experiments were approved by the Institutional Animal Care and Use Committee at Case Western Reserve University and followed the guidelines of the National Institutes of Health on the use and care of laboratory animals. C57BL/6 mice were obtained from The Jackson Laboratory (Bar Harbor, ME). 10 animals were studied, aged 5–10 months at the time of the experiments. Animals were prepared for eye movement recording by surgically implanting an acrylic head fixation pedestal as previously described (Stahl, et al., 2006). During this implantation procedure, the animals were held in a stereotactic frame. The vertical positions of lambda and bregma were measured by means of a small probe held in a calibrated micromanipulator, the pitch angle of the lambda-bregma (L-B) axis was calculated, and the pedestal was constructed so that its top surface parallels that axis. During eye movement recordings the pedestal was secured to an armature that pitches the pedestal surface (and thus, approximately, the L-B axis) 20° downward. The armature and body support were adjusted in the roll axis to place the interocular axis parallel to the earth horizontal. Just prior to eye movement recording, the eye was treated with 0.5% physostigmine salicylate to limit pupil dilation in the dark.

Eye movement recording and calibration

Eye positions were recorded using calibrated video oculography as previously described (Stahl, 2004a; Stahl, et al., 2000). Eye movements were monitored under infrared illumination using a commercial pupil tracker (ETL-200, ISCAN, Burlington, MA) operating at 60 samples/s. The IR emitter that generates the reference corneal reflection (CR) was positioned directly over the optic axis of the camera. The azimuth angle of the camera with respect to the mouse was adjusted until the CR was roughly aligned with the equilibrium horizontal position of the pupil in the light. Horizontal and vertical positions of the pupil and CR were converted offline to horizontal and vertical eye angles, using previously described trigonometric methods (Stahl, 2004a). The conversion makes use of the distance R_P0. R_P0 is the radius of the spherical surface that would be described by the pupil if it were rotated in two dimensions about the actual center of the corneal curvature. R_P0 is calculated from the relative motion of the pupil and CR as the camera is rotated about the animal over known angles; because the gimbal apparatus used for these experiments could not accommodate the rotating camera feature, R_P0 was determined for each animal in a separate experimental session on different apparatus. (Performing the calibration in a separate session is a reasonable approximation, since in a separate set of 13 mice in which R_P0 was measured on three or more days, the average session-to-session range was just 6.3% of each animal’s R_P0, with a range of ranges of 1.1–15.8%. See Supplemental figure 1.) To calculate vertical eye angle (E_V), we first corrected the raw vertical separation (ΔY_RAW) of the pupil and CR to account for the vertical separation of the reference emitter and the camera’s optical axis by the equation ΔY = ΔY_RAW + R_CORNEA sin(α/2), where R_CORNEA is fixed at 1.5 mm and α is the angular elevation of the reference emitter above the optical axis of the video camera (12.8° in this particular setup). The significance of this correction is that it renders the ultimate vertical angle the absolute elevation above the earth-horizontal plane. E_V was then calculated as arcsin(ΔY/R_P0). To calculate horizontal eye angle (E_H), we first calculated the angle of the pupil relative to the corneal reflection as arcsin(ΔX/sqrt(R_P0² – ΔY²)). We then converted this relative angle to absolute angle with respect to the mid-sagittal plane by adding the angle between the camera’s optical axis and the midline of the animal’s head.

Natural stimuli and stimulation procedure, tilt experiments

The mouse recording apparatus was mounted in a two-axis gimbal, the inner axis being vertical with respect to the mouse, and the outer axis being horizontal with respect to the earth. The orientation of the mouse was measured with a three-axis orientation sensor (3DM-G, Microstrain, Burlington, VT). The sensor was mounted to the inner axis of the gimbal and aligned to parallel the rostro-caudal axis of the mouse. Orientation angles were displayed in real-time on a laptop computer and guided our positioning of the gimbal. The mouse and oculography apparatus were enclosed in a light-tight box within the inner gimbal. For recordings in the light, the interior of the box was illuminated by white LEDs placed in the corners of the box.

During testing, each mouse was placed in body orientations spanning 360° in 15° steps, first in pitch and then in roll. The sequence of positions was randomized. All pitch tilts were done at a 0° roll orientation, and all roll tilts were done with the gimbal in its 0° pitch position. Each position was achieved by rotating the animal in the dark manually at a slow rate (to minimize semicircular canal activation) to the desired angle. After the eye position stabilized, the interior lights were turned on and the pupil position was recorded for 12 seconds, followed by 12 seconds of recording in the dark. The static horizontal and vertical eye positions were extracted in off-line analysis. Sections where pupil or CR tracking was lost or unstable were excluded. Each mouse underwent two recording sessions on different days. In the second session roll rotations were performed first. The results of the two sessions were averaged for each mouse. Throughout Results, the 0° pitch, 0° roll gimbal position is referred to as the “neutral” gimbal position. Since the head was fixed with the pedestal (and thus the L-B axis) pitched 20° down, this neutral pitch is at −20° in all plots of eye position versus pitch angle.

Determination of spontaneous head posture

Mice were video-recorded as they ambulated along a straight, narrow plank mounted in a water-filled tray. A thin aluminum plate weighing 1.6 gm and bearing high-contrast marks was screwed to the acrylic pedestal. These marks were tracked and converted to pitch angle (with respect to earth-horizontal) using a commercial video-based motion tracking and analysis system (Peak Motus, Vicon, Los Angeles). Each mouse crossed the plank 5–6 times. The video record was edited to include only periods in which the animal was ambulating and the markers were both visible. After extracting the pitch angles, we further edited the data to restrict it to the periods when the centroid of the markers was in forward motion (horizontal velocity positive). We then averaged the pitch angle during the selected data.

Post-mortem anatomical measurements and calculation of final lambda-bregma angles

Head pitch angles during both tilt and ambulation experiments were initially defined with reference to the top surface of the pedestal, which had been constructed to parallel the pitch angle of the L-B axis (see above). However, the precision of the intraoperative measurement of the L-B pitch was unknown. Consequently, we refined our pitch measurements by determining the angle between the pedestal and the L-B axis in each animal, post-mortem. After tiltMOR and ambulation data sets had been collected, animals were sacrificed by an overdose of sodium pentobarbital, decapitated, and the skull was defleshed by a combination of steaming and dissection, followed by drying in room air. The skulls were then digitally photographed from both sides. From these photographs the angle between the top surface of the pedestal (Ped) and a line connecting the atlanto-occipital joint (AOJ, equivalent to the inferior surface of the occipital condyle) to the root of the maxillary incisors (I) was measured (∠Ped/AOJ-I). Figure 3a shows one photograph with the lines marked. (For convenience, the skulls were photographed upside-down, with the pedestal surface resting on a horizontal surface.) The angles obtained from the left and right side-views were averaged to yield a single value for each mouse. Since the pedestal obscured the top surface of the skull, the average angle between the L-B line and the AOJ-I line (∠L-B/AOJ-I) was determined from the skulls of another 10 C57BL/6 mice. These skulls were x-rayed from a lateral view with their lambda and bregma locations marked by miniature ball bearings adhered to the skull by adhesive wax, and the ∠L-B/AOJ-I was measured from the radiographs as shown in figure 3b. (Measurements of ∠L-B/AOJ-I were also made from lateral photographs, yielding essentially identical results.) These angles were used to convert the pitch angle of the gimbal to the actual pitch angle of L-B with respect to earth-horizontal (∠L-B) using the formula: ∠L-B = gimbal pitch + armature pitch + ∠Ped/AOJ-I -∠L-B/AOJ-I. As noted above, armature pitch was fixed at −20°. For the ambulation experiments, the sum gimbal pitch + armature pitch was replaced by ∠Ped/horizon, the angle of the head with respect to the horizon. Note that in this equation and all figures, a negative angle denotes downward pitch. Also note that ∠Ped/AOJ-I is characteristic to each animal, whereas ∠L-B/AOJ-I is a constant determined from the skulls of the additional 10 animals not used for the tilt and ambulation experiments. ∠L-B/AOJ-I measured −6.5±1.8° (range −2.7 – −9.0°). ∠Ped/AOJ-I averaged −2.4±1.7° (range −5.1 – +0.02°). The small standard deviation of ∠Ped/AOJ-I indicates that, despite the limitations to the precision of the intraoperative measurement of the L-B pitch, the final positioning was quite consistent.

Because the standard set of gimbal angles generated slightly different ∠L-B orientations for each mouse (due to the variations in ∠Ped/AOJ-I), eye positions at the standard pitch angles had to be determined before the individual mouse curves could be averaged. These positions were obtained by interpolation on a 9-degree polynomial fit through the original data points for each mouse.

Predicting form of the relationship between eye angles and tilt angles

Because of the orientation of the mouse orbit, counter-rotation of the eye about either the pitch or roll stimulus axis would be expected to manifest, in this 2D oculography, as changes in both vertical and horizontal eye position. To aid in assessing the degree to which the eye positions reflect this geometrical consideration, we overlaid plots of eye position versus tilt with the predicted relationships. The predictions were based on the assumption that the eye rotates about an axis parallel to the stimulus axis with a gain (eye rotation/tilt angle) of 0.53 for pitch and 0.52 for roll. These gains had been selected as follows: We measured the slopes of vertical eye position vs. head orientation over the central ±30° of pitch or roll in the light, obtaining values of 0.25 and 0.46, respectively (see Results). These slopes are actually only a fraction of the tiltMOR gains; the observed ocular responses to pitch and roll should be cosX and sinX times the true gains, respectively, where X is the horizontal angle of the mouse optic axes from the midline. We found X to be 62°, based on the average of the absolute horizontal eye positions in the pitch and roll tilt series at the neutral gimbal position (roll = 0° and ∠L-B = −20°). Thus the observed ocular responses to pitch and roll should be 0.47 (cos62°) and 0.88 (sin62°) times the true gains, respectively, and we estimated the true tiltMOR gains to be 0.25/0.47 = 0.53 in pitch and 0.46/0.88 = 0.52 in roll. Finally, the predicted curves were forced to pass through the measured eye positions in the light at the neutral gimbal position. Thus for modeling the response to pitch rotations, vertical position was forced to pass through 19° and horizontal position was forced to pass through 63° at the neutral pitch orientation. For modeling the response to roll rotations, the corresponding numbers were 18° for vertical and 61° for horizontal position. Since this model was used purely to determine the expected 2D motion of an eye moving in 3D, no attempt was made to account for additional complexities such as the nonlinear relationship between firing rate and tilt angle in otolith organ primary afferents (see Discussion).

Supplementary Material

01

Supplemental figure 1: Demonstration of session-to-session variability of R_P0. R_P0 values are plotted for 13 C57BL/6 mice in which calibrations were performed on 3 or more days. Animals have been arranged in ascending order of mean R_P0.

Abbreviations

aVOR

angular vestibulo-ocular reflex

OKR

optokinetic reflex

MOR

maculo-ocular reflex

tiltMOR

tilt maculo-ocular reflex

transMOR

translation maculo-ocular reflex

L-B

lambda-bregma

CR

reference corneal reflection

AOJ

atlanto-occipital joint