Relationship of Ca²⁺ sparks to STOCs studied with 2D and 3D imaging in feline oesophageal smooth muscle cells

Abstract

1. We recorded Ca²⁺ sparks and spontaneous transient outward currents (STOCs) simultaneously in smooth muscle cells using whole-cell patch recording and a unique, high-speed widefield digital imaging system to monitor fluo-3 fluorescence in both two and three dimensions (2D and 3D).

2. In 2D imaging, the correlation between the amplitude of a spark and its corresponding STOC was a weak one, and 27 % of the sparks failed to cause STOCs. The STOCless sparks were not significantly different in amplitude from those that caused STOCs.

3. Three-dimensional imaging disclosed that STOCless sparks were located close to the cell surface, and on average their apparent distance from the cell surface was not significantly different from the sparks that cause STOCs.

4. Statistical evaluation of spark clusters disclosed that there were regions of the cell where the probability of spark occurrence was high and others where it was quite low.

Since calcium ions serve as intracellular signals for many processes, mechanisms must exist to allow cells to respond in distinct ways to different Ca²⁺ signals. One such mechanism appears to involve restricting the elevation in cytosolic Ca²⁺ concentration ([Ca²⁺]_c) to a small region of the cell, or ‘microdomain’, where the calcium ions exert their action (Berridge, 1997). These localized Ca²⁺ signals may be due either to Ca²⁺ influx from the exterior or to release of Ca²⁺ from internal stores. The latter are of two types: Ca²⁺‘puffs’ (Parker & Yao, 1991), mediated by inositol 1,4,5-tris-phosphate receptor activation, and Ca²⁺‘sparks’ mediated by ryanodine receptors (RyR) (Cheng et al. 1993; Tsugorka et al. 1995).

Ca²⁺ sparks in smooth muscle cells are of special interest because they cause synchronous activation of Ca²⁺-activated K⁺ channels, most probably of large conductance (BK channels), resulting in the appearance of spontaneous transient outward currents (STOCs; Bolton & Imaizumi, 1996). Since the BK channels underlying a STOC constitute a target for Ca²⁺ released during a spark, the spark-STOC relationship is worth examining to gain insight into how Ca²⁺ acts on a target within a microdomain. This same phenomenon is also found in neurons where the currents are called spontaneous transient miniature outward currents (SMOCs; Brown et al. 1983), although the underlying local neuronal Ca²⁺ transients have not been observed. The physiological significance of Ca²⁺ sparks in smooth muscle has been the source of considerable interest since the work of Nelson et al. (1995), which implicated sparks in mediating relaxation of arterial smooth muscle. Moreover, in a previous study we have suggested that Ca²⁺ sparks also play an important role in the stabilization of membrane potential or the generation of contraction (ZhuGe et al. 1998a) in airway smooth muscle. Hence, Ca²⁺ sparks seem to have physiological significance in their own right and are not simply elementary units of global Ca²⁺ elevation (ZhuGe et al. 1998c).

While STOCs have been studied extensively in smooth muscle, information on Ca²⁺ sparks is meager by comparison since most studies have involved recordings of STOCs alone (Bolton & Imaizumi, 1996). Furthermore, simultaneous recordings of sparks and STOCs in the same cell have appeared in only four studies, (Mironneau et al. 1996; ZhuGe et al. 1998a, 1999; Perez et al. 1999). Of these, only two examined the correlation between the magnitude of the sparks and the membrane currents recorded simultaneously (ZhuGe et al. 1998a; Perez et al. 1999).

The present study provides a characterization of Ca²⁺ sparks and STOCs recorded simultaneously in single, freshly dissociated circular smooth muscle cells from the body of the oesophagus of the cat. Characteristics of STOCs from these same cells were the subject of an earlier study from this laboratory (Sims et al. 1990), which examined properties of STOCs over a range of potentials under varying ionic conditions. In that study it was demonstrated that the zero current potential for all spontaneous currents shifted by 58.9 mV for a 10-fold difference in [K⁺]_o with a constant internal [K⁺]. Hence the STOCs in this cell type are due to an uncontaminated K⁺ current. The results of the present study add to the direct evidence that Ca²⁺ sparks cause STOCs. We also found that a substantial fraction of Ca²⁺ sparks do not elicit STOCs, and that such STOCless sparks generally occur in the vicinity of the plasma membrane. The localization of STOCless sparks was verified by 3D imaging of Ca²⁺ sparks which was carried out in this study for the first time by using a unique widefield, high-speed, digital imaging system. Finally, by means of a novel analytical tool we show that the sites of spark generation are not randomly distributed throughout the cell. Some of this work has appeared earlier in abstract form (Kirber et al. 1996, 1997, 1998).

METHODS

Preparation of dissociated cells

Adult cats were anaesthetized with ketamine (30 mg kg⁻¹; i.m.) followed by pentobarbital (30 mg kg⁻¹; i.p.). When deep anaesthesia was achieved, the stomach and oesophagus were removed intact, following which the animal was killed by exsanguination. All animal care and experimental procedures were carried out in accordance with regulations of the Animal Care Committee of Rhode Island Hospital. The stomach and oesophagus were opened with a longitudinal incision along the lesser curvature of the stomach, which was continued along the oesophagus. The mucosa and the collagen covering the circular smooth muscle layer were removed. Strips of circular smooth muscle were cut away from the longitudinal layer. The strips were approximately 0.5 to 1 mm wide and were cut along the long axis of the cells across the oesophagus, so that the length of the strips was the same as the inner circumference of the oesophagus. The dissection was carried out in modified Krebs solution, containing (mM): 118.5 NaCl, 4.7 KCl, 2.5 CaCl₂, 1.2 KH₂PO₄, 1.2 MgCl₂, 24.8 NaHCO₃, 10 glucose, continuously bubbled with 95 % O₂-5 % CO₂. Dissociation of smooth muscle cells was carried out in a Hepes buffered nutrient solution (HBNS), containing (mM): 126 NaCl, 3 KCl, 10 Hepes sodium salt, 2 KH₂PO₄, 1 MgCl₂, 0.5 CaCl₂, 0.05 EDTA, 11 glucose, soy bean trypsin inhibitor (Worthington, Freehold, NJ, USA) (40 mg (500 ml of solution)⁻¹), and amino acid supplement B6766 (Sigma, 50 × solution, 20 ml (500 ml of solution)⁻¹). Papain (Fluka, Buchs, Switzerland), dithiothreitol (DTT), bovine serum albumin (BSA) and collagenase (Worthington Type 2) were added to vials holding 4 ml of HBNS each. The final concentrations were: papain, 2 mg ml⁻¹ (based on an activity of 10-13 units mg⁻¹); DTT, 1 mM; BSA, 0.1 %; and collagenase, 50-100 units ml⁻¹. After all enzymes had been added to the HBNS, 5 to 10 strips of tissue were added to each vial. The airspace in the vial was replaced with 100 % O₂ and the vials were stored at 4°C overnight. The next day a vial was placed in a water bath at 37°C and agitated at about 1 oscillation per second for 20 min while being gently bubbled with 100 % O₂. The tissue was removed with forceps and rinsed in a vial of oxygenated HBNS for several minutes. The strips were then placed in 1-2 ml of oxygenated HBNS and gently triturated with a wide mouth disposable pipette until the solution became cloudy. The solution was examined for relaxed cells, the strips resuspended in 1-2 ml of HBNS, allowed to sit for several minutes and the trituration repeated. Vials of dissociated cells were stored at 4°C until use.

The imaging of changes in [Ca²⁺]_c was carried out with the non-ratiometric Ca²⁺ indicator fluo-3. The resting [Ca²⁺]_c was also determined ratiometrically using fura-2, and the resting value typically ranged between 70 and 100 nM. This value for resting [Ca²⁺]_c is comparable with values found in other smooth muscle cells.

Solutions

All experiments were carried out in physiological salt solutions containing (mM): 127 NaCl, 3 KCl, 1 MgCl₂, 10 Hepes, 2 CaCl₂, pH 7.4 (NaOH). Unless otherwise specified, patch pipette solutions contained (mM): 100 KCl, 3 MgATP, 20 mM Hepes, 100 μM EGTA, 50 μM fluo-3, pH 7.2. Fluo-3 and fura-2 were obtained from Molecular Probes (Eugene, OR, USA) and other chemicals unless specified were from Sigma (St Louis, MO, USA).

Instrumentation, data acquisition and analysis

Fluorescence measurements were carried out using a novel high-speed digital imaging microscope, developed by the Biomedical Imaging Group at the University of Massachusetts Medical Center. A diagram of the basic system configuration used is shown in Fig. 1, and described in the legend for that figure. The camera for the system was a high-speed, low-noise, thermoelectrically cooled charge-coupled device (CCD) camera developed in collaboration with MIT Lincoln Laboratory, Lexington, MA, USA. The array size was 128 × 128 pixels, and each pixel imaged 400 nm per side in these experiments. This camera had four digital outputs which are connected to two Data Raptor (Bit Flow Inc., Bedford, MA, USA) frame-grabber boards installed in a PC. The images were collected and stored in the frame-grabber memory, which could hold 8 Mbytes of information (200 images). The objective of the microscope travelled on a piezoelectric translator, allowing the PC to control the focus. The same PC had an analog-to-digital converter which digitized the whole-cell patch clamp current as well as the position of the objective, the image readout times and the membrane potential. Thus, the exact timing of the electrophysiological events in relation to the acquired images was known. Simultaneous patch clamp recordings were done with an Axopatch-1D amplifier (Axon Instruments Inc., Foster City, CA, USA). The current records were low-pass filtered with a cut-off frequency of 200 Hz and then sampled at 1 kHz. For 2D imaging, a 5 ms exposure was obtained every 15 or 16.76 ms. A × 40, 1.3 NA oil immersion objective was used. Three-dimensional imaging was accomplished by continuously moving the objective of the microscope so as to focus through the thickness of the cell every 26.5 ms. (See legend to Fig. 1). For the 3D imaging a × 40, 1.15 NA water immersion objective was used. In both 2D and 3D imaging, fluorescence images were normalized to represent the fractional change in fluorescence from a resting level. Thus, the fluorescence changes due to localized changes in Ca²⁺ were clearly shown, and potential uneven dye distribution was compensated for within the cell.

Figure 1. High-speed wide-field digital imaging microscope for 2D and 3D imaging.

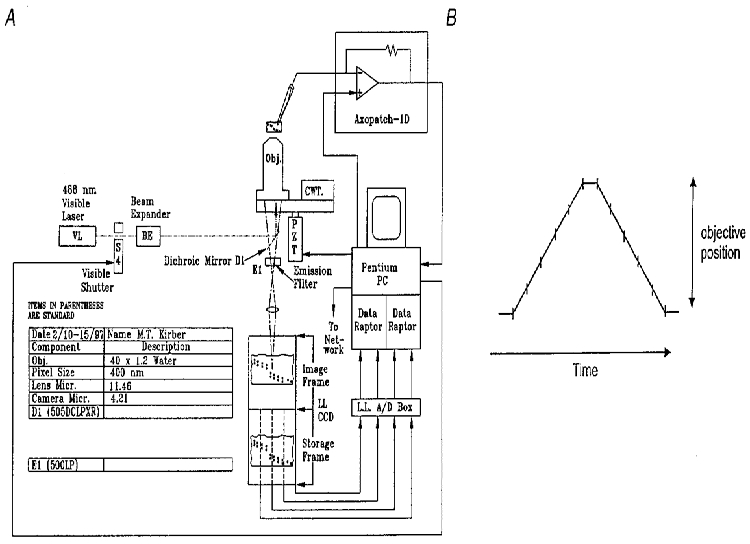
A, diagram of the system configuration. Light from a laser source (VL; argon krypton tuned to emit 488 nm light, Coherent Inc., Santa Clara, CA, USA) is passed through a beam expander (BE), electronically controlled shutter, and is used to excite the Ca²⁺ indicator fluo-3. The laser light is reflected by a dichroic mirror in the microscope body, passes through the objective and illuminates the cell. The fluorescent light emitted by the fluo-3 in the cell, which is at a longer wavelength centred near 530 nm, passes through a dichroic mirror and long-pass filter and is reflected to the camera (see Methods). The camera has four digital outputs which are connected to two frame-grabber boards installed in a Pentium PC. A piezoelectric translator is connected to the objective of the microscope, allowing the PC to control the focus. The same PC has an analog-to-digital converter which digitizes the whole-cell current, the position of the objective, the image readout times, and the membrane potential. Patch clamp recordings were done with an Axopatch-1D (Axon Instruments) patch clamp amplifier. The current records were low-pass filtered with a cutoff frequency of 200 Hz and then sampled at 1 kHz. B, schematic diagram showing method for 3D imaging. The objective was moved rapidly so that its focus scanned through the thickness of the cell in a triangular wave pattern as shown. Each image resulted from the continuous collection of light while the objective was moved over a 1 μm thickness. In some experiments five 1 μm thick planes were obtained, and in others, seven. A pause of several milliseconds was used at the top and bottom of the scans so as not to create shock waves through the water coupling of the immersion objective to the coverslip. The information collected at the top and bottom planes, when the objective was not moving, was discarded. Each exposure was 4 ms. When five image planes were acquired, a 3D set was obtained every 26.5 ms; when seven planes were acquired, a 3D set was obtained every 34 ms.

For analysis of whole-cell currents and sparks localized in 3D, STOCs were detected using a custom algorithm which detects peaks in the whole-cell current and then estimates the amplitude of those peaks. A 10 ms running average of the whole-cell current was computed to minimize noise, and the peaks in the running average were used to locate the peak in the recorded whole-cell current. Adjacent valleys in the current records were also identified using the running average. The amplitude of the STOC was then computed by taking the difference between the current at the time point identified as the peak and the average of the current in the valley occurring before and after the peak. In order to separate a STOC from random whole-cell current noise, a threshold of 10 pA was applied. Unless otherwise stated, numerical values are reported as means ± standard error of the mean, with n observations. P values less than 0.01 were considered significant.

Three-dimensional imaging and the localization of a spark within a cell

The 3D image sets were processed to remove out-of-focus fluorescence, using an algorithm developed for this purpose (Carrington & Fogarty, 1987; Carrington et al. 1995) based on an iterative, constrained, regularized least-squared error approach. This algorithm makes use of estimates of the point spread function (PSF) of the microscope system based on images collected using 0.2 μm fluorescent beads which were employed to approximate a point source of light. The algorithm estimates a non-negative object (O_xyz) that minimizes the sum of the least squares fit to the imaged data (D_xyz) and a weighted smoothing term (α||O_xyz||²):

where the asterisk denotes convolution in 3D. Before applying the restoration algorithm to 3D images of Ca²⁺ sparks, we considered two new characteristics of these 3D images that may affect the ability of the algorithm to reconstruct the 3D distribution of fluorescence due to fluo-3. First, this algorithm has been previously applied to 3D data sets composed of a series of optical sections gathered at fixed focus positions (Carrington et al. 1995). The fluorescence signals recorded here, however, have incurred additional axial blurring because the focus was continuously moved while the sparks were imaged. This additional blurring can be compensated for by altering the point spread function. Therefore, we estimated the PSF by imaging a 200 nm fluorescent bead using the same focusing protocol as was used for the 3D imaging of the sparks. Second, the changes in [Ca²⁺] being monitored should ideally be much slower than the time needed to gather a complete 3D data set. This was not always the case for the data obtained here. The effect of such relatively rapid changes in [Ca²⁺] on the restoration could not be easily analysed. Therefore, we carried out a set of computer simulations of the imaging and restoration of modelled Ca²⁺ sparks (Kirber et al. 1998). Our purpose in doing these simulations was to establish whether the algorithm which we employed would allow us to localize the site of a Ca²⁺ spark reliably in three dimensions within the cell.

The simulations were carried out as follows. A Ca²⁺ spark was modelled as a spatially symmetric, Gaussian intensity distribution with a full width, at half maximal intensity, of 1.3 μm. Images of this modelled spark were generated with a pixel size (in x,y) of 0.1 μm and 20 focal positions (in z) spaced at 0.25 μm. The intensity of the modelled spark was allowed to vary between focus positions, in order to simulate temporal changes in [Ca²⁺] in the spark data. Pixels were then summed axially and transversely to generate five optical sections having 0.4 μm by 0.4 μm by 1 μm voxels (x, y and z, respectively), which mimicked the imaging protocol used on the real sparks. Four cases were considered. In these cases the imaged spark was: (1) of constant intensity, (2) in its rising phase, (3) at its peak (i.e. rising and then falling), or (4) in its falling phase. At the beginning of the time course for each of these conditions, the focus lay at the bottom plane, where the spark was located, and moved up as the spark evolved. These simulated sparks were convolved with a theoretically derived point spread function (Tella, 1985) for a 1.15 numerical aperture water immersion lens such as the one used in our experiments. The resulting images (columns at upper right of Fig. 2) represent the raw data that would be gathered by the imaging system of a spark in isolation, without adding the complications of a cell in the background. In all cases but one, the location of the spark, taken as the position of peak intensity, was correctly identified from this output. However, when the spark intensity was rising while the focus was moving away from the spark site (Fig. 2, upper right, column labelled ‘rising’), it was not possible to determine where the spark was located from the simulated raw data.

Figure 2. Simulated Ca²⁺ sparks and their images, as would be obtained with the high-speed digital imaging system functioning in 3D mode.

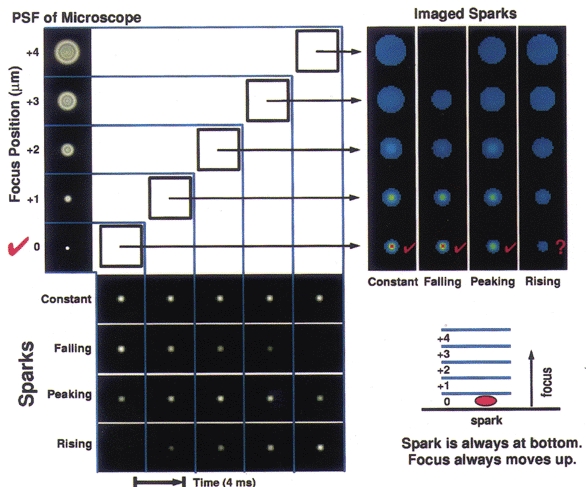
At the lower left, each of three phases of a simulated spark is shown: a rising phase, a peak (rising then falling), and a falling phase; also a control where the brightness remains constant. The spark is always located in the bottom-most plane. As shown at the upper left, the simulated sparks are then convolved with the point spread function (PSF) of the microscope for each of the five planes. At the upper right, the results of the convolution are shown, with each column representing one of the time courses shown in the rows at the lower left. Hence, when one reads each of these columns from bottom to top, one sees the series of images that would be recorded from the microscope as the objective moves away from the plane containing the spark. The scale bar indicating the relative amplitude for this figure is shown in Fig. 3. The microscope movement is represented diagrammatically at the lower right. In this simulation the microscope was focused from the bottom to the top plane at a constant velocity of 1 μm (4 ms)⁻¹. Images were recorded every 4 ms.

To complete the simulation, a smooth muscle cell was modelled as a 5 μm diameter cylinder having uniform fluorescence that was equivalent in brightness to the fluo-3 at resting Ca²⁺ levels observed in the oesophageal cells. The modelled cell was processed in the same way as the sparks in Fig. 2. The resulting images of the cell were then added, voxel by voxel, to the corresponding images of the sparks for each of the four cases in Fig. 2, thus simulating sparks occurring against a background of cellular fluorescence. The sparks represented a peak increase in fluorescence of 30 % over the background, which was a typical peak observed value in the experiments. The resulting images were then subjected to image restoration. Figure 3, left, demonstrates this process for the case of a spark of constant amplitude. The four results are summarized on the right of Fig. 3. In all cases, the location of the spark was correctly identified. Of particular note, for the case of the rising spark, location was now correctly determined even though it could not be determined from the raw data (see Fig. 2). As we might expect for this ‘worst-case’ scenario, the amplitude of the spark is not accurately estimated. However, since the decay time of actual sparks is much slower than the rise time (see Results), relatively few sparks will be captured exclusively during their rising phase as the objective is focusing away from their location during the onset. Thus, estimated amplitudes will, in general, be far more accurate than the ‘worst-case’ and we can attach considerable confidence to the localization of the sparks in the present study.

Figure 3. Simulations of sparks within a cell of constant fluorescence and the effects of image restoration.

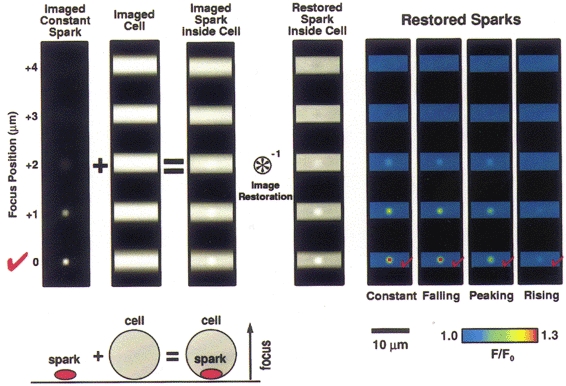
Simulated sparks (of the sort shown in Fig. 2) were added to a cylinder of constant fluorescence, simulating a spark within a cell, as represented by the diagram lower left (drawing not to scale). The upper left portion of the figure shows images of the case where the spark remains constant during the imaging sequence. The spark was then added to a simulated cell image. The cell was simulated as a cylinder 5 μm in diameter with the long axis lying perpendicular to the axis of focus; the cell was ‘filled’ with a fluorescence background equivalent to the fluo-3 fluorescence at rest (100 nM) observed in the cells used in the experiments here. The spark images represented 30 % peak changes above resting level similar to experimental data (see below). The combination was subjected to image restoration by deconvolution (see Methods). The restored, simulated sparks are shown at the right for the four different time courses considered in Fig. 2. In all cases it was possible to correctly identify the location where the spark occurred within the five plane 3D data set.

RESULTS

Simultaneous two-dimensional imaging of Ca²⁺ sparks and recording of STOCs

Ca²⁺ sparks and membrane currents were recorded simultaneously using the high-speed digital imaging system and whole-cell recording configuration shown in Fig. 1. This widefield system permitted the simultaneous imaging of a large portion of the cell and at times the whole cell. Whole-cell recording monitors currents from the membrane of the entire cell. Thus, the Ca²⁺ spark responsible for a given STOC could usually be found, and the relationship between the spark and STOC established. An example is shown in Fig. 4A and B. Here a single Ca²⁺ spark elicited a well isolated STOC. Although the Ca²⁺ spark was of substantial amplitude (almost doubling the fluorescence), it did not elicit other sparks or trigger a wave. The lower trace in Fig. 4B represents the fluorescence in a 3 × 3 pixel region (each pixel, 400 nm on a side) which was centred at the spark's brightest point.

Figure 4. Rapid 2D imaging of a Ca²⁺ spark with simultaneous whole-cell recording of the elicited STOC.

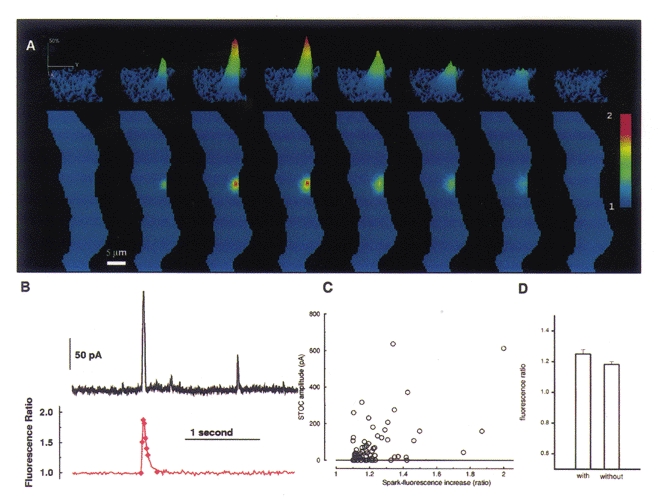
A, images of the evolution and decay of a single Ca²⁺ spark. The lower panels show the portion of the smooth muscle cell which was imaged, in this case almost the entire cell. The upper panels show a contour plot of the region of cell where the Ca²⁺ spark occurred. Each image results from a 5 ms exposure at the time indicated by the diamonds in the lower trace in B. (In the contour plots the spark appears flattened to the right where the overlying plasma membrane lies, whereas it spreads out into the cytosol to the left. The edges of the cell were estimated manually from raw fluorescence images taken before the spark occurred.) B, the time course of the Ca²⁺ spark (lower trace) shown in A and the STOC elicited by it (upper trace). The time course in the lower trace tracks the average fluorescence in a region 3 × 3 pixels (each pixel, 400 nM on a side) centred at the peak of the spark. (The diamonds on this trace mark the times that the images in A were acquired.) The rising phase of the fluorescence and of the current occurred virtually simultaneously. The membrane potential was held at 0 mV, and the current was sampled every millisecond. C, the relationship of peak spark and STOC amplitudes for a series of 71 sparks. Spark amplitudes are plotted along the abscissa and STOC amplitudes along the ordinate. STOCless sparks are assigned a zero ordinate value. D, there is no significant difference between the mean amplitude of sparks which generate STOCs and the mean of sparks that do not (P = 0.15, Student's t test).

We examined the relationship between the amplitude of 71 sparks and the STOCs they caused as shown in Fig. 4C. Nineteen of the sparks (27 % of the total) elicited no detectable STOCs, and these are shown at the zero level of the ordinate. The correlation between the amplitudes of the sparks and STOCs is weak, but statistically significant; the Spearman rank order correlation coefficient is 0.32 (P = 0.006), and 0.38 (P = 0.005) if the STOCless sparks are omitted from the calculation. If we compare the amplitudes of the sparks which generated STOCs with those that did not, we find no significant difference in the mean amplitudes (P = 0.15, Student's t test, Fig. 4D). These facts suggest that the mechanism linking sparks to STOCs is more complicated than a simple relationship between the apparent local Ca²⁺ concentration as indicated by fluo-3 fluorescence and resultant differences in the probability of the nearby BK channels being open.

Non-uniform spatial distribution of Ca²⁺ spark frequency

With the widefield imaging system, there was an impression from the first that the observed spatial pattern of sparks within a cell was non-uniform, with certain regions of the cell repeatedly generating sparks and others quiescent (Kirber et al. 1997). We therefore carried out a statistical test to determine whether this impression of clustering was real. The null hypothesis was that the observed clustering of sparks was not different from random clustering that could occur in a sample set of the same size drawn from a uniform distribution (i.e. every pixel within the 2D image of the cell had an equal probability of generating a spark). The point of the test was not to determine the probability of drawing precisely the observed pattern of sparks by chance. It was rather to determine how probable it was to draw by chance a pattern that differed to the same degree from a uniform distribution. The measure of difference was the sum of the squared differences from a uniform distribution (Cressie, 1993; Besag & Diggle, 1997). The test was carried out as follows.

To test for spark clusters of varying size, we constructed a 2D map of spark frequency and location by assigning to each pixel a value of 1, if the peak of one spark occurred there; 2, if two sparks occurred there, etc. Such maps were made for two cells where we had determined the locations of a significant number of sparks (33 sparks and 23 sparks, respectively). An example of this for one cell is shown in Fig. 5A1. We convolved the image of spark locations (such as in Fig. 5A1) with a disk of unit amplitude and varying radii. The resulting value of the convolution at each pixel is the number of sparks within the disk centred at that pixel. Figure 5A2 provides an example of the result of such a convolution using a disk with a radius of 5 pixels. The resulting plot provides a measure of the relative frequency of spark occurrence, and hence of clustering of sparks, in different regions of the cell. The convolution was repeated for disks of radii varying from 1 to 6 pixels.

Figure 5. Two-dimensional imaging reveals non-uniform spatial distribution of spark locations within the cell.

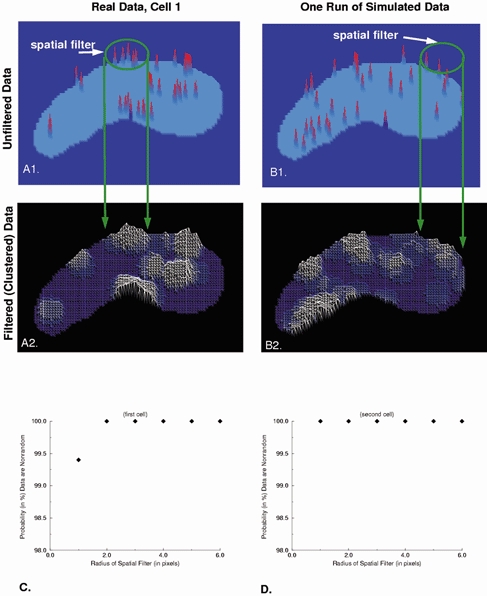
In order to assess the non-uniform nature of the distribution of spark locations quantitatively, the analysis which is described in detail in the text was carried out. A, each spark location obtained in the 2D imaging sequences was assigned a value of 1 when one spark occurred there, a value of 2 if two occurred, etc. (A1). Then the output illustrated in A1 was convolved with a disk 5 pixels in diameter and unit value (i.e. the spatial filter illustrated in A1). B, simulated outputs generated by a randomly sampled uniform distribution (using the same number of sparks) processed in an identical manner. The amplitude of the contour plots in A2 and B2 are proportional to the average number of sparks within the area of the disk. The contour plots generated from random distributions (but having the same finite number of sparks as the experimental data in A1) also show clustering behaviour. C and D, the clustering behaviour of the experimental data and simulated random data differed for each of two cells for spatial filters of different radius. The measure chosen for comparison was the sum of the squared difference at every pixel from a uniform distribution.

For comparison with these data, simulations having the same number of sparks as the real data were generated by randomly sampling from a uniform distribution. Spark locations generated from a uniform distribution will exhibit random clustering (Fig. 5B 1). Thus, it was necessary to compare the degree of clustering in the real data to that seen in the simulated data. To do so, the simulated spark maps were convolved with a disk in the same way as the real data. The resulting plot for simulated data for a disk with a radius of 5 pixels is shown in Fig. 5B 2. In order to compare them with one another, we compared the results of each of the two convolutions (i.e. for both the real and simulated spark data as illustrated in Fig. 5A2 and B2) to a uniform distribution. The measure chosen for the comparison between the output of each convolution to a uniform distribution was the sum of the squared difference, at every pixel, between the output of the convolution and the uniform distribution. This comparison was carried out for each simulation, and the simulation was repeated. If the sum of the squared differences were greater for the real data than for the simulated data 900 times out of the 1000 simulations, then we conclude that the probability that the observed sparks were not generated by a uniform distribution was 0.9 or 90 %. This same procedure was then repeated 1000 times for each disk size shown on the abscissa in Fig. 5C and D. As seen, even for a disk radius of 1 pixel (400 nm) the probability that the observed distributions were being generated by something other than a uniform distribution is greater than 99 % for cell 1 and greater than 99.9 % for cell 2. This increases to greater than 99.9 % for both cells for radii values of 2 to 6 pixels.

Given specific knowledge of the 3D geometry of the cell, there may be cases where a uniform 2D distribution is inappropriate for generating artificial random data. In addition, we might wish to incorporate prior knowledge, for example increased probability of spark generation near the membrane, and test for clustering variations tangential to the membrane surface. This can be done by analysing only an annular region including the edges of the 2D image. The diameter of the spatial filter disk is large with respect to the width of the annulus. Computations are made as the centre of the disk passes along the centre of the annular band. Clustering information depending on distance from the plasma membrane is lost (integrated out), and only variations along the length of the annular band are tested for. We applied this method to the data from the same two cells used for Fig. 5C and D. The width of the annulus used was 5 pixels (2 μm) and this was also the radius of the spatial filter disk. In 1000 trials the clustering seen in the real data exceeded clustering in the randomly generated data containing the same number of sparks in the annular region of interest. Therefore the probability that these cells contain regions which are more likely to give rise to sparks is greater than 99.9 % for these two cells.

Simultaneous three-dimensional imaging of Ca²⁺ sparks while recording STOCs

One possible explanation for the failure of some sparks to cause STOCs is that such sparks do not arise close enough to the plasma membrane. The 2D images suggested that this was not the case since some STOCless sparks were clearly located at the edge of the outline of the cell. However, it is possible that a spark might appear to lie at the cell's edge with 2D imaging but actually lie deeper inside it. (This would happen if we were not focused at the z-plane where the cell was widest (Fig. 7).) In order to address this issue, sparks were localized in the z-axis using 3D imaging. Three-dimensional images of two Ca²⁺ sparks occurring at different times and locations in the same cell are illustrated in Fig. 6A and B, with corresponding 2D projections to the left. Both these sparks caused STOCs as can be seen from the traces of Fig. 6C. The large spark in Fig. 6A is centred on the 1 μm plane second from the top; and the smaller, briefer spark in Fig. 6B is centred on the second plane from the bottom in the five plane stack. The fluorescence change in a 3 × 3 pixel region (i.e. 1.44 μm²) centred in the plane and on the location of highest intensity is shown for each spark in Fig. 6C; the simultaneously recorded whole-cell current is also shown in Fig. 6C. (The diamonds on the traces in Fig.6C correspond to the time of the images in the white frames in 6A and B, that is, the second and fourth rows from the top, respectively.) An example of a spark that failed to cause a STOC is shown in Fig. 7A. The associated current trace (showing no corresponding outward current) and fluorescence at the centre of the spark, in the plane of origin, is shown in Fig. 7D. It is apparent that this STOCless spark lies adjacent to the plasma membrane, because it is clearly flattened at the edge of the cell's silhouette. This is corroborated by the 3D imaging which shows that the location at the edge is not an artifact of the plane of focus. Figure 7B illustrates schematically how a spark could appear to be nearer the cell surface in a 2D image than it actually is. As illustrated, this can be the case even when the spark appears to lie at the lateral edge of the cell in a 2D image.

Figure 7. Localization of STOCless sparks in 3D.

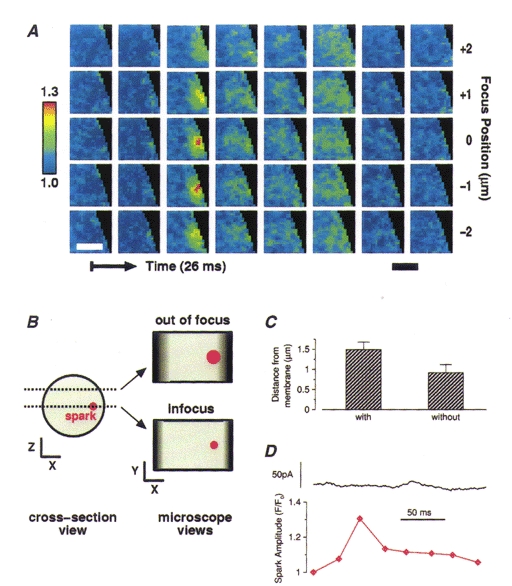
A, images from a 3D set (acquired and restored as discussed in Methods) of a spark which did not elicit a STOC. This spark occurred at a lateral surface of the cell. 3D imaging corroborated its location close to the cell surface. The same conventions are used here as in Fig. 6. B, this diagram illustrates how a spark which actually lies farther from the membrane can appear to lie at the very surface. On the left is shown a cell seen in cross-section with two z-planes marked with dotted lines; here the actual spark outline is shown in red. On the right the spark is shown as it would appear in a 2D image if the plane of microscope focus was at one z-plane or the other. The darkened areas at either side of the cell outline indicate the area where the cell outline would be ambiguous. Note that if the microscope is focused at a z plane different from where the spark lies, the spark appears to be closer to the cell surface than it actually is. 3D imaging resolves this discrepancy as illustrated above in A. C, average estimated distance to the surface membrane for those sparks that caused STOCs and those that did not. Although the mean for the STOCless sparks is smaller, the difference between the two groups is not significant (P = 0.05, Student's t test). The distance to the nearest point on the cell surface was estimated by choosing the least of three values: the distance to the closest lateral point on the surface in the plane where the spark was brightest, the distance to the ‘top’ surface, or the distance to the ‘bottom’ surface. (When the peak of the spark appeared in one of the extreme planes imaged, i.e. top or bottom plane, the distance assigned to the top or bottom surface was 0.5 μm for a 7-plane image set and 1.5 μm for a 5-plane image set.) The maximum distance to a cell surface was thus 3.5 μm. D, time course of the whole-cell current and the fluorescence at the voxel of maximum brightness ratio associated with the images in A, showing no outward or inward current associated with the change in Ca²⁺.

Figure 6. Three-dimensional images of two Ca²⁺ sparks from the same cell.

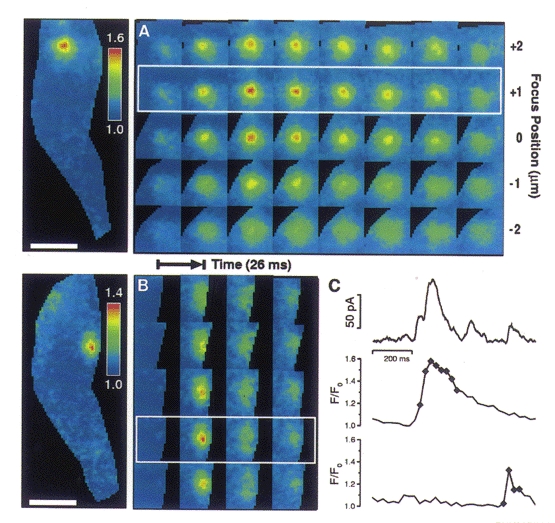
A and B, images track a large, long duration spark located near the top of the cell (A) and a smaller, shorter duration spark located near the bottom of the cell (B). Each row represents a series of images taken in one plane. Five planes with 1 μm spacing were imaged; each exposure took 4 ms, and an entire 3D set through the five planes (one column) was obtained every 26.5 ms. The image of the whole cell at the left in A and B represents a planar projection of all the images in the third column of A and the second column of B; in each case this column contains the image capturing the maximum brightness of the spark. C, time course of the membrane current from the whole cell (uppermost trace), and the time course of the change in fluorescence for the spark in A (middle trace) and for the spark in B (lowermost trace). The fluorescence in each of these traces is the mean value in a 1.44 μm² area (3 × 3 pixels, each pixel 400 nm on a side) where each spark is brightest and in the plane where that spark is localized. In both A and B, the plane of relevance is denoted by a white frame. All 3D images were background subtracted followed by image restoration with a smoothness of 0.05, to remove out-of-focus information (Carrington et al. 1995). The axial resolution of the 3D images before and after restoration is approximately 1 μm, measured as the full-width distance at half-maximal intensity along the z-axis of the PSF. Background reference areas were chosen away from the cell. After deconvolution, 3D image sets were ratioed in the following way. A resting level 3D image was generated by determining the median value for each voxel over time. After compensating for bleaching, the difference between each image and the corresponding resting image (in the same plane) was divided by the resting image. The resulting image set represented the fractional change in fluorescence due to local calcium elevations. Each image was masked by tracing the cell outlines in the fluorescence images manually. The times corresponding to the images shown are marked. Pipette solution contained (mM): 130 KCl, 10 mM Hepes, 1MgCl₂ and 50 μM fluo-3 at pH 7.4.

We used our 3D data to compare the estimated distance to the nearest cell surface for sparks with and without STOCs (Fig. 7C). The boundary of the cell (i.e. the cell surface) was determined by the extent of the basal fluo-3 fluorescence. The distance to the cell surface was determined in both the z-axis and the x-y plane (see caption for Fig. 7C). The distance plotted was the smaller of the two, and hence the distances given are the shortest apparent distances to the surface. On average the sparks without STOCs and those that produced STOCs did not differ significantly (P = 0.05, Student's t test) in their distance from the cell surface. In fact the STOCless sparks had a lower mean apparent distance. Our data suggest that factors other than distance from the cell surface contribute significantly to the determination of STOC amplitude.

DISCUSSION

The present study describes Ca²⁺ sparks and their relationship to STOCs recorded simultaneously in the same smooth muscle cell. Such simultaneous recording provides additional direct evidence that Ca²⁺ sparks cause STOCs. However many sparks fail to cause STOCs, and the relationship between a spark and the corresponding STOC appears to be more complex than previously suspected. Moreover, through the use of a high-speed, widefield digital imaging system, we have been able to localize the sparks in three dimensions within the cell. These images confirm that STOCless sparks lie close to the plasma membrane. Finally, we have developed a method to demonstrate that the sparks are not distributed uniformly in the cell.

The amplitude of a Ca²⁺ spark and corresponding STOC

Here we show that the correlation between the amplitude of the spark and the corresponding STOC is weak, suggesting that a factor or factors other than spark amplitude are significant determinants of STOC amplitude. Furthermore, there are sparks, some relatively large in amplitude and relatively close to the cell surface, which do not elicit STOCs. Hence the STOCless sparks cannot be explained simply by remoteness from the plasma membrane. These results raise several questions. Since some sparks do not cause STOCs, is there a class of sparks which have a function other than activation of BK channels? Are there microdomains which are devoid of BK channels? And is this perhaps an extreme of a spectrum of varying density of the BK channels? Or is the failure of some sparks to generate a STOC to be explained by the local regulation of BK channels, so that they become less sensitive to the elevation in [Ca²⁺] during a spark? The probability of the BK channels being in the open state (P_o) is known to be modulated by cellular processes such as phosphorylation (Kume et al. 1989; Carl et al. 1991; Robertson et al. 1993). However, in a cell at rest, it is not known whether the level of BK phosphorylation varies enough to alter the P_o of the channels sufficiently to affect spark coupling to STOCs.

Localization of Ca²⁺ sparks in 3D

In four previous studies of smooth muscle cells, it has been shown that Ca²⁺ sparks occur both close to the cell surface and relatively far from it. Mironneau et al. (1996) recorded sparks at a distance ranging approximately from 1 to 8 μm from the surface in rat portal vein myocytes. Nelson et al. (1995) found sparks at a distance ranging from 0.5 to 4 μm from the surface in rat cerebral arteries. Gordienko et al. (1998) reported that spontaneous sparks can occur far from the surface membrane; and Imaizumi et al. (1998) reported that the sites of sparks elicited by depolarization (i.e. ‘hot spots’) occur at a distance ranging from 1 to 3 μm from the surface. Whereas Mironneau et al. found the sparks fairly uniformly distributed, both Nelson et al. and Imaizumi et al. found that sparks occur more frequently near the cell surface. However, none of these studies indicated which sparks caused STOCs.

As in the studies quoted above, the present work on feline oesophageal cells indicates that Ca²⁺ sparks occur both near the surface and deeper within the cell. The distances we found ranged from less than 0.5 μm to more than 3 μm from the surface with a greater number lying closer to the surface. We found that both the sparks occurring close to the cell surface and those farther from it could cause STOCs.

While it is clear from our data that there are sparks which occur quite close to the plasma membrane but do not cause STOCS, the data on sparks which occur deeper within the cell must be interpreted with some caution. The exact location of the plasma membrane at the top and bottom could not always be unambiguously determined directly from the restored images of fluo-3 fluorescence, because the axial resolution in the images is less than the lateral resolution, even after image restoration. Hence, in those cases where the spark does not lie at the lateral edge of the cell, the apparent distance to the surface as determined from the 3D data may not correspond to the actual distance, because the surface of the cell may have bulges or depressions. That is, the cell surface may twist or fold in ways not apparent to the light microscope, so that the deep spark sites actually lie close to the sarcolemma. Another possibility is that some sparks may lie close to deep invaginations of the cell membrane. However, such invaginations, if they exist, have not yet been reported in electron microscopic studies. The deepest known invaginations in the smooth muscle membrane are caveolae, and these penetrate to a depth of less than 150 nm (Gabella, 1981). Hence caveolae do not run deeply enough to bring the sarcolemma into close apposition with the spark sites that lie several micrometres from the surface. These possibilities deserve attention, because there are a number of indications, which we have considered in detail elsewhere (ZhuGe et al. 1998b, 1999), that spark sites must lie quite close to the plasma membrane for STOCs to be elicited. For example, in amphibian gastric smooth muscle cells, STOCs are observed at membrane potentials of -80 mV or more negative. At these potentials, Ca²⁺ concentrations in the order of 10 μM are needed to achieve a P_o of 0.1 for BK channels in excised patches (Singer & Walsh, 1987). This also appears to be true of mammalian smooth muscle cells (Carl et al. 1996).

Ca²⁺ spark sites are not uniformly distributed throughout the cell

In comparing our data from 2D imaging with simulated data, we made the simplifying assumption in the simulation that a model of the cell with a uniform thickness (z-axis) was adequate. In the absence of having a membrane marker which can be simultaneously imaged with the sparks and yet not interfere with our measurements, we feel that this is a reasonable first approximation (see also Results). Any systematic error which could be generated by this approximation would most likely be associated with the edges of the cell, and there are no apparent activity changes seen at the edges throughout the images of spark clustering. In fact, the clustering is strikingly non-uniform with respect to any particular region of the cell. A previous study on guinea-pig ileal muscle noted that there were regions of the cell where there appeared to be a high probability of spark discharge (‘frequent discharge sites’) whereas there were no sparks in other regions (Gordienko et al. 1998). However, no statistical test was applied to these data to prove that the qualitative appearance of spatial non-uniformity of spark occurrence is real. In the present study we have devised and applied a statistical measure to demonstrate that spark sites are distributed in a non-random fashion, with sites where sparks occur at a relatively high rate and regions of the cell where there are no sparks. We have observed the same site (pixel) as being the source of multiple sparks. The likelihood of this being due to a uniform probability of spark occurrence within a region of the cell would be quite low. In addition, it is clear from observing Fig. 5A2 that within the areas of spark activity variations exist, with some regions showing greater activity. Consequently, areas of high spark activity probably do not simply represent irregular distribution of sarcoplasmic reticulum (SR) as has been proposed by Gordienko et al. (1998). These regions most likely represent functional differences within the SR, and/or the presence of specialized structures or local messenger molecules associated with spark generation. In the future it would be valuable to map the SR in 3D and test for regions of increased activity within the SR using the same method we have developed, extended to 3D analysis.