Modulation of primary afferent discharge by dynamic and static gamma motor axons in cat muscle spindles in relation to the intrafusal fibre types activated

Abstract

1. Recordings were made from muscle spindle primary afferents from medial gastrocnemius and soleus muscles of the cat to study the modulating effects of varying γ-motor stimulation frequency at constant muscle length. Stimulus trains had a mean frequency of 50 Hz and were sinusoidally frequency modulated at 1 Hz, with an amplitude of modulation of ± 5 to ± 30 Hz.

2. When dynamic γ-axons (γ_d) were selected for their pure effect on bag₁ fibres, they were found to have very little modulating effect on afferent firing.

3. Static γ-axons (γ_s) were tested with a random stimulus and correlation method to determine whether they acted purely on bag₂ fibres, purely on chain fibres or on both together. Pure bag₂γ_s-axons had weak modulating effects with large values of phase lag. Pure chain connections were effective in modulating with very little phase lag, but their mean gain was low. Mixed bag₂ and chain axons were most effective and showed phase shifts proportional to gain.

4. The effects of muscle length changes recorded previously from locomotor movements were also tested, with and without accompanying stimulation of mixed γ_s-axons with pulse trains recorded from γ_s-axons. This γ_s stimulation had a powerful effect in increasing afferent discharge during muscle shortening. The difference in afferent firing between the stimulated and non-stimulated conditions accurately predicted the profile of the γ_s stimulation.

5. The results are discussed in relation to the ways in which the γ-motor system may be used in natural movements.

Since the original discovery that γ-motoneurones could be divided into two classes (Matthews, 1962; Crowe & Matthews, 1964), called static and dynamic (γ_s and γ_d), there have been numerous attempts to determine their precise effects on the properties of muscle spindles and to work out how they are used in various motor tasks. There is, however, a complication; namely, the fact that there are three different intrafusal muscle fibre types, rather than just the two which were known at the time of the original γ_s/γ_d distinction (Banks et al. 1977). It was not until 1981 that the distinct functions of the two types of bag fibres were firmly established (Banks et al. 1981; Boyd, 1981), making it clear that the γ_d effect is exerted through bag₁ fibres, and the γ_s effect is produced jointly by bag₂ and chain fibres. Since the latter two are known to have very different properties, it is important to consider the function of the γ-motor innervation not simply in terms of classical static and dynamic effects, but rather to determine the separate effects of the three different intrafusal fibre types. This is now possible because of the availability of various physiological tests that can be used to indicate which intrafusal fibres are activated by a given γ-motor axon.

As a result of studies of isolated spindles from the tenuissimus muscle, changes in afferent discharge were first related to direct visualisation of which intrafusal fibres were contracting in response to γ-motor stimulation (Bessou & Pagès, 1975; Boyd, 1976, 1985). Subsequently, Boyd (1986) elaborated a physiological test for chain fibre activation based on 1:1 driving of primary afferent discharge during a ramp increase in γ-motor stimulation frequency. Since then the physiological methods of identification of bag₂ and chain fibre activation have been progressively refined (Dickson et al. 1993; Celichowski et al. 1994; Taylor et al. 1998), so that now one can determine with some confidence whether bag₂ or chain fibres or both are being activated by a given γ_s-axon.

Previous observations on γ-motor effects have generally been restricted to the action on afferent responses to stretch during constant high-frequency γ-motor stimulation, whereas during natural movements γ-motoneurone firing frequency fluctuates with particular relationships to the movements (Taylor & Appenteng, 1981; Murphy et al. 1984). In the present work, therefore, we concentrate on the effects of rhythmically varying the stimulation frequency and use frequencies of stimulation and of modulation which lie within the range observed in recordings during locomotor movements. By also using the above-mentioned physiological methods we have now been able to relate the potentiality of different γ-axons for modulating afferent discharge to the particular intrafusal fibres involved. By applying these methods to a large number of single γ-axons supplying medial gastrocnemius (MG) and soleus muscles we have obtained results which give insights into the possibilities for two types of static fusimotor output and into how γ_s activity normally interacts with muscle length changes. A preliminary account of some of the results has appeared in abstract form (Ellaway et al. 1996).

METHODS

The preparation

The cats used were adult females in the weight range 2.5-3.5 kg. They were deeply anaesthetised with sodium pentobarbitone (60 mg kg⁻¹i.p.). A tracheal cannula was provided for artificial ventilation and for monitoring end-tidal CO₂. A forelimb vein was cannulated on each side so that anaesthetic doses could be given separately from other drugs. Arterial blood pressure was measured via the right carotid artery. Body temperature was maintained close to 37 °C with a heating blanket, feedback controlled from a rectal probe. Anaesthesia was monitored by observation of blood pressure, end-tidal CO₂ and reflex responses to paw pinch, and was supplemented as necessary with intravenous doses of 12 mg sodium pentobarbitone in 1 ml saline. Particular care was taken to ensure deep anaesthesia before administration of succinylcholine (see below) and artificial ventilation was maintained during the short period of respiratory paralysis resulting from this drug. Animals were killed at the end of experiments with an intravenous overdose of pentobarbitone.

The left hip muscles and hindlimb were denervated save for the muscle in question, MG or soleus, the nerve to which was supported on a pair of silver hook electrodes for recording and stimulating. In the majority of the experiments (concerned with sinusoidally modulated stimulation), the relevant muscle tendon was separated and tied to an electromagnetic puller (Type V409; Ling Dynamic Systems Ltd, Royston, Herts, UK) operating as a displacement servo. In those experiments in which pre-recorded locomotor movements and γ stimulation patterns were involved, the tendons were left intact and controlled movements imposed by rotating the ankle joint with a servo mechanism (Taylor et al. 2000a). Pairs of 125 μm diameter silver wires were inserted into the muscle to record the electromyogram (EMG) to check for α-motor excitation. The left leg was supported by clamps on the knee and the foot. A leg pool was formed from skin flaps, filled with paraffin oil and kept at 35-37 °C by a radiant heat lamp. Leg pool temperature was checked by one thermistor probe under the sciatic nerve and another under the muscle. The animal was supported in a frame by a stereotaxic head holder and by clamps on the L2 vertebra and sacrum. After a lumbar laminectomy, the skin flaps were formed into a pool, which was filled with 3 % agar in saline. Once this was set, the centre was scooped out and filled with oil. Dorsal and ventral roots of L7 to S2 were cut close to the cord.

Afferent axon isolation

A multiple silver hook electrode array allowed for the recording from dorsal root filaments of between 6 and 12 single spindle afferent units, identified by muscle stretch, muscle twitch and by conduction velocity (CV). The latter was measured by backward spike-triggered averaging between the dorsal rootlet spike and the muscle neurogram. Spindle responses were also tested with succinylcholine (SCh: 200 μg kg⁻¹i.v. in 1 ml saline, single dose) during ramp and hold stretches, as described previously (Taylor et al. 1992a,b). The ramp stretches started from a length defined at the beginning of each experiment as L₀, the minimum in situ length, by placing a marker stitch on adjacent tissues in line with the ligature on the tendon before the tendon was cut. The maximum length was measured in some cases and found to be L₀+ 13.5 mm. Ramp stretches were of 5 mm, rising in 1 s, maintained for 1.5 s and falling in 1 s. Stretches were repeated continuously every 6 s. Spindle firing was monitored for all units as instantaneous frequency displays on the computer screen. Testing with SCh enabled each afferent to be designated as bag₁-chain, bag₁-bag₂-chain, bag₂-chain or chain, according to the evidence for its termination on the individual intrafusal fibres.

Isolation and testing of γ-axons

Natural ventral root filaments were separated and stimulated. If all-or-none action potentials could be detected in the muscle nerve in the CV range for γ-axons (15-45 m s⁻¹), the filaments were progressively subdivided until a functionally distinct unit was identified, with no evidence of α-motor involvement. During subsequent stimulation, the effectiveness of the stimulus and the absence of any further α- or γ-units were continuously checked on the muscle neurogram viewed with stimulus-triggered oscilloscope sweeps. For each γ-axon isolated the effect of stimulating at 100 Hz on the responses of the spindle afferents to ramp and hold stretches was tried. For each γ-axon with an effect on one or more of the afferents, the following tests were performed.

(1) Determination of its static or dynamic nature by stimulating at 30, 50 and 100 Hz during ramp and hold stretches, as above.

(2) Ramp frequency stimulation (Boyd & Ward, 1982) with trains of stimuli increasing linearly in frequency from 1 to 150 Hz in 2.5 s, repeated every 6 s, while maintaining length constant at L₀+ 4 mm for MG and soleus.

(3) Random frequency stimulation with a mean frequency of 50 Hz to give at least 5000 stimuli, with the length maintained constant at L₀+ 4 mm. The stimuli were triggered from a Geiger counter activated by natural uranyl acetate radioactivity. This ensured a completely random pulse train in which the inter-pulse intervals were exponentially distributed and in which the autocorrelation function was a pulse at the origin and flat elsewhere. It should be noted that no scaling or smoothing of the stimulus train was involved (cf. Petit et al. 1999). Subsequently, the firing of any spindle afferent affected was cross-correlated with the random stimuli in time bins of 1 ms. This process and its use for identifying which intrafusal muscle fibres were affected have been fully described (Taylor et al. 1996, 1998), but can be explained briefly as follows. If only chain fibres are affected, the correlogram shows a single large, narrow peak. If only bag₁ or bag₂ fibres are affected then the correlogram has only a small, broad peak or no obvious disturbance. If chain and bag fibres are both involved, a large narrow peak is present, which is accompanied by a second small, broad peak. Useful supporting evidence was obtained from examination of the results of the ramp frequency test for signs of afferent driving, indicating chain fibre activation (Boyd, 1986; Dickson et al. 1993; Celichowski et al. 1994).

(4) Frequency modulated stimulation was derived from a linear voltage-to-frequency converter with a sinusoidal input. The modulating frequency was 1 Hz. The mean stimulus frequency was set to 50 Hz and the amplitude of modulation chosen from ± 5 to ± 30 Hz. A mean frequency of 50 Hz was used rather than 100 Hz (Chen & Poppele, 1978) in order to avoid saturation effects. The conditions chosen were thus within the normal range of γ-motor firing frequencies (Taylor et al. 2000b). Muscle length was set at L₀+ 4 mm.

In a later part of the study observations were made (on preparations essentially the same as those described above) of the effects on spindle afferent discharge of naturally occurring muscle length changes alone or combined with natural patterns of γ_s stimulation. The movement and γ_s stimulation patterns had been recorded previously from experiments on treadmill locomotion in decerebrated cats (Taylor et al. 2000b). Both the ankle movements and the firing of γ_s axons from the MG nerve were recorded on magnetic tape (TEAC RD-130T, TEAC Corporation, Tokyo, Japan). The movement was reproduced exactly by playback through an electromagnetic servo arranged to rotate the ankle joint (Taylor et al. 2000a). The corresponding single unit γ_s impulse trains were used to trigger an isolated stimulator arranged for stimulating single γ_s axons in ventral rootlets, as described above. For these experiments the muscle tendons were left intact and the muscle length changes were induced by rotating the ankle joint, just as they had originally been recorded and with the same mean angle.

Data recording and analysis

Afferent spikes were discriminated and input together with trigger signals marking stimuli and the zero crossing of the modulating sine wave to a computer (66 MHz 486 PC) using a CED 1401-plus interface with Spike2 processing software (Cambridge Electronic Design, Cambridge, UK). The ramp displacement signal was sampled at 100 Hz. Data were analysed off-line using programs based on Spike2 and were also transferred to a Macintosh Centris 650 computer for curve fitting and for plotting, using Kaleidagraph software (Synergy Software Inc., Reading, PA, USA). Responses of spindle afferents to modulated γ-axon stimulation were assessed by constructing cycle-averaged frequency plots from 10 or more cycles using 32 bins per cycle. These were then fitted with sine waves by the method of least sum of squares error to give objective measures of amplitude and phase of response for comparison with similarly computed fits to the sinusoidally modulated stimulus trains. Plots were also produced by superimposing from several cycles the averaged afferent frequency against the stimulus frequency.

RESULTS

Data were derived from experiments on 15 cats, 11 of which were used primarily for another purpose (Taylor et al. 1998). The total number of muscle spindle afferents recorded was 164, of which 117 had a CV ≥ 70 m s⁻¹ and were taken to be primaries; 63 of these received contacts from the γ-axons isolated and are the subject of this report. The intrafusal fibre contacts which were made by these primary afferents were revealed by SCh testing to be: bag₁-chain, 1; bag₁-bag₂-chain, 50; bag₂-chain, 12. The total number of γ-axons isolated was 201, of which 73 acted upon at least one of the primary afferents. The conventional classification showed that the γ-axons could be divided into 59 γ_s and 14 γ_d. Because some of the γ-axons supplied more than one of the spindles, there were altogether 106 pairings between the 73 γ-axons and the 63 primary afferents, of which 84 were static effects and 22 were dynamic. Data from soleus and MG were analysed in the same way and no systematic differences were found between the two muscles. Consequently, data were pooled and are presented together.

Bag₁ effects on primary afferents

It was first established clearly by Emonet-Dénand et al. (1977) that γ_d-axons could show effects which were either pure dynamic or mixed dynamic and static. The histological basis for this was shown to be the branching of γ_d-axons to make contact with bag₂ and chain fibres (Banks et al. 1978). For the present purposes of studying the modulating effects of the individual intrafusal fibres it was therefore first necessary to establish for each γ_d-axon stimulated whether it acted purely through contraction of bag₁ fibres or whether its action involved bag₂ and/or chain contraction, caused by branches of γ_d-axons to these other fibre types. One line of evidence is given by the simple ramp and hold test during regular γ stimulation. Provided that the conditions of stretching used are those described above, particularly with regard to the regular repetition every 6 s, then activation of bag₁ fibres alone does not support primary afferent firing during the period between muscle stretches (Taylor et al. 1996). Figure 1B shows a very large dynamic effect relative to the control (A) of stimulating a γ_d-axon at 100 Hz. The afferent was, however, totally silent between stretches. The same γ-axon showed a marked dynamic effect on another primary afferent (Fig. 1D and E), but in this case firing resumed during the periods between stretches. Another γ_d-axon showed a strong dynamic action (Fig. 1G and H), also with firing returning between stretches. However, in this latter case there was an appearance of irregular driving of afferent firing at subharmonics of the stimulus frequency, whereas in E there was no sign of driving. The suggested interpretation is that only the bag₁ fibre was activated in B. In E, the bag₂ fibre was also activated, while in H, chain fibres were contracting along with the bag₁ fibre. This is supported by the correlograms shown in the right-hand column of Fig. 1 between afferent firing and random stimuli. It has been shown that in this test a large, narrow peak is characteristic of activation of chain fibres, which are fast contracting (Taylor et al. 1998). However, bag fibres contract more slowly and weakly and so produce small, broad peaks, which are sometimes difficult to detect. In Fig. 1C there is a small but definite increase in probability of firing starting with 15 ms lag time (seen clearly in the cusum), as is known to occur with a strong bag₁ activation (Taylor et al. 1996). In Fig. 1F neither the bag₁ nor the bag₂ activation was strong enough to cause a deflection in the cross-correlogram detectable at this scale of plotting (though a deflection is evident in the cusum plot). By contrast, the correlogram in Fig. 1I has a large narrow peak starting at 9 ms lag, which is characteristic of chain fibre contraction. It is not possible to be certain that no bag₂ fibre activity is involved in the example in Fig. 1H and I, though clearly the chain fibre action is dominant in periods between stretches. In the total of 22 γ_d effects recorded on primary afferents, only five were pure bag₁ fibre actions (as in Fig. 1B) and all these were from soleus.

Figure 1. Examples of dynamic effects.

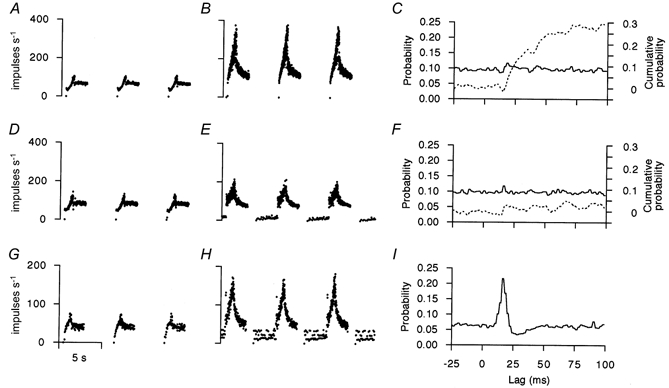
Three γ_d effects on primary afferents are shown, one in each row. The top two rows show the effect of a single γ_d-axon activating two different primary afferents, whilst the bottom row is an independent γ_d-Ia afferent pairing. A, D and G, control responses (instantaneous frequency) to ramp and hold muscle stretches repeated every 6 s (stretch records not shown). B, E and H, effects of γ_d stimulation at 100 Hz on responses to ramp and hold stretches. Stimulation continued throughout the record. The first stretch response after starting the stimulus is not shown. C, F and I, cross-correlograms (continuous lines) computed in 1 ms bins between random γ_d stimuli and primary afferent firing. The dashed lines in C and F are the cusums.

Pure bag₁ fibre contraction has only a weak tendency to bias the primary afferent discharge, so that, with a resting length of L₀+ 4 mm, in three out of the above five cases there was no maintained afferent discharge when a modulated stimulus train at a mean frequency of 50 Hz was used. The behaviour in the other two cases is shown in Fig. 2 with the 50 Hz stimulus train sinusoidally modulated by ± 30 Hz, as shown by the open circles. The afferent firing showed no detectable modulation in A and only a very small effect in B. It was concluded that, when care is taken to consider only those γ_d connections that do not have any sign of minority static effects, the dynamic γ-efferent system is essentially ineffective in modulating primary afferent firing.

Figure 2. Effects of sinusoidally modulating the stimulus frequency to two γ_d axons with pure bag₁ effects.

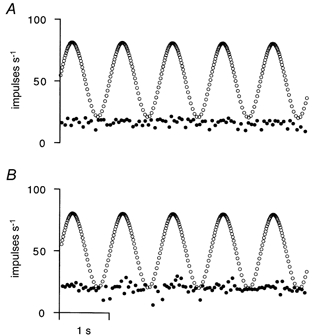
A and B each show instantaneous frequency plots of stimuli (○) and primary afferent impulses (•). Stimuli were frequency modulated sinusoidally at 1 Hz, with a mean frequency of 50 Hz and modulation depth of ± 30 Hz. A corresponds to the γ_d-Ia afferent pairing shown in the top row of Fig. 1, whilst B is a different γ_d-Ia afferent pairing, not previously shown.

Static γ effects

Static γ effects are exerted by axons which make contact with bag₂ fibres alone, chain fibres alone or both fibre types together. These different situations can be diagnosed from the effects on the responses to ramp stretches and from the form of the random stimulation cross-correlograms. Figure 3 shows the effects of three different γ-axons on spindle primary afferents. In the case of the γ effect in the top row, stimulation at 100 Hz caused increased firing, with little irregularity, in the periods between stretches with no significant change in the response to stretch (B) relative to control (A). The absence of a peak in the random stimulation correlogram (C) means that no chain fibre activation was taking place and, therefore, that the static effect must be due to bag₂ contraction. In the middle row, there were signs of driving at subharmonics of the stimulus frequency between stretches and 1:1 driving at 100 Hz during the stretch-hold phases (Fig. 3E). This indicates that the static effect in this case involved chain fibres. The single, large brief peak in the random correlogram (F) confirmed this. Finally, in the bottom row, the static effect was due to bag₂ and chain fibres acting together as indicated by the large, irregular bias of the stretch response (H) and the presence of both narrow and broad peaks in the correlogram (I). It has been demonstrated recently that correlograms such as this can be analysed as the sum of two log-normal curves. They can also be Fourier transformed to give plots of gain as a function of frequency, which can then be fitted with first-order lag curves (Taylor et al. 1998). This method also confirmed the presence of two distinct components in cases such as that in Fig. 3I.

Figure 3. Examples of γ_s action on primary afferent responses.

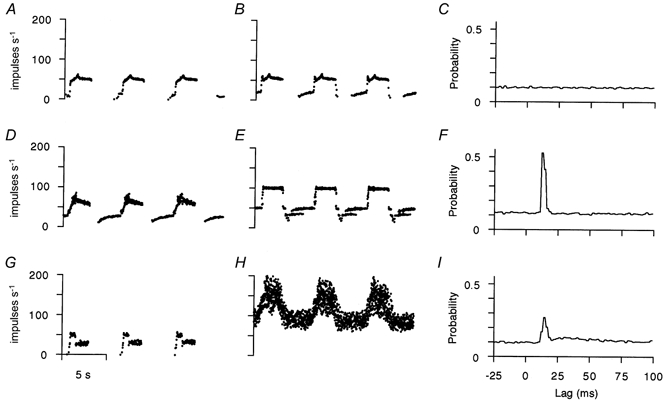
The arrangement of this figure is the same as that for Fig. 1, where each row is an independent γ_s-Ia afferent pairing. The top row shows a pure bag₂ effect, the middle row a pure chain effect and the bottom row a mixed bag₂ and chain effect.

The effects of sinusoidally modulated stimulus trains on these three γ-axons are illustrated in Fig. 4. The pure bag₂ innervation produced only a very small degree of modulation of the afferent discharge (A). The stimulation merely caused a rise in mean afferent firing frequency from a control of 41 impulses s⁻¹ (not shown) to 44 impulses s⁻¹. The γ-axon acting on the chain fibres (C) caused 1:1 driving, and hence perfect modulation, at stimulus rates above 45 Hz. At stimulus frequencies below this, the response was very irregular and gave the impression of interference between a resting natural firing frequency which was close to 40 Hz and the stimulus frequency, resulting in some paradoxically high frequencies. In Fig. 4E, it is evident that the static γ-axon acting on both bag₂ and chain fibres together produced the most complete and linear modulation of afferent discharge.

Figure 4. Effects of sinusoidally modulated stimulation of γ_s-axons.

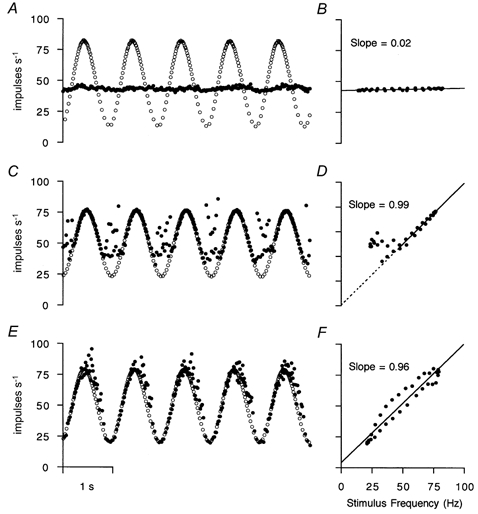
A, C and E show instantaneous frequency records of stimuli (○) and afferent impulses (•) for the three different γ_s to primary afferent pairings shown in the top, middle and bottom rows, respectively, of Fig. 3. B, D and F show plots of mean response frequency against mean stimulus frequency derived from 32 point cycle averages of data illustrated in A, C and E. The straight lines are fitted regression lines. In D, the points resulting from stimulation at frequencies < 45 Hz have been excluded from the regression, but the fitted line has been extrapolated to lower values (dashed line).

The effectiveness of the modulation can be assessed by computing the cycle-averaged frequencies at 32 points per cycle and then plotting point by point the response frequencies against the stimulus frequencies. This has been done in Fig. 4B, D and F and the straight line regressions drawn to show the very weak effect in B and slopes close to unity in D and F. Notice that in D the regression was computed for stimulus frequencies ≥ 45 Hz (continuous line) and extrapolated below that (dashed line). This confirms that, while the response was perfectly regular and linear above this frequency and some impulses followed the same relationship below it, others were irregular. This is thought to be due to interference between a resting discharge and that excited by the stimuli. The exact following, without phase shift, in the rest of the cycle is very clear and is an expression of 1:1 driving. The modulation in Fig. 4E followed the stimulus pattern closely, but was shown by the open loop in F to include some phase lag.

The linearity of the modulation caused by chain or bag₂ and chain activation was examined by comparing the effects of modulation at various depths. Data from the MG afferents of Fig. 4B, D and F are shown in Fig. 5 with the same type of plot, but with points superimposed from tests with modulation depths of ± 5, 10, 20 and 30 Hz with a mean stimulus frequency of 50 Hz. The commonest response to pure bag₂γ_s activation was the weak modulation, as seen in Fig. 5A, but the modulating effect could be larger in some cases. Thus in Fig. 5B the response from the same afferent as in A is shown for stimulation of another γ_s-axon with pure bag₂ action which yielded a mean slope of 0.23. Some phase lag in the response was evident from the open loops, which were nested inside each other. For the pure chain innervation in Fig. 5C, the points for all modulation depths lay along the same straight line except for the cluster occurring when the stimulus frequency was low, as explained for Fig. 4C and D). There was no sign of phase lag. In the mixed bag₂ and chain innervation in Fig. 5D, loops were present which expanded progressively, but the long axis remained on the same straight line, indicating that the proportional modulation of the afferent firing was constant. The slope of the relationship of output to input was close to unity, though generally the slope for mixed bag₂ and chain effects was found to vary widely from case to case, as shown below. The shape of the loops in Fig. 5D did not change appreciably as they increased in size, implying that the phase was approximately constant. The same considerations apply to Fig. 5B.

Figure 5. Effects of varying the depth of frequency modulation.

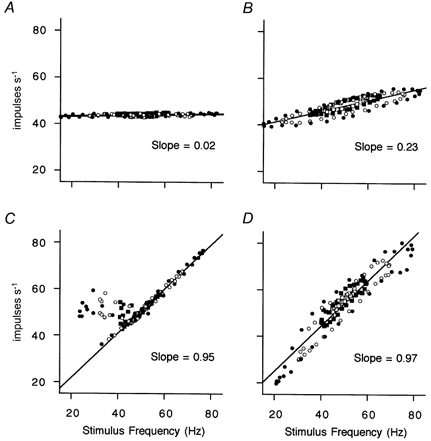
A, C and D are from the γ_s to primary afferent pairings shown in A, C and E, respectively, in Fig. 4, whilst B is a different γ_s-axon activating the same primary afferent as in A. Mean stimulus frequency is 50 Hz and modulation depths are ± 5 (□), 10 (▪), 20 (○) and 30 Hz (•). Straight lines are linear regressions fitted to all the data points, except in C, in which the outlying points occurring at low stimulus frequencies have been omitted from the calculation of the regression (slopes are shown inset).

Gain and phase shift

The above findings were confirmed as general observations and are summarised in Fig. 6 for the data pooled from the two muscles, for a modulation amplitude of ± 30 Hz. For this and subsequent figures, gains and phase shifts were estimated from sine wave fits, rather than by regression as in Fig. 5, because regression plots are not appropriate in the presence of phase shift. In Fig. 6A, it is evident that modulation gain for pure chain effects (filled bars) never exceeded unity and in these data was most usually < 0.20. The one value of modulation gain of slightly less than 1.0 was associated with 1:1 driving (Fig. 5C). The one value of 0.5 was due to 1: 2 driving and the lower gains were due to 1: 3, 1: 4 or occasional, irregular driving. In most cases of pure bag₂ effects (open bars) modulation gain was low. Those γ_s-axons exerting their effects jointly through bag₂ and chain fibres (hatched bars) were most numerous and gave the highest modulation gains, values of 0.9-1.5 being the most common. Figure 6C shows the mean values of modulation gain for the three types of γ_s action and emphasises the potency of the bag₂ and chain combination. The plot of pooled data on phase lag in Fig. 6B confirmed the very small values for pure chain action (filled bars) and the generally large values for pure bag₂ action (open bars). The mixed effects gave small to intermediate phase lags (hatched bars). These findings are summarised by the mean values in Fig. 6D.

Figure 6. Summary of modulation data for the three types of γ_s action.

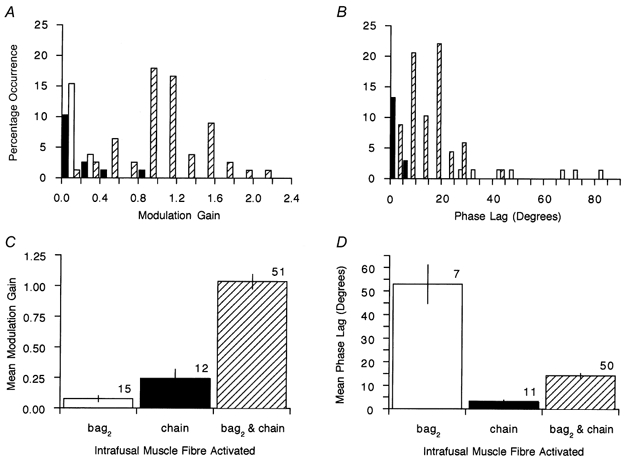
Distribution of values of modulation (A) and distribution of values of modulation phase lag (B) at 1 Hz for pure bag₂ (□), pure chain (▪) and mixed bag₂ and chain () effects. C, values of mean modulation gain for the three types of γ_s action. D, mean values of phase lag for the three types of γ_s action. In C and D, the numbers above the bars are the number of data values and the error bars are ±s.e.m.

The relationship between the estimates of gain and phase derived from the effects of stimulation modulated at 1 Hz is shown in Fig. 7, with different symbols for the three types of γ_s action. It is evident that the pure bag₂ effects (open circles) were set apart by their generally low gain and wide-ranging values of phase lag. Pure chain effects generally had small modulating gain and very small phase lags (filled circles). The mixed bag₂-chain effects (crosses) dominated and showed a significant linear regression of phase lag with gain (dashed line).

Figure 7. The relationship between phase lag and gain for the three types of γ_s action.

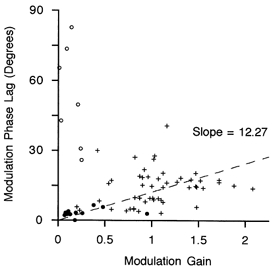
Individual points show values of phase lag and gain obtained by sinusoidally modulating 50 Hz stimulation of γ_s axons at 1 Hz by ± 30 Hz. ○, pure bag₂ effects; •, pure chain effects; +, mixed bag₂ and chain effects. The linear regression (dashed line) is drawn for the mixed data (+) only.

Natural movements and γ_s stimulation profiles

The above results clearly indicate that stimulation of γ_s-axons that act through bag₂ and chain fibres together has an effect which would be expected to oppose the unloading effect of muscle shortening. How effective this could be was tested by accurately reproducing the natural muscle length changes and γ_s discharge patterns previously recorded during treadmill locomotion in the decerebrate cat (Taylor et al. 2000b), as described in Methods. The primary afferent discharge resulting from these length changes with no γ stimulation was compared with that in the presence of the pattern of γ_s stimulation reproduced from the γ_s firing pattern, originally recorded in the same experiment. Figure 8 shows two examples, one obtained from MG (A and C) and and the other from soleus (B and D). In Fig. 8A and B, the mean afferent firing frequencies are shown with no stimulation (open circles) and in the presence of γ_s stimulation (filled circles). Figure 8C and D shows the respective difference signals (filled squares) obtained by subtracting the passive stretch response from the response with γ_s stimulation, the profile of which is shown superimposed (open squares). In Fig. 8A, it can be seen that there was a passive response to the natural pattern of muscle stretch rising to 35 impulses s⁻¹. When this was subtracted from the response to combined length change and γ_s stimulation, the profile of the difference signal in C was very similar to a scaled version of the γ_s stimulation profile. This implies a linear summation of the length and γ_s stimulation signals. In Fig. 8B, it can be seen that this particular spindle afferent from soleus, in the absence of γ-motor activity, did not respond to the natural movement pattern, presumably because the intrafusal fibres were slack. However, as shown in Fig. 8D, the natural pattern of γ_s stimulation was faithfully reproduced by the Ia afferent discharge. It should be noted that the frequency scales for the γ_s stimulation and the afferent response are different and consequently the afferent response is not merely an expression of 1:1 driving of the afferent by the stimuli. There were 11 pairings of γ_s-axons that had mixed bag₂ and chain effects with primary afferents and similar results were obtained in all cases. Thus, when bag₂ and chain fibres are excited together, with timing and extent as observed naturally for γ_s firing, not only can unloading be prevented, but also the effect may be strong enough to cause a net increase in afferent firing. The fact that, with natural length changes, the increase in afferent firing caused by a natural pattern of γ_s stimulation closely resembled a scaled copy of the stimulus profile indicates that there is effectively linear summation of the response to length change with the response to γ_s activity.

Figure 8. The effects of combining natural muscle length changes with natural γ_s activation profiles.

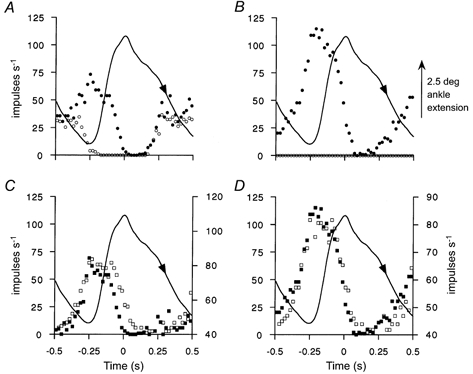
A and C are derived from a primary spindle afferent in MG and B and D from another in soleus. In each panel, the imposed ankle movement was taken from a recording made during locomotion in a decerebrate cat (Taylor et al. 2000b) and the direction of muscle stretch is shown by the arrowhead. A and B show the afferent firing frequency with no γ stimulation (○) and in the presence of stimulation of a γ_s-axon with a mixed effect on bag₂ and chain fibres (•). The γ_s stimulation profile was derived from the same experimental data which provided the ankle movement record and is shown in C and D (□, right-hand frequency scales). C and D also show the frequency difference records for the afferents obtained by subtracting the passive responses from the stimulated responses (▪, left-hand frequency scales) shown in A and B. Each record is the average of 20 similar cycles using 20 ms bins.

DISCUSSION

In the present study, it has been possible to identify physiologically which particular intrafusal muscle fibres are activated by the stimulation of a given γ-motor axon and consequently to determine how each fibre type affects the primary afferent discharge. The data have shown that bag₁ fibres acting alone have practically no capacity to bias or modulate the afferent discharge. Their functional purpose must therefore be restricted to enhancing the afferent response to muscle stretch. Bag₂ fibres do have a marked biassing action, but this cannot follow fluctuations in γ_s firing at 1 Hz at all effectively. This means that, if they are activated alone under any circumstances, then it is likely to be as part of a relatively slowly varying or tonic biassing process. Chain fibres acting alone can pass on a fluctuating bias signal, but their average modulation gain at 1 Hz is low. Mixed bag₂ and chain effects are by far the most potent in producing modulation at 1 Hz and are the most common. Thus joint activation of bag₂ and chain fibres is the type of γ-motor effect which would be most appropriate to account for the signs of fluctuating static fusimotor output seen in spindle afferent recordings during locomotion in the decerebrate cat (Taylor et al. 2000a). In previous observations on the effects of γ_s- and γ_d-axons using steps of stimulation frequency (Hulliger, 1979), it was also found that γ_s were usually much more effective than γ_d at modulating primary afferent discharge. Paradoxically, it appeared that there was no difference in the speed of the two actions. At the time of these experiments, however, the different actions of bag₂ and chain fibres were not clearly distinguished and consequently the speed of action was estimated by fitting a single exponential curve to the rise and fall of frequency. In this way the very rapid initial rise and fall following step changes in γ_s stimulation frequency (due to chain fibres) may have been missed, especially because of the use of 7 or 13 point smoothing. The mean time constant found of 58.5 ms was therefore some compromise between values for the fast and slow components. In another study in which stimuli were frequency modulated sinusoidally at various frequencies (Chen & Poppele, 1978), a single corner frequency of about 1.2 Hz was found for γ_s effects (equivalent to a time constant of 133 ms). Practical considerations limited the modulating frequency used to 20 Hz, which would not have been high enough to have revealed the effects of chain fibres. This is because, as shown by the random stimulation method, they have a mean corner frequency of 46.5 Hz (Taylor et al. 1998). Thus the low corner frequency found for γ_s effects by Chen & Poppele (1978) must actually have been due to the properties of bag₂ fibres.

When the γ_s- and γ_d-motor systems supplying mammalian muscle spindles were originally described (Matthews, 1962; Crowe & Matthews, 1964), it was natural to regard them as separate controls for different aspects of spindle afferent sensitivity. From the engineering point of view, which was becoming popular at the time, the spindle-based stretch reflex could be seen as the substrate for a negative feedback system stabilising muscle length for postural purposes or controlling length changes through a servo mechanism (Merton, 1953; Hammond et al. 1956). To regulate the gain and damping of such a mechanism it was appreciated that separate control over the length and velocity sensitivity of the spindle would be needed (Partridge, 1966; Taylor, 1972) and that this might be provided by the two parts of the γ-motor system. The original naming of these as static and dynamic for simple descriptive purposes had encouraged this attitude and consequently also encouraged attempts to express the effects of γ_s and γ_d stimulation in these terms (Lennerstrand & Thoden, 1968a,b). The use of ramp and hold stretches for testing stemmed from the desire to separate the displacement and velocity components of the response, though it was soon evident that the responses to stretches spanning the normal range of operation were so non-linear that general descriptions were impossible. Nevertheless, the attractiveness of linear systems analysis is such that numerous attempts have been made to press it into service, for example, by using sine wave stretches of small enough amplitude to stay within the linear range (Matthews & Stein, 1969; Goodwin et al. 1975) and by constructing linear models (Prochazka & Gorassini, 1998).

The dynamic fusimotor system does provide a form of control over the parameters of the spindle response to stretch (of amplitude greater than 200 μm), but the enhancement of sensitivity affects the responses to displacement and velocity approximately equally (Hulliger et al. 1977). It cannot therefore be a means by which the damping of the system is regulated. The present observations show that the dynamic fusimotor system is not effective either as a means of providing a bias signal, to compensate for unloading during active shortening, or to provide a leading signal in the sense required by the ‘length follow-up servo’ concept (Merton, 1953). Nevertheless, it has been observed that the firing frequency of γ_d-motoneurones supplying leg extensors does fluctuate rapidly during locomotion (Murphy et al. 1984; Taylor et al. 2000b). It follows that the functional value of this fluctuation must be to change rapidly the sensitivity of primary afferents to stretch at appropriate moments in the step cycle, rather than to provide a bias signal.

The static fusimotor system, on the other hand, seems to be very well adapted to bias the spindle primary discharge, in two different ways. The bag₂ fibres acting alone are most suitable for tonically maintaining a static bias, because their contraction does not occlude dynamic effects (Dickson et al. 1993). The fact that their modulating effect is weak and phase lagged (as shown here) would be of no consequence in this respect. The combined action of bag₂ and chain fibres by contrast is rapid and powerful. On this basis it may be presumed that it is by the combined activation of bag₂ and chain fibres that a patterned discharge of γ_s-motoneurones is able to offset the effects on spindle discharge of active muscle shortening, which has been shown to be such a clear feature of locomotion in decerebrate cats (Taylor et al. 2000a,b). This conclusion is very much strengthened by the present observations of the effects of combining natural length changes with natural profiles of γ_s stimulation. The effects of fusimotor stimulation in preventing silencing of muscle spindle primary afferents has also been studied by Appenteng et al. (1982). It was found that high-frequency stimulation of fusimotor fibres could compensate for high rates of shortening (2 resting lengths per second for soleus). However, which intrafusal fibres were responsible was not established, because the stimulated ventral roots contained multiple fusimotor fibres which were only classified as predominantly static or predominantly dynamic.

Another point arising from the present observations is that they confirm the linearity of the summation of the effects of muscle length change with the effects of γ_s stimulation in determining the afferent firing frequency. The linearity of summation has been implied by the recent work, referred to above (Taylor et al. 2000a), more particularly for spindle secondary afferents. It is now clear that, leaving aside the effects of γ_d stimulation, linearity in this respect is also a feature of primaries. This is an important observation in that it simplifies the interpretation of spindle afferent recordings in natural movements.

The question as to whether bag₂ fibres can be activated separately has not yet been settled, but two pieces of evidence suggest that this may be so. Firstly, a physiological study of the distribution of γ_s-motor axons to bag₂ and chain fibres in MG indicated the presence of a degree of selective innervation (Taylor et al. 1998). Secondly, recordings from γ_s-motoneurones in locomoting decerebrate cats showed the existence of two different patterns of activity (Taylor et al. 2000b). In one, the frequency fluctuated strongly, with increases timed so as to account for the main part of the observed static fusimotor effect on spindle afferents, assuming that it was acting jointly on bag₂ and chain fibres. In the other pattern, there was an increased mean frequency, but the modulation was less strong and was much more phase advanced relative to the muscle shortening. It was suggested that this pattern might be more suitable for controlling the bag₂ fibres.

The present study emphasises the advantages of using the random stimulation method for determining which intrafusal fibres are activated by a given γ-motor axon. This in turn leads to consistent interpretations of the effects of sinusoidally modulated stimulation. The mean frequencies and amplitudes of modulation have been chosen to be within the naturally occurring ranges and, consequently, point to functional interpretations of the significance of the three different intrafusal fibre types. A working proposal arising from the present work and from observations during locomotion (Taylor et al. 2000a,b) is that dynamic fusimotor activity is used to prepare spindle primaries to respond to the onset of muscle lengthening. Static fusimotor output acting jointly on bag₂ and chain fibres is modulated smoothly to offset the effects of muscle shortening on primary and secondary afferents. It is strong enough in some cases to provide a signal leading the muscle shortening. Finally, it is possible that bag₂ fibres may be activated to some extent separately by a subset of γ_s-axons to provide a tonic bias of the discharge of primary and secondary afferents, without having any substantial effect on afferent sensitivity to length changes.