Abstract
We studied the gating kinetics of Kv4.2 channels, the molecular substrate of neuronal somatodendritic A-type currents. For this purpose wild-type and mutant channels were transiently expressed in the human embryonic kidney (HEK) 293 cell line and currents were measured in the whole-cell patch-clamp configuration.
Kv4.2 channels inactivated from pre-open closed state(s) with a mean time constant of 959 ms at −50 mV. This closed-state inactivation was not affected by a deletion of the Kv4.2 N-terminus (Δ2-40).
Kv4.2 currents at +40 mV inactivated with triple-exponential kinetics. A fast component (τ = 11 ms) accounted for 73 %, an intermediate component (τ = 50 ms) for 23 % and a slow component (τ = 668 ms) for 4 % of the total decay.
Both the fast and the intermediate components of inactivation were slowed by a deletion of the Kv4.2 N-terminus (τ = 35 and 111 ms) and accounted for 33 and 56 %, respectively, of the total decay. The slow component was moderately accelerated by the truncation (τ = 346 ms) and accounted for 11 % of the total Kv4.2 current inactivation.
Recovery from open-state inactivation and recovery from closed-state inactivation occurred with similar kinetics in a strongly voltage-dependent manner. Neither recovery reaction was affected by the N-terminal truncation.
Kv4.2 Δ2-40 channels displayed slowed deactivation kinetics, suggesting that the N-terminal truncation leads to a stabilization of the open state.
Simulations with an allosteric model of inactivation, supported by the experimental data, suggested that, in response to membrane depolarization, Kv4.2 channels accumulate in the closed-inactivated state(s), from which they directly recover, bypassing the open state.
Voltage-activated potassium (Kv) channels with rapid (A-type) inactivation play important roles in pre- and postsynaptic neuronal excitation (Pongs, 1999). A-type Kv channels related to the Shal (Kv4) gene family (Baldwin et al. 1991; Pak et al. 1991; Serodio et al. 1994, 1996) mediate both the transient outward current (Ito) in cardiac myocytes (Dixon et al. 1996) and the neuronal subthreshold A-type current (Serodio et al. 1994). The Kv4 subfamily has four members, Kv4.1, Kv4.2 and two splice variants of Kv4.3, cloned from rat (Blair et al. 1991; Dixon & McKinnon, 1994; Serodio et al. 1996; Ohya et al. 1997; Tsaur et al. 1997), mouse (Pak et al. 1991; Serodio et al. 1994), dog (Dixon et al. 1996), or human cDNA libraries (Kong et al. 1998; Dilks et al. 1999; Zhu et al. 1999; Isbrandt et al. 2000).
Immunocytochemical studies have shown that the subcellular distribution of neuronal rat Kv4.2 channels is restricted to the somatodendritic area (Sheng et al. 1992), and the high abundance of Kv4.2 in the soma and dendrites led to the hypothesis that these channels may have an important influence on postsynaptic neuronal signal transduction. The discovery of Kv4.2 channel protein clusters in the postsynaptic membrane supported this view (Alonso & Widmer, 1997). Many important postsynaptic functions have been demonstrated for dendritic A-type channels. In hippocampal pyramidal neurons, where the A-type channel density increases with distance from the soma, activation of Kv4.2 channels may prevent the back-propagation of action potentials (Hoffman et al. 1997). In addition, the rapid activation of A-type channels may protect the postsynaptic membrane from excessive depolarization. On the other hand, inactivation of Kv4.2 channels by subthreshold EPSPs can lead to spike amplification, which provides a possible explanation for the Hebbian associativity found in distal dendrites (Magee & Johnston, 1997). More recently, Schoppa & Westbrook (1999) showed that A-type channels localized to the dendritic spines of GABAergic interneurons in the olfactory bulb are necessary to counterbalance fast glutamatergic EPSPs, thereby allowing a prolonged inhibitory synaptic transmission in a local feedback loop. The inhibitory synaptic transmission becomes shorter and stronger when the A-type channels are inactivated by subthreshold membrane depolarization.
The gating properties of somatodendritic A-type channels reflect their functional roles. Not only do these channels rapidly inactivate close to the action potential firing threshold, but they also recover from inactivation in the millisecond time range. This property distinguishes somatodendritic from other A-type channels. For example, Shaker-related A-type channels like Kv1.4 slowly recover from inactivation within a time range of many seconds. The inactivation mechanism of Shaker channels is well understood. It can be described as a ‘ball-and-chain’ reaction (Hoshi et al. 1990, 1991) where a tethered N-terminal inactivation domain of the Kvα subunit (Zagotta et al. 1990), or of an accessory Kvβ subunit (Rettig et al. 1994), binds to a ball receptor near the inner entrance of the pore (Isacoff et al. 1991) thereby preventing ion flux through the open channel. The fast N-type inactivation of Shaker channels is followed by a slower C-type inactivation (Hoshi et al. 1991), from which the channels recover slowly. By contrast, Jerng and coworkers (Jerng & Covarrubias, 1997; Jerng et al. 1999) showed that the inactivation of Kv4.1 channels, when expressed in vitro, does not require channel opening. The channels readily enter inactivated state(s) from pre-open closed state(s). In fact, this pathway appears to be the only one that leads to cumulative Kv4.1 channel inactivation; i.e. open channels have to close before they accumulate in the inactivated state(s). In the Kv4.1 gating model proposed by Jerng et al. (1999) this cumulative inactivation involves two sequential states, a closed-inactivated state and a deep-inactivated state.
In order to gain further insight into the gating behaviour of somatodendritic A-type channels, we investigated the kinetics of currents mediated by wild-type and N-terminally truncated Kv4.2 channels expressed in human embryonic kidney (HEK) 293 cells. We performed a detailed kinetic analysis of both closed- and open-state inactivation and recovery from inactivation.
Our results indicate that the Kv4.1 gating model of Jerng et al. (1999) cannot be used to simulate A-type currents mediated by Kv4.2 channels. In particular, the fast recovery from inactivation, a hallmark of somatodendritic A-type channels, which has been observed in our experiments, could not be simulated. Our experimental data could be most accurately reproduced by simulations based on an allosteric model of inactivation, where all closed states are connected to inactivated states, but not to a deep-inactivated state. Simulations with this model yielded fast recovery kinetics after accumulation in the closed-inactivated state(s), just as observed experimentally for Kv4.2 channels.
METHODS
Cell culture and heterologous channel expression
Both wild-type human Kv4.2 channels (EMBL data bank accession no. AJX 010969) and an N-terminal deletion mutant, which lacks amino acid residues 2-40 (Δ2-40), were transiently overexpressed in human embryonic kidney (HEK) 293 cells, as described previously (Zhu et al. 1999). Constructs of human Kv4.2 channels with a larger N-terminal truncation (e.g. Δ2-52) are non-functional (Zhu et al. 1999). The cells were grown according to standard culture protocols and plated on poly-l-lysine (50 μg ml−1)-coated 35 mm plastic dishes at densities between 1 × 104 and 1.5 × 104 cells per dish. After 7-8 h the cells were transfected using the calcium phosphate technique (Chen & Okayama, 1987) with 1 μg per dish of recombinant Kv4.2 cDNA. We cotransfected cells with 0.3 μg per dish of cDNA for an enhanced version (S56T mutant) of the green fluorescent protein as a reporter gene to identify transfected cells. The precipitate was removed 12 h later by rinsing with phosphate-buffered saline and the cells were used for electrophysiological recordings on the next 2 days.
Solutions and recording techniques
For electrophysiological recordings, cells were bathed in an external solution containing (mm): NaCl 135, KCl 5, CaCl2 2, MgCl2 2, Hepes 5 and sucrose 10, with 0.01 mg ml−1 phenol red; pH 7.4 (NaOH). Recording pipettes, pulled from thin-walled borosilicate glass using a DMZ puller (Zeitz, Augsburg, Germany) and heat polished, had bath resistances between 2.5 and 3 MΩ when filled with an internal solution containing (mm): KCl 115, KF 10, CaCl2 1, MgCl2 1, EGTA 11, Hepes 10, glutathione 2 and K2-ATP 2; pH 7.2 (KOH). All experiments were conducted in the whole-cell configration of the patch-clamp technique. In some experiments, external Na+ was replaced by K+ (130 mm; symmetrical K+), or alternatively, both internal K+ and external Na+ were replaced by Rb+ (130 mm; symmetrical Rb+). The external solutions with different ionic compositions were applied to the cell surface using a valve-controlled fast local superfusion system (Auto Mate Scientific, San Francisco, CA, USA) driven by a peristaltic pump. All experiments were conducted at room temperature (20-22 °C).
Data acquisition and analysis
Currents were evoked by voltage-jump protocols and recorded using an EPC9 patch-clamp amplifier combined with PULSE software (HEKA Elektronik, Landbrecht, Germany). Signals were filtered at 0.2-4 kHz with low-pass Bessel characteristics, amplified as required, and digitized at 50-1000 μs sample intervals. Capacitive current transients were compensated on-line, and the P/n method incorporated in PULSE was used for leak current subtraction (leak holding, −100 mV; leak size, 20 %). Data were stored on a 7600/132 Power Macintosh computer, and the program package PULSEFIT/ PULSETOOLS (HEKA Elektronik) was used to analyse current traces. The sigmoidal rising phase of Kv4.2-mediated currents was fitted using a Hodgkin-Huxley-related equation (m4) incorporated in PULSEFIT (Roeper et al. 1997). Kv4.2 current inactivation kinetics were fitted with triple-exponential functions and current relaxations caused by channel deactivation with single-exponential functions. The obtained data were further processed using Igor Pro (WaveMetrics, Lake Oswego, OR, USA) and Kaleidagraph (Synergy Software, Reading, PA, USA). Conductance values (G) at a given test potential (Vm) were calculated from the measured peak amplitude (I) and the mean reversal potential for K+ currents (Vrev = -79.9 ± 1.4 mV; n = 5) using the equation G = I/(Vm - Vrev). The voltage dependence of activation and steady-state inactivation of the expressed Kv4.2 channels were analysed with Boltzmann functions of the form G/Gmax = 1/{1 + exp[(Vm - V1/2)/k]}n, where the fraction of the maximal conductance, G/Gmax, at a given membrane potential, Vm, depends on the potential for half-maximal activation or inactivation, V1/2, and the slope factor, k. Steady-state inactivation data were fitted with a first-order Boltzmann function (n = 1). The voltage dependence of activation was fitted with both a first-order (n = 1) and a fourth-order Boltzmann function (n = 4). Statistical analyses with Student's t test were conducted using GraphPad Instat (GraphPad Software, San Diego, CA, USA), and pooled data are presented as means ± s.e.m.
Gating model and simulations
For the development of a computational model for the gating of Kv4.2 channels a custom-made program was implemented using the Borland C++ version 4.0 compiler with Intel Pentium instruction set optimization and run on a Pentium computer. We expressed the Markov-state kinetic model as a system of differential equations with voltage-dependent transitions along the activation pathway leading from CR (resting state) to C4 (final pre-open closed state; see Fig. 10A and Fig. 11A). The voltage-dependent rates are of the form α = α0exp[zαV/(RT/F)] for the forward rates and β = β0exp[-zβV/(RT/F)] for the backward rates, where α0 and β0 are the rates at 0 mV and zα and zβ are the equivalent charges moving up to the transition state. Numerical time integration was performed using eigenvalue-eigenvector decomposition of the Markov model vector field matrix. Initial conditions for each voltage-clamp sequence computation were computed by direct solving of the steady-state equations for the Markov chain, similar to the effect of a very long clamp pulse at the holding potential. We first used the gating scheme proposed by Jerng et al. (1999), which was then modified, and model parameters were allowed to vary, in order to simulate our experimental records. Parameters used in the simulations are given in Tables 1 and 2.
Figure 10. Predictions of a Kv4.1 kinetic model with adjusted parameters for Kv4.2.
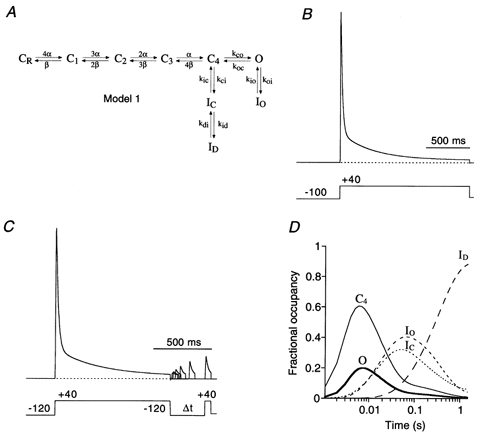
A, the K+ channel state diagram (Model 1) used for these simulations includes inactivation both from a pre-open closed state (C4→ IC) and from the open state (O → IO). The closed-state inactivation also accesses a deeper inactivated state (ID). Transitions between states are represented by arrows; the values of the simulation parameters are shown in Table 1. B, simulation, with a pulse protocol like the one used in Fig. 1, to assess the rate of channel inactivation. Entry into the inactivated states has a fast, intermediate and slow component and inactivation is largely complete for a 1.5 s depolarizing pulse to +40 mV (dotted line represents zero current). C, simulation of the recovery from inactivation. Model 1 and parameters in Table 1 were used with a recovery protocol as inF ig. 5B. The model fails to simulate experimental data because recovery is very slow, even at −120 mV. D, the fractional occupancy of Model 1 gating states is plotted as a function of the inactivation pulse time on a logarithmic time base. For clarity, only the occupancy of the pre-open closed state (C4), the open state (O) and the three inactivated states (IC, IO and ID) are shown. During the 1.5 s depolarizing pulse to +40 mV, channels largely accumulate in the deep inactivated state, ID, where they get trapped.
Figure 11. Predictions of an allosteric model for Kv4.2 channel inactivation.
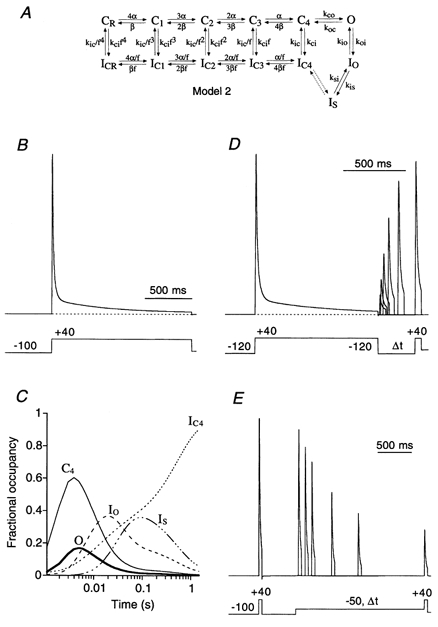
A, new Kv4 state diagram (Model 2), in which channels can inactivate from all closed states along the activation pathway. The allosteric factor f defines the coupling of closed-state inactivation and the voltage-dependent activation transitions leading from CR to C4; arrows reflect the transitions between states. Values for the simulation parameters are given in Table 2. B, simulation to assess the rate of channel inactivation with a pulse protocol like the one used in Fig. 1. Entry into the inactivated states has a predominant fast component followed by a smaller intermediate and an even smaller slow component. Inactivation is largely complete for a 1.5 s pulse to +40 mV (dotted line represents zero current). C, the fractional occupancy of Model 2 gating states is plotted as a function of the inactivation pulse time on a logarithmic time base. For clarity, only the occupancy of the pre-open closed state (C4), the open state (O) and the three inactivated states (IC4, IO and IS) are shown. By the end of the 1.5 s depolarizing pulse to +40 mV a large fraction of channels has accumulated in IC4. D, simulation of fast recovery from inactivation at −120 mV. E, simulation of the entry into closed-state inactivation with a pre-pulse to −50 mV, which did not activate a significant number of channels.
Table 1.
Values of simulation parameters used in Model 1
| Parameter | Values |
|---|---|
| α0 (s−1) | 133 |
| zα | 1.0 |
| β0 (s−1) | 4 |
| zβ | 1.58 |
| κco (s−1) | 400 |
| κoc (s−1) | 1100 |
| κoi (s−1) | 100 |
| κio (s−1) | 10 |
| κci (s−1) | 30 |
| κic (s−1) | 5 |
| κid (s−1) | 8 |
| κdi (s−1) | 0.5 |
for the backward rates, where α0 and β0 are the rates at 0 mV and zα and zβ are the equivalent charges moving up to the transition state. Channel opening and closing are defined by kco and κoc, respectively, open-state inactivation by κoi and κio, and closed-state inactivation by κci and κic. Trapping in the deep-inactivated state is defined by κid and κdi. For Model 1, see Fig. 10.
RESULTS
Currents mediated by Kv4.2 channels
A standard voltage protocol activated the currents mediated by Kv4.2 channels in HEK 293 cells with a 2.5 s pulse to +40 mV following a 2 s hyperpolarizing prepulse to −100 mV. The holding potential during the time between such voltage jumps (15 s) was −80 mV. A second voltage pulse to +40 mV was preceded by a 2 s prepulse to −35 mV to activate endogenous HEK 293 currents (Yu & Kerchner, 1998), if present, in the absence of Kv4.2 currents. The endogenous currents were subtracted from the total K+ currents if they exceeded 5 % of the total current peak amplitude. The results, which reflected exclusively Kv4.2 channel kinetics, are shown in Fig. 1A. Kv4.2 channels displayed strong inactivation with three distinct components (Fig. 1A and B). For wild-type channels the fast component of inactivation (τ1) measured at +40 mV was 11.0 ± 0.7 ms (n = 13) and accounted for 73.2 ± 1.7 % of the total decay. The fast component was followed by an intermediate and a very slow component of inactivation (Fig. 1B). The intermediate component (τ2 = 50.1 ± 2.4 ms, n = 13) accounted for 22.5 ± 1.5 % and the slow component (τ3 = 668 ± 35 ms, n = 13) for 4.3 ± 0.3 % of the total decay. When we expressed mutant channels lacking 40 amino acids of the N-terminus (Δ2-40) the resulting currents at +40 mV still exhibited decay kinetics that could be best described by the sum of three exponential terms (Fig. 1A and B). However, the time constants and their relative weights were altered in a characteristic manner. Both the fast and the intermediate components of inactivation were slowed (τ1 = 35.1 ± 4.2 ms and τ2 = 111 ± 4 ms, n = 9) and now accounted for 33.3 ± 3.1 and 55.5 ± 2.8 %, respectively, of the total decay. By contrast, the slow component of Kv4.2 Δ2-40 inactivation was slightly faster than observed for wild-type channels (τ3 = 346 ± 14 ms, n = 9; P < 0.01) and accounted for the remaining 11.2 ± 2.2 % of the total decay. These results are summarized in Fig. 1C. The slowing of the major component of outward current decay suggests a decrease in the rate of Kv4.2 channel open-state inactivation by the Δ2-40 mutation. Our findings clearly separate Kv4.2 from Shaker B channels, where a similar N-terminal deletion completely abolishes fast inactivation (Hoshi et al. 1990).
Figure 1. Inactivation kinetics of Kv4.2-mediated currents.
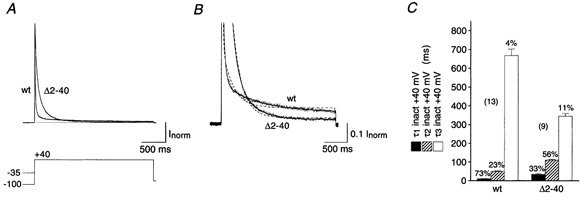
A, currents mediated by the wild-type (wt) and an N-terminal deletion mutant (Δ2-40) of Kv4.2 expressed in HEK 293 cells and recorded in the whole-cell patch-clamp configuration during a 2.5 s voltage pulse to +40 mV. Endogenous HEK 293 K+ currents recorded following a prepulse to −35 mV (not shown) have been subtracted from the total currents recorded after a prepulse to −100 mV. Traces have been normalized to peak (Inorm) and the dotted line represents zero current. Note the stronger Kv4.2 Δ2-40 inactivation, which causes a cross-over with the Kv4.2 wt trace. B, same recordings as in A on a 10-fold expanded vertical scale to illustrate intermediate and slow inactivation kinetics. Currents were fitted with three exponentials (continuous line). Inappropriate double-exponential fitting curves are shown as dashed lines. C, mean values for the fast (τ1, ▪), intermediate (τ2,  ) and slow components (τ3, □) of inactivation at +40 mV for Kv4.2 wt (n = 13) and Δ2-40 mutant channels (n = 9). The mean percentage of the total decay accounted for by each component is indicated.
) and slow components (τ3, □) of inactivation at +40 mV for Kv4.2 wt (n = 13) and Δ2-40 mutant channels (n = 9). The mean percentage of the total decay accounted for by each component is indicated.
Activation parameters of Kv4.2 channels
A series of test pulses yielded current families as shown in Fig. 2A. With these voltage-jump protocols we never observed outward currents at -60 and −50 mV, but the channels began to activate at −40 mV. The activation time constants for individual subunits obtained by fitting the sigmoidal rising phase of the current traces with a Hodgkin-Huxley-related equation (m4) were 0.72 ± 0.06 ms (n = 7) for wild-type and 0.77 ± 0.09 ms (n = 6) for Δ2-40 mutant channels at the standard test potential of +40 mV. The two channel types showed the same voltage dependence of activation kinetics (e-fold enhancement per 21 mV depolarization; Fig. 2B). In order to compare the voltage dependence of activation of the channels, we fitted Boltzmann functions to the peak conductance-voltage relationships for wild-type and Δ2-40 mutant channels (Fig. 2C). Fourth-order Boltzmann fits, which conform with the Hodgkin-Huxley-related equation used to approximate activation kinetics, yielded V1/2 values of -38.2 ± 2.4 mV (n = 8) and -39.9 ± 1.7 mV (n = 6) for Kv4.2 wild-type and Δ2-40, respectively, with slope factors of 20.6 ± 1.3 and 21.1 ± 1.2 mV. These V1/2 values for a single subunit represent the membrane potential for 6.25 % of the maximal conductance and can serve as a rough estimate of the activation threshold, which was not significantly changed by the N-terminal truncation (P = 0.58). Using the more conventional first-order Boltzmann fit we obtained V1/2 values of -1.2 ± 2.2 mV (n = 8) for wild-type and -3.3 ± 3.0 mV (n = 6) for Δ2-40 mutant channels, indicating that the midpoints of their activation curves were not significantly different (P = 0.57). The respective slope values for the fitted curves were 16.2 ± 0.9 mV (n = 8; wild-type) and 16.3 ± 0.8 mV (n = 6; Δ2-40).
Figure 2. Voltage dependence of Kv4.2 channel activation.
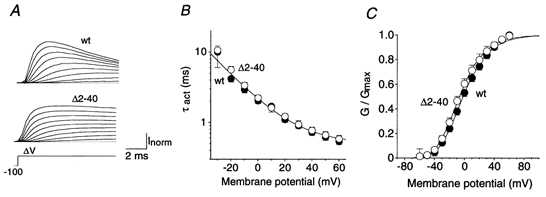
A, currents evoked by successive depolarizing steps from −100 mV to potentials between -20 and +60 mV (ΔV). Note that activation kinetics are unaffected by the N-terminal deletion while inactivation proceeds more slowly for Δ2-40 (lower traces) than for wt (upper traces). Dotted lines represent zero current. B, mean activation time constants (τact) for wt (•; n = 7) and Δ2-40 (○; n = 6) on a logarithmic scale plotted against the membrane potential applied during the test pulse. A single-exponential function was fitted to all plotted data points simultaneously. C, activation curves obtained with fourth-order Boltzmann fits to the normalized peak conductance values at different test potentials for wt (•) and Δ2-40 (○), respectively.
Closed-state inactivation of Kv4.2 channels
While in Shaker channels inactivation is tightly coupled to channel opening (Zagotta et al. 1989), Shal gene-related channels may readily inactivate from pre-open closed states as shown for Kv4.1 (Jerng et al. 1999). We intended to measure the kinetics of closed-state inactivation for both wild-type and Δ2-40 mutant Kv4.2 channels. For this purpose we applied a double-pulse protocol with an intervening conditioning pulse of variable length to a potential below the activation threshold (e.g. −50 mV; Fig. 3A). In such experiments, both the initial control pulse and the conditioning pulse were applied from a membrane potential of −100 mV (Fig. 3A), where no steady-state inactivation was observed for Kv4.2 channels (see Fig. 4B). The current amplitudes evoked by the test pulse at the end of the protocol were normalized to control and plotted against the conditioning pulse duration (Fig. 3B). The results showed that Kv4.2 channels can enter inactivated states without having been activated. Single-exponential functions fitted to the data yielded time constants for the closed-state inactivation at −50 mV of 959 ± 188 ms (n = 6) and 774 ± 79 ms (n = 5) for wild-type and Δ2-40 mutant Kv4.2 channels, respectively. At −60 mV closed-state inactivation occurred with a mean time constant of 1.03 ± 0.14 s (n = 7) for wild-type and 912 ± 138 ms (n = 5) for Δ2-40 mutant channels. The slightly higher values obtained at −60 mV may reflect the voltage dependence of closed-state inactivation, which was not further investigated, due to the small voltage range available; the inactivation observed at −70 mV was usually too small to perform reliable kinetic analyses. At −60 mV (P = 0.58) and at −50 mV (P = 0.64), the small differences between the mean closed-state inactivation kinetics for wild-type and Δ2-40 mutant channels were not significant. Thus, N-terminal truncation of Kv4.2 channels seems to have significant effects on inactivation only if the open-state is involved in the inactivation reaction, as shown by the Kv4.2 A-type current decay kinetics in Fig. 1.
Figure 3. Onset of inactivation at potentials below activation threshold.
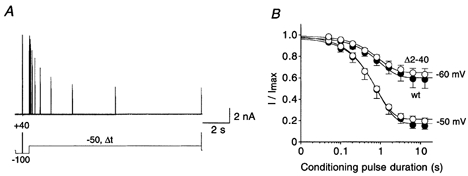
A, currents mediated by Kv4.2 wt channels recorded at +40 mV using a double-pulse protocol with a conditioning pulse to −50 mV of variable duration (Δt). B, mean current amplitudes evoked by the second pulse in protocols as shown in A, relative to the amplitude obtained by the initial control pulse, were plotted against the duration of the conditioning pulse, on a logarithmic time base. •, wt (n = 7 for −60 mV; n = 6 for −50 mV); ○, Δ2-40 (n = 5 for −60 mV; n = 5 for −50 mV). Fitting curves represent single-exponential functions. Note that subtraction of endogenous HEK 293 currents from raw data such as shown in A resulted in a lower mean steady-state value at −50 mV.
Figure 4. Summary of kinetic and steady-state analysis of Kv4.2 channel inactivation.
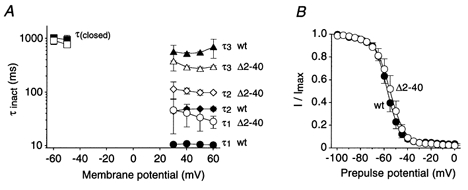
A, mean inactivation time constants (τinact) measured at different membrane potentials for wt (filled symbols) and Δ2-40 (open symbols). Circles, diamonds and triangles represent τ1, τ2 and τ3, respectively (n = 3 for wt; n = 4 for Δ2-40), obtained from triple-exponential fits to the current traces obtained during depolarizing voltage jumps. Squares represent time constants of closed-state inactivation (τ(closed); n = 5-7). Lines connect individual data points for τ1, τ2, τ3 and τ(closed). Data are presented on a semi-log scale to better illustrate the differences between wt and Δ2-40. B, voltage dependence of steady-state inactivation. Normalized current values recorded after a 5 s conditioning pre-pulse were plotted against the pre-pulse potential for wt (•; n = 6) and Δ2-40 (○; n = 5). Fitting curves represent first-order Boltzmann functions.
Figure 4A summarizes our kinetic analyses of outward current decay and closed-state inactivation over the voltage range studied, for both wild-type and Δ2-40 mutant Kv4.2 channels. It demonstrates the slowing of both the fast (τ1) and the intermediate component (τ2) of A-type current decay by the N-terminal truncation, which apparently accelerates the slow component (τ3).
The voltage dependence of Kv4.2 steady-state inactivation was studied with a 5 s prepulse protocol using a test potential of +40 mV. The normalized results are shown in Fig. 4B. Boltzmann analysis yielded V1/2 values for the steady-state inactivation of -57.4 ± 1.4 mV (n = 6) for wild-type and -54.5 ± 2.2 mV (n = 5) for Δ2-40 mutant channels. The V1/2 values were not significantly different (P = 0.29). The slope factors were 5.0 ± 0.3 mV for wild-type and 5.3 ± 0.7 mV for Δ2-40. The finding that steady-state inactivation curves were almost identical for Kv4.2 wild-type and Δ2-40 mutant channels, both above and below the activation threshold, supports the idea that the channels accumulate in an as yet undefined inactivated state, irrespective of the kinetics of inactivation transitions involving the open state. We suggest that the channels accumulate in the closed-inactivated state(s).
Recovery of Kv4.2 channels from inactivation
One of the most striking features of Shal channels, which distinguishes them from Shaker-related channels, is their fast recovery from inactivation (Pak et al. 1991; Serodio et al. 1994). We investigated the involvement of transitions between closed-inactivated and pre-open closed state(s) in the pathway of recovery from inactivation. Thus, we characterized in detail the voltage dependence of the recovery kinetics for both wild-type and Δ2-40 mutant Kv4.2 channels. In our double-pulse protocols (Fig. 5A) the membrane potential before the initial control pulse and during the recovery period was varied between -60 (Fig. 5A) and −120 mV (Fig. 5B). The recovery kinetics, obtained by plotting the relative amplitudes of the current activated by the second pulse against the duration of the interpulse interval, were always well described by a single-exponential function, although the onset of inactivation occurred with multiple components (see Fig. 1). This is consistent with an accumulation of Kv4.2 channels in one inactivated state. The recovery from inactivation was strongly voltage dependent. This is illustrated in Fig. 5C, which shows, on a logarithmic time base, the results of our analysis of recovery from inactivation at -60, -80 and −120 mV for Kv4.2 wild-type channels. The respective time constants were 656 ± 120 ms (n = 4), 285 ± 21 ms (n = 4) and 69 ± 11 ms (n = 3). The recovery time constants obtained at the same membrane potentials for Δ2-40 mutant channels were not significantly different from wild-type (P values between 0.27 and 0.83; Fig. 5D), and the voltage dependence of the Kv4.2 recovery kinetics could be described by an exponential function suggesting an e-fold enhancement of recovery from inactivation per 24 mV hyperpolarization.
Figure 5. Recovery of Kv4.2 channels from inactivation.
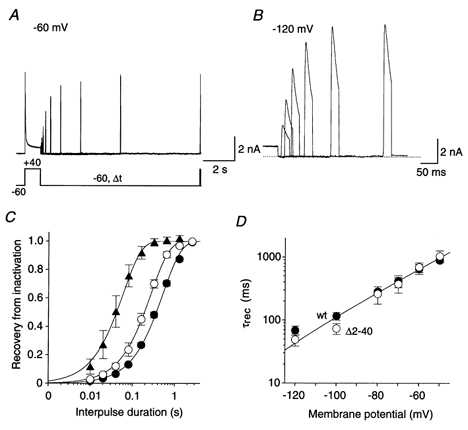
A, currents recorded with a double-pulse protocol at +40 mV. Membrane potential before the initial voltage jump and during the variable interpulse interval (Δt) was −60 mV, where a large fraction of channels were already inactivated. B, currents recorded from the same cell with a protocol as in A but with a holding potential of −120 mV, where steady-state inactivation was removed. Therefore, the maximum currents obtained at +40 mV are larger than in A. Only the second current peak following various interpulse intervals is shown, and a different time scale was chosen. Note that recovery from inactivation was almost complete after 150 ms. Dotted line represents zero current. C, mean normalized currents recorded in wt channels during the second pulse plotted against the duration of the interpulse interval, on a logarithmic time base, for recovery potentials of -60 (•; n = 4), -80 (○; n = 4) and −120 mV (▴; n = 3). Single-exponential functions fitted to the data points yielded the recovery time constants. D, voltage dependence of recovery kinetics. A mono-exponential function was fitted simultaneously to all plotted data points representing the time constants of recovery (τrec) obtained for wt (•) and Δ2-40 (○) on a logarithmic scale.
In our double-pulse protocols, a large fraction of the Kv4.2 channels passed through the open state before reaching the inactivated state(s), because the channels were quickly activated by the initial large depolarizing voltage jump. Since Kv4.2 channels also show transitions from the pre-open closed state(s) to the inactivated state(s), as shown in Fig. 3, we intended to measure the kinetics of recovery from such closed-state inactivation. For this purpose, after a short control pulse to +40 mV the channels were allowed to close and slowly reach steady-state inactivation during a 5 s conditioning pulse to −50 mV. This was followed by a variable recovery period and a subsequent test pulse to +40 mV (Fig. 6A). The membrane potential before the initial pulse and during the recovery period was varied between -80 (Fig. 6A) and −120 mV (Fig. 6B). Kinetic analysis of the recovery from closed-state inactivation revealed no differences between wild-type and mutant Kv4.2 channels (Fig. 6C). The respective time constants obtained at a recovery potential of −80 mV were 241 ± 19 ms (n = 17) and 203 ± 23 ms (n = 15; P = 0.21). Both time constants were slightly smaller than, but not significantly different from, the mean values obtained for wild-type (285 ms; P = 0.30) and mutant Kv4.2 channels (260 ms; P = 0.37) using a conventional recovery protocol as shown in Fig. 5. Figure 6D summarizes the results of our kinetic analyses of recovery from closed-state inactivation for the recovery potentials -80, -100 and −120 mV. The data suggest that the voltage dependence of recovery from closed-state inactivation is equal for wild-type and Δ2-40 mutant channels. Progressively smaller deviations from the steady-state inactivation at −50 mV prevented such analysis for recovery potentials positive to −80 mV. However, the data points representing the time constants for -80, -100 and −120 mV closely match the voltage dependence of recovery kinetics that was determined using conventional recovery protocols (compare Fig. 5D and Fig. 6D). Taken together, our results show that wild-type and Δ2-40 mutant Kv4.2 channels resemble each other with respect to all of the gating parameters tested so far, except inactivation transitions involving the open state, as revealed by the outward current decay kinetics.
Figure 6. Recovery from closed-state inactivation.
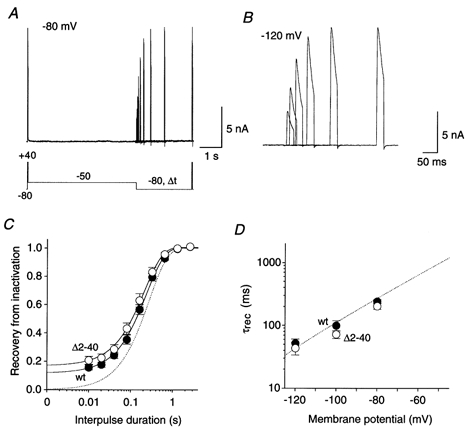
A, currents recorded at +40 mV with a specialized double-pulse protocol. Inactivation was induced at −50 mV and recovery was measured after variable times (Δt) at −80 mV. B, currents recorded with the same protocol as in A but recovery at −120 mV was measured. Only the second current response is shown on a different time scale. C, kinetics of recovery from closed-state inactivation at −80 mV. Mean normalized current amplitudes were plotted against the interpulse duration, on a logarithmic time base, for wt (•; n = 17) and Δ2-40 (○; n = 15). Fitting curves are based on single-exponential functions. The dotted line represents the fitting curve, which describes the recovery of wt channels at −80 mV from inactivation after channel opening, as shown in Fig. 5. D, mean time constants of recovery from closed-state inactivation for wt (•; n = 6-17) and Δ2-40 (○; n = 5-15) plotted against the recovery potential. The voltage and time range shown (x- and y-axis, respectively) as well as the exponential fitting curve (dotted line) were adapted from Fig. 5D.
Our recovery data presented in Fig. 5 and Fig. 6 are consistent with the idea that Kv4.2 channels always accumulate in a closed-inactivated state, from which they directly recover, bypassing the open state. Prominent tail currents as observed for Shaker channels during recovery from inactivation at very negative membrane potentials and in the presence of high external K+ concentrations (Demo & Yellen, 1991; Ruppersberg et al. 1991) should therefore be absent in Kv4.2 channels. This assumption was tested by using protocols with voltage jumps from +40 or −50 mV to −120 mV, in symmetrical 130 mm K+ (Fig. 7). As we expected, these experiments showed that progressive cumulative inactivation at +40 mV reduced the size of the initial tail currents during the recovery from inactivation at −120 mV (Fig. 7A and B). After 20 s of inactivation at +40 mV virtually no Kv4.2 channels resided in or revisited the open state during recovery from inactivation (Fig. 7C). Serving as a control experiment, the same result was obtained when the recovery from closed-state inactivation was examined at −120 mV in symmetrical 130 mm K+ (Fig. 7D).
Figure 7. No transient occupancy of open state during recovery after accumulation in closed-inactivated state(s).
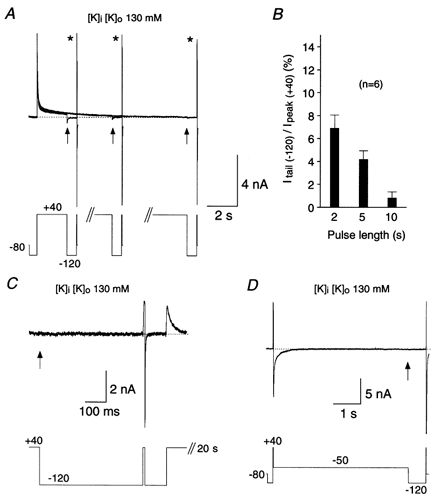
Recovery of Kv4.2 wt channels measured at −120 mV and in symmetrical 130 mm K+ to test whether channels visit the open state during recovery from inactivation. A, depolarizing pulses to +40 mV of variable duration (2, 5 and 10 s) were followed by negative voltage jumps to −120 mV. Three current traces recorded from the same cell are superimposed. Note that tail currents (arrows) vanish as cumulative inactivation proceeds. In all cases recovery from inactivation was complete after 640 ms, as indicated by the brief control outward currents (asterisks) followed by deactivating inward currents at the end of each pulse protocol. B, percentage of tail current amplitude (arrows in A) relative to the control outward current amplitude (asterisks in A) at the different pulse durations. Results from 6 cells are summarized. C, the holding potential was manually set to +40 mV, and currents were recorded every 20 s at high resolution (50 μs sample interval). Tail currents were absent at the beginning of a 640 ms pulse to −120 mV (arrow), but recovery during this period was complete. D, protocol similar to the ones used in Fig. 6, but with a fixed recovery time (640 ms) and fixed recovery potential (−120 mV). No tail currents (arrow) but complete recovery could be observed. The dotted lines in A, C and D represent zero current.
Kv4.2 wild-type and N-terminal deletion mutant differ in their deactivation kinetics
We measured the voltage dependence of the deactivation kinetics for Kv4.2 wild-type and Δ2-40 mutant channels using tail current protocols with test potentials between -110 and −50 mV following brief channel activation at +40 mV (Fig. 8A). The current decay due to channel deactivation could be fitted with a single-exponential function and the time constant at −110 mV for wild-type channels was 1.6 ± 0.1 ms (n = 15), significantly below the value for Δ2-40 mutant channels (1.9 ± 0.1 ms; n = 15; P < 0.05). For both channel types the deactivation kinetics were slowed with increasing membrane depolarization, although with apparently different voltage dependence (Fig. 8B). As inferred from exponential fitting of the obtained data, the slowing was e-fold per 44 mV depolarization for wild-type and e-fold per 30 mV depolarization for Δ2-40 mutant channels. Thus, the deactivation time constants measured at −50 mV, just below the activation threshold, differed most significantly (P < 0.01) for wild-type and mutant Kv4.2 channels. Wild-type channel closing at this membrane potential occurred with a mean time constant of 5.9 ± 0.3 ms (n = 15) while the respective value for Δ2-40 mutant channels was 11.9 ± 0.6 ms (n = 15). Our results suggest that the N-terminal truncation stabilizes the open-state of Kv4.2 channels, which causes both slowed deactivation and slowed inactivation.
Figure 8. Deactivation kinetics of Kv4.2 channels.
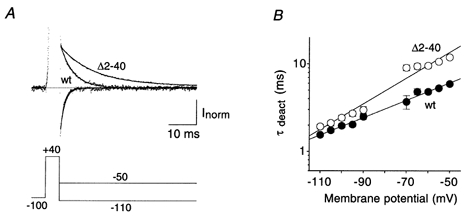
A, tail currents 5 ms after channel activation recorded during voltage jumps from +40 to −110 mV (fast decaying inward currents) and from +40 to −50 mV (slowly decaying outward currents) for wt and Δ2-40. Dotted line represents zero current and outward currents during the activation phase are truncated. Single-exponential functions were fitted to the current relaxations. Note the large difference in deactivation kinetics between wt and Δ2-40 at −50 mV, which was less obvious at −110 mV. B, mean time constants of deactivation (τdeact) for wt (•) and Δ2-40 (○) plotted on a logarithmic scale at different membrane potentials (n = 15 for both channel types). The voltage dependence of deactivation kinetics was approximated by mono-exponential functions.
The closing of K+ channels can be influenced in a voltage-dependent manner by the use of ions with different permeation properties, like Rb+ and K+ (Sala & Matteson, 1991). Rb+ ions can slow the deactivation process due to their higher pore occupancy. In order to study the permeant ion dependence of both deactivation and inactivation we recorded inward tail currents and transient outward currents, respectively, mediated by Kv4.2 wild-type channels in symmetrical 130 mm K+ and symmetrical 130 mm Rb+ (Fig. 9A and C). We used the same tail current protocol as under standard conditions. The test potential was, however, varied only between -110 and −60 mV, because the Rb+ ions caused a hyperpolarizing shift in the conductance-voltage relationship (not shown). The measured deactivation kinetics and their voltage dependence were strongly influenced by the permeant ion species. At −110 mV channel closing occurred with mean time constants of 1.3 ± 0.2 ms (n = 7) and 4.6 ± 0.7 ms (n = 10) in symmetrical K+ and symmetrical Rb+, respectively. Increasing depolarization slowed the deactivation kinetics, however, with slightly different voltage dependence for the two ion species (Fig. 9B). In symmetrical K+ an e-fold slowing per 54 mV depolarization led to a mean deactivation time constant of 3.4 ± 0.3 ms at −60 mV, while in symmetrical Rb+ a time constant of 13.6 ± 2.0 ms was reached, due to an e-fold slowing per 46 mV depolarization. Next, we measured the inactivation kinetics of outward currents at +40 mV in symmetrical K+ and symmetrical Rb+ (Fig. 9C). The inactivation kinetics obtained under symmetrical ionic conditions are summarized in Fig. 9D. As indicated in Fig. 9C, the increase in the external K+ concentration from 5 mm (standard conditions) to 130 mm caused a significant decrease in the mean time constants for fast (P < 0.01) and intermediate (P < 0.01) inactivation (5.8 ± 0.5 and 36.5 ± 2.6 ms, respectively, accounting for 63.1 ± 2.8 and 31.9 ± 2.2 % of the total decay; n = 5). The slow time constant in symmetrical 130 mm K+ was 588 ± 72 ms (n = 5), not significantly different from that in standard conditions (P = 0.36), and accounted for 5.0 ± 0.9 % of the total decay. In symmetrical 130 mm Rb+ the mean (n = 6) fast time constant was 13.9 ± 2.0 ms (66.9 ± 3.4 %), significantly slower than in symmetrical K+ (P < 0.05). Similarly, the intermediate time constant was significantly slower in symmetrical Rb+ (65.8 ± 9.4 ms; 26.0 ± 3.1 %; n = 6) than in symmetrical K+ (P < 0.05); however, the mean slow time constant was not significantly changed (693 ± 121 ms; 7.1 ± 0.5 %; n = 6) by Rb+ (P = 0.48). In summary, the high concentration of Rb+ ions caused a slowing of Kv4.2 channel deactivation and a slowing of the fast and intermediate components of Kv4.2 channel inactivation. These results are in accordance with the idea that channel closing, i.e. the occupancy of a pre-open closed state, plays a significant role in Kv4.2 channel inactivation gating.
Figure 9. Deactivation and inactivation of Kv4.2 wild-type channels under varied ionic conditions.
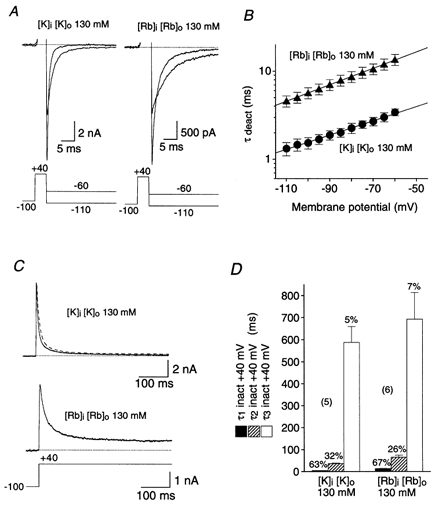
A, inward tail currents measured with the same protocol as shown in Fig. 8A but in 130 mm symmetrical K+ (left) and in 130 mm symmetrical Rb+ (right). Dotted lines represent zero current and outward currents during the activation phase are truncated. B, mean deactivation time constants obtained from single-exponential fits to the tail currents, plotted on a logarithmic scale against the membrane potential for symmetrical K+ (•; n = 7) and symmetrical Rb+ (▴; n = 10). Mono-exponential functions describe the voltage dependence of the deactivation kinetics. C, outward currents carried by K+ (upper trace) and Rb+ (lower trace) under symmetrical ionic conditions were recorded during depolarizing voltage jumps from -100 to +40 mV. The upper trace was obtained from the Kv4.2 wt-expressing cell shown in Fig. 1. The triple-exponential fit from Fig. 1B was normalized and superimposed on the current recorded in symmetrical 130 mm K+ (dashed line). Dotted lines represent zero current. D, mean values for the fast (τ1, ▪), intermediate (τ2, 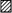 ) and slow components (τ3, □) of inactivation at +40 mV for symmetrical K+ (n = 5) and symmetrical Rb+ (n = 6). The mean percentage of the total decay accounted for by each component is indicated.
) and slow components (τ3, □) of inactivation at +40 mV for symmetrical K+ (n = 5) and symmetrical Rb+ (n = 6). The mean percentage of the total decay accounted for by each component is indicated.
Simulating Kv4.2 inactivation gating
Previously, Jerng and coworkers (Jerng et al. 1999) developed a model for Kv4.1 channel gating (Model 1; Fig. 10A), in which channels become inactivated if they visit an open-inactivated state (IO), a closed-inactivated state (IC), or a deep-inactivated state (ID). The two main kinetic features of Model 1 are, first, that Kv4.1 channels have to return from the short-lived open-inactivated state IO via the open state to the pre-open closed state before they can enter the closed-inactivated state, IC, and second, that cumulative Kv4.1 channel inactivation is a two-step reaction involving the closed-inactivated state, IC, and the deep-inactivated state, ID.
We developed a Markov state model to simulate the Kv4.2 channel currents recorded for this study (see Methods). We started with the gating scheme that Jerng and coworkers (Jerng et al. 1999) used to fit their Kv4.1 data (Model 1; Fig. 10A), and adjusted α0 and β0, in order to match the simulated activation characteristics (V1/2 = -1.9 mV; k = 16.5 mV; not shown) to our experimentally obtained G-V curves. Furthermore, we used different inactivation rates (Table 1) in order to obtain current decay kinetics that resembled more closely the experimental Kv4.2 data. Figure 10 shows the simulated currents based on voltage protocols from this study (Fig. 1A and Fig. 5B), which revealed key kinetic features of Kv4.2 channel inactivation. The currents simulated with Model 1 and the parameter values listed in Table 1 exhibited multi-exponential inactivation kinetics during a depolarizing pulse to +40 mV, very similar to those obtained experimentally (Fig. 10B). However, our simulations failed to reproduce the experimentally observed fast recovery from inactivation at −120 mV. This indicated that Model 1 was inappropriate (Fig. 10C).
We were particularly interested in the path Kv4.2 channels take to reach an inactivated state and their distribution among the different inactivated states at a given time point. To address this question, we calculated the relative occupancy of each state of the Markov chain model during the voltage pulse as a function of time (fractional occupancy time course; Fig. 10D). For ease of display, we plotted only the pre-open closed (C4), open (O) and inactivated (I) states. The fractional occupancy timecourse shows that in Model 1 channels exit both IO and IC, and by the end of the pulse all channels reside in the ID state. Since exit from ID is slow, the time course for recovery from inactivation is very slow too.
Further simulations based on Model 1 with different entry and exit rates for inactivated states failed to adequately describe Kv4.2 channel gating. The main criteria for an adequate simulation were a fast time course of recovery from inactivation at hyperpolarized potentials, and a pronounced and multi-exponential inactivation during strong depolarization. This could only be obtained when we introduced two major alterations to Model 1. First, we removed the deep-inactivated state, ID, since accumulation in ID was responsible for the extremely slow recovery from inactivation. Instead, we introduced an additional inactivated state, IS, which can be entered from IO to maintain the experimentally observed three components of current decay in the simulations. Second, we connected all closed states to inactivated states, in analogy to a Kv4.3 gating model used by Greenstein et al. (2000). We refer to the new model (Model 2; Fig. 11A) as an ‘allosteric model of inactivation’, as suggested by Beck et al. (2001). In such an allosteric model the ‘allosteric factor’f (Table 2), similar to the scaling factor used by Greenstein et al. (2000), defines the coupling of closed-state inactivation to the individual transition steps along the activation pathway (CR to C4 in Model 2). Thus, inactivation is coupled to voltage-dependent activation. The possibility that IS may connect IO and IC4, as indicated in Model 2 (Fig. 11A), was not tested in this study (but see Discussion).
Table 2.
Values of simulation parameters used in Model 2
| Parameter | Values |
|---|---|
| α0 (s−1) | 200 |
| zα | 1.0 |
| β0 (s−1) | 4 |
| zβ | 1.58 |
| κco (s−1) | 400 |
| κoc (s−1) | 1100 |
| κoi (s−1) | 300 |
| κio (s−1) | 30 |
| κci (s−1) | 30 |
| κic (s−1) | 0.1 |
| f | 0.3 |
| κis (s−1) | 30 |
| κsi (s−1) | 15 |
In the allosteric model of Kv4.2 inactivation gating, all closed states (C) are connected to inactivated states via κci and κic. The coupling of activation and inactivation is defined by an allosteric factor f (see Fig. 11A). Furthermore, a transition leading from IO to IS has been added in Model 2 (Fig. 11), which is defined by κis and κsi. The voltage-dependent reactions along the activation pathway are the same as for Model 1 (see Table 1) with the exception of the α0 term, which was shifted from 133 s−1 in Model 1 to 200 s−1 in Model 2.
The zero voltage rate term α0 for the forward direction in the closed states was adjusted (Table 2) to make the allosteric model simulate an activation behaviour (V1/2 = -1.1 mV; k = 17.4 mV) similar to that obtained experimentally for Kv4.2 channels. In order to fit the model simulations to our data, the rate of recovery from inactivation was determined by the rate constant kic. The fast decay component of simulated current traces showed a high sensitivity to koi, and while kci played the major role in setting the intermediate time constant of inactivation, ksi and kis determined the ultra slow component of inactivation. Thus, each of the components of the inactivation kinetics were found to be controlled by one or two crucial parameters in the Markov state scheme. Simulations based on Model 2 with the parameter values listed in Table 2 adequately described the Kv4.2 experimental data. The currents decayed with one fast (τ = 9 ms; 61 %), one intermediate (τ = 27 ms; 31 %) and one slow component (τ = 544 ms; 9 %), like the measured Kv4.2 wild-type currents in response to a long depolarizing pulse (Fig. 11B). Since in the allosteric model the opening step is reverse-biased (Table 2) and inactivation from the open state is relatively unstable (Table 2), channels mainly inactivate from the pre-open closed state, C4, and accumulate in IC4 during strong depolarization. Plotting the fractional occupancy time course (Fig. 11C) showed that channels start to enter IC4 early during the depolarizing pulse. After opening, the channels also occupy IO and IS, which slows the entry into IC4. Finally, the channels slowly exit IO and IS, close, and accumulate in IC4, from where the majority of channels directly recover, bypassing the open state, as soon as the membrane polarity is reversed. The simulated time course of recovery from inactivation (Fig. 11D;τ = 79 ms at −120 mV) closely resembled that measured for Kv4.2 currents. The model was also able to adequately simulate the onset of closed-state inactivation at −50 mV (Fig. 11E), albeit with slightly faster kinetics (τ = 521 ms) as seen on average experimentally.
DISCUSSION
The main conclusion that can be drawn from the results of our experiments is that in response to membrane depolarizations of variable strength, Kv4.2 channels always accumulate in the closed-inactivated state(s), from which they directly recover, bypassing the open state. The simulations done with an allosteric model nicely reproduced the measured Kv4.2 gating kinetics, especially the rapid time course of recovery from inactivation.
Inactivation reactions underlying A-type current decay
We compared our results with kinetic analyses done previously on Kv4.2 channels transiently expressed in HEK 293 cells (Perez-Garcia et al. 1999; Zhu et al. 1999). In contrast to previous studies, we have determined endogenous HEK 293 outward currents, which may contaminate decay kinetics. Thus, their subtraction is essential for a detailed kinetic analysis of macroscopic Kv4.2 currents. Furthermore, we utilized very long depolarizing pulses, in order to also cover extremely slow components of outward current decay. The results revealed triple-exponential decay kinetics for Kv4.2-mediated currents. Similar multi-exponential decay kinetics have been described for Kv4.1 channels (Jerng & Covarrubias, 1997; Jerng et al. 1999). However, Kv4.1 and Kv4.2 current inactivation kinetics are distinct. Kv4.1-mediated currents show only a small fast component, whereas in the Kv4.2 current kinetics the fast component accounts for the largest fraction of the total decay. This quantitative difference may be the reason why the slowing of fast and intermediate decay components produced by N-terminal truncation can be seen in Kv4.2-mediated currents, while similar deletion mutants of Kv4.1 apparently lack the fast component of inactivation (Jerng & Covarrubias, 1997). A complete removal of rapid inactivation after deletion of N-terminal domains can be observed in Shaker B channels (Hoshi et al. 1990); however, Kv4.1 channels do not undergo classical N-type inactivation since Kv4.1 inactivation kinetics are insensitive to internal tetraethylammonium (Jerng & Covarrubias, 1997), an open channel blocker, which interferes with Shaker N-type inactivation (Choi et al. 1991). We have not performed comparable pharmacological experiments; however, the distinct effects of the 40 amino acid N-terminal truncation observed in our experiments (slowing of both fast and intermediate components, rather than complete removal of the fast component of current decay) clearly show that inactivation of Kv4.2 channels is different from the N-type inactivation of Shaker-related channels.
Jerng & Covarrubias (1997) have also shown that external tetraethylammonium, which interferes with Shaker channel C-type inactivation (Choi et al. 1991), does not affect the Kv4.1 current decay kinetics, which are therefore unlikely to represent C-type inactivation. Similarly, the results we obtained in experiments with high K+ concentrations suggest that the slow decay phase of Kv4.2-mediated currents is distinct from Shaker-like C-type inactivation. The latter is slowed by increasing the external K+ concentration (Baukrowitz & Yellen, 1995), whereas the slow Kv4.2 inactivation component was not affected by an increase in the external K+ concentration (compare Fig. 1C and Fig. 9D). We did, however, observe an enhancement of fast Kv4.2 inactivation in symmetrical K+, which nicely compares to the effect of elevated external K+ concentration described for somatodendritic A-type currents recorded from isolated hippocampal neurons (Kirichok et al. 1998). The recovery of C-type-inactivated Shaker channels tends to be slow, occurring in the time range of many seconds, but Kv4.2 channels completely recovered from inactivation within a few hundred milliseconds (see Fig. 5). We did not study recovery from inactivation in high external K+, but Jerng & Covarrubias (1997) have shown that elevated K+ concentrations cause a slowing of Kv4.1 channel recovery, which is in contrast to the recovery-enhancing effect of high external K+ concentrations observed for Shaker-related channels (Demo & Yellen, 1991). It is obvious that Kv4 channel inactivation does not follow classical Shaker N- and C-type inactivation.
Simulations
According to Model 1 (Fig. 10A) the Kv4 current decay is a consequence of the entry into a short-lived open-inactivated state (O → IO), the accumulation in a closed-inactivated state (IC), and the final trapping in a deep-inactivated state (ID). The model simulated adequately the activation, inactivation and deactivation kinetics of macroscopic Kv4.1 currents (Jerng et al. 1999). The final trapping in a deep-inactivated state is, however, not compatible with fast recovery from inactivation (see Fig. 10C), as was experimentally observed for both Kv4.1 and Kv4.2 channels. Therefore, we used an alternative gating model (Model 2 in Fig. 11A), which was derived from Model 1 by modifying the entry and exit rates for the two inactivated states IO and IC, by deleting ID and instead coupling IO to another inactivated state, IS, and finally by connecting all closed states along the activation pathway to inactivated states (allosteric model; Beck et al. 2001). Simulations with this model produced a fast outward current component, which accounted for a large fraction of the total decay, and both recovery from inactivation and closed-state inactivation could be simulated adequately.
Involvement of channel closing in Kv4 inactivation gating
Both in Model 1 and in Model 2, the prerequisite for accumulation in the closed-inactivated state(s) is a transition from IO back to the open state, and the subsequent closing of channels, because IO and IC are not connected. In fact, when slowing the channel closing rate by a factor of 20 in Model 1, Jerng and coworkers were able to reproduce the macroscopic inactivation time course that they found in slowly deactivating Kv4.1 mutants (Jerng et al. 1999). The prominent feature of the mutant Kv4.1 inactivation was a slowing of the intermediate and slow components of decay (Jerng et al. 1999). In the Kv4.2 Δ2-40 N-terminal deletion mutant, which also exhibited slowed deactivation kinetics, we observed on average a 3-fold slowing of the fast component, a 2-fold slowing of the intermediate component, and a 2-fold enhancement of the slow component of current decay (see Fig. 1C). This is in contrast to the slowly deactivating Kv4.1 mutant studied by Jerng et al. (1999). Also, the effect of the 40 amino acid deletion on Kv4.2 current inactivation could not be exactly reproduced when K+ was replaced by Rb+, which, due to its higher pore occupancy, slows deactivation (Sala & Matteson, 1991). In symmetrical Rb+ both the fast and the intermediate components of Kv4.2 current decay were slowed on average 2-fold relative to symmetrical K+, while the slow component was unaffected by the permeant ion species (see Fig. 9D). Apparently, the effect of N-terminal truncation on Kv4.2 gating kinetics is distinct, leading to a stabilization of the open state, which causes, independently of each other, a pronounced slowing of deactivation at moderately depolarized potentials and a slowing of inactivation transitions involving the open state.
Interestingly, slowing the open-state inactivation rate (O → IO) in Model 1 and Model 2 produces single-exponential tail current kinetics, while rapidly inactivating models always deactivate with double-exponential kinetics (not shown). A prominent second component of tail current decay, probably representing channels that exit IO via the open state before they close, was observed for Kv4.1 channels (Jerng et al. 1999), but not in our experiments (see Fig. 8A), although Kv4.2 channels exhibit a fairly rapid initial component of inactivation. Therefore we envisage the possibility that open-inactivated Kv4.2 channels can close. This would be in agreement with models that have been used previously to model A-type channel gating (Solc & Aldrich, 1990; Campbell et al. 1993; Greenstein et al. 2000). Kv4 channel closing may involve one or more subconductance states, which correspond to IS. Interestingly, Campbell et al. (1993) adapted their model from one that was originally developed for voltage-dependent Na+ channels (Patlak, 1991). It has been shown that Na+ channels can inactivate from a closed state (Horn et al. 1981), and that they deactivate before they recover from inactivation (Kuo & Bean, 1994).
An important feature of both Model 1 and Model 2 is the reverse-biased opening step (koc > kco; see Tables 1 and 2 and Jerng et al. 1999). It allows cumulative inactivation in IC4 even at strongly positive membrane potentials. Such an absorbing inactivation transition, leading from C4 to IC4, implies a low peak open probability (see Fig. 10D and 11C). It is noteworthy that Solc & Aldrich (1990), who studied native Drosophila non-Shaker A-type channels, disfavoured a model with an inactivation transition occurring from the final pre-open closed state, because it produced a lower maximal open probability than was observed experimentally. Clarification of this question and the existence of a putative subconductance state(s) has to await a detailed analysis of single-channel properties.
Closed-inactivated state(s)
The recovery of Na+ channels from inactivation is fast and voltage dependent, because it occurs from a closed-inactivated state. Here we show that the same is true for Kv4.2 channels. Our experimental evidence, that Kv4.2 channels accumulate in and directly recover from a closed-inactivated state bypassing the open state, can be summarized as follows. First, wild-type and Δ2-40 mutant Kv4.2 channels recover from inactivation with identical kinetics (Fig. 5D), although their open-state inactivation kinetics are different (Fig. 1A). Second, for the two channel types, the recovery kinetics remain the same, no matter whether the channels opened (IO⇌ O → C4→ IC4; Fig. 5) or not (C4→ IC4; Fig. 6) before they inactivated. Third, the recovery kinetics are strongly voltage dependent (Fig. 5C), the voltage dependence is identical for wild-type and Δ2-40 mutant channels (Fig. 5D), and it is not changed by channel opening prior to inactivation (Fig. 6D). Finally, if cumulative inactivation of Kv4.2 channels in IC4 is complete, no inward tail currents can be observed, even in the presence of high external K+ concentrations, during recovery at very negative membrane potentials (Fig. 7). These findings exclude a prominent involvement of the open state in the recovery pathway. By contrast, Shaker channels inactivate exclusively via the open state and have to release the inactivation ball before they can close, as indicated by slow tail currents during the recovery from inactivation (Demo & Yellen, 1991; Ruppersberg et al. 1991). However, inactivation from a closed state has been described for the I2 mutant of Shaker B channels (Ayer & Sigworth, 1997). The mutation (L382I) was introduced immediately adjacent to the S4-S5 linker at the end of the S4 region. It makes Shaker B channels behave more like voltage-dependent Na+ channels and, according to this study, like Kv4.2 channels. This raises the question whether only small structural changes may underlie the distinct gating behaviours of Shaker- and Shal-related channels.
Concluding remarks
The predominant mechanism of Kv4.2 channel inactivation from a pre-open closed state is correlated with their important physiological role in dendritic signal propagation. Closed-state inactivation of somatodendritic A-type channels can lead to spike amplification since these inactivated states can be reached as a consequence of subthreshold EPSPs in dendrites (Magee & Johnston, 1997). Kv4.2 inactivation transitions involving the open state are equally important in order to counterbalance sudden extensive depolarizations. As our experiments showed, recovery will be fast irrespective of the initial inactivation reaction (C4→ IC4 or O → IO), which guarantees a high A-type channel availability. In fact, a family of Kv channel-interacting proteins (KChIPs) has recently been described (An et al. 2000), which are associated with native Kv4 channels. KChIPs dramatically increase the functional expression of Kv4 channels and markedly accelerate their recovery from inactivation. A detailed kinetic analysis of Kv4 channel gating in the presence of KChIPs will shed further light on the inactivation mechanism of these channels and the structures involved.
Acknowledgments
We would like to thank Sabine Wehrmann and Anne Schneider-Darlison for excellent technical assistance. This work was supported in part by the Deutsche Forschungsgemeinschaft, NIH grant (NS34379) to L.M.B. and a Computational Neuroscience Fellowship (University of Minnesota) to A.V.
References
- Alonso G, Widmer H. Clustering of Kv4. 2 potassium channels in postsynaptic membrane of rat supraoptic neurons: an ultrastructural study. Neuroscience. 1997;77:617–621. doi: 10.1016/s0306-4522(96)00561-1. [DOI] [PubMed] [Google Scholar]
- An W F, Bowlby M R, Betty M, Cao J, Ling H P, Mendoza G, Hinson J W, Mattsson K I, Strassle B W, Trimmer J S, Rhodes K J. Modulation of A-type potassium channels by a family of calcium sensors. Nature. 2000;403:553–556. doi: 10.1038/35000592. [DOI] [PubMed] [Google Scholar]
- Ayer R K Jr, Sigworth F J. Enhanced closed-state inactivation in a mutant Shaker K+ channel. Journal of Membrane Biology. 1997;157:215–230. doi: 10.1007/s002329900230. [DOI] [PubMed] [Google Scholar]
- Baldwin T J, Tsaur M L, Lopez G A, Jan Y N, Jan L Y. Characterization of a mammalian cDNA for an inactivating voltage-sensitive K+ channel. Neuron. 1991;7:471–483. doi: 10.1016/0896-6273(91)90299-f. [DOI] [PubMed] [Google Scholar]
- Baukrowitz T, Yellen G. Modulation of K+ current by frequency and external [K+]: a tale of two inactivation mechanisms. Neuron. 1995;15:951–960. doi: 10.1016/0896-6273(95)90185-x. [DOI] [PubMed] [Google Scholar]
- Beck E J, Bowlby M R, An W F, Rhodes K J, Covarrubias M. Modulation of Kv4 inactivation gating by a calcium binding protein (KChIP-1) Biophysical Society Abstracts. 2001;80:439a. [Google Scholar]
- Blair T A, Roberds S L, Tamkun M M, Hartshorne R P. Functional characterization of RK5, a voltage-gated K+ channel cloned from the rat cardiovascular system. FEBS Letters. 1991;295:211–213. doi: 10.1016/0014-5793(91)81420-d. [DOI] [PubMed] [Google Scholar]
- Campbell D L, Rasmusson R L, Qu Y, Strauss H C. The calcium-independent transient outward potassium current in isolated ferret right ventricular myocytes. I. Basic characterization and kinetic analysis. Journal of General Physiology. 1993;101:571–601. doi: 10.1085/jgp.101.4.571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen C, Okayama H. High-efficiency transformation of mammalian cells by plasmid DNA. Molecular Cell Biology. 1987;7:2745–2752. doi: 10.1128/mcb.7.8.2745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi K L, Aldrich R W, Yellen G. Tetraethylammonium blockade distinguishes two inactivation mechanisms in voltage-activated K+ channels. Proceedings of the National Academy of Sciences of the USA. 1991;88:5092–5095. doi: 10.1073/pnas.88.12.5092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demo S D, Yellen G. The inactivation gate of the Shaker K+ channel behaves like an open-channel blocker. Neuron. 1991;7:743–753. doi: 10.1016/0896-6273(91)90277-7. [DOI] [PubMed] [Google Scholar]
- Dilks D, Ling H P, Cockett M, Sokol P, Numann R. Cloning and expression of the human Kv4. 3 potassium channel. Journal of Neurophysiology. 1999;81:1974–1977. doi: 10.1152/jn.1999.81.4.1974. [DOI] [PubMed] [Google Scholar]
- Dixon J E, McKinnon D. Quantitative analysis of potassium channel mRNA expression in atrial and ventricular muscle of rats. Circulation Research. 1994;75:252–260. doi: 10.1161/01.res.75.2.252. [DOI] [PubMed] [Google Scholar]
- Dixon J E, Shi W, Wang H S, McDonald C, Yu H, Wymore R S, Cohen I S, McKinnon D. Role of the Kv4. 3 K+ channel in ventricular muscle. A molecular correlate for the transient outward current. Circulation Research. 1996;79:659–668. doi: 10.1161/01.res.79.4.659. [DOI] [PubMed] [Google Scholar]
- Greenstein J L, Wu R, Po S, Tomaselli G F, Winslow R L. Role of the calcium-independent transient outward current Ito1 in shaping action potential morphology and duration. Circulation Research. 2000;87:1026–1033. doi: 10.1161/01.res.87.11.1026. [DOI] [PubMed] [Google Scholar]
- Hoffman D A, Magee J C, Colbert C M, Johnston D. K+ channel regulation of signal propagation in dendrites of hippocampal pyramidal neurons. Nature. 1997;387:869–875. doi: 10.1038/43119. [DOI] [PubMed] [Google Scholar]
- Horn R, Patlak J, Stevens C F. Sodium channels need not open before they inactivate. Nature. 1981;291:426–427. doi: 10.1038/291426a0. [DOI] [PubMed] [Google Scholar]
- Hoshi T, Zagotta W N, Aldrich R W. Biophysical and molecular mechanisms of Shaker potassium channel inactivation. Science. 1990;250:533–538. doi: 10.1126/science.2122519. [DOI] [PubMed] [Google Scholar]
- Hoshi T, Zagotta W N, Aldrich R W. Two types of inactivation in Shaker K+ channels: effects of alterations in the carboxy-terminal region. Neuron. 1991;7:547–556. doi: 10.1016/0896-6273(91)90367-9. [DOI] [PubMed] [Google Scholar]
- Isacoff E Y, Jan Y N, Jan L Y. Putative receptor for the cytoplasmic inactivation gate in the Shaker K+ channel. Nature. 1991;353:86–90. doi: 10.1038/353086a0. [DOI] [PubMed] [Google Scholar]
- Isbrandt D, Leicher T, Waldschütz R, Zhu X, Luhmann U, Michel U, Sauter K, Pongs O. Gene structures and expression profiles of three human KCND (Kv4) potassium channels mediating A-type currents ITO and ISA. Genomics. 2000;64:144–154. doi: 10.1006/geno.2000.6117. [DOI] [PubMed] [Google Scholar]
- Jerng H H, Covarrubias M. K+ channel inactivation mediated by the concerted action of the cytoplasmic N- and C-terminal domains. Biophysical Journal. 1997;72:163–174. doi: 10.1016/S0006-3495(97)78655-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jerng H H, Shahidullah M, Covarrubias M. Inactivation gating of Kv4 potassium channels: molecular interactions involving the inner vestibule of the pore. Journal of General Physiology. 1999;113:641–660. doi: 10.1085/jgp.113.5.641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirichok Y V, Nikolaev A V, Krishtal O A. [K+]out accelerates inactivation of Shal-channels responsible for A-current in rat CA1 neurons. NeuroReport. 1998;9:625–629. doi: 10.1097/00001756-199803090-00012. [DOI] [PubMed] [Google Scholar]
- Kong W, Po S, Yamagishi T, Ashen M D, Stetten G, Tomaselli G F. Isolation and characterization of the human gene encoding Ito: further diversity by alternative mRNA splicing. American Journal of Physiology. 1998;275:H1963–1970. doi: 10.1152/ajpheart.1998.275.6.H1963. [DOI] [PubMed] [Google Scholar]
- Kuo C C, Bean B P. Na+ channels must deactivate to recover from inactivation. Neuron. 1994;12:819–829. doi: 10.1016/0896-6273(94)90335-2. [DOI] [PubMed] [Google Scholar]
- Magee J C, Johnston D. A synaptically controlled, associative signal for Hebbian plasticity in hippocampal neurons. Science. 1997;275:209–213. doi: 10.1126/science.275.5297.209. [DOI] [PubMed] [Google Scholar]
- Ohya S, Tanaka M, Oku T, Asai Y, Watanabe M, Giles W R, Imaizumi Y. Molecular cloning and tissue distribution of an alternatively spliced variant of an A-type K+ channel alpha-subunit, Kv4. 3 in the rat. FEBS Letters. 1997;420:47–53. doi: 10.1016/s0014-5793(97)01483-x. [DOI] [PubMed] [Google Scholar]
- Pak M D, Baker K, Covarrubias M, Butler A, Ratcliffe A, Salkoff L. mShal, a subfamily of A-type K+ channel cloned from mammalian brain. Proceedings of the National Academy of Sciences of the USA. 1991;88:4386–4390. doi: 10.1073/pnas.88.10.4386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patlak J. Molecular kinetics of voltage-dependent Na+ channels. Physiological Reviews. 1991;71:1047–1080. doi: 10.1152/physrev.1991.71.4.1047. [DOI] [PubMed] [Google Scholar]
- Perez-Garcia M T, Lopez-Lopez J R, Gonzalez C. Kvβ1. 2 subunit coexpression in HEK293 cells confers O2 sensitivity to Kv4.2 but not to Shaker channels. Journal of General Physiology. 1999;113:897–907. doi: 10.1085/jgp.113.6.897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pongs O. Voltage-gated potassium channels: from hyperexcitability to excitement. FEBS Letters. 1999;452:31–35. doi: 10.1016/s0014-5793(99)00535-9. [DOI] [PubMed] [Google Scholar]
- Rettig J, Heinemann S H, Wunder F, Lorra C, Parcej D N, Dolly J O, Pongs O. Inactivation properties of voltage-gated K+ channels altered by presence of β-subunit. Nature. 1994;369:289–294. doi: 10.1038/369289a0. [DOI] [PubMed] [Google Scholar]
- Roeper J, Lorra C, Pongs O. Frequency-dependent inactivation of mammalian A-type K+ channel Kv1. 4 regulated by Ca2+/calmodulin-dependent protein kinase. Journal of Neuroscience. 1997;17:3379–3391. doi: 10.1523/JNEUROSCI.17-10-03379.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruppersberg J P, Frank R, Pongs O, Stocker M. Cloned neuronal IK(A) channels reopen during recovery from inactivation. Nature. 1991;353:657–660. doi: 10.1038/353657a0. [DOI] [PubMed] [Google Scholar]
- Sala S, Matteson D R. Voltage-dependent slowing of K channel closing kinetics by Rb+ Journal of General Physiology. 1991;98:535–554. doi: 10.1085/jgp.98.3.535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoppa N E, Westbrook G L. Regulation of synaptic timing in the olfactory bulb by an A-type potassium current. Nature Neuroscience. 1999;2:1106–1113. doi: 10.1038/16033. [DOI] [PubMed] [Google Scholar]
- Serodio P, Kentros C, Rudy B. Identification of molecular components of A-type channels activating at subthreshold potentials. Journal of Neurophysiology. 1994;72:1516–1529. doi: 10.1152/jn.1994.72.4.1516. [DOI] [PubMed] [Google Scholar]
- Serodio P, Vega-Saenzde Miera E, Rudy B. Cloning of a novel component of A-type K+ channels operating at subthreshold potentials with unique expression in heart and brain. Journal of Neurophysiology. 1996;75:2174–2179. doi: 10.1152/jn.1996.75.5.2174. [DOI] [PubMed] [Google Scholar]
- Sheng M, Tsaur M L, Jan Y N, Jan L Y. Subcellular segregation of two A-type K+ channel proteins in rat central neurons. Neuron. 1992;9:271–284. doi: 10.1016/0896-6273(92)90166-b. [DOI] [PubMed] [Google Scholar]
- Solc C K, Aldrich R W. Gating of single non-Shaker A-type potassium channels in larval Drosophila neurons. Journal of General Physiology. 1990;96:135–165. doi: 10.1085/jgp.96.1.135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsaur M L, Chou C C, Shih Y H, Wang H L. Cloning, expression and CNS distribution of Kv4.3, an A-type K+ channel alpha subunit. FEBS Letters. 1997;400:215–220. doi: 10.1016/s0014-5793(96)01388-9. [DOI] [PubMed] [Google Scholar]
- Yu S P, Kerchner G A. Endogenous voltage-gated potassium channels in human embryonic kidney (HEK293) cells. Journal of Neuroscience Research. 1998;52:612–617. doi: 10.1002/(SICI)1097-4547(19980601)52:5<612::AID-JNR13>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]
- Zagotta W N, Hoshi T, Aldrich R W. Gating of single Shaker potassium channels in Drosophila muscle and in Xenopus oocytes injected with Shaker mRNA. Proceedings of the National Academy of Sciences of the USA. 1989;86:7243–7247. doi: 10.1073/pnas.86.18.7243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zagotta W N, Hoshi T, Aldrich R W. Restoration of inactivation in mutants of Shaker potassium channels by a peptide derived from ShB. Science. 1990;250:568–571. doi: 10.1126/science.2122520. [DOI] [PubMed] [Google Scholar]
- Zhu X-R, Wulf A, Schwarz M, Isbrandt D, Pongs O. Characterization of human Kv4. 2 mediating a rapidly-inactivating transient voltage-sensitive K+ current. Receptors and Channels. 1999;6:387–400. [PubMed] [Google Scholar]


