Skip to main content
NCBI home page
The Journal of Physiology logoLink to The Journal of Physiology
. 2001 Dec 15;537(Pt 3):949–959. doi: 10.1111/j.1469-7793.2001.00949.x

Frequency response of renal sympathetic nervous activity to aortic depressor nerve stimulation in the anaesthetized rat

Emmanuelle Petiot 1, Christian Barrès 1, Bruno Chapuis 1, Claude Julien 1
PMCID: PMC2278997  PMID: 11744767

Abstract

  1. The contribution of central baroreceptor reflex pathways to the dynamic regulation of sympathetic nervous activity (SNA) has not been properly examined thus far. The aim of this study was to characterize the transfer function of the central arc of the baroreceptor reflex (from baroreceptor afferent activity to SNA) over a wide range of frequencies.

  2. In nine baroreceptor-intact and six sino-aortic baroreceptor-denervated rats anaesthetized with urethane, the renal SNA was recorded while applying sinusoidal stimulation to the aortic depressor nerve at 26 discrete frequencies ranging from 0.03 to 20 Hz. At each modulation frequency, cross-power spectrum analysis using a fast Fourier transform algorithm was performed between the stimulation and renal SNA, which provided the transfer function of the central arc.

  3. In both baroreceptor intact and denervated rats, the transfer gain increased by a factor of about three between 0.03 and 1 Hz. At higher frequencies, the gain decreased but remained above the static gain of the system up to 12 Hz. There was a slight phase lead up to 0.4 Hz, then a continuously increasing phase lag. A three-element linear model satisfactorily described the experimental transfer function. The model combined a derivative gain (corner frequency ∼0.15 Hz), an overdamped second-order low-pass filter (natural frequency ∼1 Hz) and a fixed time delay (∼100 ms).

  4. These results indicate that the central arc of the baroreceptor reflex shows derivative properties that are essential for compensating the filtering of fast oscillations of baroreceptor afferent activity and thus for the generation of fast oscillations of renal SNA (e.g. those related to the cardiac cycle).

The overall transfer function of the arterial baroreceptor reflex combines the properties of the so-called neural arc (from arterial pressure (AP) to sympathetic nervous activity (SNA)) and those of the so-called peripheral arc (from SNA to AP). The transfer gain of the peripheral arc shows low-pass filter properties (i.e. fluctuations of vascular resistance and thus AP, attenuate progressively as the frequency of SNA fluctuations increases: Rosenbaum & Race, 1968; Ikeda et al. 1996; Bertram et al. 2000; Guild et al. 2001). In contrast, the transfer gain of the neural arc shows high-pass filter properties (i.e. the amplitude of SNA fluctuations increases as the frequency of the pressure perturbation increases: Kezdi & Geller, 1968; Harada et al. 1992; Ikeda et al. 1996). Therefore, by amplifying SNA responses, the neural arc partly compensates for the attenuation occurring at vascular neuro-effector junctions. It has been suggested that this effect improves the efficiency of the baroreceptor reflex in correcting rapid AP perturbations (Ikeda et al. 1996).

The high-pass filter (also termed rate sensitive or derivative) characteristics of the neural arc of the baroreceptor reflex can originate from arterial baroreceptors and/or from central nervous pathways. Derivative properties have been demonstrated for arterial baroreceptors using single nerve fibre recordings in isolated rabbit carotid sinus (Franz et al. 1971) and rat aortic arch (Brown et al. 1978) preparations. More recently, it was reported that in anaesthetized rabbits, the gain of the transfer function between pressure in the in situ isolated baroreceptor area and aortic depressor nerve activity increased by a factor of two to three between 0.01 and 1 Hz (Sato et al. 1998). To our knowledge, only two studies, performed on anaesthetized rabbits, examined the transfer function of the central arc (i.e. from baroreceptor afferent activity to SNA), thus excluding baroreceptor endings. In the first study (Imaizumi et al. 1994), AP was randomly perturbed by balloon inflation while recording aortic depressor nerve activity and renal SNA (RSNA). The gain of the transfer function from aortic nerve activity to RSNA was flat up to 0.3 Hz and could not be analysed at higher frequencies. In a second study, the same group described the transfer function from aortic nerve stimulation to RSNA (Kubo et al. 1996). The gain of the transfer function could be studied from 0.012 to 0.8 Hz and was claimed to be flat in this frequency range, although it showed a tendency to increase (see Fig. 4 in Kubo et al. 1996). From these observations it was concluded that central baroreceptor reflex pathways do not contribute to the high-pass filter characteristics of the neural arc. One major limitation to these studies is that the frequency range investigated did not include frequencies at which arterial baroreceptors are normally exposed to AP fluctuations, especially the frequency of the heart beat (typically, 3-4 Hz in rabbits and 5-6 Hz in rats) and its harmonics.

Figure 4. Linear modelling of the experimental transfer function.

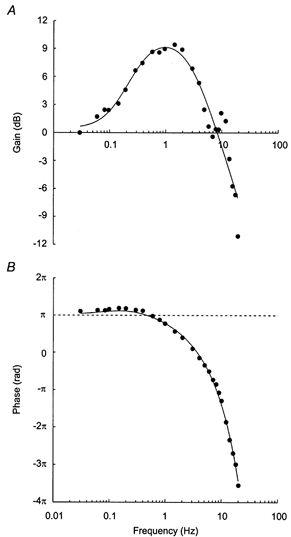
Figure 4

Open in a new tab

Graphs show gain (A) and phase (B) functions of the three-element linear model that was fitted to group-average (n = 15 rats) gain and phase values (•). The model combines a derivative gain (corner frequency, 0.127 Hz), an overdamped second-order low-pass filter (natural frequency, 1.04 Hz; damping coefficient, 1.52), and a fixed time delay (0.101 s). The 9 dB amplification of the gain at around 1 Hz indicates an almost threefold increase in the amplitude of the RSNA response from the static gain (1.05). Note that the model does not account for the increase in gain at around 10 Hz.

The aim of this study is to provide a more detailed description of the transfer properties of central baroreceptor reflex pathways, especially by expanding the range of frequencies investigated. We electrically stimulated the aortic depressor nerve in anaesthetized rats with a sinusoidal signal at discrete frequencies up to 20 Hz, while recording RSNA. We verified that this procedure allowed us to estimate correctly the open loop-transfer function by comparing data obtained in baroreceptor-intact rats and in rats after acute sino-aortic baroreceptor denervation. Finally, we investigated whether a simple linear model could provide a proper description of the experimental transfer function.

METHODS

Fifteen male Sprague-Dawley rats (300-350 g; Iffa-Credo, L'Arbresle, France) were used. All experiments conformed to the guidelines of the French Ministry of Agriculture for animal experimentation.

Animal preparation

Rats were anaesthetized with urethane (1.2 g (kg body wt)−1i.p., supplemented with 0.1 g (kg body wt)−1i.v. as needed), placed on a heating blanket to maintain rectal temperature at 37 °C, and ventilated through a tracheal cannula (7-8 ml (kg body wt)−1× 72 cycles min−1 (1.2 Hz)) with a mixture of oxygen and air (∼80/20 %), as described previously (Bertram et al. 1998). A polyethylene catheter was inserted into the lower abdominal aorta through the left femoral artery for AP measurement. A polyethylene catheter was also inserted into the inferior vena cava via the left femoral vein for the administration of drugs. The left aortic depressor nerve was carefully isolated at its junction with the superior laryngeal nerve and placed on a bipolar platinum-iridium electrode. The nerve-electrode preparation was then embedded in silicone gel (604A and B; Wacker Chemie, Munich, Germany). It was observed in this and previous experiments that after accidental displacement of the electrode (and possibly aortic depressor nerve rupture), the stimulation applied to the aortic nerve always became ineffective, whatever its intensity, which makes it unlikely that it could have spread to the superior laryngeal nerve. Through a laparotomy, a branch of the left renal sympathetic nerve was dissected free, placed on a bipolar platinum-iridium electrode and insulated with silicone gel for RSNA recording.

Sino-aortic baroreceptor denervation was performed in 6 out of 15 rats. The region of the carotid bifurcation was exposed on both sides of the trachea. On the right side, the aortic nerve, the superior laryngeal nerve and the superior cervical chain were transected. The common carotid artery, carotid bifurcation, and branches of the internal and external carotid arteries were stripped of all visible nerve fibres and wiped with 10 % phenol in ethanol. On the left side, to avoid damaging the aortic nerve used for stimulation, the superior cervical chain and the vagus nerve were transected, and the common carotid artery was tied below its bifurcation. Baroreceptor reflex responses were tested before and after denervation by means of i.v. injections of phenylephrine hydrochloride (3 μg (kg body wt)−1). Before denervation, phenylephrine raised mean AP by 35 ± 5 mmHg and decreased RSNA by 76 ± 9 %. After denervation, phenylephrine elicited an increase in AP of 46 ± 7 mmHg, and this was not accompanied by a significant change in RSNA (2.7 ± 2.7 %).

Aortic nerve stimulation

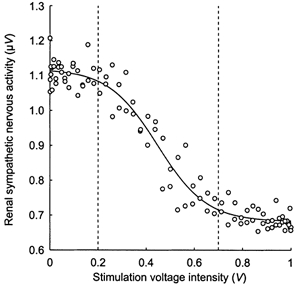
The aortic depressor nerve was stimulated by a computer through the analog output of a converter board (AT-MIO-16; National Instruments, Austin, TX, USA). The stimulation signal was composed of 2 ms impulses delivered at a 100 Hz frequency. The amplitude of impulses was modulated by a sinusoidal function using LabVIEW 5.1 software (National Instruments). In order to study the system in the linear portion of its static response (i.e. above threshold and below saturation), the stimulation had to oscillate above the minimum voltage intensity, inducing a decrease in RSNA and below the intensity inducing a maximum sympathetic inhibition. These values were determined by applying 30 s step stimulations to the aortic nerve at increasing voltage intensities. In a few rats, this procedure was validated by constructing the entire reflex curve relating RSNA to stimulation voltage intensity (Fig. 1). The aortic nerve was then stimulated at 26 discrete frequencies (0.03-20 Hz) applied in random order and separated by 3-4 min of recovery. Depending on the modulation frequency, the duration of the stimulation (1-6 min) was set so that at least 10 full cycles were applied. All aortic nerve stimulations were performed while the rats were under cardiac autonomic blockade (atropine methyl nitrate and atenolol, each at 2 mg (kg body wt)−1 h−1i.v. both from Sigma-Aldrich Chimie, Saint-Quentin-Fallavier, France). Under this condition, heart rate was remarkably stable, allowing for an accurate determination of the transfer function between AP and RSNA at cardiac frequency (see Results). On completion of the experiments, the rats received a lethal i.v. dose of urethane, and RSNA was recorded for an additional 15-20 min period to estimate the background noise level.

Figure 1. Example of relationship between renal sympathetic nervous activity (RSNA) and stimulation intensity applied to the aortic depressor nerve.

Figure 1

Open in a new tab
The aortic depressor nerve was stimulated with a continuous train of impulses (2 ms, 100 Hz), the amplitude of which varied from 0 to 1 V according to a sine wave of 0.01 Hz frequency. RSNA data were collected over one full cycle (100 s), resampled at 1 Hz by averaging, and plotted against corresponding voltage values. In this example, the background noise of RSNA (post-mortem activity = 0.6 μV) was not subtracted. A four-parameter logistic equation was fitted to experimental data:
graphic file with name tjp0537-0949-mu1.jpg
where r2= 0.958 to show the sigmoidal nature of the relationship. In the same rat, the threshold and saturation points for RSNA inhibition were determined by applying step stimulations to the aortic nerve at increasing intensities (see Methods). Using this procedure, a voltage range was chosen for sinusoidal stimulation. This range is shown by the vertical broken lines and roughly corresponds to the ‘linear’ part of the relationship.

Data acquisition

Arterial pressure was measured with a pressure transducer (Statham P23ID; Gould, Cleveland, OH, USA) coupled to an amplifier (13-4615-52; Gould). The RSNA signal was amplified (× 50 000) and band-pass filtered (300-3000 Hz: P-511.J; Grass, Quincy, MA, USA). The stimulation signal, AP and RSNA were fed into a second computer via a converter board (AT-MIO-16E-10; National Instruments), and sampled at 2000, 500 and 10 000 Hz, respectively. Using LabVIEW 5.1 software, RSNA was resampled on-line at 1000 Hz by averaging every 10 consecutive values. To avoid contamination of the recorded RSNA by an artefact due to the stimulation, all signals generated or recorded by the computers passed through an isolation device (SCM5B49 for stimulation, 5B41 for data acquisition; National Instruments).

Off-line data processing

The following analyses were performed with programs written in LabVIEW language. The RSNA signal was rectified digitally by subtracting the mean, then taking the absolute value of each data point. The three recorded signals were resampled at 50 Hz by an averaging procedure. At each modulation frequency of the aortic depressor nerve, transfer function analysis between the stimulation (input signal) and RSNA (output signal) was performed. To calculate coherence, gain and phase, cross-spectral techniques using a fast Fourier transform algorithm were employed (Bertram et al. 1998, 2000). The stimulation periods were split into segments of 2n points (n = 9-13) overlapping by half, so that at least three segments were processed. Gain and phase were taken at the peak coherence frequency that was closest to the modulation frequency of the aortic nerve. Coherence was considered significant (P < 0.05) when above 0.35 (Koopmans, 1995). Only gain and phase values associated with a significant coherence were considered. Since the absolute gain could be influenced by variations in the prestimulation levels of RSNA, it was normalized as follows. At each modulation frequency, the mean RSNA value recorded for 30 s before starting the stimulation was calculated and the background noise was subtracted. Each gain value was then divided by this value.

The modelling analysis relied on the assumption that the transfer function between aortic nerve stimulation and RSNA would show simple linear characteristics (Ikeda et al. 1996; Kubo et al. 1996; Bertram et al. 2000). Therefore, in each individual rat, the equations of first- and second-order linear systems were fitted to experimental gain and phase values using an iterative least-squares procedure (SigmaPlot 2000; SPSS, Chicago, IL, USA).

Statistical analysis

For the comparison of transfer functions obtained in baroreceptor-intact and baroreceptor-denervated rats, we used a two-way ANOVA for repeated measures with treatment and modulation frequency as factors. Results are presented as means ±s.e.m.

RESULTS

Oscillatory responses of RSNA to sinusoidal stimulation of the aortic depressor nerve

Figure 2 shows original recordings of RSNA and AP during sinusoidal stimulation of the aortic depressor nerve at two discrete frequencies in a baroreceptor-intact rat. At a low modulation frequency (0.2 Hz), the stimulation wave and resulting RSNA oscillations were seemingly out of phase. At a higher modulation frequency (2 Hz), RSNA fluctuations tended to be shifted from the cycles of stimulation.

Figure 2. Effect of sinusoidal stimulation of the aortic depressor nerve on RSNA.

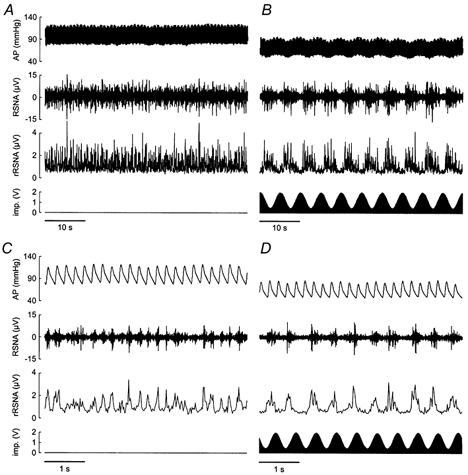
Figure 2

Open in a new tab

These traces are digital reconstructions of recordings of arterial pressure (AP, sampled at 500 Hz), RSNA (sampled at 1000 Hz), and impulses (imp., sampled at 2000 Hz) delivered to the left aortic depressor nerve in one baroreceptor-intact rat. The rectified RSNA (rRSNA, resampled at 50 Hz) is also shown. Traces were obtained before (A and C) and during sinusoidal stimulation of the aortic nerve at frequencies of 0.2 Hz (B) and 2 Hz (D). The stimulation intensity was modulated between 0.5 and 2 V. Before stimulation, the RSNA traces showed no clear pattern of slow fluctuation (A), whereas a fast rhythm, seemingly synchronous with the cardiac cycle, is often present (C). During stimulation, RSNA displayed regular oscillations at the same frequency as the stimulation wave. Note the absence of contamination of the RSNA signal by the electrical stimulus applied to the aortic nerve. At both modulation frequencies, AP showed a tonic decrease that was accompanied by an oscillation at 0.2 Hz modulation frequency only. The fast rhythm (about 1 Hz) of low amplitude in the AP trace is due to the mechanical ventilation of the rat.

Experimental transfer function of the central arc

Figure 3A shows the average coherence functions between aortic nerve stimulation and RSNA, separately in baroreceptor-intact and denervated rats. In both groups of rats, coherence was > 0.8 up to 5 Hz, demonstrating the strong linear coupling between stimulation and the resulting RSNA oscillations. At higher frequencies, coherence fell progressively, apart from an increase at around 10 Hz.

Figure 3. Experimental transfer function of the central arc.

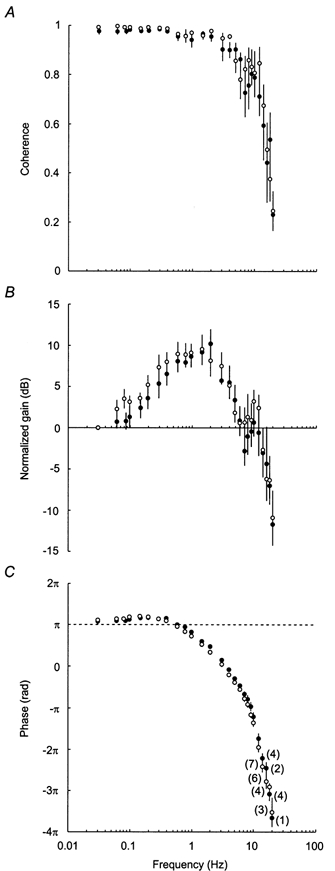
Figure 3

Open in a new tab

Graphs show average coherence and transfer functions from nine baroreceptor-intact rats (○) and six sino-aortic baroreceptor-denervated rats (•). In each rat, coherence (A), gain (B) and phase (C) between aortic nerve stimulation and RSNA were computed at 26 discrete frequencies (0.03-20 Hz). At modulation frequencies above 12 Hz, coherence was not always significant. In C, numbers in parentheses indicate, for each group of rats, the number of gain and phase values that were associated with significant coherence, and consequently were included in the calculation of group-average values. As stimulation voltage intensity differed between rats, absolute gains could not be averaged. Therefore, in each rat, all gain values were normalized by the gain measured at the lowest modulation frequency (0.03 Hz).

In both groups of rats, gain values increased at low frequencies to reach a maximum around 1 Hz (Fig. 3B). At higher frequencies, gain decreased, although there was a clear hump in the functions at around 10 Hz. Up to 12 Hz, all gain values were associated with a significant coherence, and thus could be included in a two-way ANOVA. This analysis indicated that the effect of modulation frequency on gain values did not differ significantly between baroreceptor-intact and baroreceptor-denervated rats (P = 0.47).

Phase functions (Fig. 3C) showed less inter-animal variability than gain functions. At low frequencies, RSNA and the stimulation were not completely out of phase. Actually, phase values consistently exceeded π rad up to 0.4 Hz, which points to a phase lead of RSNA oscillations in this frequency range. Then, phase decreased steadily, indicating that RSNA was progressively delayed from the stimulation. In the 0.03-12 Hz frequency range, the effect of modulation frequency on phase values tended to differ between baroreceptor-intact and baroreceptor-denervated rats (P = 0.053). However, Tukey's post hoc tests did not reveal any significant between-group differences up to 9 Hz.

Linear modelling of the transfer function of the central arc

Experimental gain and phase functions suggested a three-element model structure. The increasing gain and phase lead at low frequencies indicated that a derivative term should be included, whereas adding a low-pass filter was necessary to account for the decrease in both gain and phase at higher frequencies. Finally, the continuously decreasing phase that was observed at the highest modulation frequencies indicated the presence of a fixed time delay between aortic nerve stimulation and RSNA. Hence, the transfer function (H) of the model combined a derivative gain, a second-order low-pass filter and a fixed time delay in series. Its frequency domain expression is:

graphic file with name tjp0537-0949-m1.jpg (1)

where K is a static gain; the numerator term between parentheses corresponds to the derivative gain defined by its corner frequency (fc, in hertz); the denominator term corresponds to the low-pass filter defined by its natural frequency (fn, in hertz) and its damping coefficient (λ); the exponential term derives from the fixed time delay (T, in seconds). f and j are frequency (in hertz) and the imaginary operator, respectively. The negative sign denotes the opposite direction between changes in the input and output of the system.

This transfer function can also be represented by its gain (G) and phase (Φ), according to the following equations:

graphic file with name tjp0537-0949-m2.jpg (2)
graphic file with name tjp0537-0949-m3.jpg (3)

In each rat, eqn (2) was fitted to experimental gain values after transformation (G = 20 log(gain), expressed in dB), and eqn (3) was fitted to phase values. Since the fitting procedure was performed simultaneously for gain and phase functions, a single set of parameters was obtained (Table 1). In all cases, the equations of the three-element model could be fitted satisfactorily to experimental transfer functions. A Bode plot of the model transfer function fitted to group-average values is presented in Fig. 4.

Table 1.

Parameters of individual transfer functions

Rat no. r2 K fc (Hz) fn (Hz) λ T (s)
1 0.939 0.96 0.064 0.93 3.31 0.103
2 0.906 0.96 0.306 1.39 1.17 0.085
3 0.904 1.21 0.152 1.35 1.42 0.105
4 0.787 1.49 0.107 1.25 1.40 0.091
5 0.828 0.82 0.045 0.88 4.68 0.109
6 0.926 0.91 0.130 0.63 1.17 0.116
7 0.933 0.92 0.050 0.96 1.58 0.103
8 0.925 1.07 0.133 0.91 1.39 0.115
9 0.912 0.85 0.051 0.78 2.20 0.117
10 0.881 0.88 0.067 0.96 1.73 0.111
11 0.810 1.33 0.171 1.31 2.14 0.097
12 0.948 1.38 0.225 1.52 0.97 0.093
13 0.945 1.01 0.203 1.21 0.69 0.089
14 0.923 0.89 0.291 1.39 1.20 0.106
15 0.891 0.91 0.364 1.28 0.55 0.083
Mean 0.897 1.04 0.157 1.12 1.71 0.101
s.e.m. 0.013 0.06 0.026 0.07 0.28 0.003
Open in a new tab

In each rat, were fitted to experimental gain and phase functions, respectively. Rats 1–9 are baroreceptor-intact rats, and rats 10–15 are sino-aortic baroreceptor-denervated rats. Please note that since the static gain of the model was estimated from normalized gain values, it takes no units. Abbreviations: r2, coefficient of determination (observed vs. predicted values); K, static gain; fc, corner frequency of the derivative gain; fn, natural frequency of the second-order low-pass filter; λ, damping coefficient of the second-order low-pass filter; T, fixed time delay.

Spontaneous phase shift between AP and RSNA at cardiac frequency

A comparison of the transfer functions of the central arc (from aortic nerve stimulation to RSNA) and of the neural arc (from AP to RSNA) would provide insight into the dynamic properties of the baroreceptors. The transfer function of the neural arc can be safely determined at cardiac frequency for the following two reasons. First, RSNA oscillations related to the cardiac cycle are generated entirely by the baroreceptor reflex (Green & Heffron, 1968; Kunitake & Kannan, 2000). Second, the transfer function is open loop at cardiac frequency, because oscillations in SNA are not translated into AP oscillations at frequencies above 1 Hz in rats (Stauss et al. 1997; see also Fig. 2D). In each rat, a 2 min period before stimulation was used to compute coherence and phase between AP and RSNA. In denervated rats, there was no peak in the RSNA spectrum at cardiac frequency (6.4 ± 0.3 Hz), and coherence was extremely low (0.15 ± 0.05; Fig. 5). In baroreceptor-intact rats, coherence was maximal (0.90 ± 0.03) and phase was always positive (0.57 ± 0.11 rad) at cardiac frequency (5.5 ± 0.4 Hz). At the modulation frequency of the aortic nerve that was closest to spontaneous heart rate (5.5 ± 0.3 Hz), experimental phase was always negative (-1.49 ± 0.11 rad). In addition, in the model, the phase was also negative (-1.39 rad) at 5.5 Hz (Fig. 4B).

Figure 5. Effect of acute sino-aortic baroreceptor denervation on the spontaneous rhythms of RNSA.

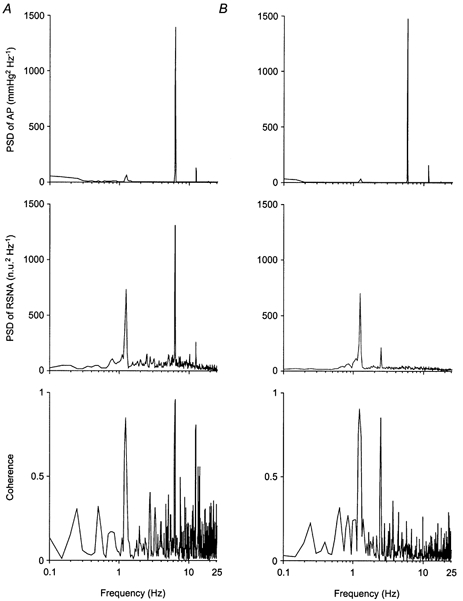
Figure 5

Open in a new tab

Power spectra of AP and RSNA were obtained from 2 min control recordings in one baroreceptor-intact rat (A) and one sino-aortic baroreceptor-denervated-rat (B). Data were resampled at 50 Hz, and power spectral density (PSD) was calculated over 11 segments of 1024 points overlapping by half. Prior to spectral analysis, RSNA data were normalized (normalized units, n.u.) by their mean value calculated over the whole 2 min period. Note in both rats the presence of three peaks in the AP spectrum, located at 1.2, 6 and 12 Hz, which corresponded to respiration, the cardiac beat and its first harmonic, respectively. In the baroreceptor-intact rat, the RSNA spectrum contains three peaks at the same frequencies, which show a strong coherence with AP, especially that synchronous with the cardiac cycle. In the RSNA spectrum of the baroreceptor-denervated rat, the 6 and 12 Hz peaks are absent, and coherence is not significant at these frequencies. The peak at 2.4 Hz corresponds to a harmonic of the respiratory cycle.

DISCUSSION

Central nervous pathways of the arterial baroreceptor reflex contain an element showing derivative properties. This element amplifies and accelerates RSNA responses to slow fluctuations of baroreceptor afferent activity, while partly compensating for the filtering of faster oscillations. This finding has several important implications regarding the dynamic control of RSNA.

Methodological considerations

The possible interference of chemoreceptor fibres

It has been shown that chemoreceptor activation can influence the central processing of baroreceptor information (Wennergren et al. 1976). There is anatomical (Cheng et al. 1997) and electrophysiological (Brophy et al. 1999) evidence that the aortic depressor nerve of the rat contains chemoreceptor afferents. However, chemoreceptors represent only ∼15 % of the fibres in the rat aortic nerve (Cheng et al. 1997), and their functional importance has been seriously questioned (Kobayashi et al. 1999). During electrical stimulation of the whole aortic nerve, both baroreceptor and chemoreceptor afferents are presumably activated, which would lead to a composite effect on RSNA, namely inhibition through baroreceptor stimulation and excitation through chemoreceptor stimulation (Dorward et al. 1987). In case of a significant involvement of chemoreceptor stimulation in the overall RSNA response to aortic nerve stimulation, what would be expected is that at the highest stimulation intensities there would be significant residual RSNA. In rats in which we applied supramaximal voltage intensities, the lower plateau of the RSNA-voltage relationship was close to the background noise level, thus indicating almost complete RSNA inhibition (see Fig. 1). This is similar to what is usually observed with a strong baroreceptor stimulus (e.g. during a large rise in AP induced by the administration of phenylephrine: Cheng et al. 2000). We therefore conclude that the effects of aortic nerve stimulation on RSNA reflect mainly, if not solely, the effects of baroreceptor stimulation.

The possible interference of functioning baroreceptors

The recommended procedure for identifying subsystems in a feedback control loop is to open the loop. Accordingly, transfer functions of the various components of the baroreceptor reflex have commonly been estimated under open-loop conditions (Kezdi & Geller, 1968; Ikeda et al. 1996; Kubo et al. 1996). In the present study, similar transfer functions were found under closed-loop (in baroreceptor-intact rats) and open-loop (in baroreceptor-denervated rats) conditions. The fact that functioning baroreceptors did not perturb the estimation of the transfer function at high frequencies was expected, because aortic nerve stimulation does not induce AP oscillations at frequencies above 0.8-1 Hz (Bertram et al. 1998), and thus cannot entrain baroreceptor afferent activity. At lower frequencies, the stimulation evoked distinct AP oscillations. However, the amplitude of these oscillations decreased exponentially as the modulation frequency of the aortic nerve increased. In accordance with a previous study (Bertram et al. 2000), we observed that the amplitude of the AP oscillations at 0.8 Hz was less than 2 % of the amplitude of the AP oscillation at 0.03 Hz (data not shown). It is therefore not surprising that the baroreceptors did not contribute to the amplification of RSNA responses in the 0.1-1 Hz frequency range, where most of the attenuation of AP oscillations occurred. Even at the lowest modulation frequencies (< 0.1 Hz), there was no indication that baroreceptors provided any amplification or acceleration to RSNA responses. This is probably because rhythmic aortic nerve stimulation induced a tonic decrease in the AP level, hence a tonic unloading of baroreceptors, a situation that resembles sino-aortic baroreceptor denervation. In accordance with this hypothesis, we observed that during aortic nerve stimulation in baroreceptor-intact rats, there was no RSNA rhythmicity at the frequency of the cardiac cycle, whatever the modulation frequency of the aortic nerve (data not shown).

The possible interference of central respiratory drive

It has been reported that central respiratory drive modulates the baroreceptor reflex at the level of the rostral ventrolateral medulla (Miyawaki et al. 1995). In the present experiments, the rats were artificially ventilated with 80 % oxygen and high tidal volume (2.1-2.4 ml for a 300 g rat), which results in normal pH, hyperoxia and an arterial partial pressure of carbon dioxide in the lower normal range (Bertram et al. 1998). Under these conditions, central respiratory drive was presumably depressed, or even absent (Chang et al. 1999).

The three-element model

The transfer function we identified combines the properties of a derivative gain, a second-order low-pass filter and a fixed time delay. The low-pass filter element indicates that the transmission from baroreceptor afferent activity to postganglionic SNA is affected by time constants. This information could not be gained from previous studies in rabbits, because RSNA responses to aortic depressor nerve stimulation were not analysed at modulation frequencies beyond 0.8 Hz (Kubo et al. 1996). In an earlier study on dogs (Kezdi & Geller, 1968), the RSNA responses to sinusoidal pressure variations in the isolated carotid sinuses was investigated at several discrete frequencies up to 5 Hz. It was reported that the gain of the system decreased at frequencies above 1 Hz. We are not aware of studies describing the transfer functions of selected baroreceptor reflex pathways within the central nervous system. It is therefore impossible to locate the anatomical substrates responsible for the time constants of the central arc. However, processes with time constants can be present at both pre- and postsynaptic levels in the nervous transmission, and it is well established that the central arc of the baroreceptor reflex is a polysynaptic pathway (Aicher et al. 2000).

The latency of central baroreceptor reflex pathways is of the order of magnitude of 200 ms in cats (Green & Heffron, 1968) and 260 ms in dogs (Kezdi & Geller, 1968). More recently, the latencies of central pathways were studied in rabbits by stimulating the aortic depressor nerve while recording simultaneously single-unit activities in the rostral ventrolateral medulla (RVLM) and multifibre RSNA (Terui et al. 1987). The onset latency was about 50 ms for RVLM inhibition and 150 ms for RSNA inhibition, thus leaving 100 ms for the conduction time of descending pathways. According to Seller (1991), most of the time delay within the central nervous system originates from the very slow conduction velocity (0.15 m s−1) between the second-order neurones in the nucleus tractus solitarii and premotor neurones in the RVLM. In the rats of the present study, the fixed time delay between changes in baroreceptor afferent activity and postganglionic RSNA was reproducibly found to be around 100 ms. We suggest that between-species differences in the latency of central baroreceptor reflex pathways is merely the result of differences in body size.

The major new finding of the present study is the presence of a derivative term in the transfer function of the central arc. This dynamic property was not apparent in the central arc of anaesthetized rabbits, at least in the 0.012-0.8 Hz frequency range (Kubo et al. 1996). In the present study, we observed a threefold increase in the transfer gain at ∼1 Hz, together with a slight but significant phase lead at lower frequencies. The influence of a derivative term in a transfer function can be modelled in the time domain. In such a system, responses of the output signal to a step change in the input signal are characterized by a sharp initial change followed by a progressive attenuation of the response towards a steady-state value that depends upon the static gain of the system. The attenuation of SNA responses to continuous baroreceptor afferent stimulation has long been recognized, and has been referred to as an adaptation or rapid-resetting phenomenon (for review see Seller, 1991). There is convincing evidence that this phenomenon takes place at the level of the first synapse between primary afferent fibres and second-order neurones in the nucleus tractus solitarii (Miles, 1986).

Functional relevance of the derivative properties

From a modelling analysis of reflex responses to a step change in AP, Ikeda et al. (1996) concluded that the high-pass filter characteristics of the neural arc of the baroreceptor reflex largely determine its ability to provide a quick and stable correction of the perturbation. However, it must be noted that AP perturbations occurring spontaneously in daily life almost never appear in the form of step changes (i.e. instantaneous increases or decreases in AP). The kinetics of spontaneous AP perturbations can be evaluated from AP recordings in conscious sino-aortic baroreceptor-denervated rats. It has been observed in these animals that AP lability is made up of rather slow AP fluctuations (< 0.15 Hz: Cerutti et al. 1994; Julien et al. 1995). Interestingly, very similar observations were made in conscious chronically sympathectomized rats (Cerutti et al. 1991; Julien et al. 1995). Therefore, the sympathetic limb of the baroreceptor reflex does not serve to buffer AP variability at frequencies where its derivative properties become apparent. On the contrary, in both sympathectomized and baroreceptor denervated rats, AP variability is decreased in the 0.15-1 Hz frequency range, mainly as a result of the disappearance of AP Mayer waves (Julien et al. 1995). We propose that the derivative properties of central baroreceptor reflex pathways play a critical role in the production of RSNA oscillations associated with AP Mayer waves, and even more so, in the generation of faster rhythms, including the cardiac-related oscillation.

After removal of the derivative term from the transfer function, it can be seen that there is a 10.5 dB deficit in the gain function at 0.4 Hz, which is the characteristic frequency of Mayer waves in rats (Brown et al. 1994), and a 30-35 dB deficit at 5-6 Hz, which is the characteristic frequency of the heart beat in conscious quiet rats (Fig. 6). This means that without the derivative term, the amplitude of RSNA oscillations induced by the baroreceptor reflex would be reduced by about 70 and 98 % at 0.4 and 5-6 Hz, respectively. The functional significance of these two RSNA rhythms remains to be established. Due to the integrator properties of the arterial vasculature, high-frequency rhythms in SNA contribute to set the level of vasoconstrictor tone, and thus to sustain AP (Malpas, 1998). It has been reported that the enhancement of the cardiac-related rhythm of RSNA makes a major contribution to the sympathetic activation induced by sodium nitroprusside infusion in conscious rats (Kunitake & Kannan, 2000). This is, however, an intriguing observation because baroreceptor unloading is expected to attenuate cardiac-related baroreceptor discharge (Charlton & Baertschi, 1982). A selective enhancement of the cardiac-related RSNA rhythm has also been reported to occur in conscious rats during exposure to an air jet stress (DiBona & Jones, 1995), and in urethane-anaesthetized cats during electrical stimulation of midbrain periaqueductal grey neurones (Gebber et al. 2000). These observations suggest that the baroreceptor reflex modulates the sympathetic activation accompanying the defence reaction, which would concur with our previous haemodynamic study in conscious sino-aortic baroreceptor-denervated rats (Zhang et al. 1996). At frequencies below 1 Hz in rats, SNA oscillations induce AP oscillations (Stauss et al. 1997). AP Mayer waves are coupled with a prominent rhythm in RSNA (Brown et al. 1994; Bertram et al. 2000). Recently, we proposed that AP and SNA oscillations at the frequency of Mayer waves are the result of instability (positive feedback) in the baroreceptor reflex loop (Bertram et al. 1998). It is still unknown whether these oscillations have a specific function, or should simply be regarded as an epiphenomenon of the normal operation of the baroreceptor reflex.

Figure 6. Influence of the derivative gain on the transfer function of the central arc of the baroreceptor reflex.

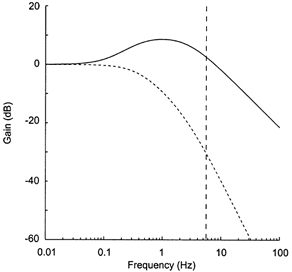
Figure 6

Open in a new tab

The graph shows the gain function of the three-element linear model describing the native transfer function of the neural arc of the baroreceptor reflex (continuous line), and the theoretical gain function obtained after removing the derivative term (dashed line). Note the 35 dB difference between the curves at cardiac frequency (5.5 Hz), as indicated by the vertical dashed line.

The amplification of the gain at 10 Hz

From 8 to 12 Hz, there was a clear amplification of the transfer gain, which could not be accounted for by the three-element model. This frequency range compares with that of the so-called 10 Hz rhythm, as described by Barman & Gebber (2000) in cats. The existence of such a fundamental rhythm has not been reported in the RSNA of conscious rats (Burgess et al. 1999; Kunitake & Kannan, 2000). However, whatever the underlying cause, a local maximum in the gain function at 8-12 Hz will favour the appearance of a reflex oscillation at this frequency, which is indeed the case in rats because the 10-12 Hz frequency range usually encompasses the first harmonic of the cardiac rhythm.

The phase shift at cardiac frequency

Derivative properties have been reported for aortic baroreceptors in rabbits (Sato et al. 1998). In this in vivo preparation, the transfer gain from pressure to baroreceptor afferent activity increased by a factor of about three between 0.01 and 1 Hz. This similarity with the transfer function of the central arc reported herein suggests that arterial baroreceptors and central nervous pathways both contribute to the overall transfer properties of the neural arc, at least at frequencies up to 1 Hz (Ikeda et al. 1996). At higher frequencies, the relative contributions of each system is difficult to delineate. In the present study, we observed that the phase shift between AP and RSNA at cardiac frequency was about 2 rad above the phase shift between aortic nerve stimulation and RSNA at the same frequency. This finding suggests strongly that an additional phase lead is introduced by arterial baroreceptors, which is consistent with the hypothesis that their derivative properties extend to the high-frequency range (Brown et al. 1978).

Conclusion

In summary, we propose that the derivative properties of the central arc of the baroreceptor reflex, by increasing the gain of the system, allow for fast rhythms of baroreceptor afferent activity to be translated into fast rhythms of RSNA, even at the cost of instability at lower frequencies.

References

  1. Aicher SA, Milner TA, Pickel VM, Reis DJ. Anatomical substrates for baroreflex sympathoinhibition in the rat. Brain Research Bulletin. 2000;51:107–110. doi: 10.1016/s0361-9230(99)00233-6. [DOI] [PubMed] [Google Scholar]
  2. Barman SM, Gebber GL. ‘Rapid’ rhythmic discharges of sympathetic nerves: sources, mechanisms of generation, and physiological relevance. Journal of Biological Rhythms. 2000;15:365–379. doi: 10.1177/074873000129001468. [DOI] [PubMed] [Google Scholar]
  3. Bertram D, Barrès C, Cheng Y, Julien C. Norepinephrine reuptake, baroreflex dynamics, and arterial pressure variability in rats. American Journal of Physiology - Regulatory, Integrative and Comparative Physiology. 2000;279:R1257–1267. doi: 10.1152/ajpregu.2000.279.4.R1257. [DOI] [PubMed] [Google Scholar]
  4. Bertram D, Barrès C, Cuisinaud G, Julien C. The arterial baroreceptor reflex of the rat exhibits positive feedback properties at the frequency of Mayer waves. Journal of Physiology. 1998;513:251–261. doi: 10.1111/j.1469-7793.1998.251by.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Brophy S, Ford TW, Carey M, Jones JFX. Activity of aortic chemoreceptors in the anaesthetized rat. Journal of Physiology. 1999;514:821–828. doi: 10.1111/j.1469-7793.1999.821ad.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Brown DR, Brown LV, Patwardhan A, Randall DC. Sympathetic activity and blood pressure are tightly coupled at 0. 4 Hz in conscious rats. American Journal of Physiology. 1994;267:R1378–1384. doi: 10.1152/ajpregu.1994.267.5.R1378. [DOI] [PubMed] [Google Scholar]
  7. Brown AM, Saum WR, Yasui S. Baroreceptor dynamics and their relationship to afferent fiber type and hypertension. Circulation Research. 1978;42:694–702. doi: 10.1161/01.res.42.5.694. [DOI] [PubMed] [Google Scholar]
  8. Burgess DE, Zimmerman TA, Wise MT, Li SG, Randall DC, Brown DR. Low-frequency renal sympathetic nerve activity, arterial BP, stationary ‘1/f noise’ and the baroreflex. American Journal of Physiology. 1999;277:R894–903. doi: 10.1152/ajpregu.1999.277.3.R894. [DOI] [PubMed] [Google Scholar]
  9. Cerutti C, Barrès C, Paultre CZ. Baroreflex modulation of blood pressure and heart rate variabilities in rats: assessment by spectral analysis. American Journal of Physiology. 1994;266:H1993–2000. doi: 10.1152/ajpheart.1994.266.5.H1993. [DOI] [PubMed] [Google Scholar]
  10. Cerutti C, Gustin MP, Paultre CZ, Lo M, Julien C, Vincent M, Sassard J. Autonomic nervous system and cardiovascular variability in rats: a spectral analysis approach. American Journal of Physiology. 1991;261:H1292–1299. doi: 10.1152/ajpheart.1991.261.4.H1292. [DOI] [PubMed] [Google Scholar]
  11. Chang H-S, Staras K, Smith JE, Gilbey MP. Sympathetic neuronal oscillators are capable of dynamic synchronization. Journal of Neuroscience. 1999;19:3183–3197. doi: 10.1523/JNEUROSCI.19-08-03183.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Charlton JD, Baertschi AJ. Responses of aortic baroreceptors to changes of aortic blood flow and pressure in rat. American Journal of Physiology. 1982;242:H520–525. doi: 10.1152/ajpheart.1982.242.4.H520. [DOI] [PubMed] [Google Scholar]
  13. Cheng Y, Planta F, Ladure P, Julien C, Barrès C. Acute cardiovascular effects of the α2-adrenoceptor antagonist, idazoxan, in rats: influence of the basal sympathetic tone. Journal of Cardiovascular Pharmacology. 2000;35:156–163. doi: 10.1097/00005344-200001000-00021. [DOI] [PubMed] [Google Scholar]
  14. Cheng Z, Powley TL, Schwaber JS, Doyle FJ. A laser confocal microscopic study of vagal afferent innervation of rat aortic arch: Chemoreceptors as well as baroreceptors. Journal of the Autonomic Nervous System. 1997;67:1–14. doi: 10.1016/s0165-1838(97)00085-4. [DOI] [PubMed] [Google Scholar]
  15. DiBona GF, Jones SY. Analysis of renal sympathetic nerve responses to stress. Hypertension. 1995;25:531–538. doi: 10.1161/01.hyp.25.4.531. [DOI] [PubMed] [Google Scholar]
  16. Dorward PK, Burke SL, Janig W, Cassell J. Reflex responses to baroreceptor, chemoreceptor and nociceptor inputs in single renal sympathetic neurones in the rabbit and the effects of anaesthesia on them. Journal of the Autonomic Nervous System. 1987;18:39–54. doi: 10.1016/0165-1838(87)90133-0. [DOI] [PubMed] [Google Scholar]
  17. Franz GN, Scher AM, Ito CS. Small signal characteristics of carotid sinus baroreceptors of rabbits. Journal of Applied Physiology. 1971;30:527–535. doi: 10.1152/jappl.1971.30.4.527. [DOI] [PubMed] [Google Scholar]
  18. Gebber GL, Zhong S, Lewis C, Barman SM. Defense like patterns of spinal sympathetic outflow involving the 10-Hz and cardiac-related rhythms. American Journal of Physiology - Regulatory, Integrative and Comparative Physiology. 2000;278:R1616–1626. doi: 10.1152/ajpregu.2000.278.6.R1616. [DOI] [PubMed] [Google Scholar]
  19. Green JH, Heffron PF. Studies upon the relationship between baroreceptor and sympathetic activity. Quarterly Journal of Experimental Physiology. 1968;53:23–32. doi: 10.1113/expphysiol.1968.sp001942. [DOI] [PubMed] [Google Scholar]
  20. Guild S-J, Austin PC, Navakatikyan M, Ringwood JV, Malpas SC. Dynamic relationship between sympathetic nerve activity and renal blood flow: a frequency domain approach. American Journal of Physiology - Regulatory, Integrative and Comparative Physiology. 2001;281:R206–212. doi: 10.1152/ajpregu.2001.281.1.R206. [DOI] [PubMed] [Google Scholar]
  21. Harada S, Imaizumi T, Ando SI, Hirooka Y, Sunagawa K, Takeshita A. Arterial baroreflex dynamics in normotensive and spontaneously hypertensive rats. American Journal of Physiology - Regulatory, Integrative and Comparative Physiology. 1992;263:R524–528. doi: 10.1152/ajpregu.1992.263.3.R524. [DOI] [PubMed] [Google Scholar]
  22. Ikeda Y, Kawada T, Sugimachi M, Kawaguchi O, Shishido T, Sato T, Miyano H, Matsuura W, Alexander JJr, Sunagawa K. Neural arc of baroreflex optimizes dynamic pressure regulation in achieving both stability and quickness. American Journal of Physiology. 1996;271:H882–890. doi: 10.1152/ajpheart.1996.271.3.H882. [DOI] [PubMed] [Google Scholar]
  23. Imaizumi T, Harasawa Y, Ando SI, Sugimachi M, Takeshita A. Transfer function analysis from arterial baroreceptor afferent activity to renal nerve activity in rabbits. American Journal of Physiology. 1994;266:H36–42. doi: 10.1152/ajpheart.1994.266.1.H36. [DOI] [PubMed] [Google Scholar]
  24. Julien C, Zhang ZQ, Cerutti C, Barrès C. Hemodynamic analysis of arterial pressure oscillations in conscious rats. Journal of the Autonomic Nervous System. 1995;50:239–252. doi: 10.1016/0165-1838(94)00095-2. [DOI] [PubMed] [Google Scholar]
  25. Kezdi P, Geller E. Baroreceptor control of postanglionic sympathetic nerve discharge. American Journal of Physiology. 1968;214:427–435. doi: 10.1152/ajplegacy.1968.214.3.427. [DOI] [PubMed] [Google Scholar]
  26. Kobayashi M, Cheng ZB, Tanaka K, Nosaka S. Is the aortic depressor nerve involved in arterial chemoreflexes in rats? Journal of the Autonomic Nervous System. 1999;78:38–48. doi: 10.1016/s0165-1838(99)00054-5. [DOI] [PubMed] [Google Scholar]
  27. Kubo T, Imaizumi T, Harasawa Y, Ando SI, Tagawa T, Endo T, Shiramoto M, Takeshita A. Transfer function analysis of central arc of aortic baroreceptor reflex in rabbits. American Journal of Physiology. 1996;270:H1054–1062. doi: 10.1152/ajpheart.1996.270.3.H1054. [DOI] [PubMed] [Google Scholar]
  28. Kunitake T, Kannan I. Discharge pattern of renal sympathetic nerve activity in the conscious rat: spectral analysis of integrated activity. Journal of Neurophysiology. 2000;84:2859–2867. doi: 10.1152/jn.2000.84.6.2859. [DOI] [PubMed] [Google Scholar]
  29. Malpas SC. The rhythmicity of sympathetic nerve activity. Progress in Neurobiology. 1998;56:65–96. doi: 10.1016/s0301-0082(98)00030-6. [DOI] [PubMed] [Google Scholar]
  30. Miles R. Frequency dependence of synaptic transmission in nucleus of the solitary tract in vitro. Journal of Neurophysiology. 1986;55:1076–1090. doi: 10.1152/jn.1986.55.5.1076. [DOI] [PubMed] [Google Scholar]
  31. Miyawaki T, Pilowsky P, Sun QJ, Minson J, Suzuki S, Arnolda L, Llewellyn-Smith I, Chalmers J. Central inspiration increases barosensitivity of neurons in rat rostral ventrolateral medulla. American Journal of Physiology. 1995;268:R909–918. doi: 10.1152/ajpregu.1995.268.4.R909. [DOI] [PubMed] [Google Scholar]
  32. Rosenbaum M, Race D. Frequency-response characteristics of vascular resistance vessels. American Journal of Physiology. 1968;215:1397–1402. doi: 10.1152/ajplegacy.1968.215.6.1397. [DOI] [PubMed] [Google Scholar]
  33. Sato T, Kawada T, Shishido T, Miyano H, Inagaki M, Miyashita H, Sugimachi M, Knuepfer MM, Sunagawa K. Dynamic transduction properties of in situ baroreceptors of rabbit aortic depressor nerve. American Journal of Physiology. 1998;274:H358–365. doi: 10.1152/ajpheart.1998.274.1.H358. [DOI] [PubMed] [Google Scholar]
  34. Seller H. Central baroreceptor reflex pathways. In: Persson PB, Kirchheim HR, editors. Baroreceptor Reflexes: Integrative Functions and Clinical Aspects. Heidelberg Germany: Springer-Verlag; 1991. pp. 45–74. [Google Scholar]
  35. Stauss HM, Persson PB, Johnson AK, Kregel KC. Frequency-response characteristics of autonomic nervous system function in conscious rats. American Journal of Physiology. 1997;273:H786–795. doi: 10.1152/ajpheart.1997.273.2.H786. [DOI] [PubMed] [Google Scholar]
  36. Terui N, Saeki Y, Kumada M. Confluence of barosensory and nonbarosensory inputs at neurons in the ventrolateral medulla in rabbits. Canadian Journal of Physiology and Pharmacology. 1987;65:1584–1590. doi: 10.1139/y87-249. [DOI] [PubMed] [Google Scholar]
  37. Wennergren G, Little R, Öberg B. Studies on the central integration of excitatory chemoreceptor influences and inhibitory baroreceptor and cardiac receptor influences. Acta Physiologica Scandinavica. 1976;96:1–18. doi: 10.1111/j.1748-1716.1976.tb10166.x. [DOI] [PubMed] [Google Scholar]
  38. Zhang ZQ, Julien C, Barrès C. Baroreceptor modulation of regional haemodynamic responses to acute stress in rat. Journal of the Autonomic Nervous System. 1996;60:23–30. doi: 10.1016/0165-1838(96)00023-9. [DOI] [PubMed] [Google Scholar]

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES