Ionophores and receptors using cation-π interactions: Collarenes

Abstract

Cation-π interactions are important forces in molecular recognition by biological receptors, enzyme catalysis, and crystal engineering. We have harnessed these interactions in designing molecular systems with circular arrangement of benzene units that are capable of acting as ionophores and models for biological receptors. [n]Collarenes are promising candidates with high selectivity for a specific cation, depending on n, because of their structural rigidity and well-defined cavity size. The interaction energies of [n]collarenes with cations have been evaluated by using ab initio calculations. The selectivity of these [n]collarenes in aqueous solution was revealed by using statistical perturbation theory in conjunction with Monte Carlo and molecular dynamics simulations. It has been observed that in [n]collarenes the ratio of the interaction energies of a cation with it and the cation with the basic building unit (benzene) can be correlated to its ion selectivity. We find that collarenes are excellent and efficient ionophores that bind cations through cation-π interactions. [6]Collarene is found to be a selective host for Li⁺ and Mg²⁺, [8]collarene for K⁺ and Sr²⁺, and [10]collarene for Cs⁺ and Ba²⁺. This finding indicates that [10]collarene and [8]collarene could be used for effective separation of highly radioactive isotopes, ¹³⁷Cs and ⁹⁰Sr, which are major constituents of nuclear wastes. More interestingly, collarenes of larger cavity size can be useful in capturing organic cations. [12]Collarene exhibits a pronounced affinity for tetramethylammonium cation and acetylcholine, which implies that it could serve as a model for acetylcholinestrase. Thus, collarenes can prove to be novel and effective ionophores/model-receptors capable of heralding a new direction in molecular recognition and host-guest chemistry.

The design of novel ionophores and receptors has attracted considerable interest in the recent past (1–5). The cation-π interaction discovered by Dougherty and coworkers (6, 7) has received much attention as a new type of binding force important in biological molecular recognition (8–15), enzyme catalysis (16, 17), and crystal engineering (3, 18). This cation-π interaction is known to be responsible for the binding of acetylcholine (ACh) to its deactivating enzyme (8, 9), acetylcholinestrase (19, 20), which has served as a target receptor in designing therapeutic agents against various ailments like myasthenia gravis, glaucoma, and Alzheimer’s disease (21–23).

A lot of effort and concern has been evinced on the disposal of nuclear wastes. A major bottleneck, however, stems from the effective separation of major hazardous isotopes (such as ¹³⁷Cs and ⁹⁰Sr, which have fairly long half-lives of ≈30 years) from these wastes (24–27). There have been extensive attempts to design and develop systems that can be used in nuclear waste separations as effective ionophores. In this context the use of various types of ionophores has been reported (25–27), and there have been extensive attempts to explore new types of ionophores that have a high selectivity for these hazardous isotopes.

It therefore is appealing to investigate the possibility of designing novel ionophores and model receptors based on the principle of the cation-π interaction. There have been reports of the systems in which π-orbitals are oriented vertically to the plane of the rings, namely belt-shape carbocyclic-conjugated systems (such as annulenes, beltenes, cyclacenes, and collarenes) (28–37). The recent discoveries of fully conjugated systems with a curved surface like fullerenes and carbon nanotubes (38, 39) further adds fuel to such a kind of study. However, belt-shape carbocyclic-conjugated systems have hardly been studied apart from the synthetic study of cyclacene precursors and collarenes (32–37).

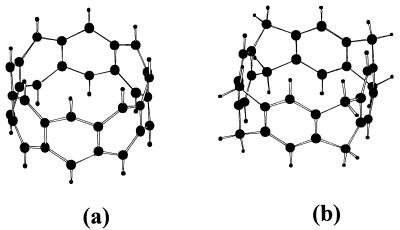
Thus, it would be of importance to investigate whether cyclacenes (comprised of only benzene moieties) and collarenes (having CH₂ linkages between benzene units) can behave as ionophores and receptors. These molecular structures can be understood from the representative structures of [8]cyclacene and [8]collarene shown in Fig. 1. We therefore have carried out extensive ab initio calculations of these structures and evaluated their interaction energies with various cations (alkali, alkaline-earth metal, and organic) in both gas and aqueous phases. Cation selectivities in aqueous solution were investigated by using Monte Carlo (MC) and molecular dynamics (MD) simulations. In the course of study, we show how these systems can be used as effective ion-specific hosts.

Figure 1.

Perspective views of [8]cyclacene (a) and [8]collarene (b).

METHODS

We investigated both [n]cyclacenes and [n]collarenes based on Hartree Fock (HF) theory and density functional theory by using Becke’s 3 parameters with Lee-Yang-Parr correlation functionals (B3LYP) (40, 41). Calculations were carried out with 3–21G and 6–31G* basis sets using the gaussian 94 suite of programs (42). (Refer to the legend of Table 1 for the basis sets of Ba⁺, K⁺, and Ca²⁺, and refs. 43 and 44.) The interaction energies are reported with 50%-basis-set-superposition-error correction, because it has proven to be useful in predicting accurate binding energies (close to the experimental values) for various systems (45–47). We find that while [n]collarenes have only singlet ground states (keeping the aromaticity of the benzene rings), small [n]cyclacenes also may have triplet ground states. The diradical character observed along the upper and lower circumferences of small cylindrical cyclacenes reflects the distortions in their structures, which are induced by high strains present in these molecules. Because small cyclacenes easily lose the aromaticity in their benzene-like building units, the cation-π interaction is found to be more effective in collarenes than cyclacenes. Therefore, our focus in this study is on the binding of [n]collarenes with alkali, alkaline-earth metal, and organic cations.

Table 1.

HF/3-21G and B3LYP/6-31G^* predicted binding energies of [n] collarenes (n = 6, 8, and 10) with various cations

Metal cation	rion	Li+ 0.68	Na+ 0.97	K+ 1.33	Rb+ 1.48	Cs+ 1.67	Be2+ 0.35	Mg2+ 0.65	Ca2+ 0.99	Sr2+ 1.13	Ba2+ 1.35
HF/3-21	G
Benzene	rmφ	1.948	2.431	2.972	3.212	3.444	1.423	2.012	2.575	2.807	3.132
	ΔE	−40.7	−27.2	−16.8	−13.8	−10.8	−204.5	−109.8	−58.7	−46.3	−34.2
[6]collarene	ΔE	−68.3	−35.7	74.6			−285.5†	−199.6	−63.8
(rc = 2.053)	ratio	1.68	1.31				1.40	1.82	1.09
[8]collarene	AE	−69.2†	−65.9	−48.1	−32.9	−6.3	−277.9†	−197.2†	−155.2	−135.3	−88.0
(rc = 2.899)	ratio	1.70	2.42	2.87	2.39	0.58	1.36	1.80	2.64	2.92	2.58
[10]collarene	ΔE			−48.7	−46.2	−40.8			−122.72	−118.71	−102.0
(rc = 3.726)	ratio			2.90	3.36	3.76			2.09	2.56	2.98
B3LYP/6-31G*
Benzene	rmφ	1.881	2.376	2.864			1.292	1.948	2.426
	ΔE	−41.1	−27.4	−17.3			−237.5	−124.1	−72.3
[6]collarene	ΔE	−67.7	−34.2				−316.1†	−218.8	−81.7
(rc = 2.057)	ratio	1.65	1.25				1.33	1.76	1.42
[8]collarene	ΔE	−65.1†	−56.0	−43.1			−311.6†	−207.6†	−162.8
(rc = 2.900)	ratio	1.59	2.04	3.54			1.31	1.67	2.25

r_ion, ionic radius (52); r_mφ, benzene centroid to metal cation distance; r_c, cavity radius of [n]collarene; ΔE, 50% basis set superposition error corrected binding energy. Distances are in Å; energies in kcal/mol. The 3–21G quality Hay-Wadt basis set (43) was used for Ba²⁺ for which the 3–21G basis set is not available; the 6–31G* quality (Ahlrichs pVDZ + 1d function) basis set (44) was used for K⁺ and Ca²⁺. The † denotes a collarene-cation complex in which the cation is displaced from the center as a result of its small size. In case of the [6]collarene-K⁺ complex, the K⁺ ion was constrained at the center of [6]collarene, because the ion is not stable in it. 

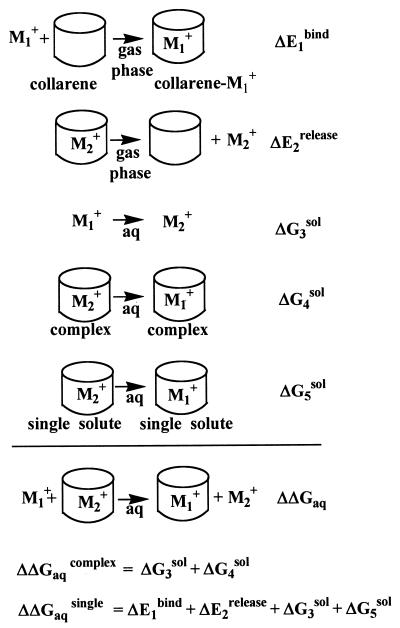
Aqueous solvation effects were investigated by using both MC and MD simulations in conjunction with statistical perturbation theory. The relative solvation-free energies of pairs of species at 298 K and 1 atm (1 atm = 101.3 kPa) were evaluated by carrying out MC simulations based on optimized potentials for liquid simulations (OPLS) (48) by using the boss suite of programs (49). The calculated results, according to the equation shown in Fig. 2, indicate the relative stabilities of [n]collarene-cation complexes (ΔΔG_aq). Because OPLS underestimates binding energies for the cation-π interaction in the gas phase, Kollman and collaborators (11, 50) have used a potential incorporating the polarization effect. This polarizable potential has proven to be useful in predicting the binding energies (close to the experimental values) for both gas and liquid phases (11, 50). Therefore, the relative solvation free energies also were evaluated by carrying out MD simulations based on the polarizable potential with the amber suite of programs (51).

Figure 2.

Scheme to calculate ΔΔG_aq^complex and ΔΔG_aq^single (refer to the legend of Table 2).

RESULTS AND DISCUSSION

Table 1 lists the HF/3–21G and B3LYP/6–31G* interaction energies of [n]collarenes (n = 6, 8, and 10) with alkali metals (Li⁺, Na⁺, K⁺, Rb⁺, and Cs⁺) and alkaline-earth metals (Be²⁺, Mg²⁺, Ca²⁺, Sr²⁺, and Ba²⁺). It can be seen that the interaction energies evaluated by using different basis sets are consistent. Because HF/3–21G energies are available for all of the systems, our discussions are based on them. The more accurate B3LYP/6–31G* energies are used where available.

The HF/3–21G interaction energies of [6]collarene with Li⁺ and Na⁺ are −68.3 and −35.7 kcal/mol, respectively. The [6]collarene-Li⁺ interaction energy is 1.7 times the benzene-Li⁺ interaction energy, whereas the [6]collarene-Na⁺ interaction energy is 1.3 times the benzene-Na⁺ interaction energy. The [6]collarene-K⁺ interaction energy is extremely positive when K⁺ is at the center of the collarene, indicating that K⁺ cannot be inside [6]collarene.

Similarly, the interaction energies of [8]collarene with Li⁺, Na⁺, K⁺, Rb⁺, and Cs⁺ are 1.7, 2.4, 2.9, 2.4, and 0.6 times that of the benzene with the corresponding cations, respectively. Thus, the ratio of the [8]collarene-K⁺ interaction energy to the benzene-K⁺ interaction energy is particularly large. Because the ratio of the interaction energies of the cation to the ionophore and its basic building unit reflects the relationship between the cavity size and the cation size, the maximum ratio is expected to appear at contact distances. Thus, the maximum ratio can be related to the maximum cation-π association, which is responsible for the ion selectivity. It will be proven later that this ratio is indeed correlated to the ion selectivity of the [n]collarenes in the aqueous phase. Accordingly, the maximum ratio of 2.9 for K⁺ in [8]collarene implies a marked preference of [8]collarene for K⁺.

The interaction energies of [10]collarene with K⁺, Rb⁺, and Cs⁺ are 2.9, 3.4, and 3.8 times that of benzene with the corresponding cations, respectively. Thus the ratio of [10]collarene-Cs⁺ binding energy to the benzene-Cs⁺ binding energy is the largest. This finding indicates that [10]collarene shows a marked preference for Cs⁺, which also will be proven by MC and MD simulations in aqueous phase.

A point to be noted from the ratio of the interaction energies is that collarenes of a certain size exhibit selectivity for a particular cation. This selectivity emerges from the structural characteristics of collarenes. The cation-π interaction in collarenes is maximum when the cavity radius is nearly equal to the optimal benzene-metal distance (r_mφ) for the maximal benzene-metal interaction. It can be seen that the cavity radius of [6]collarene (r_c = 2.1 Å) is close to the optimal distance for the benzene-Li⁺ interaction (r_mφ = 1.9 Å). However, this cavity radius is somewhat smaller than the optimal benzene-Na⁺ distance (r_mφ = 2.4 Å). Therefore, the interaction energy of [6]collarene with Li⁺ is 1.7 times the benzene-Li⁺ interaction energy, whereas with Na⁺ is similar to the benzene-Na⁺ interaction energy. The cavity radius of [8]collarene (r_c = 2.9 Å) is too large for Li⁺ to have strong binding with the π electrons of the surrounding aromatic moieties, whereas it is close to the optimal distance for the benzene-K⁺ interaction (r_mφ = 3.0 Å). Thus the interaction energy of [8]collarene with K⁺ increases (in magnitude) significantly, up to 2.9–3.5 times the benzene-K⁺ interaction energy (at the HF/3–21G and B3LYP/6–31G* levels), whereas with Li⁺ it is smaller (in magnitude) than the interaction energy of [6]collarene with Li⁺. It is reasonable to expect that Li⁺ would be more effectively captured by [6]collarene than [8]collarene, whereas K⁺ would be effectively captured by [8]collarene. In [10]collarene, the cavity radius (r_c = 3.7 Å) is close to the optimal distance for Cs⁺-π interaction (3.4 Å). Hence, the interaction energy (−40.8 kcal/mol) is 3.8 times the benzene-Cs⁺ interaction energy.

A similar trend also is observed in the complexes of [n]collarenes with alkaline-earth metals. Among the alkaline-earth divalent cations, Mg²⁺ is most favored by [6]collarene; Sr²⁺ by [8]collarene; Ba²⁺ (or possibly Ra²⁺ because the ionic radii of Ba²⁺ and Ra²⁺ are 1.35 and 1.37 Å; ref. 52) by [10]collarene. Our calculations show that [10]collarene and [8]collarene could be used as useful ionophores for the effective separation of harmful radioactive isotopes of Cs⁺ and Sr²⁺ from nuclear wastes.

Kollman and collaborators (10, 11) examined the cation-π interactions in water by using MD simulations. They showed that these cation-π associations are favorable at contact distances in aqueous solution. We also investigated whether the ion specificity of [n]collarenes prevails in aqueous solution. Hence, the Gibbs free energy changes of [n]collarenes for metal substitutions in aqueous solution evaluated by using statistical perturbation theory are listed in Table 2. The interaction energies and the relative energy changes in the gas phase also are listed in the table for comparison. It can be seen that the polarizable potential reproduces the ab initio interaction energies more reasonably than the OPLS interaction energies, which are underestimated. However, because OPLS parameters were optimized for studies in solution, the gas phase OPLS interaction energies can have large deviations from the ab initio interaction energies. Though polarization effects are important in describing the absolute gas phase interaction energies (ΔE_gas and ΔG_gas) (6–13), it can be seen from Table 2 that the relative energies (ΔΔE_gas and ΔΔG_gas) are little affected by them because the differences in polarization effect are not significant when [n]collarenes interact with different alkali cations. These results seem to lead to a situation wherein the free energy difference between the OPLS and polarization potential for [n]collarene-cation complexes does not differ significantly even in the aqueous phase. The only significant difference was noted in Na⁺-[6]collarene because the optimal Na⁺-benzene distance in the polarizable potential is too short (11) as compared with either OPLS or ab initio results. The polarization model thus underestimates the large exchange repulsion between benzene and Na⁺ despite the fact that the cavity size of [6]collarene is too small for Na⁺ to fit in. Except for this special case, all calculational results are quite consistent, whereas the results with the polarizable potential should be considered to be more reliable in the aqueous phase.

Table 2.

Relative stabilities (kcal/mol) of [n]collarene-cation complexes in the gas phase and in aqueous solution

[n]collarene		n = 6		n = 8			n = 10
		Li+	Na+	Na+	K+	Rb+	K+	Rb+	Cs+
ΔEgas	HF/3–21G	−68.3	−35.7	−65.9	−48.1	−32.9	−48.7	−46.2	−40.8
	B3LYP/6–31G*	−67.7	−34.2	−56.0	−43.1	—	—	—	—
	MC/OPLS	−44.8	−20.5	−33.6	−29.3	−24.1	−25.6	−24.5	−22.1
	MD/Polar. Pot.	−71.3	−41.8	−46.5	−40.8	−36.3	−32.8	−31.7	−29.9
ΔGgas	HF/3–21G	−58.8	−25.6	−57.7	−38.5	−22.7	—	—	—
ΔΔEgas	HF/3–21G	0	32.6	−17.8	0	15.2	−7.9	−5.4	0
	B3LYP/6–31G*	0	33.5	−12.9	0	—	—	—	—
	MC/OPLS	0	24.3	−4.3	0	5.2	−3.5	−2.4	0
	MD/Polar. Pot.	0	29.5	−5.8	0	4.4	−2.9	−1.8	0
ΔΔGgas	HF/3–21G	0	25.7	−19.3	0	16.7	—	—	—
ΔΔEaq	SCRF/HF/3-21G			7.9	0
ΔΔGaqcomplex	MC/OPLS	0	15.5	3.4	0	2.5	3.9	2.2	0
ΔΔGaqsingle	MC/OPLS	0	12.1	0.4	0	(10.8)	0.5	(−0.3)	0
ΔΔGaq	MD/Polar. Pot.	0	3.3	4.9	0	0.9	4.3	2.3	0

ΔE and ΔG are the zero-point uncorrected interaction energy and Gibbs free energy, respectively. See Fig. 2 for the definitions of ΔΔG_aq^complex and ΔΔG_aq^single. M₁ ⇒ M₂ denotes the substitution reaction in aqueous solution: [n]collarene-M₁⁺ + M₂⁺ → [n]collarene-M₂⁺ + M₁⁺. ΔΔG_aq denotes the Gibbs free energy change of the substitution reaction at room temperature and at 1 atm pressure. Positive signs of ΔΔE and ΔΔG in the free energy perturbation calculations indicate that the corresponding cation-[n]collarene complex is less stable than the reference cation-collarene complex (ΔΔE = 0, ΔΔG = 0). To calculate the free energy change between two different cation-[n]collarene systems in the MC simulations, we followed the approach used by Kumpf and Dougherty (7); ΔΔG_aq^complex is used for the cases where the interactions between a rigid [n]collarene and a cation in the complexes were explicitly taken into account in free energy perturbation calculations; ΔΔG_aq^single is used when the OPLS interactions between a rigid [n]collarene and cations were neglected by treating the complex as one single rigid solute in the free energy perturbation calculations, but the ab initio interaction energy change was added to the resulting free energy change instead of the OPLS interaction energy change. The interaction energies of cations with [6]-collarene and [8]collarene were corrected with the B3LYP/6–31G* values, and those with [10]collarene with the HF/3–21G values (because the B3LYP/6–31G* values are not available). The ΔΔG_aq^single may not be reliable when the OPLS interaction energy difference between two cation-collarene complexes is significantly different from the corresponding ab initio interaction energy difference. However, the bounds can be estimated for the errors resulting from the deficiencies in the empirical potential. The MC simulations were carried out at constant temperature (298 K) and pressure (1 atm) with the complex at the center of a cubic box 24.8 Å containing 512 TIP4P water molecules under the periodic boundary condition. The cutoff distance was 11 Å. A series of 20 simulations with double wide sampling was performed for each system. Each perturbation step involved 10⁶ configurations of equilibration followed by averaging over 5 × 10⁶ configurations. The SCRF calculations were carried out at a single point HF/3–21G level in polarized dielectric medium (water: ɛ = 78.5). The interaction energies were obtained using the equation: ΔE_SCRF = E_SCRF([n]collarene-M⁺ + (H₂O)₆) − E_SCRF ([n]collarene) − E_SCRF(M⁺ + (H₂O)₆); see Fig. 3. In case of MD simulations using the polarizable potential, we followed the approach used by Caldwell and Kollman (11); the potential was composed of charges obtained from a restrained electrostatic potential (RESP) fit of quantum mechanical electrostatic potential, the van der Waals parameters determined at the additive level, the atomic polarizabilities taken from Applequist except for the benzene sp² carbon (0.36 ų), and the POL3 water potential (11, 50, 53). The Gibbs free energy perturbation MD simulations were carried out as an NPT ensemble (298 K, 1 atm). The box sizes for the simulations of [6]-, [8]-, and [10]-collarenes were 27.0 Å × 26.6 Å × 25.3 Å, 28.9 Å × 28.9 Å × 25.3 Å, and 30.4 Å × 30.6 Å × 25.4 Å, with 487, 540, and 618 water molecules included. The cutoff distance was 10 Å. The number of simulation windows was 20. Each simulation consisted of 3 ps equilibration and 3 ps sampling. A 2-fs time step was used with all OH bonds and HOH bond angles of water molecules constrained by shake algorithm. 

When Li⁺ is replaced by Na⁺ in [6]collarene-cation complex in the gas phase, the changes of the HF/3–21G binding energy and free energy are 33 and 25 kcal/mol, respectively. In the aqueous phase, the OPLS predicted free energy change is 12–16 kcal/mol (the variation arises from different calculation methods; refer to the legend of Table 2 for details). Therefore, [6]collarene is predicted to have a good selectivity for Li⁺ in both gas and aqueous phases.

In [8]collarene, in the gas phase, Li⁺ is preferred over Na⁺, K⁺, and Rb⁺ by 3, 21, and 36 kcal/mol, respectively, whereas in aqueous solution the K⁺ ion is preferred over Li⁺, Na⁺, and Rb⁺ by 16–17, 3–5, and 1–3 kcal/mol, respectively. Thus, in aqueous solution [8]collarene shows a pronounced preference for K⁺. The selectivity for K⁺ in aqueous solution is mainly because of solvation effects. This selectivity is in consonance with the ratio of the [8]collarene-cation interaction energy to the benzene-cation interaction energy shown in Table 1.

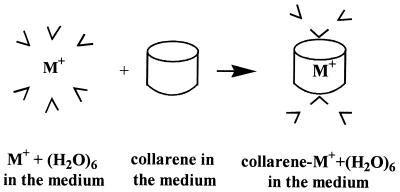
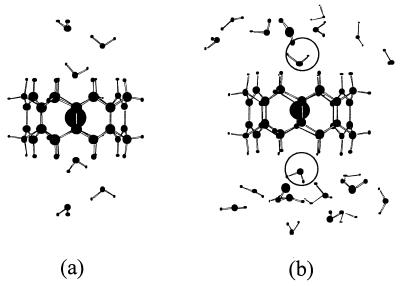
To highlight the competition between K⁺ and Na⁺ toward [8]collarene in aqueous phase, an alternative calculation method was used [HF self-consistent-reaction-field (SCRF) theory at the HF/3–21G level based on the polarized continuum model] (Fig. 3). To take into account a part of the first solvation shell structure, we carried out the SCRF calculations of the hexa-hydrated systems of the collarene-cation complexes surrounded by a polarized continuum medium of bulk water (dielectric constant of 78.5). The SCRF(HF)/3–21G optimized geometry is shown in Fig. 4; a single water molecule at each mouth of [8]collarene interacts with the cation inside the collarene, whereas the remaining two water molecules interact with it and the collarene. Such a situation also is observed in MC and MD simulations of a system comprised of an [8]collarene, a K⁺ cation, and 480 water molecules (Fig. 4). K⁺ prefers to stay inside the cavity of [8]collarene in both MC and MD simulations. In the SCRF calculations, the same preference was noted. In addition, [8]collarene exhibits a preference for K⁺ over Na⁺ by 7.9 kcal/mol (in ΔΔE_aq) at 0 K. This value implies that the corresponding free energy differences (ΔΔG_aq at 298 K and 1 atm) predicted by OPLS (3.4 kcal/mol) and the polarizable potential (4.9 kcal/mol) are reasonable. The selectivity of [8]collarene toward K⁺ therefore is confirmed by consistent results obtained from all four cases used here: the HF/3–21G and B3LYP/6–31G* predicted ratios of collarene-cation interaction energy to benzene-cation interaction energy, MC simulations, MD simulations, and SCRF method. A similar consistency of the results of the four different methods is observed in other systems.

Figure 3.

Scheme used to evaluate the binding energy of [n]collarene with cation M⁺ in polarized dielectric medium (water: ɛ = 78.5) by using SCRF calculations (see the legend of Table 2).

Figure 4.

Coordination of water molecules in the [8]collarene-K⁺ complex. (a) The HF/3–21G optimized structure of [8]collarene-K⁺ + (H₂O)₆. (b) The MC predicted instantaneous coordination of water molecules near [8]collarene-K⁺ (480 water molecules were included in the simulation). Two water molecules interact with the K⁺ cation at both portals.

In the case of [10]collarene, the free energy difference indicates that in aqueous solution Cs⁺ is more effectively captured than Rb⁺ and K⁺ by 2 and 4 kcal/mol, respectively [it should be noted that the corresponding gas phase values are −8 and −5 kcal/mol in ΔE(HF/3–21G)]. This feature also is noted from the ab initio interaction energy ratios. Rb⁺ would compete with Cs⁺ in aqueous phase to a certain extent, because the differences in interaction energy ratio and free energy are small.

It can be seen from the above discussion that the ion selectivity in aqueous phase is mainly determined by size effects or exchange repulsions, as a result of a decreased contribution from the attractive forces (because of the influence of the medium on the electrostatic forces and polarization effects). This ion selectivity in aqueous phase is in contrast to what is observed in the gas phase, where both attractive forces (electrostatic, polarization, dispersion forces, etc.) and repulsive forces (exchange repulsions) tend to influence ion binding by the collarenes. Because a large ratio of interaction energies is obtained when the optimal benzene-cation distance is nearly the same as the [n]collarene-cation distance, the energy ratio can give an indication of the size effects present in these systems. Hence, the energy ratio (a quantity obtained from ab initio calculations) can be used to represent the ion selectivity of these collarenes in aqueous solution.

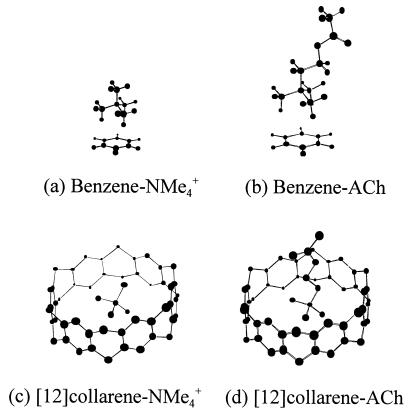
The function of large [n]collarenes also has been investigated as a possible ionophore for small organic cations. [12]collarene seems to have an adequate cavity size (4.56 Å) to capture tetramethylammonium cation (NMe₄⁺) and ACh. These cations and their complexes with aromatic compounds have been intensively investigated to shed light on the nature of the binding forces of ACh to acetylcholinestrase as well as to better understand the nature of the cation-π interaction (6–17). Fig. 5 illustrates the optimized structures of the benzene-NMe₄⁺, benzene-ACh, [12]collarene-NMe₄⁺, and [12]collarene-ACh complexes. The HF/3–21G binding energies of [12]collarene with NMe₄⁺ and ACh are 25.9 and 26.4 kcal/mol, respectively, which are 3.6 and 3.8 times those of the benzene with NMe₄⁺ and ACh. This strong binding affinity of [12]collarene toward ACh implies that [12]collarene could be used as a model receptor of acetylcholinestrase.

Figure 5.

Interactions of NMe₄⁺ or ACh with benzene or [12]collarene. In the case of [12]collarene complexes, H atoms are omitted for clarity.

CONCLUSIONS

Our results show that in contrast to [n]cyclacenes, [n]collarenes maintain the aromaticity of the benzene and therefore can be used as effective ionophores or model receptors, based on the principle of cation-π interaction. In [n]collarenes, the ratio of the interaction energies of a cation to it and the cation to its basic building unit (benzene) is found to be correlated to its ion selectivity. This selectivity toward a particular cation in the aqueous phase was revealed from MC and MD simulations carried out in conjunction with statistical perturbation theory. In sharp contrast to the gas phase wherein interaction forces like electrostatic, dispersion, and polarization effects tend to favor the maximal cation-π interactions, the ion selectivity in the aqueous phase is governed mainly by size effects related to exchange repulsions. It can be observed that cations of small ionic radius, such as Li⁺ and Mg²⁺, can be selectively captured by [6]collarene, whereas cations with intermediate ionic radius, such as K⁺ and Sr²⁺ are selectively captured by [8]collarene. Cations of relatively large radius, such as Cs⁺ and Ba²⁺ (and probably Ra²⁺), can be selectively captured by [10]collarene. Thus, [10]collarene and [8]collarene could be useful in the separation of harmful radioactive nuclear wastes like ¹³⁷Cs and ⁹⁰Sr. Organic cations of NMe₄⁺ and ACh are shown to be selectively captured by [12]collarene, which implies that [12]collarene can be used as a model receptor of acetylcholinestrase. Therefore, these collarenes that bind cations through cation-π interactions could have diverse roles with important practical applications in environmental chemistry and biology.

ABBREVIATIONS

MC

Monte Carlo

MD

molecular dynamics

NMe₄⁺

tetramethylammonium cation

ACh

acetylcholine

HF

Hartree-Fock

B3LYP

Becke’s 3 parameters using Lee-Yang-Parr correlation functionals

OPLS

optimized potentials for liquid simulations

SCRF

self-consistent reaction field