The paracellular component of water flow in the rat submandibular salivary gland

Abstract

1. The pathway of water flow during salivary secretion by the isolated, perfused rat submandibular gland was examined using a family of homologous radiodextran molecules as probes of paracellular fluid transfer.

2. The secretion/perfusate ratio (S/P) of the secreted probes versus molecular radius during fluid secretion evoked by ACh could be resolved into two components: one that fitted a free-diffusion (Stokes-Einstein) curve and indicated diffusion through large channels, and a convective component that was linearly related to radius.

3. The convective component had a cut-off point at 0.5 nm (5 Å) radius and an S/P intercept of near 1.0 at the radius of water, which indicates that most of the volume flow was paracellular.

4. The nature of such a paracellular flow is discussed together with the possible integration of this volume flow with the cellular transport of ions, resulting in an isotonic primary secretion from the gland.

The role and contribution of the paracellular pathway in isotonic fluid transport by epithelia in general, and exocrine glands in particular, is a problem that has not yet been resolved. If this pathway is of general importance then it should be possible to demonstrate and assess its magnitude in both absorbing and secreting epithelia. The salivary acinus is a ‘backwards-facing’ epithelium in which the Na⁺-K⁺-ATPase pump is located on the basolateral membranes and the secreted fluid flows from the basal to the apical side of the cells into the acinar lumen. It is a generally accepted scheme of acinar salt secretion that the Na⁺ ions move through the paracellular pathway, driven by the overall potential difference created by Cl⁻ secretion through channels on the apical membrane.

The mechanism for coupling water movement to that of the salt depends primarily upon the path of water through the acinar epithelium, but here the position remains uncertain (see pp. 1087-1088 of Cook et al. 1994). It is clear that in the two-stage model of salivary secretion the primary or acinar solution is isotonic, with little if any subsequent water flow across the ductal cells at high flow rates (Burgen, 1967; Cook et al. 1994). As the osmotic theory of fluid production is often assumed to apply to epithelia, to put the results presented here in context it is appropriate to assess the evidence to date concerning the route of water flow through the glandular epithelium.

The technique of using several non-electrolytes of differing molecular radius to assess the amount of water that passes through the paracellular pathway has been applied previously to the rabbit submandibular gland (Case et al. 1985). The principal finding was that the relative concentration of probes in the saliva (the saliva to perfusate ratio, S/P) was independent of volume flow at the higher flow rates, a finding strongly indicating a fixed ratio of probe/water traversing a non-diffusive path (see Discussion for details). The results were analysed in terms of a solvent drag model, resulting in a set of filtration coefficients versus radius, which were fitted by curves of pore radius close to 4.2 Å (0.42 nm); pseudo-solvent drag due to unstirred-layer effects was ruled out as making any significant contribution. This indicates that the fluxes of the probes were due largely to convection through such pores. Similar results were obtained subsequently (Howorth et al. 1987). However, it was shown that many of the probes, although moving paracellularly, had tissue volumes that indicated permeation into cells. In this case it was considered impossible to assume that the convective channels were wholly paracellular. It was subsequently observed that to assign such channels to the cell membranes would imply ionic permeabilities 100 times greater than those observed, and that the most likely place for them would be the tight junction (TJ; Cook et al. 1994). It is also unlikely that such convective coupling could be taking place in large membrane channels, as there are no known structures that could mediate this.

In a study using NMR relaxation methods to determine the water membrane permeability of the rabbit salivary gland membranes, the value obtained, which is almost entirely due to that of the basolateral membrane, was too small to explain the near-isotonicity of the primary secretion (Steward et al. 1990). It was concluded that the cellular route could account for only a small fraction of the water transport by osmosis during stimulation of the flow by ACh.

At the dynamic structural level, the results of light microscope studies implicate the lateral intercellular space (LIS) system as the route for water and solute transport during secretion. In studies where rat salivary glands were perfused with saline containing fluorescently labelled dextrans with molecular masses up to 500 kDa as paracellular markers, these were initially visualized only in the basolateral sections of the LIS and did not pass through the TJ into the luminal spaces without stimulation by secretagogues. However, within a few minutes after stimulation with carbachol, markers up to 10 kDa in size crossed into the lumen, and with isoproterenol (isoprenaline) stimulation, markers up to 40 kDa crossed (Segawa, 1994, 1997). It was concluded that upon stimulation, the TJ becomes permeable, enabling the passage of macromolecules and fluid.

On stimulation with ACh there is an initial cell shrinkage, although the volume of the acinus (acinar cells plus acinar lumen) swells. The application of hypotonic perfusates also creates a similar effect, with the cells swelling less than the total acinar volume (Nakahari & Imai, 1998). This was taken to indicate a primary shift of volume from the interstitium to the lumen via the LIS. In experiments in which the LIS was occluded by bicarbonate-induced cell swelling, a procedure that blocked the paracellular movement of lucifer yellow, the volume of secretion into the lumen also decreased (Nakahari et al. 1998).

In this paper we show how a homologous series of quasi-spherical dextran molecules can be used as extracellular probes of water movement, using the convection- diffusion theory. The analysis depends upon obtaining convective flows of these probes as a function of radius, when the pattern of net flow can be extrapolated to near-zero radius, yielding a value for the paracellular fluid velocity. In previous studies where this technique has been employed, the convective flow component has been measured as a net flux, the bi-directional passive diffusion fluxes being measured under conditions where they are equal (Shachar-Hill & Hill, 1993). The structure of the salivary gland is such that bi-directional fluxes cannot be measured and the flux of markers can only be determined as a unidirectional flux from the basal to the luminal side after secretion is induced. The analysis has therefore to take account of this fact and estimate the contribution of the passive diffusional flow component in a different way. In the present paper we show how this can be done in a reasonably straightforward manner to obtain a convective flux of probes as a function of radius, and from this to estimate the fraction of total fluid flow crossing the system of LIS and TJ.

METHODS

Solutions

The perfusion fluid was a buffered salt solution of the following composition (mm): Na⁺ 146, K⁺ 4.4, Ca²⁺ 1.0, Mg²⁺ 1.0, Cl⁻ 148.4, HCO₃⁻ 25 and glucose 5. Hepes at 10 mm was used for buffering the solution to pH 7.4. This saline was made freshly for each experiment and placed in a reservoir where it was equilibrated with a gas mixture containing 5 % CO₂+ 95 % O₂. The gland was stimulated to secrete by adding 1 μm ACh, which was dissolved in the perfusing saline immediately before use.

All chemicals were of analytical grade and were purchased from Sigma, apart from the radioactively labelled dextrans. These were obtained from Pharmacia as T10 dextran, and labelled by Amersham International as described previously (Shachar-Hill & Hill, 1993).

Tissue preparation and perfusion

The procedure for isolating the submandibular salivary gland of the rat has been described previously (Murakami et al. 1990). In brief, adult male Sprague Dawley rats, weighing 170-250 g, were purchased from Charles Rivers, given a standard pellet diet and water ad libitum. They were anaesthetized with pentobarbital sodium (50 mg (kg body weight)⁻¹, i.p.) and the submandibular gland was exposed surgically. The attached sublingual gland was removed after ligation of the branches of the feeding artery and draining vein. The extra-lobular main duct from the submandibular gland was cannulated with a polyethylene tube for the collection of saliva. The artery distal to the glandular branch was cannulated with a stainless steel catheter (26 gauge) and the vein from the gland was cut. The gland was isolated and transferred to an organ bath (37 °C), where the arterial catheter was connected to the perfusion apparatus. Rats were killed with an overdose of pentobarbital sodium and dislocation of the neck. The drained venous effluent was collected at the bottom of a plastic tissue dish by peristaltic pump and either re-used in the perfusion circuit or shifted to a waste container. The glands, weighing between 120 and 250 mg, were perfused arterially at a rate of 1 or 2 ml min⁻¹ using a Watson-Marlow peristaltic pump in order to supply enough O₂ during the secretory phase without using specific O₂ carriers.

The gland was perfused with saline without dextrans for 10 min and tritiated dextran T10 was added 10 min before stimulating the gland to secrete. Two perfusion regimes were used: (1) open flow perfusion (i.e. the saline leaving the gland was discarded) and (2) perfusion with re-circulation (i.e. the saline perfusing the gland was re-circulated for the duration of the experimental period to economize on the labelled dextrans). Saliva samples were collected at timed intervals into pre-weighed microfuge tubes, which were then sealed and re-weighed to determine the secretory rate. Extracellular fluid (ECF) was also collected at timed intervals, and a sample of the perfusion fluid was taken in addition for each experiment. The possible effect of re-circulation was examined by comparing plots of S/P against the molecular radius for the dextran probes in the two perfusion procedures (open n = 4, re-circulated n = 12), but there appeared to be no significant difference between the two procedures with respect to the selectivity or permeability of the preparation.

Radiochemical analysis

The samples were dried under vacuum to eliminate tritiated water, and then re-suspended in known volumes of distilled water, from which small aliquots (10 μl) were taken and assayed in a scintillation counter to estimate the total dextran flux as a function of flow rate and time. The rest of the saliva samples were combined and analysed as described previously; a detailed description of the analytical technique and the determination of dextran size and shape have been given elsewhere (Shachar-Hill & Hill, 1993). Briefly, a set volume was run on a Sephadex column for size exclusion chromatography using Pharmacia G25 calibrated for dextran. The eluted volumes were counted in a scintillation flow counter to obtain the spectrum of secreted molecular sizes. Similar runs were performed sequentially with samples of the perfusate and gland exudate, whereby the salivary fluxes could be converted to relative fluxes for each experiment.

Data analysis and theory

The activity S of the salivary samples eluted from the column was referred to dextran molecular radii using column calibration software data, and was compared with that of the corresponding perfusate P to obtain S/P ratios as a function of radius.

The relationship between the S/P ratio, the molecular radius and the width of a channel has been set out in detail for a gland in terms of the Kedem-Katchalsky theory for unidirectional secretion (Case et al. 1985) and for a planar epithelium under conditions of net flux (i.e. by convection theory; Hill & Shachar-Hill, 1993). A simple form of the latter is given here.

We consider a general theory of convection equivalent to a net flux of any particular probe species from a source bath (here the solution perfusing the blood vessels of an exocrine gland) into a sink bath (the luminal solution). The source bath is a probe solution of concentration P (perfusate). The isotonic fluid flow across the whole epithelium, J_v, may be considered to include a fluid flow through TJ and LIS equal to j_v. If the paracellular convective transport of the probe across the epithelium from the source bath is j_s, as measured experimentally by radioactive tracer, then:

(1)

where θ is a coefficient defining in very general terms the selectivity of the channel to the probe molecule during fluid flow. It is, in fact, a function of both the effective concentration of the probe in the channel and any drag effect experienced by the probe during convection through the channel. θ has the general property whereby as the probe radius r_s approaches that of water, θ→ 1.0 and the probe is passing with no selectivity compared to the solvent. If the probe is equal in radius (or half-width) to the radius of the channel then θ→ zero and there is no flux. θ would approximate to (1 - σ) of the Kedem-Katchalsky theory (where σ is the reflection coefficient of small solutes), but we are not restricted to the simple fluid convection to which this applies. Dividing eqn (1) by J_v:

(2)

and equating j_s/J_v with S, we have:

(3)

where j_v/J_v is the fraction of the total transepithelial fluid transport that is passing the TJ and LIS. The parameters S and P are experimental values, and θ is a function of r_s. If we have measurements of S/P from a series of probes, then this should rise as r_s decreases. If we have a quasi-linear relationship between S/P and r_s, as seems to hold for a homologous series of dextrans in those epithelia tested, we can extrapolate the curve to zero (or water) radius, in which case θ→ 1.0 and S/P represents the fraction of volume transport passing through the paracellular pathway.

RESULTS

S/P ratio as a function of the probe radius

The results of determining the S/P ratio as a function of molecular radius are shown in Fig. 1. The number of points generated by the analysis was high enough to indicate that the dextran series results in a smooth curve that is distinctly L-shaped. Such a relationship has been found for other epithelia when probes of increasing molecular weight were employed (Steward, 1982; Case et al. 1985; Howorth et al. 1987; Shachar-Hill & Hill, 1993; Hernandez et al. 1995). In all of these cases the L-shaped curve was only seen when unidirectional fluxes were measured as a function of probe radius, but not when net fluxes could be determined. This is due to the subtraction of the diffusive component, which must be passive and identical in each direction. In experiments with the salivary gland it is impossible to measure backfluxes, and therefore an analytical technique must be used to remove the diffusive component to obtain the convective component; the theory outlined above and embodied in eqns (1)–(3) applies only to convective paracellular fluxes.

Figure 1. Secretion/perfusate (S/P) ratio as a function of radius.

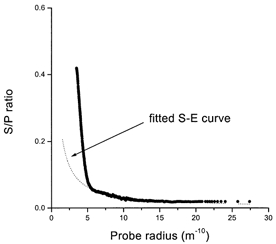
The mean S/P ratio as a function of molecular radius (all experiments n = 12). The long tail from 0.6 nm (6 Å) upwards has been fitted to a Stokes-Einstein (S-E) curve (dotted line). For details see the Discussion and Fig. 7.

Selectivity of the vascular endothelium

When the saline containing the labelled dextrans was perfused through the vasculature of the gland it is likely that the capillary walls constituted a barrier to at least some of the probes, so it was necessary to determine the molecular radius at which the endothelium began to discriminate against these molecules. It is important when calculating the S/P ratio to have the right size distribution for the dextran population in the interstitium and not to rely solely on a sample of the perfusate. Figure 2 shows that the endothelium did indeed discriminate against dextrans of higher molecular radii reaching the acini, but this was far above the radius at which the epithelium itself discriminates. This means that the endothelium does not limit the selectivity of the epithelial junctions, but it indicates that the S/P ratio should be calculated using the dextran profile of the ECF not the perfusate.

Figure 2. Selectivity of the vascular barrier to probes.

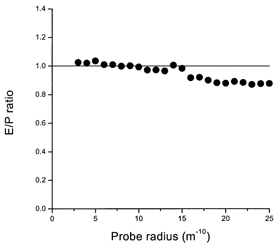
The mean exudate/perfusate activity (E/P) ratio as a function of molecular radius. Up to a radius of about 15 m⁻¹⁰, no selectivity of the vascular barrier is observed. Above this size it becomes significant.

Contribution of the first saliva sample to the S/P ratio

When the gland was stimulated to secrete, the first minute of secretion had a very high fluid flow rate and may have contained an unknown amount of dextrans, which diffused across the junctional barrier while the gland was perfused prior to the onset of fluid stimulation. This may have distorted the S/P ratio, with a concomitant overestimation of the fluid fraction accompanying the markers. Therefore, in some experiments (n = 4) the secretion during the first minute after stimulation was not pooled with the rest of the saliva, and the latter was compared with samples including saliva from the first minute of secretion. Figure 3 shows that there was no apparent difference between the two curves. This indicates that the diffusive component seen in these experiments was not due to the period prior to stimulation, and that the total saliva collected in all experiments can be pooled and used in the subsequent analysis.

Figure 3. Contribution of early samples to S/P ratios.

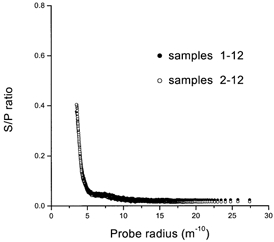
Effects of excluding the first saliva sample from the 12 samples from each experiment (n = 4).

S/P ratio as a function of the volume flow rate

The data for the S/P ratio obtained for dextrans in this study are shown against J_v rates in Fig. 4. The flow rates varied from gland to gland and fell with time after stimulation with ACh, so that a large number of points have been collected into bins. It is apparent that above 100 μl min⁻¹ (per gram of gland) there was no significant change in the S/P ratio with flow rate.

Figure 4. S/P ratios and the transepithelial flow rate.

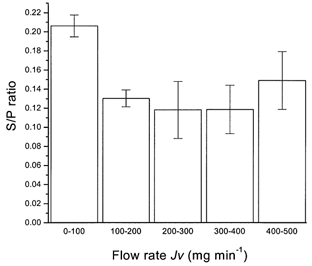
The behaviour of the mean S/P ratio as a function of flow rate (J_v; bins of rate in mg min⁻¹) found for total dextrans in all samples (n = 153) from all experiments. The S/P ratio becomes independent of J_v. The error bars are s.e.m.

DISCUSSION

Paracellular probes in other fluid-transporting epithelia have been used previously to show that there is appreciable water flow through the paracellular pathway, which comprises the TJ and LIS. A homologous series of tritiated dextrans have been used as extracellular probes during fluid transport in Necturus gallbladder and Necturus small intestine. These have shown a net transport in the direction of fluid movement, and the fraction of fluid that must accompany them to account for their net transport can be calculated (Hill & Shachar-Hill, 1993; Shachar-Hill & Hill, 1993). Gallbladder preparations are planar epithelial structures of the ‘forward-facing’ type, where the Na⁺-K⁺-ATPase pump is located on the basolateral membranes and the fluid is transported from the apical to the basal bath in the direction of salt transport. The small intestine is similar in structure, being a sheet, but fluid is transported in both directions during absorption (Hill & Shachar-Hill, 1997). In both of these tissues it is possible to perform bi-directional fluxes of probe molecules under equivalent conditions, a procedure that eliminates all passive diffusional flux components that are equal in both directions, and yields a net flux by subtraction (Hill & Shachar-Hill, 1993).

In a similar study with an excretory system of an invertebrate, the Malphigian tubule of Rhodnius, fluxes of various paracellular probes including trititated dextrans were measured in both directions by perfusion of the outer bath and the lumen of the tubule. Fluid transport at very high rates was elicited with the hormone 5-hydroxytryptamine, and by subtraction, a net flux of probes could be measured (Hernandez et al. 1995).

In glandular systems, bidirectional fluxes cannot be measured and other procedures for demonstrating and separating the convective and unidirectional components of the probe flux have to be used. These are described in detail below.

The S/P ratio versus J_v: water-probe coupling

The dextran S/P ratio of the submandibular gland shows a particular pattern in relation to the volume flow rate. We developed two models to analyse these data: (1) a separate route model that could represent cell water flow and paracellular probe flow, and (2) a coupling model representing a generalized convection of both, although not confining this to simple convection-diffusion.

(1) Let us assume that the overall fluid secretion rate is J_v and the probe flux is purely diffusive and equal to J_diff. As these are independent, then as J_v varies during the course of an experiment, the relative concentration of probe in the secretion S/P will also vary. It will be diluted by an increase in J_v because the flux J_diff must approach an upper limit as J_v→∞ and the concentration difference (P - S) attains a maximum. Eventually the S/P ratio will fall to small values at high J_v. The relationship for a simple combined model is given by:

(4)

and this would be expected for a system in which a probe diffuses through the junction and interspace, while water is driven through the cells by an osmotic difference of salt.

(2) If, however, there is a fraction of the paracellular flow of probe that is coupled to volume transport by a paracellular convective mechanism with a coupling coefficient k, the size of the fraction being J_vPk, then the same reasoning that leads to eqn (4) leads to:

(5)

These situations are shown diagrammatically in Fig. 5. Plots of S/P against the fluid flow rate J_v will not lead to a hyperbolic relationship as before, but to a curve that flattens out at the value k (Fig. 6, paracellular). Curves similar to eqn (5) have been obtained for almost all of the solutes with which the rabbit submandibular system has been tested (Case et al. 1985; Howorth et al. 1987). From the data shown in Fig. 4, it is apparent that the S/P ratio does not fall with increasing flow rates, but levels out, so it is possible to conclude that there is a linked movement of fluid and dextrans. Such results give strong independent support to the model of convective transfer of fluid through the TJ and LIS. It is predicated upon the dextran series traversing the paracellular system.

Figure 5. Two models of water flow in secretion.

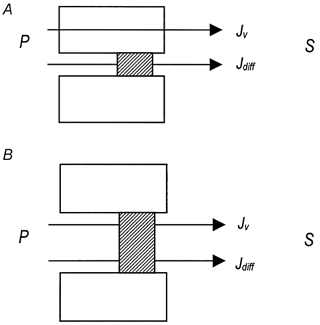
The possible coupling patterns of probe solutes and water across the gland epithelium. A, the probe diffuses through the junction (J_diff) and water moves transcellularly (J_v). B, the probe diffuses through the junction (J_diff) together with a coupled volume fraction (J_vPk).

Figure 6. Behaviour of the S/P ratio in the two models.

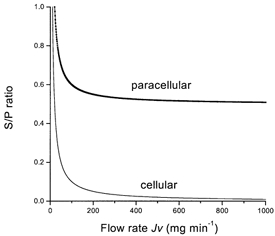
S/P ratios as a function of flow rate. Routes of water flow: cellular, water moves through the cell, as in Fig. 5A; paracellular, a fraction of the water is coupled to paracellular probe flow, as in Fig. 5B.

Subtracting the diffusive component of probe flows

For exocrine glands the backfluxes cannot be measured, for obvious reasons, but the diffusive flux can be subtracted away. The diffusion coefficient D of any one of the probes, if it were in free solution, would be expected to show a dependence upon the molecular radius r_s, known as the Stokes-Einstein relationship:

(6)

where η is the viscosity and R and T have their usual meanings. The diffusive flux J_s through any channel or pathway, per unit concentration difference, is therefore proportional to D and the area of cross-section A, or:

(7)

where K is the overall coefficient of proportionality (ART/6πη). It is an experimental fact that the unidirectional flux across all epithelia tested so far with a range of probes shows a long tail extending to high molecular weights; in Fig. 1 this is evident from a molecular radius of about 0.6 nm (6 Å). This must be a large channel that lets high-molecular weight probes across, presumably in both directions. It has been speculated that this is most probably due to holes in the epithelium made by cell damage (or replacement) and that 1 cell in 6000 with a channel width of 0.4 μm would suffice (Van Os et al. 1979). The tail in exocrine glands, where only a forward flux from perfusate to secretion can be investigated, fits eqn (7) very closely; a hyperbolic relationship indicating that the probes have virtually free diffusion through a very large channel. When it is fitted with a suitable K, as shown in Fig. 1, and subtracted from the total unidirectional flux, the linear relationship between S/P and radius shown in Fig. 7 is obtained. This is perhaps the only way of separating out diffusive and convective flows with a glandular system, but the procedure is reasonable and theoretically uncomplicated, yielding a linear curve in common with convective transfer in other epithelia (Hill & Shachar-Hill, 1993, 1997; Hernandez et al. 1995). Once one has such a flux curve for the probes as a function of radius, this must represent a paracellular ‘convective’ curve free from any diffusional components. Here, ‘convective’ is used as a general term for any non-diffusional movement, which may include schemes involving an active coupled flux of water and the solutes through the TJ and LIS. The linear relationship revealed by the subtraction of the diffusive component of the flux is not compatible with simple convection through a channel described by solutions of the convection-diffusion equation (Hill & Shachar-Hill, 1993).

Figure 7. The convective component of water flow.

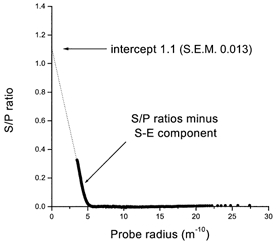
The data of mean S/P ratio as a function of molecular radius after subtraction of the diffusive S-E curve shown in Fig. 1. The S/P ratio intercept is close to 1.0 at the radius of water (0.15 nm, 1.5 Å), and the cut-off radius is close to 0.5 nm (5 Å).

Paracellular volume flow

The linearity of the S/P ratio with radius in Fig. 7 indicates that the intercept was close to 1.0 at the radius of water (0.15 nm, 1.5 Å) and the cut-off radius was close to 0.5 nm (5 Å). This latter value is in keeping with that determined in the rabbit submandibular glandular epithelium (0.4 nm, 4 Å; Howorth et al. 1987) and in rat (0.4-0.45 nm, 4-4.5 Å; Nakahari et al. 1996). The value of the intercept indicates that most of the water is flowing through the TJ and LIS. The fraction flowing transcellularly must be very small indeed, a result anticipated from the measurements of osmotic permeability and calculation of osmotic flow across the cell membranes (Steward et al. 1990).

The extent to which some pseudo-solvent drag can play a part in this result has been shown to be very small for the geometry of the rabbit gland interspace system (Case et al. 1985). Calculations applying drag effects on small dextran moieties in the interspace have been performed in detail for both Necturus gallbladder and intestinal epithelium (Shachar-Hill & Hill, 1993; Hill & Shachar-Hill, 1997), and these show that a pseudo-solvent drag model cannot explain more than a small fraction of the net flows. Application of the theory here shows a similarly small effect with the geometry of the gland epithelium.

Nature of the flow process

The fact that the dextran fluxes are a linear function of radius is interesting from the point of view of the channel geometry. Effects of partitioning into channels and the convective drag experienced by quasi-spherical probes in traversing them, which enters into the selectivity coefficient θ (eqn (1)et seq.), dictate that the channels must be parallel sided (Hill & Shachar-Hill, 1993), which concurs with our structural knowledge that the TJ is in fact a structure between parallel membranes.

It is very doubtful, however, that osmosis can be the driving force for transjunctional fluid flow. It has been commented frequently that the leakiness of junctions to ions and small molecules means that the reflection coefficient of small solutes (σ) for osmosis in these structures must be low. An osmotic flow is given by:

(8)

where the area A is very small (compared to the membrane area), the reflection coefficient is low, the driving force Δπ is very small because the transepithelial differences are of similar magnitude, and the hydraulic conductivity P_f is low because of the length of the TJ. A combination of these factors enables an estimate to be made of the volume flow by osmosis. Assuming reasonable values of these parameters, the flow rate is minute compared to the transepithelial flow rates observed.

A model has been suggested for Necturus gallbladder in which, from the drag factor operating here (a consideration of which is not within the scope of this paper), the flow cannot be simple convection (i.e. the probes cannot be swept through the junctions by a volume flow). Instead, it has been suggested that fluid must be transferred by compartmentalization of the water and solutes together (i.e. by a volume transfer), coupling the two (Hill & Shachar-Hill, 1993). The same considerations would apply to transfer through the salivary TJ. It would suggest that the TJ is an active fluid-transporting organelle and the probable source of most overall epithelial volume secretion. In such a situation it is inevitable that the junctional contribution will be hypotonic (just as the cellular contribution is almost certainly hypertonic); this is because the TJ is selective, as can be seen from Fig. 1 and 7. The fall of S/P with increasing solute radius means that water will pass the TJ faster than any (larger) solute and the junctional transportate will be more dilute than the basolateral bath.

The integration of cellular and paracellular flows

A transcellular route for water in salivary secretion involves the luminal cell membrane, which has a small surface area compared to the basolateral one. The acinar lumen, which has to provide the coupling space, is also small. If the movement of water across the luminal membrane is by osmosis, then its osmotic permeability (P_os) has to be very high indeed, and this was thought to depend upon the presence of a special water channel AQP5. Recently, mice lacking this channel were produced (Ma et al. 1999), and the rate of saliva secretion and its composition were investigated. Only total saliva could be collected and assayed, but as all the major glands have AQP5 in their luminal membrane the role of this channel could be assessed.

The results showed that the salivary flow rate in the AQP5-/- mice was only 40 % of that measured in wild-type mice, and the osmolarity rose to 420 mosmol l⁻¹, which is 125 % hypertonic to normal saliva. In addition, the ratio of Na⁺, K⁺ and Cl⁻ differed from that of wild-type mice, being higher for all three, while protein and amylase remained the same. Thus, it seems that the absence of AQP5 reduced but did not abolish salivary secretion; the salt transport was also affected substantially. The product of volume flow and salt concentration (0.4 × 125 %) was 50 % of that measured in the wild-type mice. These results are difficult to fit into a simple scheme of transcellular osmosis, especially as the removal of AQP5 does not affect lachrymal glands or alveolar re-absorption in the lung (Verkman, 2000). They are explicable, however, in a scheme where there is a reduction in the contribution of hypotonic fluid from the junctional system as a result of AQP5 removal.

The situation can be explained by using a model of paracellular fluid transport in which AQP5 acts primarily to control the tonicity of the secretion without merely being a passive water channel. AQP5 may act as a comparator of tonicity between the cell and the secretion, in which case its location on the luminal membrane is necessary. Its role could be to up-regulate the paracellular junction pump (via a cell signalling system) in response to an increase in the disparity between cytoplasm and acinar transportate. The addition of a junctional secretion, which would be hypotonic to the transcellular hypertonic salt flow (discussed above), would then bring the overall secretion back to near-isotonicity. Removal of AQP5 would remove primary control of isotonicity in this feedback loop such that fluid can still be produced but at a reduced rate and an uncontrolled tonicity. In this model, the cell tonicity closely tracks that of the plasma by partial equilibration over the considerably greater relative area of basolateral membrane - a process that would be aided by other AQPs in that membrane.

In the lachrymal gland there is also AQP5 in the apical membrane, but its removal by knockout in mice has little effect upon the volume secretion rate or tonicity of the tear fluid. A similar removal of AQPs 1, 3 and 4 also has no effect. As a result of this it has been assumed that there can be no involvement of AQP5 (and the other APQs) in the process of fluid secretion in this gland. This apparently adds a level of complexity and arbitrariness to any simple osmotic model of its function, but AQP5 may have a function in controlling the tonicity of the fluid bathing the eye surface as part of a wider feedback loop. It very much depends, a point little discussed here without recourse to a quantitative model, on the set-point to which a junctional transport system is operating without AQP control: it may be near-isotonic in some systems. What it does demonstrate is that the modulation of P_f of the membranes has only a partial effect and that fluid secretion cannot be modelled as a simple osmotic flow without invoking the paracellular route.