Effects of substituting uridine triphosphate for ATP on the crossbridge cycle of rabbit muscle

Abstract

1. Substituting uridine triphosphate (UTP) for ATP as a substrate for rabbit skeletal myosin and actin at 4°C slowed the dissociation of myosin-S1 from actin by threefold, and hydrolysis of the nucleotide by sevenfold, without a decrease in the rates of phosphate or uridine diphosphate dissociation from actomyosin.

2. The same substitution in skinned rabbit psoas fibres at 2–3°C reduced the maximum shortening velocity by 56% and increased the force asymptote of the force-velocity curve relative to force (α/P_o) by 112% without altering the velocity asymptote, β. It also decreased isometric force by 35% and isometric stiffness by 20%, so that the stiffness/force ratio was increased by 23%.

3. Tension transient experiments showed that the stiffness/force increase was associated with a 10% reduction in the amplitude of the rapid, partial (phase 2) recovery relative to the isometric force, and the addition of two new components, one that recovered at a step-size-independent rate of 100 s⁻¹ and another that did not recover following the length change.

4. The increased α/P_o with constant β suggests an internal load, as expected of attached crossbridges detained in their movement. An increased stiffness/force ratio suggests a greater fraction of attached bridges in low-force states, as expected of bridges with unhydrolysed UTP detained in low-force states. Decreased phase 2 recovery suggests the detention of high-force bridges, as expected of slowed actomyosin dissociation by nucleotide.

5. These results suggest that the separation of hydrolysed phosphates from nucleotides occurs early in the attached phase of the crossbridge cycle, near and possibly identical to a transition to a firmly attached, low-force state from an initial state where bridges with hydrolysed nucleotides are easily detached by shortening.

It is now generally accepted that force and shortening in muscle are driven by myosin crossbridges that cyclically attach to actin, pull through a structurally limited range of motion, and detach, with energy provided by the hydrolysis of ATP (Huxley, 1957; Gordon et al. 1966; Huxley & Simmons, 1971; Lymn & Taylor, 1971). It is also generally recognized that the energy extraction requires an orderly crossbridge cycle in which chemical reactions (ATP binding, hydrolysis, and the release of products) alternate with physical transitions (crossbridge attachment, power stroke, and detachment; Huxley, 1980, pp. 93-95; Taylor, 1992). A substantial part of current research in this area is directed at determining the number and order of transitions in the cycle. One way to investigate this sequence is to perturb specific transitions and assess both the mechanical and biochemical responses. In the present study, we have substituted uridine triphosphate (UTP) for ATP and compared the changes in the chemical reaction rates, which were measured with isolated myosin subfragment-1 (S1) and actin, to the changes in the contractile characteristics of skinned muscle fibres. Kinetic studies of substrate hydrolysis by isolated proteins allow alterations of specific transitions to be identified, while the skinned fibre studies show how these alterations affect physical transitions. Together, the two types of study allow us to define the order of reactions and transitions.

UTP was used because preliminary studies, as well as the work of others (Regnier et al. 1998), showed that it produced only moderate changes in force and velocity, leaving sufficient mechanical function to be studied without alteration of techniques. Chemical studies further showed that the main effect of this substitution was substantial slowing of both hydrolysis of the terminal phosphate and acto-myosin dissociation by trinucleotides. These changes could be correlated with the effects of the substitution on the contractile kinetics of the skinned fibres.

Some of the skinned fibre experiments have been presented to the Biophysical Society (Seow & Ford, 1995).

METHODS

Animals

Tissue was obtained from the carcasses of rabbits humanely killed by other investigators using methods recommended by the Panel on Euthanasia of the American Veterinary Medical Association, and under the supervision of the Animal Care and Use Committees sanctioned by the United States Department of Agriculture in the universities of the other investigators.

Isolated protein studies

Protein preparation

Rabbit skeletal actin and myosin were prepared as described previously (White & Taylor, 1976). Subfragment-1 (S1) was prepared from myosin with chymotrypsin by the method of Weeds & Taylor (1975) except that 2 mg lima bean trypsin inhibitor per milligram chymotrypsin (rather than phenylmethylsulphonyl fluoride) was used to inhibit chymotrypsin. The protein was column purified on diethylaminoethyl-52 cellulose. Fractions were pooled that contained a mixture of A1 and A2 light chains. Fluorescent phosphate binding protein was prepared as described previously (Brune et. al. 1994).

ATP and UTP hydrolysis

Steady-state hydrolysis rates were measured colourimetrically (White, 1982). Reaction velocities were determined from at least four time points per actin concentration by the method of initial rates. The data were then fitted to the steady-state kinetic equation using a Neader-Melder, non-linear, least-squares, simplex routine (White et al. 1993).

Stopped-flow measurements of ATP and UTP binding to myosin-S1 (S1) and actomyosin-S1 (acto-S1)

Nucleotides were mixed with S1 or acto-S1 using a Kintek SF-2001 stopped-flow fluorimeter equipped with a micro-stepper motor drive. Excitation light was obtained from a 75 W xenon lamp and a 0.25 m monochromator (Photon Technology). The changes in tryptophan fluorescence associated with nucleotide binding and hydrolysis were measured using excitation at 295 nm and emission within the range 320-380 nm (Corning UG-3 filter). The dissociation of acto-S1 by nucleotides was measured by light scattering at 360 nm. Four 500-point data traces were averaged and the observed rate constants were obtained by fitting single or double exponential equations using the software supplied by Kintek.

Phosphate dissociation

Dissociation rates were measured fluorimetrically in the double-mixing configuration (White et al. 1997), with fluorescent binding protein excited at 430 nm, and recording of emitted light passing through a 450 nm high-pass filter. Myosin-S1 and substrate were mixed, held in a delay-line for 2-5 s, and then mixed with actin in a second mix. The 2-5 s delay was chosen because preliminary experiments showed that this produced the maximum phosphate transient.

All solutions contained 5 μm fluorescent phosphate binding protein and a phosphate ‘mop’ consisting of 0.1 mm 7-methylguanosine and 0.02 units nucleoside phosphorylase (Sigma; White et al. 1997). The syringes and flow-cell of the stopped-flow fluorimeter were incubated overnight (12-18 h) prior to phosphate dissociation experiments, in a solution containing 1 mm 7-methylguanosine and 1 unit ml⁻¹ nucleoside phosphorylase, to remove contaminating phosphate. Buffers used in phosphate dissociation experiments were never allowed to have direct contact with the pH electrodes to avoid phosphate contamination in the buffer standards. Inorganic phosphate levels in these solutions are estimated to be < 0.1 mm.

Data analysis

The original records from the output of the photocells were initially fitted with single or double exponentials to obtain rate constants, and plots of these rate constants (k_obs) against a reactant concentration (C) were fitted with a hyperbolic function of the form:

(1)

where k_sat is the rate at infinite ligand concentration, k₀ is the rate at zero concentration and K_app is the concentration at which the rate constant was half-way between k₀ and k_sat. In general, the quantity of interest is the value of k_sat.

Skinned fibre studies

The methods were identical to those described previously (Seow et al. 1997), except that in the study solutions, UTP was substituted for ATP. Briefly, rabbit psoas fibres were chemically skinned by 6 h immersion in a low-divalent-cation relaxing solution and then stored at -20 °C in 50 % glycerol relaxing solution for later study at 2-3 °C. This low temperature has been used in all of our skinned fibre studies because we had found at the outset that striation patterns were less well maintained at only slightly higher temperatures, 5-7 °C, possibly because they also develop substantially less force. An additional benefit of the lower temperature is that there appears to be less filament compliance (C. Y. Seow & L. E. Ford, unpublished observations) than that reported by others at higher temperatures (Bagni et al. 1990; Higuchi et al. 1995). The temperatures in the isolated protein studies were chosen to closely approximate the skinned fibre conditions.

Fibres were maximally activated for study 9-11 times in an EGTA-buffered calcium-activating solution, with UTP substituted for ATP in alternate activations. Two types of mechanical studies were carried out on each fibre. Tension transients were always studied in pairs of activations, with one of the activations being in ATP and the other in UTP. Force-velocity studies were done in the same fibres after one or two pairs of activations used to define the transient tension responses. An odd number of activations was always studied in the force-velocity determinations, with the ‘reference’, ATP solution always used in the first and last activation, so that the UTP, ‘test’ contractions were bracketed by ATP, ‘reference’ contractions.

During activation, the fibres were subjected to a rapid ramp release and restretch every 2 s to maintain sarcomere homogeneity (Brenner, 1983). After full activation was achieved, nine experimental steps temporarily replaced the ramp and restretch on the same 2 s schedule. The nine steps imposed during activation were either releases to nine different isotonic loads, used to define force-velocity properties, or nine sarcomere length steps, used to define tension transients. At the end of recording following either type of step, the muscle was shortened suddenly, both to unload the transducer and define the zero force level and to allow a period of rapid shortening before restretching the muscle to its initial, isometric length.

The fibres were usually activated for 20-30 s before the study steps were applied. This delay, which was required to make adjustments to the servo apparatus, ensured that a complete exchange of nucleotide substrate occurred; any of the previous nucleotide bound to myosin would be hydrolysed and replaced during the 10-15 ramp releases and restretches imposed prior to the beginning of the study steps.

Solutions

Solution composition was calculated using a computer program kindly given to us by Dr R. E. Godt, using stability constants compiled by Godt (1974), Godt & Maughan (1988), Godt & Nosek (1991) and Andrews et al. (1991). All solutions contained either 5 mm MgATP or 5 mm MgUTP, 1 mm free Mg²⁺, 20 mm creatine phosphate, 10 mm imidazole, 56 g l⁻¹ dextran T-70 (to maintain physiological lattice spacing; Goldman, 1987; Ford et al. 1991) and sufficient potassium propionate to yield an ionic strength of 210 mm. Solutions were buffered to pH 7.0 at the temperature used (2-3 °C). The activating solution contained calcium buffered with 5 mm EGTA to pCa 4.5. A rinse solution containing 0.1 mm EGTA, and the nucleotide for the next activation (ATP or UTP) was used both to lower the EGTA concentration and to change nucleotide immediately before activation. Fibres were exposed to this rinse solution for 15-20 s before each activation.

Protocols

The nine isotonic loads used to define the force-velocity properties progressed from the lowest to the highest in the first five steps and then back to the second lowest step in the next four, and the relative loads were approximately evenly spaced, with a step occurring in nearly every 10 % increment in relative load (Seow & Ford, 1992).

Adjustment of the step sizes used to define tension transients required advance knowledge of the sarcomere stiffness of the preparation because the fibre cannot be driven to generate negative force. If a fibre is driven to shorten faster than its maximum velocity (V_max), or beyond the length where zero force is generated, the clips will come loose from their hooks, and it is possible that the fibre will buckle at the junction with the clip. If the motor is servo-controlled from the sarcomere length signal under these circumstances, it will immediately shorten to the end of its range as it tries to force the muscle to shorten faster than its V_max, and it is liable to damage both itself and the fibre. To avoid this potentially catastrophic event, the muscle was never shortened beyond the point where zero force in the fibre was approached. The largest fast release that would bring the force near to zero was first assessed to determine the largest size of release that could be applied safely. Steps were made in increments one-quarter this size. The first two steps were stretches of 2 and 1 of these increments. The next four were releases of 1-4 of these increments. These first six steps were imposed as rapidly as the apparatus would allow, 200-250 μs. The last three were 6, 8, and 10 of these increments, and they were imposed as ramps lasting ∼5 ms to avoid making the muscle go slack.

Data analysis

Individual force-velocity points obtained from multiple steps in several activations were pooled for each condition, UTP or ATP, and fitted by a Newton-Raphson least-squares method to a hyperbola (Hill, 1938). The parameters derived from these fits were V_max, the velocity asymptote (β), and the ratio of the force asymptote, α, to the zero-velocity intercept of the fitted curve, P_o (i.e. α/P_o). The value of P_o was generally slightly different from the isometric force measured immediately before the isotonic release, called T_pre. The significance of changes in the parameters of the isotonic contractions was assessed from Student's paired t test of results obtained from the individual fibres.

The transient tension responses to sudden changes of sarcomere length were analysed in two ways. In an initial analysis, responses to the same size of step under the two conditions (UTP or ATP) were scaled to make their isometric forces coincide, and then the difference between the two records was assessed. The insights gained from these difference records were then used to develop mathematical descriptions of the several components of the responses to obtain complete descriptions of the individual transients (Ford et al. 1977; Seow et al. 1997). The tension transients were also used to estimate the stiffness of the fibres under the two conditions (UTP or ATP) by comparing the slopes of the extreme tension (T₁) curves. The value of T₁ reached immediately after the length step was divided by the step size to obtain a stiffness value. This was done for the two stretches and four fast releases obtained in a single activation; the three slow releases with large step sizes were not included in the stiffness measurement. An averaged value of stiffness from the six steps was used to compare the two conditions.

RESULTS

The elements of the crossbridge cycle required to explain the present data are shown in Fig. 1. The reactions studied in the biochemical studies of isolated protein kinetics are numbered to facilitate description of those experiments.

Figure 1. Schematic representation of the crossbridge cycle.

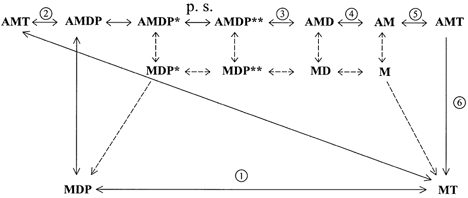
A, actin; M, myosin; T, nucleotide triphosphate; D, nucleotide diphosphate; P, inorganic phosphate. Asterisks next to some complexes reflect chemically similar but energetically different complexes. AMDP is actomyosin with hydrolysed nucleotide for which there has been no separation of the phosphate and dinucleotide moities. AMDP*, the same complex with separation of the phosphate from the dinucleotide. AMDP**, the same complex after the bridge has undergone the power stroke (p.s.). Circled numbers indicate transitions assessed in biochemical experiments. The top row represents states in which myosin is attached to actin. The bottom row represents states of myosin detached from actin. The middle row represents states of myosin detached from the corresponding attached state in the upper row.

Isolated protein kinetics

Stopped-flow fluorescence, stopped-flow light scattering and steady-state ATPase measurements were used to assess changes in the rate constants of critical steps in the actomyosin nucleotide hydrolysis mechanism when UTP was substituted for ATP. The rate and dissociation constants measured with the two substrates are listed in Table 1.

Table 1.

Reaction rates (k) or dissociation constant (K) in the presence of ATP and uridine triphosphate (UTP)

Transition constant	No. in Fig. 1	ATP	UTP
Reactions of myosin
kMT→MDP (s−1)	1	25	3.5
Reactions of actomyosin
kAMT→AMDP (s−1)	2	0.44	0.06
kAMDP→AMD+ P (s−1)	3	23	40
KAMD→AM+ D (μM)	4	50–100	>2000
kAMD→AM+ D (s−1)	4	∼500	>2000 (est)
kAM + T→AMT (M−1 s−1)	5	9 × 105	1.1 × 105
kAMT→MT (s−1)	6	∼2000	760

Nucleotide hydrolysis by S1 in the absence of actin

The time course of the increase of tryptophan fluorescence of myosin was used to measure the rate of the hydrolysis step for ATP and UTP in the absence of actin (Taylor, 1977; reaction 1 in Fig. 1). At saturating substrate concentrations and 4 °C, the substitution produced a sevenfold decrease in rate, from 25 s⁻¹ in the presence of ATP to 3.5 s⁻¹ in the presence of UTP (Fig. 2).

Figure 2. Substrate concentration dependence of rates of nucleotide binding and hydrolysis by myosin-S1.

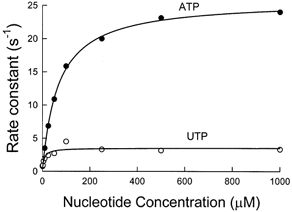
Hydrolysis was measured by tryptophan fluorescence, λ_excitation= 295 nm and λ_emission= 330-380 nm. Rabbit skeletal myosin-S1 was mixed with substrate in a stopped-flow fluorimeter with a mixing volume ratio of 2:5 myosin-S1:UTP (○) or ATP (•). The plotted rate constants were obtained by fitting a single exponential function to the original fluorescence records (not shown). The curves fitted to the data are hyperbolae defined by k_sat= 25 ± 1.1 s⁻¹ (mean ±s.d.) and K_app= 66.7 ± 3.1 μm for ATP and k_sat= 3.5 s⁻¹ and K_app= 7.2 ± 0.3 μm for UTP. Experimental conditions in the flow cell were 1 μm myosin-S1, 150 mm KCl, 5 mm Mops, 2 mm MgCl₂, pH 7, the indicated concentration of UTP or ATP, and 4 °C.

Phosphate dissociation

The rate of phosphate release from acto-S1-UDP-P was measured from the rate of fluorescence enhancement after mixing a steady-state mixture of myosin (M)-UTP and M-UDP-P with actin. This reaction was found to be biphasic, and the data were best fitted by two exponentials (Fig. 3A). The dependence of the two rates upon actin concentration is shown in Fig. 3B. At saturating concentrations, the fast component is a measure of phosphate dissociation from acto-S1-UDP-P (reaction 3 in Fig. 1) The observed maximum rate of 40 s⁻¹ is at least as fast as that previously measured with ATP as the substrate, 23 s⁻¹ (White et al. 1997).

Figure 3. Double-mixing stopped-flow measurement of phosphate dissociation from AM-UTP.

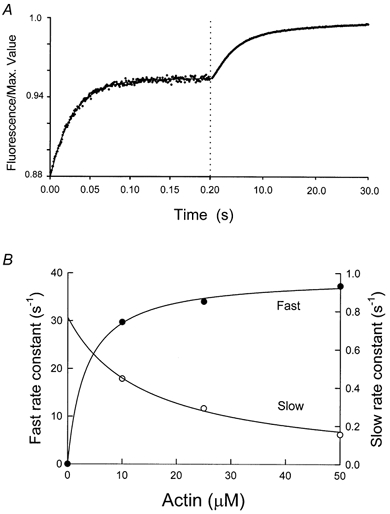
Myosin-S1 (4.5 μm) was mixed with 2.25 μm UTP and held in a delay line for 2 s before mixing with actin. Volume proportions in the final cell were myosin-S1 2, UTP 2, and actin 5. Final conditions in the flow cell were: 4 °C, 1 μm myosin-S1, 0.5 μm UTP, the indicated concentration of actin, 5 mm Mops, 2 mm MgCl₂, 5 μm PBP, 0.02 units ml⁻¹ nucleoside phosphorylase, 0.1 mm MEG, pH 7, λ_excitation= 430 nm and λ_emission > 450 nm. A, typical fluorescence record with the first 0.2 s plotted on a × 125 expanded time scale to resolve the rapid early change. As shown, the curve was fitted with two exponentials and the rate constants are plotted in B. The curves fitted in B are hyperbolae defined by k_sat= 40 ± 1 s⁻¹ and K_app= 4 ± 0.7 μm for the fast rate and k_sat= 0.04 ± 0.7 s⁻¹, K_app= 16.5 ± 0.7 μm for the slow rate.

The curve fitted to the slow component of fluorescence enhancement in Fig. 3B extrapolated to 0.04 s⁻¹ at infinite actin. This value can provide an upper limit for the attached rate of hydrolysis (reaction 2 in Fig. 1; White et al. 1997). It can also give a reliable measurement of the value if it can be demonstrated that all of the UTP is bound in the first mixing step and the rate of UTP dissociation from actomyosin is less than the observed rate obtained in this experiment. However, these criteria could not be met for UTP due to the slower second-order rate constants for UTP binding to S1 and acto-S1. The rate of the hydrolysis step on the attached bridge can, however, be estimated from the steady-state rate at low myosin and saturating actin concentrations (White et al. 1993). In these experiments, the actin dependence of steady-state UTP hydrolysis reached a maximum rate of 0.06 s⁻¹ at saturating actin concentrations (data not shown). The rate obtained at saturating actin concentrations is in reasonable agreement with the 0.04 estimated in Fig. 3, and approximately sevenfold slower than the 0.44 s⁻¹ measured previously with ATP (White et al. 1997).

Dissociation of S1 from actin by nucleotide

The dependence of the observed rate of dissociation of acto-S1 on nucleotide concentration, indicating the second-order forward rate constant for reaction 5 in Fig. 1, was measured by light scattering at 4 °C, as shown in Fig. 4. The observed rate was linearly dependent on ATP concentration up to a rate of 450 s⁻¹ and this rate was eightfold faster than the 1.1 × 10⁵ second-order dissociation rate measured for UTP (Fig. 4), suggesting that the second-order rate constant for ATP was 9 × 10⁵.

Figure 4. Substrate concentration dependence of the rates of nucleotide binding to actomyosin-S1 and dissociation of S1 from actin, measured by light scattering.

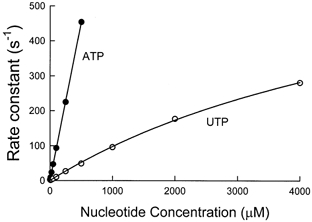
Experimental conditions in the flow cell were 1.5 μm actin, 1 μm myosin-S1, 150 mm KCl, 5 mm Mops, 2 mm MgCl₂, pH 7, the indicated concentration of ATP (•) or UTP (○) and 4 °C. λ_excitation= 360 nm and λ_emission= 360 nm. The curve fitted through the UTP data is a hyperbola defined by k_sat= 760 ± 121 s⁻¹ and K_app= 6.8 ± 0.8 mm. ATP data were fitted by a straight line with a slope of 9 (± 0.4) × 10⁵m⁻¹ s⁻¹.

The maximum rate at saturating nucleotide concentrations, indicating dissociation of actin from myosin (reaction 6 in Fig. 1), was estimated to be at least threefold slower with UTP than the 2000 s⁻¹ value measured previously with ATP. Both the second-order and maximum rates for UTP are similar to those measured using CTP and GTP (White et al. 1993).

UDP dissociation from acto-S1

ADP binding to acto-S1 was measured by the inhibition of the rate of dissociation of acto-S1 by ATP (Siemankowski et al. 1985). Using UTP to compete with ATP showed that there was no detectable binding of 2 mm UDP to actomyosin-S1 at 4 °C and the dissociation constant is therefore > 2 mm. The affinity of ADP for acto-S1 under similar conditions is 50-100 μm (20- to 40-fold greater than for UTP) and the rate of ADP dissociation from acto-S1-ADP is ∼500 s⁻¹ (Siemankowski & White, 1984).

Since the second-order rate constant for UTP binding to acto-S1 is approximately eightfold slower than for ATP, while the dissociation constant is 20-40 times higher, the rate of UDP dissociation (k_dissoc= K_dissoc×k_assoc) from actomyosin is unlikely to be slower than the rate of ADP dissociation, and could be several times more rapid, as indicated in Table 1.

Skinned fibre mechanics

Steady-state changes

Force-velocity data from each fibre were fitted with hyperbolae. The intercepts of the curves with the axes yielded the values of V_max and extrapolated isometric force (P_o), which was slightly different from the isometric force measured immediately before release to the isotonic loads (T_pre). The force and velocity asymptotes, α and β, which were also determined by the fitting procedure, were used to assess changes in contractile kinetics. The absolute reference values (±s.d.) obtained for ATP, and the values for UTP relative to those for ATP (±s.e.m.) are listed in Table 2. The reference values were very similar to those of our previous experiments carried out under similar condtions (Ford et al. 1991; Seow & Ford, 1991, 1992, 1993, 1997; Seow et al. 1997). As indicated, UTP substitution decreased V_max by 56 % and increased α/P_o by 212 %, without a change in β. It also decreased isometric force by 35 % and stiffness by 20 %, so that there was a 23 % increase in the force/stiffness ratio.

Table 2.

Contractile parameters of skinned fibres

	Tpre (kPa)	Po/Tpre	Vmax (μm (h.s.)−1s−1)	β (μm (h.s.)−1 s−1)	α/Po	Stiffness (Tpre h.s. nm−1)	Power (mW g−1)
ATP	189 ± 39	0.96 ± 0.016	1.29 ± 0.18	0.187 ± 0.014	0.147 ± 0.016	0.275 ± 0.028	16.2 ± 4.0
UTP/ATP	0.65 ± 0.07	0.91 ± 0.013	0.44 ± 0.062	0.925 ± 0.041	2.12 ± 0.080	0.798 ± 0.057	0.403 ± 0.10

The values in the upper row are absolute values ±s.d. in the presence of ATP in the units given. The values in the lower row are the ratios of the values in UTP to those in ATP ±s.e.m. h.s., half-sarcomere. Number of fibres = 12.

Tension transients

The transient tension responses to different sizes of step changes of sarcomere length (Fig. 5A) had four characteristic phases (Huxley & Simmons, 1973): phase 1 is an immediate force change in the direction of the step and is attributed to the instantaneous sarcomere stiffness; phase 2 is a rapid recovery to an intermediate level, frequently called the T₂ plateau, but which in many cases is better represented by a slightly sloped line, designated T_a(t); phase 3 is a pause or inflection in force recovery to which the T_a(t) line is fitted; and phase 4 is a slow recovery to the steady isometric level.

Figure 5. Transient tension responses to sudden changes of sarcomere length.

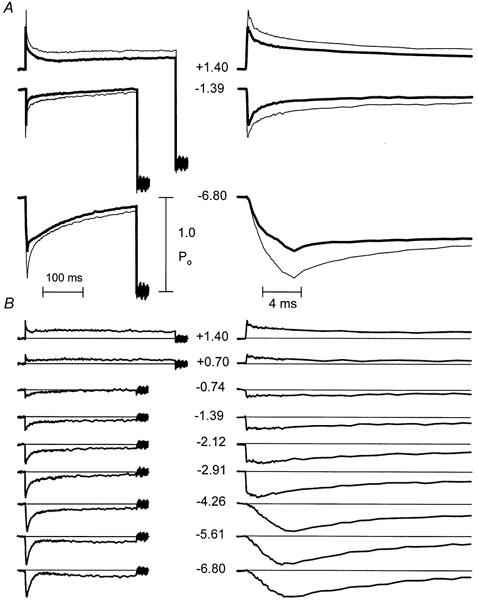
Records are the signal averages of records from 12 fibres. The size of the sarcomere-length step (in nanometres per half-sarcomere) is indicated by the numbers between traces (+ indicates stretch, - indicates release). Panels on the left display records on a slow time base, to show recording from the isometric period before the step to a period after the muscle was shortened rapidly to make the muscle go slack and zero the transducer. Note that stretches lasted longer than releases. Records on the right are displayed on a × 25 expanded time base to resolve the rapid events associated with the steps. A, representative pairs of records for same size steps in ATP (thick traces showing less deviation during the step) and UTP (thin traces) scaled to make isometric forces coincide and superimpose. B, difference between scaled pairs of records (UTP - ATP).

Difference in scaled records

For each size of step, the averaged force records for 12 fibres, obtained in the presence of UTP, have been scaled up to make the isometric forces coincide (Fig. 5A). The left-hand panels are shown on a slow time base to illustrate the entire step, while the right-hand panels are shown on a 25-times faster time base, to resolve the events associated with the steps. The upper panels (Fig. 5A) show selected paired records, while the lower panels show all of the difference records (test - reference). The numbers between the records indicate the step sizes in nanometres per half-sarcomere. As indicated by the difference records for several representative length steps (Fig. 5B), substitution of UTP altered the responses in a way that could be separated into two components that increased instantaneous relative stiffness (i.e. in the presence of UTP, the change in force during the step was larger in proportion to the isometric force). One of these components did not change after the step, and the other recovered to the level of the first component (i.e. its amplitude returned to zero) with a mono-exponential, step-size-independent rate constant of 100 s⁻¹ following the step.

It should be mentioned that the substitution produced a third effect that will not be analysed here. This was a slightly greater recovery of force during late phase 3 and early phase 4 in the largest steps made in UTP, such that the difference was slightly less than the final, steady difference level. This slight overshoot of recovery is just appreciable in the second largest release and might be considered to be within the limits of noise, except that it was very definitely present in the largest release.

Mathematical description

To quantify these changes further, the early parts of the tension transient records were fitted with a mathematical description derived from Ford et al. (1977) and Seow et al. (1997). As done previously (Seow et al. 1997), only the releases were fitted, mainly because a phase 3 inflection was not found in the stretch records, but also because an earlier study of frog fibres showed that the responses to stretches varied over time (Ford et al. 1997).

The fitting procedure was the most conservative that would give a good description; that is, the minimum number of components was used to fit the ATP reference records and then the minimum number of changes was made to fit the UTP test records. First, the phase 3 inflection was fitted with a straight line, T_a(t), with an intercept, designated T_a(0), at the time of the mid-point of the step (the fitted T_a(t) line is superimposed on the two records used to illustrate the fitting procedure in Fig. 6C). The force response up to the end of phase 3 was fitted by assuming that it consisted of several components, each of which was represented as causing force to deviate from the isometric value and then recover either towards the T_a(t) line or towards its isometric level. Thus, the response of each ith component was defined by its stiffness (S_i), its recovery rate constant (R_i), and the level to which it recovered. The equation defining the force response of each component (T_i) was:

(2)

where y is the deviation from the isometric length and A_i is the fraction of the response contributed by the component to the T_a(t) level.

Figure 6. Fits to the release force records, ATP on the left, UTP on the right.

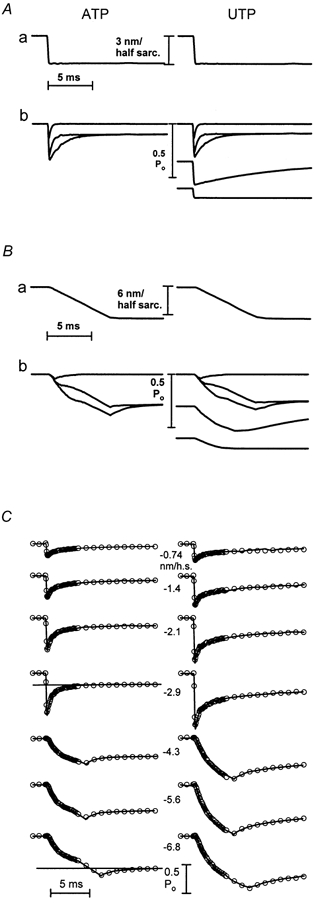
A, the sarcomere length record (a), and the responses of the individual force components (b), for the largest fast release. B, the sarcomere length record (a), and the responses of the individual force components (b), for the largest slowed release. C, sum of the individual force responses (continuous curve) superimposed on the digitized data points, represented by circles with radii equivalent to 4 % of isometric force. The lines superimposed on the fourth and seventh ATP records in C are the T_a(t) lines fitted to the phase 3 inflection of the representative records shown in A and B.

The value of A_i was assumed to be constant for all times and all steps, and for the present experiments, this value was only used to define the T_a(t) level towards which the two slower components of the tension transient recovered. The values of T_a(0), T_a(t) slope, S_i and R_i were assumed to vary with y. The first two of these were assessed by fitting the T_a(t) line to the phase 3 portion of the record (see Fig. 6C for examples). Values during the steps were determined by interpolation between values measured after the steps ended. The value of T_a(0) was assumed to be the same for both ATP and UTP. Small changes in the slope of the T_a(t) line were used to accommodate the slight over-recovery of force that occurred during phase 3 following the largest releases in the presence of UTP, so that the curves fitted this part of the force record.

The value of R_i was determined by fitting exponentials to the records after the step had ended. The value at each instantaneous length during the step was obtained by interpolation among the values obtained for the fixed lengths after the steps had ended. The value of S_i was determined by fitting the amplitudes of the responses.

The responses during reference activations in ATP could be described accurately with three components. As discussed below, and in keeping with our previous analysis (Seow et al. 1997), the two slowest components were assumed to be due to those attached crossbridges that are free to go through the power stroke during and immediately following the step. These components were assumed to have linear and identical stiffness and to have the same values of A_i. They differed from each other only in their time constants. The fastest component was assumed to be due to bridges attached in low-force states and detached rapidly by the steps. This component was assumed to have non-linear stiffness and to recover back to the isometric force level.

Fitting the responses in UTP required that the amplitudes of the two slower components of the response relative to the isometric force be reduced by 10 % and that two new components be added. Both of the new components had non-linear stiffness. One did not relax at all (i.e. it maintained constant force at each length), and the other relaxed to zero with a mono-exponential time constant that did not vary with step size.

The responses of the several components, together with their sum superimposed on the experimental record, are shown in Fig. 6: Fig. 6A shows the responses of the separate components to the largest of the rapid releases; Fig. 6B shows the responses of the same components to the largest slowed release; Fig. 6C shows the sums of the several components (continuous curves) superimposed on the digitized data points (open circles) for all six releases. The non-linear responses during the slowed steps greatly constrain the fits, and require that the individual components relax at different times and in different ways during the step. The goodness of fit can be judged from the radii of the open circles, which are equivalent to 4 % of the isometric force.

The instantaneous extension-force properties for the several components are shown in Fig. 7, and the time constants for recovery are shown in Fig. 8. Test values in UTP are plotted as filled symbols and reference values in ATP, or values that were the same for both conditions, are plotted as open symbols. The force changes in Fig. 7 are plotted as beginning either from the isometric force or from the zero-force level, reflecting the beliefs, discussed below, that some are due to force-generating bridges and that others are due to low-force, attached bridges that do not undergo the power stroke. The extension-force properties of the two slowest components of the transient were found to be the same, and thus are superimposed as the circles in Fig. 7. These had to be reduced by 10 % each (superimposed filled circles in Fig. 7) to match the phase 2 recovery in the UTP. The extension-force properties of the fastest component, which had the same relative amplitude in both ATP and UTP (open squares) are plotted as beginning from zero force, in the belief that this component is due to the detachment of low-force bridges (Seow et al. 1997). The two components added by UTP (filled triangles and diamonds) are also plotted as beginning from the zero-force baseline, as expected of bridges that are detained in low-force states and detached by the shortening. As discussed below, however, the complete identity of this component is not resolved by these experiments.

Figure 7. Extension-force properties for various components of the response.

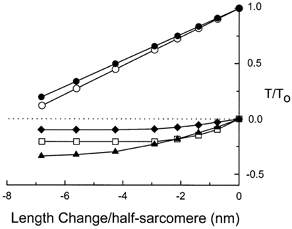
Values of the components present in the reference (ATP) records or in both the test and reference records are plotted as open symbols. Values for test (UTP) records only are filled symbols. The circles represent the sum of the two slower components of the phase 2 recovery. The two components contributed equally to the sum. The amplitude of this component was reduced by 10 % to fit the test record. Squares represent the fastest relaxing component, the amplitude of which was not altered by UTP substitution. Triangles represent the slowly relaxing component added by UTP. Diamonds represent the non-relaxing component added by UTP.

Figure 8. Rate constants for the components that relaxed.

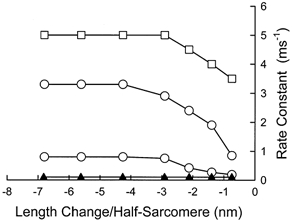
The open symbols represent values that were the same in ATP and UTP. The filled symbols represent the rate constant of the slowly relaxing component added by UTP.

The same symbol convention used for the force- extension properties is also used in Fig. 8 for the exponential time constants of the components that relaxed. As indicated by the open symbols there, the time constants for three components found under reference conditions were the same in the presence of UTP. The time constants for all three of these components reached a maximum at step sizes of about 4 nm per half-sarcomere, and their recovery rates were substantially faster than that of the relaxing component added by UTP substitution.

DISCUSSION

Based in part on unpublished observations, Huxley (1980, pp. 93-95) proposed that crossbridges pass through a cycle in which chemical reactions (substrate binding, hydrolysis and release) alternate with physical transitions (bridge attachment, power stroke and detachment). A variant of such a cycle is shown in Fig. 1, which attempts to reconcile a schism between biochemists and physiologists. Physiologists frequently draw their schemes as including only the relevant states (e.g. Huxley, 1980, Fig. 16, p. 94). In contrast, biochemists assert, correctly, that every attached state must have a corresponding detached state (e.g. Hill, 1974). The problem with such complete schemes is that they are very complex, particularly when an effort is made to describe the entire cycle. Figure 1 includes these largely unoccupied detached states, but in a separate row connected by dotted lines to indicate that this pathway is not usually followed. It might be expected, however, that these states would be occupied under some infrequent conditions, as for example when rapid length changes forcibly detach bridges in the middle of the attached phase of the cycle. The possible pathways taken by these forcibly detached bridges are indicated by the interrupted arrows in Fig. 1, showing that they might either re-attach unaltered to actin sites further along the filaments or undergo chemical changes that bring them to the normal detached state. An example of rapid re-attachment is described under the heading of ‘skidding bridges’, below.

Correlation between mechanical and biochemical studies

The biochemical studies described here show that UTP substitution significantly slowed two categories of reactions. Acto-S1 dissociation by nucleotide was slowed because UTP binding and dissociation of the complex were eight- and threefold slower, respectively. The observed rate of dissociation of acto-S1 by ATP was linear to a rate of 450 s⁻¹, and this rate was eightfold faster than the second-order dissociation rate in UTP. The true maximum rate, which would be a measure of myosin- ATP dissociation from actin, was too rapid to be measured and was likely to have been > 2000 s⁻¹, at least threefold more rapid than the 760 s⁻¹, obtained with UTP (k_max in Fig. 3). In addition, UTP hydrolysis was seven times slower, both in the absence of actin (Fig. 2) and when attached to actin (steady-state experiments). In contrast, the rates of dissociation of hydrolysis products from acto-S1-UDP-P were equal to or greater than from acto-S1-ADP-P (fast process in Fig. 3). The two categories of slowed reactions can be correlated with transitions identified from changes in the mechanical responses of skinned fibres using the scheme shown in Fig. 1.

Low-force bridges with unhydrolysed nucleotide

The 20 % reduction in sarcomere stiffness (Table 2) produced by UTP substitution indicates a decreased number of attached bridges. The greater decrease in force than stiffness, producing a decreased force/stiffness ratio, indicates a reduced force per bridge, and therefore a lower fraction of attached bridges in high-force states (Table 2). Together, these findings suggest that bridges are detained in low-force states where they increase stiffness without contributing to force and where they decrease the number of attached bridges by slowing progress to other parts of the attached phase of the cycle. Slowing of the transitions numbered 1 and 2 in Fig. 1 will increase the fraction of attached bridges with unhydrolysed nucleotide in low-force states. The sevenfold reduction in the rate of the hydrolysis step on the detached bridge (transition 1) is likely to increase the fraction of bridges that initially attach to actin with unhydrolysed nucleotide. This fraction is further increased by the sevenfold reduction in the rate of the hydrolysis step on the attached bridge (transition 2).

In addition to producing force and stiffness changes, UTP substitution produced an additional component of the transient that had non-linear compliance, and relaxed with a step-size-independent rate constant of 100 s⁻¹. It seems very likely that this component is attributable to the detained bridges that are detached by shortening. The apparent non-linearity of the force-extension properties of this component would be caused by detachment, even if the bridges themselves have linear stiffness; once detached, bridges no longer contribute to stiffness, so that the stiffness decreases progressively with larger releases. The step-size independence of the rate constant is likely to be due to its being the rate constant for detachment over the limited range of a few nanometres of shortening, with bridges that are shortened more being torn off much more rapidly.

In the presence of ATP, there was very little, if any, component of the transient responses that relaxed at a rate of 100 s⁻¹, suggesting that very few ATP bridges attach with unhydrolysed nucleotide.

The finding of an increased α/P_o ratio in the force- velocity relationship without a change in β (Table 1) suggests that the velocity slowing produced by UTP was due to an internal load (Seow & Ford, 1993). A very likely source of this internal load is the bridges detained by unhydrolysed nucleotide.

Other low-force states

In both ATP and UTP, there was a very rapid component of the transient that relaxed with a rate constant of 3-5 ms⁻¹, which had non-linear stiffness and amplitude proportional to force. In previous experiments with ATP as the substrate, where initially attached crossbridges would have almost all nucleotide in a hydrolysed state, we have associated this component with a low-force state that is detached rapidly by shortening but not by stretch (Seow & Ford, 1993; Seow et al. 1997). Regnier et al. (1995) and Morris et al. (2001) have postulated a similar weak-binding to strong-binding transition of low-force bridges with hydrolysed nucleotide. This component has the properties of the initial attachment state first proposed by Huxley (1973) to account for A. V. Hill's (1964) experiments showing that the extra heat of shortening declines at high shortening velocities. The non-linear stiffness of this state suggests that it is different from those in which the bridges relax by passing through the power stroke. Thus, our previous and present mechanical experiments suggest at least two low-force attached states for bridges with hydrolysed nucleotide, one easily detached by shortening and one that relaxes by passing through the power stroke. In Fig. 1, the transition from the first to the second would occur near separation of the hydrolysed products: AMDP→AMDP*. Two aspects of the present experiments allow the interpretation that the first of these attached states is occupied by bridges with hydrolysed nucleotide bound. First, bridges with unhydrolysed nucleotide produce the new state, from which they detach with a time constant of 100 s⁻¹. The absence of a detectable component with this relaxation rate in ATP suggests that there is very little unhydrolysed ATP bound to attached bridges. Second, the relative amplitude of the very rapid component is unchanged, suggesting that it is a property of bridges with hydrolysed nucleotide that react normally to a quick release. Thus, it appears to be a state with hydrolysed nucleotide separate from the state that relaxes by moving through the power stroke.

The finding of a transition from a loosely to a firmly attached low-force state very near a point in the cycle where separation of the reaction products occurs suggests that the hydrolysed reaction products help to form bonds that strengthen the attachment of low-force bridges in a way that allows the power stroke to occur. A similar conclusion was reached by Regnier et al. (1995) and by Morris et al. (2001). Another interesting feature of the transition from unhydrolysed to hydrolysed nucleotide, is that the bridges move from a state where they are more resistant to shortening to one where they detach rapidly following shortening.

High-force bridges

The reduced ratio of phase 2 amplitude to isometric force caused by UTP substitution suggests that bridges were also detained in high-force states after they had undergone the power stroke, as would be caused by slowing of the transitions labelled 4-6 in Fig. 1. Such detained bridges increase force but do not contribute to phase 2 force recovery following releases. They may also contribute to the internal load that reduces velocity when shortening is sufficiently rapid to bring them to negative force positions before they detach. These considerations lead to an interesting conclusion when correlated with the rates in Table 1.

Table 1 shows that the slowing of transitions that might be invoked to explain the detention of bridges in high-force states are, by far, the fastest observed in the isolated protein experiments. They are so fast that if the reactions proceeded at even a modest fraction of these rates in the intact muscle, there would be very few high-force bridges and almost no isometric force. One obvious and likely explanation of this apparent disparity is that one or more of these reactions is strongly strain dependent, as proposed in the original crossbridge model (Huxley, 1957). The present experiments cannot distinguish which of these reactions possess the strain dependence needed to account for the apparent increase in the relative fraction of attached bridges in high-force states. The observation that UTP substitution increased dinucleotide dissociation (reaction 4) suggests that bridges were detained in later states, such as the AM (rigor) state, but in the absence of specific data on strain dependence, this conclusion cannot be made. Furthermore, we have shown previously that elevated ADP concentrations, which would be expected to slow reaction 4, increase the force out of proportion to the amplitude of the phase 2 transient (Seow & Ford, 1997) in a manner very similar to that caused by UTP substitution.

Bridges that contribute to phase 2 force recovery

In their description of the tension transients, Huxley & Simmons (1971) postulated that the speed of phase 2 recovery is dependent upon the energy stored in the bridges as the result of ATP hydrolysis, and the activation energy required for the bridges to go between two attached states is separated by several nanometres in the axial direction. Since this axial movement in the shortening directions stretches a compliant element somewhere in the bridge, the activation energy required for this movement includes the potential energy stored in the bridge compliance as the result of the movement. It is the decrease in energy stored in the bridge with greater shortening steps that accounts for the higher speed of phase 2 following these steps. Since neither the bridge stiffness nor the energy available from substrate hydrolysis are expected to be changed by nucleotide substitution, the speed of phase 2 recovery would not be expected to change, as was found in the present study. Furthermore, later experiments (Ford et al. 1977) showed that the phase 2 recovery was adequately described by assuming that the bridges had linear stiffness, as found here. The appearance of non-linearity was due largely, if not entirely, to the more rapid recovery force following larger releases truncating the force response during the step. In the present experiments, much of the overall non-linearity of the sarcomere stiffness is explained by this same mechanism, but some is also due to the detachment of initially attached bridges with hydrolysed nucleotide.

In their original description, Huxley & Simmons (1971) speculated that bridges undergo at least two power strokes during a cycle in which a single ATP molecule is hydrolysed. This speculation was derived from the consideration that the energy of the single power stroke was substantially less than half that available from ATP. The two components with linear stiffness and equal amplitude that contribute to phase 2 recovery in the present experiments could be explained by there being two separate power strokes. A deficiency of the scheme shown in Fig. 1 is that it does not include these separate steps, and the reason for the omission is a lack of knowledge of how they occur. Huxley (1980, pp. 93-95) has postulated that the two power strokes occur in series during a single cycle of attachment and detachment, with phosphate release occurring between them. In contrast, the more recent work of Lombardi et al. (1992), as well as our own work (Seow & Ford, 1994), suggests that crossbridges detach between power strokes, such that there is more than one cycle of attachment and detachment during a single cycle of nucleotide hydrolysis. But at present, there is no knowledge of how these separate power strokes are related to the chemical reactions.

Phosphate release

This release is drawn on Fig. 1 as occurring after the power stroke, in keeping with the interpretations of Fortune et al. (1991), Kawai & Halvorson (1991) and Dantzig et al. (1992). While we have some reservations about this interpretation, we adopt the scheme in Fig. 1 because it provides a convenient way of showing cleavage of the terminal phosphate bond as a transition that is distinct from dissociation of phosphate from the bridge.

A second reason for placing phosphate release after the power stroke is that we believe that there must be at least one transition between the initial high-force state and the release of dinucleotide, and it was economical to include this extra state as the phosphate release. Our belief is derived, in part, from our experience with a program for producing a mathematical description of the force generated by various models of the crossbridge cycle (Slawnych et al. 1994). Our experiments with decreasing ATP and increasing ADP concentrations showed that force was increased by both interventions (Seow & Ford, 1997). On the other hand, our unpublished attempts to model this showed that if there was no slowly reversible transition immediately following the power stroke, slowing of either ADP release or ATP binding will lower rather than increase isometric force. While it required some experience with the computer program to derive this insight, it might have been anticipated without modelling. The lower force results from rapid reversibility of the power stroke compared with the chemical transitions, such that there are fewer high-force bridges unless this backward movement is prevented by a slowly reversible transition that slows backward movement through the power stroke.

Non-relaxing component

The final mechanical change found in the skinned fibre experiments, the addition of a non-relaxing component with apparent non-linear force-extension properties, is likely to arise from at least three mechanisms, and the present experiments cannot distinguish the relative contributions of the three.

Detained, high-force bridges

These bridges will increase stiffness to a lesser extent than force. They will also appear to have non-linear force-extension properties if their detachment rate from thin filaments is greatly increased when filament sliding brings them to zero-force positions. Such a strain dependence of detachment is expected (Huxley, 1957). Furthermore, the rapid detachment of bridges having little or no force would not alter the time course of phase 2 force changes because there would be little force change when they detached. Thus, the response of these bridges to sudden shortening is likely to appear to have little effect on the time course of phase 2 force recovery and to make the T₁ curves appear non-linear, even if the force-extension properties of the individual bridges are linear and they detach with a finite time course. On the other hand, they are likely to contribute no more than about 15-20 % of the overall non-relaxing component. This factor is estimated from the relative stiffness of this component and from the consideration that bridges detained in a high-force state increase force about 2.5 times as much as bridges normally distributed between high- and low-force states (Seow & Ford, 1997). The conclusion that about 10 % of the isometric force in UTP is generated by bridges detained in high-force states suggests that they would make up about 4 % of the attached bridges, if the other attached bridges were normally distributed between high- and low-force states. By comparison, the stiffness of this component, estimated from the force-extension relationship for the smallest steps in Fig. 7, was about 14 % of the combined stiffness of the two components that contribute to phase 2. The remaining 10 % of stiffness in this non-relaxing component requires further explanation.

Skidding bridges

Bridges that resist shortening for small strain, but detach and quickly re-attach further along thin filaments for larger strain will produce the appearance of a time-invariant, non-linear stiffness, even when bridge stiffness is linear and detachment has a finite rate constant. Such a mechanism is represented by the connections between the top and middle rows of Fig. 1, where bridges that are forcibly detached re-attach in the same state. This mechanism has been proposed to account for the flat force-extension relationships seen when both active (Seow & Ford, 1993) and relaxed (Brenner et al. 1982) muscle fibres are subjected to rapid length changes.

Filament compliance

A final mechanism that would contribute to a non-relaxing and non-linear component is a recently described filament compliance (Bagni et al. 1990; Huxley et al. 1994; Wakabayashi et al. 1994; Higuchi et al. 1995). The same size step applied to sarcomeres developing lower isometric force will cause less length change in the series compliance because the absolute force change is less, and more of the step will be applied to the bridges. The persistent difference in relative force difference following the step is then due to the step applied to the crossbridges being larger. The force-extension properties of this component of the response will appear to be non-linear, even if the filament stiffness is linear, when the steps are slowed to avoid making the muscle go slack. In the case of the larger steps that are slowed progressively to avoid making the muscle go slack, the length changes in the compliant filaments during the steps are constant and the force change associated with this component of the response reaches a constant value.

Relationship to other work

Substitution of substrate analogues

The selective detention of bridges in different states through slowing of specific transitions allows the order of the transitions to be identified. Previous studies have compared different nucleotides with regard to their effects on different contractile parameters (Pate et al. 1993; Regnier & Homsher, 1998; Regnier et al. 1998; Amitani et al. 2001). These studies concluded, as do we, that nucleotide substitution alters the chemical reactions that limit the rate of crossbridge access to the power stroke. This conclusion is in keeping with the crossbridge model of Huxley & Simmons (1971), where rates through the power stroke are determined largely by the activation energy required to stretch the crossbridge spring, and the amount of energy available in the energized crossbridge.

A very recent study by Amitani et al. (2001) comparing steady-state nucleotide hydrolysis rates with single filament sliding in motility assays of rabbit actomyosin at 25 °C showed agreement with the relative changes produced by UTP substitution for ATP at 2-4 °C here. UTP substitution reduced the sliding rate to 32 % in the single-filament study and to 44 % in the skinned fibres studied here. As expected of the higher temperature in the other study, single-filament velocity was higher than found in skinned fibres here, but the increase in speed, ∼threefold, was substantially less than expected from the usual Q₁₀ of 2-4 for muscle velocity. This reduced velocity almost certainly results from the lack of coordinated effort of multiple crossbridges in the single-filament study and from the relatively greater viscous drag on the single filaments.

Structural studies

The structure of myosin S1 (Rayment et al. 1993a,b) suggests domains within the protein head that rotate relative to each other during the force-generating power stroke of the crossbridge. It also seems very likely that this power stroke involves structural movements of at least several nanometres. On the other hand, other structural studies suggest that the phosphate binding site does not move more than a few tenths of a nanometre from the dinucleotide binding site (Dominguez et al. 1998; Houdesse et al. 2000). To the extent that this is so, separation of these products of hydrolysis cannot occur concomitantly with the power stroke unless the binding sites are located very near the fulcrum of the pivoting structures. This leads to the interesting speculation that the separation of reaction products is associated with another transition between low-force states.

Conclusion

The major conclusions of this work are that the substitution of UTP for ATP slows nucleotide hydrolysis by myosin and actomyosin and that this slowed hydrolysis detains bridges in low-force states that precede the power stroke. Others have concluded that phosphate release occurs after the power stroke, in a way that locks the bridge in a high-force state (Fortune et al. 1991; Kawai & Halvorson, 1991; Dantzig et al. 1992). Together, these conclusions suggest that hydrolysis and phosphate release occur at two distinct points in the crossbridge cycle, one before the power stroke and one after. The hydrolysis step seems to precede, but be very close to an initial state from which bridges are easily detached by shortening to one that is more firmly attached, and from which the bridges are able to undergo the power stroke. This conclusion suggests that nucleotide hydrolysis products immediately form new bonds that strengthen crossbridge attachment in preparation for the power stroke.