Regulation of the calcium release channel from rabbit skeletal muscle by the nucleotides ATP, AMP, IMP and adenosine

Abstract

1. Nucleotide activation of skeletal muscle ryanodine receptors (RyRs) was studied in planar lipid bilayers in order to understand RyR regulation in vivo under normal and fatigued conditions. With ‘resting’ calcium (100 nm cytoplasmic and 1 mm luminal), RyRs had an open probability (P_o) of ∼0.01 in the absence of nucleotides and magnesium. ATP reversibly activated RyRs with P_o at saturation (P_max) ∼0.33 and K_a (concentration for half-maximal activation) ∼0.36 mm and with a Hill coefficient (n_H) of ∼1.8 in RyRs when P_max < 0.5 and ∼4 when P_max > 0.5.

2. AMP was a much weaker agonist (P_max∼0.09) and adenosine was weaker still (P_max∼0.01–0.02), whereas inosine monophosphate (IMP), the normal metabolic end product of ATP hydrolysis, produced no activation at all.

3. Adenosine acted as a competitive antagonist that reversibly inhibited ATP- and AMP-activated RyRs with n_H∼1 and K_i∼0.06 mm at [ATP] < 0.5 mm, increasing 4-fold for each 2-fold increase in [ATP] above 0.5 mm. This is explained by the binding of a single adenosine preventing the cooperative binding of two ATP or AMP molecules, with dissociation constants of 0.4, 0.45 and 0.06 mm for ATP, AMP and adenosine, respectively. Importantly, IMP (≤ 8 mm) had no inhibitory effect whatsoever on ATP-activated RyRs.

4. Mean open (τ_o) and closed (τ_c) dwell-times were more closely related to P_o than to the nucleotide species or individual RyRs. At P_o < 0.2, RyR regulation occurred via changes in τ_c, whereas at higher P_o this also occurred via changes in τ_o. The detailed properties of activation and competitive inhibition indicated complex channel behaviour that could be explained in terms of a model involving interactions between different subunits of the RyR homotetramer.

5. The results also show how deleterious adenosine accumulation is to the function of RyRs in skeletal muscle and, by comparison with voltage sensor-controlled Ca²⁺ release, indicate that voltage sensor activation requires ATP binding to the RyR to be effective.

In vertebrate skeletal muscle, dihydropyridine receptors (DHPRs) in the transverse-tubular (T) system membrane act as voltage sensors, detecting depolarization of an action potential and opening adjacent ryanodine receptor (RyR)/Ca²⁺ release channels in the apposing sarcoplasmic reticulum (SR) membrane, thereby releasing Ca²⁺ into the cytoplasm and activating the contractile apparatus (Tanabe et al. 1990; Melzer et al. 1995). In contrast to cardiac muscle, the influx of extracellular Ca²⁺ through the DHPR is not necessary for initiating Ca²⁺ release, as the DHPR/voltage sensors directly activate the RyRs by some protein-protein interaction. Studies on isolated RyRs in lipid bilayers (Smith et al. 1986) and on ryanodine binding and Ca²⁺ release in SR vesicles (Meissner et al. 1986) have shown that millimolar levels of ATP potently activate the skeletal muscle RyR in the virtual absence of cytoplasmic Ca²⁺, and in conjunction with Ca²⁺ can cause almost full activation. By-products of ATP hydrolysis, such as ADP and AMP, are less effective agonists of skeletal muscle RyRs (Meissner, 1984) and evidently compete with ATP for its site(s) on the RyR (Rousseau et al. 1988). However, it is uncertain whether such ATP stimulation is important to voltage sensor activation of the RyRs.

The cytoplasm of resting muscle fibres contains approximately 6-8 mm ATP (Hood & Parent, 1991; Nagesser et al. 1992, 1993; Fitts, 1994). With vigorous or sustained exercise, phosphocreatine stores in the fibre become depleted and the [ATP] can decline to less than 1 mm (Karatzaferi et al. 2001) on average in the cytoplasm and possibly even lower in particular local areas if there is restricted diffusion and a relatively high rate of ATP utilisation, as may be the case near the RyRs (see Discussion). Under these conditions much of the ADP is hydrolysed to AMP, rather than being reconverted to ATP, and the AMP is normally deaminated to inosine monophosphate (IMP) by myoadenylate deaminase, such that the [IMP] increases in an almost equimolar manner with the decline in [ATP] (Nagesser et al. 1992; Allen et al. 1995; Sabina & Holmes, 1995). The role of these changes in muscle fatigue is not well understood. Muscle fatigue is a multi-faceted phenomenon to which many factors contribute (Fitts, 1994; Allen et al. 1995). The decline in force occurring with sustained exercise is produced by changes in the response of the contractile apparatus and eventually also by a decline in Ca²⁺ release from the SR (Allen et al. 1995). It has been reported that local depletion of ATP near the RyRs (with the concomitant build-up of metabolic products) may contribute to this reduced Ca²⁺ release (Westerblad & Allen, 1992; Owen et al. 1996; Allen et al. 1997; Duke & Steele, 1998; Blazev & Lamb, 1999a,b), though it was unclear whether this effect was mediated by a mechanism involving ATP hydrolysis (Allen et al. 1997) or was related to interference with ATP stimulation of the RyR (Owen et al. 1996; Duke & Steele, 1998; Blazev & Lamb, 1999a,b).

To further investigate this, we examined here the regulation of single skeletal muscle RyR channels by ATP, AMP, IMP and adenosine in the absence of Mg²⁺. (It was necessary to omit Mg²⁺ because it is a potent inhibitor of RyRs in the absence of voltage sensor stimulation, see Discussion.) Adenosine is known to inhibit caffeine-induced Ca²⁺ release in permeabilised fibres from frog muscle (Duke & Steele, 1998) and to inhibit both caffeine-induced and voltage sensor-controlled Ca²⁺ release in rat muscle fibres, with IMP having no noticeable effect (Blazev & Lamb, 1999b). We show here that the effects of ATP and its metabolites on voltage sensor release of Ca²⁺ are all well explained by their competitive effects directly on the RyR. This provides strong evidence that (a) voltage sensor activation of the RyR requires concurrent stimulation of the RyR by cytoplasmic ATP and (b) that competition between ATP and its metabolites for the stimulatory binding sites on the RyR could well be responsible for reduced Ca²⁺ release in fatigue in normal individuals and for the early onset of fatigue in individuals with myoadenylate deaminase deficiency (MDD), where AMP cannot be deaminated to IMP and there are increased levels of adenosine (Sabina et al. 1984). Finally, this study describes and models findings that suggest that potent activation of the RyR occurs by simultaneous activation of its four subunits. A brief, preliminary report of some of these findings has been published previously (Laver et al. 2000a).

METHODS

Preparation of SR microsomes

SR vesicles were prepared from the back and leg muscles of New Zealand White rabbits killed by captive bolt prior to muscle removal. The procedure was carried out by the holder of a current licence granted under ACT State legislation. Native SR vesicles were isolated using techniques based on those of Chu et al. (1988) as previously described in Laver et al. (1995). Briefly, the muscle was differentially centrifuged to yield a crude microsomal fraction, which was fractionated by loading it onto a discontinuous sucrose gradient. Heavy SR vesicles were collected from the 35-45 % (w/v) interface, centrifuged, resuspended in buffer then snap frozen and stored in liquid N₂ or at -70 °C.

Lipid bilayers, chemicals and solutions

Lipid bilayers were formed from phosphatidylethanolamine and phosphatidylcholine (4:1) (Avanti Polar Lipids, AL, USA) in n-decane, across an aperture of ∼200 μm diameter in a Delrin cup (Cadillac Plastics, NC, USA). The bilayer separated two solutions: cis and trans (∼1 ml). Vesicles were added to the cis solution and incorporation with the bilayer occurred as described by Miller & Racker (1976). Due to the orientation of RyRs in the SR vesicles, RyRs added to the cis chamber incorporated into the bilayer with the cytoplasmic face of the channel orientated to the cis solution. During SR vesicle incorporation the cis (cytoplasmic) solution contained 250 mm Cs⁺ (230 mm CsCH₃O₃S, 20 mm CsCl) with 1 mm CaCl₂ and the trans (luminal) solution contained 50 mm Cs⁺ (30 mm CsCH₃O₃S, 20 mm CsCl), 1 mm CaCl₂. The caesium salts were obtained from the Aldrich Chemical Company and CaCl₂ from BDH Chemicals. The osmotic gradient across the membrane and the Ca²⁺ in the cis solution helped vesicle fusion with the bilayer. During measurements the cis solution contained 250 mm Cs⁺ (230 mm CsCH₃O₃S, 20 CsCl) with 100 nm Ca²⁺ (4.5 mm BAPTA, obtained as a tetra-potassium salt from Molecular Probes, 1 mm CaCl₂) and various nucleotide concentrations at pH 7.4. The trans solution was the same as that used during vesicle incorporation. All solutions were pH buffered with 10 mm Tes (ICN Biomedicals) and solutions were titrated to pH 7.4 using CsOH (optical grade from ICN Biomedicals). The free [Ca²⁺] was estimated using published association constants (Marks & Maxfield, 1991) and the program ‘Bound and Determined’ (Brooks & Storey, 1992). ATP, AMP, IMP and adenosine were obtained in the form of sodium salts from Sigma Chemicals.

Solution changes

During experiments the composition of the cis solution was altered either by addition of aliquots of stock solutions or by perfusion of the bath near the bilayer. The local perfusion method allowed solution exchange between sixteen available solutions in random sequence. Details of the perfusion method are given by Laver et al. (2000b).

Data acquisition and analysis

Bilayer potential was controlled and currents recorded using either an Axopatch 200B amplifier (Axon Instruments) or a Bilayer Clamp-525C (Warner Instruments). The cis chamber was electrically grounded to prevent electrical interference from the perfusion tubes and the potential of the trans chamber was varied. However, all electrical potentials are expressed here using standard physiological convention (i.e. cytoplasmic side relative to the luminal side at virtual ground).

Unless otherwise stated, single channel recordings were obtained using a bilayer potential difference of +40 mV. RyRs with open probabilities in excess of ∼0.2 exhibit voltage-dependent inactivation (see Laver & Lamb, 1998) that depends on P_o rather than on the specific channel activator. The occurrence of inactivation was minimised by application of brief (∼1 s) voltage steps to -40 mV at ∼15 s intervals.

During the experiments, the bilayer current was recorded after low pass filtering at 5 kHz, sampled at 50 kHz and simultaneously stored on computer disk using data interfaces (DT301 or DT3001, Data Translation, MA, USA) under the control of in-house software written in Visual Basic. For measurements of unitary current, P_o and dwell times, the current signal was digitally filtered at 1 kHz with a Gaussian filter and sampled at 5 kHz. Unitary current and time-averaged currents were measured using Channel2 software (Professor P. W. Gage and Mr M. Smith at the Australian National University). To calculate P_o from single channel records, a threshold discriminator was set at 50 % of channel amplitude to detect channel opening and closing events. For experiments in which bilayers contained several strongly activated RyRs, the time-averaged current was divided by the unitary current and the number of channels. This method of calculating P_o gives a similar result to that obtained when measuring P_o of single channels using a threshold discriminator (Laver et al. 1997a). Frequency histograms of dwell-time duration were compiled from channel records varying in duration from 30 to 120 s. Event durations were extracted from the data using 50 % threshold detection which, in conjunction with the filtering, had a dead-time of ∼200 μs. The histograms are presented as probability distributions using variable bin widths with equal separation on a log scale as described by Sigworth & Sine (1987).

The activation of RyRs by the nucleotides ATP and AMP was characterised by fitting (by least squares) a Hill equation (eqn (1)) to the relation between P_o and nucleotide concentration:

(1)

where n_H is the Hill coefficient, K_a is the concentration of half-activation and P_max is the open probability at maximum activation. Fitting was usually carried out using the pooled results from normalised data of several experiments (the averaged data points presented in the figures were not used for fitting). K_a was determined from data that were normalised for P_max while n_H was determined from data that were normalised for both P_max and K_a. Inhibition of RyRs by adenosine was characterised by fitting an alternative form of the Hill equation (eqn (2)) to the relation between P_o and adenosine concentration:

(2)

where P_max is the open probability of the uninhibited channel and K_i is the concentration for half-inhibition.

Unless otherwise stated the data are presented as means ± standard error of the mean (s.e.m.). The quality of fit parameter used was the root mean square of the residuals.

RESULTS

Activation of RyRs by nucleotides

The open probability of RyRs responded to changes in nucleotide concentration within the time expected for solution change at the bilayer surface (∼10 s). The open probability was determined from recordings of steady RyR activity lasting 30-120 s under each experimental condition. The response of individual RyRs to cytoplasmic nucleotides is shown in Fig. 1 and 2. The mean activation of RyRs by ATP and AMP is shown in Fig. 3A. The activating effects of different nucleotides were investigated on different groups of channels which, on average, showed slightly different levels of activity in the absence of nucleotides. In the absence of nucleotides, RyRs were relatively inactive at 100 nm cytoplasmic Ca²⁺ with an overall P_o of 0.02 ± 0.02. Addition of ATP up to a concentration of 8 mm strongly activated RyRs to a P_max of 0.33 ± 0.04, whereas AMP (up to 10 mm) was a less potent activator, giving rise to a mean P_max of 0.09 ± 0.02. Adenosine (5-10 mm) produced only a slight activation of RyRs (2.1 ± 0.7-fold change by paired analysis, with P_max= 0.008 ± 0.001) and IMP (up to 8 mm) produced no activation at all (0.9 ± 0.15-fold change by paired analysis, P_max= 0.0012). Since the absolute values of P_o in the adenosine and IMP experiments were extremely low (P_o < 0.01) we endeavoured to obtain higher precision measurements of the IMP and adenosine effects by examining RyRs activated by 100 μm Ca²⁺, where P_o= 0.28 ± 0.08 (n = 8) prior to nucleotide activation. RyRs in the presence of 5 mm IMP and 100 μm Ca²⁺ had a P_max= 0.24, which was 85 ± 13 % (n = 4) of that in the absence of IMP. Similar analysis of adenosine activation showed that 5 mm adenosine, in the presence of 100 μm Ca²⁺, increased P_max on average to 0.52, which represents an increase of 130 ± 30 % (n = 4). Thus, adenosine is a much weaker RyR agonist than ATP and AMP, and IMP has no discernible effect at all.

Figure 1. Representative segments of an experiment showing the competitive effects of ATP and adenosine on a single skeletal RyR.

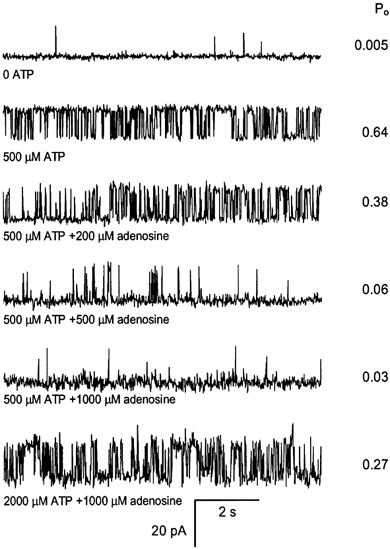
The cis (cytoplasmic) solution contained 250 mm Cs⁺ (230 mm CsCH₃O₃S, 20 mm CsCl) with 100 nm Ca²⁺ (4.5 mm BAPTA, 1 mm Ca²⁺) and various concentrations of ATP and adenosine at pH 7. 4. The trans (luminal) solution contained 50 mm Cs⁺ (30 mm CsCH₃O₃S, 20 mm CsCl), 1 mm CaCl₂ at pH 7. 4. All solutions were pH buffered with 10 mm Tes. The membrane potential was held at +40 mV and channel openings are shown here by upward deflections of the current from the baseline. The RyR open probability (P_o) determined from > 30 s recordings is shown at the right of each trace. Top trace, RyRs were relatively inactive in 100 nm Ca²⁺ in the absence of ATP. Second trace, addition of 500 μm ATP to the cis bath (aliquot addition) markedly activated the channel. Traces 3-5, subsequent addition of adenosine reduced channel activity. Bottom trace, subsequently increasing [ATP] to 2000 μm reversed the inhibitory effect of 1000 μm adenosine.

Figure 2. Reversibility of ATP activation and adenosine inhibition of RyRs.

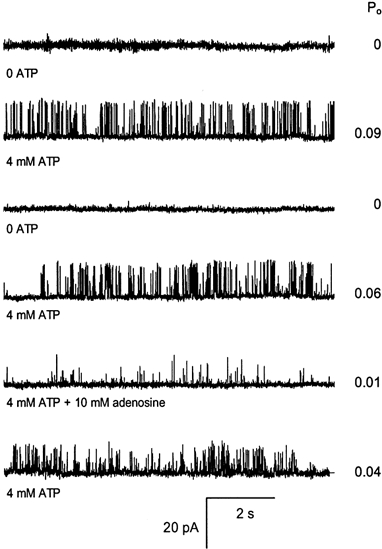
The experimental conditions are given in the legend to Fig. 1 and the nucleotide concentrations are given at the left of each trace. The P_o, determined from > 30 s recordings, is shown at the right of each trace. Top trace, RyRs were found to be inactive in 100 nm Ca²⁺ in the absence of ATP (control solution) at the start of the experiment. Trace 2, addition of 4 mm ATP to the cis bath (local perfusion) activated the channel. Traces 3-6, after 8 min the channel activation by ATP could be completely reversed by flowing the control solution onto the channel. In the same experiment, solutions containing 4 mm ATP plus adenosine reversibly inhibited channel activity. Note the higher concentrations of adenosine used compared to Fig. 1.

Figure 3. The response of RyR P_o to ATP and AMP.

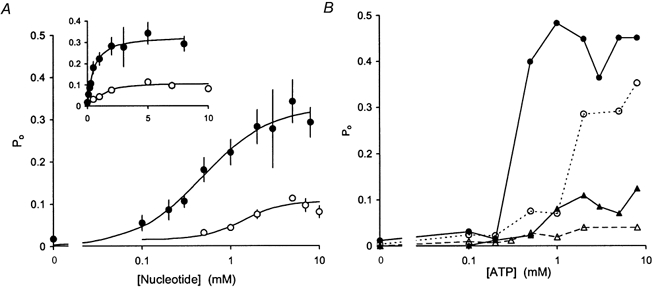
Experimental conditions are given in Fig. 1. A, the average response of RyR P_o to ATP and AMP. The data points show the means and s.e.m. of RyRs when exposed to cis ATP (•, n = 32) or to cis AMP (○, n = 19). The continuous curves show Hill curves (eqn (1)) fitted to the data. For ATP the fit parameters are P_max= 0.33 ± 0.04, K_a= 0.48 ± 0.17, n_H= 1.1 ± 0.7 and for AMP P_max= 0.09 ± 0.02, K_a= 1.4 ± 0.3, n_H= 1.9 ± 0.5. The inset shows the same data plotted with a linear abscissa. B, examples of the response to ATP of individual RyRs spanning the full range of observed P_max.

Maximal activation achieved with either ATP or AMP showed considerable variation between individual channels (e.g. Fig. 3B). In the presence of 100 nm Ca²⁺ and 4-8 mm AMP or 1-8 mm ATP, RyRs reach near-maximal activation for that nucleotide, with P_o being within 20 % of the respective P_max. The frequency distributions of P_max in Fig. 4 suggest continuous unimodal distributions that are skewed to low values. Thus, the P_max distributions gave no indication that there were two or more distinct populations of RyRs present in these experiments. We also measured RyR activation by ATP in the presence of 1 nm Ca²⁺ to test the possibility that variations in P_max in 100 nm Ca²⁺ reflected variations in RyR sensitivity to cytoplasmic Ca²⁺. In 1 nm Ca²⁺ the frequency distribution of P_max was similar to that seen in 100 nm Ca²⁺. The Wilcoxon-Mann-Whitney test showed that there was no significant difference between the distributions (P = 0.5) indicating that variations in P_max were not related to activation by cytoplasmic Ca²⁺.

Figure 4. Frequency distribution of maximum open probability (P_max) of RyRs activated by ATP and AMP, showing the considerable variation between individual channels.

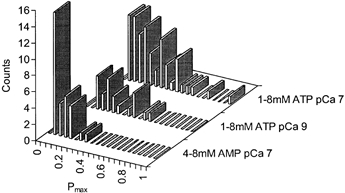
RyR activity was measured under experimental conditions given in Fig. 1 at cytoplasmic Ca²⁺ and nucleotide concentrations indicated. Over these ranges of [ATP] and [AMP] RyRs were near-maximally activated so that P_o values approximate the P_max for that RyR and nucleotide (see eqn (1)).

The dose-response of RyRs to ATP was examined by least squares fitting of the Hill equation, eqn (1), to the concentration dependencies of P_o shown in Fig. 3. The average dose-response of RyRs to ATP (Fig. 3A) gave values of P_max= 0.33 ± 0.04, K_a= 0.48 ± 0.17 mm and n_H= 1.1 ± 0.7 (These values of K_a and n_H from fits to the non-normalised, averaged data are not as accurate as those found when fitting to normalised data as done below, in particular causing n_H to be underestimated - see Discussion on this point in Laver et al. 2000b). Since the variation in P_max was relatively large, we separately pooled RyRs with high P_max (> 0.5) from those with low P_max (P_max < 0.2) and intermediate P_max (P_max= 0.2-0.5) in order to test for possible correlations between P_max and K_a and n_H. Values of K_a obtained from data normalised for P_max did not significantly differ between the three RyR groups (see Table 1) and had a weighted mean value of 0.36 mm. In order to get accurate values of the Hill coefficient, Hill fits were made to dose-responses that had been normalised to both P_max and K_a for each RyR individually. RyRs in the lower activity groups had Hill coefficients for ATP activation of approximately 2 (Table 1) and RyRs with P_max > 0.5 gave values of n_H∼4.

Table 1.

Summary of Hill parameters obtained from fits of eqn (1) to the [nucleotide] dependencies of RyR P_o

RyR activation	Pmax	Ka (mM)	nH
ATP
Pmax= 0.5–0.9, n = 4	0.54 ± 0.05	0.35 ± 0.08*	3.8 ± 1.3 †
ATP
Pmax= 0.2–0.5, n = 5	0.33 ± 0.02	0.48 ± 0.08*	1.7 ± 0.5 †
ATP
Pmax= 0–0.2, n = 9	0.07 ± 0.02	0.29 ± 0.04*	1.8 ± 0.7 †
AMP
Pmax= 0–0.4, n = 19	0.09 ± 0.02	1.4 ± 0.3 ‡	1.9 ± 0.5 ‡

P_max is the saturating level of P_o, K_a is the nucleotide concentration that produces 50 % activation and n_H is the Hill coefficient.

^*K_a values were determined from least squares fit to P_o data that were normalised to 8 mM ATP.

^†n_H values were determined from data in which P_o was normalised to 8 mM ATP and [ATP] was normalised to K_a.

^‡Values were obtained from data that were normalised to 5 mM AMP.

AMP activated RyRs at concentrations up to 10 mm, but to a lesser extent than did ATP. Maximal activation commonly occurred at 5 mm AMP and, at concentrations above this, RyR activity decreased in a similar way to that reported previously for cardiac RyRs (Ching et al. 1999). In 6 out of 10 experiments RyR activity decreased by 50 -80 % in the presence of 5-10 mm AMP, while in four others channel activity increased by 10-30 % over this concentration range. The average [AMP]-dependent activation of all 10 RyRs is shown in Fig. 3A. The inactivation at high [AMP] made it difficult to obtain a reliable estimate of K_a and n_H from a Hill fit to the AMP data in Fig. 3. Therefore we determined K_a to be 1.4 mm from the [AMP] at which P_o was 50 % of that at 5 mm AMP.

We also analysed AMP activation of RyRs in high- and low-activity groups using an arbitrary threshold of P_max= 0.04 to define the two groups. The two groups gave identical values of K_a= 1.4 mm indicating that K_a for the AMP-activated RyRs did not depend on P_max over the range 0 to 0.4. In summary, the average AMP data in Fig. 3A had values of P_max= 0.09 ± 0.02, K_a= 1.4 ± 0.3, n_H= 1.9 ± 0.5.

Effects of adenosine and IMP on RyRs activated by ATP or AMP

Adenosine inhibited the activity of RyRs activated by either ATP or AMP. This inhibition could be partially reversed by increasing the concentration of ATP or AMP. This is shown for the case of adenosine and ATP in Fig. 1. Thus, it appears that adenosine acts by competing with ATP and AMP for a common set of binding sites on the RyR. The adenosine inhibition dose-response curves of RyRs activated by 0.2-8 mm ATP are shown in Fig. 5A. Hill fits (eqn (2)) to these data show inhibition, with Hill coefficients ranging from 0.9 to 1.2 (Table 2) and a half-inhibiting [adenosine] (K_i) with biphasic dependence on [ATP] (see Fig. 5B). Over the range 0.2-0.5 mm, ATP had little effect on K_i (∼0.06 mm), whereas at higher [ATP], K_i increased ∼4-fold for each 2-fold increase in [ATP]. We found no significant difference between K_i values obtained from channels with high and low activity over the full range of [ATP] used in these experiments. Analysis of the competition between these nucleotides (see Discussion) indicates dissociation constants for adenosine, ATP and AMP of 0.06, 0.4 and 0.45 mm, respectively. This estimate of the dissociation constant for ATP is similar to the K_a for ATP activation (0.36 mm), whereas the dissociation constant for AMP is significantly lower than the K_a found when activating with AMP (1.4 mm, see earlier). The effect of IMP on ATP-activated RyRs was markedly different from that of adenosine. At concentrations up to 8 mm, IMP produced no inhibitory effect on RyRs that were activated by either 0.5 or 2 mm ATP (Fig. 6).

Figure 5. The inhibitory effect of adenosine in the presence of various concentrations of ATP and AMP.

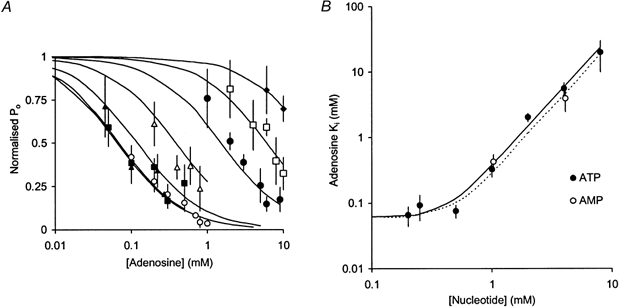
A, pooled data showing the inhibitory dose-response behaviour of RyRs to adenosine in the presence of ATP at the following concentrations (mm): 0.2 (○, n = 5), 0.25 (▴, n = 5), 0.5 (▪, n = 14), 1 (▵, n = 5), 2 (•, n = 9), 4 (□, n = 9) and 8 (♦, n = 3). Channel activity is given as the mean and s.e.m. of open probability normalised in each experiment to that in the absence of adenosine. B, the half-inhibitory concentration of adenosine (K_i) in the presence of various concentrations of ATP (•) and AMP (○). Means and s.e.m. of K_i were determined from least squares fits of the individual adenosine dose-response data combined from all experiments under each experimental condition. K_i shows biphasic dependence on [ATP]. Over the range 0.2-0.5 mm, ATP has little effect on K_i whereas at higher [ATP], K_i increases ∼4-fold for each 2-fold increase in [ATP]. K_i for adenosine was similar in the presence of either ATP or AMP. The curves in A and B show model fits to the ATP data (continuous lines) and the AMP data (dotted line) based on Scheme 2. The values for the parameters of Scheme 2 are: K_ATP= K_ATP2= 0.4 mm, K_AMP= K_AMP2= 0.45 mm, K_ad= K_ad2= 0.06 mm.

Table 2.

Summary of the parameters obtained from fitting eqn (2) to the adenosine inhibition data (see Fig. 5)

	Ki for adenosine (mM)	nH	n
[ATP] (mM)
0.2	0.066 ± 0.022	0.9 ± 0.3	5
0.25	0.093 ± 0.04	0.6 ± 0.5	5
0.5	0.076 ±. 017	1.0 ± 0.3	14
1	0.33 ± 0.08	1.2 ± 0.6	5
2	2.0 ± 0.3	1.2 ± 0.4	9
4	5.6 ± 1.2	0.9 ± 0.4	9
8	20 ± 10	—	2
[AMP] (mM)
1	0.43 ± 0.12	1.5 ± 0.7	7
4	4.0 ± 1.5	1.2 ± 0.8	5

K_i is the [adenosine] that produces 50 % inhibition, n_H is the Hill coefficient and n is the number of RyRs observed.

Figure 6. Pooled data showing that cis IMP has no significant effect on the activity of RyRs activated by either 0.5 mm ATP (•, n = 5) or 2 mm ATP (○, n = 4).

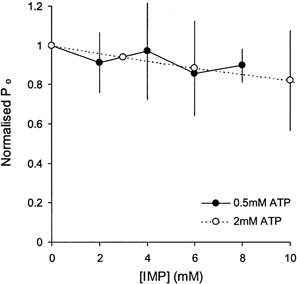
Experimental conditions are given in Fig. 1. Channel activity is shown by the mean and s.e.m. of P_o normalised in each experiment to that in the absence of IMP.

Reversibility of nucleotide effects

The effects of ATP and adenosine were reversible in most cases (Fig. 2). In 18 experiments, RyR activity was measured under control conditions (∼100 nm Ca²⁺ in the absence of nucleotides) both at the beginning of each experiment and after several minutes exposure to ATP. In 15 of these experiments RyR activity returned to low levels upon washout after 5-18 min exposure to ATP. In the remaining three experiments RyRs showed greater activity (P_o > 0.05) under control conditions after 5, 12 and 18 min exposure to ATP than at the start of the experiments (P_o= 0.005). In these cases ATP, adenosine and Ca²⁺ also failed to regulate RyR activity. In the last of these three experiments, six RyRs had incorporated into the bilayer but only one channel showed irreversible behaviour. Thus, after more than 5 min exposure to ATP, ∼15 % of RyRs appeared to be activated by unknown factors other than the presence of nucleotides and were not included in the present analysis. Due to premature ruptures of the lipid bilayer, we were unable to test for reversibility of ATP activation in half of our experiments. However, in these experiments the exposures of RyRs to ATP were generally of less than 5 min duration, so that it was unlikely that these RyRs were not regulated by nucleotides in the normal manner.

Analysis of dwell times

Information about the mechanisms of nucleotide regulation of RyRs can be gained from analysis of dwell times, beginning here with mean closed and open dwell times (τ_c and τ_o, respectively) and then following with a more detailed analysis of dwell time distributions. Activation of RyRs by ATP occurred via a decrease in τ_c (Fig. 7B). In channels that were activated to P_o > 0.2, activation was also associated with an increase in τ_o (Fig. 7A). These dependencies of τ_o and τ_c on P_o are shown in Fig. 7C and D. The same behaviour was also found for AMP-activated RyRs, as well as those inhibited by adenosine (see below).

Figure 7. Effect of nucleotides on the mean open and closed dwell times of RyRs.

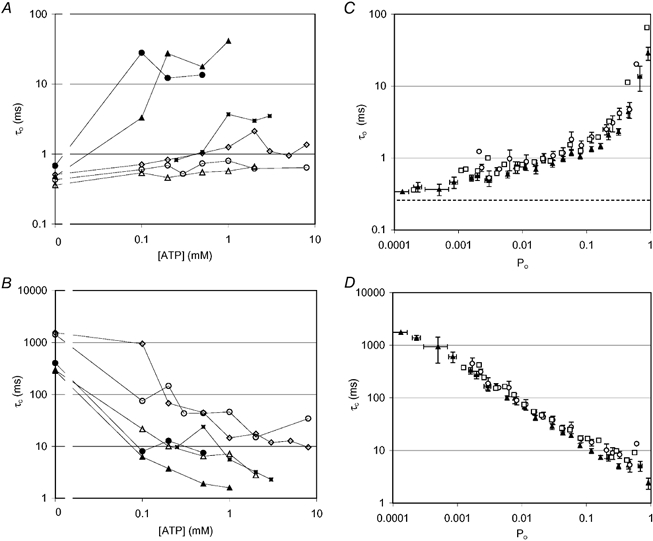
A and B, effect of ATP concentration on the mean open (τ_o, A) and closed (τ_c, B) dwell times of representative RyRs. P_max values shown here cover the full range of activating levels induced by ATP. P_max values obtained for each RyR are as follows: ▴, -0.96; •, -0.64; ▪, -0.6; ⋄, -0.12; ▵, -0.11; ○, -0.02. C and D, summaries of all mean open (τ_o, C) and closed (τ_c, D) dwell times data, showing the effect of ATP (0-8 mm, ▴) and AMP (0-5 mm, □) activation and adenosine (0-10 mm, ○) inhibition of RyRs. Here, dwell times are plotted against the degree of channel activation (P_o) rather than nucleotide concentration. In all cases, nucleotide regulation of P_o was associated with changes in mean closed dwell times. However, when P_o exceeded ∼0.2, nucleotides had a relatively strong effect on the mean open dwell times. The dashed line in C shows the duration of the shortest detectable gating events.

Since two or more ATP molecules are evidently involved in RyR activation (see n_H for nucleotide activation and the [ATP] dependence of K_i for adenosine inhibition), we analysed the [ATP] dependence of τ_c in order to estimate the number of ATP molecules that must bind to the closed channel before it can open. These data were fitted with eqn (3), in which N represents the number of ATP molecules needed to open the channel, K is the average dissociation constant for the ATP molecules and τ_c,max and τ_c,min are the mean closed times in the absence of ATP and at maximal ATP activation, respectively:

(3)

This analysis of the data gave values of N = 2.0 ± 0.2 (n = 8), which indicates that the binding of at least two ATP molecules is required to open RyRs. Values of N did not show any significant dependency on P_max. The N values for high activity RyRs (N = 2.0 ± 0.5, n = 3, P_max > 0.5) were similar to those for low activity RyRs (N = 1.9 ± 0.3, n = 5, P_max < 0.2). ATP clearly had an effect on τ_o under some circumstances (see above), which indicates that ATP also interacts with the RyR in its open state. The ATP-dependent increase in τ_o was usually quite abrupt, the full increase occurring between sampled ATP concentrations. Consequently we were unable to obtain reliable estimates of N from a similar analysis to that used for τ_c. However, the abrupt increase in τ_o indicated N > 2.

The effect of adenosine inhibition on τ_o and τ_c of ATP-activated RyRs is shown in Fig. 8. Adenosine inhibition had a similar effect to that of a decrease in the activating nucleotide concentration, in that in all cases adenosine increased τ_c but only produced a decrease in τ_o when τ_o had increased with ATP- or AMP-induced activation (see Fig. 7C).

Figure 8. Effects of adenosine inhibition on the mean open (τ_o, A) and closed (τ_c, B) dwell times of four representative RyRs.

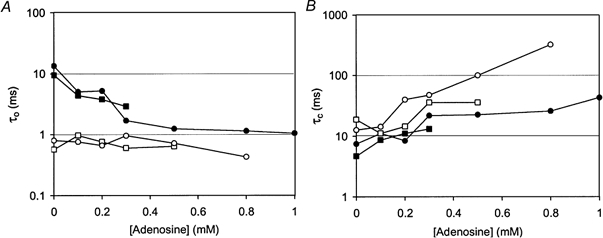
Adenosine inhibition was produced in the presence of 0.5 mm ATP and is shown here for two RyRs that were strongly activated by ATP (•, P_max= 0.64; ▪, P_max= 0.67) and for another two that were weakly activated by ATP (○, P_max= 0.03; □, P_max= 0.06). In all cases adenosine increased the mean closed dwell times but only decreased the open dwell times of RyRs that had been strongly activated by ATP.

ATP activation and adenosine inhibition mechanisms were investigated in more detail by analysing the open and closed dwell-time distributions. These were compiled from 10 channels, five of which could be activated to medium and high levels by ATP (P_o > 0.2) and five of which could only be activated to lower levels. Open dwell-time distributions obtained from low activity, ATP-activated channels had two exponential time constants of 0.7 and 2.5 ms (see Table 3 and also Fig. 9D). These open time distributions did not depend on either the ATP or adenosine concentration. This is in contrast to the ATP dependence seen in the dwell times of RyRs that could be activated to medium or high activity. These RyRs, while at relatively low levels of nucleotide activation (i.e. at low [ATP] where P_o < 0.1), also exhibited two time constants (0.9 ± 0.1 and 4.0 ± 0.5 ms) in their open dwell time distributions, which had relative weightings of 64 % and 36 %, respectively. However, at higher levels of activation (P_o > 0.2) the same RyRs exhibited an additional one or two open time constants of the order of 10 and 100 ms. Thus, out of the five RyRs in this group, three channels showed a total of three exponential components, while another two showed four components. The ATP concentration had no significant effect on the values of the fitted time constants but it did alter their relative weightings (i.e. the relative areas). The long time constant components had combined relative areas (A_L) which were proportional to the level of activation and, on average, were ∼0.4 in maximally activated channels (i.e. ∼40 %, see Table 3 and Fig. 9B). A_L was proportional to the degree of RyR activation (P_o) regardless of whether RyRs were activated by ATP (A_L= (0.7 ± 0.08)P_o) or inhibited by adenosine (A_L= (1.0 ± 0.148)P_o). Thus, as seen with mean open times, the effect of adenosine inhibition on A_L was effectively the same as a decrease in the ATP concentration.

Table 3.

Summary of parameters from multi-exponential fits to open and closed dwell time probability distributions obtained from RyRs that were near-maximally activated by ATP

	Closed dwell times		Open dwell times
Exponential component	Relative area (%)	Time constant (ms)	Relative area (%)	Time constant (%)
Low Pmax RyRs
No. 1	25 ± 4	2.4 ± 0.5	72 ± 20	0.7 ± 0.2
No. 2	48 ± 3	15 ± 5	26 ± 20	2.5 ± 0.4
No. 3	26 ± 5	66 ± 7	—	—
High Pmax RyRs
No. 1	40 ± 5	0.90 ± 0.13	38 ± 5	1.0 ± 0.14
No. 2	40 ± 3	4.8 ± 0.7	37 ± 2	6.4 ± 0.8
No. 3	16 ± 3	25 ± 7	27 ± 5	43 ± 9
No. 4	—	—	10 ± 5	180 ± 12

Data are grouped from five RyRs with medium to high activity (P_max > 0.2) and another five with low activity (P_max < 0.2).

Figure 9. Dwell-time probability distributions obtained from RyRs activated by ATP and inhibited by adenosine.

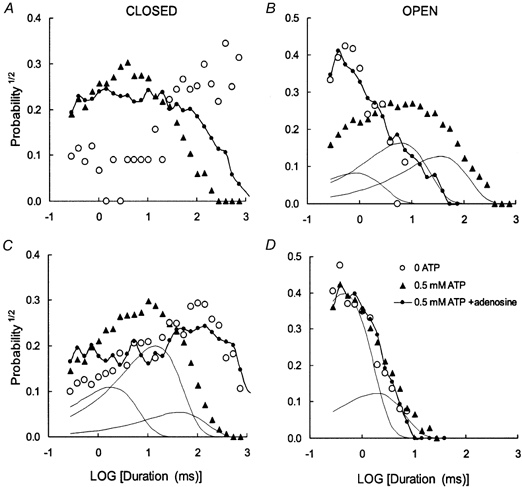
These RyRs showed behaviour representative of the high activity (A and B) and low activity (C and D) RyRs seen in this study. Probability distributions were constructed using the method of Sigworth & Sine (1987) where data were grouped into bins that are equally spaced on a log scale. Using this method, an exponentially decaying distribution is transformed to peaked distribution, where the peak is located at a time equal to its time constant. The continuous curves show examples of the individual exponential components of theoretical curves fitted with the data. A and B, ○, P_o= 0.0017. Data were compiled from 123 gating events in an 80 s recording, in the absence of nucleotides. ▴, P_o= 0.63. Data compiled from 1910 gating events in a 60 s recording, in the presence of 0.5 mm ATP. There is a considerable increase in the probability of long open events and short closed events. The individual exponential components of an exponential fit to the open data are shown by the continuous curves. •, P_o= 0.05. Data compiled from 2920 gating events in a 100 s recording, in the presence of 0.5 mm ATP plus 0.8 mm adenosine. Inhibition increases the probability of long closures and short openings. The open dwell time distribution of the RyR in the presence of ATP and adenosine is very similar to that in the absence of nucleotides. C and D, ○, P_o= 0.0084. Data were compiled from 548 gating events in a 60 s recording, in the presence of low (0.1 mm) ATP. ▴, P_o= 0.07. Data compiled from 3630 gating events in a 60 s recording, in the presence of 0.5 mm ATP. As with the high activity RyR, there is a considerable increase in the probability of short closed events. However, the open time distribution is unchanged. The individual exponential components in the open and closed data are shown by the continuous curves. •, P_o= 0.0089. Data compiled from 670 gating events in an 80 s recording, in the presence of 0.5 mm ATP plus 0.5 mm adenosine. Inhibition increases the probability of long closures but unlike the high activity channel adenosine has no effect on the openings. Once again, the open dwell time distribution of the RyR in the presence of ATP and adenosine is very similar to that in the absence of nucleotide. The parameters of the fitted curves (i.e. the time constants, τ (ms), and relative areas, A, of each exponential component) in each panel are listed in pairs (τ, A): B, 1.0, 0.22; 7.3, 0.44; 41, 0.34; C, 2.2, 0.30; 17, 0.55; 52, 0.15; D, 0.54, 0.76; 2.2, 0.24.

Closed times were mostly described by three exponential components, with time constants over the range 0.5-200 ms depending on their degree of activation (e.g. Fig. 9C and D). RyRs that maximally activated to P_o < 0.2 all had very similar closed dwell-time distributions with evenly weighted time constants at 2.4, 15 and 66 ms. RyRs with higher P_o had ∼3-fold shorter time constants in their closed dwell-time distributions (see Table 3). The closed dwell time distributions varied in a complex manner with ATP and adenosine and it was not possible to track the individual [ATP] and [adenosine] dependencies of the exponential parameters.

DISCUSSION

This study provides new and detailed information about the regulation of the skeletal muscle RyR by ATP and related nucleotides and presents the first detailed study of adenosine inhibition of RyRs. We describe the mechanism of action of ATP, AMP and adenosine, showing how the distinctive properties can be explained by a scheme based on competitive activation. Then we interpret this scheme in terms of a mechanism in which the overall activation of a RyR depends on nucleotide binding to each of its four subunits. Finally, we discuss the physiological significance of the results, showing how important ATP is to the normal mechanism of excitation-contraction (E-C) coupling in skeletal muscle and how this nucleotide modulation could play a role in muscle fatigue.

General properties of nucleotide regulation of skeletal and cardiac RyRs

The overall characteristics of nucleotide activation of skeletal RyRs measured from our single channel experiments are consistent with those seen previously by studies of ⁴⁵Ca²⁺ release from SR vesicles (Morii & Tonomura, 1983; Meissner, 1984; Meissner et al. 1986). The sequence of activation efficacy of ATP, AMP and adenosine is the same as that reported by Meissner (1984). Activation of skeletal RyRs by ATP and its non-hydrolysable analogue AMP-PCP has been reported to have a K_a= 0.3-1 mm with Hill coefficients of ∼2 (Meissner, 1984; Meissner et al. 1986), which are consistent with our findings that K_a= 0.36 mm and that, for the lower activity RyRs, n_H∼2. Values of n_H that we measured for strongly activated RyRs (n_H∼4) have not been previously reported. We report here AMP activation of RyRs with K_a= 1.4 mm, which is similar to that reported by Morii & Tonomura (1983) for Ca²⁺ release from SR vesicles (K_a= 2 mm), although we found a Hill coefficient of n_H∼2 compared to their value of n_H∼1, which is an expected consequence of fitting RyRs individually rather than fitting the population response (see Laver et al. 2000b).

Rousseau et al. (1988) found that adenine reduced ATP-induced Ca²⁺ release from SR vesicles and suggested that adenine and ATP compete for a common binding site on the RyRs. We found that adenosine competes with AMP and ATP for common nucleotide binding sites and we used these competitive interactions to probe the mechanism of nucleotide activation of skeletal RyRs.

Measurements of Ca²⁺ release from SR vesicles showed that inosine triphosphate (ITP) does not activate skeletal RyRs and, if anything, slightly inhibits them (Meissner, 1984), which potentially could be very important in muscle fatigue. Our single channel measurements, however, show that the physiologically important monophosphate form (IMP) does not directly activate or inhibit RyRs, nor does it interfere with adenine nucleotide activation of the RyRs. Thus, it appears that deamination of the adenosine group to inosine abolishes nucleotide binding to RyRs, rendering the nucleotide functionally inert.

Jona et al. (2001) recently reported the first detailed measurements of ATP activation of rat skeletal RyRs from single channel experiments. They found that ATP in the presence of ∼0.5 μm cytoplasmic Ca²⁺ activated RyRs to an average P_max= 0.28, which is similar to our value of P_max= 0.33 for rabbit RyRs in 1-100 nm Ca²⁺. Jona et al. (2001) report a biphasic dependence of P_o on ATP, the first phase having a P_max of 0.1 and a K_a of 0.05 mm and the second phase with a P_max of 0.28 and a K_a of 0.35 mm. We did not observe any feature in the ATP activation of rabbit RyRs that corresponded to the first phase. This was not seen in the activation of individual RyRs or in pooled data, regardless of the method for normalising the data. However, our value for the K_a of ATP activation is close to the value quoted for the second phase of ATP activation of RyRs in rat. The reason for the difference in ATP activation is not clear. It may be due to the species difference or to the different Ca²⁺ concentrations present during the experiments (cytoplasmic [Ca²⁺] was 472 nm compared to our 100 nm and luminal [Ca²⁺] was 50 μm compared to our 1 mm). Another reason may stem from the different experimental protocols used in the two studies. In this study ATP concentrations were varied in pseudorandom order and channels showing irreversible activation during experiments were not included in the analysis. In the study by Jona et al. (2001) ATP concentrations were varied by increments so that activation by ATP or by other factors would not be distinguishable in their data.

Cardiac RyRs are also activated by millimolar concentrations of adenine nucleotides, and adenosine and ADP have also been found to antagonise ATP-induced activation of cardiac RyRs by a mechanism in which adenosine and ADP are relatively weak agonists that compete for ATP sites on the RyR (Kermode et al. 1998; Chan et al. 2000). However, the activation characteristics differ in a number of important respects from those seen in skeletal RyRs. One major difference we see, that is already recognised (Meissner et al. 1988; Kermode et al. 1998; Murayama et al. 2000), is that adenine nucleotides activate skeletal RyRs in the absence of Ca²⁺ while cardiac RyRs also require Ca²⁺ to be active (see below). This study also finds several other differences. Firstly, adenosine is a much poorer activator of skeletal RyRs than of cardiac RyRs. Adenosine has been reported to activate cardiac RyRs to a P_max of ∼0.1 (Chan et al. 2000) or 1 (McGarry & Williams, 1994). In either case, the degree of activation (10- to 40-fold) well exceeds the 2-fold activation seen here with skeletal RyRs. Secondly, nucleotides activate the two RyR isoforms with different apparent affinities. In skeletal muscle the affinities we obtained for ATP, AMP and adenosine were 0.36, 1.4 and 0.06 mm, respectively, compared with 0.22, 3 and 0.2 mm, respectively, for cardiac RyRs (Kermode et al. 1998; Ching et al. 1999; Chan et al. 2000). Thus, the relative affinities of the nucleotide cardiac and skeletal RyRs are quite different. In skeletal RyRs the ratio of the dissociation constants for the binding of ATP and of adenosine to RyRs (K_ATP/K_ad) ∼6 whereas in cardiac RyRs K_ATP/K_ad∼1. In the light of these one would expect adenosine to be a much more potent inhibitor of skeletal RyRs than cardiac RyRs.

The mechanism for ATP activation and adenosine inhibition of RyRs

Here we evolve a model to explain the nucleotide activation and adenosine inhibition of RyRs and interpret this model in terms of the homotetrameric RyR structure. Our data indicate that adenosine inhibits skeletal muscle RyRs by acting as a competitive antagonist to ATP and AMP activation. Adenosine, on its own, is an extremely weak agonist of the RyRs and so in the presence of ATP acts as a channel inhibitor. Furthermore, this inhibition could be partially reversed by increasing the nucleotide concentration (Fig. 1 and 5), which is similar to findings in cardiac RyRs (McGarry & Williams, 1994; Ching et al. 1999; Chan et al. 2000). The Hill coefficients of ≥ 2 (depending on P_max) for ATP and AMP activation indicate that activation results somehow from the cooperative binding of two or more such molecules to the RyR. More precise information about the mechanism of ATP binding comes from analysis of open and closed dwell-times and of the competition between ATP and adenosine. The [ATP] dependence of τ_c (N∼2 in eqn (2), see Fig. 7) also indicates that the binding of at least two ATP molecules is needed to cause channel openings. The potency of adenosine inhibition is inversely proportional to the second power of [ATP] (Fig. 5B, 0.5-8 mm ATP), which points to a mechanism whereby the binding of one adenosine molecule can prevent the binding of two activating ATP molecules. Here again is evidence that at least two ATP molecules are needed to activate the channel. These properties are embodied in Scheme 1, which describes the way in which adenosine can act as a competitive agonist to ATP and AMP.

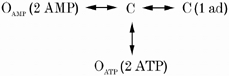
The state C indicates the poorly activated states (i.e. P_o < 0.01) and O_AMP and O_ATP represent the AMP- and ATP-activated states of the RyR. K_ATP, K_AMP and K_ad are the dissociation constants for the binding of ATP, AMP and adenosine to RyRs, respectively. The open probability, based on Scheme 1, is given by eqn (4) in which P_AMP and P_ATP represent the maximal open probabilities attained by AMP and ATP activation, respectively:

(4)

Scheme 1 can account for the nucleotide regulation of RyRs that activate to low levels. It predicts that AMP and ATP activation would have a Hill coefficient of 2 and that n_H= 1 for adenosine inhibition. It gives a good fit to the ATP dependence of adenosine inhibition shown in Fig. 5. The best fit to the data was achieved for K_ATP= 0.4 mm, K_AMP= 0.45 mm and K_ad= 0.06 mm. (The model fit is not shown but it is very similar to the fit shown for Scheme 2, see below.)

However, Scheme 1 does not explain all our data. It does not account for: (1) n_H ∼4 seen in high activity channels, (2) the significant increase in τ_o when P_o exceeds ∼0.2 and (3) the decrease in τ_o that occurs when adenosine inhibits RyRs with high activity (Scheme 1 predicts that inhibition would occur purely by an increase in τ_c and that τ_o would be independent of adenosine concentration). In order to explain these phenomena we need to consider more complex nucleotide regulation mechanisms. Scheme 2 (shown for ATP binding only) is an extension of Scheme 1 in which there is an additional site where ATP, AMP and adenosine molecules can bind competitively to the RyR. The binding of additional ATP (or AMP) can produce an activation state (5) of the RyR that produces relatively long channel openings.

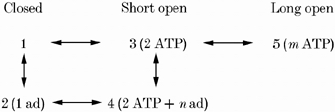
In this scheme, m and n represent the total number of ATP and adenosine molecules, respectively, bound to the RyR. K_ATP2 and K_ad2 are the dissociation constants for the binding of ATP and adenosine to 3, respectively. In Scheme 2, low activity RyRs can only adopt 1-3 whereas high activity RyRs can also adopt 4 and 5. We tried fitting this model to the data in Fig. 5 using different combinations of values of m (3 and 4) and n (1 and 2). A satisfactory fit was obtained only when m = 4 and n = 2. In other words, once RyRs have been partly activated by two ATP molecules, the binding of two additional ATPs may activate them further or they may bind one adenosine molecule and remain only partially activated. The combination of m and n (m, n) of (4, 1) gave a fourth order dependence of adenosine inhibition on [ATP] while (3, 1) and (3, 2) predicted dependencies of adenosine inhibition on [ATP] that were too weak to explain the data in Fig. 5B. In order to explain our finding that K_i for adenosine inhibition is the same in high and low activity RyRs it was necessary to have K_ATP2≈K_ATP and K_ad2≈K_ad. This model for nucleotide regulation predicts that for RyRs activated to high activity by ATP (or AMP) n_H is ∼4 while for low activity RyRs n_H is ∼2. It also predicts that adenosine will decrease τ_o in high activity RyRs via a decrease in the proportion of long channel openings, which is consistent with our findings. However, this model still does not explain the significant difference between K_AMP and the K_a for AMP activation of RyRs.

In Scheme 2, 3-5 appear to represent a very similar binding mechanism to 1-3, suggesting that similar nucleotide binding mechanisms may be operating in different parts of the RyR. Since the RyR is a homotetramer it is quite possible that four identical groups of ATP binding sites exist in the RyR. A physical basis for the Scheme 2 mechanism might be as follows. Each subunit of the RyR binds nucleotides according to Scheme 1. When one subunit in the RyR tetramer becomes activated, the channel opens with a mean dwell time of ∼1 ms. If two subunits are simultaneously active then the channel complex enters a more stable open state with longer mean duration. Though not explicitly included in Scheme 2, simultaneous activation of more subunits could further stabilise the open state to create even longer channel openings. The four time constants seen in the open time distributions (∼1, 10, 40 and 200 ms, see Table 3) may correspond to the simultaneous activation of one to four subunits. There is good evidence that this type of mechanism actually occurs in the cyclic nucleotide gated channel (Ruiz & Karpen, 1997, 1999). Stabilisation of channel openings by simultaneous activation of individual subunits would also explain (1) why changes in τ_o occur via changes in the fraction of events associated with long time constants and (2) why there is a significant increase in τ_o only when P_o exceeds ∼0.2 (Fig. 7C and D). As the activation probability for each subunit exceeds ∼33 %, the probability that two or more subunits are simultaneously active becomes greater than the probability that only one subunit is active. As subunit activation levels cross this threshold during ATP activation or adenosine inhibition the RyR gating switches between being dominated by the longer open states associated with multiple active subunits and by the shorter open states associated with a single active subunit. This model predicts that as RyRs are activated to even higher levels they will tend to do so with larger Hill coefficients and that in the extreme case when RyRs is activated to P_max∼1 the Hill coefficient could reach a maximum of eight. This would happen because at very high levels of ATP activation it is likely that all four subunits are simultaneously active and hence channel openings would be controlled by cooperative binding at eight ATP sites. However, quantitative validation of this homotetrameric model awaits more direct information on subunit interactions within the RyR complex.

The three features of nucleotide regulation of RyR gating listed above are evidently general properties of RyR gating, given that trends similar to those shown for nucleotide-regulated RyRs in Fig. 7C and D have also been seen in cardiac and skeletal RyRs activated by Ca²⁺ (D. R. Laver, unpublished observations;Sitsapesan & Williams, 1994; Copello et al. 1997) and by suramin (Sitsapesan & Williams, 1996).

Physiological relevance

The properties of nucleotide regulation of the RyR described here give important insight into the basis of E-C coupling in skeletal muscle. In vertebrate skeletal muscle, the DHPR/voltage sensors in the T-system in some way directly activate the adjacent RyRs, and the influx of extracellular Ca²⁺ is not required as it is in cardiac muscle (see Introduction). The voltage sensors are able to activate some or all of the RyRs to some degree even when the cytoplasmic [Ca²⁺] is initially only ∼100 nm or lower. Here, the importance of a key difference in the ATP regulation of skeletal and cardiac RyRs becomes apparent. Cardiac RyRs are not appreciably activated by ATP in the presence of resting levels of cytoplasmic Ca²⁺ (e.g. ∼100 nm) (Meissner et al. 1988; Kermode et al. 1998) and, though cytoplasmic ATP augments activation, channel opening can be viewed as being primarily gated by cytoplasmic Ca²⁺, with the influx of extracellular Ca²⁺ activating the RyRs to some degree and the released Ca²⁺ triggering further channel activation and Ca²⁺ release. In contrast, skeletal RyRs are activated appreciably (e.g. P_o∼0.3) by millimolar [ATP] when the cytoplasmic [Ca²⁺] is only at resting levels (∼100 nm) (e.g. Fig. 3 and Meissner et al. 1986, 1988). Thus, the strong activating effect of ATP on the skeletal RyR can explain how the channel can be opened without there being any influx of extracellular Ca²⁺ to act as a trigger.

Furthermore, comparison of the inhibitory effect of adenosine on ATP activation of the RyR found here (Fig. 1 and 5) with that of voltage sensor-mediated Ca²⁺ release indicates that the normal E-C coupling mechanism in skeletal muscle absolutely requires up-regulation of the RyR by ATP. Blazev & Lamb (1999a,b) found that cytoplasmic adenosine inhibited voltage sensor control of Ca²⁺ release in rat skinned muscle fibres, with 0.4 mm adenosine causing some inhibition of release at 2 mm ATP, and 3 mm adenosine virtually eliminating all Ca²⁺ release at 0.5 mm ATP. In skinned fibres, reducing the cytoplasmic [ATP] to 0.5 mm caused significant inhibition of depolarization-induced Ca²⁺ release in rat fibres at 3 mm Mg²⁺ (Blazev & Lamb, 1999a) and an almost 2-fold reduction in amphibian muscle fibres at 1 mm Mg²⁺ (Owen et al. 1996). In contrast to adenosine, IMP did not interfere with voltage sensor-mediated Ca²⁺ release (Blazev & Lamb, 1999b). ATP is also necessary for caffeine-induced Ca²⁺ release and the ability of other nucleotides to interfere is in the following order: adenosine ≫ AMP ≫ IMP (Duke & Steele, 1998; Blazev & Lamb, 1999b). The above results on depolarization-induced and caffeine-induced Ca²⁺ release in skinned fibres are all in good quantitative agreement with the results found in this study on nucleotide activation and inhibition in single skeletal RyRs. These strongly suggest that (a) the effects of nucleotides observed in the skinned fibre studies were due to actions on the RyRs and (b) that ATP stimulation of the RyRs is essential for normal E-C coupling in skeletal muscle fibres in vivo, with the voltage sensor/DHPRs being unable to activate the RyRs in the absence of such ATP stimulation.

Given the strong stimulatory effect of ATP on the skeletal RyRs at ∼100 nm Ca²⁺, the question immediately arises as to why the channels are not largely open in a muscle at rest (i.e. with no voltage sensor stimulation of the RyR). This is evidently because the skeletal RyR has an inhibitory site for Ca²⁺/Mg²⁺ which has a K_i of ∼0.05-0.1 mm (at physiological ionic strength and [Cl⁻], Laver et al. 1997b; Meissner et al. 1997), with the consequence that in the presence of physiological [Mg²⁺] (1 mm) the RyR cannot be substantially activated by cytoplasmic Ca²⁺ and ATP (e.g. maximum P_o≤ 0.1, Meissner et al. 1986, 1988; Donoso et al. 2000) unless the SR is overloaded with Ca²⁺ (Lamb, 2000; Lamb et al. 2001). Thus, as the high peak rate of Ca²⁺ release occurring in vivo is unlikely to be achieved with such a limited P_o (Mejia-Alvarez et al. 1999), the voltage sensor activation of the RyR must overcome or bypass this inhibitory effect of Mg²⁺ at the Ca²⁺/Mg²⁺ site (Lamb & Stephenson, 1991, 1994; Lamb, 2000). Given the above conclusion, that ATP stimulation of the RyRs is required for the voltage sensors to be able to activate the RyRs, and given that such ATP stimulation would be present in a resting fibre, it may be that the voltage sensors could trigger Ca²⁺ release simply by removing the inhibitory effect of Mg²⁺ exerted at the Ca²⁺/Mg²⁺ inhibitory site, possibly by lowering its affinity for Mg²⁺ as suggested previously (see Lamb, 2000). The released Ca²⁺ could then reinforce further activation, increasing P_o to close to unity. Mg²⁺ also binds at the Ca²⁺-activation site on the RyR (Meissner et al. 1986; Laver et al. 1997a) and if this inhibits RyRs even with ATP present, voltage-sensor activation of the RyRs would have to also decrease or remove this second type of Mg²⁺ inhibition (Lamb & Stephenson, 1991). Note that in the present experiments where the RyRs are not being stimulated by the voltage sensors, we had to omit Mg²⁺ in order to measure the activating effects of nucleotides.

Ca²⁺ release in fatigue

The results here also give insight into how changes in the intracellular milieu occurring in exercise can affect RyR function and Ca²⁺ release in skeletal muscle. In agreement with Ca²⁺ release measurements in SR vesicles (Meissner et al. 1986), the results here suggest that activation of the RyR would not be deleteriously affected by a decrease in [ATP] from 8 to 1 mm (Karatzaferi et al. 2001) if it occurred in isolation. However, in a muscle fibre such a decline in [ATP] would be accompanied by an increase in the concentration of the metabolic byproducts of ATP hydrolysis (see Introduction). Accumulation of AMP would be deleterious not only because it would lead to an increase in [ADP] (because of back-inhibition of the reaction 2ADP → AMP + ATP), but also because it would interfere with optimal ATP activation of the RyR, because AMP is a competitive, weak agonist (Fig. 3). (Accumulation of ADP will also be deleterious because it is likely to be a competitive agonist on the RyRs (Kermode et al. 1998). The effect of ADP was not explicitly examined here because the experiments were specifically designed to match the voltage sensor-induced calcium release experiments of Blazev & Lamb (1999a,b).) If AMP were simply further hydrolysed to adenosine, it is clear that the competitive inhibition with ATP at the RyR would be far worse (Figs 1 and 5). In normal skeletal muscle, the problem of adenosine competition with ATP is avoided by rapidly deaminating virtually all AMP to IMP (Sabina et al. 1984; Nagesser et al. 1992, 1993), which has no detectable inhibitory effect on the skeletal RyR (Fig. 6 and Blazev & Lamb, 1999b). The likely importance of this deamination process to normal E-C coupling would explain why myoadenylate deaminase is localised at the junction of the A-I band in mammalian muscle fibres (van Kuppevelt et al. 1994), where the triad junction is also located.

Finally, it is possible that adenosine accumulation does interfere with ATP activation of the RyR in individuals with myoadenylate deaminase deficiency (MDD) and hence contributes to the more rapid onset of muscle fatigue observed in some such individuals (Sabina et al. 1984). Though the average concentration of adenosine measured in the cytoplasm in such cases is relatively low (reaching only ∼50-200 μm with exercise in MDD subjects, cf. < 10 μm in normal subjects), it is quite possible that this is a considerable underestimate of the concentration reached in a restricted space such as the triad junction. (The [adenosine] may also be underestimated owing to measurement problems arising from the rapid resynthesis of adenosine → AMP → ADP → ATP, driven by hydrolysis of the remaining creatine phosphate.) Likewise, the [ATP] in the triad junction may decrease substantially below the minimum measured in the cytoplasm as a whole, particularly as the rate of ATP hydrolysis may be relatively high owing to the high density of ATPases in the terminal cisternae of the SR (Franzini-Armstrong & Jorgensen, 1994) and the T-system. The results of this study indicate that, in such a situation, ATP stimulation of the RyR would be markedly hindered (Fig. 5), thus possibly contributing to reduced Ca²⁺ release and muscle fatigue (Blazev & Lamb, 1999b).