Gap Junction Channels Exhibit Connexin-specific Permeability to Cyclic Nucleotides

Abstract

Gap junction channels exhibit connexin dependent biophysical properties, including selective intercellular passage of larger solutes, such as second messengers and siRNA. Here, we report the determination of cyclic nucleotide (cAMP) permeability through gap junction channels composed of Cx43, Cx40, or Cx26 using simultaneous measurements of junctional conductance and intercellular transfer of cAMP. For cAMP detection the recipient cells were transfected with a reporter gene, the cyclic nucleotide-modulated channel from sea urchin sperm (SpIH). cAMP was introduced via patch pipette into the cell of the pair that did not express SpIH. SpIH-derived currents (I _h) were recorded from the other cell of a pair that expressed SpIH. cAMP diffusion through gap junction channels to the neighboring SpIH-transfected cell resulted in a five to sixfold increase in I _h current over time. Cyclic AMP transfer was observed for homotypic Cx43 channels over a wide range of conductances. However, homotypic Cx40 and homotypic Cx26 exhibited reduced cAMP permeability in comparison to Cx43. The cAMP/K⁺ permeability ratios were 0.18, 0.027, and 0.018 for Cx43, Cx26, and Cx40, respectively. Cx43 channels were ∼10 to 7 times more permeable to cAMP than Cx40 or Cx26 (Cx43 > Cx26 ≥ Cx40), suggesting that these channels have distinctly different selectivity for negatively charged larger solutes involved in metabolic/biochemical coupling. These data suggest that Cx43 permeability to cAMP results in a rapid delivery of cAMP from cell to cell in sufficient quantity before degradation by phosphodiesterase to trigger relevant intracellular responses. The data also suggest that the reduced permeability of Cx26 and Cx40 might compromise their ability to deliver cAMP rapidly enough to cause functional changes in a recipient cell.

INTRODUCTION

Gap junction channels represent the only selective intercellular communication pathway that is exclusive of the extracellular space allowing ions and various solutes to pass from one cell interior to another. There are three families of proteins that potentially are able to form gap junction channels. These are the connexins, innexins, and pannexins. The connexins form gap junction channels in chordates, while innexins perform the same function in many invertebrate species. Pannexins are also found in chordates but their ability to form gap junctions has only been documented in vitro and their in vivo functions are not yet completely defined (Bruzzone et al., 2003; Barbe et al., 2006).

Of particular interest are the connexins that are able to coordinate activity such as action potential propagation in cardiac muscle and nerve (Barr et al., 1968; Weidmann, 1970; Bennett and Goodenough, 1978). Two key features of gap junction channels that facilitate action potential propagation are permeability to monovalent cations (Veenstra et al., 1995; Brink, 1996; Valiunas et al., 1997; Wang and Veenstra, 1997) and open probabilities approaching unity (Brink et al., 1996; Christ and Brink, 1999; Ramanan et al., 2005). In tissues such as vascular smooth muscle, vasomotor tone is, in part, reliant on gap junction permeability to metabolites and solutes such as Ca²⁺, IP₃, and cAMP (Christ et al., 1993; Christ et al., 1996; Melman and Rehman, 1999).

There are over 20 identified connexins within the human genome and all appear to be permeable to monovalent cations and to a lesser extent, anions (Harris, 2007). In addition, connexins also allow the passage of a variety of solutes, including second messengers, polypeptides, and siRNA (Niessen et al., 2000; Goldberg et al., 2004; Valiunas et al., 2005; Bedner et al., 2006). Permeability/selectivity to exogenous and endogenous solutes has been found to be connexin specific (Valiunas et al., 2002; Goldberg et al., 2004; Valiunas et al., 2005; Harris, 2007). In most cases where permeability/selectivity has been assessed, the approach has been to compare a probe's permeability for two different connexins (Elfgang et al., 1995; Niessen et al., 2000; Goldberg et al., 2004), but in some cases simultaneous measurement of junctional conductance and probe permeability to a specific connexin has been determined (Valiunas et al., 2002; Brink et al., 2006). The permeability of gap junction channels to the cyclic nucleotides cAMP and cGMP is of particular interest as both are important messengers in many cellular and tissue processes, including normal bone development, cardiac myocyte contractility and pacing, vascular tone, and intercellular signaling in the cochlea (Tsien and Weingart, 1976; Caverzasio and Bonjour, 1996; Christ et al., 1996; Zhao, 2005; DiFrancesco, 2006). To better understand the permeability properties of homotypic connexin gap junction channels and their role in defining coordinated tissue function we have chosen to measure junctional conductance while simultaneously monitoring the permeability of the second messenger cAMP in three cell lines expressing wild type Cx43, Cx40, or Cx26. To accomplish this we use patch clamp methods on cell pairs where one cell of a pair had been transfected with the cyclic nucleotide reporter gene SpIH and the other, nontransfected cell, is the source of cAMP delivered by a patch pipette.

MATERIALS AND METHODS

Cells and culture conditions

Experiments were performed on HeLa or N2A cells stable transfected with wild type Cx26, Cx40, or Cx43. Production and characterization of these cells, culture conditions, and staining methods for identification of specific cells have been described previously (Valiunas et al., 2000; Valiunas et al., 2001; Gemel et al., 2004; Valiunas et al., 2004). Electrophysiological measurements and cAMP flux studies were performed on cells cultured for 1–3 d.

Electrophysiological Measurements

Experiments were performed on cell pairs. A dual voltage-clamp method and whole-cell/perforated patch recording were used to control the membrane potential of both cells and to measure currents (Valiunas et al., 2001, 2002). For electrical recordings, glass coverslips with adherent cells were transferred to an experimental chamber mounted on the stage of an inverted microscope (Olympus IX71) equipped with fluorescence imaging system. The chamber was perfused at room temperature (∼22°C) with bath solution containing (in mM) NaCl, 150; KCl, 10; CaCl₂, 2; HEPES, 5 (pH 7.4); glucose, 5; 2 mM CsCl and BaCl₂ were added. The patch pipettes were filled with solution containing (in mM) K⁺ aspartate⁻, 120; NaCl, 10; MgATP, 3; HEPES, 5 (pH 7.2); EGTA, 10 (pCa ∼8); filtered through 0.22-μm pores. In some experiments K⁺ aspartate⁻ was replaced by an equimolar amount of Na⁺ aspartate⁻. For perforated patch experiments, the pipette solution contained 30–50 μM β-escin (Fan and Palade, 1998). Patch pipettes were pulled from glass capillaries (code GC150F-10; Harvard Apparatus) with a horizontal puller (DMZ-Universal, Zeitz-Instrumente). When filled, the resistance of the pipettes measured 2–5 MΩ.

cAMP Flux Studies

cAMP transfer through gap junction channels was investigated using cell pairs. For cAMP detection, the recipient cells were transfected with a reporter gene, a cyclic nucleotide-modulated channel from sea urchin sperm (SpIH) (Gauss et al., 1998; Shin et al., 2001). cDNA of SpIH (a gift of G. Yellen, Harvard Medical School, Boston, MA) was subcloned into the eukaryotic expression vector pIRES2-EGFP (CLONTECH Laboratories, Inc.). For later identification, another population of cells was transfected with red fluorescent protein (RFP) (pIRES2-DsRed2, CLONTECH Laboratories, Inc.). SpIH and RFP-transfected cells were co-cultured. Green eGFP and red RFP signals were visualized under a fluorescent microscope and only pairs consisting of one SpIH and one RFP-transfected cells were chosen for cAMP transfer measurements.

cAMP was introduced via patch pipette into the cell of the pair that did not express SpIH, and SpIH-derived currents were recorded from the cell expressing SpIH. cAMP (Sigma-Aldrich) was dissolved in the pipette solution to reach a concentration of 500 μM. To prevent cAMP degradation a membrane-permeable phospodiesterase inhibitor IBMX (200 μM, Sigma-Aldrich) was added to the bath solution. Additionally, an adenylate cyclase inhibitor 2’,5′ dideoxyadenosine (5 μM, Calbiochem) was added to the pipette and bath solutions to inhibit intracellular cAMP production. The quantitative channel permeability was determined using simultaneous measurement of junctional conductance and intercellular transfer of cAMP.

Signal Recording and Analysis

Voltage and current signals were recorded using patch clamp amplifiers (Axopatch 200B). The current signals were digitized with a 16 bit A/D-converter (Digidata 1322A; Molecular Devices) and stored with a personal computer. Data acquisition and analysis were performed with pClamp9 software (Molecular Devices). Curve fitting and statistical analyses were performed using SigmaPlot and SigmaStat, respectively (Jandel Scientific). The results are presented as means ± SEM.

RESULTS

Characterization of Reporter Gene Currents

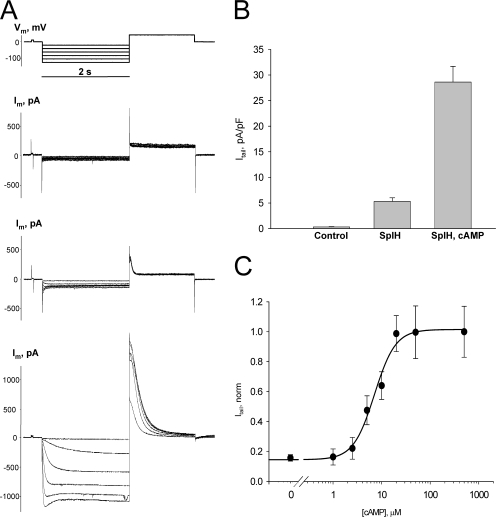
To detect intercellular cAMP permeation, HeLa or N2A cells expressing Cx40, Cx43, or Cx26 were transfected with a reporter gene, the cyclic nucleotide-modulated channel from sea urchin sperm (SpIH) (Gauss et al., 1998; Shin et al., 2001). The activity of SpIH channels in transfected cells was first determined using single whole cell patch clamp. Fig. 1 A shows the voltage protocol (top) along with the resultant nonjunctional membrane currents (I_m) recorded from three different HeLa cells: the upper most currents are from a cell not transfected with SpIH, the middle current record is from an SpIH-transfected cell with no cAMP in the patch pipette and the lower current recording is from an SpIH-transfected cell with 50 μM cAMP in the pipette. Hyperpolarizing voltage pulses delivered from a holding potential of 0 mV to test potentials between −20 and −120 mV produced time and voltage-dependent inward and tail currents (V_m = +50 mV) in SpIH-transfected cells (middle and bottom current records), whereas the SpIH-lacking cell (top current trace) showed negligible currents. When cAMP was present in the pipette solution, SpIH-transfected cells exhibited larger currents. The tail current amplitudes recorded after a voltage step to V_m = −100 mV for all three types of cells are summarized in Fig. 1 B. Intracellular application of cAMP increased the peak current level by more than fivefold on average in comparison to the SpIH-transfected cells not treated with cAMP (28.6 ± 3.1 pA/pF versus 5.3 ± 0.7 pA/pF). To generate a dose–response curve for the cyclic nucleotide-gated SplH channel, SpIH currents were recorded from single cells in whole cell patch clamp configuration where the patch pipette contained known concentrations of cAMP. Intracellular perfusion with cAMP increased SpIH currents in a dose-dependent manner. The dose–response curve for SpIH is summarized in Fig. 1 C. SpIH current density varied over an order of magnitude between 1 and 25 μM cAMP and the Hill equation was fit to the data with E_C50 of 7.1 μM and a Hill slope of 2.01. A calculated E_C90 of ∼20 μM was assumed as a saturating concentration of cAMP for SpIH channel in our experimental conditions. All experiments done to generate the dose–response curve were performed in the presence of phosphodiesterase and adenylate cyclase inhibitors IBMX and 2’,5′ dideoxyadenosine, respectively.

Figure 1.

Properties of SpIH channels. (A) Voltage protocol (V_m) and whole cell currents (I_m) recorded in control, untransfected (top), and SpIH-transfected HeLa cells in the absence (middle) or presence (bottom) of 50 μM cAMP. I_m were elicited by 2-s voltage pulses delivered from a holding potential of 0 mV to test potentials between −20 and −120 mV, in 20-mV increments, and returning to a tail potential of +50 mV. I_m increased in SpIH-transfected cells when cAMP was present in the pipette solution. (B) Average of tail current densities measured after voltage step to V_m = −100 mV from control cells (0.3 ± 0.05 pA/pF, n = 7), SpIH-transfected cells (5.3 ± 0.7 pA/pF, n = 13), and SpIH-transfected cells with 50 μM cAMP in the pipette (28.6 ± 3.1 pA/pF, n = 13). Data represent means ± SEM. (C) Dependence of the SpIH current on intracellular cAMP concentration. Solid line represents best fit of data to the Hill equation with E_C50 = 7.1 μM, Hill slope = 2.01. Data represent means ± SEM, obtained from a total 48 cells at V_m = −100 mV. The experiments were performed in the presence of IBMX and 2’,5′ dideoxyadenosine.

Detection of Intercellular Transfer of cAMP

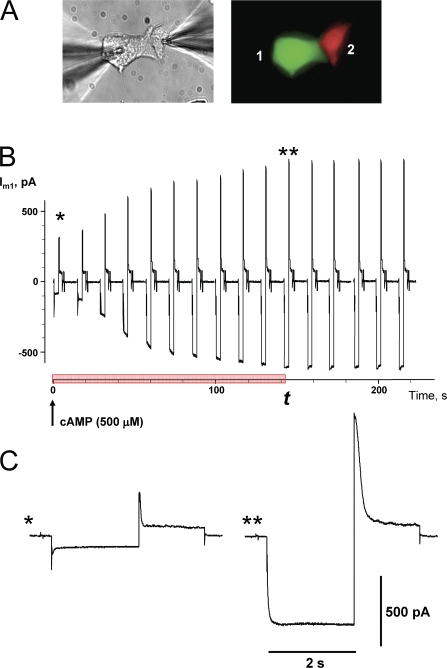
The detection of cAMP transfer between cells of a pair was accomplished by coculturing HeLa or N2A cell pairs where one cell expressed eGFP and SpIH, while the other expressed RFP only (green and red cells, respectively in Fig. 2 A). This allowed assessment of cAMP transfer by monitoring the activity of SpIH current while measuring junctional conductance using dual patch clamp. In this configuration one pipette was in whole cell mode and contained 500 μM cAMP and the recipient cell, containing SpIH, was in perforated patch mode. An example of the activation of SpIH current in recipient cell is shown in Fig. 2 B. Currents recorded from the SpIH-expressing cell were derived in response to voltage pulses from a holding potential of 0 to −100 mV and returning to a tail potential of +50 mV. SpIH currents increased over time to a new steady-state value due to cAMP diffusion from cell 2 to cell 1. Examples of the SpIH current activation for the record shown in Fig. 2 B are shown in Fig. 2 C, one at the time the whole cell patch was opened (*) and the other 135 s later when the SpiH current became saturated with cAMP from cell 2 (**).

Figure 2.

Detection of intercellular transfer of cAMP. (A) Cell pair where one cell expressed SpIH-eGFP (green cell) and the other expressed RFP only (red cell). 500 μM cAMP was delivered via patch pipette into the red cell that did not express SpIH and SpIH currents were recorded from cell expressing SpIH in perforated patch mode. Both cells express Cx43. (B) Current recorded from the SpIH-expressing cell, in response to voltage pulses from a holding potential of 0 to −100 mV, returning to a tail potential of +50 mV. The arrow indicates the opening of the patch into whole cell recording mode and the beginning of cAMP delivery into the donor cell. SpIH current over time increased to steady state. The red bar on time axis indicates SpIH current activation time interval t during which current reaches saturation.(C) Segments of SpIH current records when the whole cell patch was opened (*) and 135 s later with saturated current (**).

cAMP Diffusion through Homotypic Cx26, Cx40, and Cx43 Channels

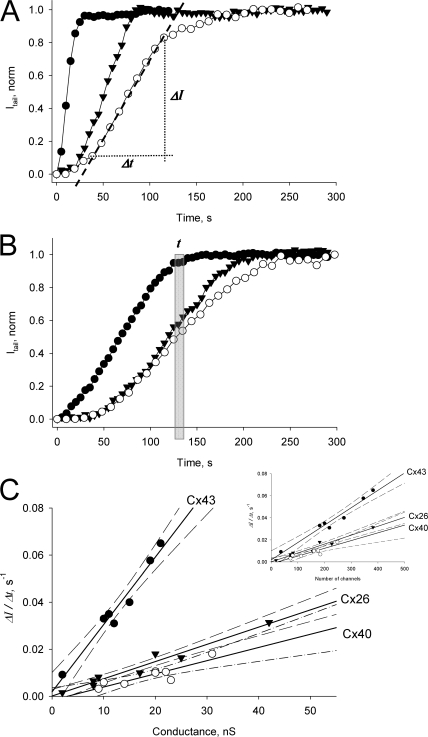
cAMP transfer experiments were performed on HeLa cell pairs expressing wild-type Cx26, Cx40, or Cx43 as illustrated in Fig. 2. SpIH cAMP-dependent currents were recorded from the recipient cell during cAMP application. Fig. 3 (A and B) shows examples of normalized SpIH tail currents in the recipient cell plotted versus time for Cx43 (•), Cx40 (○), and Cx26 (▾) at different conductance values. Since saturation of SpIH current occurs with 20 μM cAMP in the recipient cell as indicated by the dose–response curve (Fig. 1 C), it is clear from Fig. 3 (A and B) that cAMP accumulates in Cx43-expressing cells faster than for Cx40 or Cx26 cells.

Figure 3.

(A and B) Plots of normalized tail current versus time recorded from the recipient cells after cAMP injection into the source cell for cell pairs expressing Cx43 (•): g_j = 19 nS (A), and 2 nS (B); Cx26 (▾): g_j = 25 nS (A), and 8 nS (B); and Cx40(○): g_j = 22 nS (A) and 10 nS (B). SpIH activation time, t corresponds to the time when SpIH current reaches saturation in the recipient cell. The first order regression over the linear part of the plots (dashed line shown in Cx40 plot, A) was used to determine current activation rate ΔI/Δt. (C) Summarized plots of the SpIH tail current activation rate (ΔI/Δt) versus junctional conductance for Cx43 (•), Cx26 (▾), and Cx40(○). The solid lines correspond to the first order regressions with the following slopes: (30.0 ± 2.5) · 10⁻⁴ s⁻¹/nS for Cx43, (7.3 ± 0.6) · 10⁻⁴ s⁻¹/nS for Cx26, and (4.8 ± 1.1) · 10⁻⁴ s⁻¹/nS for Cx40. The dashed lines are the 95% confidence intervals. The experiments were performed in the presence of IBMX and 2’,5′ dideoxyadenosine. Insert: current activation rate (ΔI/Δt) versus channel number for all three connexins with slopes of (1.6 ± 0.1) · 10⁻⁴ s⁻¹/channel for Cx43 (•), (0.8 ± 0.07) · 10⁻⁴ s⁻¹/channel for Cx26 (▾), and (0.6 ± 0.1) · 10⁻⁴ s⁻¹/channel for Cx40 (○).

We monitored the time course of SpIH cAMP dependent current activity relative to junctional conductance and calculated the parameter ΔI/Δt, which is defined as the change in SpIH tail current divided by the time to attain the maximum current increase rate. ΔI/Δt was obtained by fitting the linear part of the SpIH current–time relationship as shown in Fig. 3 A. It represents the SpIH current increase due to cAMP accumulation in the recipient cells, after it has permeated through gap junction channels between the source cell and the recipient cell. The ratio ΔI/Δt was then plotted versus measured junctional conductance (g_j), as summarized in Fig. 3 C for Cx43 (•), Cx40 (○), and Cx26 (▾). There is a distinct relationship between ΔI/Δt and g_j for each connexin. The solid lines represent a linear fit with the following slopes: (30.0 ± 2.5) · 10⁻⁴ s⁻¹/nS for Cx43, (7.3 ± 0.6) · 10⁻⁴ s⁻¹/nS for Cx26, and (4.8 ± 1.1) · 10⁻⁴ s⁻¹/nS for Cx40, and the dashed lines represent the 95% confidence intervals. Comparison of regression lines by analysis of covariance (Prism, GraphPad) revealed that the differences between Cx43 slope and Cx26 or Cx40 slopes were extremely significant (P < 0.0001). Analysis of Cx26 and Cx40 regression lines showed that the slopes are not significantly different (P = 0.099), although the differences between the elevations were significant (P = 0.0025). Since unitary conductances of all three connexins are known, the ratio ΔI/Δt then was plotted versus channel number for all three connexins (Fig. 3 C, inset). The slope analysis for ΔI/Δt versus the number of channels revealed the same pattern. All of the data shown in Fig. 3 were collected in the presence of 200 μM IBMX and 5 μM 2’5′dideoxyadenosine to inhibit endogenous degradation or biosynthesis of cAMP in the cytoplasm.

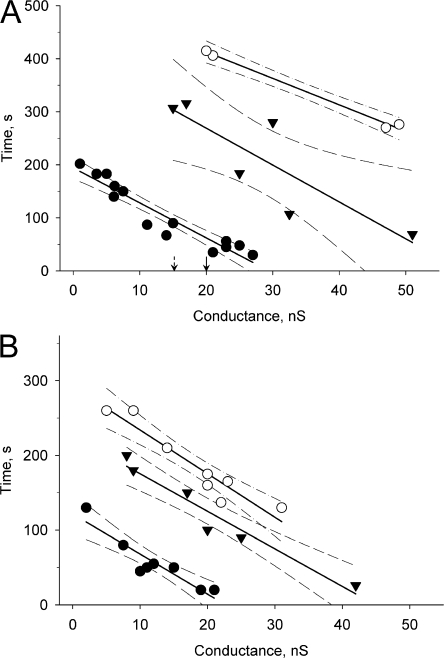
We also compared cells under physiological conditions without IBMX and 2’5′dideoxyadenosine with those in a pool of IBMX and 2’5′dideoxyadenosine-exposed preparations to assess whether or not there was significant degradation of cAMP over the time course of our experiments. For this analysis we measured time t (see Fig. 2 B and Fig. 3 B), for the SpIH current to reach saturation in the recipient cell (i.e., ∼20 μM of cAMP) after cAMP delivery to the donor cell. Fig. 4 shows the datasets for non-IBMX–treated and IBMX-treated cell pairs plotted versus g_j for all three connexins. These data show that there is a reduction in the delivered cAMP without inhibition of phospodiesterase. The time to SpIH current saturation is reduced in IBMX and 2’5′dideoxyadenosine-treated cells for all three connexins, indicating that the effective free pool of cAMP delivered to the reporter gene SpIH is reduced if IBMX and 2’5′dideoxyadenosine are not present. Interestingly, we found that without IBMX or 2’5′dideoxyadenosine, cAMP transfer was detected only in well-coupled cell pairs of Cx26 (>15 nS) and Cx40 (>20 nS). In Fig. 4 A the arrows pointing to 15 and 20 nS on the X axis indicate the minimal coupling to detect cAMP transfer for Cx26 and Cx40, respectively.

Figure 4.

Plots of the SpIH activation time versus junctional conductance for Cx43 (•), Cx26 (▾), and Cx40 (○) in the absence (A) and presence (B) of phosphodiesterase (IBMX) and adenylate cyclase inhibitors (2’,5′ dideoxyadenosine). The SpIH activation times were reduced in IBMX and 2’5′dideoxyadenosine-treated cells and were reciprocally proportional to junctional conductance. The solid lines correspond to the first order regression and the dashed lines are the 95% confidence intervals. The arrows pointing to 15 and 20 nS indicate the threshold for detection of cAMP in recipient cell for Cx26 and Cx40, respectively.

cAMP Effect on Junctional Conductance

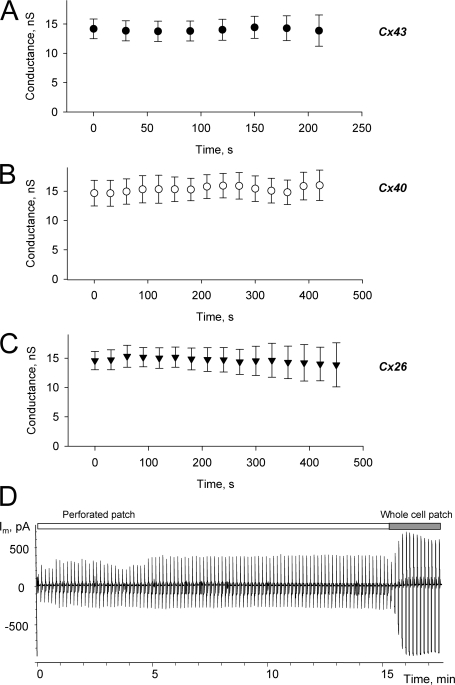
An important control experiment is the determination of cAMP effects, if any, on junctional conductance. Junctional conductance was monitored in all experiments using a V_j step of 10 mV with a duration of 50 ms. Fig. 5 shows summarized plots of g_jversus time for cell pairs expressing Cx43, Cx26, or Cx40, measured during the delivery of cAMP to the donor cell. All measurements were done in the presence of IBMX and 2’5′dideoxyadenosine. Over the time course of the experiment, no statistically significant alteration in junctional conductance was observed for Cx43, Cx40, or Cx26. This is in apparent contradiction to previous studies that showed a rapid (minutes) increase in junctional conductance of ∼25% for Cx40 transfected into SKHep1 cells using dual whole cell patch (Van Rijen et al., 2000). We used a perforated patch mode with one cell of the pair (recipient cell), which might represent a reason for the apparent difference. It is also quite possible that HeLa cells do not possess the same molecular machinery as SKHep1 cells, since we were not able to distinguish any difference on junctional conductance between IBMX- and 2’5′dideoxyadenosine-treated or nontreated cell pairs.

Figure 5.

(A–C) Plots of junctional conductance versus time from Cx43 (•, n = 9), Cx40 (○, n = 12), and Cx26 (▾, n = 12) expressing cell pairs, measured during the application of cAMP to the donor cell. Data represent means ± SEM. (D) Current recorded from the single SpIH-expressing cell with 20 μM cAMP in the pipette in perforated patch mode. There was no detectable SpIH current increase in perforated patch mode, and SpIH current increased dramatically when perforated patch was converted to the conventional whole cell patch clamp (around 15 min time mark). See text for details. All measurements were done in the presence of IBMX and 2’5′dideoxyadenosine.

Another important issue is the possibility of cAMP diffusion through the pores formed by β-escin in the pipette tip of the recipient cell. Although there are reports that larger molecules can diffuse through β-escin pores, the perforating efficacy is concentration and time dependent (Kobayashi et al., 1989; Iizuka et al., 1994; Tansey et al., 1994). In previous studies we did not detect significant Lucifer yellow (LY) diffusion into the pipette from recipient cell when β-escin was used for perforated patch (Valiunas et al., 2002). To determine if cAMP was able to diffuse through β-escin pores we performed a number of single whole cell experiments to estimate if there was significant cAMP diffusion through β-escin pores in the perforated recording mode. An example of one experiment is shown in Fig. 5 D. A single SpIH transfected cell was patched with 50 μM β-escin and 20 μM cAMP in the pipette. There was no detectable SpIH current increase for ∼10 min after complete formation of the perforated patch (between 4 and 5 min time mark). However, there was a dramatic increase of SpIH currents when the perforated patch mode was converted to the conventional whole cell patch by purposely breaking the patch after 15 min. The stability of the SpIH current using perforated patch for over 10 min is sufficiently long to allow reasonable estimates of cAMP in the recipient delivered from a coupled source cell without concern that the cAMP concentration in the recipient cell will be diluted by diffusion into the volume of the pipette. In addition, Arnould et al. (1996) reported that the exposure of endothelial cells to β-escin does not cause loss of ATP. Thus we conclude that cAMP washout from the cell was insignificant and/or beyond the time frame of duration of our experiment.

Lucifer Yellow Transfer through Cx26 Channels

Previously, we reported the permeability of LY, relative to the ubiquitous monovalent cation K⁺, for Cx43 and Cx40 channels (Valiunas et al., 2002).

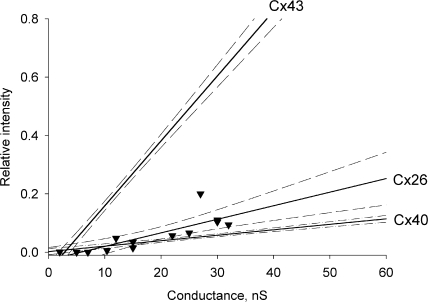
To compare cAMP transfer to LY transfer for all three connexins, using the same method of simultaneous measure of g_j and LY transfer as in Valiunas et al. (2002), we determined LY permeability for Cx26-transfected HeLa cells. Fig. 6 presents a summary of data from (Valiunas et al., 2002) for Cx43 and Cx40 where the ratio of recipient cell fluorescence intensity relative to the source cell is plotted versus measured g_j 12 min after introduction of LY into the source cell. The new data obtained from HeLa Cx26 cell pairs are shown as individual points (▾) and were fit by a first order regression (solid line) with a slope of 0.0035/nS. Thus, Cx26 has permeability characteristics for LY that are similar to Cx40.

Figure 6.

Summary of LY flux data versus junctional conductance for Cx43, Cx26, and Cx40 cell pairs. Each data point for Cx26 (▾) represents a recipient cell fluorescence intensity over injected cell fluorescence intensity 12 min after LY injection (Valiunas et al., 2002). The solid lines correspond to the first order regressions and the dashed lines represent confidence intervals (95%) for each plot. See text for references on derivation of regression lines for Cx40 and Cx43.

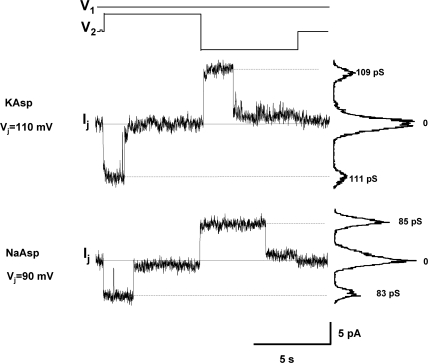
For later assessment of Cx26 selectivity properties (see below) and determination of LY flux per channel, the unitary conductance of channel has to be defined. Fig. 7 shows single channel recordings from Cx26 cell pairs. Using 120 mM K⁺ aspartate⁻ solution, single channel conductance (γ_j) was 109–111 pS. With 120 mM Na⁺ aspartate⁻ pipette solution, γ_j was 83–85 pS. These data are consistent with Cx26 unitary conductance values reported previously (Suchyna et al., 1999; Valiunas et al., 1999; Yum et al., 2007).

Figure 7.

Single channel properties of Cx26 channels. Voltage protocol (top) and single channel currents recorded from homotypic Cx26 cell pairs with pipette solutions of different ionic compositions. Top: K⁺ aspartate⁻ pipette solution. Transjuctional voltage V_j = 110 mV, the current histograms yielded γ_j of 111pS/109 pS for negative/positive V_j. Bottom: Na⁺ aspartate⁻ pipette solution, V_j = 90 mV, γ_j = 83 pS/85 pS for negative/positive V_j.

Determination of cAMP Permeability for Cx26, Cx40, and Cx43

The majority of connexins are permeable to monovalent cations but lack selectivity between them (Beblo and Veenstra, 1997; Wang and Veenstra, 1997; Brink et al., 2000). In contrast, the permeability to monovalent anions, exogenous anionic probes and labeled endogenous species such as metabolites has been shown to be connexin specific (Veenstra et al., 1995; Beblo and Veenstra, 1997; Wang and Veenstra, 1997; Suchyna et al., 1999; Valiunas et al., 2002; Goldberg et al., 2004; Valiunas et al., 2005), and the data presented here further demonstrate the specificity of connexin permeability/selectivity for a universal second messenger, cAMP. To illustrate this point we calculated the transfer rates of cAMP molecules or K⁺ ions per channel per second (species/channel/second) and then computed the ratio of cAMP to K⁺ for Cx43, Cx40, and Cx26. We used a 23.4-mV voltage step, which is approximately equivalent to a 10× concentration gradient, to calculate the number of K⁺ ions transported/channel/second. The ionic flux for a 10× concentration gradient in the absence of a voltage gradient is j = pΔC, where j-flux (moles/s), p-single channel permeability (cm³/s), ΔC-concentration gradient (moles/cm³). The ionic flux driven by a voltage gradient (ΔΨ) to create a flux equivalent to a 10× concentration when the concentrations are in fact equal on either side of a membrane is defined as j = pCΔΨ/(RT/F), where C is the concentration, R is the universal gas constant, F is the Faraday constant, T is temperature, and RT/F = 26 mV. Combining the two equations and rearranging to solve for ΔΨ yields the following: ΔΨ = (ΔC/C)(RT/F). For any 10× gradient ΔC/C = 0.9, and solving for ΔΨ gives a voltage of 23.4 mV.

The unitary current for a 55 pS Cx43 channel in 120 mM K⁺ solution (Valiunas et al., 2002) with a transjuctional voltage step of 23.4 mV is then 1.29 pA. To determine the total number of K⁺ ions moving through a channel for 1 s, the electron charge (e = 1.6 · 10⁻¹⁹ C) is divided into the unitary current (1.29 · 10⁻¹² A) to yield 8.0 · 10⁶ ions/channel/second for Cx43. Using a unitary conductance of 125 pS for Cx40 (Valiunas et al., 2002) yielded 18.2 · 10⁶ K⁺ ions/channel/second. Similarly, using a unitary conductance of 110 pS for Cx26 (Fig. 7 and Valiunas et al., 1999) gave 16.1 · 10⁶ K⁺ ions/channel/second for Cx26. Based on published studies for the anion/cation conductance ratio (Beblo and Veenstra, 1997; Wang and Veenstra, 1997; Suchyna et al., 1999) for all three connexins we have assumed that the major current carrier is K⁺ and aspartate conductance is insignificant.

The assay method for determining cAMP transfer yields a time course to saturation for SpIH current in the recipient cell (Fig. 2) that is dependent on the magnitude of junctional conductance (Fig. 3). Determination of ΔI/Δt allowed an estimate of the intracellular concentration of cAMP in the recipient cells via utilization of normalized dose–response curve for the tail currents (Fig. 1 C). The fit of the linear part of cAMP concentration dose–response curve (Fig. 1 C) between 5 and 10 μM yielded a slope for SpIH normalized tail current of 0.048/μM. This linear part of dose–response curve corresponds to the linear part of normalized SpIH tail current increase over time (Fig. 3 A). The normalized SpIH current increase over time (ΔI/Δt) is g_j dependent and for Cx43 it yields a slope of 0.003 s⁻¹/nS (Fig. 3 C). Thus the cAMP flux permeating Cx43 junctions can be calculated as follows: 0.003 s⁻¹/nS · 10⁻⁶ M/0.048 = 6.2 · 10⁻⁸ M/s/nS . The total number of cAMP molecules (MN) that transfer from the injected or source cell to the recipient cell can be determined: MN = V_c·ΔC·N_A, where V_c is the cell volume, ΔC is the flux concentration, and N_A is Avogadro's number. The average cell volume for HeLa cells we assumed to be 1.8 pL (Rackauskas et al., 2007). A similar cell volume range (1.6–2.2 pL) for HeLa cells was determined by Hernandez et al. (2007). Then the total number of cAMP molecules that transfers to the recipient cell in 1 s for a Cx43 junctional conductance of 1 nS is 67,183 (6.2 · 10⁻⁸ M/s/nS · 1.8 pL ·N_A). Assuming a 55 pS unitary conductance for Cx43, the number of cAMP molecules passing per channel per second becomes 3,732 molecules/channel/second. Analogous cAMP flux calculations using slopes obtained from data in Fig. 3 C (0.00074 s⁻¹/nS for Cx26 and 0.00048 s⁻¹/nS for Cx40) yielded 1,805 and 1,355 molec/chann/sec for Cx26 and Cx40, respectively. These fluxes represent experimental conditions and are not corrected to equivalent concentration gradients.

To allow an accurate determination of cAMP permeability relative to K⁺, both species concentrations must be normalized. After whole cell patch configuration is established on the donor cell, the cAMP diffuses from the pipette to the cell reaching the equilibrium concentration, which equals pipette concentration. The rate of cAMP concentration change in the injected cell depends on the entry via the pipette (Oliva et al., 1988) and the diffusion time constant from the pipette can be calculated: τ_p = R_p·V_c/D·p, where R_p is the pipette resistance (Ω), V_c is the cell volume (cm³), D is the diffusion coefficient (cm²/s), and p is the resistivity of the pipette filling solution(Ωcm) (Mathias et al., 1990). Assuming our experimental conditions (R_p = 4 MΩ, V_c = 1.8 pL, D_cAMP = 2.7 · 10⁻⁶ cm²/s [Chen et al., 1999] and p_Kasp = 120 Ωcm) τ_p turned out to be ∼22 s. If we assume no flux across the membrane, then the cAMP concentration in the injected cell (C_i) at any time (t) can be simply calculated: C_i(t) =C_p(1 − e ^{− t/τp}), where C_p is the cAMP concentration in the pipette. At g_j ∼20 nS for Cx26 and Cx40 in the presence of IBMX, the SpIH current in the recipient cell saturates at times greater than 100 s (Fig. 4 B) while the cAMP concentration in injected cell is within 10% of the pipette concentration, i.e., 500 μM. This is not the case for Cx43, where junctional conductances of 20 nS result in saturated SpIH currents over a shorter time interval (∼20 s), where the calculated concentration of cAMP C_i in the source cell is 275 μM.

For a comparison of cAMP with K⁺ the differences in concentrations in the pipette, i.e., in the donor cell, must therefore be taken into account, 120 mM for K⁺ versus 500 μM for cAMP (240×), raising the cAMP transfer rate to 4.33 · 10⁵ molec/chann/sec and 3.25 · 10⁵ molec/chann/sec for Cx26 and Cx40, respectively. In the case of Cx43 at g_j ∼20 nS, a factor of 436× (120 mM for K⁺ versus 275 μM) yielded 16.3 · 10⁵ molec/chann/sec. For junctional conductances ≥10 nS, with times to saturation for the recipient cells that were shorter than 50 s, a source cell concentration was computed for the time to saturation to allow for an accurate estimate of the cAMP/K⁺ ratio. Accordingly the calculated averaged cAMP/K⁺ ratios for Cx43, Cx40, and Cx26 were 0.180, 0.018, and 0.027, respectively. cAMP fluxes corrected to the 500 μM cAMP concentration together with unitary conductances and LY (2 mM) fluxes for all three connexins are given in Table I.

TABLE I.

Permeability Properties of Cx26, Cx40, and Cx43 Channels to cAMP and LY

	Cx26	Cx40	Cx43
Unitary conductance (pS)	110	125	55
cAMP flux (molecules/channel/sec)a	1870	1355	5880
LY flux (molecules/channel/sec)a	1166	720	3744

^aCorrected for concentrations of 500 μM (cAMP) and 2 mM (LY).

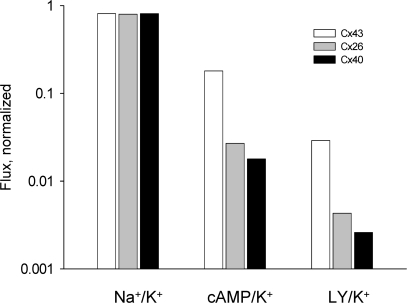
Fig. 8 compares the selectivity properties of Cx43, Cx40, and Cx26 to various solutes relative to K⁺ ions. The bars represent cAMP/K⁺, LY/K⁺ (Valiunas et al., 2002), and Na⁺/K⁺ ratios plotted on log scale for Cx43 (white bar), Cx26 (gray bar), and Cx40 (black bar). All three homotypic channels are poorly selective toward monovalent cations as illustrated by the Na⁺/K⁺ conductance ratios. The Na⁺/K⁺ unitary conductance ratios were determined by comparison of unitary conductance in NaCl and KCl solutions (Beblo and Veenstra, 1997; Wang and Veenstra, 1997) for Cx43 and Cx40 and the data for Cx26 is derived from Fig. 7. Interestingly, both LY and cAMP showed a similar permeability order: Cx43 > Cx26 ≥ Cx40, suggesting that these channels have distinct selectivity for larger solutes.

Figure 8.

Selectivity properties of Cx43, Cx40, and Cx26 to various solutes relative to K⁺. The bars represent Na⁺/K⁺, cAMP/K⁺, and LY/ K⁺ ratios plotted on log scale for Cx43 (white bar), Cx26 (gray bar), and Cx40 (black bar).

DISCUSSION

We have used a reporter gene (SpIH) that is cyclic nucleotide gated to determine cAMP concentration in SpIH-transfected cells. cAMP was delivered to the SpIH-transfected cell via gap junction channels from a second non-SpIH–expressing cell where the latter was also the source of cAMP. Homotypic Cx43, Cx40, or Cx26 gap junction channels were used to study cAMP permeability between cell pairs.

Cx43 is a ubiquitously distributed connexin found in many organs and tissues of the body including the heart. The data for cAMP permeability determined here for Cx43 corresponds well with data for ventricular myocytes determined by Tsien and Weingart (1976). They did not directly calculate cAMP permeability to the intercalated disc, but rather determined an effective diffusion coefficient of 1.12 · 10⁻⁶ cm²/s (with phosphodiesterase inhibitor). Weidmann and Hodgkin (1966) had previously determined the effective diffusion coefficient for K⁺ in the same tissue to be 7.9 · 10⁻⁶ cm²/s. The ratio of the effective diffusion coefficients (cAMP/K⁺) yields an apparent permeability ratio of ∼0.14, assuming the gap junctions within the intercalated discs are the major determinant of longitudinal diffusion. This is similar to the value we have determined in this study, 0.18 (Table II). The effective diffusion coefficient of 3.0 · 10⁻⁷ cm²/s for LY in ventricle was reported by De Mello (2007). There, the ratio of the effective diffusion coefficients (LY/K⁺) yields a value of 0.038 similar to the value of 0.029 (Table II) we determined for Cx43 in this study and earlier (Valiunas et al., 2002).

TABLE II.

Relative Permeability to cAMP and LY and Estimated Pore Diameter of Cx26, Cx40, and Cx43 Channels

	Cx26	Cx40	Cx43
cAMP/K+	0.027	0.018	0.180
LY/K+	0.0043	0.0026	0.029
cAMP/LY	6.3	6.9	6.2
Estimated pore diameter (nm)
from cAMP (0.52 nm, minor diameter)	0.69	0.65	1.12
from LY (0.95 nm, minor diameter)	1.1	1.08	1.25

Cx40 is another cardiac connexin that is more limiting than Cx43 relative to cAMP permeation, 0.028 versus 0.18. It is found in the atria and portions of the conducting system (van Veen et al., 2001). Analysis showed that Cx40 is roughly 10–11 times more restrictive to cAMP permeation than Cx43. Cx26 is also found in many organs and tissues (Beyer, 1993), and is also approximately seven times more restrictive to cAMP relative to Cx43. The permeability of cAMP to Cx26 has recently been determined and compared with LY, yielding a ratio of LY/cAMP of 0.15 (Hernandez et al., 2007). The data from Table II also allows determination of the LY/cAMP ratio for Cx26 which is 0.16. While different analytical approaches were used by Hernandez et al. (2007) and ourselves to calculate fluxes and/or permeabilities, the ratios generated values that are essentially the same. Bedner et al. (2003, 2006) compared cAMP permeability of different connexin channels measuring cytosolic Ca²⁺ concentration increase due to cyclic nucleotide-gated Ca²⁺ channel activation via photolysis of caged cAMP. They reported that diffusion of a similar amount of cAMP from cell to cell requires approximately three to four times more Cx26 channels than Cx43 channels. However, the relationship between permeability and junctional conductance as well as single channel permeability were not determined. The results of Bedner et al. (2006) cannot be directly compared with cAMP flux (molecules/channel/sec) through Cx43 and Cx26 single channels in the present study (Table I) where cAMP flux through Cx43 channel is approximately three times greater than through Cx26 channel. While direct comparison is not possible because Bedner et al. (2006) did not use phospodiesterase inhibitors, it is worth noting that a similar result was obtained.

Fig. 8 graphically illustrates Na⁺, LY, or cAMP flux relative to K⁺ flux for all three connexins. The Na⁺/K⁺ ratio is nearly the same for each connexin regardless of the unitary conductance, consistent with the original observations of Veenstra et al. (1995) and the notion of poor selectivity. For larger solutes such as cAMP and LY, as cytoplasmic mobility decreases, the permeability of gap junction channels declines as well, but it is much more dramatic for Cx40 and Cx26 than Cx43. If all three channels were equally nonselective and had pore diameters of equal dimension then no differences in flux/channel/second would be predicted. None of the data presented suggests such a circumstance. To further compound the issue the two channels with larger unitary conductances are less permeable to cAMP and LY than Cx43. Interestingly, the permeability ratios for Cl⁻ relative to K⁺ (Cl⁻/K⁺ ratio) for Cx43 and Cx40 are similar, 0.13–0.14 (Beblo and Veenstra, 1997; Wang and Veenstra, 1997). The anion/cation permeability ratio for Cx26 is 0.38 (Suchyna et al., 1999). The sequence for these three connexins is Cx26 > Cx40 ≥ Cx43. This ratio is not the same as that for cAMP or LY (Cx43 > Cx26 ≥ Cx40), further demonstrating that selectivity/permeability is not related to unitary conductance nor necessarily apparent pore size (Veenstra et al., 1995).

How can channels with larger unitary conductances and poor, or nonexistent, selectivity for monovalent cations be more selective or restrictive for solutes such as cAMP or LY? One explanation is that the larger conducting channels have shorter channel lengths and smaller channel diameters. This could result in a channel with a larger unitary conductance that is apparently more selective than a lesser conductive channel. This hypothesis is consistent with the results of Valiunas et al. (2002) where a pore diameter of 1.2 nm was calculated for Cx43 and 1.0 nm for Cx40 using LY (minor diameter of 0.95 nm) as the experimental probe and applying an equation derived from general continuum theory for multiple ions within a channel (Levitt, 1991a,b). In apparent contradiction to this hypothesis Wang and Veenstra (1997) and Beblo and Veenstra (1997) determined the effective channel diameters for Cx43 and Cx40 as 1.26 and 1.32 nm, respectively, using experimental data derived from monovalent cation permeability and the equation derived by Levitt (1991b). The differences in calculated pore diameter for Cx40 estimated from monovalent cation data (Beblo and Veenstra, 1997; Wang and Veenstra, 1997) or the larger divalent anionic probe LY were suggested by Valiunas et al. (2002) to arise from channel properties not accounted for in the Levitt model such as selectivity/screening effects.

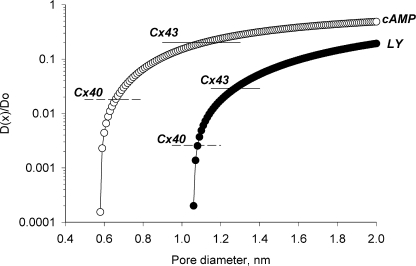
Does the data generated in this study illustrate apparent differences in pore diameter for LY and cAMP? Using the same analysis to determine pore diameter for cAMP where its minor diameter is ∼0.52 nm (Hernandez et al., 2007) yields a channel diameter of ∼1.12 nm for Cx43, which is consistent with the value determined by Valiunas et al. (2002) for LY. The calculated pore diameter determined from the cAMP data for Cx40 is not consistent with the value calculated for LY determined by Valiunas et al. (2002). Instead, a calculated pore diameter of ∼0.65 nm for Cx40 is obtained from the cAMP data while a value of ∼1.1 nm is obtained from the LY data. The data for LY and cAMP when applied to the Levitt model (Levitt, 1991b) for Cx26 also generate two different apparent pore diameters, 0.69 nm for cAMP and 1.1 nm for LY. The estimates of pore size determined from the Levitt model (Levitt, 1991b) assume that the ratio D(x)/D(o) is roughly equivalent to the flux ratios for cAMP/K⁺ or LY/K⁺ by assuming that the diffusion coefficients for cAMP, LY, and K⁺ in the cytoplasm are similar. D(x) is the diffusion coefficient of a solute within the pore, and D(o) indicates the diffusion coefficient in cytoplasm. Fig. 9 shows plots for cAMP and LY derived from the Levitt equation (Levitt, 1991b) where the ordinate is the ratio D(x)/D(o) and the abscissa is diameter of the pore. As the minor diameter of the solute and the diameter of the pore approximate each other, the diffusion coefficient within the channel declines. Table II also includes the dimensions of the solutes tested and the calculated pore size from the Levitt equation based on the cAMP/K⁺ or LY/K⁺ ratios.

Figure 9.

Levitt model plotting D(x)/Do versus pore diameter for cAMP (○) and LY (•), where D(x) is the diffusion coefficient for a solute within the channel and Do is the equivalent within the cytoplasm. D(x)/Do is assumed to be approximated by the calculated flux ratios for cAMP/K⁺ and LY/K⁺. The continuous and dashed lines represent cAMP/K and LY/K⁺ ratios for Cx43 and Cx40, respectively.

One possible explanation, suggested by Valiunas et al. (2002) for the calculated differences in pore diameter derived from the Levitt model are differences in selectivity or filtering between Cx43, Cx40, and Cx26 that are not related to channel diameter. Screening effects due to different fixed charge density at or near the orifice of the channels is one potential explanation. Human Cx37 unitary conductance does not linearly follow monovalent cation concentration but rather behaves in a manner consistent with an influence of fixed charge groups at the channel opening (Banach et al., 2000). It is then tenable to consider differences in screening properties where fixed charge density around the orifice of the channels differs from connexin to connexin, in this case for the homotypic forms of Cx43, Cx40, and Cx26.

In Valiunas et al. (2002) we suggested that the selectivity properties of connexins might exclude the rapid transfer of specific solutes and cAMP would be a possible candidate. This study confirms that Cx40 and Cx26 are less effective in allowing permeation of cAMP in comparison to Cx43. Only the inhibition of phosphodiesterase activity unmasked cAMP diffusion in weakly and moderately coupled cell pairs expressing Cx26 (<15 nS) and Cx40 (<20 nS) (Fig. 4). These data suggest that Cx43 permeability allows for rapid delivery of cAMP from cell to cell in sufficient quantity before degradation by phosphodiesterase to possibly trigger relevant intracellular functions. The reduced permeability of Cx26 and Cx40 to cAMP suggests that those connexins would not be able to rapidly deliver cAMP to effect functional changes in a recipient cell. Alternatively, both Cx26 and Cx40 functional channel number would have to be significantly greater than Cx43 to result in the same rapid delivery of cAMP from cell to cell. Interestingly, Ponsioen et al. (2007) also concluded that depending on cell type, phosphodiesterase activity in receiving cells can critically determine the concentration of cAMP.

Defining the permeability and selectivity characteristics for connexins is essential to our understanding of the normal physiological state of cells and is clearly an important factor in understanding the potential role of connexins in disease states. Oculodentodigital dysplasia or ODDD and accompanying neurological complications and congenital heart disorders have been attributed to mutations of Cx43 (Paznekas et al., 2003), and mutations of Cx40 correlate with atrial fibrillation and other arrhythmias (Gollob et al., 2006). Cx26 is another example where mutations have been shown to be instrumental to cochlear dysfunction associated with hearing loss (Mese et al., 2004; Zhao, 2005).