No effect of recombination on the efficacy of natural selection in primates

Abstract

Population genetic theory suggests that natural selection should be less effective in regions of low recombination, potentially leading to differences in rates of adaptation among recombination environments. To date, this prediction has mainly been tested in Drosophila, with somewhat conflicting results. We investigated the association between human recombination rates and adaptation in primates, by considering rates of protein evolution (measured by d_N/d_S) between human, chimpanzee, and rhesus macaque. We found no correlation between either broad- or fine-scale rates of recombination and rates of protein evolution, once GC content is taken into account. Moreover, genes in regions of very low recombination, which are expected to show the most pronounced reduction in the efficacy of selection, do not evolve at a different rate than other genes. Thus, there is no evidence for differences in the efficacy of selection across recombinational environments. An interesting implication is that indirect selection for recombination modifiers has probably been a weak force in primate evolution.

Genetic linkage couples the fates of mutations that are located near one another on a chromosome. As a result, natural selection is unable to operate independently on linked loci, leading to a decrease in the efficacy of natural selection dependent on the rate of recombination (Hill and Robertson 1966; Felsenstein and Yokoyama 1976). The relationship between the efficacy of selection and recombination can be seen by considering a pair of linked loci. When two beneficial mutations arise on different genetic backgrounds, and unless there are repeated mutations or recombination, they compete or “interfere” with one another, and only one of the two mutations can reach fixation in the population. Whereas if there is sufficient recombination, both mutations can recombine onto the same background and subsequently reach fixation. Thus, recombination decreases the strength of interference, leading to an increase in the rate of adaptation (cf. Otto and Lenormand 2002 and references therein). Similarly, recombination can lead to more effective purifying selection: When multiple deleterious mutations segregate in a population, recombination can lead to the creation of haplotypes with fewer such mutations, thereby retarding or preventing the fixation of harmful alleles (Fisher 1930; Muller 1932; Felsenstein 1974).

All else being equal, the strength of interference among selected alleles, referred to as Hill–Robertson interference (HRI) (Hill and Robertson 1966), should vary among recombination environments, potentially leading to differences in rates of evolution. However, while HRI has received extensive theoretical attention, notably because of its possible role in the origin of sex and recombination (Otto and Lenormand 2002), in practice it remains unknown how important a force it has been in influencing rates of adaptation across genomes. Answering this question has important implications for our understanding of adaptation and the evolution of recombination (Otto and Lenormand 2002; Coop and Przeworski 2007; Gaut et al. 2007).

To date, the best evidence for the effects of HRI stems from extreme examples, in which there is a complete or near-complete absence of recombination, such as heterogametic sex chromosomes and endosymbionts. In these cases, deleterious mutations appear to accumulate at a high rate, presumably because purifying selection is unable to purge them effectively from the population (cf. Charlesworth and Charlesworth 2000; Bachtrog 2006).

The role of HRI has also been evaluated by comparing rates of evolution between species across recombination environments. Surprisingly, however, given the extensive body of theoretical work on this subject, there have been few such studies, most of which have been conducted in Drosophila. Early investigations of variation in the efficacy of selection focused on the strength of codon bias within a single genome (Kliman and Hey 1993; Hey and Kliman 2002), finding weaker codon bias in regions of low recombination. While consistent with a lower efficacy of selection, the interpretation of these observations is not clear-cut (Marais et al. 2003; Singh et al. 2005).

More recently, studies have used divergence data, in particular the rates of nonsynonymous and synonymous substitution (d_N and d_S, respectively) (Yang and Nielsen 1998), as their main measures of the rate of adaptation. The ratio d_N/d_S, also referred to as ω, reflects the selective pressures acting on nonsynonymous sites relative to synonymous ones (cf. Li 1997). Synonymous sites are thought to be neutral or nearly neutral in many species, including primates (Lu and Wu 2005); indeed, while there is some evidence that they evolve under selection (Chamary et al. 2006; Comeron 2006), they tend to be much less constrained than do nonsynonymous sites (Hellmann et al. 2003b). Thus, a high ratio of d_N/d_S (close to or greater than one) indicates relatively little constraint on replacement sites, while a lower ratio points to greater constraint.

Considering the relationship between d_N/d_S and recombination, there are a number of possible predictions: (1) If nonsynonymous substitutions are largely beneficial and favored mutations occur at a high enough rate that they cannot be fixed sequentially or if their dynamics are affected by the segregation of deleterious alleles (Peck 1994), then increased recombination will tend to increase the rate of adaptation. In this case, all else being equal, there should be a positive correlation between the rate of protein evolution (d_N/d_S) and the rate of recombination. (2) Alternatively, if most nonsynonymous mutations tend to be slightly deleterious, then more such mutations would reach fixation where selection is less effective, leading to a higher d_N/d_S ratio in regions of low recombination. This scenario would then result in a negative correlation between d_N/d_S and recombination rate. In practice, both adaptation and purifying selection may have occurred at numerous genes, with the direction of the relationship between d_N/d_S across the genome reflecting whichever form of HRI is predominant. Finally, it is also possible that most or all recombining regions of the genome experience enough genetic exchange that the precise rate does not influence the efficacy of selection. If so, there may be no relationship between the recombination environment and rate of protein evolution.

The first two studies that used divergence data (Betancourt and Presgraves 2002) or divergence and polymorphism data (Presgraves 2005) focused on genes in Drosophila melanogaster and Drosophila simulans, many of which were chosen because of prior evidence for positive selection. For these subsets of the Drosophila genome, consisting of 255 and 98 genes, respectively, the investigators found a number of relationships between recombination and selection consistent with widespread HRI. Specifically, they found (1) higher d_N in regions of higher recombination (but no such pattern for d_S), suggesting a higher rate of protein adaptation in regions of higher recombination (Betancourt and Presgraves 2002); (2) less codon bias in genes with more rapid protein evolution, potentially indicating that strong selection at amino acid sites reduces the efficacy of purifying selection at linked sites (Betancourt and Presgraves 2002; but see Marais et al. 2004); and (3) combining inter- and intra-species data from coding regions, fewer beneficial substitutions and more weakly deleterious polymorphisms in regions of low recombination (Presgraves 2005). In turn, a more recent, genome-wide study of d_N/d_S between D. melanogaster and Drosophila yakuba found that the most pronounced effect of recombination was a reduction in the efficacy of purifying selection on the fourth chromosome, which completely lacks crossing-over (Haddrill et al. 2007). Among regions with some recombination, there was little evidence for variation in the efficacy of selection. These seemingly conflicting findings have been partially reconciled in a recent genomic study by Larracuente et al. (2008), who report evidence both for ineffective purifying selection in regions of low recombination and, possibly, for an increased rate of adaptation among strongly positively selected genes in regions of higher recombination. In summary, it appears as if there is evidence for interference in Drosophila, but much of the effect may be in regions of highly reduced or no crossing-over.

A more general understanding of the role of HRI requires one to examine its role over many species. As a first step in this direction, we conducted a study of the relationship between recombination and selection in primates. The recent availability of human, chimpanzee, and rhesus macaque genomes provides high-quality data for three closely related species, allowing us to evaluate the evidence for HRI with genome-wide divergence data. Moreover, population genetic parameters for primates differ markedly from those of Drosophila: The ratio of recombination rate to mutation rate is thought to be smaller in primates than in Drosophila (Andolfatto and Przeworski 2000; Kong et al. 2002), genome sizes differ by an order of magnitude, potentially affecting the density of selection targets, and the human effective population size is roughly two orders of magnitude smaller than those in Drosophila (Aquadro et al. 2001; Eyre-Walker 2006). Thus, these primate data provide an opportunity to test predictions of HRI in primates and to gain more general insights into its importance in shaping rates of adaptation.

Results

Gene-centric alignments and recombination rate estimates

We used coding region divergence data from high-quality alignments of orthologous human, chimpanzee, and rhesus macaque genes (Gibbs et al. 2007). The divergence time for human and chimpanzee is ∼6–7 million years (Myr) (Chimpanzee Sequencing and Analysis Consortium 2005) and for human–rhesus macaque 25–30 Myr (Gibbs et al. 2007), so that the phylogeny of these species represents a total of ∼60–70 Myr of primate evolution. In all, we analyzed ∼10,000 trios of orthologous genes, affording high power to detect even small differences in the efficacy of selection across recombination environments.

Because of uncertainty in a number of important parameters, notably the distribution of fitness effects, we did not have a clear a priori expectation about the genomic scale over which interference may be important. Indeed, if selection tends to be strong, only loci far away from the target of selection will escape its effects through recombination, such that the relevant recombination environment may be over megabases. In contrast, if selection tends to be weak, the effects of HRI may exert themselves on a much finer scale. To try to evaluate both possibilities, we performed all our analyses using estimates of human recombination rates obtained for two different scales, hereafter referred to as broad and fine (recombination rate estimates are not available for chimpanzees and are only available over an extremely broad scale in rhesus macaques) (Rogers et al. 2006). Broad-scale recombination rates per gene were estimated using the deCODE pedigree-based human recombination map (Kong et al. 2002), by interpolating between markers separated by a median distance of 925 kb. Thus, these estimates provide rates on the scale of a megabase (for details, see Methods). In turn, fine-scale recombination rates for each gene were obtained from a recombination map inferred from human linkage disequilibrium (LD) data (Myers et al. 2005). Each gene was assigned a rate based on a 40-kb window centered on the gene (see Methods). Using these two scales allowed us to test for an effect of interference over scales that differ by two orders of magnitude.

We note that the recombination estimates reflect only or primarily the cross-over rate, rather than rates of both crossing-over and gene conversion (although the LD-based estimates may reflect some contribution of gene conversion as well) (Przeworski and Wall 2001). Both crossing-over and gene conversion events can break down allelic associations, thereby uncoupling the fates of linked alleles. However, while a cross-over anywhere between two sites will decrease the association, a gene conversion event will only do so if the conversion track (on the order of ∼100 bp) overlaps one of the two sites. Thus, even if the per base pair rate of gene conversion is several fold higher than crossing-over (Jeffreys and May 2004), the allelic association between sites that are more than a couple of hundred base pairs apart will primarily be broken down by crossing-over (Przeworski and Wall 2001). In other words, crossing-over should be the primary determinant of the strength of HRI, unless the cross-over rate is very low (or the sites are very close). This exceptional case may apply to the tip of the X chromosome in Drosophila melanogaster, where gene conversion events are believed to be orders of magnitude more frequent than cross-overs (Langley et al. 2000; Gay et al. 2007). In our data, however, all of our genes experience some level of cross-over, so we expect the cross-over rate (hereafter referred to simply as the recombination rate) to be the salient parameter influencing the strength of HRI.

The relationship between the recombination environment and the rate of protein evolution

We assessed whether the rate of protein evolution, d_N/d_S, is correlated with the recombination rate. To do so, we excluded genes on the X, as differences in the effective population sizes of the X versus autosomes and the hemizygous nature of the X in males are expected to lead to systematic differences in selection pressures (Charlesworth et al. 1987) and the inclusion of X-linked genes would therefore complicate the interpretation.

Across autosomes, both d_N and d_S separately are strongly positively correlated with recombination rate in primates (see Supplemental Table 1). The correlation between recombination rate and d_S (and d_N) could reflect a mutagenic effect of recombination (Hellmann et al. 2003a, 2005) or could reflect nonequilibrium GC content, e.g., caused by biased gene conversion (Duret et al. 2002; Webster et al. 2003; Spencer et al. 2006). Regardless of the reason, measuring the rate of protein evolution using the ratio d_N/d_S should control at least partially for mutation rate variation, assuming d_S is largely a reflection of the fixation of neutral alleles. Whether it fully accounts for mutation rate variation, however, is unclear (see the discussion of GC content as a covariate below).

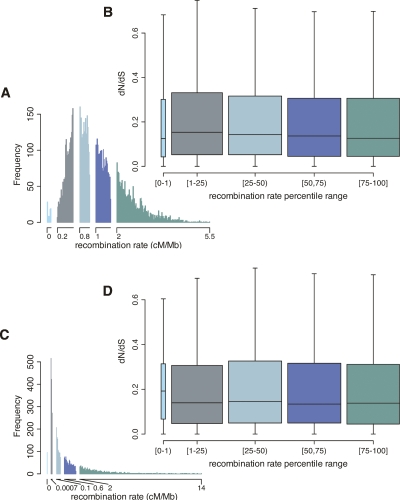
To examine whether interference is shaping rates of protein evolution, we took two approaches. First, given that interference is best documented in asexual genomes and nonrecombining chromosomes, we hypothesized that the reduction in the efficacy of selection may be highly nonlinear in the recombination rate, with most of the reduction in efficacy occurring in regions with very low recombination rates. If so, most of the signal for interference may come from genes in the lowest recombination-rate bin. Figure 1 shows box-plots of d_N/d_S partitioned by recombination rate into quartiles, with the lowest 1% tail of the distribution separated out as its own bin. As can be seen, even genes with recombination rates in the lowest 1% tail do not have a significantly different d_N/d_S than the genes in the other 99% (Wilcoxon rank sum test; broad-scale rates: P = 0.6, fine-scale rates: P = 0.4). We also investigated other partitions of the distribution (i.e., using other cutoffs than 1%), and reached the same conclusion (see Supplemental Fig. 1).

Figure 1.

Summary of the relationship between d_N/d_S and the recombination rate. Colors correspond to recombination rate bins, which consist of the first percentile of the distribution and then four bins comprising the remaining 99% of the recombination rate distribution. Broad-scale rates are depicted in panels A and B and fine-scale rates in panels C and D. (A,C) The distribution of recombination rates for the ∼10,000 genes; (B,D) box plots of d_N/d_S by recombination rate bin. The boxes span the 25%–75% d_N/d_S quantiles with the internal horizontal line indicating the median rate; whiskers extend to the most extreme data point that is less than 1.5 times the length of the box. Outliers beyond the whiskers are not shown.

In Drosophila, much of the genome-wide signal for HRI stems from genes in regions of the genome that experience very little or no crossing over (Haddrill et al. 2007) and contain many genes (Noor et al. 2001). In humans, gene density is significantly positively correlated with recombination rate (Kong et al. 2002), raising the possibility that regions with less recombination could have fewer targets of selection (see the discussion on gene density below). In particular, centromeric regions, which experience suppressed recombination, tend to be gene poor. However, the genes in our low recombination bin lie mostly outside centromeric regions (only 25% of genes with recombination rates in the lowest 1% tail are within 2 cM of a centromere; see Supplemental Fig. 2). More generally, the genes with low recombination are not in gene poor regions: If we consider the 1% of genes with the lowest broad-scale recombination rates, they do not contain fewer genes on average than other regions (median 12 and mean 17 genes/Mb in the low 1% tail vs. median 13 and mean 17 genes/Mb in the remaining 99%; Wilcoxon test, P = 0.5; similar results hold for the 5% tail, data not shown). Thus, our lack of evidence for an effect of recombination on HRI in the lowest 1% tail is unlikely to simply reflect a lack of potential selection targets.

Next, we considered the correlation of d_N/d_S and recombination rates, over both fine and broad scales. We found that d_N/d_S is significantly negatively correlated with broad-scale recombination rates (Spearman ρ = −0.03, P = 0.003) but not with fine-scale recombination rates (Spearman ρ = −0.002, P = 0.8). At face value, the broad-scale findings might suggest a slight increase in the efficacy of purifying selection with recombination.

One of the complications of this type of genomic analysis, however, is that many genomic features are correlated. In particular, GC content is positively correlated with both recombination rates (Kong et al. 2002) and substitution rates (see Supplemental Fig. 3) (Hellmann et al. 2003a). Using d_N/d_S estimates from PAML, there is a strong, nonlinear correlation between GC content and d_N/d_S (see Supplemental Fig. 4). The correlations with GC content probably arise from the manner in which codon-based d_N/d_S is calculated (Bierne and Eyre-Walker 2003), nonequilibrium GC content (Duret et al. 2002; Webster et al. 2003), or CpG effects. In any case, after correction for the linear and quadratic effects of GC content estimated from fourfold degenerate silent sites in each gene, broad-scale recombination rates are uncorrelated with d_N/d_S (partial correlation; ρ = 0.02, P = 0.07). The reverse is not true: GC content is still highly correlated with d_N/d_S after correction for recombination rates (partial correlation; broad-scale: ρ = −0.20, P < 10⁻¹⁶). These observations strongly suggest that the observed relationship between broad-scale rates of recombination and d_N/d_S is attributable to the correlation of both d_N/d_S and recombination rate with GC content, rather than resulting from HRI.

We note that, after correction for GC content, fine-scale recombination rates actually become weakly but significantly positively correlated with d_N/d_S (partial correlation; ρ = 0.04, P = 0.0002). Closer inspection, however, reveals that this correlation arises because genes with no observed nonsynonymous substitutions (i.e., for which d_N = 0) tend to be in regions of low recombination. When d_N = 0, genes are assigned a d_N/d_S ratio of 0.0001 by the program PAML. Since this is probably an underestimate of the true value were enough time to pass for nonsynonymous substitutions to occur, we chose to exclude these genes, which comprise ∼10% of the data. Excluding genes with d_N = 0 removes the positive correlation seen between fine-scale rates and d_N/d_S (partial correlation, accounting for linear and quadratic effects of GC content, ρ = 0.02, P = 0.049) and does not affect the relationship between broad-scale rates and d_N/d_S (partial correlation, accounting for linear and quadratic effects of GC content, ρ = 0.008, P = 0.45).

A concern is that the exclusion of genes with d_N = 0 could mask a true signal of HRI. Several arguments suggest that this is not the case: (1) If interference due to purifying selection were predominant, then genes with no observed nonsynonymous substitutions should have higher recombination rates. Yet, as mentioned above, the genes with no nonsynonymous substitutions tend to have a lower mean recombination rate (two-tailed t-test; broad-scale: P = 0.0003, fine-scale: P = 6 × 10⁻⁵) and a lower median recombination rate (Wilcoxon rank sum test; broad-scale: P = 0.002, fine-scale: P = 1 × 10⁻⁵). (2) If, instead, most HRI involves positively selected mutations, then the lower recombination rate for these genes would be consistent with an effect of interference. However, since these genes have no observed nonsynonymous substitutions, they probably have not experienced extensive HRI. (3) Finally, the observations could be consistent with a more complex model of interference (Peck 1994) in which many weakly deleterious alleles (which are not able to fix due to purifying selection) prevent the fixation of any beneficial mutations, thereby leading to d_N = 0. While this scenario is possible, it would require a very specific distribution of selection coefficients, which ensures that HRI is sufficiently strong to prevent the fixation of any beneficial mutations in 60–70 Myr, and yet not strong enough to allow for the fixation of any weakly deleterious mutations by drift. A simpler explanation for most of these d_N = 0 genes may be that genes with a lower recombination rate tend to have a lower substitution rate (Hellmann et al. 2003a, 2005). Consistent with this hypothesis, d_S is much lower in genes with d_N = 0 (broad-scale: P = 4 × 10⁻⁸; fine-scale: P = 1 × 10⁻⁹ by a two-tailed t-test). In summary, while it remains possible that some signal for HRI is lost by the exclusion of these genes, interpreting this pattern as evidence for an effect of recombination on HRI requires some special pleading.

Effect of gene density

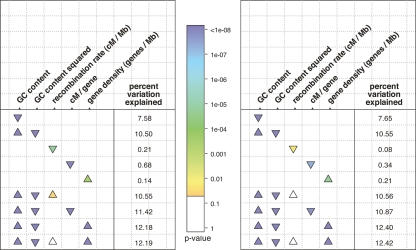
The strength of interference depends on the number of mutations subject to selection within a given genetic distance. The measure cM/gene could thus be a better predictor of interference than cM alone, as it may more accurately capture the number of selection targets within a linked region (assuming that the number of genes in a region is a good proxy for the number of potential selection targets). The measure of cM/gene based on broad-scale rates is significantly negatively correlated with d_N/d_S, even after adjusting for linear and quadratic effects of GC content (partial correlation; ρ = −0.09, P < 10⁻¹⁶). In turn, cM/gene based on fine-scale rates is marginally negatively correlated with d_N/d_S after correcting for GC content (partial correlation; ρ = −0.02, P = 0.03). However, the measure cM/gene appears to be correlated with d_N/d_S because gene density completely dominates the combined measure. Indeed, controlling for GC effects, d_N/d_S and gene density are far more correlated (partial correlation; ρ = 0.10, P < 10⁻¹⁶) than are d_N/d_S and the recombination rate. Moreover, if GC content, gene density, and recombination rate are all modeled as separate predictors of normalized d_N/d_S in a linear model framework, the coefficient for the recombination rate is consistently insignificant (Fig. 2). These findings remain unchanged if we use exon density instead of gene density in these analyses (data not shown). That gene density is an excellent predictor of d_N/d_S while the recombination rate is not, suggests either that (1) gene density correlates with d_N/d_S for reasons unrelated to the recombination rate or (2) HRI is pronounced, but both human broad- and fine-scale recombination rates are very poor predictors of the effect, and the most relevant predictor is how many genes are present in a given physical interval (for more discussion, see “Relevance of Observed Recombination Rates”). Even if gene density is a good proxy of the number of selected mutations within a region, and should therefore influence the strength of HRI, the recombination rate within this region should also be predictive, as interference is a function of the genetic linkage (not merely physical linkage) among selected mutations.

Figure 2.

Summary of linear models, with normalized d_N/d_S as a response variable. The left and right panels show broad- and fine-scale recombination rates, respectively. Each row describes a linear model used to explain variation in quantile-normalized d_N/d_S. The columns list the predictor variables, and the presence of absence of a triangle indicates if a particular variable was used in the model. For example, the last model includes four terms: GC content, GC content squared, recombination rate, and gene density. The color of the triangles displays the P-value, coded by the colored bar in the center; it is based on a Student’s t-test, which tests whether the coefficient for that term differs significantly from zero. White triangles represent nonsignificant coefficients at the 0.05 level. The orientation of the triangles indicates the sign of the coefficient, with upward- and downward-pointing triangles indicating positive and negative coefficients, respectively. The column of numbers on the right of each panel is the percentage of the variation in quantile-normalized d_N/d_S that is explained by the model i.e., 100r². GC content refers to GC4 content (see Methods). A more extensive summary of the linear models that we investigated is provided in Supplemental Figure 6.

The relationship between d_N/d_S and gene density is intriguing. If not due to HRI, it could reflect a clustering in the genome of rapidly-evolving genes (perhaps due to gene duplication or coregulation). For example, immunity genes (as defined by their PANTHER category) tend to have higher d_N/d_S than average and reside in regions of higher gene density (see Supplemental Fig. 5). However, even after controlling for both GC content and PANTHER category, there is still a highly significant correlation between d_N/d_S and gene density (partial correlation; ρ = 0.11, P < 10⁻¹⁶).

Evaluating the joint effects of recombination, gene density and GC content

Our findings are summarized in Figure 2, which shows the results for a subset of the linear models that we considered (for a more extensive set of linear models, see Supplemental Fig. 6). In all models, we used quantile-normalized d_N/d_S as the response variable (see Methods). When only broad- or fine-scale recombination rates are used as a predictor, there is a slight negative correlation between d_N/d_S and the recombination rate. However, if we take into account the linear and quadratic effects of GC content on d_N/d_S (see above), d_N/d_S is no longer significantly correlated with recombination rates (at either broad or fine scales). A measure that combines recombination rate and gene density (in effect normalizing the size of a genetic interval by an estimate of the number of selection targets) is a highly significant predictor of d_N/d_S. However, if recombination rate and gene density are considered as separate predictors, gene density alone explains a similar amount of the variation as the combined measure, while recombination rate is not a significant predictor (see Fig. 2). That GC content and gene density together explain so much of the variation in d_N/d_S across genes is somewhat surprising and warrants further investigation.

A concern is whether our findings are robust with respect to the (unknown) genomic scale over which different effects could be operating. To examine this, we also considered log recombination rate, log gene density, log cM/gene, 1/gene density (see Supplemental Fig. 6). The qualitative results do not differ if d_N/d_S itself, rather than quantile-normalized d_N/d_S, is used (data not shown). Because the correlation between d_N/d_S and GC content could reflect the way in which d_N/d_S is estimated (Bierne and Eyre-Walker 2003), we also used a simpler method by Nei and Gojobori (1986). Using the Nei–Gojobori distance, d_N/d_S is much less, although still significantly, correlated with GC content (Spearman ρ = −0.08, P < 10⁻¹⁶). Other qualitative conclusions are unchanged (see Supplemental Fig. 7). Finally, regardless of the model employed, there is no significant contribution of recombination rate toward explaining variation in d_N/d_S; in other words, we see no evidence for an effect of recombination on HRI among amino acid substitutions.

Relevance of human recombination rates

Both broad- and fine-scale recombination rates are estimated from extant human data, raising the question of their applicability to the three primate species. For broad-scale rates, this seems unlikely to be problematic, as the broad-scale genetic map is similar between human and rhesus macaque (Rogers et al. 2006), with high rates near telomeres and low rates near centromeres. However, a number of chromosome fusions and fissions have occurred on the phylogeny that could affect broad-scale rates, and potentially weaken the signal for HRI. We therefore repeated two of our analyses after excluding genes on seven human chromosomes: 7 and 21 (3 in rhesus), 14 and 15 (7 in rhesus), 20 and 22 (10 in rhesus), and 2 (12 and 13 in rhesus, 2a and 2b in chimpanzee). For both broad- and fine-scale rates, genes in the low 1% of recombining regions do not have a significantly different d_N/d_S (Wilcoxon sign rank test; broad-scale: P = 0.6, fine-scale: P = 0.1). Also, after correcting for GC-content, broad-scale rates are not correlated with d_N/d_S (Spearman ρ = −0.004, P = 0.8), and fine-scale rates are only marginally positively correlated (Spearman ρ = 0.02, P = 0.0503). Finally, linear models on this reduced data set are consistent with earlier results; i.e., both broad- and fine-scale recombination are not significant predictors of d_N/d_S when considered with other covariates (see Supplemental Fig. 8).

To hone in on regions where the broad-scale rates are likely to have remained very similar throughout the phylogeny, we concentrated on centromeric regions, which experience low levels of recombination, contrasting genes within 2 cM of the centromere (Supplemental Fig. 2) to all other genes. We see a very weak, nonsignificant increase in the normalized, GC-corrected d_N/d_S in centromeric regions compared with other regions (Wilcoxon sign rank test, P = 0.07), with a similar result (Wilcoxon sign rank test, P = 0.2) if we exclude chromosomes (2, 7, 14, 15, 20, 21, and 22) that have been involved in chromosomal fusions or fissions since the common ancestor of human, chimpanzee, and macaque. Thus, low recombination does not appear to contribute to HRI, even in regions that (likely) experience stable recombination rates.

At a finer scale, recombination rates may have changed substantially: Although fine-scale rates may be partially conserved (Myers et al. 2005; Ptak et al. 2005), hotspot locations seem to differ markedly between human and chimpanzee (Wall et al. 2003; Ptak et al. 2004, 2005; Winckler et al. 2005). Rapid turnover of hotspots could lead human fine-scale rates to be poor proxies for the fine-scale recombination environment for much of the phylogeny. If true, then a stronger signal of HRI might emerge if we restrict our attention to the human lineage. To investigate this possibility, we looked at the rates of d_N/d_S estimated for the human branch, again finding no correlation with the rate of protein evolution (Spearman ρ = −0.0005, P = 0.96; for a set of linear models, see Supplemental Fig. 9). Given the relatively short human branch (mean d_S = 0.007), however, estimation of d_N/d_S is very noisy, so we may have limited power to detect an association.

Another concern about the use of fine-scale recombination rates is that these are estimated from patterns of LD, which can be shaped by natural selection as well as by recombination (Stephan et al. 2006, but see McVean 2007). The bias in LD-based estimates of recombination will depend on the true recombination rate and the strength, rate, and mode of selection. While such a bias remains to be fully investigated, it is unlikely to obscure a correlation between LD-based estimates of recombination and d_N/d_S (and under certain circumstances might actually enhance or produce an apparent correlation). In this respect, it is interesting to note that the correlation (and linear relationship) between broad-scale (pedigree-based) and fine-scale (LD-based) rates is not noticeably different between regions of low, medium, or high d_N/d_S (see Supplemental Table 2). This observation suggests that LD estimates are not strongly biased in regions of strong historic selection (as measured by d_N/d_S). Thus, while LD-based rates of fine-scale recombination may be affected by natural selection, this concern seems minor for our analyses.

Could different signals of interference cancel each other out?

Widespread interference predicts either a positive or negative correlation between recombination rate and d_N/d_S, depending on the unknown distribution of fitness effects. Thus, if our sample includes genes that experience both positive and purifying selection, as is likely, the conflicting signals due to interference could in principle cancel each other out and mask the evidence for HRI. To test this possibility, we partitioned the ∼10,000 genes in our data set into genes with the highest d_N/d_S and genes with the lowest. For both broad- and fine-scale rates, no significant positive correlations were observed in the high d_N/d_S tail, regardless of how the tail was defined (see Supplemental Fig. 10). For broad-scale rates, significant negative correlations were detected in the low tail of the distribution when the low tail included at least 35% of the genes. This reflects the overall negative correlation observed for the whole data set and so, as before, can be explained by covariates such as GC content. Fine-scale rates consistently show a positive correlation in the high tail and a negative correlation in the low tail, but none of the tested correlations are significant at the 1% level, even without correction for multiple tests. These results suggest that any canceling effect is negligible.

Of course, using d_N/d_S to classify genes into sets under positive vs. purifying (negative) selection may not be ideal. To use an alternative approach, we also classified genes based on estimates of the population genetic selection parameter, γ = 2N_es, obtained from human variation data and human–chimpanzee divergence data (using a variant of a McDonald-Kreitman approach) (Bustamante et al. 2005). Specifically, we considered a gene to be under positive selection if the estimated Bayesian credible interval (CI) of γ lay entirely above zero and under purifying selection if the CI lay entirely below zero. Among the ∼5500 genes for which we had γ estimates and alignments for all three primate species, neither the set of 124 negatively selected genes nor the set of 384 positively selected genes shows a significant correlation between d_N/d_S and broad-scale recombination rate (Spearman correlation test; negatively selected: ρ = −0.05, P = 0.6, positively selected: ρ = 0.03, P = 0.6). Similarly, neither set shows a correlation with fine-scale rates (Spearman correlation test; negatively selected: ρ = −0.01, P = 0.9, positively selected: ρ = −0.03, P = 0.6). Given that broad-scale rates show slight (nonsignificant) correlations with d_N/d_S in the expected direction for both positively and negatively selected genes, we hypothesized that our original criteria for classifying genes based on the mode of selection were too strict to have enough power. We therefore relaxed the criteria, testing partial correlations between recombination rate and GC-corrected d_N/d_S in successively larger sets of positively and negatively selected genes (see Methods). However, again, no set yielded a significant correlation at the 1% level (see Supplemental Fig. 11). Thus, if there is an effect of recombination rate on HRI, it is a very weak one.

Another approach to stratifying the data is by functional gene categories. Functional classes of genes differ in their mean recombination environments (Frazer et al. 2007). Moreover, some functional categories are thought to undergo repeated positive selection, while other classes of genes are strongly constrained, experiencing widespread purifying selection; indeed, 17 of the 25 functional categories with more than 80 members in our data set have a mean d_N/d_S that differs significantly from the mean across all genes (see Supplemental Fig. 12). To test whether a signal of HRI was lost by pooling genes across categories, we examined the correlations between d_N/d_S and recombination rate within each top-level PANTHER molecular function category. For broad-scale rates, the only functional category to have a marginally significant correlation is transcription factors (see Supplemental Fig. 14). For fine-scale rates, four categories are marginally significant: ligases, transporters, oxidoreductases, and unclassified (see Supplemental Fig. 15). However, for both the broad- and fine-scale rate analyses, no functional category shows a significant correlation after correction for multiple tests (data not shown). In summary, even within functional categories, there is no evidence for a relationship between recombination and rates of protein evolution.

Next, we investigated whether there is a signal of HRI in genome-wide polymorphism data (Bustamante et al. 2005), focusing on the ratio of nonsynonymous to synonymous mutations observed in each gene. This ratio is likely to reflect almost exclusively the effects of weak purifying selection, as beneficial and strongly deleterious mutations spend little time segregating in the population. If selection is less effective in regions of low recombination due to HRI, there may be a greater number of weakly deleterious alleles segregating in such regions. To test this, we used a linear model to try to predict the number of nonsynonymous polymorphisms as a function of either broad- or fine-scale recombination rate, the number of silent segregating sites, linear and quadratic GC content, and gene density. Our results seem not to support the hypothesis of less effective purifying selection in regions of low recombination: At both broad and fine scales, the recombination rate had a marginally significant positive coefficient, while our hypothesis predicts a negative coefficient (see Supplemental Table 3). We also obtained similar results after excluding genes that may be under positive selection based on γ estimates (Bustamante et al. 2005; data not shown). The very weak positive correlation that we do observe is not easily explained by HRI and could reflect the effects of biased gene conversion or other evolutionary processes. Finally, we note that gene density, while a significant predictor of d_N/d_S, does not have a significant effect on the number of nonsynonymous polymorphisms, suggesting that the relationship between protein divergence and gene density is not due to ineffective purifying selection in gene dense regions.

Patterns on the X chromosome

We analyzed genes on the X chromosome separately, for the reasons discussed above. Genes with the lowest 10% of recombination rates on the X chromosome do not evolve at a significantly different rate from other genes on the X (Wilcoxon rank sum test; broad-scale: P = 0.5, fine-scale: P = 0.2). Moreover, there is no correlation between either broad- or fine-scale recombination rates and d_N/d_S (Spearman correlation test; broad-scale: ρ = −0.07, P = 0.3, fine-scale: ρ = −0.09, P = 0.2), including after correction for GC content (partial correlation; broad-scale: ρ = −0.05, P = 0.4, fine-scale: ρ = −0.1, P = 0.1). The only potential evidence for HRI on the X chromosome is that genes close to the centromere have higher d_N/d_S (correcting for GC content) than genes outside the centromere, but only slightly so (Wilcoxon rank sum test, P = 0.04). A caveat of these X chromosome analyses is that we may have relatively low power, given the smaller number of genes for which we have data (∼230).

Discussion

Considering rates of protein evolution, there is very weak or no evidence for a consistent effect of recombination on the efficacy of natural selection in primates. This result holds whether we analyzed coding regions across all autosomes or focused on subsets of genes that, a priori, may be thought to experience more interference (such as those in low recombination environments, those in specific functional categories, or those thought to have experienced extensive purifying or positive selection). It also holds whether we use broad- or fine-scale recombination rates and measured these on a linear or log scale, suggesting that the finding does not stem from an incorrect choice of scale. Moreover, the lack of a detectable relationship between recombination and rates of protein evolution is not due to lack of data: With ∼10,000 orthologous genes (approximately half the genes in the human genome), including hundreds of genes in regions of very low crossing-over, the study is probably not underpowered.

In our analyses, we focused on d_N/d_S to investigate the link between evolutionary rates and recombination, to the exclusion of noncoding DNA—largely because it remains unclear how to define functional categories of noncoding DNA a priori. This omission is unlikely to mask a signal for HRI, however: If selection on noncoding changes is common, this should lead to additional interference with mutations in coding regions and should therefore contribute to increased efficacy of selection in regions of high recombination. We also did not consider additional measures, such as codon bias, which have been used to assess the efficacy of selection in Drosophila because, despite some evidence for selection on silent sites in primates (Comeron 2006), their applicability to primates is unclear (Duret 2002). A concern with the use of d_N/d_S might be that synonymous sites are not strictly neutral in primates (Chamary et al. 2006; Comeron 2006). However, even if this were true, selective pressures on synonymous sites are highly unlikely to be as strong as on nonsynonymous sites (Hellmann et al. 2003b; Lu and Wu 2005). Thus, using d_S as a denominator should not mask the signal of interference.

In addition to the approaches that we took to categorize genes, there may be other approaches that are informative with respect to HRI. For example, it may be productive to stratify genes based on gene expression (breadth or intensity), as a proxy for selective pressures experienced by a gene, e.g., genes that are broadly expressed are thought to be under more constraint (Duret and Mouchiroud 2000). While such an analysis would clearly be worthwhile, patterns of gene expression are correlated with both gene density and recombination rates (perhaps for mechanistic reasons) (Holmquist and Ashley 2006) and so picking apart the causal factors will likely be challenging.

An additional caveat of our analysis is the use of human recombination rates, which may not be an ideal proxy for the recombination environment in all three primate species. Comparison of the human genetic map to a preliminary map in rhesus macaques (Rogers et al. 2006) suggests that rates over megabases may be similar. Moreover, centromeric regions tend to experience low rates of recombination, and telomeric regions tend to experience high rates across mammals (Jensen-Seaman et al. 2004). These considerations suggest that our assumption is probably valid for the broad scale. But the assumption may not be as applicable to the fine scale. Indeed, analyses of LD data in humans and chimpanzees indicate that although rates >50 kb are weakly correlated (Ptak et al. 2005), hotspot locations differ markedly between the two species (Wall et al. 2003; Ptak et al. 2004, 2005; Winckler et al. 2005). If HRI exerts its effects over very short distances, and fine-scale rates have changed markedly between species, some of the signal could be masked as a result. This scenario seems unlikely, however: Most of the signal for HRI is expected to come from regions of very low recombination (e.g., near centromeres) that are likely to be shared across species, and there is no evidence for an effect in this subset of genes. Finally, we note that using more distantly related species (than human, chimpanzee, and rhesus macaque) might provide slightly better estimates of rates of protein evolution, but would only accentuate the problem of using human recombination rates for the entire phylogeny.

We note that we also used polymorphism data, for which contemporary recombination rates are more clearly appropriate, to test for an effect of the recombination environment on HRI. Our hypothesis was that, if weak selection is common, ineffective purifying selection due to HRI should lead to a higher number of nonsynonymous polymorphisms in regions of low recombination. Again, this pattern is not observed.

Although recombination is not a significant predictor of rates of protein evolution, gene density is. This finding could be explained by an effect of HRI if the physical density of selection targets rather than the density over genetic distance is important, but this seems unlikely as genetic linkage is an essential aspect of HRI. More plausible possibilities are (1) that current recombination rates in humans are surprisingly poor predictors of HRI, while gene density is a good proxy for the number of selection targets, or that (2) some explanation other than HRI need be invoked to explain the relationship of gene density and rates of protein evolution. The lack of a relationship between nonsynonymous polymorphism and gene density lends some support to the latter, but further investigation is needed.

The lack of relationship between recombination and the efficacy of selection in primates contrasts with findings in Drosophila. In multiple Drosophila species, there is a strong correlation between diversity levels (i.e., N_e) and recombination rates, but no correlation between divergence and recombination, suggesting that some form of variation-reducing selection (e.g., background selection or repeated adaptations) is shaping patterns of genetic variation genome wide (Aguade et al. 1989; Begun and Aquadro 1992; Shapiro et al. 2007). One way to view this observation is that levels of genetic drift (or genetic draft; Gillespie 2000) differ across recombination environments, implying that the strength of HRI and the efficacy of selection may also vary along the genome. In humans, however, there is only a very weak correlation between recombination and diversity after controlling for divergence (i.e., variation in the nucleotide substitution rate) (cf. Hellmann et al. 2005). Moreover, this weak correlation may be due to a very localized effect of biased gene conversion in recombination hotspots (Spencer et al. 2006). Thus, in humans, there is little evidence for differences in rates of genetic drift across recombination environments. Consistent with the diversity patterns, our findings suggest no or few differences in the efficacy of selection among autosomal recombination environments.

An interesting question is then which factors explain the greater evidence for HRI effects in Drosophila. Assuming that the signal in Drosophila comes mainly from regions with little or no recombination, as suggested by a recent study (Haddrill et al. 2007), one possibility is simply that in Drosophila, there are more or larger gene rich environments with very low rates of recombination (e.g., the fourth chromosome) than in humans. Alternatively, it may reflect differences in the salient parameters in the two species. The sex-averaged recombination rates per base pair are similar in Drosophila and humans (∼1 cM/Mb), but the census and effective population (N_e) sizes are much larger in Drosophila (Eyre-Walker 2006). For a given rate of adaptation, the larger effective population size in Drosophila results in relatively less genetic drift and should therefore lead to decreased HRI relative to humans. However, there may be many more selected mutations in Drosophila between which HRI can occur, including potentially more deleterious amino acid replacement polymorphisms, which would increase the strength and prevalence of background selection (Loewe and Charlesworth 2007). Indeed, if we assume a similar distribution of selection coefficients (s) in primates and in Drosophila, then the larger population size would result in a larger input of beneficial mutations as well as a higher fraction of newly arising mutations whose fate is governed primarily by selection rather than drift (i.e., alleles for which |N_es| > 1). Consistent with this prediction, estimates of the fraction of replacement sites fixed by positive selection in primates are lower than in Drosophila (Eyre-Walker 2006). Another relevant factor in comparing primates to Drosophila species may be the tighter physical spacing of genes and more intense selection on noncoding DNA in Drosophila (Andolfatto 2005; Keightley et al. 2005). Finally, it is not clear whether the presence of recombination hotspots in humans, which appear to be absent or weak in Drosophila, could play a role in the apparent difference in the strength of HRI. Systematic surveys of other genomes and further developments of theory are needed to understand how these factors combine to shape rates of adaptive evolution, as well as the effects of selection on diversity and divergence genome-wide.

Our findings also have implications for the evolution of recombination rates. Indeed, HRI is thought to play a fundamental role in shaping the evolution of recombination rates in small effective populations, such as those found in these three primate species (Stone and Verrelli 2006; Hernandez et al. 2007), as modifier alleles that increase recombination locally can be selected if they reduce HRI (Felsenstein 1974; Felsenstein and Yokoyama 1976; Otto and Lenormand 2002; Barton and Otto 2005). Intuitively, this phenomenon occurs because a modifier allele produces, and so resides on, haplotypes with greater fitness (e.g., with fewer deleterious or more advantageous mutations) and as a result tends to hitchhike to fixation. Consistent with this notion, Iles et al. (2003) demonstrated that HRI can lead to consistent selection on modifiers for increased recombination rate when many tightly linked loci are simultaneously under positive selection, while Keightley and Otto (2006) showed that a constant influx of deleterious mutations can select for increased rates of recombination. Our findings, however, suggest that there is no detectable effect of recombination on rates of protein evolution in primates, implying that HRI is likely to exert little selection pressure on modifiers of recombination. One implication is that other selective pressures, e.g., related to karyotype changes or to the risk of nondisjunction (Coop and Przeworski 2007), are likely to have influenced the evolution of recombination rates in primates.

Methods

Sequence analysis

We used a highly vetted set of genic alignments for human, chimpanzee, and rhesus macaque (Gibbs et al. 2007). For each of the 10,376 trios of orthologous genes (Gibbs et al. 2007), we calculated maximum likelihood estimates of ω (the d_N/d_S ratio), κ, and d_N and d_S using the CODEML program provided with version 3.15 of PAML (Yang 1997) with control parameters as follows: ω is constrained to be the same on all branches of the human/chimp/rhesus rooted tree; the transition/transversion ratio, κ, is estimated for each gene; d_N and d_S estimates are per branch; and there is assumed to be no variation in ω across sites within a gene. The assumption of a single ω for the entire phylogeny could not be rejected for almost all genes (data not shown). The codon-based maximum likelihood method (Yang and Nielsen 1998) assumes stationarity, and the equilibrium codon frequencies were calculated using the F3x4 method, which is to say that they were calculated from the nucleotide frequencies at each of the three codon positions, as observed in the data.

The program CODEML provides default values for estimated parameters when they cannot be directly estimated in a meaningful way from the data. In our data, there are 45 orthologous trios of genes (0.4% of the data) with zero observed synonymous changes, for which CODEML sets ω to 999. In all analyses with the exception of when ω values are quantile-normalized, we discarded these genes. Additionally, there are 1009 trios of genes with zero observed nonsynonymous changes, for which ω is set to 0.0001, and there are 406 trios with zero observed transversions, for which CODEML sets κ to 99. For the human-lineage specific rates, we allowed CODEML to vary ω per branch and used only the ω estimate for the human-specific lineage.

We also calculated d_N and d_S using the Nei–Gojobori method (Nei and Gojobori 1986), based on human–rhesus macaques, as provided by PAML. By this approach, 74 genes have d_S = 0 and 1144 genes have d_N = 0.

We excluded genes with d_N = 0 from three analyses: (1) when testing the partial correlation between d_N/d_S and recombination rates, controlling for GC content; (2) when using the linear model analyses; and (3) when testing for correlations between d_N/d_S and recombination rate in the high and low tails of the d_N/d_S distribution and when partitioning by γ values. PAML assigns genes with no observed nonsynonymous substitutions a d_N/d_S estimate of 0.0001 (see above), regardless of the value of d_S. This value of d_N/d_S is arbitrary and probably lower than the true d_N/d_S parameter, were enough time to pass for both synonymous and nonsynonymous substitutions to occur. We therefore chose to exclude these genes, which comprise ∼10% of the data (see Results).

We located the centromeres by downloading the centromere-labeled nonbridgeable gaps from the UCSC Genome Browser build March 2006 (Kuhn et al. 2007).

Finally, to assess if genes were positively or negatively selected when looking at within-selection-class correlations between d_N/d_S and the recombination rate, we used the Bayesian CI around the γ estimates from (Bustamante et al. 2005). As our criterion for positively selected genes, we required the CI to lie entirely above zero and similarly for negatively selected genes, we required the CI to be entirely below zero. To relax the criteria, we ordered genes based on the lower edge of the CI for genes in the positively selected tail and the upper edge of the CI for genes in the negatively selected tail, successively adjusting the number of genes in the tails between 100 and 2000 in increments of 50. Only autosomal genes were included in this analysis.

Recombination rates

Broad-scale recombination rates are based on the best available pedigree-based recombination map in humans (Kong et al. 2002). To estimate recombination rates for specific genes, we calculated broad-scale recombination rates by linearly interpolating between the two markers flanking the center of each gene. The median distance between flanking markers was 925 kb, with 90% of the distribution between 180 kb and 2.8 Mb. Thus, the broad-scale rates represent an estimate of recombination on the megabase scale.

In turn, the fine-scale recombination rates are based on a human recombination map inferred from HapMap Phase I linkage-disequilibrium data, using the program LDhat (Myers et al. 2005). We estimated fine-scale recombination rates by averaging the smoothed rates between pairs of markers within a 40-kb window centered on each gene. The center of each gene was determined as the midpoint between the first and last base, the coordinates of which are specified in the alignments (Gibbs et al. 2007).

Calculation of gene density and GC content

We calculated the gene density by counting the number of genes for which exons overlap or are contained in the 1-Mb window around the gene center. We used gene models downloaded from Ensembl 45 (Hubbard et al. 2007) to determine which genes were contained within the 1-Mb window; this build of Ensembl is based on NCBI build 36 of the human genome. Similarly, we computed exon density as the number of distinct exons contained in a 1-Mb window centered on each gene. The GC content attributed to each trio of orthologs was calculated from the human gene. Throughout this article, GC refers to GC4, which is the percentage of guanines and cytosines in third codon positions that are fourfold degenerate. Eighty-four percent of genes have at least 50 fourfold degenerate codons, making GC4 an accurate estimate of putatively neutral GC content for most genes.

PANTHER category analysis

We used gene function annotations from version 6.1 of the PANTHER ontology (Mi et al. 2007). For each gene, we used only the broadest tier of classifications. Genes can be assigned to more than one annotated molecular function, resulting in some correlation between categories. For analyses that required a single molecular function annotation per gene, we chose one function at random in the cases where the gene had multiple function annotations.

Calculation of partial correlation coefficients

We calculated partial correlation coefficients between variables X and Y by calculating the correlation between the two sets of residuals formed by two linear models X ∼ Z and Y ∼ Z, where Z is the variable that we wish to hold fixed. We used a Spearman rank correlation test to estimate the correlation coefficient and obtain a P-value. For correlations that involve d_N/d_S, we used quantile-normalized d_N/d_S because in controlling for a third variable, Z, the linear model used to regress out d_N/d_S Z is sensitive to the highly non-normal distribution of d_N/d_S estimates (see below). For partial correlation estimates involving PANTHER categories, a problem is that many genes have more than one top-tier molecular function annotation, which makes it difficult to treat PANTHER category as a factor in the linear model. For genes with more than one molecular function annotation, we randomly picked one and then computed the partial correlation. We repeated this 1000 times and considered the median correlation estimate from these permutations and the associated P-value.

Linear model analysis

We compared a number of linear models, using as the response variable either quantile-normalized d_N/d_S (PAML or Nei–Gojobori), the raw d_N/d_S (PAML only), or human-specific d_N/d_S and using as the predictor variables various combinations of the recombination rate, GC content, gene density, log gene density, 1/gene density, cM/gene, log cM/gene, and PANTHER category. The predictor variable centimorgans per gene is simply the recombination rate estimate (cM/Mb) divided by gene density (genes/Mb). The distribution of d_N/d_S values is approximately exponential, which is a problem in a least-squares linear model framework because the residuals will be highly non-normal, making the results difficult to interpret. Therefore, we quantile-normalized the d_N/d_S values, replacing the estimates of d_N/d_S with their theoretical quantiles based on a normal distribution. For the original distribution of d_N/d_S estimates, the log-transformed distribution, and a depiction of the quantile normalization, see Supplemental Figure 16.

We also used a linear model framework to investigate the effects of HRI on polymorphism data, relying on the genome-wide resequencing data set of Bustamante et al. (2005), for which 39 humans were surveyed for variation in the exons of ∼11,000 genes. The response variable was the number of nonsynonymous segregating sites observed in each gene and the predictor variables included broad- or fine-scale recombination rate, linear and squared GC content, gene density, and the number of silent segregating sites observed in each gene. We chose not to model the ratio of nonsynonymous to synonymous sites (p_N/p_S) in order to include the numerous genes with zero observed synonymous segregating sites. We used genes for which we had polymorphism data and for which we could unambiguously match to corresponding genes in our other datasets (i.e., ∼5,000 genes). The γ estimates used in this analysis are also from Bustamante et al. (2005).