Abstract
The availability of various types of genomic data provides an opportunity to incorporate this data as prior information in genetic association studies. This information includes knowledge of linkage disequilibrium structure as well as which regions are likely to be involved in disease. In this paper, we present an approach for incorporating this information by revisiting how we perform multiple-hypothesis correction. In a traditional association study, in order to correct for multiple-hypothesis testing, the significance threshold at each marker, t, is set to control the total false-positive rate. In our framework, we vary the threshold at each marker ti and use these thresholds to incorporate prior information. We present a numerical procedure for solving for thresholds that maximizes association study power using prior information. We also present the results of benchmark simulation experiments using the HapMap data, which demonstrate a significant increase in association study power under this framework. We provide a Web server for performing association studies using our method and provide thresholds optimized for the Affymetrix 500k and Illumina HumanHap 550 chips and demonstrate the application of our framework to the analysis of the Wellcome Trust Case Control Consortium data.
Whole-genome association is an important first step in discovering the genetic basis of human disease (Devlin and Risch 1995; Risch and Merikangas 1996; Collins et al. 1998; Altshuler et al. 2005). These studies are often followed up by examining the molecular function of associated loci to identify whether they play a biological function in disease. Recently developed genomic resources such as those generated by the ENCODE project (ENCODE Project Consortium 2007) provide a tremendous amount of information on molecular function. These resources provide an opportunity to incorporate prior information into genetic association studies, including which regions are more likely to be involved in disease. Despite recent progress (Pe’er et al. 2006; Roeder et al. 2006, 2007), questions remain on how to incorporate this information into the design of association studies. In this paper, we present an approach for incorporating this information by revisiting how we perform multiple-hypothesis correction. Surprisingly, our approach increases statistical power not only in the presence of prior information, but also only using information on the linkage disequilibrium structure obtained from human variation reference sets such as the HapMap (Altshuler et al. 2005).
Due to the number of markers collected in an association study, correcting for multiple-hypothesis testing is a major challenge in large association studies. The goal of these studies is to detect a causal polymorphism from a subset of putative causal polymorphisms while controlling the overall false-positive rate, α, of the association study. In a typical association study, genotype data are collected for a set of M markers, each of which is a proxy for a subset of the polymorphisms, and a statistic is evaluated over the data at each collected marker. In order to correct for multiple-hypothesis testing, the significance threshold at each marker is set to control the total false-positive rate of the complete study. The Bonferroni approximation for this threshold, t = (α/M), is a reasonable estimate if the markers are independent and M is large.
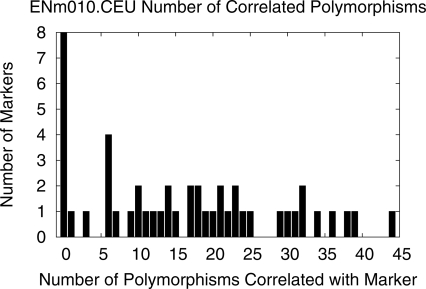
The traditional approach treats each of the markers identically by setting each marker’s significance threshold to t. However, in practice, the markers are not identical. Different markers have differing probabilities for serving as a proxy for causal variation for several reasons. Some polymorphisms are in regions more likely to be involved in disease than other polymorphisms, based on previous candidate gene or linkage studies. Even if we assume all polymorphisms are equally likely to be involved in disease, the markers are not identical. Some markers are correlated with few polymorphisms while others are correlated with many polymorphisms (Fig. 1), and these differences affect the likelihood that a marker serves as a proxy for a causal polymorphism. By treating each marker identically, traditional association approaches do not take advantage of differences between markers.
Figure 1.
Marker heterogeneity in the ENm010 ENCODE region in the CEU population. Histogram of the count of SNPs for which each marker is a proxy.
In this paper, we present a method for incorporating information about markers into association studies to increase statistical power. Information about markers is classified into two types: intrinsic and extrinsic. Intrinsic information includes information on linkage disequilibrium patterns between markers and the polymorphisms they are correlated with, as well as the allele frequencies of the markers and correlated polymorphisms, all of which can be estimated from the HapMap (Altshuler et al. 2005). Extrinsic information encodes prior beliefs about which polymorphisms are likely to be causal and may include information from previous linkage studies, genes thought likely to be involved in specific diseases, and which single nucleotide polymorphisms (SNPs) have known molecular function, such as nonsynonymous coding SNPs.
We present an association framework that can leverage both of these types of information. The main idea behind our approach is that instead of using a constant threshold t for each marker, we instead set a different threshold, ti, at each marker that reflects both intrinsic and extrinsic information on the markers. We present a novel multi-threshold association study analysis (MASA) method for setting these thresholds to maximize the statistical power of the study in the context of the additional information. The simplest approach for encoding extrinsic information is through assuming a causal probability distribution. In this setting, we assume that the causal polymorphism is chosen from this distribution and only one polymorphism is causal. We refer to the probability that the polymorphism is causal as its causal probability, ci. If the marker i is causal, the power at marker i or the probability of detecting the association is dependent on the per-marker threshold ti. Given the causal probabilities, using the approach presented in this paper, we can numerically solve for the marker thresholds that maximize power. By taking advantage of this information, we show how our multi-threshold framework can significantly increase the power of association studies while still controlling the overall false-positive rate, α, of the study as long as ∑ ti = α. Counterintuitively, higher causal probabilities do not always translate into higher thresholds; i.e., there is a complex relationship between causal probabilities and optimal thresholds. We can gain intuitions on our method by considering the following analogy to investing: Our algorithm must choose how to distribute a total budget of α (corresponding to the overall false-positive rate) among M possible investments (corresponding to the markers), and each investment has a certain return (corresponding to the power at the marker). Not surprisingly, the optimal overall return is achieved when the marginal rate of return is equal in each investment. Returning to our setting, the derivative of the power function at each marker at the marker’s optimal threshold is equal for all markers. We use this insight to motivate our numerical procedures for obtaining the thresholds. Our optimization algorithm is very efficient, and we can obtain thresholds for whole-genome associations in minutes.
Even in the case that all polymorphisms are equally likely to be causal, this framework can take advantage of differences in marker minor allele frequency and density of putative casual polymorphisms relative to markers to increase power over traditional association studies. Since this framework sets the thresholds based on the assumption of independent markers, the true false-positive rate of the designed association studies will be more conservative than expected. We present a permutation-based procedure to correct for this assumption to achieve a desired false-positive rate that increases computational time only slightly relative to traditional permutation tests.
Our method makes the assumption that the relative risk of the causal polymorphism is known. We show that even if the true relative risk of the causal polymorphism differs from the assumed relative risk, in most cases our method still increases the power over traditional association studies. Similarly, consistent with previous studies (Roeder et al. 2006), if the causal likelihoods are incorrectly specified, the amount of power lost is very small compared with the power gains if the causal likelihoods are correctly specified.
Incorporating prior information into association studies by modifying multiple-hypothesis testing was pioneered by Roeder et al. (2006) using a modified false discovery rate procedure. More recently, Wasserman and Roeder (Wasserman and Roeder 2006; Roeder et al. 2007) presented a modified Bonferroni approach. Our approach has some similarities to the Wasserman and Roeder (Wasserman and Roeder 2006; Roeder et al. 2007) approach, which presents an elegant analytical solution for setting thresholds assuming a Bonferroni correction, but it differs in several important ways. Our approach explicitly takes into account proxies, which complicates the optimization and requires a numerical solution for determining the thresholds. In fact, much of the power gains from our method stem from taking advantage of information derived from the HapMap on the tremendous heterogeneity among markers with respect to the linkage disequilibrium patterns between markers and polymorphisms and the heterogeneity among allele frequencies of polymorphisms. This accounts for why our approach provides more significant power increases compared with the more modest power increases of previous approaches such as those of Wasserman and Roeder (Wasserman and Roeder 2006; Roeder et al. 2007) and Rubin et al. (2006), which use sample splitting to estimate the equivalent information. Our approach also handles the effect of correlated markers on the overall false-positive rate and develops methods for determining the overall false-positive rate of a study.
An alternative framework for incorporating prior information into association studies is through the use of Bayesian hypothesis testing (Pe’er et al. 2006; Marchini et al. 2007). Our approach, as well as those of Wasserman and Roeder (Wasserman and Roeder 2006; Roeder et al. 2007) and Rubin et al. (2006), fundamentally differ from the Bayesian approach. A key difference is that our approach, by design, provides strong control of the false-positive rate regardless of the accuracy of the prior information. In other words, incorrect information will lead to a reduction in statistical power, but not an increase in the rate of false positives. While Bayesian hypothesis testing methods provide an estimate of the number of false positives, they do not provide such control of the false-positive rate. One of the advantages of the Bayesian framework is how straightforward it is to incorporate priors. In that light, a major contribution of our and related approaches is the ability to both incorporate prior information and provide strong control of false-positive rates. Other approaches to increasing power by modifying multiple-hypothesis testing include that of Van Steen et al. (2005).
We benchmark our methods using many simulated case-control data sets created using the HapMap project data and demonstrate that our multi-threshold approach significantly increases the power both for small regions such as a candidate gene region and in whole-genome association studies by taking into account both intrinsic and extrinsic information. In order to measure the effect of intrinsic information, specifically linkage disequilibrium patterns in the HapMap, we assume that each polymorphism is equally likely to be causal and observe on average an increase in power that is equivalent to an increase in the number of individuals by 9%. In simulations of whole-genome association studies with the Affymetrix 500k chip using this information, our method increases the power equivalently to increasing the number of individuals by 5%.
We measure the effect of extrinsic information by encoding this information as causal likelihoods in the association study. By assuming that genes suspected of being involved in a disease are more likely to harbor causal polymorphisms, we can increase power equivalent to an increase of the number of individual by 27%, and, by assuming that nonsynonymous coding SNPs account for 20% of causal polymorphisms, we can increase power equivalent to increasing the number of individuals by 17%. Surprisingly, there is a relationship between the distribution of likely causal polymorphisms among proxies and the power gained by incorporating the prior information. If the same marker serves as a proxy for both likely and unlikely causal variation, some of the gains in using the prior information are mitigated. The reason for this effect is that the linkage disequilibrium structure constrains the flexibility of setting different thresholds for correlated markers. This suggests that “region-specific” information such as the results of previous linkage scans (Roeder et al. 2006) or candidate genes is more useful in an association study than “polymorphism-specific” information such as specific polymorphisms that have suspected molecular function (Botstein and Risch 2003).
We provide a Web server for performing association studies using this method at http://masa.cs.ucla.edu/. On the Web site, we provide thresholds optimized for the Affymetrix 500k and Illumina HumanHap 550 chips (Matsuzaki et al. 2004; Gunderson et al. 2005).
Methods
Standard association studies
Given an association study that collects genotype information on M markers in N/2 cases and N/2 controls individuals, we denote the minor allele frequency of a specific marker fi. We assume that the causal polymorphism has a relative risk of γ and low penetrance. To simplify the analysis, we make the standard assumptions that all markers are independent, and one of the markers, d, is the actual causal polymorphism. We will relax these assumptions below.
A causal polymorphism with relative risk γ, low penetrance, and minor allele frequency fd will induce an allele frequency difference between the cases and controls. We denote the true case and control allele frequency for each marker 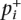 and
and 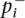 , respectively. In the case of the causal marker d,
, respectively. In the case of the causal marker d,
 |
Note that 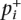 =
= 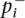 if i ≠ d. We denote the observed frequencies in the case and control sample
if i ≠ d. We denote the observed frequencies in the case and control sample 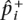 and
and 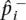 and their mean
and their mean 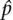 i = (
i = (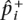 −
− 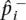 /2).
/2).
In a case and control study with N individuals, the following statistic is evaluated at each marker
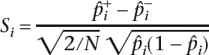 |
and is approximately normally distributed with variance 1 and mean
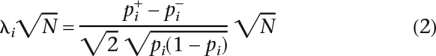 |
where pi = (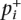 +
+ 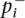 /2) and λi
/2) and λi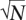 is the non-centrality parameter that increases with both the allele frequency difference and the number of individuals in the study for the casual polymorphism, and λi = 0 otherwise. The non-centrality parameter is dependent on both the marker’s minor allele frequency and the relative risk.
is the non-centrality parameter that increases with both the allele frequency difference and the number of individuals in the study for the casual polymorphism, and λi = 0 otherwise. The non-centrality parameter is dependent on both the marker’s minor allele frequency and the relative risk.
The power of an association study at a given marker depends on this non-centrality parameter. The power at a single marker Ps(t, λi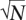 ) or the probability of detecting an association in a study with N individuals at P-value or significance threshold t, and non-centrality parameter λi
) or the probability of detecting an association in a study with N individuals at P-value or significance threshold t, and non-centrality parameter λi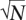 is
is
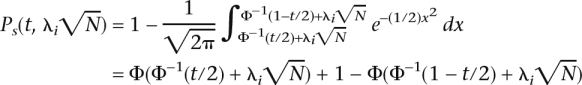 |
where P and Φ−1(t) is the cumulative distribution function and quantile of the standard normal distribution.
The standard approach to association studies over multiple markers fixes the false-positive rate or P-value threshold at each marker such that after correcting for multiple-hypothesis testing, the total false-positive rate or adjusted P-value is α. In a standard association study, assuming the Bonferroni correction for multiple-hypothesis testing, t = (α/M). Let c1, c2, . . . , cM, ∑ ci = 1 be the probability distribution over which of the M markers is causal and let fi represent the minor allele frequency of marker mi. In traditional association studies, each marker is assumed to be equally likely to be causal; i.e., ci = (1/M) for ∀i. If a marker is causal, we denote its non-centrality parameter computed using Equations 1 and 2, and λi = 0 otherwise. We measure the “expected power” of the association study, which is
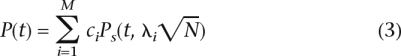 |
with an adjusted false-positive rate of α when t = (α/M). Equation 3 differs from the traditional definition of the statistical power since it measures the probability of rejecting the correct null hypothesis and not the probability of rejecting any null hypothesis. However, the “expected power” is a more meaningful measure of performance for the design of association studies. For a well motivated discussion of “expected power” and its relation to traditional measures of power, see Rubin et al. (2006).
Multi-threshold association studies
Since the power at each marker depends on its minor allele frequency, which influences λi, not all of the terms in Equation 3 contribute equally to the power even when all markers are equally likely to be causal. We can exploit this observation to increase the power of an association study. Instead of using the same threshold t for all markers, we instead allow a different P-value significance threshold ti for each marker. Under the null hypothesis, the chance of a false positive is 1 −  (1 − ti) ≈
(1 − ti) ≈  ti for small ti if the markers are independent. This motivates a similar multiple-hypothesis correction to the Bonferroni correction; i.e., if
ti for small ti if the markers are independent. This motivates a similar multiple-hypothesis correction to the Bonferroni correction; i.e., if 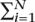 ti = α then the multiple-hypothesis testing adjusted false-positive rate remains α.
ti = α then the multiple-hypothesis testing adjusted false-positive rate remains α.
In this formulation, the power of an association study is
 |
with multiple-hypothesis testing adjusted false-positive rate 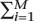 ti = α. A traditional association study is a special case of this framework where ti = tj = (α/M) and ci = (1/M) for ∀i, j. The distribution ci can be used to encode prior information on which polymorphisms are likely to be causal. By varying ti, we can leverage this information in the association study.
ti = α. A traditional association study is a special case of this framework where ti = tj = (α/M) and ci = (1/M) for ∀i, j. The distribution ci can be used to encode prior information on which polymorphisms are likely to be causal. By varying ti, we can leverage this information in the association study.
Since the overall power of an association study depends on the values of ti, we can set the values for ti to maximize the power of the association study by maximizing Equation 4 subject to the constraints 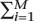 ti = α and ti ≥ 0. As we show below, we can numerically solve this optimization problem to find the global maximum of this function. The optimal set of thresholds (ti) reflects both differences in non-centrality parameters (λi) and differences in causal probabilities (ci).
ti = α and ti ≥ 0. As we show below, we can numerically solve this optimization problem to find the global maximum of this function. The optimal set of thresholds (ti) reflects both differences in non-centrality parameters (λi) and differences in causal probabilities (ci).
Maximizing the association study power
In order to maximize Equation 4, we consider the vector of thresholds T = {t1, t2, . . . , tM}. Since each threshold is contained in only one term of the sum, the gradient is simply the vector of partial derivatives
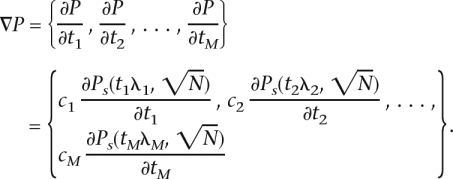 |
The partial derivative of the power function with respect to the significance threshold at a single marker is
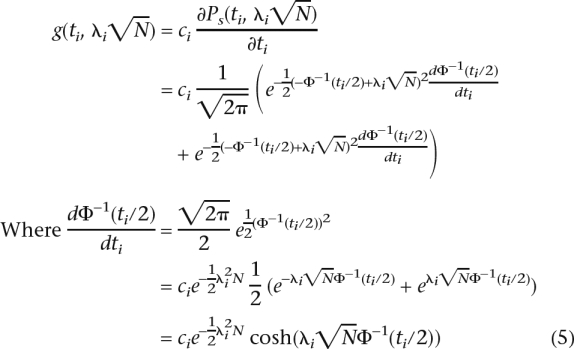 |
Since second derivative of the power function is negative for all ti from 0 to 1 (at ti = 1, the second derivative is 0), the function Ps(ti, λi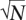 ) is concave and the sum of concave functions, Equation 4, is concave. Since we are maximizing a concave function over a convex set, there exists a unique maximum point. Since the power function at each marker is monotonically increasing with the threshold, the maximum will be achieved on the plane where ∑ ti = α. At each ti = 0 the derivatives go to positive infinity; therefore, the maximum point will occur where all ti are positive. The maximization can be solved using Lagrange multipliers, and at the maximal point all components of the gradient will be equal; i.e., for the optimal threshold
) is concave and the sum of concave functions, Equation 4, is concave. Since we are maximizing a concave function over a convex set, there exists a unique maximum point. Since the power function at each marker is monotonically increasing with the threshold, the maximum will be achieved on the plane where ∑ ti = α. At each ti = 0 the derivatives go to positive infinity; therefore, the maximum point will occur where all ti are positive. The maximization can be solved using Lagrange multipliers, and at the maximal point all components of the gradient will be equal; i.e., for the optimal threshold 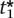 , . . . ,
, . . . , 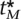 , g(
, g(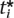 , λi
, λi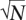 ) = g(
) = g(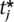 , λj
, λj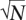 ) for all i, j and ∑
) for all i, j and ∑ 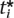 = α. We use this observation to numerically estimate the optimal point. Given a value of the gradient, we solve for the threshold at each marker to achieve that gradient. We denote the inverse of the gradient g−1(β, λi
= α. We use this observation to numerically estimate the optimal point. Given a value of the gradient, we solve for the threshold at each marker to achieve that gradient. We denote the inverse of the gradient g−1(β, λi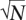 ) = ti if β = g(ti, λi
) = ti if β = g(ti, λi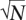 ). For any value of the gradient β, the sum of the optimal thresholds corresponding to the gradient is ∑ g−1(β, λi
). For any value of the gradient β, the sum of the optimal thresholds corresponding to the gradient is ∑ g−1(β, λi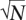 ). We perform binary search over the values of the gradient until the thresholds sum to α.
). We perform binary search over the values of the gradient until the thresholds sum to α.
Maximizing power for proxies
In the previous section, we made the assumption that the markers themselves are causal. In practice, the markers are more likely to be tags for the causal variation. Given K polymorphisms, we can assign each potential causal polymorphism to the best marker. We associate each polymorphism vk to a single marker i, using the notation vk ∈ Ti. From Pritchard and Przeworski (2001), the effective non-centrality parameter of the indirect association is reduced by a factor of |rki|, where rki is the correlation coefficient between polymorphism k and marker i. Each polymorphism k has a probability of being causal ck. If a given polymorphism vk is causal, the power function when observing proxy marker i is Ps(t, |rki|λk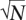 , N). Using a reference data set such as the HapMap (Altshuler et al. 2005), we can obtain estimates for these correlation coefficients. We can then denote the total power captured by each marker i as Pm(ti, Ti, N) = ∑vk∈Ti ckPs(ti, |rki|λk
, N). Using a reference data set such as the HapMap (Altshuler et al. 2005), we can obtain estimates for these correlation coefficients. We can then denote the total power captured by each marker i as Pm(ti, Ti, N) = ∑vk∈Ti ckPs(ti, |rki|λk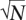 ). In this case, the total power of the association study is
). In this case, the total power of the association study is
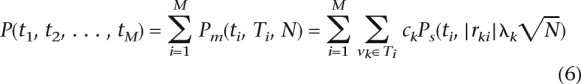 |
The power of the study taking into account indirect association can be maximized using the same approach as above. If a marker has more than one proxy, finding the threshold that achieves a certain gradient must be solved numerically. If a marker has only one proxy, we can analytically derive the inverse of the Equation 5 (function g−1), which results in an algorithm that is comparable in terms of computational complexity to the approach of Wasserman and Roeder (Wasserman and Roeder 2006). Equation 6 makes the assumption that each causal polymorphism has a unique marker proxy. In reality, some polymorphisms are covered by multiple markers, which causes our estimate of power to be conservative.
Assessing statistical significance in multi-threshold studies
If the statistical significance at a marker is below its threshold, we declare an association at the marker, and, as shown above, the overall significance of this association is below α. Since the thresholds differ at each marker, it is not immediately clear how to assign a multiple-testing adjusted P-value to each marker.
Consider the case where at marker i with threshold ti we observe an association with significance level 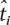 ≤ ti. We can obtain a multiple-testing adjusted significance level α* at this marker using a similar optimization procedure to obtaining the optimal thresholds. The multiple-hypothesis adjusted significance level is the probability under the null hypothesis of observing a more significant association at any marker. Intuitively, if
≤ ti. We can obtain a multiple-testing adjusted significance level α* at this marker using a similar optimization procedure to obtaining the optimal thresholds. The multiple-hypothesis adjusted significance level is the probability under the null hypothesis of observing a more significant association at any marker. Intuitively, if 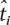 = ti, then by definition, the multiple-testing adjusted significance level is α. For
= ti, then by definition, the multiple-testing adjusted significance level is α. For 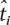 ≤ ti, we want to determine the significance level α* < α. Estimating this significance level is equivalent to discovering the α* and a new set of thresholds
≤ ti, we want to determine the significance level α* < α. Estimating this significance level is equivalent to discovering the α* and a new set of thresholds 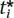 such that when we maximize Equation 6 with the constraint ∑j
such that when we maximize Equation 6 with the constraint ∑j 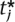 = α*, the threshold for marker i is the observed threshold,
= α*, the threshold for marker i is the observed threshold, 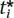 =
= 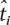 . We denote the gradient at the observed threshold
. We denote the gradient at the observed threshold 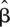 = g−1(
= g−1(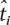 , λi
, λi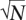 ). At the optimal solution, the gradient at each markers will be equal to
). At the optimal solution, the gradient at each markers will be equal to 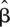 and the threshold is
and the threshold is 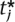 = g−1(
= g−1(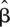 , λj
, λj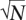 ). Thus, the multiple-hypothesis corrected significance level for observed significance level
). Thus, the multiple-hypothesis corrected significance level for observed significance level 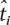 at marker i is
at marker i is
Accommodating correlated markers
Due to the linkage disequilibrium structure of the genome, the Bonferroni assumption of independent markers is not realistic. In the case of correlated markers, setting the threshold to t = (α/M) will achieve an overall false-positive rate lower than α. Using the procedure above to obtain the multiple-hypothesis corrected significance threshold, we can apply a permutation procedure to discover thresholds that take into account the false-positive rate. This procedure works as follows: We first permute the case and control samples, and for each marker we compute the multi-threshold significance level. We record the most significant association and repeat for each permutation. We then observe the empirical distribution of these significance levels (minimum P-values) and use this distribution to determine the true significance level that corresponds to a given observed significance level.
A problem with this procedure is that it is not computationally feasible since it requires obtaining the significance level at each marker in each permutation. We take advantage of the observation that at the optimal solution for a set of thresholds, the gradient of the power function with respect to the significance level at each marker is equal. Thus, the most significant multi-threshold association will correspond to the marker with the highest gradient. We can then obtain the same empirical distribution by computing the gradient at each marker and recording the maximum value of the gradient in each permutation. The quantile of the empirical distribution of maximum gradient and the minimum P-value are equivalent, which allows us to efficiently compute the permutation-adjusted multiple-threshold P-values.
Results
Candidate gene study associations
We simulate association studies in a candidate gene-sized region using the HapMap data ENCODE regions (Altshuler et al. 2005) by following the evaluation protocol presented in de Bakker et al. (2005). In these simulations, we generate 1000 cases and control individuals by randomly sampling from the pool of haplotypes from HapMap samples in the ENCODE regions. The disease status for each individual is determined by randomly designating a SNP from this region as causal with a certain relative risk. We simulate the scenario where we are using a whole-genome genotyping product such as the Affymetrix 500k SNP chip (Matsuzaki et al. 2004) and assume that the study collects as markers the subset of genotypes from this region that are present on the chip. Using the HapMap data, we uniquely assign each SNP to a proxy by choosing the marker with the highest correlation coefficient with the SNP. We perform this simulation over the four HapMap populations in each of the 10 ENCODE regions. Over the 10 ENCODE regions, there are 34–120 polymorphic SNPs on the Affymetrix gene chip, and the total number of SNPs ranges from 607 to 1841.
We first consider power estimates of traditional versus multi-threshold association studies where we assume that the markers are independent. Consider, for example, the ENCODE region ENm010 for the CEU population. In this region, there are 47 markers on the Affymetrix 500k gene chip that serve as proxies for the 756 SNPs. The number of proxies for each tag varies from 1 to 50. If we assume 1000 cases and controls genotyped at each tag and a relative risk of 2.0 for the causal SNP, a traditional association study using the Bonferroni correction to set the threshold to achieve a false-positive rate at α = 0.05 will have an average power of 0.683. We obtain this estimate by repeatedly sampling 1000 case and control individuals from the HapMap following the simulation procedure described in de Bakker et al. (2005). If we apply MASA to optimize the thresholds of the study, the average power increases to 0.711. An increase of power of 3% may not seem that significant, but the average power is a misleading indicator. In fact, most of the SNPs in the region either have very high or very low power. Of the 756 SNPs, 425 have a power >0.9, and 138 have a power <0.1 in a traditional association study. In the multi-threshold association study, for both of these sets of high- and low-powered SNPs, the power changes only slightly. However, for the 193 SNPs with power in a traditional study between 0.1 and 0.9, the multi-threshold association study significantly increases the average power of these SNPs from 0.459 to 0.556. A more informative measure is the increase in the number of individuals that a traditional association study would need to achieve an equivalent power increase. On average, the power increase due to optimizing the thresholds is equivalent to increasing the number of individuals by 9%. This measure can be computed by repeatedly simulating traditional association studies with an increasing number of individuals until the traditional study power equals the multi-threshold study power.
Previous methods for weighted hypothesis testing did not take into account proxies, which makes it difficult to compare MASA directly with previous methods. We can measure the relative importance of taking proxies into account by applying the optimization method using only information from the markers and then measuring the power considering all SNPs including SNPs correlated with the markers. The thresholds we obtain are equivalent to those that we would obtain using the method presented in Roeder et al. (2007). Using these thresholds, the power decreases to 0.678, which is not surprising considering that in this case the method is optimizing the power only at the 47 SNPs that are markers, while we are measuring the power over the 756 SNPs in the region.
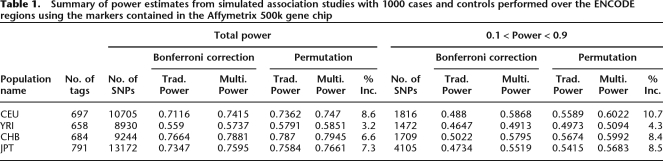
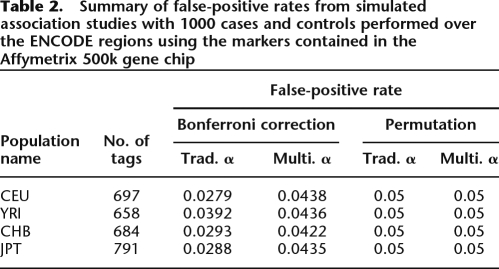
Since the SNPs on the Affymetrix SNP chip are correlated, our use of the Bonferroni approximation for the threshold results in a conservative estimate of the false-positive rate. We empirically measure our false-positive rate by repeatedly sampling 1000 case and control individuals from the HapMap data and observe that our true false-positive rates for our thresholds set using the Bonferroni correction are 0.031 and 0.046 for traditional and multi-threshold association studies, respectively. We apply a permutation procedure to obtain the correct false-positive rate. To set the traditional permutation threshold, we compute the empirical distribution of the minimum P-value from each simulated association study and use this distribution to set the threshold that empirically achieves a false-positive rate of 0.05. To set the weighted thresholds, we apply our gradient permutation procedure (see Methods). We empirically verify the false-positive rates for our permutation-based threshold using simulations and obtain false-positive rates of 0.050 for both traditional and multi-threshold association. Our power using these adjusted thresholds for a traditional study is 0.705 and is increased to 0.714 using the multi-threshold association, which is equivalent to the power gain of increasing the number of individuals by 8%. For SNPs with power between 0.1 and 0.9, the power increase is more dramatic, going from 0.517 to 0.566, equivalent to increasing the number of individuals by 13%. Tables 1 and 2 summarize the comparison over all 10 ENCODE regions.
Table 1.
Summary of power estimates from simulated association studies with 1000 cases and controls performed over the ENCODE regions using the markers contained in the Affymetrix 500k gene chip
Table 2.
Summary of false-positive rates from simulated association studies with 1000 cases and controls performed over the ENCODE regions using the markers contained in the Affymetrix 500k gene chip
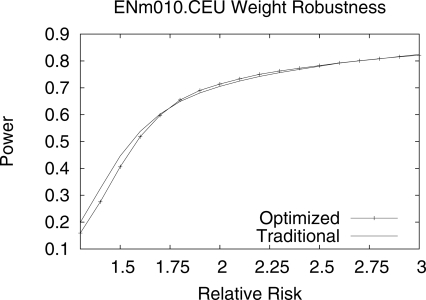
Our approach makes the unrealistic assumption that we know the relative risk of the causal polymorphism, and this assumption is used to set the optimal thresholds. We measure the effect of an incorrect assumption of the relative risk by obtaining optimal thresholds assuming the relative risk is 2.0 and measuring the power of these thresholds under a wide range of relative risks. Figure 2 shows the power under different relative risks. Even if the assumption is incorrect, the multi-threshold association method increases the power for a wide range of relative risks, in this case from 1.65 to >3.0, compared with traditional association studies.
Figure 2.
Comparison of multi-threshold power compared with traditional power over a range of relative risks. The weights were optimized for a relative risk of 2.0, and power was measured over a range of relative risks to measure performance if relative risk is incorrectly specified. Multi-threshold power outperforms traditional power for a range of relative risks. In this case, multi-threshold association outperforms traditional methods for relative risks >1.65.
Whole-genome association experiments
We simulate whole-genome multi-threshold association studies using the Affymetrix 500k gene chip by generating simulated 1000 case and 1000 control data sets using the HapMap data. We assume that each of the 2,614,057 SNPs polymorphic in the CEU population in the HapMap are equally likely to be causal with a relative risk of 2. The power of a traditional association study with false-positive rate α = 0.05 is 0.593, and the average power for the 916,380 SNPs that have power between 0.1 and 0.9 is 0.568. The power of a multi-threshold association study is 0.610 overall and 0.615 for the 916,380 SNPs. This power increase is equivalent to an increase of individuals by 5% and 7%, respectively.
We measure the impact on extrinsic information on whole-genome scans by considering two types of extrinsic information. We first consider the assumption that coding SNPs (cSNPs), regardless of where they occur in the genome, are more likely to be involved in disease. Second, we consider adding information on a set of genes that are more likely to be involved in specific diseases. We consider the set of 30,700 cSNPs among the polymorphic SNPs in the HapMap. In a traditional association study, the power for detecting an association if a cSNP is causal is 0.500, and the overall power is 0.593. For SNPs that have power between 0.1 and 0.9, the power for detecting association at a cSNP is 0.560, and the overall power is 0.568. If we assume that the 30,700 cSNPs contribute to 20% of the disease-causing variation, the causal likelihood of these SNPs is 21 times the causal likelihood of the remaining SNPs. In this case, the overall power of a traditional association study is 0.583 (and 0.567 for mid-range power SNPs). If we take this information into account, the multi-threshold power increases the power of detecting an association if a cSNP is causal is increased to 0.545 (and 0.681 for mid-range power causal SNPs). This increase is equivalent to increasing the number of individuals by 16% (17%). The overall power of a multi-threshold association increases to 0.602 (and 0.619 for mid-range power SNPs), which is equivalent to increasing the number of individuals by 5% (7%). If our prior information on the causal likelihood of cSNPs is incorrect and they are not any more likely to be involved in disease than remaining SNPs, the overall multi-threshold power is 0.608 (compared with the power of a traditional study 0.593). In fact, the power is increased compared with a traditional study regardless of the contribution of cSNPs to the disease-causing variation. Thus, the potential gains of using prior information are much larger than the loss in power if the information is incorrect.
We measure the impact of information on which genes are more likely to be involved in disease by simulating association studies using the Cancer Gene Census (CGC) (Futreal et al. 2004). The CGC contains a list of 363 genes in which mutations have been implicated in cancer. Using the CGC as prior information in the context of a whole-genome scan for variation that affects cancer susceptibility, we make the assumption that SNPs in these genes are more likely to be involved in cancer susceptibility than SNPs in other genes. These genes contain 34,475 SNPs within 50 kb of the genes. We simulated an association study where we assume that 20% of the causal variation in cancer is located in these genes. Under this assumption, these SNPs are 18 times more likely to be the causal variation. A traditional association study under these assumptions would have a power of 0.588 and 0.567 for mid-range power SNPs; those with power in a traditional association study between 0.1 and 0.9. Taking advantage of this prior knowledge improves the power of an association to 0.612 and 0.632 for mid-range SNPs, which is equivalent to an increase of the number of individuals by 7% and 9%, respectively. Over the cancer gene SNPs, the power is increased to 0.641 (0.746 for mid-range SNPs) from 0.566 (0.565) in the traditional study, which is an increase in the number of individuals by 27% (28%). Over the remaining SNPs, the power is 0.605 (0.605) compared with 0.593 (0.568), which is an increase of 4% (5%) individuals. On the other hand, if we assume this prior information when setting the thresholds, but in fact the CGC genes are no more likely than other genes to be involved in disease, the power of the method decreases to 0.606, which is still higher than the power in a traditional association study (0.593). Despite the incorrect assumptions about which SNPs are likely to be involved in disease, the gains due to taking advantage of the correlation structure result in an increase in overall power compared with the traditional approach.
Application to the WTCCC data
We apply our method to the Wellcome Trust Case Control Consortium (WTCCC) data (Wellcome Trust Case Control Consortium 2007). This data set contains genotypes for ∼2000 individuals for each of seven diseases and genotypes for 3000 control individuals, which is equivalent to a study with 2400 case and control individuals in a balanced study. We consider the 400,266 SNPs that pass the quality control filters and map to a unique SNP in the HapMap.
We first examine the increase in power of applying our method to take into account the linkage disequilibrium structure. If we assume a relative risk of 1.5, the power of the association study is 0.472. If we apply our method to optimize the thresholds to take into account the linkage disequilibrium structure, the power increases to 0.494, which is an increase in power equivalent to increasing the number of individuals by 5%. For SNPs with power between 0.1 and 0.9, the power increases from 0.573 to 0.620, equivalent to an increase of 6% of the number of individuals. If we assume that nonsynonymous coding SNPs account for 20% of the causal SNPs, using that information increases the power for cSNPs from 0.393 to 0.450, equivalent to increasing the number of individuals by 17%. For cSNPs with power between 0.1 and 0.9, the power increases from 0.560 to 0.685, equivalent to increasing the number of individuals by 18%. Adjusted P-values for associations using MASA applied to the WTCCC data are available at http://masa.cs.ucla.edu/.
Discussion
We have presented a method for incorporating prior information into association studies that uses multiple thresholds when correcting for multiple-hypothesis testing. For the case where the prior information can be represented in the form of causal probabilities, or the probability that a specific polymorphism is causal with respect to the disease, we present an efficient algorithm that can solve for the thresholds that maximize power. We show that even in the case where each polymorphism is equally likely to be causal, our approach increases the power by adjusting the thresholds due to differences in non-centrality parameters caused by differences in minor allele frequencies and the linkage disequilibrium structure. In our experiments, our method provides the equivalent gain in power as increasing the sample size on average by 19%. Prior information represented in terms of causal probabilities can provide a further increase in power.
Our approach builds on recent work in incorporating prior information in association studies (Pe’er et al. 2006; Roeder et al. 2006, 2007). The closest method to what is presented is that of Wasserman and Roeder (Wasserman and Roeder 2006; Roeder et al. 2007), which is also a modified Bonferroni approach. An advantage of the Wasserman and Roeder (Wasserman and Roeder 2006; Roeder et al. 2007) approach is that they have a very elegant analytical solution for setting the thresholds given the non-centrality parameter, which is dependent on a single constant that can be numerically computed from the data, resulting in a much more computationally efficient algorithm for setting the thresholds. However, their approach is not applicable to the practical case where the markers are proxies for causal variation. Since both methods are based on the Bonferroni correction, the optimal thresholds are too conservative due to the independence assumptions of the correction. We provide an iterative procedure that incorporates empirical estimates of the false-positive rates to achieve the desired false-positive rate.
Acknowledgments
I thank the anonymous reviewers for helpful comments. E.E. is partially supported by National Science Foundation grants nos. 0513612 and 0731455 and National Institutes of Health Grant no. 1K25HL080079. Part of this investigation was supported using the computing facility made possible by the Research Facilities Improvement Program grant no. C06 RR017588 awarded to the Whitaker Biomedical Engineering Institute, and the Biomedical Technology Resource Centers Program grant no. P41 RR08605 awarded to the National Biomedical Computation Resource, UCSD, from the National Center for Research Resources, National Institutes of Health. Additional computational resources were provided by the California Institute of Telecommunications and Information Technology (Calit2).
Footnotes
[MASA is available at http://masa.cs.ucla.edu.]
Article published online before print. Article and publication date are online at http://www.genome.org/cgi/doi/10.1101/gr.072785.107.
References
- Altshuler D., Brooks L., Chakravarti A., Collins F., Daly M., Donnelly P., Consortium I.H., Brooks L., Chakravarti A., Collins F., Daly M., Donnelly P., Consortium I.H., Chakravarti A., Collins F., Daly M., Donnelly P., Consortium I.H., Collins F., Daly M., Donnelly P., Consortium I.H., Daly M., Donnelly P., Consortium I.H., Donnelly P., Consortium I.H., Consortium I.H. A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botstein D., Risch N., Risch N. Discovering genotypes underlying human phenotypes: Past successes for mendelian disease, future approaches for complex disease. Nat. Genet. 2003;33 (Suppl.):228–237. doi: 10.1038/ng1090. [DOI] [PubMed] [Google Scholar]
- Collins F.S., Brooks L.D., Chakravarti A., Brooks L.D., Chakravarti A., Chakravarti A. A DNA polymorphism discovery resource for research on human genetic variation. Genome Res. 1998;8:1229–1231. doi: 10.1101/gr.8.12.1229. [DOI] [PubMed] [Google Scholar]
- de Bakker P., Yelensky R., Pe’er I., Gabriel S., Daly M., Altshuler D., Yelensky R., Pe’er I., Gabriel S., Daly M., Altshuler D., Pe’er I., Gabriel S., Daly M., Altshuler D., Gabriel S., Daly M., Altshuler D., Daly M., Altshuler D., Altshuler D. Efficiency and power in genetic association studies. Nat. Genet. 2005;37:1217–1223. doi: 10.1038/ng1669. [DOI] [PubMed] [Google Scholar]
- Devlin B., Risch N., Risch N. A comparison of linkage disequilibrium measures for fine-scale mapping. Genomics. 1995;29:311–322. doi: 10.1006/geno.1995.9003. [DOI] [PubMed] [Google Scholar]
- ENCODE Project Consortium Identification and analysis of functional elements in 1% of the human genome by the ENCODE pilot project. Nature. 2007;447:799–816. doi: 10.1038/nature05874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Futreal P., Coin L., Marshall M., Down T., Hubbard T., Wooster R., Rahman N., Stratton M., Coin L., Marshall M., Down T., Hubbard T., Wooster R., Rahman N., Stratton M., Marshall M., Down T., Hubbard T., Wooster R., Rahman N., Stratton M., Down T., Hubbard T., Wooster R., Rahman N., Stratton M., Hubbard T., Wooster R., Rahman N., Stratton M., Wooster R., Rahman N., Stratton M., Rahman N., Stratton M., Stratton M. A census of human cancer genes. Nat. Rev. Cancer. 2004;4:177–183. doi: 10.1038/nrc1299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gunderson K., Steemers F., Lee G., Mendoza L., Chee A., Steemers F., Lee G., Mendoza L., Chee A., Lee G., Mendoza L., Chee A., Mendoza L., Chee A., Chee A. A genome-wide scalable SNP genotyping assay using microarray technology. Nat. Genet. 2005;37:549–554. doi: 10.1038/ng1547. [DOI] [PubMed] [Google Scholar]
- Marchini J., Howie B., Myers S., McVean G., Donnelly P., Howie B., Myers S., McVean G., Donnelly P., Myers S., McVean G., Donnelly P., McVean G., Donnelly P., Donnelly P. A new multipoint method for genome-wide association studies by imputation of genotypes. Nat. Genet. 2007;39:906–913. doi: 10.1038/ng2088. [DOI] [PubMed] [Google Scholar]
- Matsuzaki H., Dong S., Loi H., Di X., Liu G., Hubbell E., Law J., Berntsen T., Chadha M., Hui H., Dong S., Loi H., Di X., Liu G., Hubbell E., Law J., Berntsen T., Chadha M., Hui H., Loi H., Di X., Liu G., Hubbell E., Law J., Berntsen T., Chadha M., Hui H., Di X., Liu G., Hubbell E., Law J., Berntsen T., Chadha M., Hui H., Liu G., Hubbell E., Law J., Berntsen T., Chadha M., Hui H., Hubbell E., Law J., Berntsen T., Chadha M., Hui H., Law J., Berntsen T., Chadha M., Hui H., Berntsen T., Chadha M., Hui H., Chadha M., Hui H., Hui H., et al. Genotyping over 100,000 SNPs on a pair of oligonucleotide arrays. Nat. Methods. 2004;1:109–111. doi: 10.1038/nmeth718. [DOI] [PubMed] [Google Scholar]
- Pe’er I., de Bakker P., Maller J., Yelensky R., Altshuler D., Daly M.J., de Bakker P., Maller J., Yelensky R., Altshuler D., Daly M.J., Maller J., Yelensky R., Altshuler D., Daly M.J., Yelensky R., Altshuler D., Daly M.J., Altshuler D., Daly M.J., Daly M.J. Evaluating and improving power in whole-genome association studies using fixed marker sets. Nat. Genet. 2006;38:663–667. doi: 10.1038/ng1816. [DOI] [PubMed] [Google Scholar]
- Pritchard J.K., Przeworski M., Przeworski M. Linkage disequilibrium in humans: Models and data. Am. J. Hum. Genet. 2001;69:1–4. doi: 10.1086/321275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risch N., Merikangas K., Merikangas K. The future of genetic studies of complex human diseases. Science. 1996;273:1516–1517. doi: 10.1126/science.273.5281.1516. [DOI] [PubMed] [Google Scholar]
- Roeder K., Bacanu S., Wasserman L., Devlin B., Bacanu S., Wasserman L., Devlin B., Wasserman L., Devlin B., Devlin B. Using linkage genome scans to improve power of association in genome scans. Am. J. Hum. Genet. 2006;78:243–252. doi: 10.1086/500026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roeder K., Devlin B., Wasserman L., Devlin B., Wasserman L., Wasserman L. Improving power in genome-wide association studies: Weights tip the scale. Genet. Epidemiol. 2007;31:741–747. doi: 10.1002/gepi.20237. [DOI] [PubMed] [Google Scholar]
- Rubin D., Dudoit S., van der Laan M., Dudoit S., van der Laan M., van der Laan M. A method to increase the power of multiple testing procedures through sample splitting. Stat. Appl. Genet. Mol. Biol. 2006;5 doi: 10.2202/1544-6115.1148. Article19. [DOI] [PubMed] [Google Scholar]
- Van Steen K., McQueen M., Herbert A., Raby B., Lyon H., Demeo D., Murphy A., Su J., Datta S., Rosenow C., McQueen M., Herbert A., Raby B., Lyon H., Demeo D., Murphy A., Su J., Datta S., Rosenow C., Herbert A., Raby B., Lyon H., Demeo D., Murphy A., Su J., Datta S., Rosenow C., Raby B., Lyon H., Demeo D., Murphy A., Su J., Datta S., Rosenow C., Lyon H., Demeo D., Murphy A., Su J., Datta S., Rosenow C., Demeo D., Murphy A., Su J., Datta S., Rosenow C., Murphy A., Su J., Datta S., Rosenow C., Su J., Datta S., Rosenow C., Datta S., Rosenow C., Rosenow C., et al. Genomic screening and replication using the same data set in family-based association testing. Nat. Genet. 2005;37:683–691. doi: 10.1038/ng1582. [DOI] [PubMed] [Google Scholar]
- Wasserman L., Roeder K., Roeder K. 2006. Weighted hypothesis testing. Archive: http://arxiv.org/abs/math/0604172v1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wellcome Trust Case Control Consortium Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature. 2007;447:661–678. doi: 10.1038/nature05911. [DOI] [PMC free article] [PubMed] [Google Scholar]