On the inference of ancestries in admixed populations

Abstract

Inference of ancestral information in recently admixed populations, in which every individual is composed of a mixed ancestry (e.g., African Americans in the United States), is a challenging problem. Several previous model-based approaches to admixture have been based on hidden Markov models (HMMs) and Markov hidden Markov models (MHMMs). We present an augmented form of these models that can be used to predict historical recombination events and can model background linkage disequilibrium (LD) more accurately. We also study some of the computational issues that arise in using such Markovian models on realistic data sets. In particular, we present an effective initialization procedure that, when combined with expectation-maximization (EM) algorithms for parameter estimation, yields high accuracy at significantly decreased computational cost relative to the Markov chain Monte Carlo (MCMC) algorithms that have generally been used in earlier studies. We present experiments exploring these modeling and algorithmic issues in two scenarios—the inference of locus-specific ancestries in a population that is assumed to originate from two unknown ancestral populations, and the inference of allele frequencies in one ancestral population given those in another.

Recent advances in genotyping and sequencing technologies have resulted in exciting discoveries of links between genes and diseases via whole-genome association studies (Bonnen et al. 2006). In these studies, cases and controls are collected and single nucleotide polymorphisms (SNPs) are genotyped across the entire genome of these two populations. A discrepancy in the allele distribution across the cases and the controls serves as evidence for an association between the SNP and the condition studied.

One of the main caveats of such association studies is their sensitivity to confounding effects. In particular, the ancestral background of the cases and the controls may affect the results. In order to overcome this problem, one could infer the ancestral background of each individual using the genotypes and then apply a correction to the statistical tests based on this information (Price et al. 2006).

The inference of ancestral information is a nontrivial problem, and the accuracy of existing methods on this task is currently limited. Our focus in the present paper is on the setting of recently admixed populations in which every individual is composed of a mixed ancestry (e.g., African Americans in the United States, Hispanic populations, and recently mixed populations in large metropolitan areas such as New York or the San Francisco Bay Area). These populations originate from two or more ancestral populations that were separated for a long time, and then started mixing a small number of generations ago (e.g., 10–20 generations ago). Owing to recombination events, the genome of every such admixed individual is a mosaic of haplotypes that originated from the original ancestral populations. Thus, in order to describe their overall ancestry, we have to find the locus-specific ancestry for each individual, or the ancestral origin of every locus in the genome of each of the individuals.

Given the genetic underpinnings of the ancestral origin problem, it is natural to consider inference methods based on probabilistic models. Indeed, most previous work has made use of hidden Markov models (HMMs), where the states are the ancestral populations, the transitions roughly correspond to historical recombination events, and the emission matrix models population-specific allele frequencies (Pritchard et al. 2000; Falush et al. 2003; Hoggart et al. 2004; Patterson et al. 2004). Such Markovian models capture the linkage disequilibrium (LD) among alleles that arises owing to admixture, but they fail to account for within-population linkage disequilibrium (the HMM assumes that alleles are independent once the ancestries are known). It is possible, however, to augment the HMM to include additional Markovian dependencies among the observed alleles to attempt to account for the latter form of LD; such a model has been referred to as a Markov Hidden Markov Model (MHMM) and has been implemented in the program SABER (Tang et al. 2006).

In this study, we consider an augmented form of the HMM/MHMM framework for modeling admixture that includes explicit indicators for recombination events. Specifically, if a recombination event occurs between SNPs, then the ancestries of the SNPs are chosen independently; if recombination does not occur, then the ancestries are set equal. These explicit indicators serve several purposes. First, they make it possible to estimate the location of recombination events; the set of events is generally a strict superset of the set of change-of-ancestry events that are captured by the state sequence. The use of explicit indicators within an admixture model thus makes it possible to use admixture data to make inferences regarding historical recombinations and recombination rates. Second, recombination indicators can yield improvements in the estimates of haplotype frequencies. Note in particular that the MHMM used in SABER conditions on the ancestral state to decide whether to use pairwise or singleton allele probabilities (if the state does not change, then the pairwise probabilities are used; otherwise singleton probabilities are used). However, haplotypes are broken up by recombination, not only by change of ancestry, and it would seem desirable to be able to condition on these more fine-grained events.

One of the goals of the paper is thus to investigate the role of recombination indicators in HMM/MHMM models. Another goal of the paper is to consider more broadly whether the HMM/MHMM modeling and inference framework provides a practical computational solution to the problem of modeling of admixture and LD. In these models, inference of ancestry is tractable once its parameters are determined, but the need to estimate various hyperparameters is a challenging problem that has led researchers to Markov chain Monte Carlo (MCMC) sampling procedures. These procedures have desirable theoretical properties in the limit of large numbers of samples, but in practice they can be overly slow for realistic data sets.

To tackle the computational problem, Sankararaman et al. (2008) have recently presented a rather different, non-model-based approach to inferring locus-specific ancestries. This method (referred to as “LAMP”) is based on running a window over the genome, computing the local ancestry of each individual within each window based on a local-likelihood model, and combining the results from the windows overlapping a given SNP using a majority vote. Sankararaman et al. (2008) have shown empirically that this approach provides estimates of ancestry that significantly improve on the HMM-based methods. This improvement may be due to the inadequacy of the Markovian assumptions, but it may also arise because the HMM models are being initialized randomly and the MCMC procedures are not mixing on a practical timescale.

To address this issue, note that practical applications of HMMs in other literature, most notably the speech and signal processing literature (Huang et al. 2001), emphasize the critical need for effective initialization of parameter estimation procedures for HMMs. Practical inference for HMM-based admixture models may also require effective initialization. Accordingly, we investigate the possibility of using the solution from LAMP to initialize an HMM. Hill-climbing in likelihood from the LAMP solution may provide an effective way to retain the advantages of a model-based method while not sacrificing performance.

A final issue that we investigate concerns the modeling of background LD when the data are a dense set of SNPs. As alluded to earlier, the HMM does not attempt to model background LD. The MHMM models background LD via a simple first-order Markov chain that links neighboring alleles. To evaluate the adequacy of this model of background LD, we compare the MHMM to an alternative approach that prunes SNPs with a heuristic that discards highly correlated SNPs and then uses these SNPs as input to an HMM.

Our experimental work focuses on the problem of inferring locus-specific ancestries in a population that is assumed to originate from two unknown ancestral populations (Falush et al. 2003; Sankararaman et al. 2008). We also consider a less-studied scenario in which we assume that one of the ancestral populations is unknown, or its genotypes are not given, and we wish to infer the allele frequencies in this population. This scenario may be appropriate in situations in which it is difficult to obtain external estimates of the allele frequencies of one of the ancestral populations. This is the case, for example, in many modern Caribbean populations (such as Puerto Ricans), where the native American population has vanished.

Methods

In this section, we describe the augmented HMM that serves as the basis of our experiments. We also describe an MHMM that incorporates a model of background LD along the lines of SABER (Tang et al. 2006). We then describe various forms of inference algorithms for these hidden Markov models, emphasizing the use of the EM procedure for parameter estimation.

Probabilistic model

To simplify our presentation, let us assume that the number of populations that have been admixed is two (the notation is slightly more involved in the case of more than two populations, but no new ideas are needed). Also, again for simplicity of presentation, we restrict our attention to haplotypes; genotypes can be handled in a straightforward manner as described in the Appendix.

Let m denote the number of haplotypes, and let n denote the number of SNPs. Let X be the observed binary matrix of SNPs; that is, X_i,j is the jth SNP of the ith haplotype. Let p and q be the vectors of the allele frequencies in the ancestral populations. Hence, p_j is the probability to obtain 1 in the jth SNP in the first population, and q_j is the corresponding probability in the second population. The matrix Z denotes the ancestry information of each haplotype at each SNP: Z_i,j ∈ {0, 1} holds the ancestry of haplotype i at the jth SNP (0 if SNP j of haplotype i originated from the first population and 1 if it originated from the second). We use the matrix W to denote recombination events. Specifically, W_i,j equals 1 if at least one recombination event occurred during the history of the admixture process in the ith haplotype in the interval between the (j − 1)-th SNP and the jth SNP, and 0 otherwise. The (n − 1)-dimensional vector θ denotes the probability of at least one such recombination event, with θ_j corresponding to the interval between the (j − 1)-th and the jth SNPs. The fraction of the first population in the ancestral population, which we call the “admixture fraction,” is denoted by α. Finally, g denotes the number of generations of the admixed process (in the sense that 1/[g − 1] models the average length of ancestral chromosome blocks in the current admixed population).

Given the parameters g, α, p, q, and θ, we model a haplotype as being generated as follows: Recombination points are generated on each chromosome based on a Poisson process whose rate parameter depends on g and the recombination rate r. This process corresponds to setting some of the Ws to 1. Then the ancestries of the resulting chromosomal blocks are determined independently for each block, with α being the probability to choose the first ancestry. We assume that the mating is random across the populations. Given the ancestry at a particular position, an allele is generated using the corresponding ancestral allele frequency. We assume that the alleles are generated independently in a block.

We now describe the marginal and conditional distributions of the model. We assume a uniform prior over the interval [0, 1] for each of the parameters α, p, q. The parameter g is assumed to be distributed uniformly over the interval [g_min, g_max] for some g_max > g_min > 1. Given the ancestry and given the allele frequencies of a specific SNP j in haplotype i, X_i,j is a Bernoulli random variable with distribution:

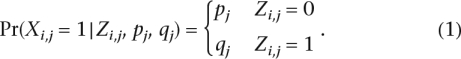The distribution of the ancestry of a specific SNP depends on the occurrence of a recombination event. On the occurrence of a recombination between SNPs j and j − 1 of haplotype i, the ancestry Z_i,j is chosen with probability α to be 0 and 1 otherwise. If there was no recombination, the ancestry stays the same as that at the previous SNP:

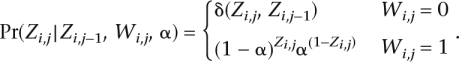where δ(x, y) = 1, if x = y.

Since we assume that the recombination process is a Poisson process, the variables W_i,j and W_i,k are independent for k ≠ j and the probability for a specific location between SNPs j − 1 and j to have at least one recombination depends solely on θ_j. For j > 1, we have Pr(W_i,j = 1|θ_j) = θ_j and θ_j = 1 − e^{−(g−1)l_jr_j}, where l_j is the distance between the (j − 1)-th SNP and the jth SNP and r_j is the recombination rate in that region. In our specific problem, θ_j is a deterministic function of g. In other situations, it may be more appropriate for g to parameterize a prior over θ_j.

Marginalizing over the recombination indicator W_i,j, we obtain the mixture distribution that is used as a transition matrix by programs such as STRUCTURE (Falush et al. 2003) and SABER (Tang et al. 2006).

Modeling background LD

The HMM framework assumes that alleles are conditionally independent given the states and thus is not able to capture within-population LD. The MHMM model implemented in SABER (Tang et al. 2006) attempts to capture such background LD by allowing additional dependencies directly between the observable X_i variables. The form of these dependencies differs depending on the ancestries Z_i,j−1 and Z_i,j. In particular, if these ancestries are the same, then a pairwise emission probability is used. If these ancestries are different, then a singleton emission probability is used. SABER estimates the pairwise probabilities using ancestral haplotypes (which are assumed to be available).

Given that our model makes use of explicit recombination indicators W_i,j, we can condition on these variables instead of the ancestry variables Z_i,j. Formally, we define the following transition matrix for j > 1:

The transition matrix is defined so that if W_i,j = 1 (i.e., a recombination has occurred between SNPs j − 1 and j), then the allele seen at position j is independent of the allele at position j − 1. If W_i,j = 0, the SNPs at position j − 1 and j belong to the same ancestral haplotype, and the emission probability of the allele at position j depends on the allele at j − 1. Here p_j−1,j and q_j−1,j are the pairwise (conditional) SNP frequencies at positions j − 1 and j in the haplotypes from the two respective populations.

Why do we condition on recombination events instead of ancestries (as in SABER)? Note that the conditioning in SABER ignores recombinations that do not change the ancestries. Such recombinations are expected to be common when the admixture fraction α ≪ ½. In that case, assuming random mating, an expected fraction α² + (1 − α)² of recombinations will not lead to a change in the ancestry. Ignoring such events can be problematic. Consider a scenario where the haplotype frequencies are estimated from an ancestral population. Assume that 00 and 11 are the only haplotypes present in this ancestral population. In the admixed population, a new haplotype, say 01, may arise because of a recombination event that is not accompanied by a change in the ancestry. By ignoring the recombination event and assuming that the two loci share a haplotype, the MHMM would assign a small probability (indeed, a zero probability in our example) to the new haplotype 01. On the other hand, in a model that conditions on the recombination indicators W_i,j, the new haplotype is assigned a frequency that is the product of the allele frequencies at the two loci.

Inference problems

In this section, we focus on two inferential problems that can be framed within the HMM/MHMM formalism. In both problems, we seek the maximum a posteriori (MAP) estimates of a subset of the variables in the model, and we find parameter estimates via the EM algorithm. For simplicity, we assume that the number of generations g is constant and known, and therefore θ is known. This is often the case for admixed populations. The two problems that we consider are: (1) The admixture fraction is known, the allele frequencies are unknown, and the goal is to find the local ancestries for each SNP in each haplotype. The optimization problem is to find (W, Z) such that Pr(W, Z|X, α, g) is maximized. We refer to this problem as the “local ancestries inference problem.” (2) The allele frequencies are known for one of the ancestral populations, and the goal is to find the allele frequencies of the other as well as the admixture fraction. Here, the local ancestries are missing variables. The optimization problem is to find (q, α) such that Pr(q, α|X, p) is maximized. We refer to this problem as the “ancestral allele frequencies inference problem.”

Local ancestries problem

To compute the local ancestries, we would like to compute the MAP estimates of Z and W by solving the following optimization problem:

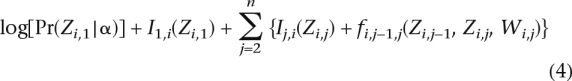In each iteration of EM, the updates to Z and W are computed by a Viterbi algorithm with the emission probabilities Pr(X_i,j|Z_i,j, p_j, q_j) replaced by an integral over p_j, q_j. The E-step involves computing the posterior probabilities of p_j, q_j; that is, Pr(p_j, q_j, |X_i,j, Z^(t)_i,j). This can be done easily using Bayes’ theorem. The M-step involves solving m separate optimization problems in Z_i, W_i, i ∈ {1, . . . , m} where Z_i denotes the vector of ancestries for the ith haplotype and W_i denotes the corresponding vector of recombination events:

where

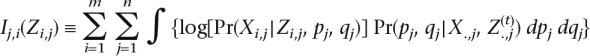corresponding to log transition probabilities and

are expectations of the log emission probabilities.

Generally, the values of I_j,i(z) can be tabulated for each i, j, z by computing the integral over a grid on the {p_j, q_j}. For our setting, we have a uniform prior over p_j and q_j which permits the integral to be evaluated analytically as shown in the Appendix. We can maximize Equation 4 by dynamic programming. The values obtained for Z, W are then used to recompute the integrals I_j,i(Z_i,j) and the procedure is iterated.

Ancestral allele frequencies problem

To compute the ancestral allele frequencies, we compute the MAP estimates of q and α:

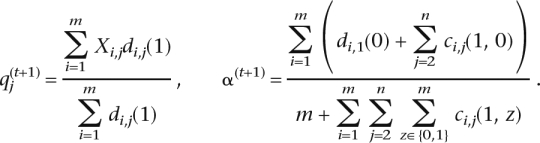since we have a uniform prior on q and α. We assume g and p to be known. Let q^(t), α^(t) denote the current estimates of q, α. The EM algorithm produces new estimates q^(t+1), α^(t+1) that improve the objective function:

Here

and

are the posterior probabilities of (W, Z) and Z at the jth SNP of haplotype i, respectively, and are computed by an application of the forward–backward algorithm in the E-step.

These updates have an intuitive interpretation. At each position j, the new value of q_j is the fraction of SNPs that are 1 out of all SNPs belonging to the second population (weighted by their posterior probabilities). The update for α is the fraction of ancestries chosen from the first population whenever a new haplotype is chosen (weighted by their posterior probabilities).

Experiments

We have implemented the HMM and the EM algorithm that we have described in a program that we term “SWITCH.” We have also implemented a program that we refer to as “SWITCH-MHMM” that is based on the MHMM. In this section, we describe experiments aimed at evaluating these procedures.

These experiments were run on data sets generated from HapMap data (http://www.hapmap.org). We used SNPs found in the Affymetrix 500K GeneChip Assay (http://www.affymetrix.com/products/arrays/specific/500k.affx) from Chromosome 1 for each of the HapMap populations; that is, Yorubans (YRI), Japanese (JPT), Han Chinese (CHB), and western Europeans (CEU). For a pair of populations, we simulated admixture by picking individuals from two ancestral populations in the ratio α:(1 − α). In each generation, individuals mate randomly and produce offspring. The rate of the recombination process is set to 10⁻⁸ per base pair per generation (Nachman and Crowell 2000). The mixing process is repeated for g generations. We generated data sets consisting of admixtures of YRI-CEU, CEU-JPT, and JPT-CHB populations. We set g to 7 and α to 0.20 since these roughly correspond to the admixing process in African-American populations as estimated in Falush et al. (2003), Patterson et al. (2004), and Tian et al. (2006). For each of the problems, we use only genotype data. Since the HMM underlying SWITCH assumes that the SNPs are conditionally independent given the states, in the input to SWITCH we greedily remove SNPs that have a high correlation coefficient, r² > 0.1, with any other SNP. We refer to this usage of SWITCH as “uSWITCH.” (When the entire set of SNPs is used, we refer to the usage simply as “SWITCH.”) Ancestry estimates at the discarded SNPs were filled in from the highly correlated SNP that was retained.

The remainder of this section is organized as follows. First, we compare the performance of various methods on the local ancestries problem. The role of the inference algorithms and background LD models are discussed in the next two sections, respectively. The performance of methods on the problems of predicting recombination events and the ancestral allele frequencies problem are then discussed in the following sections.

Local ancestries problem

We first compare the estimates of the ancestries obtained from SWITCH to the estimates obtained from SABER and LAMP. In these experiments, the methods are given g and α. We consider two settings depending on whether the ancestral frequencies, (p, q), are available. Even when the frequencies of the ancestral populations are available, it is still advantageous to use the data to update the frequency estimates, which may have drifted from the ancestral frequencies.

When they are available, uSWITCH uses a maximum-likelihood classification based on these frequencies as initialization. We refer to this variation of uSWITCH as uSWITCH-ANC. SABER also requires the ancestral allele frequencies. The version of LAMP that uses ancestral frequencies is termed “LAMP-ANC.”

When the ancestral allele frequencies are not known, LAMP can still be used, as can uSWITCH. For the latter, we use the estimates of ancestries from LAMP to initialize the EM algorithm.

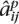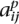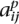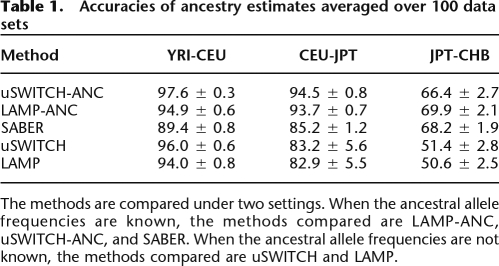
For each individual i and SNP j, each method finds an estimate ∈ {0, 0.5, 1} for the true ancestry . We measure the accuracy of a method as the fraction of triplets (i, j, p) for which = 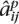. The first half of Table 1 compares the accuracies of SABER, LAMP-ANC, and uSWITCH-ANC on 100 random data sets of YRI-CEU, CEU-JPT, and JPT-CHB. uSWITCH-ANC improves significantly over LAMP-ANC and SABER on the YRI-CEU data set. On the CEU-JPT, uSWITCH-ANC and LAMP-ANC have comparable performance, and both methods are more accurate than SABER. All methods perform poorly on the JPT-CHB data set because of the closeness of the two populations. The second half of Table 1 compares the accuracies of uSWITCH and LAMP. On the YRI-CEU data, uSWITCH, with an accuracy of 96.0%, improves significantly over LAMP, which has an accuracy of 94.0% (Wilcoxon Paired Signed Rank test P-value of 3.89 × 10⁻¹⁸). Interestingly, uSWITCH improves significantly over LAMP-ANC even though the latter uses the ancestral allele frequencies. On the CEU-JPT and the JPT-CHB data sets, uSWITCH seems to have slightly higher accuracies than LAMP. We believe that using more informative priors on the variables (p, q) should yield further improvements by improving the estimation of low-frequency alleles. These results indicate that the HMM is most useful when the mixing populations can be easily distinguished as is the case with the YRI-CEU admixture.

Table 1.

Accuracies of ancestry estimates averaged over 100 data sets

The methods are compared under two settings. When the ancestral allele frequencies are known, the methods compared are LAMP-ANC, uSWITCH-ANC, and SABER. When the ancestral allele frequencies are not known, the methods compared are uSWITCH and LAMP.

Although the versions of uSWITCH have a factor of five to 10 increase in running time compared to LAMP, they still run under an hour on large data sets, making them feasible for genome-scale problems.

Role of the inference algorithm

To understand the impact of the inference algorithm and the initialization, we compared uSWITCH to STRUCTURE. While the model used in uSWITCH is the same as the model used in STRUCTURE when the recombination indicators W are integrated out, the inference algorithms differ. uSWITCH obtains the posterior mode of the ancestries Z using an EM algorithm with LAMP providing the initialization. STRUCTURE computes the posterior marginals of each Z_i,j using an MCMC algorithm to integrate out the unknown parameters. To evaluate the output from STRUCTURE, we threshold the posterior mean to obtain the actual ancestry estimates; that is, position i, j is assigned 0, 1, or 2 alleles from one of the populations depending on whether the posterior marginal E(Z_i,j|X) lies in [0, 0.5), [0.5, 1.5), or [1.5, 2]. We compared the ancestry estimates produced by the two methods on the YRI-CEU data set. STRUCTURE was run for 10,000 burn-in and 50,000 MCMC iterations (see below for further discussion of this choice). The linkage model was used. STRUCTURE was run on non-overlapping sets of 4000 SNPs covering 36,000 of the 38,000 initial SNPs because of numerical instabilities when larger numbers of SNPs were used.

On the YRI-CEU data set, uSWITCH achieved an accuracy of 97%, while STRUCTURE achieved an accuracy of 84%. To isolate the reason for this difference, we evaluated MCMC algorithms that differ from STRUCTURE in varying degrees. First, we ran MCMC from a random starting point for 1000 iterations with 100 iterations of burn-in and used the posterior mean as the ancestry estimates. This yielded estimates with an accuracy of 91.13%. When the LAMP estimates were used as a starting point, the accuracy was 94.9%. This suggests that the chain has not mixed in our STRUCTURE runs. To test this suggestion formally, we simulated five such chains each from different random starting points. We then computed a multivariate potential scale reduction factor (PSRF) (Brooks and Gelman 1998) for random sets of 100 ps and qs and found it to be consistently large (>1.2). When the Markov chain is unable to converge quickly, the initialization influences the ancestry estimates. Given that the MCMC algorithms do not converge even after being run for several days (in particular, the STRUCTURE runs required a little less than 3 d, while the other MCMC runs took about a day to run), good initialization becomes essential.

Two other differences between STRUCTURE and the MCMC algorithm that we implemented are that the latter discards correlated SNPs and fixes the hyperparameters. We modified the MCMC runs to retain the correlated SNPs, and the accuracy falls to 74.9%. We conclude that the pruning of highly correlated SNPs can have a large impact on the accuracy of models that do not attempt to account for background LD. Another approach to this problem is to attempt to account for background LD via the MHMM approach; we discuss this approach in the following section.

Modeling background LD

As discussed above, we refer to our implementation of an MHMM model based on the recombination indicators W_i,j as SWITCH-MHMM. We also implemented a version of the model based on the ancestries Z_i,j instead of the recombination indicators. We refer to this model as “MHMM”; it is the same as the model underlying SABER. (Our implementation differs from SABER in the inference procedures that we used; in particular, the ancestry estimates were computed by a Viterbi algorithm.)

In the first scenario that we studied, both the MHMM and the SWITCH-MHMM were given the ancestral haplotypes. The ancestral haplotypes were used to estimate the pairwise SNP emission probabilities. The single SNP frequencies were estimated using LAMP-ANC. In this experiment, SWITCH-MHMM achieved an accuracy of 91.9%, while the MHMM yielded an accuracy of 88.9%. This demonstrates that improvements can be obtained by conditioning on recombination indicators instead of conditioning on ancestral states.

In a second scenario, the pairwise SNP emission probabilities were estimated directly from the admixed data. In this case, the accuracies of SWITCH-MHMM and MHMM were both 95.7%. It is interesting to note that these accuracies are higher than in the case that ancestral haplotypes were used to estimate parameters. This is presumably because the estimates of haplotype frequencies are more accurate when estimated from the admixed population itself. Finally, we also measured the accuracy of ancestry estimates from SWITCH (i.e., when the entire set of SNPs was taken as input) and observed that the accuracy drops to 93.1%. This improvement in accuracies when background LD is taken into account has been observed before (Tang et al. 2006). However, the accuracy of uSWITCH is higher than SWITCH-HMM. Thus, the heuristic of removing highly correlated SNPs and then running SWITCH appears to be competitive, in practice, to the methods based on explicit (but simplified) models of background LD.

Predicting recombinations

Another advantage of the use of the recombination indicators W is that they open the possibility of inference of historic recombinations created by the mixing process after the initial admixture event. While a change in the ancestry between two SNPs implies a recombination event, many recombination events do not result in a change in the ancestry. When α is small, this happens quite often. To study this issue, we measured the accuracy of uSWITCH in predicting such recombinations. If a predicted recombination falls within 5 kb of the SNPs flanking a true recombination, it is called a true positive. If multiple recombinations are predicted within this window, only one is counted as a true positive. False positives and false negatives are defined similarly. The precision and recall of the predictions are then computed as

and

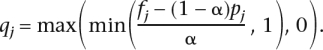We combine these numbers by taking a harmonic mean, reporting

As a baseline, we use a null model that predicts recombinations based on the exponentially distributed lengths of the haplotypes. The total number of recombinations in the null model is set to the number of predicted recombinations, and the precision and recall of the predictions are computed similarly.

On the YRI-CEU data set, uSWITCH attains an F-score of 70.8, while the null model attains an F-score of 52.8. uSWITCH was found to be consistently more accurate than the null model on the CEU-JPT and JPT-CHB data sets as well (data not shown).

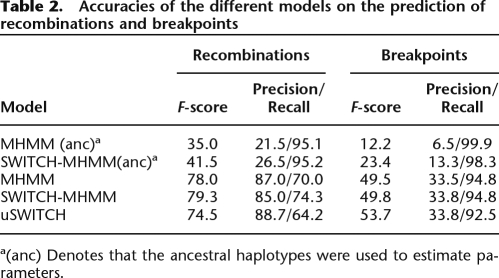
We now consider models that attempt to account for background LD. For the MHMM model, since the model does not explicitly represent recombinations, the recombinations are inferred (naively) based on a change in the ancestry labels. The results are shown in Table 2. When we use the ancestral haplotypes to estimate parameters, the MHMM and SWITCH-MHMM achieve F-scores of 35.0 and 41.5, respectively. Using the admixed data to estimate parameters, the two models achieve F-scores of 78.0 and 79.3, respectively. We see that the explicit W variables allow more accurate prediction of recombinations in the admixed genomes. When we restrict attention to breakpoints (recombinations that change the ancestry), the difference between the models is diminished although the relative performance is the same.

Table 2.

Accuracies of the different models on the prediction of recombinations and breakpoints

^a(anc) Denotes that the ancestral haplotypes were used to estimate parameters.

As discussed in the previous section, SWITCH-MHMM (and the other models that incorporate background LD) has lower accuracy than uSWITCH, which ignores background LD and uses a heuristic to prune correlated SNPs. However, SWITCH-MHMM predicts recombinations more accurately (while uSWITCH is more accurate in predicting breakpoints). This result suggests that models that incorporate background LD (albeit imperfectly) may be useful in inferring recombinations in admixed genomes.

Ancestral allele frequencies problem

We now turn to the problem of inferring ancestral allele frequencies. To obtain a benchmark, we implemented a naive algorithm. The naive algorithm is given the true value of α (which is not available to the model). The idea behind the naive algorithm is as follows. For a position j with minor allele frequency f_j, and allele frequencies p_j and q_j in the two populations, if the number of individuals is large, f_j can be written as f_j = (1 − α)p_j + αq_j. Thus we compute the allele frequency q_j at position j as

We used two different estimates of α, yielding algorithms that we refer to as “Naive1” and “Naive2.” Naive1 uses the value of α = 0.20, which is the admixture fraction in the first generation of admixture. Naive2 uses an α measured from each data set.

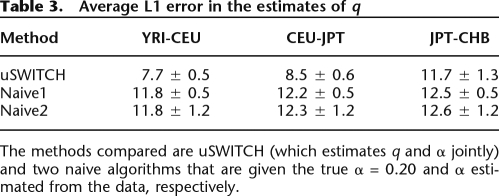
We calculated the L1 error (the sum of the absolute values of the errors) between the estimated 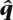and the true q. The L1 error averaged over 100 data sets of YRI-CEU, CEU-JPT, and JPT-CHB is shown in Table 3. We see that uSWITCH reduces the L1 error by ∼30% in the YRI-CEU and the CEU-JPT data sets, while there is no significant difference for the JPT-CHB data set.

Table 3.

Average L1 error in the estimates of q

The methods compared are uSWITCH (which estimates q and α jointly) and two naive algorithms that are given the true α = 0.20 and α estimated from the data, respectively.

We also compared the ancestry estimates from uSWITCH with those from STRUCTURE on single instances of YRI-CEU, CEU-JPT, and JPT-CHB data sets (the running time of STRUCTURE prohibited multiple runs). The L1 errors for uSWITCH are 7.1%, 8.3%, and 12.7% on the respective data sets. STRUCTURE obtains errors of 25.8%, 29.0%, and 25.2%, respectively.

Conclusions

Markovian models such as HMMs and MHMMs are a natural approach to admixture that aim to strike a balance between predictive performance and inferential complexity. We have explored several variations on the HMM/MHMM theme with the aim of identifying combinations of model specification, inference procedure, and data preprocessing that are most effective in realizing this balance.

We have found that explicit indicators of recombination events can be useful. These indicators allow us to provide a more fine-grained version of the MHMM that allows new haplotypes to emerge when recombinations occur, and not only when ancestral state changes. We found that this approach yielded better estimates when haplotype emission probabilities are inferred from ancestral populations. Also, by making the recombination events explicit in our model, we are able to infer historic recombinations. While being interesting in and of themselves, these predictions may be helpful in allowing admixture data to be used in the inference of recombination hotspots.

HMM and MHMM models require the estimation of model hyperparameters. One approach to estimating these hyperparameters is to use MCMC algorithms, but these algorithms can be impractical on realistic data sets. We have shown that an EM-based approach starting with an accurate initialization (the non-model-based procedure LAMP) yielded high accuracy at reasonable cost. Indeed, this approach yielded the best results of any algorithm that we studied.

Our conclusions regarding background LD are mixed. If an MHMM model is to be used to attempt to capture background LD, then we recommend conditioning on explicit recombination indicators. On the other hand, we found that a heuristic approach, in which highly correlated SNPs are discarded before running an HMM, yielded higher accuracy than the MHMM. One possible direction for future research is to consider richer MHMM models than the pairwise model considered here and in SABER.

An important caveat of our work is that we have not studied the robustness of our methods to factors such as variable recombination rates, continuous gene-flow models, and nonrandom mating. The extent to which the Markovian models that we have studied here are robust to such factors is currently unknown, and this is an essential direction for future research.