Integrated modeling of the major events in the MHC class I antigen processing pathway

Abstract

Rational design of epitope-driven vaccines is a key goal of immunoinformatics. Typically, candidate selection relies on the prediction of MHC–peptide binding only, as this is known to be the most selective step in the MHC class I antigen processing pathway. However, proteasomal cleavage and transport by the transporter associated with antigen processing (TAP) are essential steps in antigen processing as well. While prediction methods exist for the individual steps, no method has yet offered an integrated prediction of all three major processing events. Here we present WAPP, a method combining prediction of proteasomal cleavage, TAP transport, and MHC binding into a single prediction system. The proteasomal cleavage site prediction employs a new matrix-based method that is based on experimentally verified proteasomal cleavage sites. Support vector regression is used for predicting peptides transported by TAP. MHC binding is the last step in the antigen processing pathway and was predicted using a support vector machine method, SVMHC. The individual methods are combined in a filtering approach mimicking the natural processing pathway. WAPP thus predicts peptides that are cleaved by the proteasome at the C terminus, transported by TAP, and show significant affinity to MHC class I molecules. This results in a decrease in false positive rates compared to MHC binding prediction alone. Compared to prediction of MHC binding only, we report an increased overall accuracy and a lower rate of false positive predictions for the HLA-A*0201, HLA-B*2705, HLA-A*01, and HLA-A*03 alleles using WAPP. The method is available online through our prediction server at http://www-bs.informatik.uni-tuebingen.de/WAPP.

Activation of cytotoxic T-cells in the immune system requires presentation of endogenous antigenic peptides by MHC class I molecules (Pamer and Cresswell 1998; Kloetzel 2001; Lankat-Buttgereit and Tampe 2002). The processing pathway of MHC class I restricted antigens involves three major steps: cleavage, transport, and MHC binding. Cytosolic proteins are cleaved into smaller peptides by the proteasome. A subset of these peptides can be transported into the endoplasmatic reticulum (ER) by the transporters associated with antigen processing (TAP), where they can bind to MHC molecules. The MHC–peptide complex is subsequently translocated to the cell surface, where it may activate cytotoxic T-cells. Understanding and predicting the whole antigen processing pathway leading to these peptides is extremely valuable in epitope-driven vaccine development. While prediction methods for these individual steps have been described for quite some time, the performance is still low for some of the steps, and combining them into a single joint prediction is not trivial. We will now briefly describe the current state of the art for the individual processing steps.

The proteasome is a barrel-shaped protease complex described to have trypsin-like, chymotrypsin-like, and peptidylglutamyl-peptide hydrolytic activity (Uebel and Tampe 1999). The 20S proteasome can be found in two different forms, the constitutive form and the immunoproteasome induced by IFN-γ (Gaczynska et al. 1993). The proteasome cleaves ubiquitin-protein conjugates into smaller peptides and is responsible for generating the correct C terminus of MHC class I binding peptides (Niedermann et al. 1996; Craiu et al. 1997).

Several computational approaches for elucidating the cleavage specificity of the proteasome have been presented. They are all based on experimentally verified cleavage sites within protein substrates and analysis of the flanking region of such sites. Holzhütter et al. (1999) used a statistical method to analyze the cleavage sites found in a set of peptide substrates with lengths ranging from 22 to 30 amino acids. The method is a part of the MAPPP prediction server. PAProC (Kuttler et al. 2000; Nussbaum et al. 2001) is a method based on proteasomal degradation of the enolase protein. Up to 10 flanking amino acids around verified cleavage sites are used by an evolutionary algorithm to create the network-based model used for prediction. A third method for proteasomal cleavage prediction, NetChop, uses a neural network for prediction (Kesmir et al. 2002). There are two different sets of training data used by NetChop: verified cleavage sites within proteins on one hand and naturally processed MHC ligands on the other. MHC class I ligands for studying proteasomal cleavage were previously introduced by Altuvia and Margalit (2000).

After cleavage, peptides are transported into the ER by TAP, the transporter associated with antigen processing. TAP belongs to the large family of ATP-binding cassette (ABC) transporters and actively transports peptides from the cytosol into the ER. The transport is most efficient for peptides of 8–12 amino acids (Koopmann et al. 1996), and a correlation between TAP affinity and transport rates of peptides has been observed (Gubler et al. 1998). Several studies point out the importance of the three N-terminal and the C-terminal amino acids of a peptide for TAP binding (Uebel et al. 1997).Methods to predict TAP affinity include simple scoring matrices (Peters et al. 2003) and more complex machine learning methods (Brusic et al. 1999; Bhasin and Raghava 2004). Peters et al. (2003) recently presented a stabilized matrix method (SMM) for prediction of TAP affinity. The method is based on a set of 9-mer peptides with known binding affinity. They also applied their prediction to peptides longer than nine amino acids by using the parts of the 9 × 20 scoring matrix that corresponds to the three N-terminal and the C-terminal amino acids. In an attempt to combine TAP prediction and MHC binding predictions for HLAA* 0201, they found only a marginal increase in prediction accuracy.

A number of different prediction methods for MHC binding peptides have been developed. The first methods were based on the identification of allele-specific anchor residues (Falk et al. 1991; Rotzschke et al. 1992; Rammensee et al. 1995). These simple motif-based methods were later replaced by different weight matrix-based methods (Parker et al. 1994; Rammensee et al. 1997). Different types of machine learning algorithms have also been applied for prediction, including hidden Markov models (Mamitsuka 1998), support vector machines (SVMs) (Dönnes and Elofsson 2002), and artificial neural networks (Gulukota et al. 1997; Honeyman et al. 1998). There are also methods using structural information for prediction of MHC binding peptides, e.g., MHC-peptide threading (Schueler-Furman et al. 2000) and molecular dynamics-based approaches (Rognan et al. 1994).

While there is a large number of prediction methods for the individual steps of the MHC class I antigen processing pathway, there has been little success in combining these into an integrated class I prediction system. The majority of presented epitopes have to pass all three steps of antigen processing in order to be immunogenic, so there is little doubt that an accurate prediction of the overall process is immensely valuable. We have developed WAPP (whole antigen processing prediction), which combines new methods for proteasomal cleavage prediction and TAP transport with our well-established method for MHC binding prediction, SVMHC (Dönnes and Elofsson 2002).

Our proteasomal cleavage prediction method is based on experimentally verified cleavage sites in whole protein sequences. Using the verified cleavage sites and their flanking amino acids, we have constructed proteasomal cleavage matrices (PCMs). In a comparison to existing proteasomal cleavage prediction methods, we show that PCM is more accurate and more robust than comparable methods. The method for TAP prediction (SVMTAP) is based on support vector regression (SVR) and was trained on a set of more than 400 peptides with measured binding affinity to TAP. The correlation between experimental and predicted binding affinities for SVMTAP is improved in comparison to the prediction method presented by Peters et al. (2003). We combine all three methods using a filtering approach mimicking natural MHC class I processing.

Peptides predicted by WAPP are likely to have a C terminus generated by the proteasome, a high affinity for TAP, and finally a high affinity for a specific MHC allele. This increases the specificity of our method by reducing the rate of false positives. In a benchmark for the MHC alleles HLA-A*0201, HLA-B*2705, HLA-A* 01, and HLA-A*03, we show an increase in prediction accuracy using WAPP over MHC binding prediction alone. We used naturally processed and T-cell epitopes extracted from the SYFPEITHI database for this evaluation (Rammensee et al. 1997). For example, the Matthews correlation coefficient (MCC) (Matthews 1975) for HLA-A* 0201 reaches 0.74 using WAPP, which can be compared to 0.68 using MHC binding prediction alone. The improvement in MCC is due to the increase in specificity, 0.86 for WAPP compared to 0.78 for SVMHC. For HLA-B* 2705, MCC increases from 0.85 to 0.88 and the specificity increase from 0.76 to 0.82. We also show how WAPP can be used to identify three experimentally verified HLA-A*0201 epitopes (Kim et al. 1999) from a Chlamydia trachomatis protein.

Results

Proteasomal cleavage prediction

Prediction of proteasomal cleavage sites is challenging, as the amount of data available is very limited. Currently, there are data from three different cleavage experiments of single proteins available: enolase (E) (Nussbaum 2001), β-casein (C) (Emmerich et al. 2000), and the prion protein (P) (Tenzer et al. 2004). A number of machine-learning techniques have been employed for predicting proteasomal cleavage. Unfortunately, the lack of data makes the true assessment of a method’s prediction performance very difficult. One critical aspect of prediction performance is the robustness of the method. With most machine-learning methods, it is quite simple to overfit the model to reproduce the exact cleavage sites of the training set. If these models are then applied to proteins not contained in the training set, their prediction performance is hardly better than random. Typically, this problem is assessed by evaluating prediction performance in a cross-validation experiment, where a significant portion—say a third—of the data set is set aside for independent validation. The algorithm is then trained on the remaining data set only and the performance is evaluated on the validation set.

We have developed a new method for proteasomal cleavage site prediction using a probability-based model encoded by proteasomal cleavage matrices. These PCMs were derived from observed cleavage probabilities (see Materials and Methods). The method is less prone to overfitting in general and thus well suited for this type of problem. When assessing the performance of these PCMs, we put special emphasis on the validation of the method’s robustness. As a measure of prediction performance, we used MCC. Large values for MCC indicate good prediction performance, while values of zero indicate random results and values below zero anti-correlated results (most cleavage sites are predicated as noncleavage sites and vice versa). We trained our method on all combinations of two proteins and then assessed its performance on the third protein. The results of these predictions are given in Table 1, where MCC, specificity (SP), and sensitivity (SE) are presented along with the total accuracy (ACC) of predicting both cleavage and noncleavage sites. The average total accuracy for the three proteins of the PCM method, when no training data were used for evaluation, reaches 65%. While the overall MCCs are not all that impressive (ranging from 0.18 to 0.32), our method is fairly robust.

Table 1.

Proteasomal cleavage site prediction

	Enolase (E)				Casein (C)				Prion (P)
Method	MCC	SP	SE	ACC	MCC	SP	SE	ACC	MCC	SP	SE	ACC
PCM(ALL)	0.54	0.74	0.57	0.81	0.51	0.58	0.67	0.83	0.40	0.58	0.77	0.69
PCM(E + C)	0.59	0.64	0.80	0.82	0.50	0.69	0.51	0.85	0.18	0.51	0.44	0.61
PCM(E + P)	0.48	0.70	0.56	0.79	0.38	0.43	0.67	0.74	0.41	0.63	0.54	0.72
PCM(C + P)	0.19	0.35	0.69	0.57	0.51	0.67	0.53	0.85	0.46	0.62	0.78	0.73

Results of proteasomal cleavage site prediction for the PCM method. Several different PCMs were constructed in order to compare methods.

We have also compared the robustness of our method to that of other methods for cleavage site prediction. We compared our method to PAProC N1, PAProC N2, PAProC N3 (Kuttler et al. 2000; Nussbaum et al. 2001), NetChop 20S, NetChop C-term 2.0 (Kesmir et al. 2002), and MAPPP (Holzhütter et al. 1999). In each case, we used all proteins that were not included in the respective method’s training set in order to assess their prediction performance. It turns out that all methods are considerably less robust than the PCM method. While PAProC and NetChop 20S achieve very high MCC values (0.88–0.95) on the proteins they were trained on (enolase for PAProC; enolase and casein for NetChop 20S), their performance drops to values between −0.03 and 0.07 when validated with other proteins. This is a clear indication of overfitting on the training data. MAPPP and NetChop C-term 2.0 are clearly more robust, but their prediction performance is well below the performance of our method (see Table 2). The average total accuracies of all external methods, when no training data were used for evaluation, were also calculated. The MAPPP method has an average accuracy of 47%; PAProC, 60%; and NetChop, 61% (PCM 65%). We therefore conclude that PCM combines comparable or slightly better prediction accuracy with improved robustness.

Table 2.

Proteasomal cleavage site prediction

	Enolase (E)				Casein (C)				Prion (P)
Method	MCC	SP	SE	ACC	MCC	SP	SE	ACC	MCC	SP	SE	ACC
MAPPP	0.09	0.30	0.75	0.45	0.12	0.24	0.77	0.45	0.03	0.40	0.56	0.50
PAProC N1	(0.95)	(0.98)	(0.95)	(0.98)	0.17	0.29	0.53	0.64	−0.03	0.36	0.33	0.52
PAProC N2	(0.95)	(0.97)	(0.97)	(0.98)	0.27	0.35	0.63	0.68	0.07	0.44	0.34	0.58
PAProC N3	(0.94)	(0.96)	(0.96)	(0.98)	0.15	0.27	0.56	0.61	0.08	0.44	0.39	0.57
NetChop 20S	(0.88)	(0.85)	(0.99)	(0.95)	(0.76)	(0.71)	(0.93)	(0.91)	0.12	0.47	0.41	0.59
NetChop C	0.18	0.37	0.49	0.64	0.18	0.29	0.58	0.63	0.07	0.44	0.33	0.58

Results from the proteasomal cleavage site prediction using already existing methods; values in parentheses are prediction performances for data used in method development and should not be used to compare methods. A large difference in performance can be seen for data contained in the training set vs. data not in the training set for the PAProC and NetChop methods.

Our PCM method also allows the easy extraction of proteasomal cleavage motifs based on amino acid preferences in a specific position. The three proteolytic sites of the proteasome have been described as having trypsinlike, chymotrypsin-like, and peptidylglutamylpeptide hydrolytic (PGPH) activity (Uebel and Tampe 1999). Figure 1 ▶ shows the preferences for specific amino acids at positions surrounding the cleavage site. This figure has been prepared from the values of the PCM derived from all three proteins and thus reflects the current knowledge on the cleavage preference of the proteasome (see Supplemental Material for more details). Tryptic activity would imply cleavage immediately after Lys and Arg; however, we observe only Arg to be favorable, whereas Lys seems to have a negative effect on cleavage probability. Chymotryptic activity (cleavage after Phe, Tyr, and Trp) and PGPH activity (cleavage after Asp and Glu) is quite obvious from the very favorable values for these amino acids. In addition, we observe very unfavorable effects of Pro on the two positions immediately preceding the cleavage site; and Val, Ile, and Phe, immediately following the cleavage site. Due to the low abundance of Met, Cys, and Trp in the source proteins, we do not want to interpret the effects seen for these three amino acids; they might be artifacts of the analysis.

Figure 1.

The effect of specific amino acids on proteasomal cleavage. High values (black) contribute to proteasomal cleavage, whereas white inhibits cleavage. The cleavage occurs between the P1 and P′1 positions (Met, Cys, and Trp have been omitted due to insufficient statistical basis). Numerical values can be found in the supplemental material.

TAP affinity prediction

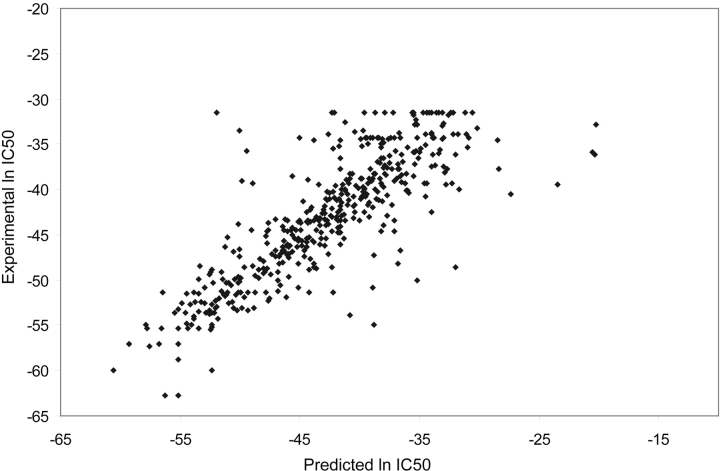
For TAP affinity prediction, we propose a new approach (SVMTAP) based on support vector regression (see Materials and Methods for details). SVMTAP was trained to predict peptide binding affinity to TAP. The performance of SVMTAP was evaluated and compared to the matrix approach (MATRIX) presented by Peters et al. (2003). Leave-one-out cross-validation was applied for SVMTAP, using a linear SVM kernel. The correlation between predicted and experimentally verified ln IC₅₀ values was used to evaluate prediction accuracy. A plot of predicted values versus experimentally verified values for the SVMTAP method can be seen in Figure 2 ▶. The correlation coefficient for predicted versus experimental values reaches 0.82 for SVMTAP, which can be compared to 0.79 for the MATRIX method. A further method, TAPPred, based on cascading SVMs, has also been presented (Bhasin and Raghava 2004). The reported performance of TAPPred reaches 0.88, but the method uses a pregrouping of data and two layers of SVMs. Hence, a direct comparison of the methods is not possible.

Figure 2.

Predicted binding affinities plotted against experimentally verified affinities for the SVMTAP method. The correlation of predicted and experimental values is 0.82.

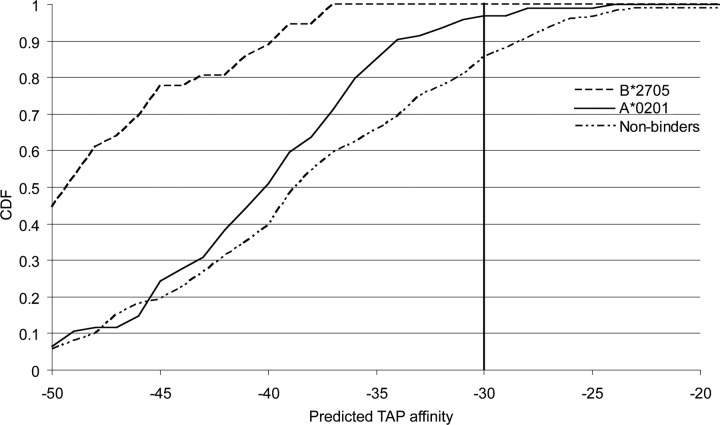
In addition we predicted TAP affinity for known epitopes of HLA-A*0201 and HLA-B*2705, as well as for nonbinding peptides (see Figure 3 ▶). We observe a very distinct difference between the three classes, where the known HLA binders show a higher affinity for TAP than the nonbinders.

Figure 3.

Predicted TAP affinity for the HLA-A*0201 and HLAB* 2705 data sets, represented as cumulative distribution functions (CDFs) going from high to low affinity binders. The value of the CDF corresponds to the fraction of data with values below a given TAP affinity. A clear difference in the distribution of TAP affinity can be seen between known epitopes and nonepitopes. Only a small fraction of the known epitopes has a TAP affinity higher than −30 (corresponding to an IC₅₀ of 5000 nM).

Both experimental and computational studies have previously shown that HLA-B*2705 peptides have a high TAP affinity, whereas HLA-A*0201 has relatively low TAP affinity (van Endert et al. 1995; Brusic et al. 1999). This difference is to be expected, as HLA-A*0201 is a TAP-inefficient allele, whereas HLA-B*2705 is TAP efficient.

However, a threshold for TAP affinity can be defined that reduces the number of false positives while keeping all true positives. This threshold can be chosen in an allele-specific manner or by the allele showing weakest TAP affinity. In this example a cutoff of −30, corresponding to an IC₅₀ value of approximately 5500 nM, can be chosen for both alleles. For the HLA-B*2705 allele this cutoff could even be set lower.

Whole pathway prediction

Prediction of the individual steps of class I antigen processing alone is of limited use, in particular for proteasomal cleavage and TAP transport, as these steps are known to be less specific than the final MHC binding. Nevertheless, by combining these predictions into a three-step prediction, we could improve performance for the prediction of natural MHC epitopes. In order to be presented by MHC, each epitope ought to possess a C terminus created by the proteasome, possess at least moderate TAP affinity, and show some affinity to MHC. After exploring several probability-based approaches, we have settled for a simple filtering approach combining the three processing steps (see Materials and Methods). We have named this joint approach WAPP and made the method available as a WWW-based prediction service on our Web site, http://www-bs.informatik.uni-tuebingen.de/WAPP/.

In order to assess the performance of the joint method, we use four alleles (HLA-A*0201, HLA-B*2705, HLAA* 01, and HLA-A*03) where a sufficient number of naturally processed ligands have been known to allow a statistically valid analysis. We extracted the protein sequences containing these alleles from the SYFPEITHI database and predicted the epitopes using WAPP. We compared the performance of WAPP to that of its constituent method, SVMHC, a highly accurate method for MHC class I prediction. We found a significantly improved performance of WAPP over SVMHC alone (MCC increases from 0.68 to 0.74 for HLA-A*0201, from 0.85 to 0.88 for HLA-B*2705, and from 0.80 to 0.82 for HLA-A*03) (see Table 3). This improvement is mostly due to a smaller number of false positives, i.e., peptides that could bind to MHC but are either not cleaved by the proteasome or not transported by TAP. The improvement for HLA-A*01 is somewhat smaller; however, the overall prediction accuracy for this allele is very high.

Table 3.

Prediction accuracies of WAPP

	SVMHC			WAPP			PC+MHC	TAP+MHC
Allele	MCC	SP	SE	MCC	SP	SE	MCC	MCC
HLA-A*0201	0.68	0.78	0.78	0.74	0.86	0.79	0.71	0.71
HLA-B*2705	0.85	0.76	1.00	0.88	0.82	1.00	0.86	0.86
HLA-A*01	0.92	0.94	0.96	0.93	0.95	0.98	0.93	0.93
HLA-A*03	0.80	0.84	0.90	0.82	0.92	0.89	0.81	0.81

Prediction accuracies for the two alleles using different approaches. An increase in all three cases can be seen for WAPP compared to SVMHC. Furthermore, the results from combining the MHC prediction with either proteasomal cleavage (PC) or TAP are shown.

The best performance is achieved when both proteasomal cleavage and TAP filtering is used. The largest increase in prediction performance is achieved for the HLA-A*0201 allele where the MCC increases from 0.68 to 0.74. Using either proteasomal cleavage or TAP as a filter shows worse results for the HLA-A*0201, HLA-B*2705, and HLA-A*03 alleles. The main feature of the combined approach is a reduction in false positives in the prediction, i.e., removal of peptides that actually could bind to MHC but are unlikely to be generated by the proteasome or transported by TAP. The specificity increases from 0.78 to 0.86 for the HLA-A* 0201 allele and from 0.76 to 0.82 for HLA-B*2705. The only allele that shows slightly different results is HLA-A*01. The peptides binding to these alleles almost exclusively have a Tyr in position 9. This means that a high specificity can be obtained by MHC prediction alone; however, it should be pointed out that the prediction accuracy is not negatively affected by taking proteasomal cleavage and TAP transport into account.

A well-characterized Chlamydia trachomatis protein, containing three experimentally verified HLA-A*0201 epitopes, further shows the usefulness of WAPP. The three epitopes are identified as potential binders by the SVMHC method along with seven other peptides. These 10 candidates are reduced to six by applying SVMTAP, and, after final filtering for peptides with C termini likely to be generated by the proteasome, only the three known epitopes remain. This exemplifies the use of WAPP to identify peptides likely to pass all major processing steps and thereby increase the specificity of the prediction.

Discussion

We have presented an integrated prediction method, WAPP, for the major events in the processing pathway of MHC class I antigens. WAPP mimics the series of biological events by predicting peptides with a proteasomal cleavage site at the C terminus, moderate to high affinity to TAP, and an affinity to MHC.

The three steps modeled here are generally thought to be the major determinants in class I antigen processing, although several alternative processing events have been described in literature. Luckey et al. (2001) showed that for some MHC alleles, a significant amount of peptides were generated even in the presences of proteasome inhibitors. These results clearly indicate an important effect of other cytosolic proteases (Beninga et al. 1998; Geier et al. 1999). TPPII is one such protease that has important effects in the trimming of proteasomal degradation products (Reits et al. 2004). A further example points out the importance of TPPII in the generation of a known HIV-Nef (73–82) epitope (Seifert et al. 2003). Some alternative ways of peptide transport into the ER have also been suggested. Lautscham et al. (2003) described TAP-independent transport of hydrophobic peptides and suggested that these might enter the ER by passive diffusion or by an unknown transport protein within the ER membrane. Furthermore, they pointed out that many known MHC binding peptides are derived from protein signal sequences and suggested Sec61 as a potential transporter. A recent study showed that peptides for some MHC alleles have a low TAP affinity (Petrovsky and Brusic 2004). We also observe this for the HLA-A*0201 and HLA-B*2705 alleles, described as TAP inefficient and TAP efficient, respectively. It is likely that some of the TAP-inefficient alleles utilizes the routes described by Lautcham et al. (2003), but it is still possible to combine TAP and MHC prediction to reduce the number of false positives.

The overall increase in performance obtained by adding TAP affinity prediction and proteasomal cleavage site prediction to MHC binding prediction is significant, although these steps are clearly less specific than MHC binding itself. Thus, improved overall performance for a combined model can only be achieved through high-quality models for proteasomal cleavage and TAP affinity. Previous attempts to combine the different steps yielded only a small increase in performance combining TAP prediction with MHC binding predictions and even a decrease in performance if proteasomal cleavage was predicted together with MHC binding (Peters et al. 2003). At least for the case of proteasomal cleavage, we argue that this might be largely due to an overfitting of the cleavage models, as insufficient data were available.

The existing methods for proteasomal cleavage prediction, NetChop and PAProC, can reproduce their training data with high accuracy, while their performance on external validation data is much lower. This implies an overfitting of the model, which typically results in lower generality of the models. Our PCM method presented has thus been carefully designed to be more robust at the cost of slightly reduced accuracy on the training set. The robustness, however, turns out to be key to a successful combination with the other prediction steps.

Future challenges in the prediction of proteasomal cleavage are likely to include splicing events (Hanada et al. 2004; Vigneron et al. 2004). Splicing within the proteasome can generate a peptide from two noncontiguous parts of its source protein. The mechanisms under-lying proteasomal splicing are not fully understood and currently there are not enough data available to model this in the predictions.

Prediction of TAP transport by SVMTAP shows an increase in performance compared to the MATRIX method. It is also likely that some of the peptides transported into the ER have extended N terminals that can be trimmed by ER aminopeptidases (Serwold et al. 2001). Peters et al. (2003) used parts of the matrix for predicting peptides longer than nine amino acids. They explored a weighting of the N-terminal scores in order to improve prediction. For some alleles the weighting improved accuracy, whereas the effect was negative in other cases. It should also be pointed out that the study of the relationship of TAP affinity and TAP transport was done using a library of 9-amino-acid-long peptides (Gubler et al. 1998). Further considerations of this relationship might need to be taken into account for longer peptides. The problem of predicting TAP affinity for peptides longer than 9 amino acids is still unsolved and more data are needed for a thorough investigation.

In summary, we are able to show improved prediction performance for two MHC alleles using an integrated approach including the three major processing steps. We intend to extend our method to other alleles in the future.

We hope that whole-pathway predictions, as presented here with WAPP, will improve the rational design of epitope-driven vaccines in the future. WAPP increases the prediction specificity and hence reduces the number of peptides that have to be tested experimentally. Future improvements on the prediction will largely be data driven, as the lack of data for TAP transport and for proteasomal cleavage are currently the issues limiting predictive power.

Materials and methods

Prediction of proteasomal cleavage

The proteasomal cleavage prediction method is based on proteasomal degradation experiments of the β-casein (Emmerich et al. 2000), enolase (Nussbaum 2001), and prion proteins (Tenzer et al. 2004). Peptides generated by the proteasome are analyzed by mass spectrometry and the cleavage sites determined. Verified cleavage sites were used to create proteasomal cleavage matrices. Four N-terminal and two C-terminal amino acids flanking each cleavage site were extracted from the source protein. These small peptides, all containing a cleavage site between the fourth and fifth positions, were used to create a position-specific scoring matrix (PSSM). The score s_i,j of amino acid i at position j is defined as

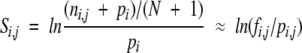(1)

where f_i,j is the frequency of amino acids i at position j and p_i,j is the prior probability of amino acid i in position j (Hertz and Stormo 1999). The priors used are based on the amino acid composition of the source proteins. The score for a new sequence is calculated as the sum of individual position-specific scores for the amino acid in the sequence.

Different types of PCMs were created in order to fairly compare the performance of the different methods. Matrices based on all three proteins as well as a combination of two sets were used for performance evaluation. A comparison of the PCM based on the enolase and casein proteins, PCM(E+C) can be used to compare the performance of all methods for the prion protein. The cutoff for distinguishing between cleavage and noncleavage sites was chosen at maximum MCC.

In order to compare the PCM method to other available prediction methods, all proteins were submitted to the prediction servers MAPPP, PAProC, and NetChop. The predicted scores were compared to the experimentally verified cleavage sites to estimate the performance of each method. The MAPPP prediction server offers only one type of proteasomal cleavage prediction, but both PAProC and NetChop provide several options for prediction. Three different models from the PAProC server were used for prediction: N1–N3. The N1 model is based on cleavages in enolase, the N2 model is based on cleavages in enolase and ovalbumin, and the N3 model is based on cleavages of enolase and a different set of ovalbumin cleavages. Two different types of networks were used from the NetChop server: 20S and C-term 2.0. The 20S network was trained on in vitro degradation of the enolase and casein proteins, whereas the C-term 2.0 network was trained on MHC ligands. For MAPPP and NetChop a cutoff of 0.5 was used. This is the default cutoff used by the MAPPP server and a recent study by the developers of NetChop used 0.5 to discriminate between cleavage and noncleavage sites (Saxova et al. 2003).

Prediction of TAP affinity: SVMTAP

A method based on support vector regression (SVR) (Vapnik 1999; Cristianini and Shawe-Taylor 2000), SVMTAP, was developed in order to predict TAP affinity. The data used for training and evaluation consist of 446 peptides (9 amino acids long) with experimentally verified IC₅₀ values (Daniel et al. 1998). Peptides were represented using sparse binary encoding (Dönnes and Elofsson 2002). As has been shown elsewhere (Rognan et al. 1999), there is a correlation between the binding energy and ln IC₅₀ values (Gubler et al. 1998). For this reason, ln IC₅₀ was used to train SVMTAP and for comparison to the matrix method (MATRIX) presented by Peters et al. (2003). Performance was evaluated as the correlation coefficient R between predicted and experimental values. Several different kernels were optimized in the SVR procedure, and the simple linear kernel turned out to reproduce the data best. The SVM implementation used was SVMLIGHT (Joachims 1998).

Prediction of MHC binding

The SVMHC method was used for predicting MHC binding (Dönnes and Elofsson 2002). SVMHC is a SVM-based method trained on verified MHC binding peptides from the SYFPEITHI (Rammensee et al. 1997) and the MHCPEP (Brusic et al. 1998) databases. The version of SVMHC used in this study was trained on data from the SYFPEITHI database, containing only naturally processed and T-cell epitopes. For more details of SVMHC implementation and performance, see Dönnes and Elofsson (2002).

Combination of the prediction methods

The separate prediction methods were combined in order to model the whole processing pathway of MHC class I antigens. Predicted peptides should have a C terminus generated by the proteasome, a relatively high TAP affinity, and some affinity to MHC molecules. The final step of MHC binding prediction can be done with high accuracy, and, hence, the other methods were used as a filter removing candidate peptides unlikely to be generated by the proteasome and/or transported by TAP. Peptides with a length of 9 amino acids were extracted from the SYFPEITHI database. The peptides were mapped back to their source protein in order to extract extended C termini needed for proteasomal cleavage prediction. A set of nonbinders was constructed by randomly extracting peptides from real protein sequences. This is a reasonable approach since it has been estimated that only 1 in 100–200 potential peptides actually bind to a MHC molecule (Mamitsuka 1998).We used the alleles HLA-A*0201, HLA-B*2705, HLA-A*01, and HLA-A*03 to evaluate our method, and the number of binders were 96, 36, 47, and 71, respectively. All peptides were predicted with the PCM, SVMTAP, and SVMHC methods. In order to reduce the number of false positives, we used the values predicted by PCM and SVMTAP for filtering: Any peptide with a score below the threshold of either method was removed. These thresholds were chosen (as described above for TAP affinity) very conservatively in order to remove false positives only. The final cutoffs chosen for HLA-A*0201 were −4.8 for proteasomal cleavage and −27 for TAP affinity. The corresponding values for HLA-B* 2705, HLA-A*01, and HLA-A*03 were −2.0 and −35.

Furthermore a membrane protein from C. trachomatis (SWISSPROT ID P17451) was used to exemplify the usefulness of WAPP. This protein contains three experimentally verified HLA-A*0201 epitopes (Kim et al. 1999).

Prediction accuracy measures

The aim of most prediction methods is to discriminate between two classes, e.g., cleavage and noncleavage sites in the case of proteasomal cleavage. A good prediction method will have a high number of correctly predicted cleavage sites and at the same time a low number of noncleavage sites predicted as cleavage sites (false positives). A measure that captures these characteristics is the Matthews correlation coefficient (Matthews 1975). It is defined as

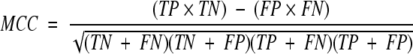(2)

where TP is the number of cleavage sites correctly predicted, FP is the number of noncleavage sites predicted as cleavage sites, TN is the noncleavage sites predicted as such, and FN is the number of cleavage sites predicted as noncleavage sites. Two other measures, specificity (SP) and sensitivity (SE) can also be defined:

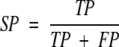(3)

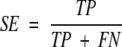(4)

SE is the fraction of known binding sites that are actually predicted as such. SP is the fraction of correctly predicted binding sites among all predicted binding sites.

The correlation between predicted binding affinity and experimentally verified was used to evaluate the performance of SVMTAP.

Electronic supplemental material

The supplement consists of the PCM created for proteasomal cleavage prediction using data from all three proteins. Figure 1 ▶ in the manuscript is created using this position-specific scoring matrix.

Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.051352405.