Skip to main content
PMC home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2004 Aug;13(8):2120–2129. doi: 10.1110/ps.04748404

H-bonding in protein hydration revisited

Michael Petukhov 1,2, Georgy Rychkov 1, Leonid Firsov 1, Luis Serrano 2
PMCID: PMC2279814  PMID: 15238635

Abstract

H-bonding between protein surface polar/charged groups and water is one of the key factors of protein hydration. Here, we introduce an Accessible Surface Area (ASA) model for computationally efficient estimation of a free energy of water–protein H-bonding at any given protein conformation. The free energy of water–protein H-bonds is estimated using empirical formulas describing probabilities of hydrogen bond formation that were derived from molecular dynamics simulations of water molecules at the surface of a small protein, Crambin, from the Abyssinian cabbage (Crambe abyssinica) seed. The results suggest that atomic solvation parameters (ASP) widely used in continuum hydration models might be dependent on ASA for polar/charged atoms under consideration. The predictions of the model are found to be in qualitative agreement with the available experimental data on model compounds. This model combines the computational speed of ASA potential, with the high resolution of more sophisticated solvation methods.

Keywords: protein, hydration, water, H-bonding, solvent-accessible surface area

Determination of solvation contribution to the free energy of folding remains a difficult problem, complicated by the wide variety of phenomena concerning water–protein interactions such as hydrogen bonding effects (Feyereisen et al. 1996; Martin and Derewenda 1999; Chatake et al. 2003; Walsh et al. 2003), screening of electrostatic forces (Finkelstein 1977; Gilson and Honig 1991; Warshel and Papazyan 1998), and hydrophobic interactions (Scheraga 1998). The high number of solvent degrees of freedom results in the existence of a variety of different water local structure motifs, such as clathrate-like structures near hydrophobic segments of the protein surface (Scheraga 1998), or stable water bridges between two polar atoms often found in proteins (Thanki et al. 1990, 1991; Morris et al. 1992; Petukhov et al. 1999). Water–protein interactions have been the subject of many recent experimental (Otting et al. 1991; Israelachvili and Wennerstrom 1996; Pal et al. 2002; Bhattacharyya et al. 2003; Walsh et al. 2003) and theoretical studies (Hummer et al. 1996; Kovacs et al. 1997; Lazaridis and Karplus 1999; Lomize et al. 2002; Deep and Ahluwalia 2003; Efimov and Brazhnikov 2003; Walsh et al. 2003). Many theoretical approximations have been developed to account for solvation contribution to the free energy of protein folding. It is routine to perform molecular dynamics simulations of a protein in an explicit water box (Kovacs et al. 1997; Bonvin et al. 1998; Cheng and Rossky 1998). Also, a variety of continuum approximation models based on the accessible protein surface area (Eisenberg and McLachlan 1986; Ooi et al. 1987; Wesson and Eisenberg 1992; Williams et al. 1992; von Freyberg et al. 1993) and as well as several electrostatic models (Warshel and Russell 1984; Sharp and Honig 1990) are used to describe water–protein interactions.

Although explicit water models have proven to adequately account for protein solvation in molecular dynamics simulation, they are extremely computationally demanding and require long computation times for equilibration of the water box itself, to obtain the hydration energy of a protein. The continuum electrostatic models are less computationally demanding; however, they do not properly account for hydrogen bonding between protein and water.

Water–protein H-bonding is known to play a major role in hydration of many polar and charged groups exposed to solvent. ASA-based models are fast enough, and would be the method of choice. However, it suffers from the lack of atomic details, and therefore cannot account for stable local water structures near the protein surface and proper H-bond geometry requirements in water–protein interactions. The later contribution to the free energy of hydration depends not only on available ASA of protein polar atoms, but also on a disposition of the protein solvent-exposed segments and on the existence of intraprotein hydrogen bonds. In our previous work we presented a correction term for ASA-based solvation models that allows to account for a water bridge motif where a water molecule mediates a hydrogen bond bridge with two protein atoms (Petukhov et al. 1999). The calculation of a water bridge free energy is based on probabilities of water bridge formation derived from molecular dynamics simulations performed for a series of short peptides in an explicit water box. The accounting for a water bridge contribution to the solvation free energy of small pentapeptides was found to be essential to correctly reproduce the equilibrium coupling constants and chemical shifts of the central amino acid in random coil pentapeptides. In this work we have extended this approach for water–protein hydrogen bonding without a water bridge formation, and we have built a simple and computationally effective model correctly describing the main peculiarities of H-bonding of protein polar and charged groups with water.

Results and Discussion

Although protein crystal structures usually include a large number of water molecules, its positions are not usually preserved in different crystal forms. The analysis of many protein crystal structures indicates that protein surface topology plays an important role for highly ordered water molecules. These ordered water molecules are usually located in deep grooves of the protein surface (Kuhn et al. 1992). On the other hand, water molecules near exposed polar areas are not usually conserved, undergoing fast exchange with bulk water. For instance, only 6 out of 60 water molecules were found to be conserved in three crystal forms of the pancreatic trypsin inhibitor (Otting et al. 1991), showing the importance of the particular crystal environment. MD simulation revealed that hydration of nonpolar groups depends on the surface topology where clathrate-like structures are predominant near convex nonpolar surface areas, while the hydration shells near flat surfaces are mostly unordered (Cheng and Rossky 1998). Additionally, in many protein conformations stable water molecules form water bridges between the amino acid side chains and the backbone (Thanki et al. 1990, 1991; Morris et al. 1992; Petukhov et al. 1999).

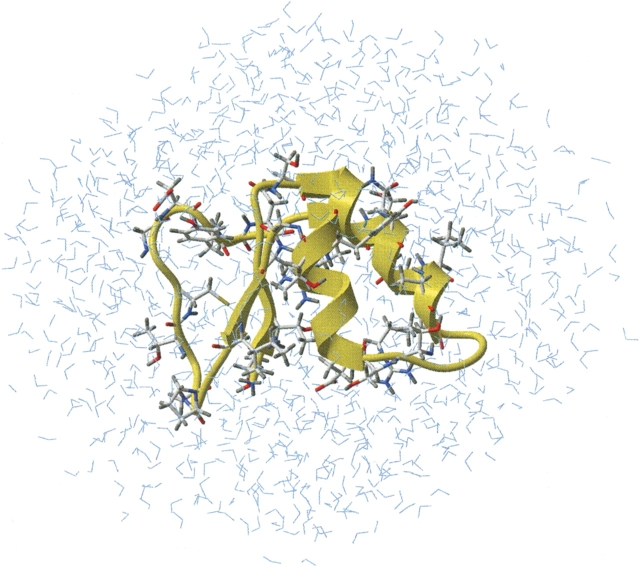
A very detailed analysis of hydrogen bonding in proteins (including water–protein hydrogen bonding) was published by several groups (Ippolito et al. 1990; Thanki et al. 1990, 1991; Morris et al. 1992; Petukhov et al. 1999). However, some details, particularly the distribution of dihedral angles between two or more water molecules bonded to the same protein atom, were not analyzed. To better understand the basic principles of protein solvation, we used a combination of Protein Data Base analysis and MD simulations of a small protein, Crambin, from an Abyssinian cabbage (Crambe abyssinica) seed, in an explicit water box. The spatial structure of this protein was obtained by X-ray crystallography at 0.87 Å2, and include protein hydrogens. Figure 1 ▶ shows structure details of the molecular model used in MD simulations. The protein immersed in a water box of 1084 water molecules is shown in a ribbon diagram, and side chains of the amino acid having at least one water-exposed atom capable for H-bonding with the solvent are shown in sticks.

Figure 1.

Figure 1.

Open in a new tab

Molecular model of Crambin in an explicit water box used in this study. Amino acids where at least one atom of both main and side chain can form a water–protein H-bond are shown in sticks.

H-bonds where water donates its protons to protein

Carbonyl/carboxyl and hydroxyl oxygen atoms are the primary acceptors of water hydrogen atoms in proteins. However, in some current force fields (ECEPP, for instance) NH and NH2 groups are considered to be capable of accepting a hydrogen in an H-bond (Momany et al. 1975; Nemethy et al. 1983). However, in protein crystal structures the cases where these groups play a role of acceptor in a hydrogen boding are very rare, and normally considered to be artifacts (Ippolito et al. 1990). Sulfurs in Met and Cys are also capable of forming H-bonds with water. However, such bonds are known to be very long and weak compared to water–water H-bonds, and therefore are not expected to contribute significantly to the solvation of amino acids (Gregoret et al. 1991). Also, there have been few cases of “exotic” hydrogen bonds reported in proteins where the aromatic ring of Phe acts as an acceptor playing an important role in conformational stabilization of peptide α-helices (Armstrong et al. 1993). However, this type of H-bond acceptor is rather weak, and unlikely plays a significant role compared to many ordinary hydrogen bonds between water and protein surface hydroxyl and carbonyl/carboxyl oxygen atoms.

In natural amino acids there are basically two chemical groups containing oxygen atoms—sp2 hybridized carbonyl/ carboxyl, and sp3 hybridized hydroxyl groups. The car-bonyl/carboxyl oxygen atoms are found in the main chain of all residues and in the side chains of Asp, Asn, Glu, and Gln. There are basically three stereochemical requirements (Ippolito et al. 1990) for a hydrogen bonding between sp2-hybridized protein carbonyl/carboxyl oxygen atoms and water: (1) The distance between the protein and water oxygen atoms must be in the range of 2.8–3.0 Å2; (2) the hydrogen bond angle (Protein-O. . .Water) is in the range of 100°–140°; (3) if there is a second hydrogen bond to an oxygen atom, it should occupy a symmetrical position to the first hydrogen bond position (dihedral angle around 180°). The statistical analysis regarding the first two requirements has been published already (Ippolito et al. 1990; Thanki et al. 1990, 1991; Morris et al. 1992). Figure 2A ▶ shows the statistical data of the dihedral angle distribution between two hydrogen bonds with a carbonyl/carboxyl group found in the protein crystal structures. The dihedral angle between the two hydrogen bonds is above 100° in more than 90% of the cases, having its frequency maximum, as expected for an sp2-hybridized oxygen, at 180°. The average hydrogen bond angle was found to be 133°, with standard deviation of 18°, which is in agreement with previously published data requirements (Thanki et al. 1990, 1991).

Figure 2.

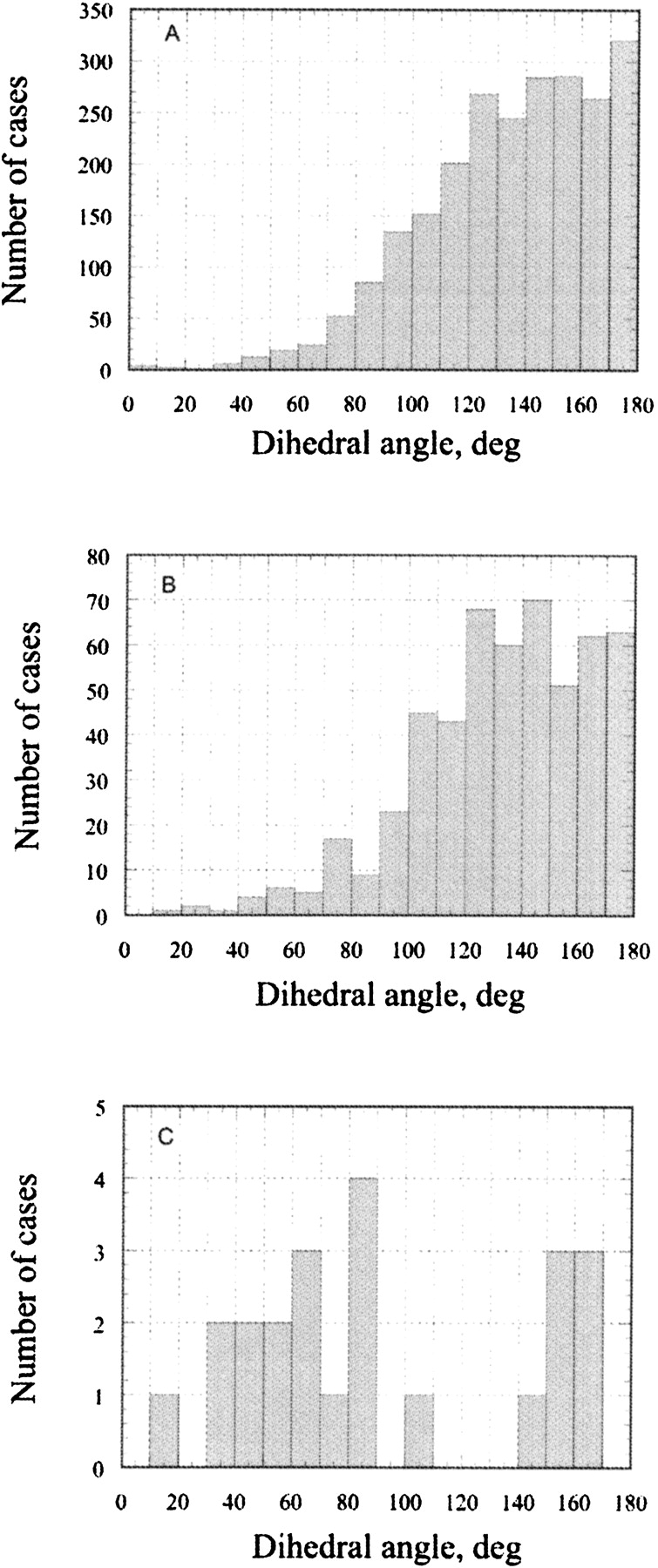
Figure 2.

Open in a new tab

The statistical survey of a dihedral angle between the two hydrogen bonds in 315 protein crystal structures at high resolution: (A) carbonyl oxygen atoms in the main chain and COO and CONH2 groups of the amino acid side chains; (B) hydroxyl oxygen atoms in Ser, Thr, and Tyr; (C) sulfur atoms in Cys and Met.

Hydroxyl groups are present in the side chains of Ser, Thr, and Tyr. The distance between the hydroxyl oxygen and water and the hydrogen bond angle are very similar to that of a carbonyl/carboxyl oxygen atoms. However, due to sp3 hybridization of Ser and Thr hydroxyls, the dihedral angle between two hydrogen bonded waters is expected to be somewhat different compared to sp2-hybridized oxygen atoms. Although Figure 2B ▶ indeed shows a small maximum at around 120° to 140°, the whole area above 100° is populated, and the overall distribution looks similar to that for the carbonyl/carboxyl oxygen atoms. Other stereochemical requirements are the same for both carbonyl/carboxyl and hydroxyl oxygen atoms. Therefore, in our analysis the ste-reochemical requirements for H-bonds where both carbonyl/carboxyl and hydroxyl oxygen atoms accept water protons are considered to be the same. Very similar patterns for the dihedral angle distributions of carbonyl/carboxyl and hydroxyl groups were also found in MD runs, indicating that the explicit water box as implemented in the AMBER force field indeed reproduces well the water behavior at the water–protein surface (data not shown). In addition to this, H-bonds where hydroxyl groups donate its proton to water will be considered separately based on water accessibility of the hydrogen atoms and the possible presence of intraprotein H-bonds (see Discussion below).

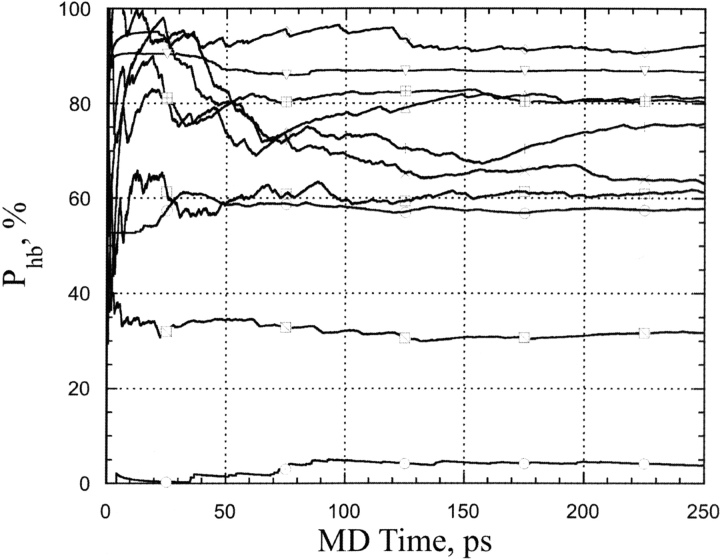
Figure 3 ▶ shows typical time courses of hydrogen bond occupancies as obtained from MD simulations for a representative set of water–protein hydrogen bonds in a box of explicit TIP3P waters (Cornell et al. 1995; Pearlman et al. 1995). One can see that 250 psec of MD simulations were long enough to reach an equilibrium plateau of the occupancies of the typical hydrogen bonds between protein and water. MD simulations showed occupancies of different water binding sites in peptides and proteins have diverse stability depending on its chemical nature, water accessibility, and protein (peptide) conformation. Average residence times of water molecules having one hydrogen bond at any given time were approximately 15–22 psec. It is noteworthy that in the case of peptides, similar hydrogen bonds had significantly shorter residence times in the range of approximately 4–6 psec (Petukhov et al. 1999). This difference is probably due to the presence of exposed hydrophobic patches in close proximity of H-bonding water sites, which significantly decrease the possibility for a water molecule to migrate from the protein sites under consideration. The above results are also in agreement with experimental results indicating that mobility of water is significantly lower at close proximity of the side chain of Trp-113 in Subtilisin than that at the surface of a free aqueous Trp analog (Pal et al. 2002).

Figure 3.

Figure 3.

Open in a new tab

Time course of H-bond occupancies for a typical set of hydrogen bonds of water molecules at the protein surface obtained from the MD simulations of Crambin (see Materials and Methods).

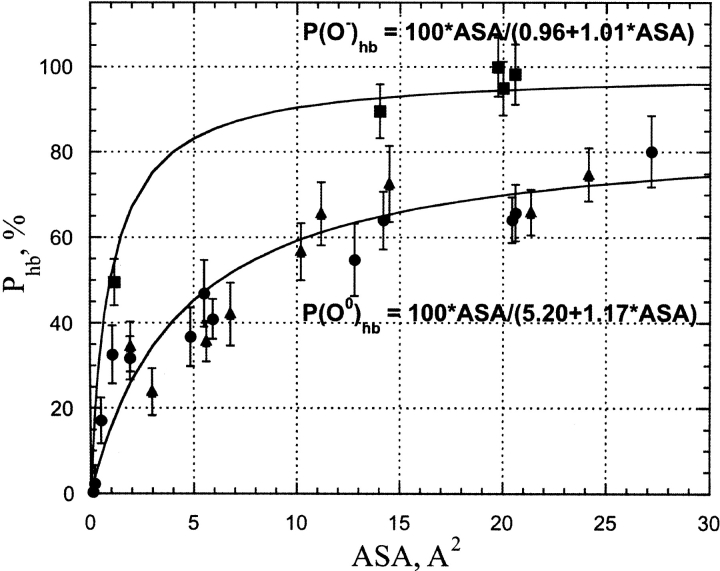
Figure 4 ▶ shows the correlation between the H-bond probability of water–protein hydrogen bond formation, Phb and the accessible surface area (ASA) of protein oxygen atoms (both sp2 and sp3 hybridized) that are not involved in water bridges as derived from MD simulations of Crambin (see Materials and Methods). The carbonyl/carboxyl and hydroxyl oxygen atoms are capable of accepting a maximum of two hydrogen bonds from water, and therefore, the expected maximum value for the H-bond occupancy is 200%. Indeed, for many solvent-exposed oxygen atoms having upper end ASA values MD simulations showed total H-bond occupancies to be in the range of 120% to 180%. However, because water molecules bind at their respective H-bond sites independently, total H-bond occupancies are divided by factor 2 to obtain Phb values shown in Figure 4 ▶.

Figure 4.

Figure 4.

Open in a new tab

The correlation between per H-bond probability of the water–protein hydrogen bond and accessible surface area for protein carbonyl, hydroxyl, and carboxyl oxygen atoms as derived from MD simulations of Crambin in an explicit water box. The filled circles and triangles show uncharged main-chain carbonyl and side-chain hydroxyl groups, respectively, where oxygen atoms are involved in water–protein hydrogen bonding. The filled squares show charged carboxyl oxygen atoms in side-chain Asp and Glu involved in water–protein H-bonds. In all cases only the data for atoms without possibilities of water bridge formation were shown. The parameters of the approximation function are shown in the figure.

As expected, atoms involved in water bridges showed no simple dependence of Phb on ASA (data not shown). The method to obtain the free energy contribution of protein atoms involved in water bridges is explained in Petukhov et al. (1999). Therefore, hereafter the protein atoms involved in water bridges are removed from the consideration.

The stability of the hydrogen bond mainly depends on the chemical nature of its donor/acceptor participants. However, the number of opportunities for the water molecule for H-bonding with a protein polar/charged group is directly proportional to the available ASA of a particular protein donor/acceptor. Thus, it is expected that for a particular group the fraction of time when a water–protein hydrogen bond is formed (or, in other words, hydrogen bond probability), Phb should be strongly dependent on ASA. At least a few Å2 of ASA are required to place a hydrogen bonded water molecule. The lower the ASA, the higher the entropy penalty must be paid for fixing a water molecule in position to allow hydrogen bond formation. This effect is probably the main reason behind the increase of H-bond occupancy with increasing ASA shown in Figure 4 ▶ and Figure 5A, B, and C ▶. There should be a certain value of ASA above which H-bonding to a protein acceptor does not really change the entropy of the water molecule compared to that in bulk water. On the other hand, due to the covalent structure of carbonyl/carboxyl and hydroxyl groups, the maximum ASA of a fully exposed oxygen atom is approximately 50 Å2. Given the fact that the requirement of the dihedral angle between two hydrogen bonded water molecules must be higher than 100°, the maximum ASA per one H-bond in a fully exposed oxygen atom is approximately 50 Å2/3.6 ≈ 5 Å2. The same estimate is also valid for H-bonding between water molecules in pure water. Thus, for ASA values below 15 Å2, only one hydrogen bond is expected to be formed with water. Above this ASA value a possibility of the second H-bond appears. However, the spatial disposition of the H-bonds is far from perfect, and also the limited per H-bond ASA require a significant loss of the water entropy. As a result, the stability of H-bonds, as reflected in the H-bond occupancy, is relatively low. However, as expected, it increases with ASA increase, reaching its maximum at 80% per H-bond in the ASA range above 30 Å2 for oxygen atoms of polar carbonyl/carboxyl and hydroxyl groups. Although unfortunately there are only three solvent-exposed carboxyl groups (side chains Glu23 and Asp43 and the C-terminal COO− group), in Crambin, clearly the maximum H-bond probability of fully hydrated oxygen atoms of these groups is higher than that of polar carbonyl/carboxyl and hydroxyl groups, and most probably is in excess of 90%. This is in agreement with many observations that COO−–water H-bonds are much stronger than that in protein amide, amine, and hydroxyl groups (Jeffrey and Saenger 1991).

Figure 5.

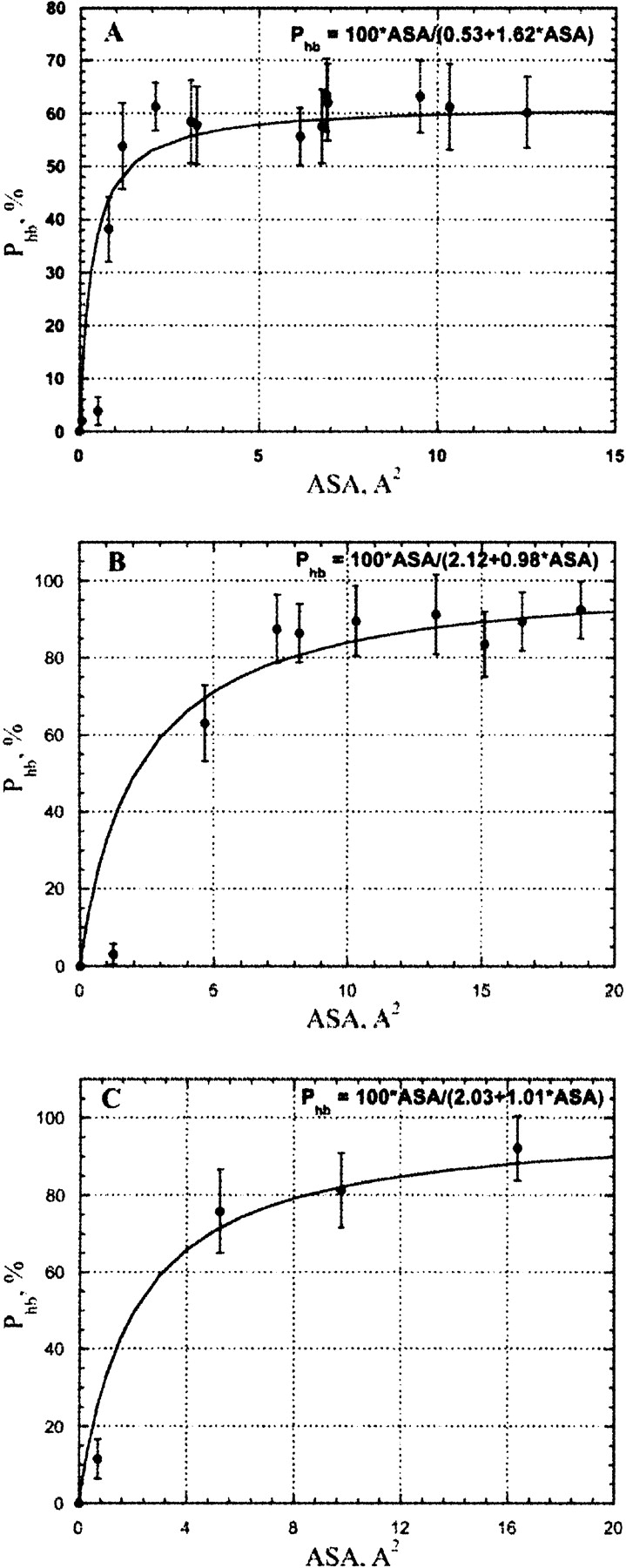
Figure 5.

Open in a new tab

The correlation between an H-bond probability of water–protein hydrogen bond and accessible surface area for hydrogen atoms in (A) uncharged NH, NH2 in protein main and side chains; (B) uncharged OH groups in side chains Ser and Thr; (C) charged NH2+ and NH3+ groups as derived from MD simulations of Crambin in an explicit water box. The accessible surface was calculated with explicit hydrogen atoms.

The mole fractions of water molecules involved in four, three, two, etc., hydrogen bonds in pure water have been experimentally determined from heat capacity data and Ra-man spectroscopy measurements at several temperatures between 0°C and 100°C (Walrafen 1972). At room temperature (22°C), approximately 52% of water molecules were found to have four hydrogen bonds, while 48% have three hydrogen bonds and having fewer number of H bonds were below a detectable level. Thus, in pure water the probability of a water molecule of satisfying its full hydrogen-bond potential is Phb = 100 * (0.52 * 4 + 0.48 * 3)/4 = 88%. This number is in a good agreement with the estimate (≈80%) derived from the MD simulations for carbonyl/carboxyl and hydroxyl groups.

H-bonds where water accepts protons from the protein

The amine, amide, and hydroxyl groups are the primary protein donors of protons to water. These groups are present in the protein backbone (NH) and in the side chains of Trp, His (NH), Asn, Gln (NH2), Arg (NH and NH2), Lys+ (NH3), Ser, Thr, and Tyr (OH). Depending on the pH, they can participate in one, two, or three hydrogen bonds with water. The maximum hydrogen bond lengths between non-hydrogen atoms and these hydrogen bonds are very similar for both amine/amide and hydroxyl groups (≈3.0 Å2). The acceptor water molecules are clustered along the N—H. . .O line, and therefore, the dihedral angle between water molecules bounded to NH2 groups is 180° ± 30°, as has been discussed by Ippolito et al. (1990). The dihedral angle distribution between water molecules bounded to hydroxyl groups is in the range of 100°–180°, as indicated by Figure 2B ▶.

Available ASA-based solvation potentials have been derived without considering protein hydrogen atoms, whose contribution to total ASA was included into the ASA of the related protein heavy atoms (Eisenberg and McLachlan 1986; Ooi et al. 1987; Wesson and Eisenberg 1992; Williams et al. 1992; Juffer et al. 1995). However, unlike solvation of carbonyl/carboxyl and hydroxyl oxygen atoms, where water donates a hydrogen bond at different positions, the position of the hydrogen atoms of NH, NH2, NH3, and OH groups is fixed. Therefore, it is expected that the probability of hydrogen bond with water should mainly depend on the ASA of the donated hydrogen atoms rather then on that of its heavy atoms. Explicit accounting for the hydrogen atoms in ASA calculations better corresponds to the physical reality. Also, it significantly affects the results of ASA calculations for all other protein atoms. Thus, ASA of protein hydrogen atoms as an important part of protein total ASA must be included into solvation potentials to accurately reproduce protein hydration. Therefore, in this work all calculations of protein ASA are performed in the presence of protein hydrogen atoms.

Figure 5, A, B, and C ▶, shows the dependence of Phb on ASA (A) for backbone NH and side chain NH2 groups of Asn and Gln; (B) for hydroxyl groups in side chains of Ser, Thr, and Tyr; (C) for charged side chains of Arg+; derived from MD simulations of Crambin in explicit water box (see Materials and Methods). The general form of dependence is the same for the all H-bond types shown in Figure 4 ▶ and Figure 5 ▶; however, the maximum levels of Phb are significantly different. It is well known from crystallography that O. . .HO bonds have shorter distances and higher strength compared to the NH. . .O H-bond, and also H-bonds are stronger if one or two H-bonded groups are charged (Jeffrey and Saenger 1991). Therefore, hydroxyl groups of Ser, Thr, and Tyr and charged groups of Arg+ have approximately the same level of maximal Phb (≈90%), although uncharged NH/NH2 groups in the protein backbone and in side chains of Asn and Gln can reach only 60% probability of H-bond formation with water, indicating relatively low stability of this H-bonds and its contribution to free energy of protein hydration (see Discussion).

Solvation of SH and S-CH3 groups

The sulfur groups are presented in the side chains of Cys and Met. The side chains of Cys are often found in the protein core forming S–S bridges that are essential to stabilize protein structures. Met is usually considered to be a hydrophobic amino acid. Although sulfur atoms are capable of hydrogen bonding with water both as a donor and acceptor, the bonds are relatively long and weak compared with those of O, OH, NH, NH2, and NH3 groups. The maximum length of the hydrogen bond is 3.6 Å2 and the hydrogen bond angle is 104° ± 30° (Ippolito et al. 1990). Unfortunately, in our set of proteins, the number of cases where sulfur groups of Cys and Met have at least two hydrogen bonds to water was only 26, and that is not enough to draw reliable conclusions about preferential areas. Figure 2C ▶ shows that dihedral angles of 60° ± 30° and 155° ± 15° seem to be the most probable. However, due to the relative weakness of sulfur H-bonds with water, it is expected that water molecules will prefer to form H-bonds between themselves rather than with protein sulfur groups, and therefore will behave more as hydrophobic groups than polar ones.

Hydrogen bond contribution to solvation

Presence, or absence, of hydrogen bonds with water, significantly contributes to free energy of protein hydration. For instance, the hydrophobic effect that is thought to be the main driving force for protein folding is mainly due to the lack of H-bonding capabilities of the amino acid residues in the protein core. The discrete nature of the effect is complicated by several stereochemical requirements and the presence, or absence, of intraprotein hydrogen bonding, as discussed above. In the case of a single water–protein hydrogen bond, standard free energy of H-bond formation, ΔGhb can be calculated using the classical relation between the change of free energy of a two state chemical reaction and its equilibrium constant:

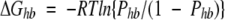graphic file with name M1.gif (1)

where R is gas constant, T is temperature in Kelvin, and Phb is the probability of formation of a particular hydrogen bond between a protein atom and a water molecule. Providing an approximate based on ASA formula describing Phb for any solvent exposed protein polar and charged groups one can accurately and efficiently calculate H-bonding contribution to protein hydration. We have to note that our goal here is to describe equilibrium kinetics of water H-bonding under conditions when ASA of “receptor” can vary only using approximate empirical formulas suitable for computationally effective free energy calculations. To do that we will use equilibrium kinetics analysis of classical multisite-receptor/ligand binding reaction using a standard approach (Edsall and Wyman 1958; Tsai 2002).

Figures 4 ▶ and 5 ▶ show that all dependencies of Phb on ASA derived from MD simulations have similar saturation Michaelis-Menten shapes. Therefore, following the formalism by (Tsai 2002) for a simple reaction of a “ligand” (L) (i.e., water) binding by a “receptor” (R) (i.e., protein donor/acceptor groups) having n sites of binding:

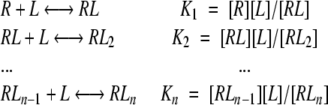graphic file with name M2.gif

For the case of a single binding site one can obtain the following formula for dependence of moles of ligand bound per mole of receptor binding sites, ν (Tsai 2002), or in other words, probability of binding:

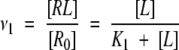graphic file with name M3.gif (2)

where [R0] is total molar concentration of bound and non-bound receptor and K1 is dissociation constant. In the case of n noninteracting equivalent binding sites, dissociation constants are the same for all binding sites, and therefore, its binding probabilities, νi are equal as well. Therefore, the total average number of occupied sites per molecule of “receptor” is ν = ∑νi = nν1. The probability that any arbitrary site of a receptor is occupied by a ligand is (Edsall and Wyman 1958):

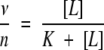graphic file with name M4.gif (3)

However, because efficiency of ligand binding is dependent on the receptor’s ASA due to entropical contributions to free energy of binding, the dissociation constant, K should be also dependent on ASA. Let’s introduce a factor F (from 0 to 1) describing the binding efficiency which:

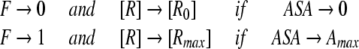graphic file with name M5.gif

and is approximately proportional to ASA if ASA → 0 Here, Rmax is equilibrium concentrations of free acceptor at conditions of maximal receptor efficiency. The simplest function possessing all above requirements is,

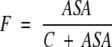graphic file with name M6.gif

where C is a constant. Given that

[R] =[R0](1 − F) + F[Rmax] one can obtain that:

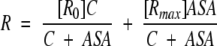graphic file with name M7.gif (4)

and, therefore, K can be approximated by the following formula describing its dependence on ASA:

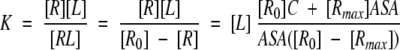graphic file with name M8.gif (5)

Substituting formula 5 into formula 3 gives approximate dependence of per H-bond probability of H-bond formation, Phb = ν/n on ASA as a simple hyperbolic function:

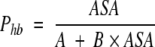graphic file with name M9.gif (6)

where A and B are constants depending on types of donor/ acceptor groups.

Figure 4 ▶ and Figure 5A, B, and C ▶ show the best-fit parameters of the above formula obtained for the available data on H-bond probabilities for different types of protein polar and charged groups. Because there is very high correlation (>0.9) between Phb derived from MD simulations and that calculated using the formulas shown in the figure legends free energy of the protein hydration at any given protein conformation can be calculated as follows:

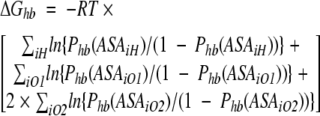graphic file with name M10.gif (7)

where Phb(ASA) are respective functions of ASA; ASAiH is the exposed surface area of a protein polar hydrogen atoms; and ASAiO1, ASAiO2 are solvent-accessible surface areas of protein oxygen atoms capable for one and two H-bonds with water, respectively, in a given protein conformation.

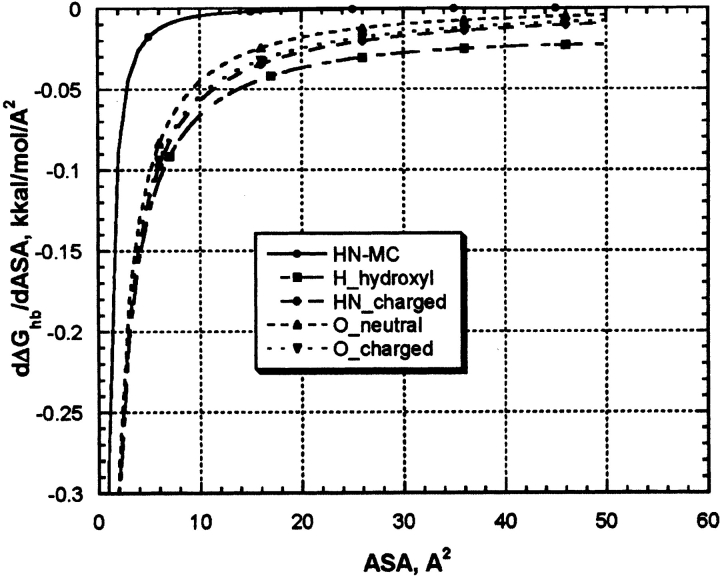
As one can see from the Figure 4 ▶ and Figure 5A, B, and C ▶, first derivatives of the protein hydration function are not a constant and highly depend on ASA of an atom under consideration. Nevertheless, it was assumed so in many continuous approximation models for protein hydration by introduction of constant atomic solvation parameters for each basis atom types (Juffer et al. 1995). Therefore, it would be interesting to compare the derivatives of protein hydration functions of our work with that from other models. Due to simplicity of mathematical functions used in our model it is easy to obtain its first derivative of ASA:

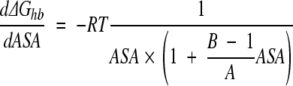graphic file with name M11.gif (8)

where A and B are respective constants from equation 6, R is the gas constant, and T is the temperature.

Figure 6 ▶ shows dependence of the derivatives of protein hydration function on ASA for five types of parameterizations shown in Figure 4 ▶ and Figure 5A, B, and C ▶. All derivative functions have hyperbolic-like saturation shapes. All functions show a steep increase in ASP values between zero and approximately up to 10 Å2 and a plateau above 10 Å2. Because most of the continuous hydration models were parameterized using experimental data on transfer of small organic molecules modeling amino acid side chain and peptide backbone where respective atoms have maximal values of ASA belonging to the plateau section, it is understandable why the authors could successfully parameterize their model using assumption of constant ASP. In proteins, however, many of the solvent-exposed atoms capable of H-bonding with water are shadowed by neighboring protein atoms, and their ASA are shifted to the low ASA with a steep slope of the ASP function. Table 1 shows the results of the ASA statistical survey of a representative protein set for atom types under consideration. One can see that, indeed, major parts of the distributions belong to the steep slope areas between 0 and 10 Å2, where models with constant ASP seem are not applicable. This explains why continues hydration model with constant ASPs are so inaccurate in calculations of protein hydration (Juffer et al. 1995).

Figure 6.

Figure 6.

Open in a new tab

The first derivatives of H-bonding functions for protein hydration with respect to ASA for five types of basic parameterizations shown in the legends of Figures 4 ▶ and 5A, B, and C ▶.

Table 1.

Statistical survey of solvent-exposed groups capable for H-bonding with water in a set of protein crystal structures

Number of atoms with nonzero ASA Total ASA (Å2) Average ASA per atom (Å2) Standard deviation (Å2)
Hydrogen atoms in mainchain NH groups 1548 4817 3.1 2.8
Hydrogen atoms in hydroxyl groups of Ser,Thy, and Tyr side chains 883 7131 8.1 6.4
Hydrogen atoms in charged groups of Arg+ and Lys+ side chains 715 6117 8.6 6.0
Oxygen atoms in uncharged carbonyl groups in main chain and side chains of Asn and Gln 5928 61000 10.3 9.4
Oxygen atoms in charged groups of Asp and Glu side chains 638 8860 13.9 10.1
Open in a new tab

List of PDB codes for 42 protein crystal structures from representative set of structure nonrelated proteins at better than 1.5 Å2 resolution, with less than 25% homology and with R-factor below 0.19 (PDB-SELECT, Vriend 1990) used in this statistical survey: 1rb9, 3lzt, 2pvb, 1bxo, 1cex, 1nls, 1a1y, 1psr, 2erl, 2igd, 1lkk, 1aho, 1rge, 1ctj, 1bkr, 1bpi, 1arb, 1atg, 7rsa, 1amm, 7fd1, 1aac, 1plc, 5ptp, 1xso, 1rcf, 3ebx, 1awd, 3sdh, 2ctc, 256b, 2izh, 2end, 2olb, 1xyz, 1eca, 2phy, 3vub, 1xnb, 1bgf, 1g3p, 3seb.

H-bond ASP derived from our model for five atom types using its average atomic ASA in proteins (see data in Table 1) are: −0.044 kcal/mole/Å2 (HN/NH2-uncharged groups), −0.066 kcal/mole/Å2 (H in hydroxyl groups), −0.072 kcal/ mole/Å2 (NH2/NH3-charged groups), −0.045 kcal/mole/Å2 (O-uncharged carbonyl/hydroxyl groups), and −0.04 kcal/ mole/Å2 (O-charged carboxyl group). Proper accounting for the number of possible water–protein H-bonds for each protein hydrophilic group in our model converts the data to total H-bonding–based ASP, which are in energy range (0.044–0.216 kcal/mole/Å2) for different protein polar and charged groups. The energy range is very close to that used in most of ASP parameter sets discussed in the literature (Juffer et al. 1995), indicating that H-bonding with water is a main contributor to the free energy of hydration of these groups. It is of interest that ranking of H-bonding stability of different protein hydrophilic groups (data is shown in Figs. 4 ▶ and 5 ▶) in our model correctly reproduces relative ranking of protein–water H-bonding potential: COO− > NH3+ > OH > NH/NH2 as was found in experiments with gradually increasing Lysozyme solvation (Jeffrey and Saenger 1991). We have to note, therefore, that despite the fact that this model is totally based on computational results, its predictions are in a reasonably good agreement with available experimental data on protein hydration. In addition, the model is simple, based on first physical principles and very computationally efficient. Therefore, we hope it can help to greatly improve the accuracy of energy functions used in molecular modeling and dynamics of proteins.

Materials and methods

MD simulations

The Molecular Dynamics (MD) calculations were performed with AMBER 4.1 package (Cornell et al. 1995; Pearlman et al. 1995). MD simulations of small globular protein Crambin from the Abyssinian cabbage (Crambe abyssinica) seed (PDB entry code 1AB1) at a resolution of 0.89 Å2 were done as follows: Original PDB structure of Crambin (1AB1) was regularized to remove minor van der Waals clashes using a standard regularization protocol of the ICM package for molecular modeling and design (Abagyan and Totrov 1994). Both N and C termini were uncharged. Each protein structure was immersed in a box of explicit TIP3P waters, with walls at least 10 Å2 away from any peptide atom. The water box was then truncated to an octahedron, and periodic boundary conditions were employed to eliminate boundary effects. All protein conformations were kept rigid during the simulations. Non-bonded interactions were evaluated at every step, applying a 12 Å2 residue-based cutoff. The SHAKE algorithm (van Gunsteren and Berendsen 1977) was used to constraint all bonds during the MD simulations, and the time step was set to 0.002 psec. All calculations were performed on a Silicon Graphics Octane/R10000 workstation. MD simulations were calculated at 293 K for at least 350 psec, and Cartesian coordinates were saved on disk every 0.04 psec during the course of the trajectories, leading to sets of 8500 frames. The following strategy was used to prepare each system to the MD runs: All water molecules were minimized, subjected to 10 psec of MD at constant volume to allow for the reorientation and relaxation of the water dipoles, and minimized again. After this procedure to randomize the water box, the system was heated gradually from 10 K to 293 K for 20 psec, and then the temperature was maintained at 293 K for the rest of the constant-pressure MD simulations. Analysis of H-bonds was performed with the CARNAL module from the AMBER 4.1 package. The probability of hydrogen bond, Phb was calculated as the fraction of time that a H-bond between a water molecule and the corresponding protein atom is formed. It was evaluated during the last 250 psec of the MD simulations (~5000 frames), thus allowing the system to equilibrate during the initial 100 psec. In the analysis of MD trajectories the H-bonds were considered to be formed when the distance between heavy atoms of a donor and an acceptor was ≤3.1 Å2 for NH. . .O and ≤3.0 Å2 for OH. . .O H-bonds, respectively. The H-Donor-Acceptor angle was ≤30°. The hydrogen bond geometry criteria are in accordance with data derived from studies of amino acid hydration in protein crystal structures (Thanki et al. 1990, 1991; Morris et al. 1992). In the case of NH2 groups and carbonyl/carboxyl oxygen atoms of main chain and side chains of Asp, Asn, Glu, and Gln where two water molecules are expected to occupy symmetrical positions, the additional requirement for dihedral angle between the water molecular (according to statistical survey of the protein database to be >120°) was used. To estimate the errors in the H-bond probabilities, the partial Phb were calculated for five consecutive 50 psec intervals in the last 250 psec of the MD trajectory.

Statistical survey of the protein database

The atomic details of water–protein interactions were derived from 42 proteins from a representative set of proteins crystal structures at better than 1.5 Å2 resolution, with less than 25% homology and with R-factor below 0.19 (PDB-SELECT; Vriend 1990). The crystal structures of the proteins were taken from the Brookhaven Protein Data Bank (Bernstein et al. 1977). Similar to analysis of MD simulations H-bonds between water and protein were accepted when distance between heavy atoms of a donor and an acceptor was ≤3.1 Å2 for NH. . .O and ≤3.0 Å2 for OH. . .O H-bonds, respectively. The H-Donor-Acceptor angle was ≤30° in all the cases. The hydrogen bond geometry criteria are in accordance with Thanki et al. (1990, 1991) and Morris et al. (1992).

Acknowledgments

This work was supported by research grants from St. Petersburg Scientific Center, the Russian Academy of Sciences of 2002–2003, and from the Russian Foundation for Basic Research (Grants No. 02-04-49259 and 02-04-50058).

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

Abbreviations

  • ASA, solvent-accessible surface area

  • MD, molecular dynamics

  • PDB, Brookhaven Protein Data Bank

  • ASP, atomic solvation parameters

Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.04748404.

References

  1. Abagyan, R. and Totrov, M. 1994. Biased probability Monte Carlo conformational searches and electrostatic calculations for peptides and proteins. J. Mol. Biol. 235 983–1002. [DOI] [PubMed] [Google Scholar]
  2. Armstrong, K.M., Fairman, R., and Baldwin, R.L. 1993. The (i, i + 4) Phe–His interaction studied in an alanine-based α-helix. J. Mol. Biol. 230 284–291. [DOI] [PubMed] [Google Scholar]
  3. Bernstein, F.C., Koetzle, T.F., Williams, G.J., Meyer Jr., E.E., Brice, M.D., Rodgers, J.R., Kennard, O., Shimanouchi, T., and Tasumi, M. 1977. The Protein Data Bank: A computer-based archival file for macromolecular structures. J. Mol. Biol. 112 535–542. [DOI] [PubMed] [Google Scholar]
  4. Bhattacharyya, S.M., Wang, Z.G., and Zewail, A.H. 2003. Dynamics of water near a protein surface. J. Phys. Chem. 107 13218–13228. [Google Scholar]
  5. Bonvin, A.M.J.J., Sunnerhagen, M., Otting, G., and van Gunsteren, W.F. 1998. Water molecules in DNA recognition II: A molecular dynamics view of the structure and hydration of the trp operator. J. Mol. Biol. 282 859–873. [DOI] [PubMed] [Google Scholar]
  6. Chatake, T., Ostermann, A., Kurihara, K., Parak, F.G., and Niimura, N. 2003. Hydration in proteins observed by high-resolution neutron crystallography. Proteins 50 516–523. [DOI] [PubMed] [Google Scholar]
  7. Cheng, Y.K. and Rossky, P.J. 1998. Surface topography dependence of biomo-lecular hydrophobic hydration. Nature 392 696–699. [DOI] [PubMed] [Google Scholar]
  8. Cornell, W.D., Cieplak, P., Bayly, C.I., Gould, I.R., Merz, J.K.M., Fergusson, D.M., Spellmeyer, D.C., Fox, T., Caldwell, J.W., and Kollman, P.A. 1995. A second generation force field for the simulation of proteins and nucleic acids. J. Am. Chem. Soc. 117 5179–5197. [Google Scholar]
  9. Deep, S. and Ahluwalia, J.C. 2003. Theoretical studies on solvation contribution to the thermodynamic stability of mutants of lysozyme T4. Protein Eng. 16 415–422. [DOI] [PubMed] [Google Scholar]
  10. Edsall, J.T. and Wyman, J. 1958. Biophysical chemistry, pp. 610–614. Academic Press, New York.
  11. Efimov, A.V. and Brazhnikov, E.V. 2003. Relationship between intramolecular hydrogen bonding and solvent accessibility of side-chain donors and acceptors in proteins. FEBS Lett. 554 389–393. [DOI] [PubMed] [Google Scholar]
  12. Eisenberg, D. and McLachlan, A.D. 1986. Solvation energy in protein folding and binding. Nature 319 199–203. [DOI] [PubMed] [Google Scholar]
  13. Feyereisen, M.W., Feller, D., and Dixon, D.A. 1996. Hydrogen bond energy of the water dimer. J. Phys. Chem. 100 2993–2997. [Google Scholar]
  14. Finkelstein, A.V. 1977. Electrostatic interactions of charged groups in water environment and their influence on the polypeptide chain secondary structure formation. Mol. Biol. (Mosk) 10 811–819. [PubMed] [Google Scholar]
  15. Gilson, M.K. and Honig, B. 1991. The inclusion of electrostatic hydration energies in molecular mechanics calculations. J. Comput. Aided Mol. Des. 5 5–20. [DOI] [PubMed] [Google Scholar]
  16. Gregoret, L.M., Rader, S.D., Fletterick, R.J., and Cohen, F.E. 1991. Hydrogen bonds involving sulfur atoms in proteins. Proteins 9 99–107. [DOI] [PubMed] [Google Scholar]
  17. Hummer, G., Garcia, A.E., and Soumpasis, D.M. 1996. A statistical mechanical description of biomolecular hydration. Faraday Discuss. 103 175–189. [DOI] [PubMed] [Google Scholar]
  18. Ippolito, J.A., Alexander, R.S., and Christianson, D.W. 1990. Hydrogen bond stereochemistry in protein structure and function. J. Mol. Biol. 215 457–471. [DOI] [PubMed] [Google Scholar]
  19. Israelachvili, J. and Wennerstrom, H. 1996. Role of hydration and water structure in biological and colloidal interactions. Nature 379 219–225. [DOI] [PubMed] [Google Scholar]
  20. Jeffrey, G.A. and Saenger, W. 1991. Hydrogen bonding in biological structures, pp. 459–486. Springer-Verlag, Berlin.
  21. Juffer, A.H., Eisenhaber, F., Hubbard, S.J., Walther, D., and Argos, P. 1995. Comparison of atomic solvation parametric sets: Applicability and limitations in protein folding and binding. Protein Sci. 4 2499–2509. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kovacs, H., Mark, A.E., and van Gunsteren, W.F. 1997. Solvent structure at a hydrophobic protein surface. Proteins 27 395–404. [DOI] [PubMed] [Google Scholar]
  23. Kuhn, L.A., Siani, M.A., Pique, M.E., Fisher, C.L., Getzoff, E.D., and Tainer, J.A. 1992. The interdependence of protein surface topography and bound water molecules revealed by surface accessibility and fractal density measures. J. Mol. Biol. 228 13–22. [DOI] [PubMed] [Google Scholar]
  24. Lazaridis, T. and Karplus, M. 1999. Effective energy function for proteins in solution. Proteins 35 133–152. [DOI] [PubMed] [Google Scholar]
  25. Lomize, A.L., Reibarkh, M.Y., and Pogozheva, I.D. 2002. Interatomic potentials and solvation parameters from protein engineering data for buried residues. Protein Sci. 11 1984–2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Martin, T.W. and Derewenda, Z.S. 1999. The name is bond—H bond. Nat. Struct. Biol. 6 403–406. [DOI] [PubMed] [Google Scholar]
  27. Momany, F.A., McGuire, R.F., Burgess, A.W., and Scheraga, H.A. 1975. Energy parameters in polypeptides. VII. Geometric parameters, partial atomic charges, nonbonded interactions and intrinsic torsional potential for the naturally occurring amino acids. J. Phys. Chem. 79 2361–2381. [Google Scholar]
  28. Morris, A.S., Thanki, N., and Goodfellow, J.M. 1992. Hydration of amino acid side chains: Dependence on secondary structure. Protein Eng. 5 717–728. [DOI] [PubMed] [Google Scholar]
  29. Nemethy, G., Pottle, M.S., and Scheraga, H.A. 1983. Energy parameters in polypeptides. 9. Updating of geometrical parameters, nonbonded interactions and hydrogen bond interactions for the naturally occurring amino acids. J. Phys. Chem. 87 1883–1887. [Google Scholar]
  30. Ooi, T., Oobatake, M., Nemethy, G., and Scheraga, H.A. 1987. Accessible surface areas as a measure of the thermodynamic parameters of hydration of peptides. Proc. Natl. Acad. Sci. 84 3086–3090. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Otting, G., Liepinsh, E., and Wuthrich, K. 1991. Protein hydration in aqueous solution. Science 254 974–980. [DOI] [PubMed] [Google Scholar]
  32. Pal, S.K., Peon, J., and Zewail, A.H. 2002. Biological water at the protein surface: Dynamical solvation probed directly with femtosecond resolution. Proc. Natl. Acad. Sci. 99 1763–1768. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Pearlman, D.A., Case, D.A., Caldwell, J.C., Ross, W.S., Cheatham, T.E., Fergusson, D.M., Seibel, G.L., Chandra Singh, U., Weiner, P., and Kollman, P.A. 1995. AMBER 4.1. University of California, San Francisco, CA.
  34. Petukhov, M., Cregut, D., Soares, C.M., and Serrano, L. 1999. Local water bridges and protein conformational stability. Protein Sci. 8 1982–1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Scheraga, H.A. 1998. Theory of hydrophobic interactions. J. Biomol. Struct. Dyn. 16 447–460. [DOI] [PubMed] [Google Scholar]
  36. Sharp, K.A. and Honig, B. 1990. Electrostatic interactions in macromolecules: Theory and applications. Annu. Rev. Biophys. Biophys. Chem. 19 301–332. [DOI] [PubMed] [Google Scholar]
  37. Thanki, N., Thornton, J.M., and Goodfellow, J.M. 1990. Influence of secondary structure on the hydration of serine, threonine and tyrosine residues in proteins. Protein Eng. 3 495–508. [DOI] [PubMed] [Google Scholar]
  38. Thanki, N., Umrania, Y., Thornton, J.M., and Goodfellow, J.M. 1991. Analysis of protein mainchain solvation as a function of secondary structure. J. Mol. Biol. 221 669–691. [DOI] [PubMed] [Google Scholar]
  39. Tsai, C.S. 2002. An introduction to computational biochemistry, pp. 107–111. J. Wiley, New York.
  40. van Gunsteren, W.F. and Berendsen, H.J.C. 1977. Algorithms for macromolecular dynamics and constraint dynamics. Mol. Phys. 34 1311–1327. [Google Scholar]
  41. von Freyberg, B., Richmond, T.J., and Braun, W. 1993. Surface area included in energy refinement of proteins. A comparative study on atomic solvation parameters. J. Mol. Biol. 233 275–292. [DOI] [PubMed] [Google Scholar]
  42. Vriend, G. 1990. WHAT IF: A molecular modeling and drug design program. J. Mol. Graph. 8 52–56. [DOI] [PubMed] [Google Scholar]
  43. Walrafen, G.E. 1972. Raman and infrared spectral investigations of water structure. In Water, a comprehensive treatise (ed. F. Franks), pp. 151–215. Plenum Press, New York.
  44. Walsh, S.T., Cheng, R.P., Wright, W.W., Alonso, D.O., Daggett, V., Vanderkooi, J.M., and DeGrado, W.F. 2003. The hydration of amides in helices; a comprehensive picture from molecular dynamics, IR, and NMR. Protein Sci. 12 520–531. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Warshel, A. and Papazyan, A. 1998. Electrostatic effects in macromolecules: Fundamental concepts and practical modeling. Curr. Opin. Struct. Biol. 8 211–217. [DOI] [PubMed] [Google Scholar]
  46. Warshel, A. and Russell, S.T. 1984. Calculations of electrostatic interactions in biological systems and in solutions. Q. Rev. Biophys. 17 283–422. [DOI] [PubMed] [Google Scholar]
  47. Wesson, L. and Eisenberg, D. 1992. Atomic solvation parameters applied to molecular dynamics of proteins in solution. Protein Sci. 1 227–235. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Williams, R.L., Vila, J., Perrot, G., and Scheraga, H.A. 1992. Empirical solvation models in the context of conformational energy searches: Application to bovine pancreatic trypsin inhibitor. Proteins 14 110–119. [DOI] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES