Database searching by flexible protein structure alignment

Abstract

We have recently developed a flexible protein structure alignment program (FATCAT) that identifies structural similarity, at the same time accounting for flexibility of protein structures. One of the most important applications of a structure alignment method is to aid in functional annotations by identifying similar structures in large structural databases. However, none of the flexible structure alignment methods were applied in this task because of a lack of significance estimation of flexible alignments. In this paper, we developed an estimate of the statistical significance of FATCAT alignment score, allowing us to use it as a database-searching tool. The results reported here show that (1) the distribution of the similarity score of FATCAT alignment between two unrelated protein structures follows the extreme value distribution (EVD), adding one more example to the current collection of EVDs of sequence and structure similarities; (2) introducing flexibility into structure comparison only slightly influences the sensitivity and specificity of identifying similar structures; and (3) the overall performance of FATCAT as a database searching tool is comparable to that of the widely used rigid-body structure comparison programs DALI and CE. Two examples illustrating the advantages of using flexible structure alignments in database searching are also presented. The conformational flexibilities that were detected in the first example may be involved with substrate specificity, and the conformational flexibilities detected in the second example may reflect the evolution of structures by block building.

One of the most important tasks in structural biology is to discover similarities between three-dimensional structures of proteins (Goldsmith-Fischman and Honig 2003; Zhang and Kim 2003). Once a new structure is determined, usually the first question asked is: Is the new structure similar to any known protein structures? Only when the answer is yes is the next question asked: What are the similarities/differences between the new structure and its homologs/analogs?

Over 50 different structure comparison programs have been developed to answer the latter question (for review, for instance, see Guerra and Istrail 2000). Significantly fewer programs can also answer the first question, at least in a reasonable time and with verified accuracy. The most popular ones are DALI (Holm and Sander 1993), CE (Shindyalov and Bourne 1998), and VAST (Madej et al. 1995; Gibrat et al. 1996). Sensitivity and selectivity of the popular structure comparison programs have been compared recently (Sierk and Pearson 2004). Resources such as SCOP (Murzin et al. 1995) and CATH (Orengo et al. 1997) address the same question, but were created on the basis of both human analysis and automated comparison programs. For comparing two structures, we need to search for the optimal alignment between them, whereas for identifying a similar structure in a database, we need to answer a different and more difficult question: Is the similarity between proteins A and B more significant than the similarity between A and C? To answer this question, one has to develop an estimate of the statistical significance of the structural alignment, whereas most structure comparison programs simply report the length of the alignment and a similarity measure, such as root mean square deviation (RMSD). For instance, the most popular programs, DALI and CE, both report a Z-score as the similarity measurement, but they do not provide proof that the distribution of their raw scores is Gaussian. Only one algorithm (Gerstein and Levitt 1998) has been extensively analyzed in this respect (Levitt and Gerstein 1998).

A large number of existing structure comparison programs is the best proof that the structural comparison problem is far from being solved (Holm and Sander 1993; Boutonnet et al. 1995; Madej et al. 1995; Shindyalov and Bourne 1998; Eidhammer et al. 2001). There is no unique and objective measure for structural similarity between proteins (Yang and Honig 2000), and there is not even a unique way of aligning two protein structures (Godzik 1996). Existing structure comparison algorithms differ by minimization strategy and the similarity function being optimized (Holm and Sander 1993). But despite all the differences, most of them share a fundamental limitation: They compare proteins as rigid bodies and thus concentrate on the question of identifying the largest common substructure between two proteins. At the same time, it is well known that proteins are flexible and undergo significant structural changes as part of their normal function and as a result of mutations (Wuthrich and Wagner 1978; Schulz and Schirmer 1979; Bennett and Huber 1984; Jacobs et al. 2001). Only very few methods, such as least-squares fitting (Wriggers and Schulten 1997), multiple linkage clustering (Boutonnet et al. 1995; Ochagavia et al. 2002), FlexProt (Shatsky et al. 2002), and FATCAT (Ye and Godzik 2003) treat protein structures, true to their real nature, as flexible. Such programs ask: How can one of the structures be rearranged to make it more similar to the other one? instead of the usual, What is the largest similar part of two proteins? This seemingly simple change has profound consequences, for instance, in applying results of flexible structure alignments to modeling.

None of the current flexible protein structure comparison algorithms has been used for database searches because of a lack of an accurate statistical estimate of alignment significance. For instance, in FATCAT, the similarity score describes how well two structures are superimposed, but the score is strongly correlated with the length of the structures being compared. As a result, protein A may seem to be more similar to protein B than to protein C just because B is longer than C, whereas in fact the alignment between A and B may be worse. In this paper, we describe a method to evaluate the significance of structural similarity that is independent of the length of proteins, which makes database searching using FATCAT possible.

It is well known that the alignment score between random sequences follows the extreme value distribution (EVD; Pearson 1998). This was rigorously proven only for alignment without gaps (Altschul and Gish 1996), but empirically it was shown to hold for a variety of alignment algorithms and gap penalty functions (Pearson 1998). The EVD parameters can be fitted to an empirical distribution of random scores and used for a statistical estimate of the significance of the particular score. In two rigid-body structural alignment programs used for database searches, DALI (Holm and Sander 1993) and CE (Shindyalov and Bourne 1998), Z-score is used for similarity evaluation—apparently assuming that the score distribution is Gaussian. Levitt and Gerstein (1998) have shown that the score of their simple structure comparison algorithm (Gerstein and Levitt 1998) behaves like a sequence similarity score, following EVD, whereas RMSD follows a different distribution and does not perform as well as the structural alignment score. However, their method is a generalization of the Needleman-Wunsch sequence alignment, using repeated cycles of dynamic programming and least-squares superimposing of two structures in which dynamic programming is performed on the distance matrix derived from least-squares superimposing; it was not really tested against other genuine structure comparison methods (Gerstein and Levitt 1998). Recently, Dewey and colleagues (Y. Jia, G.T. Dewey, I.N. Shindyalov, and P.E. Bourne, in prep.) showed that in gapless alignments of structural fragments of the same length, the RMSD of their optimal superposition follows the EVD type of distribution. In this paper, we show that the FATCAT similarity score between two unrelated structures also follows the EVD. On the basis of this, a statistical significance evaluation method was developed for a FATCAT-based database-searching tool (FATCAT-search) and tested on a large benchmark. Also, we show the results of applying FATCAT-search to several protein structures that were recently determined by Protein Structure Initiative Centers (Lesley et al. 2002). Despite successful structure determination, the functions of these proteins remain unknown. The advantages of flexible structural alignments in structure-similarity-based functional annotation are illustrated in these cases. FATCAT-search was able to identify similar structures and align active site residues for protein 1ufh (PDB code), which led to a reliable prediction of its function as an acetyltransferase. In addition, flexibility was detected, which we hypothesize correlates with the substrate specificity of acetyltransferase. In the second case, FATCAT-search results suggest that the original annotation of the structures with an unusual trefoil knot as an early prototype of a TIM barrel (Zarembinski et al. 2003) may be wrong; instead, the similarity between knot structures and TIM barrel proteins is probably caused by the similarity in the building blocks they share, because significant similarities (some even stronger) were also detected between knot structures and structures from other folds.

Materials and methods

Flexible structure alignment

We have recently developed a new method, FATCAT, for flexible protein structure alignment (Ye and Godzik 2003). FATCAT builds a structural alignment from aligned fragment pairs (AFPs) and it considers solutions involving gaps, twists, and simple extensions using a unified scoring function. FATCAT performs the alignment and hinge detection simultaneously. The entire algorithm has been implemented in a fast and efficient computer program and systematically tested on large alignment benchmarks. In an extensive comparison with other structure alignment programs, it was shown that FATCAT is not biased toward introducing twists into the structure, achieving performance that matched that of the rigid structure alignments for all of the test cases. At the same time, it outperformed the only other comparable flexible alignment algorithm, FlexProt (Shatsky et al. 2002), by producing longer alignments with a smaller number of twists in most cases (Ye and Godzik 2003). In the following paragraph, we present a short synopsis of the FATCAT algorithm:

Flexible structure alignment is formulated as the AFP chaining process (Gusfield 1999), allowing at most t twists, and the flexible structure alignment is reduced to a rigid structure alignment when t equals 0. Dynamic programming is used in the chaining process, which can combine gaps and twists between consecutive AFPs, each with its own score penalty. We denote S(k) as the best score ending at AFP k, which can be calculated from the best ending at previous AFPs that can be connected with AFP k subject to the constraints of the consecutive,

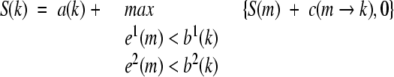(1)

s.t. T(k) ≤ t

where a(k) is the score of AFP k itself; c(m → k) is the score of introducing a connection between AFP m and AFP k; T(k) is the number of twists required to connect the chain of AFPs leading up to S(k), which is calculated by,

(2)

where t(m → k) is 1 if a twist is required to connect AFP m and k and 0 if no twist is required. Denote the maximum S(k) as the chaining score of FATCAT, cs, which will be used following.

Extreme value distribution

The EVD of a random variable s has the probability density of

(3)

where μ is the location parameter and λ is the scale parameter. These parameters can be determined by either the analytic formula or empirical simulation (Altschul and Gish 1996; Pearson 1998). Here we follow the latter route. Once the parameters are determined, they can be used to compute the probability that the variable X takes a value greater than s (survival function; Evans et al. 2000):

(4)

It has been reported that different fitting methods give almost identical results in determining the parameters (Altschul and Gish 1996). In this study, we use the fitting function based on the Nelder-Mead simplex method “fmins,” implemented in Matlab (Nelder and Mead 1965).

Significance estimate of FATCAT score

We have developed the significance estimate for both FATCAT rigid-body mode (i.e., t = 0) and FATCAT flexible mode (i.e., t = 5). We did this in order to check the influence of introducing flexibility into structural comparison in terms of sensitivity and specificity in recognizing similar structures.

A good structural similarity measure should describe both the local structure similarity and the global structure similarity between two proteins. On the basis of this requirement, we have designed a similarity score of FATCAT in such a way that it takes into account factors such as the FATCAT chaining score (describing mainly the local and medium-range structure similarity; see equation 1), the global structure similarity between two structures described by the overall RMSD (which is defined as the root mean square deviation of all of the aligned C_α atoms, based on the rigid-body superposition after one structure is modified according to the FATCAT alignment), and the number of equivalent positions in the alignment and the number of twists. The similarity score is computed as

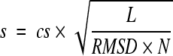(5)

where cs is the FATCAT chaining score; L is the number of equivalent positions in the alignment; RMSD is the overall RMSD between two structures when one structure is rearranged at the positions where twists are detected by FATCAT; N is the number of blocks in the alignment (number of twists + 1).

We collected a set of unrelated structure pairs for the simulation to determine the location and scale parameters of the EVD distributions based on the SCOP classification (Murzin et al. 1995). We assume that any two structures from different SCOP folds constitute a pair of unrelated structures. Sometimes two structures from different SCOP folds could be similar (Shindyalov and Bourne 2000); a few exceptions, however, will not significantly influence the parameter fitting. We need to fit parameters of the EVD for random structures cataloged into different lengths separately because the parameters are dependent on the length of structures. Although there are >20,000 structures in PDB (Berman et al. 2000), there are not enough nonredundant protein structures with the same length to fit distribution parameters for all lengths. To overcome this problem, we randomly cut regions of length m from structures that are longer than m, and used this region as an individual structure for the parameters simulation of length m. In this way, we prepared a set of structure libraries for lengths of 40, 70, 100. . .400 amino acids, with each library having up to 10,000 random structure pairs (the full lists are available at the FATCAT Web site).

Database searching

We implemented the FATCAT-search, a FATCAT-based database searching tool to identify structural analogs for a given query structure. We used the 95% nonredundant SCOP database (Murzin et al. 1995) as the target database for searching instead of PDB (Berman et al. 2000) because SCOP provides a well-maintained annotation and classification of the structures and divides larger structures into domains. Although 0.05 is a typical significance level, we may also keep candidates with lower significance (for example, with P-value < 0.1) for further manual inspection to explore distantly similar structures.

Results and Discussion

Statistical estimate of FATCAT score

First we show that the similarity scores of rigid FATCAT and flexible FATCAT follow the EVD. Figures 1A ▶ and 2A ▶ show the distributions of FATCAT similarity scores of protein structures with a length of 160 amino acids by rigid FATCAT and flexible FATCAT, respectively. A simple visual inspection confirms that both distributions closely resemble EVD. Quantile–quantile plots (Chambers et al. 1983) are further presented to show how well the data follow the fitted distribution. For both flexible and rigid FATCAT, the vast majority of structural similarity scores follow EVD very well, except for the two regions of extreme low scores and extreme high scores (Figs. 1B ▶, 2B ▶). Poor fitting in these two regions, however, will not have a big influence in database searching for similar structures: We are not interested in the extreme low scores (which mean dissimilar structures), and structure pairs with very high scores are significant no matter if the similarity is significant at the 1e-10 level (P-value) or the 1e-20 level. The scale and location parameters of EVD are shown to be linearly correlated with the length of the proteins, as shown in Figures 1C ▶ and 2C ▶. This is different from the EVD behavior of the sequence similarity score, in which the scale parameter remains essentially constant (Altschul and Gish 1996). Such a simple relation provides a simple way to compute the location and scale parameters for any protein length. Given a FATCAT similarity score, we can compute the P-value of the FATCAT alignment with equation 4. The smaller the P-value, the more statistically significant the similarity.

Figure 1.

EVD fitting of the rigid FATCAT scores. (A) The EVD distribution of FATCAT scores for protein structures with a length of 160 amino acids. (B) Quantile–quantile plot for fitting A. (C) μ (upper line) and λ (lower line) as functions of the length of proteins with linear coefficients of 0.993 and 0.992, respectively.

Figure 2.

EVD fitting of the flexible FATCAT scores. (A) The EVD distribution of FATCAT scores for protein structures with a length of 160 amino acids. (B) Quantile–quantile plot for fitting A. (C) μ (upper line) and λ (lower line) as functions of the length of proteins with linear coefficients of 0.997 and 0.988, respectively.

The significance estimate introduced earlier was tested by a benchmark (available at the FATCAT Web site) constructed on the basis of the SCOP version 1.61 40% protein set. The benchmark has 6233 pairs of similar proteins and 8769 pairs of dissimilar proteins (proteins from different folds). The collection of similar protein pairs includes 830 pairs of family-level similarities, 3146 pairs on the superfamily level, and 2257 on the fold level. The collection of dissimilar proteins includes pairs of proteins from different folds. We emphasize that the definition of structural similarity used in the benchmark is based on the SCOP classification, which has some inherent problems, as we will see from the following discussion. For instance, some protein pairs from different SCOP folds have actually very similar structures, an observation made several times previously (Shindyalov and Bourne 2000; Harrison et al. 2002). However, SCOP is one of the best classifications of protein structures and it has essentially become a standard in structure analysis. Therefore, here we use the SCOP classification to evaluate the FATCAT results.

The evaluation of the significance estimate here is focused on the ability of FATCAT to recognize similar structures in the benchmark described earlier as compared with CE and DALI. We adopted the ROC (Receiver Operating Characteristic) curve (Bradley 1997) to show the specificity and sensitivity of identifying similar structures for all of these programs. P-values of FATCAT and Z-scores of DALI and CE are used for ROC analysis. For each method, the protein pairs of both similar structures and dissimilar structures were sorted by the P-values or Z-scores, and then the true-positive fractions and false-positive fractions were calculated at different cutoffs. The performances of the three methods are shown in Figure 3 ▶, in which a random performance corresponds to the main diagonal, and the better the performance of a method, the farther the corresponding curve is from the main diagonal. It is obvious that FATCAT using P-value performed better than FATCAT using the raw chaining score (cs). Both rigid FATCAT and flexible FATCAT have better discriminating ability than CE, but they are worse than DALI, at least in this benchmark. We conclude that FATCAT works relatively well in database search, comparable to the two most popular structural comparison programs (DALI and CE). The introduction of flexibility in the FATCAT only results in a small decrease in performance, laying to rest the worries that flexible alignment will significantly increase the number of false positives in recognition of similar structures.

Figure 3.

The ROC curves for CE, DALI, rigid FATCAT, and flexible FATCAT.

Similarities between structures from different SCOP folds

It is well known that structures from different SCOP or CATH folds can be similar at some levels (Shindyalov and Bourne 2000; Harrison et al. 2002). This is also observed in our calculation. Among the 8769 pairs of “dissimilar” proteins mentioned earlier, statistically significant structural similarity has been detected in 475 pairs by FATCAT at the 5% significance level (see a list at the FATCAT Web site). Seventy of the 475 pairs are further confirmed by both DALI (Z-score ≥ 2.0) and CE (Z-score ≥ 3.5), and another 122 pairs are confirmed by either DALI or CE. Selected examples are described following (see Table 1 and Fig. 4 ▶).

Table 1.

Selected structure pairs from different SCOP folds that are similar according to structure alignment programs FATCAT, and/or CE, and/or DALI

	Structure 1		Structure 2				FATCAT
ID	Code	Fold	Code	Fold	CE Z-score	DALI Z-score	P-value	n(twists)	RMSD (Å)
A	d1grj_1	a.2	d1nfn_	a.24	4.7	4.9	2.4e–5	0	3.08
B	d1tig_	d.68	d1seia_	d.140	3.5	5.0	1.1e–3	0	2.84
C	d1cola_	f.1	d1bm1_	f.2	3.7	3.7	7.1e–4	4	3.07
D	d1jbea_	c.23	d1dv1a2	c.30	3.9	5.2	5.3e–3	2	2.44
E	d1fvka1	a.44	d1jhga_	a.107	2.8	1.7	8.3e–4	1	1.53
F	d2cbla2	a.48	d1ak4c_	a.73	2.3	1.1	8.3e–3	2	2.39
G	d1hd8a1	b.105	d1qasa2	b.7	2.0	1.2	4.6e–2	0	3.28
H	d1di2a	d.50	d1r16a1	d.141	2.3	1.2	9.2e–3	1	1.73

The number of twists, n(twists), and RMSD of the alignment are also shown for FATCAT. Refer to the text for descriptions of proteins represented by the SCOP codes (release 1.61) for pairs with ID A–D (the same as the index of the subgraphs in Fig. 4 ▶). Descriptions for the proteins for pairs with ID E–H are as follows: d1fvka1, disulphide-bond formation facilitator (DSBA), insertion domain from E. coli; d1jhga_, Trp repressor from E. coli; d2cbla2, N-terminal domain of cbl from H. sapiens; d1ak4c_, HIV-1 capsid protein; d1hd8a1, C-terminal domain of penicillin-binding protein 5 from E. coli; d1qasa2, C-terminal domain of PI-specific phospholipase C isozyme D1 from R. norvegicus; d1di2a_, double-stranded RNA-binding protein A from X. laevis; d1r16a1, ribosomal protein L6 from B. stearothermophilus. Descriptions of the folds are as follows: a.2, long α hairpin; a.24, four-helical up-and-down bundle; a.44, disulphide-bond formation facilitator (DSBA), insertion domain; a.48, N-cbl–like; a.107, DNA/RNA-binding 3-helical bundle; b.7, C2 domain-like; b.105, penicillin-binding protein 5, C-terminal domain; c.23, flavodoxin-like; c.30, biotin carboxylase N-terminal domain-like; d.45, ribosomal protein L7/12, C-terminal domain; d.50, dsRBD-like; d.68, IF3-like; d.140, ribosomal protein S8; d.141, ribosomal protein L6; f.1, toxins’ membrane translocation domains; f.2, membrane all-α.

Figure 4.

Superposition of (A) d1grj_1 and d1nfn__; (B) d1tig__ and d1seia_; (C) d1co1a_ and d1bm1__; (D) d1jbea_ and d1jw9b; (E) d1fvka1 and d1jhga_; (F) d2cbla2 and d1ak4c_; (G) d1hd8a1 and d1qasa2; and (H) d1di2a_ and d1rl6a1. In A, B, and G, one structure is shown in gray ribbons and the other structure in yellow; in C, D, E, F, and H, one structure is shown in gray, and the other structure is modified according to the FATCAT alignment and its different blocks are shown in different colors.

In the most typical cases, structures having similar regions, which can be detected by automatic comparison programs, are classified into different folds because one of them has additional secondary structure elements or domains. For instance, the N-terminal domain of GreA transcript cleavage protein (SCOP code d1grj_1) and apolipo-protein E3 (d1nfn__) have two similar helices, with d1nfn__ having two additional helices (Fig. 4A ▶); ribosomal protein S8 (d1seia_) is similar to the C-terminal domain of translation initiation factor IF3 (d1tig__) except that d1tig__ has an additional domain (Fig. 4B ▶). In some other cases, structures can be aligned well by FATCAT by introducing twists. For instance, RUNT domain of acute myeloid leukemia 1 protein (AML1; d1co1a_) and bacteriorhodopsin (d1bm1__), two transmembrane proteins, are superimposed by FATCAT with four twists, 165 aligned positions, and an RMSD of 3.07 Å (Fig. 4C ▶); CheY protein (d1jbea_) and biotin N-domain of carboxylase subunit of acetyl-CoA car-boxylase (d1dv1a2) share three very similar building blocks but a slightly different mutual arrangement (Fig. 4D ▶). In the latter two cases, flexible structural alignment allows us to see relations between folds that otherwise would go unnoticed.

Significant similarity between the structures in the examples shown earlier was detected by all three programs, FATCAT, CE, and DALI. In the 283 pairs that are found to be similar only by FATCAT, twists are present in 224 cases (detailed results are available at the FATCAT Web site). Selected examples are shown in Table 1 (E–H) and Figure 4 (E–H) ▶. Because these similarities are not very strong (P-value > 1e-4) and they are not confirmed by either DALI (i.e., Z-score < 2.0) or CE program (i.e., Z-score < 3.5), we believe that they mostly reflect marginal similarity of analogous groups of secondary structure elements. For instance, similarities can often be found between two structures with the same number of helices even though their topologies are different because helices themselves are similar and introducing twists easily transforms one into another. Indeed, such extreme cases are represented in our calculation. In 238 of 283 structure pairs, one or both structures are mainly composed of helices. In contrast, in only five cases, one or two structures are mainly composed of β-sheets. This suggests that, from a practical view, additional attention should be paid to the low significance similarity between helical structures, and that a P-value cutoff smaller than 0.05 may be needed for detecting the structural similarity so that it can also be detected by rigid-body comparison programs.

These and other related studies suggest that the current hierarchical classification of protein structures with strict division on separate fold-islands such as that used in SCOP (using a hierarchy of four levels; Murzin et al. 1995) and CATH (using a hierarchy of five levels; Orengo et al. 1997) does not necessarily reflect the actual hierarchy of protein structures (Ouzounis et al. 2003). Additional levels (for instance building blocks) between the fold and class may be necessary; neighborhoods of folds may share smaller structural units such as helical hairpins.

FATCAT-search examples

As mentioned in the introduction, a primary application of any protein structure similarity search procedure is to search for proteins that are similar to a newly determined protein structure. This type of analysis may provide helpful information for the functional study of the proteins, as distant homology can sometimes be recognized on the basis of structure similarity only. In this section, two cases are presented to demonstrate the FATCAT-search application for this task.

1ufh, a new acetyltransferase

The FATCAT-search shows that 1ufh (PDB code), a hypothetical protein in Bacillus subtilis, is similar to N-acetyl transferases (SCOP code d.108.1.1) from the acyl-coA N-acyltransferases fold. The highest similarity is found between 1ufh and histone acetyltransferase HPA2 from Saccharomyces cerevisiae (SCOP code d1qsma_), with a FATCAT alignment of 133 positions with an RMSD of 3.08 Å (P-value 5.05e-10). Twists are found in comparing 1ufh with some of the acyltransferases. For instance, when comparing 1ufh with the tabtoxin resistance protein from Pseudomonas syringae (SCOP code d1ghea_), a twist was introduced by FATCAT to get an alignment of 139 aligned positions with an RMSD of 2.66 Å, which covers the whole structure (P-value 5.05e-08); otherwise, only the acyl coenzyme A (ACO) binding regions can be well superimposed because the remaining two helices (cap helices) have slightly different orientations in the two structures (Fig. 5 ▶). With the FATCAT alignments, the GANT motif (involved with ACO binding activity; He et al. 2003) and two of three putative active sites were confirmed to be conserved in 1ufh. The two conserved active sites are His 128 (could be Asp or His according to the known structures with acetyl-transferase activity) and Tyr 97, and the site not conserved is Phe 90 (corresponding to Glu in the known acetyltransferases). We conclude that 1ufh may have the acetyltransferase activity on the basis of these results. Furthermore, the conformational changes detected by FATCAT in comparing 1ufh with other acetyltransferases suggest that different acetyltransferases may have different substrate specificity, which is related to the different orientations of the cap helices; it provides an efficient way to change the size of the substrate binding pocket by simply changing the packing between the two helices and the cofactor binding region.

Figure 5.

(A) The comparison between 1ufh (light ribbons) and d1ghea_ (dark ribbons), in which the acyl coenzyme A from d1ghea_ is shown in ball and sticks, and (B) the frequency of twists along 1ufh that can be detected in comparing 1ufh with the structures from the 95% nonredundant SCOP database. The original frequency of twists is shown in the black curve and the smoothed frequency of twists using a window length of 7 is shown in the gray curve.

Structures with an unusual trefoil knot

The structures of hypothetical protein Mt0001 from Methanobacterium thermoautotrophicum (PDB code 1k3r; Zarembinski et al. 2003), hypothetical protein Yggj_Haein from Haemophilus influenzae (PDB code 1nxz), and Ybea from Escherichia coli (PDB code 1ns5), determined by different structural genomics centers, have a deep trefoil knot, a very unusual feature in the structure universe (Nureki et al. 2002). SCOP version 1.63 groups the common knot domain of 1k3r and 1ns5 into a separate α/ β knot fold. 1k3r, however, was described as a TIM-barrel-like structure in the original paper (Zarembinski et al. 2003). This annotation was based on the DALI comparisons, which show that 1k3r is significantly similar to TIM-barrel structures (1b5t with Z-score of 5.7, 1ezw with Z-score of 5.4, and 1a49 with Z-score of 4.6). The investigators further suggested that the knot structure of 1k3r may be an early prototype of a TIM barrel.

FATCAT-search results provide a different scenario. The knot domains of these three structures are very similar to each other and they are most similar to the two knot structures that were collected by SCOP version 1.63, d1ipaa1 and d1mxia_. More important, FATCAT-search shows that these structures are also very similar to structures from some other folds (Table 2). For instance, significant similarities are found by FATCAT between 1nxz and d1chd__ from fold c.40 and d1g8la3 from fold c.57 (Table 2, Fig. 6 ▶), which are even stronger than the similarities between 1nxz and some other knot structures, 1ns5, 1mxi, and 1ipa. Although low similarities were also found between these three structures and structures from TIM-barrel fold (c.1), the similarities are less significant than the knot structures and structures from fold c.40, c.57, and so forth. Twists were detected in some of the alignments (Table 2, Fig. 6 ▶). Inspection of these structural similarities shows that many of these folds share building blocks, in this case, α/β/α modules (Fig. 6 ▶). We conclude that the knot structure is a type of gregarious fold (Harrison et al. 2002) that has significant overlap with structures from many other SCOP folds, and the similarities between knot structures with structures from other folds could be the result of their common ancestors or just a result of construction of protein structures from limited building blocks. However, we cannot derive a more detailed functional annotation for these gregarious knot structures when no dominant structural homologs/analogs with known functions can be reliably found.

Table 2.

Similar structures of knot fold (excluding the structures of the knot fold)

	Structural analogs			FATCAT alignment
Knot structure	Code	Fold	Length	n(twist)	RMSD (Å)	P-value
1nxz	d1k3ra2	c.116	151	0	2.86	1.80e–06
1nxz	d1chd_	c.40	119	0	3.09	9.37e–04
1nxz	d1g81a3	c.57	104	0	3.48	2.43e–03
1nxz	d11dg_1	c.2	111	1	2.89	4.78e–03
1nxz	d1rvv1_	c.16	105	2	2.91	1.45e–02
1nxz	d2tpsa_	c.1	146	3	3.23	1.86e–02
1k3r	d1mxia_	c.116	141	0	3.00	5.99e–05
1k3r	d1h4xa_	c.13	75	0	3.02	3.27e–02
1ns5	d1ipaa1	c.116	115	0	3.06	1.94e–06
1ns5	d1aoxa_	c.62	128	2	3.03	2.39e–03
1ns5	d1o97d2	c.31	79	0	3.01	4.08e–03
1ns5	d1di0a_	c.16	94	3	1.95	4.73e–03
1ns5	d1mjha_	c.26	89	1	3.09	5.16e–03
1ns5	d1nksa_	c.37	113	2	2.68	5.44e–03

Only one structure from each fold with the highest P-value is represented and up to five similar structures (with P-value < 0.05) are listed for each knot structure. Descriptions of the folds are as follows: c.116, α/β knot; c.1, TIM β/α-barrel; c.2, NAD(P)-binding Rossmann-fold domains; c.13, SpoIIaa-like; c.16, lumazine synthase; c.26, adenine nucleotide α hydrolase-like; c.31, DHS-like NAD/FAD-binding domain; c.37, P-loop containing nucleotide triphosphate hydrolases; c.40, methylesterase CheB, C-terminal domain; c.57, molybdenum cofactor biosynthesis proteins; c.62, integrin A (or I) domain.

Figure 6.

The structure of 1nxz and the superposition of 1nxz with its structural homologs/analogs from different folds. For each superposition, 1nxz is shown in gray ribbons and the other structure in yellow if no twists are detected; otherwise, the other structure is modified according to the FATCAT alignment and its different blocks are shown in different colors. The SCOP codes for each structure and its fold (in parentheses) are shown along with the structure. Refer to Table 2 and text for the descriptions of the folds and the FATCAT alignments.

Conclusion

A statistical estimate of FATCAT alignment has been developed and tested on a large benchmark. On the basis of this, a new database protein structural similarity searching tool, FATCAT-search, has been developed by extending a flexible protein structure alignment algorithm, FATCAT. FATCAT-search offers additional clues in structure-based functional annotation as compared with the usual rigid structure comparison tools, such as DALI and CE, by considering the structure flexibility. In addition, structure alignment that allows us to naturally include flexibility is very useful in detecting functionally related rearrangements within protein structures because protein structures are naturally flexible.

The study of similarities between different structures is the most important application of protein comparison programs. To date, we still do not know much about the overall properties of the fold space even though there have been more than 20,000 structures in PDB and more than 700 folds defined in SCOP. For instance, it is not clear if the fold space is continuous or hierarchical; we do not know how many folds there are in the universe. Whatever the results, the rules of how proteins change and evolve have to start from describing fold flexibilities, such as provided by the FATCAT program.

Electronic supplemental material

The FATCAT and FATCAT-search servers are available at http://fatcat.burnham.org (FATCAT Web site). All of the supplementary data is also available at the same Web site.