Structural alignment of proteins by a novel TOPOFIT method, as a superimposition of common volumes at a topomax point

Abstract

Similarity of protein structures has been analyzed using three-dimensional Delaunay triangulation patterns derived from the backbone representation. It has been found that structurally related proteins have a common spatial invariant part, a set of tetrahedrons, mathematically described as a common spatial subgraph volume of the three-dimensional contact graph derived from Delaunay tessellation (DT). Based on this property of protein structures, we present a novel common volume superimposition (TOPOFIT) method to produce structural alignments. Structural alignments usually evaluated by a number of equivalent (aligned) positions (N^e) with corresponding root mean square deviation (RMSD). The superimposition of the DT patterns allows one to uniquely identify a maximal common number of equivalent residues in the structural alignment. In other words, TOPOFIT identifies a feature point on the RMSD N_e curve, a topomax point, until which the topologies of two structures correspond to each other, including backbone and interresidue contacts, whereas the growing number of mismatches between the DT patterns occurs at larger RMSD (N_e) after the topomax point. It has been found that the topomax point is present in all alignments from different protein structural classes; therefore, the TOPOFIT method identifies common, invariant structural parts between proteins. The alignments produced by the TOPOFIT method have a good correlation with alignments produced by other current methods. This novel method opens new opportunities for the comparative analysis of protein structures and for more detailed studies on understanding the molecular principles of tertiary structure organization and functionality. The TOPOFIT method also helps to detect conformational changes, topological differences in variable parts, which are particularly important for studies of variations in active/ binding sites and protein classification.

The comparison of proteins is a fundamental approach to understanding the biological, physical, and chemical properties of proteins and their various functionalities. Protein structure comparison dates back to the first X-ray solutions of protein structures and has resulted in a tremendous impact on biological and biomedical research. Structural alignments help researchers to determine the relationships between the biological functionality of proteins and their primary sequence and three-dimensional structure, to understand protein architecture and identify common structural folds and structural families, to build models by homology, and to reveal evolutionary relationships between species.

Significant progress has been made in both the methodology and algorithms of comparative structure analysis. Superimpositions of the structures and consequent structure-based sequence alignments have been characterized from different points, and several methods and databases on protein structural alignments have been developed. Systematic comparison of all available protein structures has led to the development of several different protein structure classification schemes. Each classification scheme is derived from different algorithms, with slightly different goals in mind. FSSP (Holm and Sander 1996) is based on the DALI (Holm and Sander 1993) algorithm, whereas CATH (Orengo et al. 1997) has its roots in the SAP algorithm (Taylor et al. 1994), SCOP (Murzin et al. 1995) is derived primarily by visual inspection, MMDB (Ohkawa et al. 1995) uses the VAST algorithm (Gibrat et al. 1996), and CE-ALL (Shindyalov and Bourne 2001) uses the CE algorithm (Shindyalov and Bourne 1998). Many other methodologies and classifications have been reported (for reviews, see Madej et al. 1995; Godzik 1996; Holm and Sander 1999; Shindyalov and Bourne 2000; Koehl 2001). Those highlighted here provide Web-accessible resources that are kept current as new structures become available from the Protein Data Bank (PDB; Berman et al. 2000).

With the numerous methods available, one might think the structure superimposition problem has been solved, but upon close examination, there are many unresolved questions. The structural alignment problem has proven to be NP-hard (Lathrop 1994; Godzik 1996). Despite the significant progress, current methods produce different results. A one-target function cannot be defined to evaluate an alignment; therefore, two criteria for the similarity between three-dimensional structures have been developed, namely root mean square deviation (RMSD) and number of equivalent (aligned) positions (N_e). The “right” alignment is some-where on the two-dimensional space representing relations between those two values, RMSD and N_e. All the methods of comparative structure analysis are facing this problem and are developing different “heuristics” to find a proper balance between lower RMSD and a larger number of aligned positions (Shindyalov and Bourne 1998). This leads to different alignments for the same proteins; consequently, the methods do not produce the same results. For example, the overlap between the alignments from the popular methods FSSP/DALI and CE is just 40% (Shindyalov and Bourne 2000); therefore, there are still many unknowns in the structural alignment problem. Taking into account the above, we thought it would be useful to approach this problem from a different point of view.

We present here an application of a different mathematical model to produce structural alignments. Similarity between protein structures has been analyzed using three-dimensional Delaunay triangulation patterns (Delaunay 1934) derived from the backbone representation of protein structure. The Delaunay triangulation (DT) has been known for a long time in mathematics, computer science, protein studies, and many other scientific fields. DT is topologically linked to Voronoi tessellation, originally developed by Voronoi (1908) and first applied to proteins by Richards (1974). Since then, both tessellations have been used successfully in the calculation of standard volumes of protein residues, characterizing protein–protein interactions, understanding protein motions, analyzing cavities in protein structure (Chothia 1975; Finney 1975 Finney 1977; Gerstein et al. 1994; Harpaz et al. 1994), and in the analysis of volume of atoms on the protein surface (Gerstein et al. 1995). Delaunay simplexes were also used to develop four-body potential for statistical analysis of protein structures (Singh et al. 1996) and for studies on protein-specific correlations to protein stability changes by hydrophobic core mutations (Carter et al. 2001).

Presented here is a study on the application of the three-dimensional DT model for the structural alignment of proteins, based on our novel TOPOFIT method, which superimposes protein structures by identification of the common volume subgraph of Delaunay triangulation.

Results and Discussion

The first result is that the TOPOFIT method actually identifies proteins with similar structure (see Fig. 1 ▶). It was unobvious ab initio that the Delaunay tessellation patterns would be the same or similar for slightly different proteins (e.g., those which have some movements, shifts of secondary structure, mutations, etc.). The initial idea of TOPOFIT was to test whether proteins retain their unique internal interconnectivity between amino acids, the spatial distribution and the network of the interresidue contacts in their family of structural neighbors. The results presented below show that structurally related proteins do share common volumes with the same topological substructure. This common volume can be used to find and evaluate those relations.

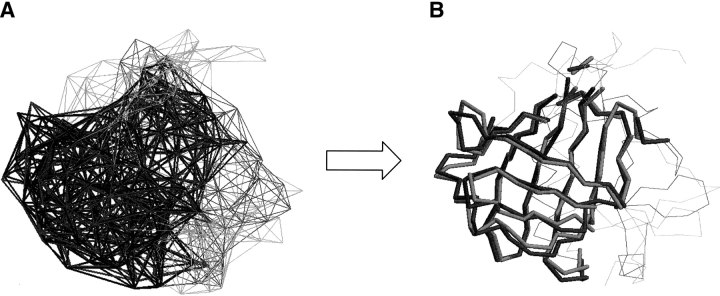
Figure 1.

(A) An example of the TOPOFIT superimposition between two protein structures: Neutrophil gelatinase (PDB code 1qqs chain A) is shown by dark gray and β-lactoglobin (PDB code 1beb chain A) is in light gray. Number of aligned points is 109 with RMSD = 1.4 Å; the superimposed tessellation contacts are in bold. (B) The resulting structural alignment of Neutrophil gelatinase in dark gray and β-lactoglobin in light gray.

Topomax point on the RMSD/N_e curve

As was mentioned in the introduction, the comparison of two protein structures requires two parameters: RMSD and N_e (number of equivalent residues). Most methods try to balance between lower RMSD and larger alignment length. Usually the complete dependence (a curve) of RMSD via N_e is necessary for an evaluation of a structural alignment. The major result of the TOPOFIT method is a feature point on this curve, a “topomax” point, which reflects the beginning of the topological mismatch.

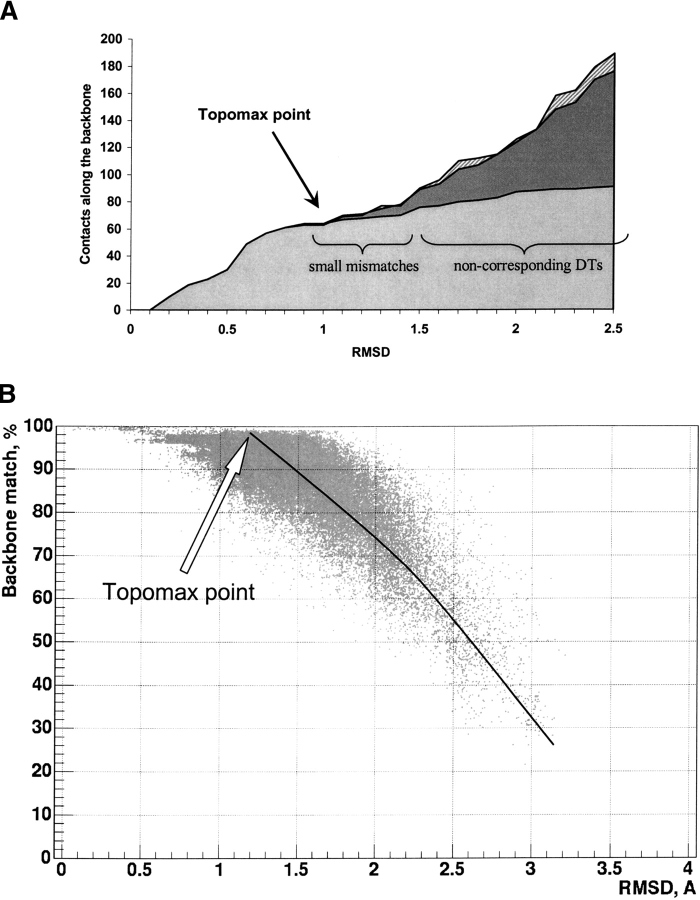
The conformity of the backbone topologies in the tessellation patterns has been analyzed for the growing seed of the structural alignment. An example of the seed growth is shown on Figure 2A ▶. One can see that the number of aligned positions (N_e) is growing along with an increase of the joint distance (RMSD; see Materials and Methods), and more and more aligned residues are associated with the seed. The backbone contacts in both proteins match each other from the beginning, but their topological correspondence remains the same only until some point, after which the topologies of the backbones start to diverge. The divergence begins at RMSD 1–1.5 Å (pointed by arrow in Fig. 2A ▶) at the joint distance of 3 Å. The topology of the growing seed is equivalent in both compared proteins until this point, and then there is a small area when the topology is almost the same with some small number of mismatches. After this area, the topology starts to deviate dramatically: The growing seed includes more and more mismatches; backbone contacts in one protein correspond to nonbackbone contacts or do not have correspondence with any contacts in another protein at all. The number of mismatches increases rapidly up to 50%, which is shown as the darker region in Figure 2A ▶. We will refer to the place on the RMSD/N_e curve where topology starts to deviate as a topomax point, a point on the curve where the growing seed of topologically equivalent spatial volumes reaches its maximum.

Figure 2.

(A) An example of the dependence of the number of matching backbone contacts vs. RMSD in the growing seed of the superimposition between two proteins 1bt3 chain A and 1hc2. The proteins have been aligned step by step with different values of the joint distance parameter ranging from 0.5 to 4.5 Å with the step 0.1 Å. The resulting RMSD and the number of the backbone contacts of the growing seed are plotted on the curves. The number of contacts in the first protein is shown by the dashed area and in the second protein by the dark gray area, and the number of matched contacts in both proteins is shown by the light gray area. (B) Correspondence of the backbone matches between aligned proteins for different RMSD of the alignments during the growth of seeds. The test set of 2905 protein pairs (see Materials and Methods) has been processed by TOPOFIT at different values of joint distance from 1.0 to 7.0 Å by steps of 0.5 Å. All the alignments with alignment size larger than 30 residues and Z-score >3.0 have been collected, resulting in a total of 87,618 seeds shown as dots. Each dot represents the resulting RMSD of the superimposition at a particular joint distance and percentage of matching backbones between aligned proteins.

The conformity of the backbone topology shown in Figure 2B ▶ has been checked on a larger scale for a test set of 2905 protein pairs (see Materials and Methods), which includes proteins for all-α, all-β, and α/β classes of protein structures and their structural neighbors. Each protein pair has been aligned several times by the TOPOFIT method at joint distances ranging from 1 Å to 7 Å by 0.5 Å steps, and all the statistically significant seeds for the pair have been collected according to Z-score and the size. The distribution of the matching backbones versus the resulting RMSD of the alignment for each seed is shown in Figure 2B ▶ for a total of 87,618 seeds. The same behavior of the growing seed and the presence of the topomax point (as in the example in Fig. 2A ▶) have been observed for all proteins from different structural classes, which is clearly seen from the plot in Figure 2B ▶. The location of the topomax point varies from protein to protein with the distribution of RMSD value ranging from 0.7 to 1.6 Å, with an average of 1.2 Å. After the topomax point, the topological mismatches between backbones are dramatically increasing and the alignments at 3 Å of RMSD already contain approximately 50% topological mismatches.

It should be noted that the topomax point on the RMSD/N_e curve defined by the TOPOFIT method is actually not a point in a geometrical sense, it is rather a small region where the topology starts to deviate. In this area there are a small number of mismatches (see Fig. 2A ▶) and the graph volumes in both proteins are almost the same. The existence of this small region is logical because protein structures are defined by experiment and have some experimental errors, which produce small deviations in sensitive DT patterns. The DT patterns can also be affected by small conformational movements and mutations present in the structural neighbors. Taking into account the small region of mismatches, based on the results from Figure 2 ▶, we consider it reasonable to identify the topomax point at a position with up to 80%–85% matches, allowing up to 15%–20% mismatches, which corresponds to the joint distance parameter of 3 Å.

It is particularly worth emphasizing that the topomax point is not an input threshold in the algorithm; it is not defined a priori. This feature point has been obtained as an output result of the comparison of the topological patterns between two structures and the determination of maximal common topologically invariant volumes between the structures. Therefore, the TOPFIT method presents an objective way to identify common parts of proteins that are identical in the topology of the DT patterns.

Evaluation of the TOPOFIT method to identify structural neighbors

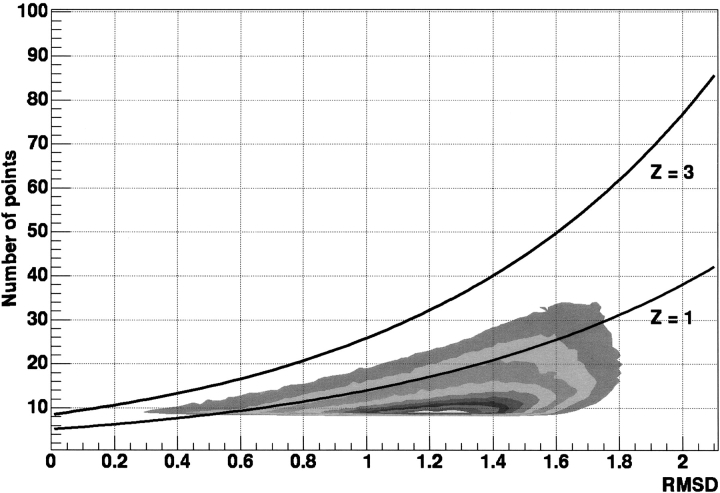
The statistical significance of the TOPOFIT alignments has been evaluated on a data set of 10,731 structurally nonrelated protein pairs where 1,393,272 seeds have been extended as described in Materials and Methods, and a Z-score to identify structural neighbors has been derived (see Fig. 8 ▶ below).

Figure 8.

Frequency distributions of RMSD and N_e for TOPOFIT alignments for structurally nonrelated proteins in the nonredundant set. The set consists of 147 protein chains selected from the representative list excluding all the proteins with duplicated or missing atoms, structural gaps, or with a total number of residues lower than 100 (Hobohm et al. 1992). All these proteins share a sequence identity below 25% and have been solved by X-ray crystallography with a resolution better than 3.0 Å. We evaluated 10,731 protein pairs and 1,393,272 seeds have been extended. Frequency distribution is represented as levels of the same frequency value. There are also curves representing levels at different Z-scores for the TOPOFIT method (see text).

To evaluate the sensitivity of the TOPOFIT method to detect structurally related proteins, the test set of 2905 proteins was compiled from the lists of known structural neighbors detected by the popular methods DALI and CE (see Materials and Methods). Those representatives and their structural neighbors of the different structural classes have been processed by the TOPOFIT method.

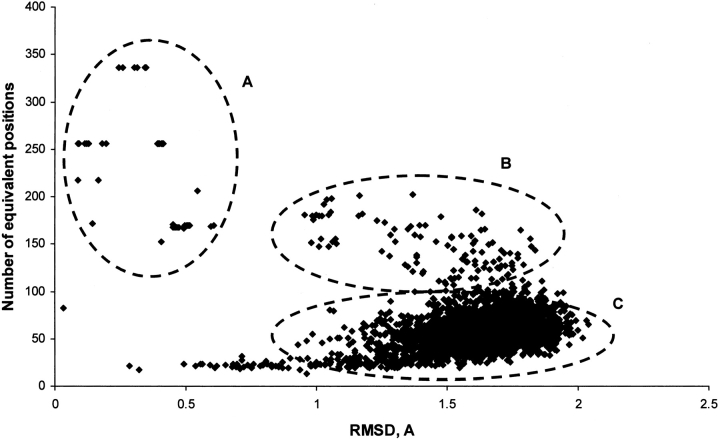
The results of the TOPOFIT alignments are shown in Figure 3 ▶ on the RMSD/N_e plot. The majority of the alignments are distributed from 1 to 2 Å of RMSD while few alignments are found at RMSD equals 2 Å or more. The distribution also shows three distinct areas of the structural neighbors. An initial analysis of the contents of these three clearly separated areas suggests the following: In area A, an exact match, the pairs include matches between mutant proteins, different crystal forms of the same protein or its closest homologs; in area B, structural subfamily, a strong correlation of two or more domains between proteins is present; in area C, structural superfamily, proteins with at least one similar domain structure up to 100 residues are present, and this area contains the majority of all the alignments. A more detailed analysis of the contents in the observed areas is one of the future directions in the research by the TOPOFIT method.

Figure 3.

Distribution of RMSD and N_e values of the TOPOFIT alignments for structurally related proteins. The alignments were calculated for proteins representing different structural classes against the test set of 2905 proteins (see Materials and Methods). All the TOPOFIT alignments show RMSD better than 2 Å. The distribution also shows three distinct areas of the structural neighbors, which are circled by the dashed ellipses: A, exact match; B, structural subfamily; and C, structural superfamily.

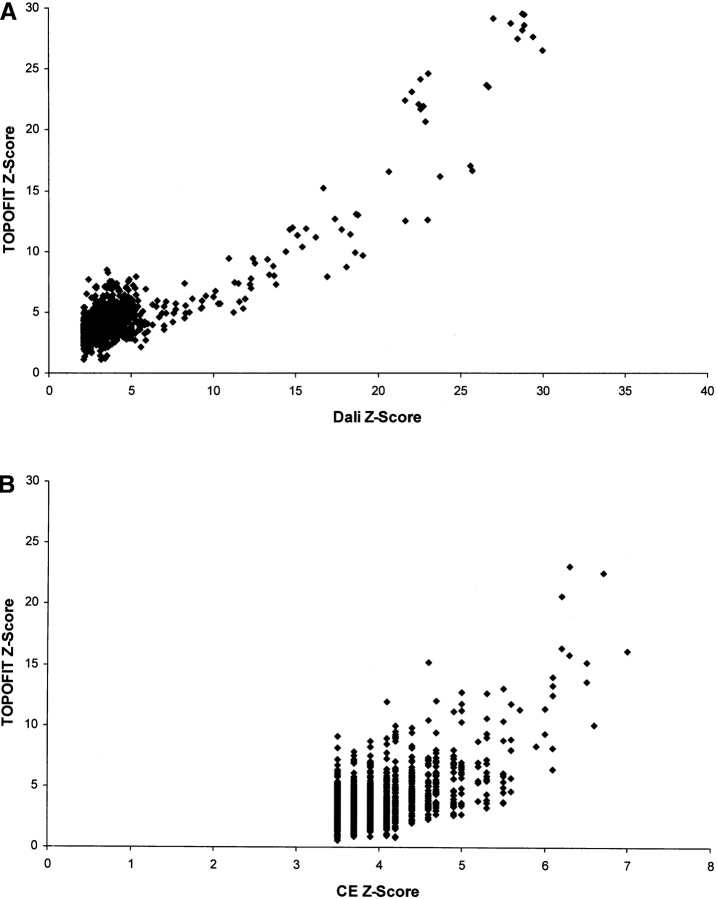
A comparison of the above TOPOFIT alignments with the original results from other methods has also been performed (Fig. 4 ▶). The results on the test data set show that the Z-scores derived from the TOPOFIT method strongly correlate with the Z-scores from the DALI and CE methods. TOPOFIT correlates significantly with other methods when matching protein pairs are highly related by structure (with Z-score >4.5; Fig. 4A,B ▶). The correlation between methods is not seen clearly at lower Z-scores, which is probably a “Twilight Zone” for all the methods. There are always structural neighbors that one method finds and the others miss, which is a common feature for all the methods (see, e.g., O’Hearn et al. 2003). Therefore, the ability of the TOPOFIT method to identify structurally related proteins is similar to other popular methods. TOPOFIT picks slightly different residues and the size of the TOPOFIT alignments is usually smaller. The performance of the TOPOFIT algorithm has also been compared on a set of “difficult” structures (Fischer et al. 1996). The results in Table 1 show that the TOPOFIT method also identifies these difficult cases. An illustration of structural alignments by different methods is shown in Figure 5 ▶, which clearly shows that the overlap regions of structural similarity identified by the different methods are very similar (many other examples can be found from our public TOPOFIT server at http://mozart.bio.neu.edu).

Figure 4.

(A) Correlation of the Z-scores between the TOPOFIT and DALI alignments. (B) Correlation of the hits between TOPOFIT and CE methods. Each point on the graph represents a structural alignment of two protein structures. The correlations are calculated based on the structural alignments of the query proteins of different structural types against the test set of 2905 proteins (see Materials and Methods).

Table 1.

Comparison of the alignments of difficult structures as cited in Fischer et al. (1996) and Shindyalov and Bourne (1998) by different methods

PDB code	PDB code	TOPOFIT	Dali	CE
1fxi:A	1ubq:_	55/1.6	60/2.6	64/3.8
1ten:_	3hhr:B	81/1.4	86/2.0	87/1.9
3hla:B	2rhe:_	47/1.6	70/3.2	82/3.6
2aza:A	1paz:_	72/1.7	81/2.5	85/2.9
1cew:I	1mol:A	73/1.6	81/2.3	74/2.1
1cid:_	2rhe:_	69/1.5	97/3.2	96/3.4
1crl:_	1ede:_	143/1.9	211/3.5	219/3.8
2sim:_	1nsb:A	207/2.0	291/3.3	295/3.2
1bge:B	2gmf:A	68/1.7	95/3.2	107/4.0
1tie:_	4fgf:_	88/1.6	114/3.1	128/3.2

The data for DALI and CE alignments were obtained from the publicly available databases. In cases when compared structures were not present in the databases, Web accessible DALI and CE services were used to compare structures. Structures are identified by their PDB code and chain. The format of the superimposition results is “N_e/RMSD.”

Figure 5.

An example of the structural alignments produced by different methods. Proteins are identified by their PDB codes, 1ngl chain A and 1beb chain A, and have only 17% sequence identity. Each superimposition is evaluated by the number of equivalent points/RMSD. Common parts of the two proteins used in the superimposition are displayed in bold. The orientation of one structure in each picture is kept constant. All methods find this match with high scores: TOPOFIT gives 97/1.7, CE gives 139/3.2, and DALI gives 136/3.4 (CE and DALI alignments were obtained using CE and DALI Web services).

Structural comparison of active and binding sites

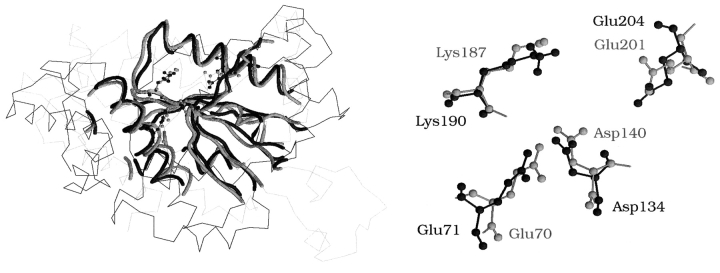
The ability of the TOPOFIT method to produce alignments with RMSD <2 Å allows one to use the structural superimpositions from TOPOFIT not only for the fold recognition and structural classification of proteins, but also for more detailed analysis of the functional sites. Usually amino acids are tightly packed in protein structure with an approximate distance between two neighboring residues of 4–7 Å. Therefore, when two structures are aligned at RMSD of 4–5 Å (which is the commonly accepted value in many structural alignment methods) it is not always feasible to associate the proper residues in three-dimensional space. The active site residues from one protein can be spatially misaligned with the residues surrounding the active site in the other protein, which has a dramatic effect on active/binding site studies, because the mismatch of functional residues from one protein with the neighboring residues from another will mislead functional characterization. TOPOFIT alignments with RMSD less than 2 Å might provide an insight on the functional comparison. An example in Figure 6 ▶ shows the active sites of two endonucleases (PDB codes 1fiu chain A and 1cfr) aligned by TOPOFIT. The overall structural alignment places the functional site residues in the endonuclease active sites in close proximity with overall RMSD <2 Å. The active site residues can be unambiguously correlated between the two proteins, making it possible to study the roles of the catalytic residues and compare the structural basis for functional activity of the endonucleases.

Figure 6.

An example of the quality of the overall structure superposition for the active site comparison. View of superimposed residues in the active sites of two endonucleases (PDB codes 1fiu chain A and 1cfr). The structure 1fiu is in green and 1cfr is in violet. Alignment of protein structures is shown on the left, and superposition of the active site residues is shown on the right in “ball and stick” mode. TOPOFIT gives the superimposition with the distances between atoms in corresponding active site residues less than 1 Å.

Conclusions and future directions

Superimposition of protein structures by the common structural subgraph-volume method (TOPOFIT) presents several new results:

1. Structurally similar proteins have a common volume with invariant three-dimensional tessellation patterns including interresidue contacts. The conformity of these patterns can be used as a measure of structural similarity between proteins.

2. The TOPOFIT method identifies this common volume as a feature point on the RMSD/N_e curve of the growing seed of the alignment, a topomax point, where the alignment has a maximal number of aligned positions with topologically the same patterns between the compared proteins. The topology in these common volumes are equivalent between proteins until the topomax point, whereas the alignments after the topomax point (with higher RMSD) have a significant number of topological mismatches; therefore, the common subgraph volume, defined at the topomax point by the TOPOFIT method, represents a topological invariant.

3. It is shown that the topological invariants defined by TOPOFIT have a good geometrical correlation with low RMSD <2Å for the resulting structural alignments.

The TOPOFIT structural alignments will be used for a general classification of protein folds based on the topological structural invariants across the structural families, detection of the variations in the topology between proteins, which will be provided by automated large-scale calculations, and for studying sequence–structure features and mapping variations in gene sequences onto structural families of the encoded proteins. A strong geometrical correlation between the topological invariants extends the usability of the method, for example, to more detailed comparative analysis of the functional sites between proteins, and for active and binding sites mapping, characterization, and classification, which will be useful for biomedical studies. The common subgraph volumes can also be used to help better understand the problem of protein folding and protein stability, which will result in applications of the TOPOFIT methods for comparative modeling of proteins. This is based on identification of the common graph volume by TOPOFIT methods derived from the alignment of target sequence with one or more structural templates, producing structural models. Therefore, the TOPOFIT method will be insightful for a wide range of protein studies.

Structure comparison using the TOPOFIT method is implemented in our integrated multiple structure-sequence viewer, Friend (Abyzov et al. 2003), and also publicly available from our TOPOFIT Web server at http://mozart.bio.neu.edu.

Materials and methods

Delaunay tessellation (DT) of protein structures

The Delaunay tessellation (Fig. 6 ▶) can be uniquely derived from more familiar Voronoi cells (Schuster and Stadler 1999). Given a finite set of points in A ⊆ Rⁿ, the Voronoi cell of x ∈ A is

(1)

where d denotes the Euclidean distance in Rⁿ. The nearest neighbor set N(x) of x ∈ A is the set of points that are closest to x in Euclidean distance. For each point u ∈ Rⁿ define nb(A, u) as the set of points x′ A\{u}. A point v ∈ Rⁿ is a Voronoi vertex (corner of the Voronoi cell) if |nb(A, v)| is maximal over all nearest sets. The Delaunay cell of v is the convex hull conv(nb(A, v)). The complex (or triangulation) of A is therefore a partition of the convex hull conv(A) into the Delaunay cells of its Voronoi vertices. The Delaunay complex is derived from the Voronoi diagram in the sense that there is a natural bijection between the two complexes that reverses the face inclusions. Apart from degenerate cases, in three-dimensional space each Delaunay cell is a tetrahedron with four points of A at its corners. This procedure therefore defines 4-edges (sets of 4 “mutually adjacent” vertices) in a (protein) structure in a parameter-free way. The 2-edges of a contact graph and 3-edges can, of course, be derived directly from the tessellation by considering subsets. We use C_α atoms of the backbone chain of a protein for computation. The tessellation has been calculated using QHULL (Barber et al. 1996).

Therefore, the Delaunay tessellation of protein structure uniquely identifies close spatial neighbors to each particular point. This is the most important feature of DT used for the TOPOFIT method.

Contact graphs

The three-dimensional structure of a linear biopolymer, such as a protein, can be approximated by their contact structure, that is, by the list of all pairs of monomers that are spatial neighbors. Contact structures of polypeptides were introduced by Ken Dill and coworkers in the context of lattice models of protein folding (Chan and Dill 1990,Chan and Dill 1991). The structures of proteins form a special class of contact structures. We assume that the monomers, amino acids alike, are numbered from 1 to n along the backbone. For simplicity we shall write [n] = {1, . . . , n}. The adjacency matrix of the backbone B has the entries B_i,j+1 = B_i+1,i = 1, i ∈ [n − 1]. In a more general context, polymers with cyclic or branched backbones could be considered. A contact structure is represented by the contact matrix C with the entries c_ij = 1 if the monomers i and j are spatial neighbors without being adjacent along the backbone, and c_ij = 0 otherwise. Hence, C_ij = 0 if |i − j| ≤ 1. Note that both B and C are symmetric matrices. We define the (contact) diagram ([n],Ω) to consist of n vertices labeled 1 to n and a set of arcs that connect nonconsecutive vertices. The diagram is simply a graphical representation of the contact matrix. As an example, we show the conventional backbone diagram of the protein crambin together with its discretized structure represented by the contact matrix and contact graph (Fig. 7 ▶). The contact graph has the adjacency matrix A = B + C. The contact graph is used as an internal two-dimensional representation of protein contacts and is useful in many intermediate calculations.

Figure 7.

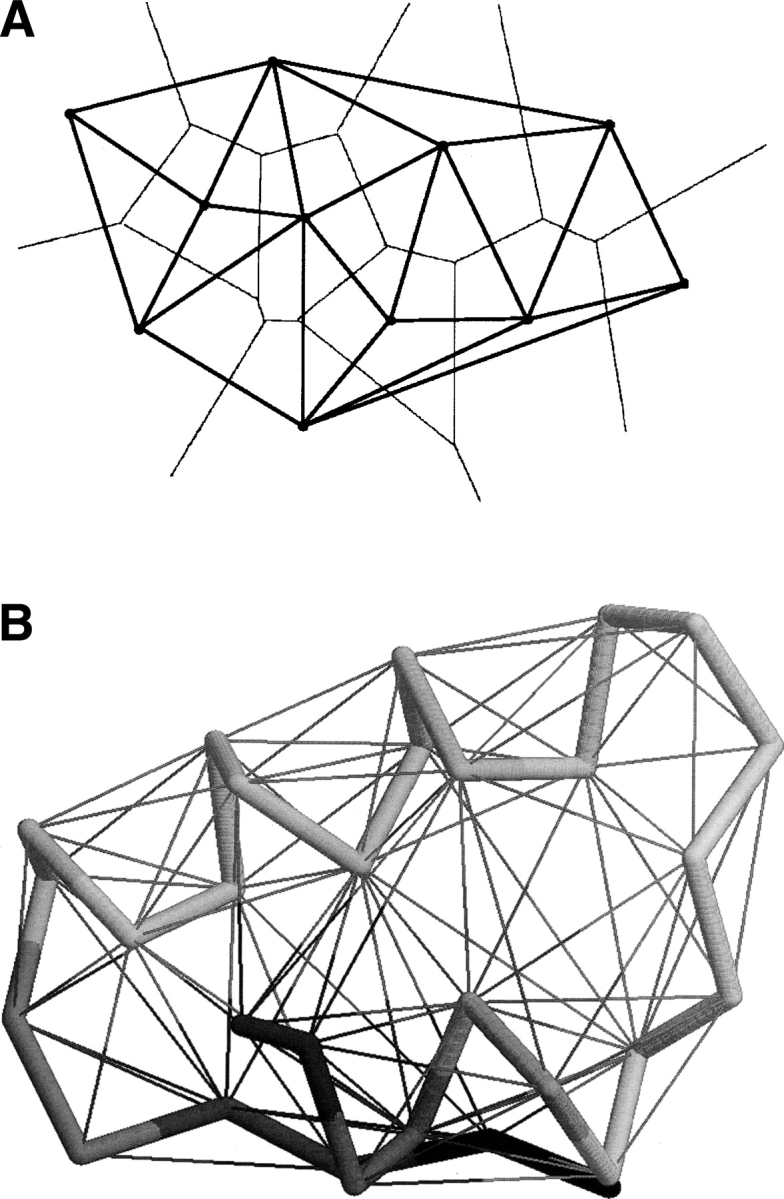
An example of a Delaunay tessellation (A) set of points in two-dimensional space. The Delaunay tessellation is shown by thick lines and the corresponding Voronoi polihedra, by thin lines. (B) DT of C_α atoms of crambin (PDB code 1crn) in three-dimensional space. The Delaunay tessellation is shown by thin lines. The backbone of the protein is displayed by thick lines and colored from N terminus to C terminus by gradually changing color.

We define the common topological volume as a common subgraph between contact graphs approximating different protein structures. The subgraph volume can be one tetrahedron or a set of neighboring tetrahedrons in the Delaunay tessellation representing one continuous volume. To superimpose two DT patterns from two proteins, one protein is fixed and a transformation is applied to the other, which is determined in three-dimensional space by a rotation matrix and translation vector. To superimpose corresponding points in the subgraph, the least-squares fit method (Kabsch 1978) is used and the superimposition is evaluated by RMSD.

The comparison algorithm

Consider two proteins labeled A and B. The superimposition algorithm has three steps. The first step is a Delaunay tessellation of points representing the proteins. The set of tetrahedrons for proteins A and B we call T_A and T_B, respectively. The second step includes initial classification of the tetrahedrons by shape, volume, and backbone topology and then systematic pairwise superimposition of all the tetrahedrons inside the different types in both proteins. For each tetrahedron t_a of a particular type from the protein A, the best matched tetrahedron t_b of the same type from the protein B is found. The pair of tetrahedrons (t_a,t_b) is called a “seed” and is used in the next step of the algorithm. The goal of the third step is to iteratively add as a many points to the seed as possible. The seed extension is a volume extension algorithm, not a backbone extension; each step adds one or more new tetrahedrons to the growing seed. Each new pair of points is chosen from the neighboring DT pattern by the topology and a restriction parameter called “joint distance,” D. Because points are always added to both growing subgraphs, they can always be superimposed and the lowest RMSD is recalculated. If there are pairs of points (x_a,x_b), x_a ∈ t_a, x_b ∈ t_b with superimposition distance d′x_a,x_b) > D, then they are excluded from t_a and t_b. The number of matching tessellation contacts is also evaluated for all points. The match is defined when the contacts are present in both proteins and they are the same in type; either both are backbones or both are interresidue contacts, if not it is a mismatch.

The algorithm stops when there are no more new points or when the number of mismatches exceeds the threshold (15%); in other words we grow the seed a little further from the beginning of the topological mismatch.

Collecting a test set for different structural classes

The structural neighbors of seven proteins representing different structural classes have been collected up to the lowest scores from current popular methods DALI and CE, resulting in a total of 2905 proteins. PDB codes for the query proteins are 1bt3 chain A (mainly α helices), 1at0 (β sheets), 1hxn (mainly β sheets), 1huw (α helices), 1qj4 chain A (β sheets and α helices), 1zin (α helices and β sheets), and 451c ( αhelices). The results from DALI were obtained from their Web server (Holm and Sander 1996), and the results of the CE calculations were downloaded from the CE Web site (Shindyalov and Bourne 2001).

Statistical significance of TOPOFIT alignments

To evaluate the statistical significance of the TOPOFIT structural alignments and derive a scoring function for identification of structurally related proteins, the frequency distribution for N_e and RMSD for a set of structurally nonrelated proteins has been analyzed (a second test set). All-to-all alignments for a known nonredundant set of nonhomologous proteins (Hobohm et al. 1992) have been calculated. To minimize bias, only nonoverlapping seeds were extended. The frequency distribution of 10,731 alignments is shown in Figure 8 ▶ on the RMSD/N_e plot. The observed frequency distribution has been analytically approximated. The distribution of N_e for each value of RMSD was approximated by Gaussian distribution with mean μ(RMSD) and σ(RMSD) depending on RMSD. The parameters μ and σ were obtained from the least-squares fit of the experimental distributions for each RMSD. The Gaussian approximation describes the data very well: Typical values of χ² for the approximation are ranging from the 0.95 to 1.2 per degree of freedom. The dependences μ(RMSD) and μ(RMSD) + σ(RMSD) were approximated by exponents:

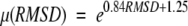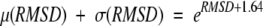For a given RMSD and N_e the Z-score was calculated as deviation of N_e from the Gaussian average μ normalized to the Gaussian σ

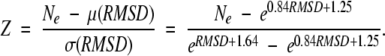The obtained relation between N_e and RMSD for a Z-score equal to 3 is shown in Figure 8 ▶. Alignments above Z-score 3 are considered to have a statistically significant structural correlation.

The complexity of TOPOFIT algorithms is n × m; the calculation varies significantly with an average of 15 sec per alignment based on the data set in Figure 3 ▶ on a 2.4-GHz Linux box with 512 Mb of memory, which is comparable to other methods.