Some fundamental aspects of building protein structures from fragment libraries

Abstract

We have investigated some of the basic principles that influence generation of protein structures using a fragment-based, random insertion method. We tested buildup methods and fragment library quality for accuracy in constructing a set of known structures. The parameters most influential in the construction procedure are bond and torsion angles with minor inaccuracies in bond angles alone causing >6 Å CαRMSD for a 150-residue protein. Idealization to a standard set of values corrects this problem, but changes the torsion angles and does not work for every structure. Alternatively, we found using Cartesian coordinates instead of torsion angles did not reduce performance and can potentially increase speed and accuracy. Under conditions simulating ab initio structure prediction, fragment library quality can be suboptimal and still produce near-native structures. Using various clustering criteria, we created a number of libraries and used them to predict a set of native structures based on nonnative fragments. Local CαRMSD fit of fragments, library size, and takeoff/landing angle criteria weakly influence the accuracy of the models. Based on a fragment’s minimal perturbation upon insertion into a known structure, a seminative fragment library was created that produced more accurate structures with fragments that were less similar to native fragments than the other sets. These results suggest that fragments need only contain native-like subsections, which when correctly overlapped, can recreate a native-like model. For fragment-based, random insertion methods used in protein structure prediction and design, our findings help to define the parameters this method needs to generate near-native structures.

By predicting the regular secondary structure elements, Corey and Pauling helped to simplify the complexities of a protein fold into a collection of smaller, more tractable parts (Pauling and Corey 1951; Pauling et al. 1951). The theoretical community did not immediately accept and apply this idea that a protein’s fold is made up of fragments (Johnson et al. 1994). Not until a method using known folds to aid in structure refinement (Jones and Thirup 1986) was developed that fragment-based structure prediction methods began being developed. The underlying approach uses parts of known proteins, or protein fragments, as the building blocks to construct and predict new protein structures. Several groups independently of each other developed such fragment-based structure prediction methods that showed a great deal of promise (Jones and Thirup 1986; Claessens et al. 1989; Unger et al. 1989; Simon et al. 1991; Levitt 1992; Sippl et al. 1992; Wendoloski and Salemme 1992; Bowie and Eisenberg 1994). Continual development of this approach, refinement of fragment libraries (Han et al. 1997; Kleywegt 1999), the increase in structural information provided by the Protein Data Bank (Berman et al. 2002) eventually produced an algorithm, Rosetta (Simons et al. 1997), that showed significant and consistent improvement at predicting new protein folds (Simons et al. 1999a; Bonneau et al. 2001) as well as success in accurately designing new folds (Kuhlman et al. 2003). Effectively, Rosetta splits structure prediction up into two steps: generation of a set of models, and selection of the nearest native structures. Although Rosetta certainly generates ensembles of near native structures, especially for globular helical proteins (Bonneau and Baker 2001), the advancements made by the Rosetta algorithm have primarily been in potential functions and filtering schemes for selecting correct models (Plaxco et al. 1998; Shortle et al. 1998; Simons et al. 1999b; Bonneau et al. 2002; Ruczinski et al. 2002; Schueler-Furman and Baker 2003; Tsai et al. 2003). Improvements to structure generation have been more difficult to address because they involve more fundamental issues such as adequate sampling of conformational space. As one step towards understanding these issues, we have studied some of the factors that limit the accuracy of fragment-based structure generation methods.

An effective structure generation method should produce a set of candidate models highly populated with native like members, so that the selection method has a higher probability of choosing a near native model. Limitations to generating near-native structures using a fragment-based method depend upon two factors: the construction procedure and the fragment library. Obviously, given values matching a particular target structure, the construction procedure should be able to exactly recreate a target protein’s structure. Because the construction procedure also needs to build thousands of models to adequately sample conformational space, the level of accuracy is usually balanced against speed in building models. Approaches satisfying this balance must make certain approximations. Usually, structures are built in torsion angle space using a standard set of bond angles and bond lengths for the protein main chain atoms with a centroid replacing the entire side chain. The centroid approximation reduces the total number of atoms per residue to exactly five (four main chain and the centroid) from an average of 10. Also, using torsion angles instead of Cartesian coordinates reduces the minimum number of parameters needed to properly place a residue to three torsion angles (φ–ψ–ω, since ω is not always exactly 0° or 180°) from nine Cartesian coordinates (x, y, and z of three atoms—N, Cα, and C). Another significant difference between building with torsion angles versus Cartesian coordinates is the reliance of torsion angles buildup routines on an ideal/regular backbone geometry, which is usually the values calculated by Engh and Huber (1991). Although backbone regularization is well accepted in protein structure refinement (Linge et al. 2003; Wedemeyer and Baker 2003), and validation (Lovell et al. 2003), the effects of idealization on backbone accuracy have not been rigorously assessed in methods predicting protein structure. In this study, we compare building models using torsion angles versus Cartesian coordinates to find the limitations of each method in adequately constructing native-like structures.

The fragment library also sets limits to how well a fragment-based method can recreate native protein structures. For ab initio predictions, fragment libraries are constructed to sample as many protein folds/environments as possible. From such libraries, the standard procedure is to select a subset of fragments that best matches the native fragment in order to build near-native models. Therefore, a number of fragments (usually in the hundreds) are selected to cover every stretch of residues in the target protein (based on the size of the fragment). Optimally, one if not most of the selected fragments closely matches the same stretch of amino acids or fragment in the native structure. As a test of the coverage necessary for a fragment library, recent work has shown that fragments from a fragment library clustered based on shape can closely approximate the local structure of proteins (Hunter and Subramaniam 2003). In another quite rigorous study, clustering fragments using a k-means method and using an optimized building procedure further showed that fragment library size does not need to be very large to approximate local structure as well as construct near native models (Kolodny et al. 2002). To find the best model structure from their fragments, both of these studies used an optimized method (fragment addition guided by the native structure) to generate their models. We wanted to test fragment libraries under the same conditions used in predictive studies (where the target is not known). Therefore, structures were built using only nine residue fragments (9mers) and with a search algorithm similar to the one used by the Rosetta method (Simons et al. 1997). This algorithm is meant to test the capabilities of each fragment library under conditions similar to those encountered in ab initio prediction. It consists of randomly inserting fragments into a protein, and comparing to native after each insertion (see Materials and Methods). Using this approach, we investigated what characteristics of a fragment are required to accurately rebuild a native structure. The common assumption is fragments in a library that are closer to the native fragment (local similarity) will generate more native-like models (global similarity). The standard measure of this similarity is backbone α-carbon root-mean-squared deviation or CαRMSD. For local structure, we find that similarity in CαRMSD shape is part of the criteria, but takeoff and landing angles also play an important role. Another important aspect of a good fragment library is how well do its member’s cover fold space? A number of fragment libraries that differed in coverage and complexity were created to test the depth required to accurately reproduce native backbones. Overall, these tests of the construction procedure and fragment library help to understand the limitations in using a fragment-based method for the prediction and design of protein structures.

Results

Evaluating construction procedure in torsion angle space

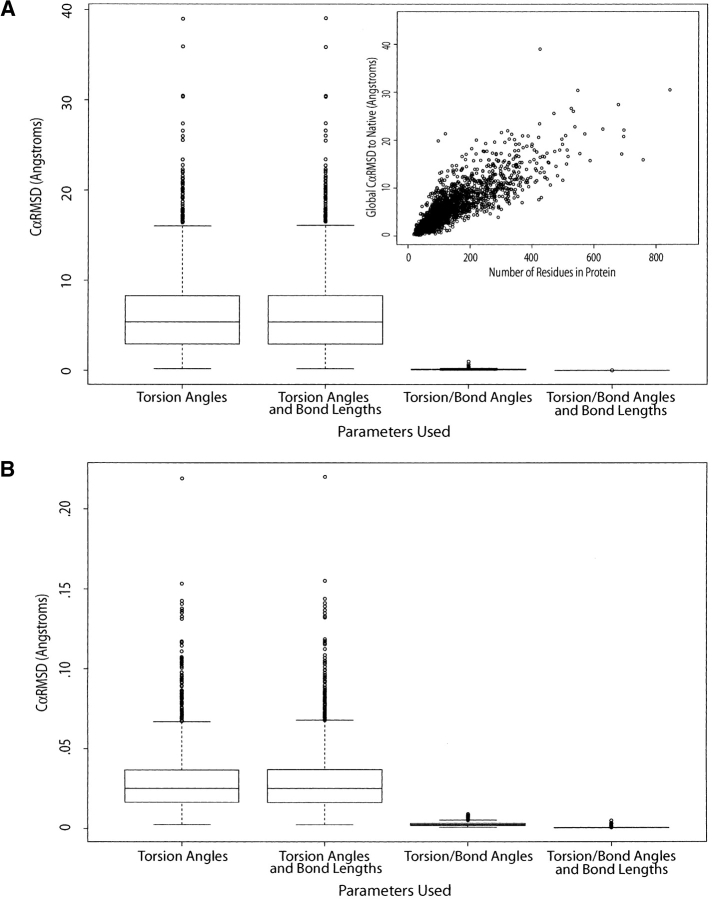
Historically, torsion space has been used to reduce the memory requirements of building up a protein backbone by eliminating six parameters (nine Cartesian coordinates to three torsion angles). This decrease in parameters was also assumed to provide an increase in speed upon construction of a peptide backbone. In this section, we show the results from a test of the accuracy of torsion angle space by using increasing levels of information about the native protein to rebuild its structure. A list of 1894 native proteins were taken, in part, from previous work (Kolodny et al. 2002), and will be further referred to as the Kolodny set. Each protein in the Kolodny set was rebuilt based on three levels of information about the native structure, and standard or ideal values for each residue (Engh and Huber 1991) were used in the absence of native bond angles and bond lengths (Ramachandran et al. 1974). Figure 1A ▶ shows the distribution of backbone deviations for each of the builds over the Kolodny set. First, only native φ–ψ–ω torsion angles were applied. The average CαRMSD of rebuilt structures to native was 6.2 Å and highly dependent upon the length of the protein (Fig. 1A ▶, inset). The addition of native bond lengths did not improve the accuracy. The addition of native bond angles helped tremendously and decreased the CαRMSD to 0.1 Å. As a control, all native torsion angles, bond angles, and bond lengths were applied in reconstructing the protein and the limit of our precision was reached at a CαRMSD of 0.0005 Å.

Figure 1.

Testing parameters used to build models with torsion angles. Both box-and-whisker plots indicate the effect on the global CαRMSD (between the original structure and reconstructed model) of specifying precise bond angles and bond lengths instead of using ideal values (Engh and Huber 1991). The R statistical computing environment was used to create all box-and-whisker plots (http://www.rproject.org/). The whiskers are set to either 1.5 the interquartile length or the most extreme data point if it is less. (A) Distribution of the CαRMSD for 1894 native protein structures rebuilt using increasing amounts of native information. The length dependence of the reconstruction routine is shown in the inset. In all of the box plots, we saw longer proteins near the high extremes of CαRMSD and smaller proteins near the lower extremes. (B) The same plot as the previous, except it was created using 1894 idealized protein structures.

We repeated the same reconstruction experiment on the idealized structures from the Kolodny set. Idealized structures are the result of minimizing the native backbone to ideal or standard bond angles and bond lengths by changing the backbone torsion angles. Although not all the bond angle and lengths converge to a single value, the distribution is much smaller. Because the idealized structures differ slightly from native (see Discussion), we compared our rebuilt structures to the idealized fold, because we used idealized torsion/bond angles and bond lengths. Results of the various builds are shown in Figure 1B ▶. Because of the standardization of bond angles and lengths, this allowed for a much more accurate reconstruction with less information. Using only the φ–ψ–ω torsion angles from idealized structure reproduced the idealized native structures to an average of 0.03 Å CαRMSD. Once again, adding bond length information does not improve the accuracy, although in this case it is to be expected as the bond lengths have been standardized. Adding the bond angle information makes the rebuilding more accurate by an order of magnitude to an average of 0.003 Å CαRMSD. Again, we reach the accuracy limit of 0.0006 Å CαRMSD when we use torsion angles with bond angle and length information.

Fragment libraries

In this section, we created a number of different fragment libraries to understand the qualities that make a fragment library optimal for building near-native models in the context of ab initio prediction. Each library and their results are shown in Table 1. To properly assess such attributes of a good fragment library, the construction procedure needs to (1) mimic realistic prediction conditions, and (2) provide a true measure of how well the fragment library approximates a native structure. To accomplish the first objective, we decided to use a method imitating Rosetta (Simons et al. 1997), where the scoring function is based on structural similarity to native. To address the second goal, our construction procedure built backbones in Cartesian space. Building in Cartesian space tests the absolute accuracy of a fragment library’s ability to reproduce a native structure. We also chose to construct proteins in Cartesian space because it provides a speed enhancement with rebuilds. Although it has been commonly thought that Cartesian space rebuilds are slower, we conservatively find an order of magnitude increase in speed. This increase in speed is a trade off with heavier requirements on memory: nine coordinates for three atoms instead of three torsion angles. A more detailed discussion explaining the reasons for this speed up is in Materials and Methods.

Table 1.

Clustered libraries loosely ordered by number of clusters

	C3RMSD cutoff/Å
Cluster library	Helix	Non-Helix	Number of clusters	Average local CαRMSD	Average global CαRMSD	Number <7 Å to native	Average CαRMSD of <7 Å structures
Unclustered	—	—	135,298	0.41	11.35	110	3.63
Unclustered IDLa	—	—	127,275	0.41	11.29	113	3.71
SC stringent	0.75	1.75	53,002	0.48	11.77	101	3.99
SC Loose	1.75	2.50	20,995	0.56	12.06	88	3.90
SC 2.50	2.50	2.50	11,300	0.62	12.27	81	4.11
SC 5.00	5.00	5.00	2308	0.78	12.49	78	4.11
SC 7.50b	7.50	7.50	1982	0.82	12.46	73	4.02
General clustering	2.25	2.25	187	1.08	13.37	110	5.63
To/L clusteringc	13.00		49,800	2.24	13.50	49	4.37

^a IDL: Idealized Native Proteins are used to create fragment library.

^b The SC 7.50 cluster basically had a cluster cutoff so large that all fragments sorted into their superclusters.

c Distance cutoff specific for To/L (Takeoff/Landing) clustering. The cutoff used for the summation of N₁ to N₁ when overlaying the ninth residue and C₉ to C₉ distances while overlaying the first residue was 13 Å (see Materials and Methods). All other libraries are created from native-fold proteins. Each clustered library is shown with its CαRMSD cutoff (exception To/L clustering; see above) in Ångstroms. The average local CαRMSD when selecting the best nonnative replacement fragment is shown as well as the average global CαRMSD from the best models generated for each of the target structures in the PISCES set when reconstructing using each library (see Materials and Methods). Both of these columns are reported in Ångstroms. Because our global average was so high and differences were so slight, we also counted the number of the target proteins where a model was generated under 7 Å as well as the average CαRMSD of these best models. The values are reported in the last two columns, respectively.

Our base or Unclustered fragment library was constructed from a more current set of 686 nonhomologous proteins structures chosen using the PISCES server (Wang and Dunbrack Jr. 2003), which is further referred to as the PISCES set (see Materials and Methods). This Unclustered library consists of 135,298 9mer fragments created from the PISCES set (Table 1). For the construction of models, the subset of fragments chosen to build models differed, but generally, the closest fragment to the native based on CαRMSD was chosen, where the native fragment was properly jackknifed out of the selection. Fragment libraries have been assessed on average local fit of the fragments to the native ones and the average global fit of the best model to the native structure using CαRMSD. Local fit indicates how close the replacement fragment is to the native fragment, while global fit reflects how well the construction procedure was able to use the fragment library in reconstructing the native backbone. Global fits were an average of the best model generated for each of the proteins in the PISCES set. If we used all 135,298 fragments, we found an average local fit of 0.41 Å for all the fragments and an average global fit of 11.35 Å of the best models to the PISCES set (Table 1). To test the effects of idealization on model building, we idealized the PISCES structure set (see Materials and Methods) to create an idealized fragment library (Unclustered IDL in Table 1). As explained in more detail in the methods, this library had fewer fragments because we had to break some structures up into domains to idealize them. Local and global fits were very similar for the idealized structures at 0.41 Å and 11.29 Å, respectively (Table 1).

In the following sections, we created a number of different fragment libraries from the above library based on certain criteria for clustering, such as backbone CαRMSD or takeoff/landing angles. The centers of clusters were used as representatives for selection of the subset of fragments used to build models. In this way, we were able to test a fragment library’s complexity as well its effects on building native-like models.

Backbone CαRMSD space clustering

Before clustering on CαRMSD, we first grouped the 9mer fragments into superclusters based on their secondary structure make up. We used a three-state secondary structure model (α-helix [H], β-sheet [E], coil [C]) as defined by PROMOTIF (Hutchinson and Thornton 1996). The distribution of each type of secondary structure from all 135,298 fragments was very even: 33% H, 32% E, and 35% C. Based on this three-state model, a possible 19,683 (3⁹) secondary structure combinations exist for each 9mer. However, the fragments from the PISCES set only populated 1982 (10%) out of the possible 19,683 superclusters. Of the unpopulated superclusters, 95% consisted of superclusters composed of all three secondary structure states occurring at least once in the 9mer fragment. These types of fragments containing all three secondary structure types were also scarce in the existing superclusters and populated only 7% of the 1982 groups. As expected, we did not find superclusters containing isolated helical residues such as CCC CCC CHC, because the definition of a helix requires four adjacent helical residues. Therefore, we only found consecutive helical residues of less than four at the beginning or end of a fragment. On the other hand, sheets and coils could occur individually. Of the existing superclusters, 63% contained an isolated sheet residue and 65% contained an isolated coil residue. Sheet and coil residues generally were more likely to be isolated next to coils and sheets, respectively, than in helical stretches (67% and 62% when isolated, respectively). Fragment libraries using these super-clusters are denoted with an SC for superclustering in Table 1.

Within each supercluster, we chose to cluster based on the CαRMSD between 9mer fragments. Table 1 gives a description of each of these supercluster (SC) libraries that were created by showing the relationship between the cutoffs used and the number of clusters produced. Increasing the CαRMSD cutoff allows for more members to be included in a cluster. Figure 2A ▶ is an example of one such cluster from the all β-strand supercluster (EEE EEE EEE). Every member of the cluster possesses the same bent shape, which is to be expected from a Cartesian space-based clustering method. As a validation of our clustering, we found results similar to previous studies (Han et al. 1997), which are to be expected, such as helical fragments cluster more tightly together than other fragments. Because of this more compact helical clustering, we set the cluster width (cutoff point at which two fragments are sorted into the same cluster) lower for helical fragments in the two SC libraries with most clusters. The SC Stringent possesses helix and nonhelix CαRMSD cutoffs of 0.75 Å and 1.75 Å, respectively, and the SC Loose has values of 1.75 Å and 2.50 Å, respectively. The remaining clusters used the same value for helix and nonhelix superclusters stepping up from 2.50 Å to 5.00 Å to 7.50 Å. Because a single fragment represented each cluster, the total number of members in a library decreases until the SC 7.50 library, where there is one fragment for every supercluster at a CαRMSD cutoff of 7.50 Å. For this extreme, the SC 7.5 library has the minimum of 1982 members or basically the number of superclusters. To create a library with even fewer fragments, we clustered without superclusters based on a 2.25 Å CαRMSD cutoff to create the General Clustering library with 187 members.

Figure 2.

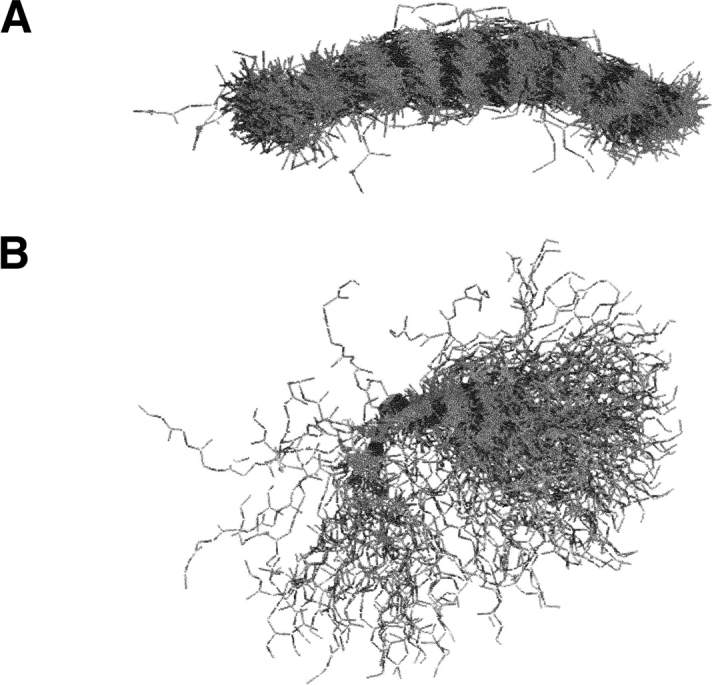
A β-strand (EEE EEE EEE) fragment cluster. This is one cluster from the all β-strand supercluster. (A) The 9mers are shown superimposed. It is in this position that a CαRMSD between two 9mers is calculated and clustering is executed. (B) The cluster is shown when the first residue of each 9mer is artificially superimposed. The latter more closely represents the effect of inserting 9mers into a protein structure.

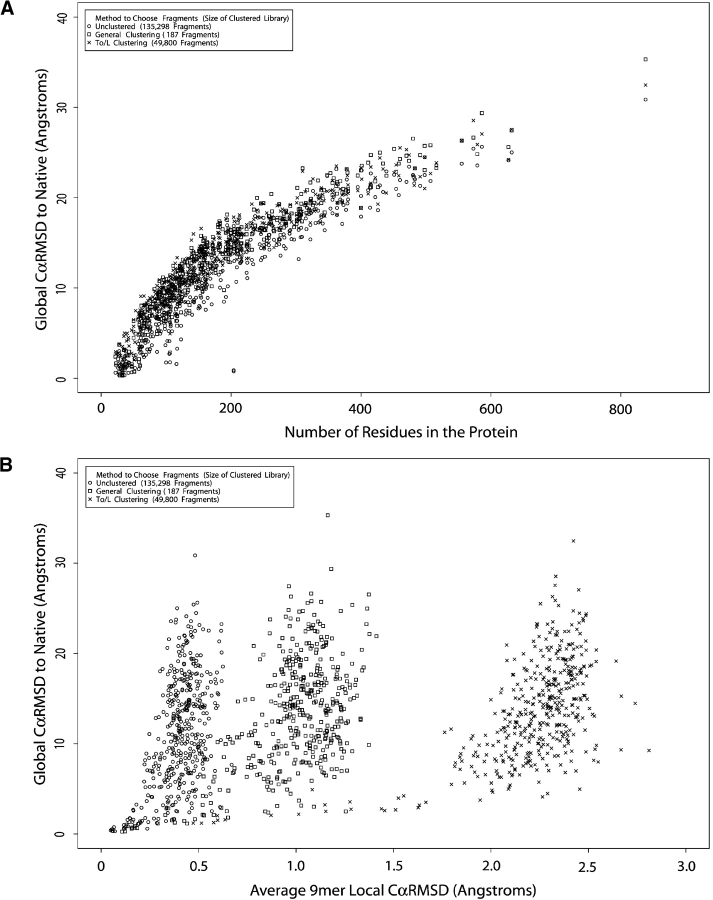
Using these libraries, we explored reconstructing proteins from nonnative 9mer fragments. We chose one nonnative 9mer fragment to replace each native 9mer fragment. Table 1 also reports the average values for the local and global fits over the PISCES set in addition to the description of each library. As expected, and has been shown previously (Kolodny et al. 2002; Hunter and Subramaniam 2003), an inverse relationship exists between the number of cluster members and local fit of fragments to native 9mers. Decreasing the number of cluster members increases the local CαRMSD or fit of the representative fragment to the native fragment from 0.41 Å for the Unclustered library with the most members to 1.08 Å for the General Clustering library with the fewest members. Surprisingly, the average global fit of the rebuilt structure to the native structure seems to only have a slight dependence on the average local fit: increasing from an average of 11.35 for the Unclustered library to 13.37 for the general clustering library. To provide more detail, we compare in Figure 3 ▶ the results of rebuilding native structures from the Unclustered library to the general clustering library. As shown in Figure 3A ▶, the best structure rebuilt from either fragment library depends strongly on the length of the native target, where longer proteins generally produce higher CαRMSD values. Figure 3B ▶ depicts the poor local similarity of the fragments from the general clustering library in comparison to the Unclustered library, but the distribution in global CαRMSD is very similar between the two as plotted by the Y-axis. Because of the magnitude of the global CαRMSD values and their relatively minor differences with each other, we decided to calculate the number and average of good models generated (those below 7 Å CαRMSD), as shown in the last two columns of Table 1. The general trend is that the number of accurate models decreases and the average CαRMSD increases as the fragment library complexity decreases. However, the General Clustering library produces the same number (110) of good models as the Unclustered library, albeit with a worse average CαRMSD of 5.63 Å.

Figure 3.

Testing the accuracy of fragment libraries. We analyzed the impact of the size of our fragment library as well as the method used to select the best replacement fragment. (A) The relationship between protein size and the global CαRMSD is shown. (B) The relationship between local CαRMSD (9mer to 9mer) and global CαRMSD is shown.

Takeoff/landing angle space clustering

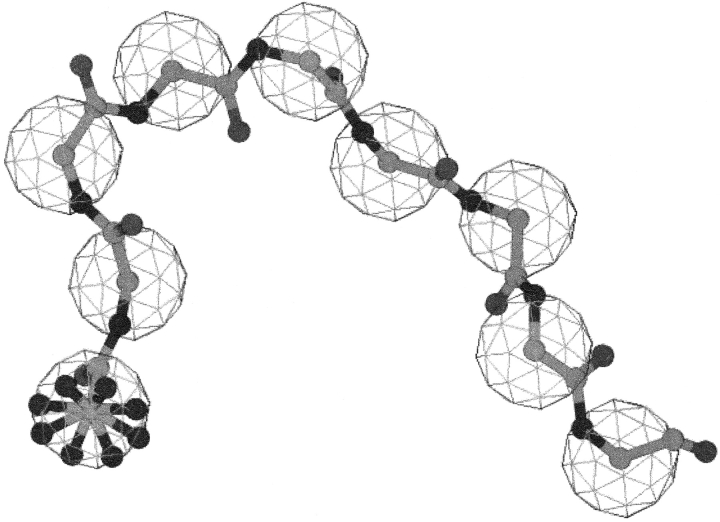
An interesting consequence of clustering in Cartesian space is that large perturbations in the initial ψ (takeoff) and final φ (landing) angles can radically redirect the way in which a fragment affects the protein topology upon insertion. As illustrated in part B of Figure 2 ▶, the same fragments as in the cluster pictured in Figure 2A ▶ are displayed, but this time, the first residue of every fragment is overlaid. Portraying the fragments in this manner provides a better picture of the effect of inserting these fragments into the middle of a protein. Because these differences in the takeoff/landing angles do not move the α-carbons, they are not considered in our CαRMSD based clustering (Fig. 4 ▶). To address the influence of takeoff and landing angles, we created a clustering score that solely focused on these angles (see Materials and Methods). We clustered this takeoff/landing (To/L) library to a width of 13 Å (Table 1). The To/L library contained 49,800 members. Even though the To/L score exhibits the worst local CαRMSD score of all the libraries at 2.24 Å, the average global RMSD of 13.50 Å is not much worse than the other libraries. The poorer local fit is plainly evident by the X-axis in Figure 3B ▶, while the similarity in global fit average and distribution is shown by the Y-axis. Also in Table 1, the number of good models was the worst of any library at 49.

Figure 4.

Effect of takeoff angles on building protein models. The initial ψ torsion angle of each 9mer has an effect on any protein into which it is inserted when compared to the same fragment with a different takeoff angle. Eight 9mers with identical main chain atoms but differ by their initial ψ torsion angle. The α-carbons all perfectly overlay (large spheres), so the CαRMSD between these would be 0 Å. The figure was created using the Spock molecular graphics program (http://quorum.tamu.edu/spock/).

Artificial takeoff/landing angle libraries

To further investigate the influence of takeoff and landing angles on the performance of a fragment library, we created a set of artificial libraries based on 9mers taken from the native structure that differ in their initial takeoff, ψ angle or in their final landing, φ angle. Figure 4 ▶ depicts one set of fragments with their initial ψ angle changed by 45° increments from the native fragment. Including the native fragment, seven synthetic fragments are overlaid, where all eight α-carbons are also superimposed exactly on top of each other (large spheres in Fig. 4 ▶). We had seven angle changes for each torsion angle that gave a total of 14 permutations of a native fragment. This basically created 14 artificial libraries. Initially, we wanted to measure how a set of fragments (all native but with a single takeoff or landing change) would affect the construction of models in the buildup procedure. Doing this produced essentially native structures. The result is not so surprising once we thought about it. For a given library, all the native torsion angles were present. To obtain a native structure with a random insertion method, the structure needed enough moves to insert all native angles and move the nonnative permutation to one of the termini. (A sequential fragment insertion method would have found this result immediately, depending on which side it started from and which type, ψ or φ, of angle change was made.) Therefore, we decided to look at this effect in a more straightforward manner.

To measure the influence of takeoff or landing angle changes on the buildup of structures, we used these fragments to rebuild each structure in the PISCES set of proteins. For each structure, every 9mer fragment was replaced with a permuted native fragment. In effect, the structure was rebuilt with one of its ψ or φ angles changed, and the resulting structure was then compared to the native structure by CαRMSD. For a given 45° ψ or φ angle permutation, we averaged over all CαRMSD changes in a structure and over all structures. Averages and standard deviations of the global fit from rebuilding these structures using each of the 15 fragment libraries (14 synthetic + 1 native) are shown in Table 2. Because only the takeoff or landing angle was changed, the local CαRMSD was 0.0 between the native and permuted fragment (for every 45° change). As a control of our buildup procedure, the native 9mer fragments always reconstructed a perfect native structure. The other 14 libraries exhibited expected behavior. The farther from native ψ or φ angles that we moved the fragments, the worse the model structures became with the peak being at a change of 180°. Additionally, like the previous libraries, the global CαRMSD depended highly upon protein length, where the maximum and minimum global CαRMSDs were the largest and smallest protein tested, respectively (data not shown).

Table 2.

Values and deviations from takeoff and landing angle permutations

	Takeoff		Landing
Angle permutation	Average	Std. Dev.	Average	Std. Dev.
0°	0.00	0.00	0.00	0.00
45°	4.45	1.04	4.43	1.03
90°	8.34	1.95	8.83	1.93
135°	11.18	2.62	11.18	2.58
180°	12.31	2.88	12.31	2.84
225°	11.25	2.61	11.25	2.58
270°	8.40	1.94	8.39	1.92
315°	4.46	1.03	4.45	1.02

Values and deviations are in Å based on a CαRMSD comparison to the native structure.

Native insertion fragment selection

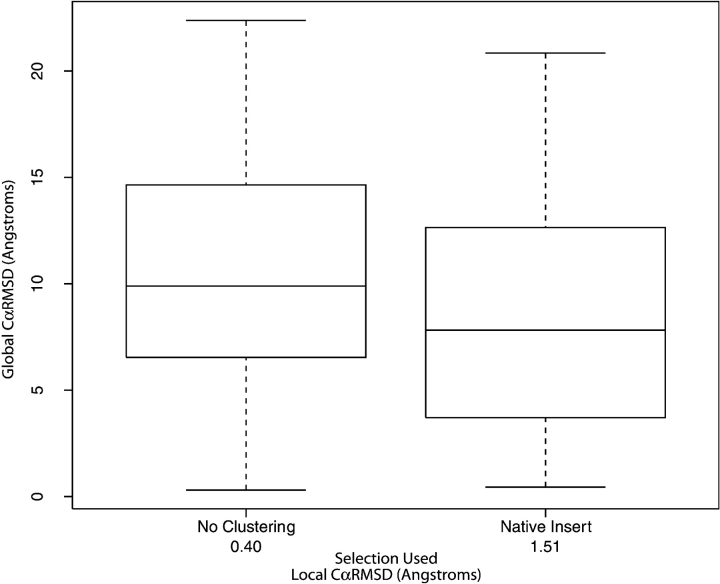
Based on the previous results, the selection of the best fragment at a position is a balance in matching the native fragment’s backbone as well as its takeoff/landing angles. Knowing the native structure, a simple yet optimal approach that considers a fragment’s local fit to the native fragment with its global effects on the structure is to identify the fragment that makes the smallest perturbation to a native backbone. To find such fragments, we inserted a fragment into a native backbone, rebuilt the structures, and measured the overall CαRMSD back to native. The fragment producing the smallest CαRMSD was considered the best fragment. This was repeated at each position in every native structure for all 135,298 fragments of the Unclustered library. Eventually, for larger structures, calculating the CαRMSD for every fragment at every position became computationally prohibitive. We hit a limit at 434 residues, and so we only used 161 proteins from the PISCES set. From these 161 proteins, the distribution of CαRMSD to native for the nearest native rebuilt structures using the native insert selection is compared to the Unclustered library’s CαRMSD selection in Figure 5 ▶. What is striking from the plot is that the global fit is better for fragments selected using the native insertion method than the CαRMSD (8.61 Å versus 10.25 Å over the 161 proteins, respectively), even though the native insertion fragments’ local fit is worse than CαRMSD ones (1.51 Å versus 0.40 Å over 161 proteins, respectively).

Figure 5.

Testing of the native insert algorithm. The native insert 9mer selection algorithm (where 161 proteins from the PISCES set were used) is compared to the CαRMSD selection algorithm. The numbers under the X-axis labels indicates the average local CαRMSD calculated from the 161 proteins for comparison. The global CαRMSD is calculated between the native coordinates and the model constructed from the selected 9mers. Interestingly, a lower local CαRMSD has a higher global CαRMSD.

Discussion

Building in torsion space versus Cartesian space

Although it is commonly assumed that native folds can be rebuilt by only using information from their backbone φ–ψ–ω torsion angles, our results indicate that torsion angle information is not enough to accurately reproduce the native backbone. Using φ– ψ–ω torsion angles, 90% of the native structures could be reconstructed under 13 Å (Fig. 1A ▶), and this inaccuracy only worsens with longer proteins (Fig. 1A ▶, inset). Because building proteins using only torsion angles must assume standard bond angles and lengths, inconsistencies in native bond angles and lengths are the fundamental cause of this imprecision. Although While these deviations have been characterized previously (Laskowski et al. 1993), we show average values and deviations for bond lengths and angles in Table 3. Of the two, we have found that the variability found in bond angles contributes more to the inaccuracy than the variability in bond lengths. Table 3 shows this deviation in bond angle values (on the order of degrees) in comparison to the deviation in the bond lengths (on the order of thousandths of an Å). When bond angles are used along with torsion angles, native structures can be accurately rebuilt within an angstrom (Fig. 1A ▶). However, building proteins using only torsion angle information is currently the most accepted approach to generating structures. The common work around to the problems created by variations in bond angles and lengths is to use idealized proteins to produce fragments, where the backbone bond angles and lengths have been fit to standard values. Reproducing the native idealized fold is much more accurate, where 90% of the idealized structures were rebuilt under 0.06 Å CαRMSD to the idealized, native fold. Of course, to accomplish this standardization, the backbone torsion angles are changed. As shown in Figure 6 ▶, the idealized fold is not exactly like the native fold. For the Kolodny set, the average CαRMSD of the idealized structure to native is 0.5 Å. Thus, the absolute limit for predicting a protein structure using torsion angles and a standard set of bond angles and lengths is at least 0.5 Å or worse. Although this is a small effect on modeling protein backbones, the change in torsion angles will have an impact on correctly positioning and packing side chains (Chung and Subbiah 1996). On the other hand, constructing proteins using torsion angles and idealized fragments has proven successful at approximating native folds in tests of ab initio, protein structure prediction (Simons et al. 1999a; Bonneau et al. 2001), and design (Kuhlman et al. 2003).

Table 3.

Values and deviations in the PISCES structure set’s bond lengths and bond angles

	Value	Deviation
Bond angle
N–Cα–C	110.96°	2.81°
Cα–C–N	114.91°	1.20°
C–N–Cα	120.64°	1.51°
Bond lengths
N–Cα	1.46 Å	0.0091 Å
Cα–C	1.52 Å	0.0095 Å
C–N	1.32 Å	0.0062 Å

The values and deviation of the nontorsion angle torsion space data is shown for the PISCES data set.

Figure 6.

Global CαRMSD differences between idealized and native data structures. For the Kolodny structure set, the CαRMSD of the idealized structure to the native is plotted against number of residues.

Although moves in torsion space are described by fewer parameters than moves in Cartesian space (per residue it is three torsion angles versus nine coordinates, respectively), both types of moves describe the same complexity. For torsion angle moves, idealization of the backbone angles and lengths helps to reduce the search space, but as shown by comparing the results from the Unclustered to the Un-clustered IDL libraries in Table 1, idealization does not significantly help in finding the native fold. Although the advantage of working in torsion angle space is that it reduces memory requirements, Cartesian space builds allow a conservative 10-fold speed up in builds (see discussion in Materials and Methods). In the absolute sense, building with Cartesian coordinates can exactly reconstruct a native protein, so Cartesian space models have the potential to be more accurate than models built with torsion angles and idealized residues. This ability to exactly build a native fold has a downside, because structures have to be able to match the deviation seen in protein backbone angles and lengths as shown by Table 3. To be able to build all native folds, a fragment library would be expected to contain every possible residue variation in every combination. Although such a library could be constructed artificially, searching through such a large space is impracticable and approaches the same complexity as predicting a protein’s overall fold. Realistically, the fragment library will need to be more tractable, so Cartesian space builds will be just as approximate as torsion angle builds with idealized fragments. Although building models in Cartesian space is slightly more favorable because of faster model construction, overall, these advantages and disadvantages do not strongly favor one method over the other one.

Characteristics of a fragment library for generating near-native models

Ideally, a good fragment library should be able to reconstruct native folds from nonnative fragments, that is, contain fragments that match all the target protein’s fragments and be tractable to search. One way to increase a fragment library’s effectiveness is to remove the redundancy in the library, so that conformational space can be sampled more efficiently. This was shown by two recent studies of fragment clustering. One showed that small nonredundant libraries could have good fit to local structure when clustering by shape (Hunter and Subramaniam 2003). The other study clustered fragments with a k-means method and, in a thorough test over a large set of target structures, found that only a few fragments are needed to build models that are very close to native (Kolodny et al. 2002). To build their models, the last report used a sequential fragment buildup that was fit against the native structure after each addition. In this study, we used a construction procedure that is not optimized to find the native structure but mimics currently used structure prediction methods (Simons et al. 1997) under mostly ab initio conditions. Described in Table 1, our clustered fragment libraries were created to investigate fragment redundancy effects on creating near native models. They are similar to the previous studies in that they test library size and complexity. Because our construction method is different in that it is not optimized to find the native structure, we cannot directly compare our results in building nearest native structures. However, this does somewhat explain why our method produces such poor global fits. In fact, we believe that our approach indicates how well a fragment library can perform in reproducing near native folds under conditions more similar to ab initio structure prediction.

Two measures were used to assess our fragment libraries: (1) the local fit or the 9mer CαRMSD of the closest fragments to their native counterparts, and (2) the global fit or the CαRMSD of the nearest native model to the native structure. In terms of local fit, the Unclustered library, where every member could be considered, sets the accuracy limit. The average local fit was 0.41 Å CαRMSD between the best match and the native fragment (Table 1), and these matches to native ranged between 0.05 and 0.67 Å CαRMSD, suggesting that they adequately covered local fragment space. As expected, increasing the clustering width reduces the size of the fragment library, and thereby decreases the local fit, most likely because the near-native fragments are now lost somewhere in the cluster. In terms of global fit, all of these libraries followed the trend of producing worse native-like models as the complexity of the fragment library decreased. When we chose from our library of only 187 fragments, the global CαRMSD to native was only slightly worse than when choosing from our entire 9mer library of 135,298 fragments (Table 1; Fig. 3 ▶). We did confirm our suspicion that fewer fragments in a library will lead to worse models, but were not expecting how little the change would be in the overall global fit with smaller libraries. To reassure ourselves that the comparison of such high CαRMSD values was true, we also looked at the number of good models generated. These measures also followed the trend of producing fewer and worse models the less complex the fragment library was. The only anomaly is the General Clustering library, which produced as many good structures as the Unclustered library, which is visually corroborated by the plots in Figure 3 ▶. This result suggests that the superclustering by secondary structure type is not favorable to fragment base structure generation and possibly adds a deleterious constraint upon fragment selection. The fact that Rosetta type algorithms are still able to produce a native-like model indicates that the proper fragments exist. We have shown that those fragments are generally not the best local fit fragments, because the lack of the ability for best local fit fragments to reproduce native-like models. Ultimately, because we know that we are searching for the native φ–ψ–ω torsion angles, local fit by CαRMSD is an incomplete measure for choosing the best replacement fragment.

This result led us to start thinking about whether we were choosing the best substitution fragment from the library. The standard similarity measure between two fragments is based on their backbone CαRMSD, and does not account for takeoff and landing angles, as illustrated in Figure 2 ▶. To test the influence of takeoff and landing angles, we created a set of artificial libraries that did not change the Cα positions (and so were perfect in terms of local CαRMSD) but did contain either a permuted takeoff or landing torsion angle. Clearly, the results from only changing the takeoff angle of native fragments shows that takeoff and landing angles are important (see Table 2). Therefore, we used a score just based on takeoff/landing angles to cluster fragments. This takeoff/landing angle clustering produces a fragment library with a very poor local fit of 2.24 Å, but the global fit of 13.50 Å is not much worse than our worst CαRMSD clustered set (General Clustering) with a better local fit (see Table 1; Fig. 3 ▶). The To/L clustered library did not improve the global fit most likely because this score was too focused on these takeoff/landing angles and ignored the local Cartesian similarities of two fragments. Therefore, if an α-helix and a β-sheet fragment had the same takeoff and landing angles, they could be chosen as a substitute for one another. So, a score must be devised that balanced both of these factors together: local Cartesian similarity, and take-off/landing angle similarity. We decided the best measure of a fragment’s similarity to the native would be to see how much a fragment perturbs the overall fold upon insertion into the native backbone. This worked reasonably well, as shown by Figure 5 ▶. Compared to the Unclustered fragment library that produces the lowest global fit, the native insert library exhibits a worse local fit, but better global fit. This different trend indicates that this score did much to find a better, more suitable, substitutionary fragment. However, longer proteins of lengths greater than 300 residues still had a global Cα RMSD of ~20 Å.

Although CαRMSD is a good measure for global fit, these results show that measuring similarity of fragments using CαRMSD is not an optimal method for choosing the nearest native fragment. This weakness in CαRMSD is mostly due to this measure’s strong dependence on length. Ultimately, the best fragment needs to insert all the native φ–ψ–ω torsion set at the proper point in the protein. For local structure similarity, takeoff and landing angles are no more important than any of the other 25 dihedral angles within the 9mer fragment. All of the angles matter equally as much. However, we believe takeoff and landing angles are often overlooked because they cause no visible torque in the 9mer fragment except in the initial nitrogen and terminal carbonyl carbon. Because no Cα shifts (e.g., see Fig. 4 ▶) a CαRMSD metric cannot distinguish between two such fragments. If you change any other torsion angle beside the first ψ and last φ (let’s say the fourth ψ by 180°), you will clearly see a difference between fragments.

Indeed, our results suggest that the emphasis on local structure similarity to assess a fragment library’s abilities at producing near-native models is misplaced. We find that near native models can still be generated with about the same likelihood for fragment libraries that are not complex, if we compare the results from the Unclustered to the General Clustered libraries. This result is corroborated by the simple library developed by Kolodny et al. (2002), where low global similarities were found. Basically, methods for generating protein structures using random insertions of fragments do not need optimal fragment libraries, that is, require a complete native fragment to necessarily exist in the library. Using the Rosetta algorithm as an example, this approach chooses 200 fragments at each position or per 9mer (Simons et al. 1997). Therefore, including overlap, each residue can in effect choose from 1800 φ–ψ–ω sets, or there are 1800 chances to find a native or near-native set of φ–ψ–ω values. Our results suggest that this redundancy is a fundamental asset to structure building using fragment-based, random insertions. Fragments in a library need only contain one native-like set of dihedral angles at each residue. More likely, fragments exist with stretches of contiguous native-like torsion angles. As long as the fragments are put together in the right order, a native-like model can be constructed. The importance of the sequence in which the fragments are inserted emphasizes the strong influence of the guiding potential function. Using CαRMSD as a guide has not produced the most native structures in this study, and suggests that these structures are trapped in deep local minima. The function used by Rosetta considers many qualitative aspects of protein structure (Simons et al. 1999b) that finds the correct sequence of fragments to build near native structures. The only place where a fragment based insertion method to build protein models would fail is if the φ–ψ–ω values were not present in the library. This is suggested by the result that Rosetta can build helical structures more accurately than those containing sheets (Bonneau and Baker 2001), because helical torsion angles are more regular and are better represented than sheet torsion angles in fragment libraries. Continuing with the same reasoning, the best fragment library would have complete coverage of fold space for fragments. Instead of generating the library from known structures, the library could be produced artificially like a recent library created for loop modeling (DePristo et al. 2003).

Conclusion

In this study, we have tried to understand what qualities are important when using a fragment-based method for prediction of protein structure. Specifically, we looked at construction procedure and fragment libraries. For construction procedure, we found that building models in torsion angle space only provides an advantage in simplifying the search to matching three parameters (φ–ψ–ω), but the complexity or degrees of freedom is essentially the same as building in Cartesian space. In terms of accuracy, the idealization of backbone coordinates places a lower limit to the accuracy of the backbone and will pose problems to eventual side chain packing (Chung and Subbiah 1996). Using Cartesian coordinates ultimately allows for exact accuracy and in our hands provides a more efficient buildup of models.

The important characteristic of a fragment library is that it contains near-native fragments or subfragments, but does not need to maximize local structure similarity. For construction procedures used in ab initio structure prediction, we have shown that selection of fragments based on local similarity (measured by CαRMSD) to the native fragment should be considered about equally with what the replacement fragment will do to the global fold (measure by take-off/landing angles). This leads us to an important point about the construction procedure and building nearest native structures. Because random insertion of fragments leads to overlapping and sometimes even complete elimination, it is interesting that takeoff and landing angles have an effect. In a study using random insertions of native fragments with permuted takeoff or landing angles, all native angles were available in the fragment library, but still native-like models were not made (data not shown). This indicates that using the global CαRMSD as a score is not optimal and probably restricts the random insertion search for the correct structure to deep local minima. Random fragment insertion has shown success in constructing near native structures (Simons et al. 1999a; Bonneau et al. 2001; Bradley et al. 2003) and in accurate design of a new protein fold (Kuhlman et al. 2003). These results, coupled with our work in this study, suggest that a strength of this buildup procedure is that it can use suboptimal fragment libraries. With a potential function (Simons et al. 1999b; Kortemme et al. 2003) and filters (Plaxco et al. 1998; Shortle et al. 1998; Ruczinski et al. 2002) favoring protein-like features, such suboptimal fragment libraries are more than adequate for generating near-native structures.

Materials and methods

Protein data sets

The studies conducted in this paper are based on two protein structure data sets:

1. For building protein structures in torsion angle space, we used the Kolodny set, an augmented set of idealized protein structures consisting of 1894 structures, 350 of which were used in Kolodny et al. (2002). Coordinates for native structures were obtained directly from the Protein Data Bank (Berman et al. 2002).

2. For the creation of the 9mer library as well as for testing fragment libraries, we used a list of 686 structures obtained using the PISCES server (Wang and Dunbrack 2003), which we called the PISCES set. This set has a 1.8 Å resolution and less than 20% internal structural homology. The subset of structures consists of single chains without any breaks, and contains coordinates for all backbone atoms: nitrogen, α-carbon, and carbonyl carbon. The structures in this set ranged in length from 51 to 838 residues. The PDB codes for the set used in this study have been supplied as supplemental material.

Idealization of the PISCES set

The Rosetta idealization implementation (Simons et al. 1997) was applied to the PISCES set. We go over it briefly here. The Rosetta idealization implements the Broyden-Fletcher-Goldfarb-Shanno variant of the Davidson-Fletcher-Powell (DFP) minimization algorithm as described in Numerical Recipes (Press et al. 1992). This algorithm is a quasi-Newtonian, variable metric method for multidimensional minimization. Rosetta makes three passes over the structure’s bond angles. These angles are minimized against Engh and Huber values (1991) while modifying the torsion angles to maintain the original three-dimensional shape. One limitation of the Rosetta implementation is that the proteins must be under 200 residues in size. Therefore, any protein greater than 200 residues was separated based on its domain structure into approximately 200 residue pieces. However, each split eliminated nine 9mers that otherwise existed in the native library. This contributed to having a slightly smaller 9mer library than the native library in terms of total number of fragments. Once the idealized 9mer library was created, the same routine was followed as with the Unclustered native library: selection of the lowest CαRMSD 9mer fragment for each 9mer position followed by a random insertion of the Cartesian coordinates of the fragment, minimizing to the native fold. It is important to note that we did not minimize to the idealized fold, but rather minimized a structure with the Engh and Huber standard values to approximate the nonideal native coordinates.

Creation of the 9mer library

For the 9mer Library, the PISCES set was systematically sliced into all possible 9mer fragments. Careful attention was paid to breaks in the chains created by nonstandard residues, so as not to create a 9mer fragment spanning a break in the native fold from which it was taken. Also, each residue of the 9mer fragment was classified based on a three-state model of secondary structure (helix H, sheet E, and coil C) as determined by PROMOTIF (Hutchinson and Thornton 1996). This classification was used to group fragments based on identical secondary structure assignments: superclusters. Using this scheme, we created 1982 of these super-cluster groups.

Clustering of the 9mer library

Within each supercluster, fragments were further clustered using a greedy multicentered clustering algorithm. The CαRMSD cutoff for the supercluster stringent library was set at 0.75 Å for helical superclusters (defined as >1/3 helical residues) and 1.75 Å otherwise. If a fragment did not meet the cutoff with any existing cluster center, the fragment would create its own cluster, and become the center of the new cluster. With each addition to the cluster, the cluster center was updated to the fragment with the smallest sum total CαRMSD to every other fragment within the cluster. Other clustered libraries (within superclusters) were created with varying CαRMSD cutoffs for purposes of reconstruction. We also created a library with 187 clusters that clustered across superclusters, that is, considered all 135,298 fragments as a whole.

For the To/L clustering, we used a gross score. We overlaid the first three atoms of the fragment, and then measured how far apart (in Å) the final carbonyl carbons were from one another, and than overlaid the final three atoms, and added the distance between the initial nitrogens. Because we wanted to compare these results with our SC library, a 13 Å cutoff was chosen to produce a similar number of clusters (49,800) as the supercluster Stringent library (53,002).

Because we used a greedy algorithm, not all fragments ended up clustered to their nearest (in CαRMSD space) cluster center. If two clusters had overlapping areas, a fragment could be first assigned to the cluster with the second best score, if the better scoring cluster center has not yet been created.

Computer implementation of library clustering

Due to the large number of fragments to be clustered (>135,000 9mers), a method was desired that was quick, but primarily memory efficient. A linked list solution was decided upon despite linked list’s reputation for being slow to access and use in comparison to arrays. For one linked list, each node held information for a cluster, only being created and allocated when a new cluster was discovered. Each of these cluster nodes pointed to:

1. Another linked list consisting of a node for each 9mer member of the cluster;

2. The individual 9mer node of the linked list above (1) acting as the current “cluster center”;

3. The final 9mer node in the linked list above (1) allowing for rapid addition of 9mer fragments to a cluster.

The nodes of the second linked list contained the name of the 9mer file as well as that 9mer’s sum CαRMSD to every other 9mer in the cluster. Thus, for a cluster consisting of only a single, unique 9mer, two nodes exist in computer memory: the individual 9mer node (with sum CαRMSD of 0) and the cluster node with three pointers to the single 9mer node.

Reconstruction of proteins in torsion space

The Kolodny set was rebuilt using increasing degrees of native structure information, and then the CαRMSD to native was calculated. Each nitrogen/α-carbon/carbon atom was appended to the previous atom of the main chain using basic geometric rules and quaternion rotations.

More specifically, the Cartesian coordinates of the three previous atoms to the atom being inserted were used to create two unit vectors. A third unit vector was created by duplicating the second one. It was then rotated using quaternion rotation around the axis created by the cross-product of vector one and two by the supplement of the bond angle. Next, it was rotated (again, using a quaternion rotation) around the axis of the second vector by the appropriate torsion angle. Finally, it was shifted down vector two by the bond length of the second vector, and lengthened by multiplying by its own bond length.

We used this process for four applications. First, we only calculated the torsion angles of the protein to be rebuilt, and supplemented the bond angle and bond length data with standard data (Ramachandran et al. 1974). Next, we also calculated the bond lengths of the protein, but still used the standard bond angles. Then, we calculated the bond angles of the protein, but still used the standard bond lengths. Finally, after calculating all three torsion angles, all three bond angles, and all three bond lengths, we rebuilt the proteins using all of the data.

One thousand eight hundred ninety-four protein chains from the Kolodny idealized set were also used. Instead of using ideal or standard bond lengths and bond angles, we used the values to which the data set was minimized. This time, the variation was in the bond angles was only ±0.03°, because each residue had been minimized to a common set of six numbers.

Reconstruction of proteins from nonnative 9mer fragments in Cartesian space

First, a list of a protein’s best nonnative replacement fragments was created. We would do this by looking at the 9mer library of interest and finding the fragment with the lowest CαRMSD to the native 9mer (best local fit). A subset of 421 structures with continuous chains from the PISCES set was used. This selection was properly jackknifed to prohibit the selection of the native fragment. Thus, for a 100-residue protein, 92 9mer fragments would be chosen from nonnative proteins. The total number of combinations of these 92 fragments, considering overlapping fragments, is near 10⁹⁰, which is currently computationally intractable. Therefore, we randomly sampled these possibilities with hopes that the structures would converge onto the native fold. The method for using these “nonnative, best local fit” fragments is as follows:

1. A “straightened” model would be created with φ–ψ–ω angles of 180° while preserving the native bond angles and bond lengths of the original structure.

2. A randomly chosen fragment was placed into its associated position in the straightened protein. For example, the best local fit fragment for residues 40–49 would be at those positions.

3. The CαRMSD of the model (with the new insertion) to native was calculated.

   1. If the model is further from native, reject the replacement.
   2. If the model is closer to native, accept the replacement.

4. Continue for 5000 insertions.

5. Repeat this procedure 1000 times, each time restarting from a straightened model, and ultimately saving the best model.

The Cartesian space replacement of a 9mer fragment was accomplished by the following algorithm, which is very similar to the Rosetta method (Simons et al. 1997). We would use the initial and final residue of the 9mer fragment (nitrogen, α-carbon, and carbonyl carbon) to overlay with the corresponding residues of the protein chain into which we were inserting the 9mer fragment. A rotational/translational matrix was calculated to overlay the first residue of the fragment onto the corresponding residue in the original model. This matrix was calculated by first overlaying the nitrogen to α-carbon vectors onto one another, followed by a rotation around the nitrogen/α-carbon vector to place the corresponding carbonyl carbons into the same plane. This calculated rotational/ translational matrix was applied to every atom in the fragment. Another rotational/translational matrix was calculated for placing the original terminal residue’s nitrogen, α-carbon and carbonyl carbon onto the corresponding terminal residue of the now-rotated fragment. If the insertion was closer to the end of the model, this matrix was applied to every atom from the terminal residue + 1 to the end of the protein. Otherwise, the inverse of this matrix was applied to residue 1 through the terminal residue of the fragment.

Because we were using a knowledge-based system, it was important that we insert the fragment exactly as we found it in the native fold from which it was taken. We made sure to preserve every φ–ψ–ω torsion angle, even at the ends of the fragment. If we allowed the algorithm to freely rotate the fragment upon insertion, we would move away from the restraints of a knowledge-based system, and towards the combinatorial problem of freely sampling conformational space.

With regard to the speed up by building in Cartesian space as opposed to Torsion space, we must consider each routine. Considering only main chain atoms, there are three general steps for Cartesian space builds:

1. Calculate a matrix to rotate the fragment onto the protein at one end.

2. Apply this matrix to 27 atoms.

3. Append the rest of the protein onto the other end of the fragment.

The steps for the best torsion space algorithm build currently in use are to:

1. Calculate the position of 27 atoms based on dihedral angles.

2. Append the rest of the protein onto the other end of the fragment.

The last step of each method is the same and may be ignored in this comparison. Thus, we are left with the other steps.

Steps 1 and 2 of a Cartesian space build require:

• 384 Multiplications (141 and 243, respectively)

• 252 Additions (90 and 243, respectively)

• 10 Divisions (Step 1)

• 6 square roots (Step 1)

Step 1 of a Torsion Space build, using quaternion rotations, requires:

• 1755 Multiplications

• 1350 Additions

• 297 Divisions

• 27 Square Roots

• 216 Trig Operations

Based on this breakdown, it is fair to say that a torsion space build is slower than inserting fragments stored in Cartesian space.

Variation of takeoff and landing angles of native 9mer fragments

To simulate the effects of takeoff angles on a fragment reconstruction method of building proteins, we first started with a protein’s set of native 9mer fragments taken from any given protein. We then sequentially inserted one fragment at a time to the native fold, each time, and averaged all of the CαRMSDs. As one would expect, the average CαRMSD at this point was 0 Å. We then changed the initial ψ or final φ by 45° increments for every native 9mer, effectively changing the orientation by which the fragment would be appended to the protein. We again sequentially inserted one fragment at a time to the native fold, each time, and averaged all of the CαRMSDs. For this test, we ran over the structures in the PISCES set.