Abstract
Analyzing the stability of a multimeric protein is challenging because of the intrinsic difficulty in handling the mathematical model for the folded multimer-unfolded monomer equilibrium. To circumvent this problem, we introduce the concept of effective stability, ΔGeff (= −RTlnKeff), where Keff is the equilibrium constant expressed in monomer units. Analysis of the denaturant effect on ΔGeff gives new insight into the stability of multimeric proteins. When a multimeric protein is mostly folded, the dependence of effective stability on denaturant concentration (effective m-value) is simply the m-value of its monomeric unit. However, when the protein is mostly unfolded, its stability depends on denaturant concentration with the m-value of its multimeric form. We also find that the effective m-value at the Cm is a good approximation of the apparent m-value determined by fitting the equilibrium unfolding data from multimeric proteins with a two-state monomer model. Moreover, when the m-value of a monomeric unit is estimated from its size, the effective stability of a multimeric protein can be determined simply from Cm and this estimated m-value. These simple and intuitive approaches will allow a facile analysis of the stability of multimeric proteins. These analyses are also applicable for high-throughput analysis of protein stability on a proteomic scale.
Keywords: protein stability, m-value, multimeric protein, oligomeric protein
Determining protein stability is the first step in investigating the thermodynamic properties of proteins. The only requirement is that the protein establishes a reversible equilibrium between the folded and unfolded states. Most proteins whose stabilities have been studied so far are monomeric. Despite the prevalence of multimeric proteins, stability determinations of multimeric proteins are quite rare, mostly because of the inherent difficulty in the treatment and analysis of their equilibrium behavior. Enhancing our knowledge of the stability of multimeric proteins requires the development of new and facile ways to analyze their equilibria.
The equilibrium between an n-mer protein and its unfolded monomer without any intermediate state1 is shown in equation 1:
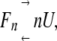 |
(1) |
where the equilibrium constant of the reaction is
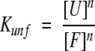 |
The fraction of unfolded protein, fD, is defined as in equation 2.
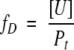 |
(2) |
where Pt is the total protein concentration in monomer units. Kunf and ΔG° can be expressed as functions of fD:
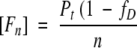 |
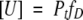 |
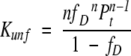 |
(3) |
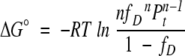 |
(4) |
The challenge in studying multimeric proteins results from their reaction order. Even for multimeric proteins, ΔG° can be directly calculated from an experimentally determined fD by equation 4 (Silinski et al. 2001). However, calculation of fD from a given ΔG° is nontrivial, because equation 4 is n-th order. Solving the equation is feasible for monomeric and dimeric proteins. However, even for trimeric proteins, deriving a general expression of fD as a function of Kunf is challenging (Backmann et al. 1998; Silinski et al. 2001; Güthe et al. 2004):
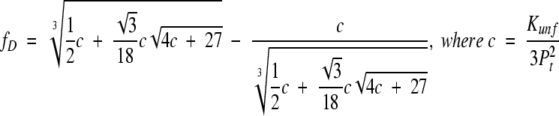 |
For n > 3, the equation needs to be solved numerically (Johnson et al. 1995; Boudker et al. 1997; Panse et al. 2000). This problem precludes the development of a general description for the stability of multimeric proteins. Moreover, since Kunf is not unitless for multimeric proteins, it is much less intuitive and less useful for comparative purposes than is Kunf for monomeric proteins.
The effective stability
Is there a more intuitive approach similar to that used for monomeric proteins to understand the thermodynamic stability of multimeric proteins? To address this question, we have developed an approach using an effective ΔG (ΔGeff), instead of ΔG° for the standard condition:
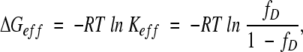 |
(5) |
where fD is defined as in equation 2. Keff is simply the ratio of unfolded protein concentration to folded protein concentration in monomer units. ΔGeff and Keff are pseudo-thermodynamic parameters where the actual order of chemical equation is ignored. Unlike ΔG°, ΔGeff and Keff are dependent on the total protein concentration of the system. However, these pseudo-thermodynamic parameters are more intuitive in that they relate directly to the amount of folded protein in the system. For example, ΔGeff is always zero when half of protein is unfolded, that is, fD = 0.5, while ΔG° of a multimeric protein has a nonzero value when fD = 0.5.
Next, we derive a general equation for ΔGeff(H2O). As mentioned earlier, analytical derivation of ΔGeff(H2O) from ΔG°(H2O) in an n-mer system is mathematically impossible. If one assumes that in water fD will be very small (a reasonable assumption for a stable protein under aqueous condition), then ΔG°(H2O) can be directly related to ΔGeff(H2O). From equations 4 and 5,
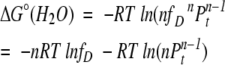 |
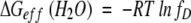 |
Therefore,
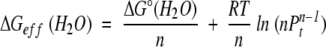 |
(6) |
Here, ΔG°/n is the ΔG° per monomer unit (Boudker et al. 1997), which is concentration-independent and an intrinsic property of the protein. The second term, however, is not protein-specific; it depends only on the total protein concentration and the number of monomer units in the multimer. This second term is identical for any n-meric protein under identical total protein concentration. Therefore, ΔGeff can be dissected into two terms: a protein-specific term, and a concentration-dependent term.
The separate terms in equation 6 allow a facile comparison of protein stability across proteins with different oligomeric states, which is not feasible with ΔG°. Table 1 showsΔG°/n extracted from experimental data available for several multimeric proteins. While ΔG° values vary significantly, ΔG°/n values are all between 5 kcal/mole and 12 kcal/mole, which is also the usual range for monomeric protein stability. The ΔGeff values at 100 μM monomer concentration were also calculated for the same proteins (Table 1). When two proteins in different oligomeric states have the same ΔG°/n values, the second term of the equation 6 explains the difference in ΔGeff, which is directly related to the unfavorable oligomerization at a nonstandard concentration. For example, ΔG°/n of Trp aporepressor and 4-oxalocrotonate tautomerase (4-OT) are quite similar: 11.7 kcal/mole and 11.3 kcal/mole, respectively (Table 1). However, because Trp aporepressor is a dimer and 4-OT is a hexamer, folding of 4-OT involves a bigger loss of entropy than does Trp aporepressor. When the two proteins are at the same concentration, the effective stabilities of 4-OT and Trp aporepressor differ mostly in the second term of equation 6 (2.1 kcal/mole at 100 μM in monomer units).
Table 1.
Comparison of ΔG°, ΔG°/n and ΔGeffof various multimeric proteins
| Proteins | Oligomeric state | ΔG° (kcal/mole of n-mer) | ΔG°/n (kcal/mole of monomer) | ΔGeff (kcal/mole of monomer) |
| Trp aporepressor | 2 | 23.3 ± 0.9a | 11.7 ± 0.5 | 9.1 ± 0.5 |
| HIV-1 protease | 2 | 14.2 ± 1.4b | 7.1 ± 0.7 | 4.6 ± 0.7 |
| Arc repressor | 2 | 11c | 5.5 | 3.0 |
| Adenylate kinase | 3 | 30.5d | 10.2 | 6.8 |
| T4 fibritin | 3 | 21.3 ± 0.1e | 7.1 ± 0.03 | 3.7 ± 0.03 |
| p53 | 4 | 29.5 | 7.4h | 3.5 |
| SecB | 4 | 28 ± 2f | 7.0 ± 0.5 | 3.1 ± 0.5 |
| 4-Oxalocrotonate tautomerase | 6 | 68 ± 3g | 11.3 ± 0.5 | 7.0 ± 0.5 |
| GroES | 7 | 63 | 9.0i | 4.5 |
The ΔG° value for each protein was collected from the literature. For p53 and GroES, ΔG° values were calculated from the ΔG°/n reported in the literature. The ΔGeff value of each protein was calculated with equation 6, with a protein concentration of 100 μM in monomer units.
aGittelman and Matthews 1990; bGrant et al. 1992; cBowie and Sauer 1989; dBackmann et al. 1998; eGüthe et al. 2004; fPanse et al. 2000; gSilinski et al. 2001; hJohnson et al. 1995; iBoudker et al. 1997.
ΔG°/n values can easily be used to analyze the effect of mutations on the stability of multimeric proteins, because mutations do not affect the free energy change of the second term in equation 6. Therefore, the effect of mutations on ΔGeff is described simply as:
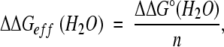 |
which shows that the mutational effect on ΔG°/n reflects directly the change in ΔGeff at any protein concentration. This relationship also supports the utility of ΔGeff and ΔG°/n in stability analysis of multimeric proteins.
The effect of denaturant on ΔGeff
The simplest method for determining protein stability is by monitoring chemical-induced denaturation profiles, combined with a two-state approximation and linear extrapolation (Greene and Pace 1974).
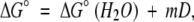 |
(7) |
where D is the denaturant concentration and m is the dependence of the stability on denaturant. Unfolding equilibrium constants, Kunf, can be measured directly in the transition zone, where detectable amounts of folded and unfolded proteins are in equilibrium. Then, ΔG°(H2O) can be determined by extrapolating ΔG° values (=RTlnKunf) from varying concentrations of denaturant.
To show how denaturant affects ΔGeff of multimeric proteins, we define meff as:
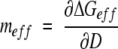 |
(8) |
By using equation 5,
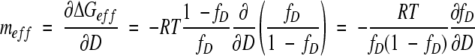 |
(9) |
∂fD/∂D can be derived by using equations 4 and 7. The two equations are combined to yield:
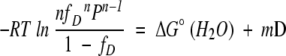 |
(10) |
By differentiating equation 10 with respect to D,
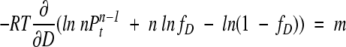 |
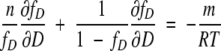 |
 |
(11) |
From equations 9 and 11,
 |
(12) |
This simple equation clearly shows the denaturant dependence of multimeric proteins. For a monomeric protein (n =1), meff is equal to m and constant with respect to denaturant. For multimeric proteins (n > 1), meff is not a constant. When the protein is mostly folded (fD ??0), meff is close to m/n. When the protein is mostly unfolded (fD ??1), meff is close to m.
Interestingly, m/n is approximately the expected m-value for a monomeric unit of an n-mer. Based on a study of reported m-values, Myers et al. demonstrated that m-values show a strong correlation with the size or the number of amino acids in a protein (Myers et al. 1995). It follows that the expected m-value for a hypothetical folded monomeric unit of an n-mer would be 1/n of the value of the n-mer protein (m/n). Therefore, when the protein is mostly folded, meff is approximately the expected m-value of the monomeric unit.
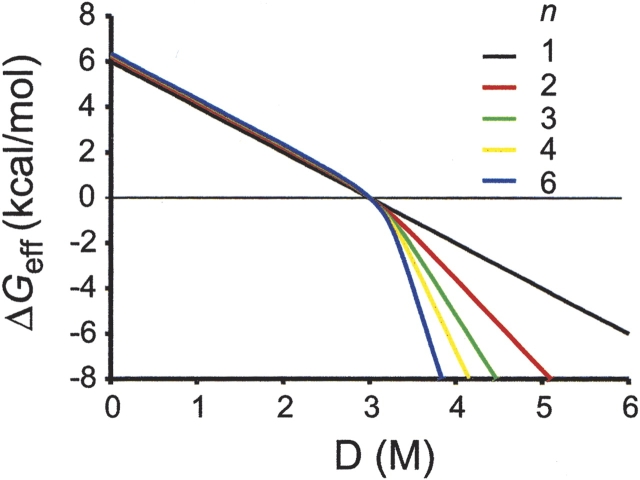
This denaturant-dependent behavior of meff is shown clearly in Figure 1 ▶. In this simulation, ΔGeff of each multimeric protein was determined numerically using equations 4 and 5. All the proteins were given the same expected m-value for a monomeric unit of 2 kcal/(mole•M) (m/n =2). For ease of comparison, all proteins were assigned to have the same Cm value (the denaturant concentration where fD =0.5) of 3 M. As shown in Figure 1 ▶, under native condition (D < Cm), the denaturant dependence of ΔGeff shows a slope of 2, regardless of the oligomeric state. As predicted by equation 12, this slope corresponds to the expected m-value of the monomeric unit. Under denaturing conditions (D > Cm); however, the slope of the denaturant dependence for ΔGeff corresponds to the m-value of each oligomeric protein.
Figure 1.
The effect of denaturant on effective ΔG of multimeric proteins. n represents the oligomeric state of each protein. The m/n values and Cm of all the proteins were set to be 2 kcal/(mole•M) and 3 M, respectively, for comparison. ΔG°(H2O) was determined with equation 14 by using these parameters. The fraction of unfolded protein, fD, was determined from ΔG° by solving equation 4 numerically. ΔGeff was calculated with this fD by equation 5. Total protein concentration was set to be 2 μM in monomer units. However, the result is indifferent to total protein concentration, because Cm was fixed.
The behavior predicted by equation 12 agrees with published data using hydrogen exchange and mass spectrometry to evaluate the stability of multimeric proteins (Powell et al. 2002). When this technique, called SUPREX (Ghaemmaghami et al. 2000), was applied for multimeric proteins, the observed m-values were noted to be 1/n-th of the m-value expected for the multimeric proteins. These m-values were derived at the CmSUPREX, which is lower than the actual Cm because of the kinetics of hydrogen exchange (Ghaemmaghami et al. 2000):
 |
which suggests that fD is close to 1 at CmSUPREX. Therefore, meff determined by SUPREX is meff at fD ??1, which is close to m/n as shown in equation 12.
Analysis of denaturation data from multimeric proteins
The simplest treatment of chemically induced denaturation data from multimeric proteins would be to use the simple two-state monomer model. What m-values would result from this curve fitting? Even though this approach clearly uses an incorrect model, the curve fitting would yield the correct Cm, because this parameter is model-free. Moreover, only a limited range of ΔGeff can be determined by experiment—those in the transition zone where D is near Cm. Therefore, experimental ΔGeff values are unlikely to show the biphasic patterns shown in Figure 1 ▶. Rather, experimentally determined plots of ΔGeff versus D would show a more or less linear tendency unless n is very large. The m-value from the simplified curve-fitting with a monomer model would be close to the meff at Cm. From equation 12, meff at Cm can be calculated by setting fD =0.5:
 |
(13) |
Table 2 shows that indeed the m-values obtained by this incorrect, yet simple, monomer model correlate extremely well with the expected meff at the midpoint determined by the above equation. The m-values in Table 2 were determined by fitting the fD values used to generate Figure 1 ▶ with a two-state monomer model.
Table 2.
Comparison of meffat Cmwith m-values determined with a two-state monomer model
| Oligomeric state | m-value used for generating simulation data | meff at Cm | m-value from curve fitting with a monomer model |
| 1 | −2.0 | −2.0 | −2.0 ± 0.0 |
| 2 | −4.0 | −2.7 | −2.7 ± 0.1 |
| 3 | −6.0 | −3.0 | −3.1 ± 0.1 |
| 4 | −8.0 | −3.2 | −3.3 ± 0.1 |
| 6 | −12.0 | −3.4 | −3.5 ± 0.2 |
The fractions of unfolded protein, fD, were calculated by assuming m/n = −2 kcal/(mole • M) and Cm = 3 M for imaginary n-mer proteins (Fig. 1 ▶). These fD values were fit with a two-state monomer model to determine m-values. The meff at Cm were also calculated with equation 13 from the m-values used to calculate fD. The unit of m-values is kcal/(mole • M).
The above analysis demonstrates that the m-value of multimeric proteins can be reasonably determined by applying a two-state monomer model and calculating meff at the midpoint. This monomer model does a better job of approximating meff at the Cm when n is smaller. Because meff is not actually constant, one caveat to this approach is that the curve-fitting will depend on the distribution of data points in the transition zone. Introducing more data points on the unfolded side of the transition (0.5 < fD < 1) results in m-values bigger than meff at Cm. It is also important to stress that the stabilities that result from this curve fitting with the monomer model are meaningless, because the slope is treated as a constant, yet meff depends on denaturant.
Determination of ΔGeff from Cm
Can ΔGeff(H2O) be determined simply by knowing the mid-point? As mentioned earlier, with the statistical data from the study by Myers et al. (1995), one can estimate m-values simply from the size of proteins. In monomeric proteins, ΔGunf can be reasonably approximated by multiplying the estimated m-value and Cm. Is this approach valid for multimeric proteins? The simulated data in Figure 1 ▶ suggest that ΔGeff in H2O might be approximated by Cm and m/n, the m-value for monomeric unit, regardless of the oligomeric state of a protein.
To verify this observation, we derive an equation for calculating ΔGeff from the Cm and m-value. In multimeric proteins, ΔG° is not zero at the Cm. Rather, according to equation 4, ΔG° at the Cm is expressed as (Backmann et al. 1998; Ragone 2000):
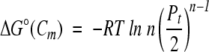 |
By using equation 7,
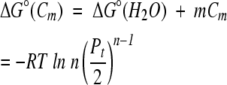 |
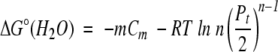 |
(14) |
By using equations 6 and 14, ΔGeff can be expressed in a simple equation:
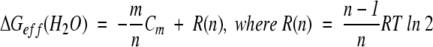 |
(15) |
R(n) is a residual function of n. This function is responsible for the slight differences in ΔGeff(H2O) values between different oligomers in Figure 1 ▶. For monomeric proteins, R(n) is zero. In all cases, R(n) is smaller than RTln2 (?0.41 kcal/mole at 25°C), which is quite negligible in most practical applications, and as shown in Figure 1 ▶. Because m/n is simply the m-value of a monomeric unit of the n-mer, ΔGeff(H2O) can be deduced from two parameters: the m-value of a monomeric unit calculated from the statistical data by Myers et al. and the experimentally determined Cm. Surprisingly, knowing the number of monomers in the multimer is not necessary to determine ΔGeff(H2O), because the two parameters, the m-value of the monomeric unit (m/n) and the Cm, are model-free.
Conclusions
We show here that the use of effective ΔG and effective m-value provides valuable information about the stabilities of multimeric proteins. ΔGeff is a useful parameter that gives an intuitive appreciation of the stability of multimeric proteins; one can calculate the fraction of unfolded protein from ΔGeff of a multimeric protein as easily as doing so from the ΔG° of a monomeric protein. To understand the effect of denaturant on the stability of multimeric protein, we define meff as the derivative of ΔGeff with respect to denaturant concentration. Analysis of meff shows that denaturant affects ΔGeff in a biphasic way. When the m-value of an n-mer protein is m, meff of this protein is m/n under folding conditions and m under denaturing conditions. Thus, although direct analysis of ΔG° is not feasible for multimeric proteins, ΔGeff and meff provide a facile alternative way to compare the stability of these proteins. Additionally,ΔGeff can be determined without prior knowledge of the oligomeric state of a protein. This unique property of ΔGeff could facilitate high-throughput analysis of protein stability on a proteomic scale.
Acknowledgments
This work was supported by an NIH grant. We also thank D.E. Wildes and E.A. Shank for helpful discussions and comments on the manuscript. We also thank reviewers for their productive comments.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.04811004.
Footnotes
An alternative unfolding mechanism is also observed in multimeric protein unfolding in which dissociation into monomers and unfolding are not coupled:
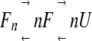 |
The unfolding transition in this mechanism is nothing but an unfolding transition of a monomeric protein, which can be analyzed with conventional methods. Therefore, here we only focus on the mechanism shown in equation 1.
References
- Backmann, J., Schafer, G., Wyns, L., and Bonisch, H. 1998. Thermodynamics and kinetics of unfolding of the thermostable trimeric adenylate kinase from the archaeon Sulfolobus acidocaldarius. J. Mol. Biol. 284 817–833. [DOI] [PubMed] [Google Scholar]
- Boudker, O., Todd, M.J., and Freire, E. 1997. The structural stability of the cochaperonin GroES. J. Mol. Biol. 272 770–779. [DOI] [PubMed] [Google Scholar]
- Bowie, J.U. and Sauer, R.T. 1989. Equilibrium dissociation and unfolding of the arc repressor dimer. Biochemistry 28 7139–7143. [DOI] [PubMed] [Google Scholar]
- Ghaemmaghami, S., Fitzgerald, M.C., and Oas, T.G. 2000. A quantitative, high-throughput screen for protein stability. Proc. Natl. Acad. Sci. 97 8296–8301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gittelman, M.S. and Matthews, C.R. 1990. Folding and stability of trp aporepressor from Escherichia coli. Biochemistry 29 7011–7020. [DOI] [PubMed] [Google Scholar]
- Grant, S.K., Deckman, I.C., Culp, J.S., Minnich, M.D., Brooks, I.S., Hensley, P., Debouck, C., and Meek, T.D. 1992. Use of protein unfolding studies to determine the conformational and dimeric stabilities of HIV-1 and SIV proteases. Biochemistry 31 9491–9501. [DOI] [PubMed] [Google Scholar]
- Greene, R.F. and Pace, C.N. 1974. Urea and guanidine-hydrochloride denaturation of ribonuclease, lysozyme, α-chymotrypsin, and β-lactoglobulin. J. Biol. Chem. 249 5388–5393. [PubMed] [Google Scholar]
- Güthe, S., Kapinos, L., Möglish, A., Meier, S., Grzesiek, S., and Kiefhaber, T. 2004. Very fast folding and association of a trimerization domain from bacteriophage T4 fibritin. J. Mol. Biol. 337 905–915. [DOI] [PubMed] [Google Scholar]
- Johnson, C.R., Morin, P.E., Arrowsmith, C.H., and Freire, E. 1995. Thermodynamic analysis of the structural stability of the tetrameric oligomerization domain of p53 tumor suppressor. Biochemistry 34 5309–5316. [DOI] [PubMed] [Google Scholar]
- Myers, J.K., Pace, C.N., and Scholtz, J.M. 1995. Denaturant m values and heat capacity changes: Relation to changes in accessible surface areas of protein unfolding. Protein Sci. 4 2138–2148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panse, V.G., Swaminathan, C.P., Aloor, J.J., Surolia, A., and Varadarajan, R. 2000. Unfolding thermodynamics of the tetrameric chaperone, SecB. Biochemistry 39 2362–2369. [DOI] [PubMed] [Google Scholar]
- Powell, K.D., Wales, T.E., and Fitzgerald, M.C. 2002. Thermodynamic stability measurements on multimeric proteins using a new H/D exchange- and matrix-assisted laser desorption/ionization (MALDI) mass spectrometry-based method. Protein Sci. 11 841–851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ragone, R. 2000. How the protein concentration affects unfolding curves of oligomers. Biopolymers 53 221–225. [DOI] [PubMed] [Google Scholar]
- Silinski, P., Allingham, M.J., and Fitzgerald, M.C. 2001. Guanidine-induced equilibrium unfolding of a homo-hexameric enzyme 4-oxalocrotonate tau-tomerase (4-OT). Biochemistry 40 4493–4502. [DOI] [PubMed] [Google Scholar]