Trypsin specificity as elucidated by LIE calculations, X-ray structures, and association constant measurements

Abstract

The variation in inhibitor specificity for five different amine inhibitors bound to CST, BT, and the cold-adapted AST has been studied by use of association constant measurements, structural analysis of high-resolution crystal structures, and the LIE method. Experimental data show that AST binds the 1BZA and 2BEA inhibitors 0.8 and 0.5 kcal/mole more strongly than BT. However, structural interactions and orientations of the inhibitors within the S1 site have been found to be virtually identical in the three enzymes studied. For example, the four water molecules in the inhibitor-free structures of AST and BT are channeled into similar positions in the S1 site, and the nitrogen atom(s) of the inhibitors are found in two cationic binding sites denoted Position1 and Position2. The hydrophobic binding contributions for all five inhibitors, estimated by the LIE calculations, are also in the same order (−2.1 ± 0.2 kcal/mole) for all three enzymes. Our hypothesis is therefore that the observed variation in inhibitor binding arises from different electrostatic interactions originating from residues outside the S1 site. This is well illustrated by AST, in which Asp 150 and Glu 221B, despite some distance from the S1 binding site, lower the electrostatic potential of the S1 site and thus enhance substrate binding. Because the trends in the experimentally determined binding energies were reproduced by the LIE calculations after adding the contribution from long-range interactions, we find this method very suitable for rational studies of protein–substrate interactions.

The binding of protein and peptide substrates to the pancreatic serine proteinases is characterized by well-defined binding sites, including a primary specificity pocket (S1 site, nomenclature from Schechter and Berger 1967) and subsites (secondary binding sites), anchoring the polypeptide chain of the substrate at both sides of the primary binding residue (P1). The primary specificity of the serine proteinases is to a large extent determined by the shape and charge of the S1 pocket. It is well documented that Asp 189, at the bottom of the active site pocket of trypsin, is the major determinant for the narrow specificity of trypsin for positively charged substrates. In addition, the hydrophobic walls of the pocket create a favorable environment for the long aliphatic and unbranched parts of the basic arginine and lysine side chains. In contrast, chymotrypsin possesses a wider and uncharged S1 pocket, and prefers large hydrophobic and aromatic P1 side chains. However, a number of studies have revealed that several residues distal to the S1 site are essential for the specificity (see, for example, Hedstrom 1996; Perona and Craik 1997). Attempts to convert trypsin into a chymotrypsin-like or elastase-like enzyme (Hedstrom et al. 1992, 1994a,b; Hung and Hedstrom 1998) have all shown that the specificity of serine proteinases is much more complex than previously thought, and the structural sources of the substrate discrimination are still not fully understood.

Measurements of the association constants (K_a) for complexes between 18 different P1 variants of the BPTI and four serine proteinases (bovine chymotrypsin, human neutrophile elastase, AST, and BT) revealed that both BT and AST had, as expected, a specific and narrow affinity for the cognate Lys and Arg side chains (Krowarsch et al. 1999). However, K_a-values for AST were 100-fold higher than the corresponding values for BT for both P1 Lys and Arg, whereas binding of the noncognate P1 residues was not significantly different in the two trypsins. Another comparative kinetic study of AST and BT, using a small synthetic substrate (benzoyl-D,L-arginine p-nitroanilide), showed that the salmon enzyme possessed a 35-fold higher catalytic efficiency (measured by the k_cat/K_m ratio) at 4°C compared with BT (Outzen et al. 1996). The catalytic efficiency for CHST is lower than for AST (22-fold higher than BT at 5°C; Sekizaki et al. 2000^; Toyota et al. 2002), even if there are only four differences in the amino acid sequences (positions 28, 125, 152, and 244) of the fish enzymes, and the RMSD value for the main-chain atoms of the two structures is 0.36 Å (Toyota et al. 2002). Residue 152 is Ser in AST and Lys in CHST, which changes the overall charge from −4 (AST) to −3 (CHST), and the electrostatic potential of the S1 site in the latter is slightly altered. For AST, the K_m value is reduced in the catalysis, implying a stronger binding of the substrate in the S1 site. Increased substrate affinity has also been observed for other cold-adapted trypsins (Kristjansson et al. 1997), whereas higher catalytic efficiency appears to be a general feature of cold-adapted enzymes; see, for example, Smalås et al. (2000). Comparison of the crystal structures of the AST-BPTI and BT-BPTI complexes (Helland et al. 1998) revealed small differences in binding modes of the two enzymes, both at primary and secondary binding sites. The P1 Lys Nζ atom of BPTI forms a hydrogen bond directly to the carboxyl group of Asp 189 in AST-BPTI, whereas it only interacts via a water molecule in the BT-BPTI complex. Differences in the secondary binding sites indicate looser binding of the S′side of AST-BPTI. The P1 Gly variant of the BPTI complex has no side chain penetrating the S1 pocket of trypsin, and is therefore expected to give an estimate of the contribution to the binding energy from secondary binding sites only. The similar association energy between the BPTI P1 Gly variant bound to BT and AST, both in the order of 6 kcal/mole (Krowarsch et al. 1999), suggests that these interactions are similar in the two homologs and that they contribute significantly to the overall complex formation.

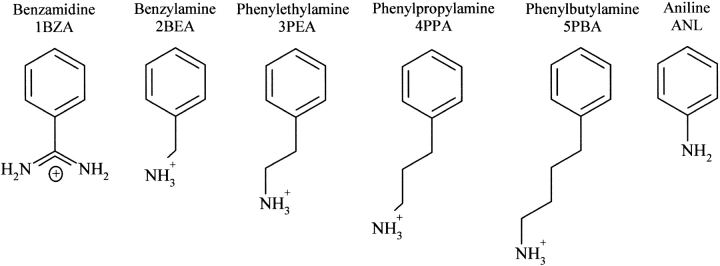
The observations mentioned earlier suggest that the higher substrate affinities of AST mainly arise from stronger interactions within the S1 site. This encouraged us to further investigate the nature and the differences among the primary binding sites of trypsins. The association capacities and binding patterns for three different trypsins (AST, CST, and BT), in complex with a series of small synthetic inhibitors that are only in contact with the S1 site, have been investigated. In this study, four AST and four BT crystal structures have been determined; association constants have been measured for the inhibitors bound to AST, CST, and BT; and the binding free energies have been calculated using the LIE approach (Åqvist et al. 1994). The structures have in detail been compared with a series of corresponding BT complexes (Marquart et al. 1983; Kurinov and Harrison 1994), BT complexed with BPTI P1 Gly and P1 Phe, (Helland et al. 1999b) and the AST-BPTI complex (Helland et al. 1998). The synthetic inhibitors included in this study are, in addition to 1BZA, all amines of various lengths attached to a phenyl group (Fig. 1 ▶).

Figure 1.

Structural formulas of the synthetic trypsin inhibitors included in the study. The numbers 1–5 refer roughly to the strength of the inhibitors.

Results

Association constants

The measured association constants (K_a) for the synthetic inhibitors in complex with AST, CST, and BT clearly rank 1BZA as the most potent inhibitor of all the trypsins followed by 2BEA and 3PEA (Tables 1a, 1b). The 4PPA binds more favorably than 5PBA (the longest one) to both AST and BT, whereas the reverse is found for CST. The cold-adapted and overall negatively charged AST (pI = 4.7; Outzen et al. 1996) binds the two smallest inhibitors stronger than the cationic CST and BT (pI above 10; Outzen et al. 1996). The association constants of 1BZA and 2BEA bound to AST are 1.4–3.5 times higher compared with CST and BT. CST is found to have the highest affinity for the longer inhibitors, and is, for example, for 5PBA 20 times higher compared with BT. The association constants for 4PPA and 5PBA are, however, very weak (up to several thousand fold lower K_a-values than for 1BZA), and the accuracy may therefore be expected to be somewhat lower for these measurements compared with the best inhibitors. The differences among the weakly bound complexes should therefore only be taken as relative indications. We have introduced numbers 1–5 in the abbreviations (1BZA, 2BEA, 3PEA, etc.), which roughly refer to the lengths of the inhibitors. See Figure 1 ▶ and Table 1b for more details.

Table 1a.

The steady-state parameters for the hydrolysis of the sensitive trypsin substrate Tos-Gly-Pro-Arg-pNA, in 100 mM Tris, 20 mM CaCl₂(pH 8.3) for AST, CST, and BT

	AST	CST	BT
kcat (S−1)	30.4	87.5	88.0
Km (M)	8.96 * 10−7	2.61 * 10−6	5.19 * 10−6
kcat/Km (S−1M−1)	3.39 * 107	3.35 * 107	1.70 * 107

Table 1b.

Experimental association constants (K_a, M⁻¹) for small molecule inhibitors bound to AST, CST, and BT

Inhibitor	AST	CST	BT	BTa
1BZA	1.65 * 105	1.06 * 105	4.71 * 104	1 * 104
2BEA	6940	4870	3120
FBA				2326
AMC				855
3PEA	1029	1150	188	91
4PPA	293	520	38	31
5PBA	243	573	28	50

The K_a is 1/K_d where K_d is found from the Dixon plot equation defined in

Materials and Methods.

^a Previously reported values are from Kurinov and Harrison (1994).

X-ray structures

Crystals were obtained for three AST complexes (AST-2BEA, AST-3PEA, AST-4PPA) and three BT complexes (BT-2BEA, BT-3PEA, BT-5PBA) in addition to the inhibitor free enzymes (AST-Free, BT-Free). The two latter are from unsuccessful trials of crystallization with ANL and 4PPA for AST and BT, respectively. All of the structures diffracted to high resolution (1.15–1.83 Å) and were refined to R-values between 11.3% and 18.9%. The corresponding R-free values are not more than 5.5% higher than the conventional R-factors. Mean coordinate errors are estimated to be in the range of 0.06–0.17 Å and RMS deviations in the range of 0.008–0.015 Å for bond lengths. See Tables 2 and 3 for more details. All inhibitors have been refined with full occupancy so that the relative B-factors (Tables 4, 5) reflect both the binding affinity and the occupancy in the structures (in addition to dynamic and static disorder). The relative B-factor is:

Table 2.

Data collection statistics of the AST and BT complexes

	Anionic salmon trypsin				Bovine trypsin
Inhibitor	Benzylamine	Phenylethylamine	Phenylpropylamine	No inhibitor	Benzylamine	Phenylethylamine	Phenylbutylamine	No inhibitor
Abbreviation	AST-2BEA	AST- 3PEA	AST-4PPA	AST-Free	BT-2BEA	BT-3PEA	BT-5PBA	BT-Free
Max. diffraction (Å)	1.83	1.5	1.7	1.53	1.15	1.15	1.3	1.15
Temperature (K)	295	295	295	120	120	100	100	100
Beamline	SNBL MAR	DESY X31 MAR	SNBL MAR	SNBL	SNBL	ID14-EH4 ADSC	ID14-EH4 ADSC	ID14-EH4 ADSC
Detector	18 cm	18 cm	18 cm	MAR345	MAR345	CCD	CCD	CCD
Wavelength (Å)	0.873	1.070	0.873	0.873	0.800	0.932	0.932	0.932
Cell (Å)	a = 45.03	a = 74.94	a = 44.94	a = 71.43	a = 54.15	a = b 3 54.59	a = b = 54.60	a = b = 54.51
	b = 48.18	b = 85.09	b = 48.27	b = 83.26	b = 56.73	c = 107.19	c = 107.10	c = 107.28
	c = 83.01	c = 32.19	c = 83.10	c = 30.87	c = 66.25	γ = 120	γ = 120	γ = 120
Space group	P212121	P21212	P212121	P21212	P212121	P3121	P3121	P3121
No. of observations (∞-max. resol.)	68,761	111,508	51,387	156,549	801,482	633,227	638,726	608,228
No. of unique reflections	14,865	32,883	19,106	28,477	71,444	63,049	41,821	62,502
Rmerge (%)	6.8 (12.2)	4.8 (27.1)	7.0 (24.3)	7.5 (36.1)	5.5 (35.6)	7.8 (40.1)	5.9 (16.1)	5.4 (35.3)
I/σI	8.5 (5.5)	10.1 (2.8)	8.3 (3.0)	2.6 (2.0)	7.2 (1.9)	4.0 (1.8)	5.1 (1.4)	6.4 (2.1)
Completeness (%)	90.6 (57.0)	97.9 (93.4)	93.8 (96.4)	99.5 (98.2)	97.3 (91.6)	94.8 (84.2)	91.5 (87.5)	94.6 (85.7)
Wilson B-factor (Å2)	10.58	14.25	11.32	11.43	10.17	11.21	12.25	10.88

The outer shell values (10^th bin) are shown in parentheses.

Table 3.

Final refinement statistics for the AST and BT structures

	AST-2BEA	AST-3PEA	AST-4PPA	AST-Free	BT-2BEA		BT-3PEA	BT-5PBA	BT-Free
Refinement program	X-PLOR	X-PLOR	X-PLOR	SHELXL	SHELXL		SHELXL	SHELXL	SHELXL
Resol. in final refinement (Å)	8.0–1.83	8.0–1.50	8.0–1.70	8.0–1.53	8.0–1.15		8.0–1.15	8.0–1.3	8.0–1.15
No. of reflections	14,637	32,682	18,880	28,246	70,363	62,855		41,657	62,277
% used for R-free calculations	10	7	10	7	5		5	5	5
R-factor including all data (%)	16.2	18.9	17.6	17.74	11.32		13.92	14.13	13.77
R-free (%)	20.7	21.7	21.6	22.91	15.48		18.73	18.30	18.75
No. of protein atoms	1670	1684	1666	1697	1728		1699	1670	1687
No. of water molecules	75	109	73	179	286		225	194	254
No. of other solvent molecules	—	—	1 MPD	2 SO42−	5SO42−, 2 GOL, 1 Tris		1 GOL	1 GOL	1 GOL
No. of alternative side-chain conformations	1	5	—	4	14		10	6	7
Mean B-factors (Å2)
All atoms	11.06	15.68	11.98	14.16	15.47		16.94	17.42	18.08
Protein	10.71	14.84	11.49	12.86	13.21		15.77	16.97	16.98
Water molecules	18.99	27.60	20.44	24.60	27.49		26.00	23.04	24.87
Inhibitor	7.57	22.01	19.96	—	17.54		24.48	47.00	—
RMS deviations from ideal geometry
Bond lengths (Å)	0.008	0.011	0.008	0.009	0.015		0.015	0.011	0.015
Angles	1.726°	1.756°	1.753°	0.024 Å	0.032 Å		0.031 Å	0.028 Å	0.032 Å
Luzatti (1952) coordinate error (Å)	0.15	0.17	0.17	0.13	0.06		0.07	0.08	0.08

Table 4.

Intermolecular hydrogen bonds (Å) involving the inhibitor atom(s) NH1, NH2, or Nζ, or the OW3 molecule in the anionic salmon trypsin structures

	AST-1BZA		AST-2BEA	AST-3PEA	AST-4PPA	AST-Free	AST-BPT1
Contacts to	NH1	NH2	NH1	NH1	NH1	OW3	Nζ
Asp 189 Oδ1	2.87	(3.73)	3.33	3.14	3.46	2.85	3.35
Asp 189 Oδ2	(3.55)	2.84	2.70	(3.55)	(3.73)	3.18	(3.73)
Ser 190 O	3.17	3.34	2.86	3.16	3.07	2.93	2.78
Ser 190 Oγ	3.04			3.15	3.01	3.40	3.07
Gly 219 O		2.87	3.13
OW1			2.97	2.79	2.75	2.72	2.96
OW2	2.95			2.94	3.08	3.45	3.05
Cys 191 C-Trp 215 C		7.83	8.05	8.46	8.23	8.10	8.28
Relative B-factor of inhibitor		1.03	0.71	1.48	1.74		0.48a

Distances longer than 3.5 Å are given in parentheses, and the width of the pocket is taken as the Cys 191 C to Trp 215 C distance. Relative B-factors the inhibitors (〈B-factor_inhib〉/〈B-factor_prot〉) are also included.

^a Side-chain atoms only.

Table 5.

Intermolecular hydrogen bonds (Å) involving the inhibitor atom(s) NH1 or NH2, or the OW3 molecule in the bovine trypsin structures and cationic salmon trypsin (CST-1BZA)

	BT-1BZA		BT-2BEA	BT-ANL	BT-3PEA	BT-5PBA	BT-Free	CST-1BZA
Contacts to	NH1	NH2	NH1	NH1	NH1	NH1	OW3	NH1	NH2
Asp 189 Oδ1	2.87	(3.78)	3.34	3.48	3.35	3.36	2.93	2.88	(3.78)
Asp 189 Oδ2	(3.51)	2.92	2.79	(3.99)	(3.74)	(3.61)	3.12	(3.48)	2.89
Ser 190 O	3.22	3.40	2.77	3.10	3.00	2.78	2.66	3.17
Ser 190 Oγ	3.04			2.97	3.14	3.16	3.21	3.01
Gly 219 O		2.82	2.90						2.86
OW1			2.94	2.84	2.90	2.99	2.81
OW2	3.13			2.86	3.11	3.44	(3.81)	3.28
Cys 191 C-Trp 215 C		7.98	8.35	8.33	8.30	8.22	8.25		7.83
Relative B-factor of inhibitor		1.56	1.33	2.30	1.55	3.22			0.78

Distances longer than 3.5 Å are given in parentheses, and the width of the pocket is taken as the Cys 191 C to Trp 215 C distance. Relative B-factors for the inhibitors (〈B-factor_inhib. 〉 /〈B-factor_prot.〉) are also included.

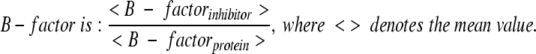The electron density maps of the AST structures given in Figure 2 ▶ show that the smallest inhibitor (2BEA) is best defined in the 2F_o–F_c map, whereas the longer (3PEA, 4PPA) have poorer electron density. This is particularly pronounced for the carbon attached to the amine nitrogen of the inhibitor (the NH1 atom), which implies some degree of flexibility in this region. Also, the phenyl rings of 3PEA and 4PPA are not fully defined in the electron density maps, reflected through higher relative B-values for the inhibitors (Table 4). On the contrary, the electron density of the inhibitor in the previously reported AST-1BZA is very precise (Fig. 2A ▶; Leiros et al. 2001).

Figure 2.

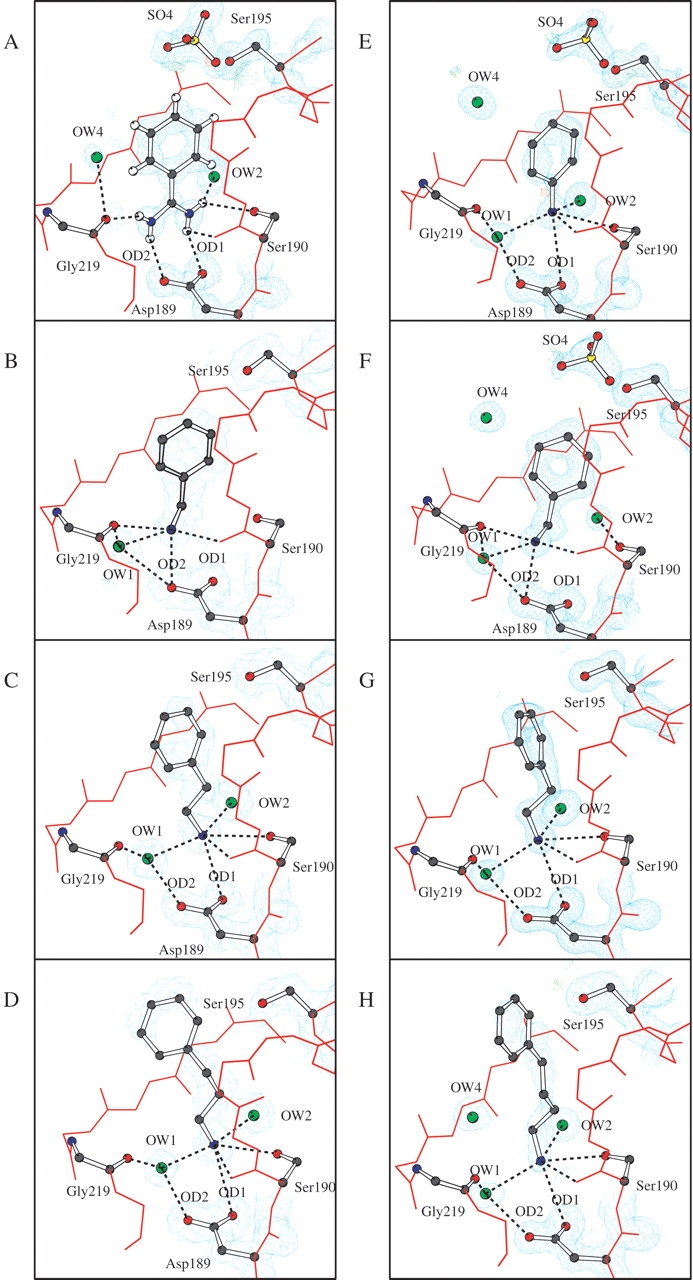
Structural arrangements, 2F_o–F_c (cyan) electron density maps and Fourier difference maps (Fo–F_c) at +4σ(green) and -4σ (red) of the active site of AST (A–D) and BT (E–H). The inhibitors are (A) benzamidine AST-1BZA, (B) benzylamine AST-2BEA, (C) phenylethylamine AST-3PEA, (D) phenylpropylamine AST-4PPA, (E) aniline BT-ANL, (F) benzylamine BT-2BEA, (G) phenylethylamine BT-3PEA, and (H) phenylbutylamine BT-5PBA. Ser 190 is not covered by electron density and only selected hydrogen bonds are included to simplify the figure created by BobScript (Esnouf 1997). The sigma levels of the 2F_o–F_c maps are 1.1–1.5 (AST) and 1.5–1.7 (BT).

The BT-ANL structure has been presented elsewhere (Leiros et al. 2001), but details of the inhibitor interactions will be discussed here. The observed negative difference electron density adjacent to NH1 and one poorly defined C-C bond in the ring (Fig. 2E ▶) is likely to be explained by a genuine occupancy of the inhibitor lower than 1. The inhibitor and three surrounding water molecules are well defined in the electron density maps in the BT-2BEA structure (Fig. 2F ▶). When BT is inhibited by 2BEA, the amine is very well defined in electron density maps and three water molecules surround the inhibitor (Fig. 2F ▶). For the two longer inhibitors, 3PEA and 5PBA, the carbon next to NH1 is well defined (Fig. 2G,H ▶), which is not the case for AST-3PEA or AST-4PPA. Although the phenyl ring of BT-5PBA could be placed at different positions, we chose the one that best fitted the observed 2F_o–F_c electron density.

Five water molecules with well-defined electron densities are found in the S1 binding site of the AST-Free structure. OW5 has a somewhat larger density compared with the other water molecules, and could be a disordered ANL molecule (data not shown). In the BT-Free structure, there are four water molecules filling the active site. These waters in both structures superimpose very well on the corresponding solvent molecules in BT-K15G, which also has an “empty” active site because the P1 residue of BPTI is mutated.

Structural comparison

The superposition of the present trypsin amine inhibitor complexes onto the respective AST-1BZA (Fig. 3A ▶) and BT-1BZA (Fig. 3B ▶) complexes shows that the inhibitor amine nitrogen persistently occupies one of the guanidine nitrogen positions of 1BZA. The amine group is turned toward Gly 219 (Position1) in the BEA and its analogs (AST-2BEA, BT-2BEA, BT-AMC, BT-FBA; Fig. 4C ▶), whereas it is turned in the opposite direction (Position2), toward Ser 190, in the complexes with longer inhibitors (3PEA, 4PPA, 5PBA; Fig. 3A,B ▶). The principal interactions in Position1 involve contacts to Asp 189 Oδ2, Ser 190 O, Glu 219 O, and OW1, whereas the main interactions in Position2 are with Asp 189 Oδ1, Ser 190 O, Ser 190 Oγ, OW1, and OW2 (Tables 4, 5; Fig. 4 ▶). The latter orientation is also in accordance with the binding of the lysine side chain in the trypsin BPTI complexes (Rühlmann et al. 1973; Helland et al. 1998). The water mediated (OW1) hydrogen bonds between the inhibitor amines and Asp 189 are replaced with direct bonds to Asp 189 and Gly 219 in the 1BZA complexes. The water molecule (OW2) that bridges the amine nitrogen and the carbonyl oxygens of Val 227 and Trp 215 of AST and BT is also present in the 1BZA complexes. A second water molecule (OW2) that bridges the amine nitrogen and the carbonyl oxygens of Val 227 and Trp 215 of trypsin is also present in the 1BZA complexes. To summarize, there are no significant differences between the AST and BT inhibitor binding interactions as judged from the crystal structures, and the 1BZA binding pattern is identical among AST, CST, and BT, as previously reported (Smalås et al. 1994; Schrøder et al. 1998).

Figure 3.

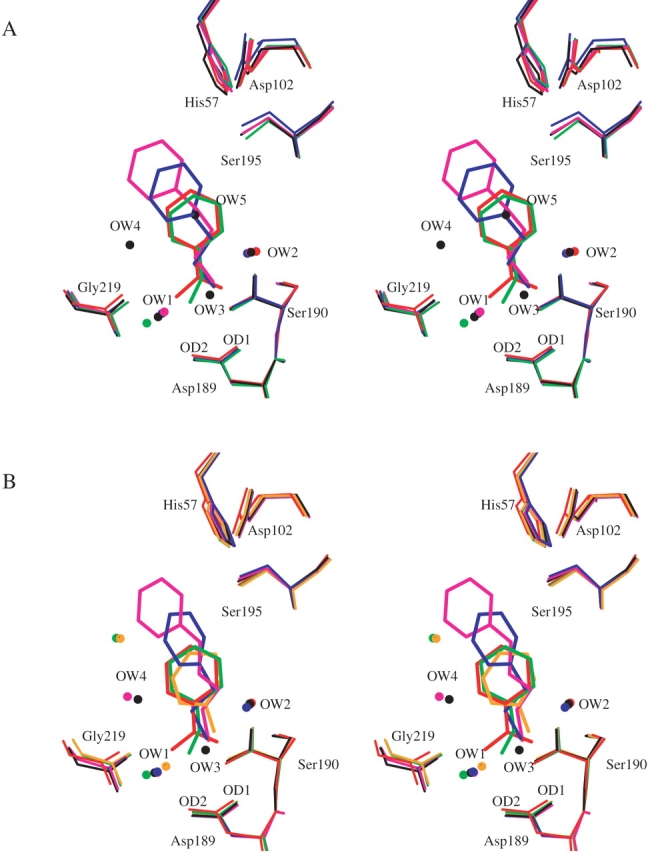
(A) Superposition of the active site clefts of the five AST structures AST-1BZA (red), AST-2BEA (green), AST-3PEA (blue), AST-4PPA (magenta), and no inhibitor AST-Free (black). (B) The S1 site of BT with BT-1BZA (red), BT-2BEA (green), BT-ANL (orange), BT-3PEA (blue), BT-5PBA (magenta), and no inhibitor BT-Free (black).

Figure 4.

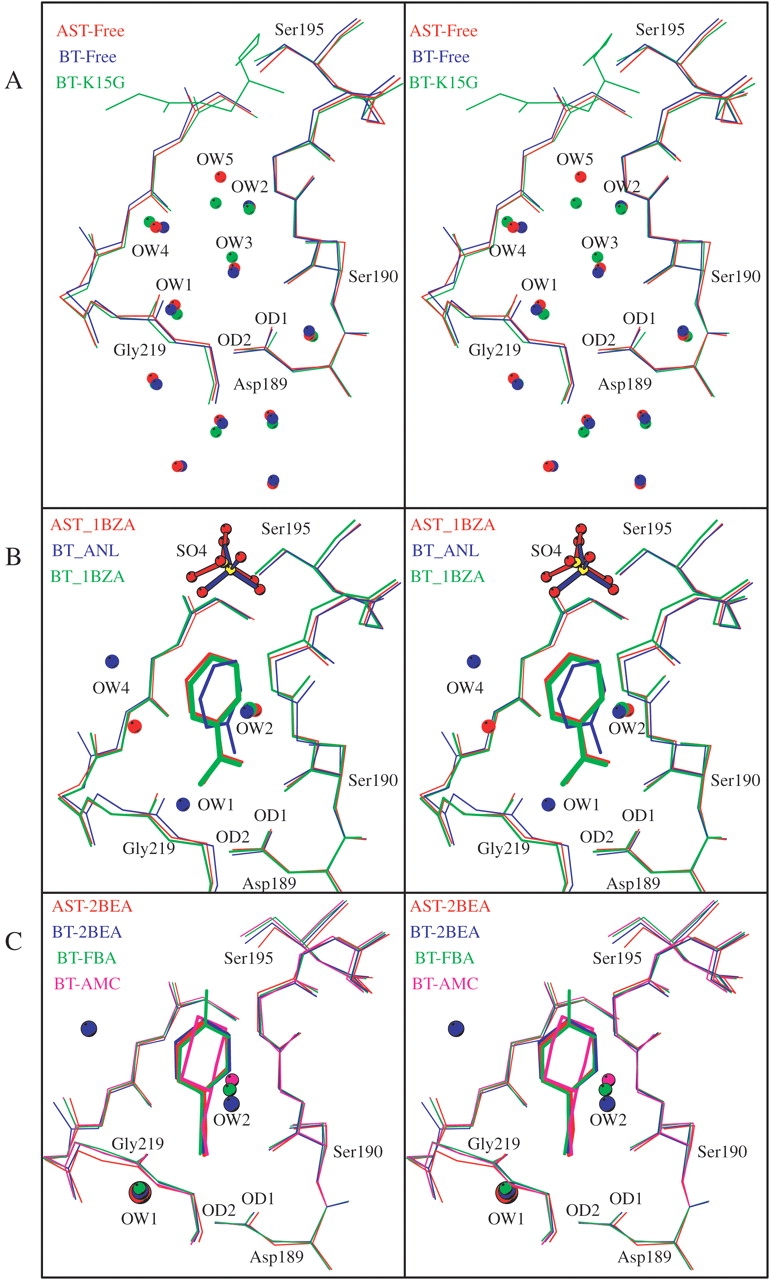
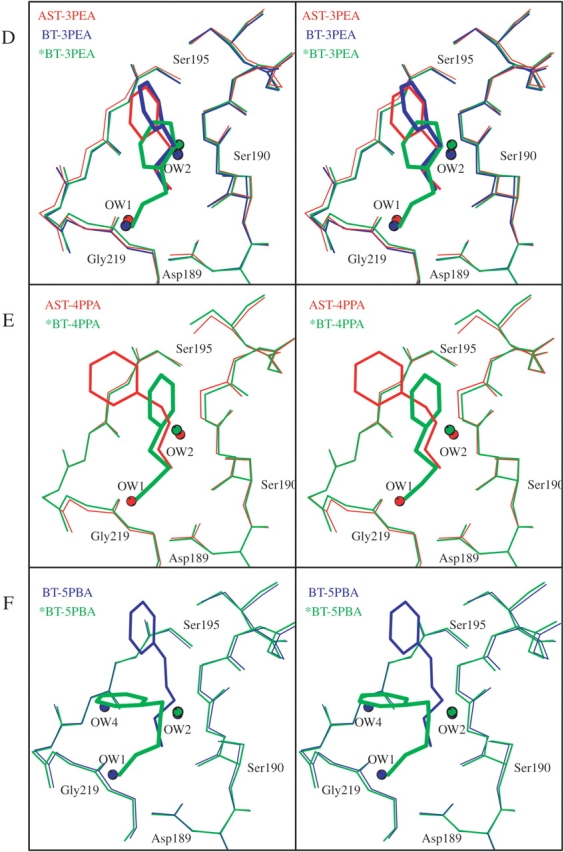
Arrangement of the superimposed S1 binding pockets and water molecules of (A) AST-Free (red), BT-Free (blue), and BT-K15G with the main chain of the BPTI residues 14–16 (green); (B) AST-1BZA (red), BT-ANL (blue), and BT-1BZA (green); (C) AST-2BEA (red), BT-2BEA (blue), BT-FBA (green), and BT-AMC (magenta); (D) AST-3PEA (red), BT-3PEA (blue), and *BT-3PEA (1TNJ; green); (E) AST-4PPA (red) and *BT-4PPA (1TNK; green); and (F) BT-5PBA (blue) and *BT-5PBA (1TNI; green). The structures with an asterisk (*) are from Kurinov and Harrison (1994).

The orientations and positions of the phenyl groups are to a high degree conserved for all the short-chain inhibitors (1BZA, 2BEA, ANL, AMC, FBA), whereas the phenyl groups of the longer inhibitors are moved toward the active site entrance according to their increasing length (Fig. 3A,B ▶). The latter will thus be much more exposed to solvent when bound to the active site of the trypsins as compared with the short chain. Although the phenyl group of ANL in the BT-ANL complex is slightly rotated compared with the other short-chain inhibitors, it is buried equally deep in the pocket, as shown in Figure 4B ▶.

Kurinov and Harrison (1994) have previously reported a specificity pocket arrangement corresponding to our observations for the short-chain synthetic inhibitors (AMC, FBA) in complex with BT, where the amine group at Position1 interacts with Gly 219, similar to the situation in AST-2BEA and BT-2BEA. For the longer inhibitors of that study (3PEA, 4PPA, 5PBA), however, a binding pattern different from ours was reported (Fig. 4D ▶–F). They report the three inhibitors to bind deeper in the pocket, with the amino group at the position of our OW1, forming direct interactions to Asp 189 Oδ2 (2.7–2.8 Å), and the second carbon atom attached to NH1 located <3.0 Å from Ser 190 O flanking Position2. In addition, 5PBA in the previously reported BT-5PBA structure have the phenyl group bent toward one of the pocket walls, covering the OW4 water position in our BT-5PBA structure (Fig. 4F ▶).

Calculated binding constants

The free energies for binding five of the synthetic inhibitors given in Figure 1 ▶ to AST, CST, and BT, respectively, have been calculated with the LIE method (Åqvist et al. 1994). The individual contributions from polar (V_el) and nonpolar (V_vdw) interactions are shown in Table 6, and the resulting calculated association energies (ΔG_calc) are shown in Table 7. To facilitate the discussion, we transformed the measured association constants (K_a-values in Table 1b) into ΔG_exp in kcal/mole (ΔG_exp = −(RT ln K_a)), as given in the table. The LIE calculations correctly predict that 1BZA binds far more strongly than any of the other synthetic inhibitors studied here for all three trypsins. Furthermore, the calculations also show that 1BZA binds more favorably to AST and CST as compared with BT. In terms of absolute free energies, the calculated values for 1BZA deviate up to about 1.3 kcal/mole from the measured values. The ΔG_calc for 1BZA is in the order of 4–5 kcal/mole more favorable than the second strongest inhibitor, whereas the measured energies show corresponding differences in the range of 1.6–1.9 kcal/mole for the three trypsins. The relative order of association for the weaker amine inhibitors is also reproduced. The largest deviation is found for BT bound to 2BEA, for which the calculations predict a binding free energy of −2.4 kcal/mole, a value 2.3 kcal/mole more positive compared with the experimental value (−4.7 kcal/mole). In this case, the BT-2BEA simulation started from the X-ray structure with the amine nitrogen in the position where it binds to Gly 219, but during the MD simulations, the inhibitor amine switches interaction pattern and a water molecule gets trapped at the initial amine position. Thus, the calculated too positive binding free energy for this inhibitor with BT is caused by a significant change in the principal hydrogen-binding network. Once this network of hydrogen bonds is broken, the amine flips and interacts with Asp 189 from the second position toward Ser 190. However, this is also observed in both AST and CST, but here the inhibitor alternates between the two positions.

Table 6.

Averaged ligand-surrounding interaction energies (kcal/mole) from the MD simulations

	AST		CST		BT		Water
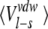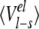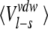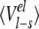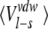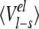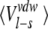1BZA	−141.7	−12.6	−142.5	−12.5	−142.6	−12.1	−129.9	−1.5
2BEA	−139.3	−16.3	−141.4	−16.5	−138.4	−16.5	−136.6	−4.5
3PEA	−142.8	−16.4	−142.1	−17.1	−142.4	−16.5	−139.4	−6.1
4PPA	−141.8	−20.4	−144.0	−18.9	−141.6	−19.4	−141.5	−7.7
5PBA	−143.2	−22.4	−142.5	−20.6	−144.4	−21.5	−142.2	−9.5

Table 7.

Calculated binding constants (ΔG_calc) for the inhibitors bound to AST, CST, and BT

	AST					CST					BT
	ΔGel	ΔGvdw	Suma	Gcalcb	ΔGexp	ΔGel	ΔGvdw	Suma	Gcalcb	ΔGexp	ΔGel	ΔGvdw	Suma	Gcalcb	ΔGexp
1BZA	−5.9	−2.0	−7.9	−8.6	−7.1	−6.3	−2.0	−8.3	−8.0	−6.8	−6.4	−1.9	−8.3	−7.6	−6.3
2BEA	−1.4	−2.1	−3.5	−4.2	−5.2	−2.4	−2.2	−4.6	−4.3	−5.0	−0.9	−2.2	−3.1	−2.4	−4.7
3PEA	−1.7	−1.9	−3.5	−4.2	−4.1	−1.3	−2.0	−3.3	−3.0	−4.1	−1.5	−1.9	−3.3	−2.6	−3.1
4PPA	−0.1	−2.3	−2.4	−3.1	−3.3	−1.2	−2.0	−3.2	−2.9	−3.7	0.0	−2.1	−2.1	−1.4	−2.1
5PBA	−0.5	−2.3	−2.8	−3.5	−3.2	−0.2	−2.0	−2.2	−1.9	−3.7	−1.1	−2.2	−3.3	−2.6	−2.0

Δ G_exp = (−RT ln K_a)/4180 (kcal/mole), and K_a is from Table 1b.

^a Long-range contribution from interactions between the ligand and the protein outside the simulations sphere, estimated using a Coulombic potential with high dielectric constant.

^b The error in the calculated binding free energies is between 0.5 and 1.0 kcal/mole based on the difference in the free energies calculated from the first and the second half of the production phase of the simulations.

Discussion

The characterization of the three-dimensional structure and the energetics involved is one of the key elements required to understand many biological functions, and the interplay between experimental and theoretical research plays a central role in the understanding of molecular recognition at the atomic level. In this study, we have determined association constants for binding of five different inhibitors to three different trypsins, and eight X-ray structures have been solved to high resolution. The energetics of these complexes have further been examined by carrying out free energy calculations using molecular dynamics simulations and the LIE method.

The role of the primary binding (S1) site of trypsin is well documented from mutation studies and from crystal structure analysis. Previous studies have shown that a number of factors are responsible for binding of ligands to the S1 site of trypsin. The electrostatic interaction between Asp 189 and positively charged ligands is the primary specificity determinant, but effects from hydrophobic interactions, solvation energies, and optimization of water-mediated hydrogen bonding networks are also important factors in mediating binding specificity. Crystal structures of protein–ligand complexes at atomic resolution, and thermodynamic studies, are an important source of information for further exploring such fundamental questions. Resolving such issues is of great importance in a number of different fields and plays a fundamental role in studies of molecular recognition in general. When it comes to structure-based ligand design, information at the atomic level along with thermodynamic data are the only way to calibrate and develop more accurate scoring functions and efficient docking algorithms.

Overall binding pattern

The present study demonstrates that a wide range of amine and amidiniumtype molecules inhibits trypsin, but the great variation in inhibition potential is not fully understood. For example, the P1-Arg mutant of BPTI binds in the order of ~10¹⁵ M⁻¹ (K_a, Krowarsch et al. 1999), whereas 1BZA binds in the range of ~10⁵ M⁻¹ and the similar amine inhibitors have a K_a <~10² M⁻¹. By using the trypsin 1BZA complex as a reference, the amine group of all the other inhibitors superimposes approximately with one of the amidinium nitrogens of 1BZA. In general, the crystal structures show that the amine group of the inhibitor is directed toward one particular side of the S1 pocket, bound to Gly 219 O (Position1), in the 2BEA complexes, whereas it is directed toward the opposite side, and bound to Ser 190 Oγ(Position2), in the other complexes (Fig. 4C ▶–F). The interaction distances to Asp 189 are, however, significantly longer for the inhibitors bound at Position2 (3.1–3.5 Å) compared with 1BZA and 2BEA (2.7–2.9 Å; c.f. Tables 4,5), which in part give rise to the marked drop in association energy (Table 1b). No significant difference in the interaction pattern among the three trypsins is observed on accommodating the various ligands; the same binding mode is observed for each ligand with all three trypsins.

Kurinov and Harrison (1994) have studied binding of 2BEA analogs to BT (BT-FBA and BT-AMC) using X-ray crystallography, and a binding arrangement with the amine nitrogen atoms in Position1 is observed for these analogs. However, their interpretation of complexes with longer amine inhibitors shows a totally different binding pattern compared with our results. Superimposing their models of BT complexed with 3PEA, 4PPA, and 5PBA onto our models (Fig. 4D ▶–F) reveals that the inhibitors are placed deeper into the pocket. Their NH1 atoms have replaced the OW1 molecule and the second carbon connected to NH1 occupies Position2, which is usually a cation-binding site. The results from Kurinov and Harrison thus show a highly unusual binding arrangement of an amine type of ligand to trypsin, and to our knowledge this has not been seen for any other trypsin inhibitor complexes, neither with proteinase inhibitors (Rühlmann et al. 1973; Helland et al. 1998, 1999a,b) nor with complexes with small molecules (Whitlow et al. 1999; Maignan et al. 2000; Toyota et al. 2001). Our crystallization conditions are identical to those of Kurinov and Harrison, but nevertheless resulted in different space groups, P2₁2₁2₁ and P3₁21, respectively. It is not obvious that a change in space group alone could give rise to such a difference, but we have no other plausible explanation for the dissimilarities in inhibitor binding pattern.

Experimental and theoretical association energies

The association measurements show that 1BZA is the most potent trypsin inhibitor of the five ligands included here, and it binds 1.6–1.9 kcal/mole more favorably than the second-best inhibitor, depending on the trypsin. The association energies for the amines increase with increasing chain length, making them less potent as trypsin inhibitors. The trend is similar for all three trypsins, but the reduction is more pronounced for BT than for AST and CST. In order to address the variation in the binding capacity among these ligands, free energy calculations were carried out using the LIE approach. With this method, the binding free energy is estimated as a sum of polar and nonpolar contributions, making the method a good choice to study the difference in binding capacity. Furthermore, the method is also one of few that allows the absolute binding free energy to be estimated, not only the relative such as with free energy perturbation and thermodynamic integration techniques (for reviews, see Kollmann 1993; Brandsdal et al. 2003).

All of the ligands investigated are ionizable and carry a net charge at pH 8.3 where the association measurements were performed. Because these ligands, except for 1BZA, are highly flexible, the estimation of the absolute binding free energies was very challenging. In particular, it was difficult to obtain stable and converged ligand-surrounding energies for the bound state, as the ligand is involved in an extensive hydrogen bonding network with several water molecules as well as with charged residues in the protein. This delicate water-mediated hydrogen bonding network is actually the key to obtaining the correct binding free energies. The failure to reproduce the interaction pattern is clearly demonstrated by the 2BEA simulation when bound to BT, yielding a binding free energy 2.3 kcal/mole too positive. Nonetheless, the LIE method gave ΔGs that agree well with the experimental data, particularly for AST and CST, in which not only is the deviation from experiments low, but also the ranking of the ligands is very well reproduced. From the calculated free energies, the variation in the inhibition potency among the ligands seems to arise predominantly from subtle differences in the electrostatic interactions. As mentioned previously, the association constant becomes smaller (i.e., weaker binding or inhibition) when the length of the aliphatic chain of the amine increases. The LIE calculations clearly show that this is mainly caused by a change in the polar contribution to the free energy of binding (i.e., of electrostatic origin). In fact, the nonpolar contribution varies only with 0.2 to 0.4 kcal/mole, whereas the experimental free energy varies with 3.1 to 4.3 kcal/mole, depending on the ligand and the trypsin. The nonpolar contribution to the binding free energy is therefore virtually constant regardless of the ligand and trypsin, emphasizing the role of electrostatic interactions when explaining the variation in binding strength.

Cold-adaptation

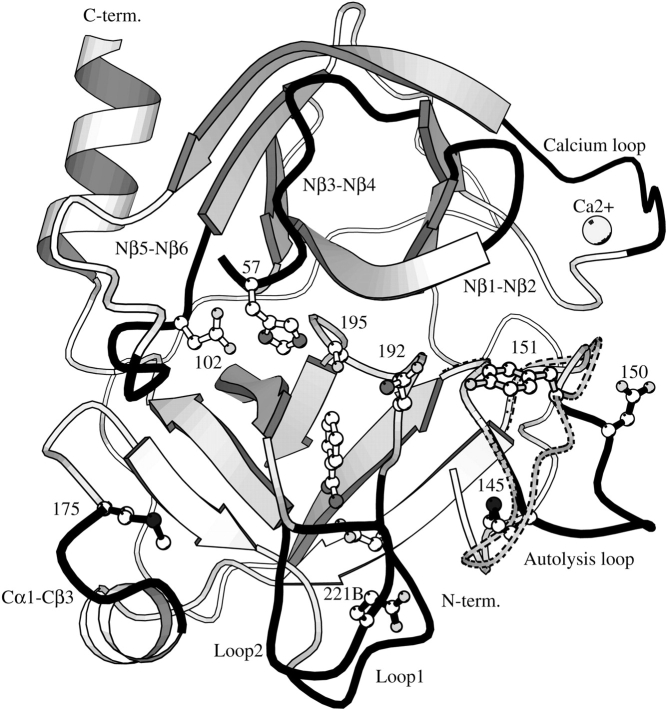
Electrostatic interactions have been found to be an important feature of the cold-adaptation of the AST (Smalås et al. 1994; Leiros et al. 2000; Brandsdal et al. 2001b). Indeed, enhanced primary binding has been suggested to be an important factor when explaining the higher catalytic efficiency of AST relative to CST, BT, and porcine trypsin (Outzen et al. 1996). Increased catalytic activity is also observed for other cold-adapted trypsins (Osnes and Mohr 1985; Genicot et al. 1988; Ásgeirsson et al. 1989) and mainly attributed to lower K_m values. Continuum electrostatics calculations showed that the active site of AST is more negatively charged in comparison to BT. This is primarily caused by the negative charges of Asp 150 and Glu 221B (shown in Fig. 5 ▶), indicating that enhanced electrostatic interactions could be a source of the observed 10-fold reduction in K_m (Gorfe et al. 2000). Our previous LIE calculations (Brandsdal et al. 2001b), where 1BZA and P1 Arg and Lys variants of BPTI were bound to AST and BT, showed that the more favorable binding of these ligands to AST was caused by more optimized electrostatic interactions.

Figure 5.

Ribbon diagram defining secondary structure element of AST. The loops that determine the S1 and subsite specificity of the chymotrypsin fold class of serine proteinases (Perona and Craik 1997) are colored in black: Nβ1-Nβ2 loop (res. 34–41), Nβ3-Nβ4 loop (56–64), the calcium binding loop (74–80), Nβ5-Nβ6 loop (97–103), autolysis loop (143–151), Cα1-Cβ3 loop (169–175), Loop1 (185–188A), and Loop2 (217–225). The most important cold-adapted determinants are shown in black (Met 145, Met 175, Asp 150, Glu 221B), along with the catalytic triad (Asp 102, His 57, Ser 195), Asp 189, the 1BZA inhibitor, the calcium ion, and Gln 192. The autolysis loop (dotted lines) and Tyr 151 of BT are also included.

The main contribution to the total binding free energy is expected to arise from interactions within the S1-binding site for all of the ligands regardless of which trypsin they bind to, and that these forces are predominantly of short-range nature. The association measurements clearly show that the cold-adapted trypsin (AST) is more strongly inhibited by the positively charged ligands studied here, as compared with its warm-active counterpart (BT). This effect is most pronounced for binding of 1BZA, but it is also consistent for the less potent inhibitors. Despite this difference in binding capacity, the principal interactions in the active site cleft are virtually identical as judged from the high-resolution structures presented here, and also further supported by the free energy calculations, which show more or less the same interaction energies among the different enzymes for a given ligand (Tables 6, 7). However, the relative differences in binding are reproduced only when the contribution from distant ionic residues is added to the free energy (yielding ΔG_calc in Table 7). This contribution is −0.7, 0.3, and 0.7 kcal/mole for AST, CST, and BT, respectively, with the sign of this contribution reflecting the overall charge of the molecule. Other explanations for the increased catalytic capacity of AST compared with BT and CST have been found among the residues and structural features unique to the cold-adapted trypsins that are not found in CST (Leiros et al. 2000). These include the lack of Tyr 151 in AST, the unique orientation of residues 145–153 in the autolysis loop, the reduced interactions for the C-terminal residues, and the presence of the long residues Met 145 and Met 175 (Fig. 5 ▶), which together give the cold-adapted AST and CHST increased local flexibility that can explain the higher catalytic abilities.

Thus, the present study adds strong support to the hypothesis that electrostatic interactions play an important role in explaining the cold-adaptation of AST and its higher catalytic efficiency. It also confirms that the primary binding pattern is highly conserved but subtle differences arising from long-range effects cause the differences in binding affinities among the three trypsins studied here.

Materials and methods

Association constant measurements

AST and CST used for the binding constants measurements and structure determination were purified from the pancreatic tissue of Atlantic salmon (Outzen et al. 1996) and BT was purchased from Sigma (Type III).

The determination of association constants for the interactions between synthetic inhibitors and trypsin was performed using the Dixon method. Concentration of trypsins was determined by titration with 4-nitrophenyl 4-guanidinobenzoate (Chase and Shaw 1970). First, the steady-state parameters for the hydrolysis of the sensitive trypsin substrate Tos-Gly-Pro-Arg-pNA was determined in 100 mM Tris, 20 mM CaCl₂ (pH 8.3) with a diode array spectrophotometer HP 8452A, as given in Table 1a. The calculated initial rates of the reaction were fitted by application of the nonlinear least squares analysis to the Briggs-Haldane equation. The final volume of the reaction mixture (1.8 mL) included 1 × 10⁻¹⁰ M to 4 × 10⁻¹⁰ M trypsin, and the substrate concentration varied from 0.1 × K_m to about 3 × K_m. The dissociation constants (K_d) were determined in similar experiments, keeping the substrate at a constant concentration. The inhibitor concentration varied from K_d to 0.3 × K_d. The dissociation constants were determined from the Dixon plot:

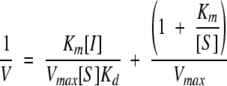Finally, the association constants (K_a) were calculated (K_a = 1/K_d), and given in Table 1b.

Crystallization and data collection

Cocrystallization of AST and BT with the synthetic inhibitors (Fig. 1 ▶) was done by the hanging drop method. Crystals of AST were grown at 37°C with reservoir solutions of 0.7 M ammonium sulfate, 10 mM CaCl₂, and 50 mM sodium citrate-phosphate (pH 6.0), and an initial protein concentration of 10 mg/mL (Berglund et al. 1995). One hundred millimolar of the inhibitors was added to the reservoirs, and, in order to dissolve the longest inhibitors (3PEA, 4PPA, 5PBA), it was necessary to add 10%–15% MPD. Crystals of BT were grown at room temperature with reservoir solutions containing 23%–25% polyethylene glycol 8000, 0.2 M ammonium sulphate, 0.1 M Tris buffer (pH 8) and 100 mM inhibitor, and an initial protein concentration of 15 mg/mL (Kurinov and Harrison 1994). Data were collected at ID14-EH4 and the Swiss Norwegian Beamline (SNBL), both at the European Synchrotron Radiation Facility (ESRF) in Grenoble, France, and at X31, DESY-lab, Hamburg, Germany. All data were integrated using DENZO (Otwinowski 1993), and scaling and merging were performed with SCALA from the CCP4 program suite (Collaborative Computational Project, No. 4 1994). Low R-merge values (4.8%–7.8%) and high completeness (90%–99%) were obtained for all complexes. See Tables 2 and 3 for details.

Phase determination and refinement

A new and third crystal form was found for the AST structures AST-2BEA and AST-4PPA. Initial phases for AST-2BEA were found by molecular replacement in AMoRe (Navaza 1994) with the AST crystal form II (PDB entry 1BIT) as a search model. The cross rotation and translation searches were done with data from 15–4.0 Å and an integration radius of 20 Å. The resulting Crowther angles and fractional translation vectors were α= 38.83, β= 65.97, γ= 263.42, T_x= −0.6188, T_y = 0.4560, and T_z = 1.0888. For the other AST structures, rigid body optimization from previously refined AST structures was sufficient (PDB entry 1BIT or 1HJ8; Berglund et al. 1995^; Leiros et al. 2001). The phases for the BT structures were obtained using rigid body optimization from 1TNK (P2₁2₁2₁) or 1C1Q (P3₁21) (Kurinov and Harrison 1994; Katz et al. 1998).

All structures were subjected to one cycle of simulated annealing (3000 K) in X-PLOR (Brünger 1992) using all data from 15 Å to the maximum resolution. Further refinement included alternate cycles of conjugated-gradient minimization and restrained temperature factor refinement with data from 8.0 Å to maximum resolution and rebuilding of the models using the graphics program O (Jones et al. 1991). Five percent to 10 percent of the data was kept out of refinement for cross validation, and the models were refitted on the basis of σ_a-weighted (Read 1986) 2F_o–F_c and F_o–F_c electron density maps. Solvent molecules were added to the models in which the difference density exceeded 3.5σ. For the structures refined with SHELXL (Sheldrick and Schneider 1997), rigid hydrogen atoms were added on all residues except the hydroxyl groups of Ser, Thr, and Tyr and the nitrogen atoms of the His side chains. Anisotropic B-factors were refined for the structures resolved to the highest resolution: AST-Free (free refers to no inhibitor), BT-2BEA, BT-3PEA, BT-5PBA, and BT-Free.

Structural comparison

The structures were compared by using the LSQKAB and CONTAC programs of the CCP4 program suite (Collaborative Computational Project, No. 4 1994) and O (Jones et al. 1991). Criteria for hydrogen bonds were a maximum distance of 3.5 Å between donor and acceptor, and a maximum angle of 120° O^…H-N bonds and 90° O^…O-C bonds.

Computational analysis

The interactions between the five synthetic inhibitors (Fig. 1 ▶) and AST, CST, and BT were subjected to computational analysis by the LIE method (Åqvist et al. 1994, 2002; Brandsdal et al. 2003).

The LIE approach estimates the polar and nonpolar contribution to the binding affinity separately using:

where < > is the molecular dynamics average of the nonbonded van der Waals (vdw) and electrostatic (el) interactions between the ligand and its surrounding environment (l-s). The Δ represents the change in these average energies between the bound and free states, and α and β are weight coefficients for the nonpolar and polar contribution, respectively. Here, we have used α = 0.18 and β = 0.5, because these values have previously been applied to trypsin with success (Wang et al. 1999; Brandsdal et al. 2001a).

Calculation of the absolute binding free energies of the ligands binding AST, CST, and BT was initiated from the six complex crystal structures presented here (Tables 3, 4), along with the high-resolution-resolved AST-1BZA and BT-ANL complexes (entries 1HJ8, 1HJ9; Leiros et al. 2001) and the CST-1BZA crystal structure (PDB entry 1A0J, Molecule B; Schrøder et al. 1998). The remaining complexes (AST with 5PBA, BT with 4PPA, CST in complex with the four amine inhibitors) were constructed from corresponding crystal structures with preservation of the hydrogen binding network and water molecules in the binding pocket (Fig. 4 ▶).

The free energy calculations were performed using the molecular dynamics program Q (Marelius et al. 1998) with the OPLS-AA force field (Jorgensen et al. 1996). Atomic charges for the ligands were set according to the force field scheme. The computational protocol used throughout the calculations is identical to the protocol described by Brandsdal et al. (2001a) except that an 18 Å simulations sphere was used here. The simulation center was defined to be the nitrogen atom of the amine ligands, and the carbon atom in the amidinium group of 1BZA. The nonbonded potentials involving the ligands were not subjected to any truncation schemes. Ionizable residues within 15 Å of the simulation center were considered charged along with the N-terminal residue, whereas distant ionizable residues were described using a neutral charge set. The contributions from these charges were taken into account using a screened Coulombic potential with ɛ = 80, because this has been found (Brandsdal et al. 2001b) to yield essentially the same contribution as with the sigmoidal dielectric function of Mehler and Eichele (1984). The production phase in which the ligand-surrounding interaction energies were sampled was 375 psec for all of the simulations.

Abbreviations

• AST, anionic salmon trypsin

• CST, cationic salmon trypsin

• BT, bovine trypsin

• CHST, chum salmon trypsin

• 1BZA, benzamidine

• 2BEA, benzylamine

• ANL, aniline

• AMC, aminomethylcyclohexane

• FBA, 4-fluorobenzyl

• 3PEA, phenylethylamine

• 4PPA, phenylpropylamine

• 5PBA, phenylbutylamine

• BPTI, bovine pancreatic trypsin inhibitor

• AST-BPTI, AST complexed with BPTI (1BZX)

• BT-1BZA, BT complexed with benzamidine (3PTB)

• BT-FBA, BT with 4-fluorobenzylamine (1TNH)

• BT-AMC, BT with amino-methylcyclohexane (1TNG)

• BT-3PEA, BT with phenylethylamine (1TNJ)

• BT-4PPA, BT with phenylpropylamine (1TNK)

• BT-5PBA, BT with phenylbutylamine (1TNI)

• BT-K15G, BT complexed with BPTI and P1 Gly (3BTG)

• BT-K15F, BT complexed with BPTI and P1 Phe (3BTP)

• LIE, linear interaction energy

• MPD, 2-methyl-2,4-pentanediol

• GOL, glycerol

• MD, molecular dynamics