Mimicking the action of folding chaperones in molecular dynamics simulations: Application to the refinement of homology-based protein structures

Abstract

A novel method for the refinement of misfolded protein structures is proposed in which the properties of the solvent environment are oscillated in order to mimic some aspects of the role of molecular chaperones play in protein folding in vivo. Specifically, the hydrophobicity of the solvent is cycled by repetitively altering the partial charges on solvent molecules (water) during a molecular dynamics simulation. During periods when the hydrophobicity of the solvent is increased, intramolecular hydrogen bonding and secondary structure formation are promoted. During periods of increased solvent polarity, poorly packed regions of secondary structures are destabilized, promoting structural rearrangement. By cycling between these two extremes, the aim is to minimize the formation of long-lived intermediates. The approach has been applied to the refinement of structural models of three proteins generated by using the ROSETTA procedure for ab initio structure prediction. A significant improvement in the deviation of the model structures from the corresponding experimental structures was observed. Although preliminary, the results indicate computationally mimicking some functions of molecular chaperones in molecular dynamics simulations can promote the correct formation of secondary structure and thus be of general use in protein folding simulations and in the refinement of structural models of small- to medium-size proteins.

There is a pressing need for theoretical methods to that can be used to predict protein structure from sequence. Ideally, one would like to numerically simulate the process of folding itself under reversible conditions. However, given current computational resources, this is only possible for systems containing a very small number of amino acids (Daura et al. 1998; Rao and Caflisch 2003). Alternative approaches involve generating a population of possible structures (i.e., by threading) and attempting to select the best solution based on some free energy function (Lemer et al. 1995; Rost et al. 1997; Vorobjev and Hermans 2001; Fain et al. 2002; Feig and Brooks 2002; Felts et al. 2002). Such approaches have proved effective in certain cases, in particular for predicting the packing within the core of the protein. However, normally only part of the protein can be correctly modeled, with other regions remaining grossly misfolded. As it is not possible to reliably predict protein structure from sequence by taking a truly ab initio approach, the structures of unknown proteins are generally modeled based on the fact that sequence homology often implies structural similarity. The difficulty is that unless the sequence similarity between the target and the template is very high, a homology model will, by definition, contain errors (Baker and Sali 2001; Schonbrun et al. 2002). It is clear that in each of the examples above, the refinement of the initial structural models to experimental resolution remains of fundamental importance (Kolinski et al. 1999).

In principle, given a sufficiently accurate inter-atomic force field, classical molecular dynamics (MD) simulation techniques performed in an appropriate environment would be the method of choice for the refinement of protein models with several groups having reported promising results (Simmerling et al. 2000; Lee et al. 2001a; Flohil et al. 2002). For example, Lee et al. starting from a ROSETTA model of a 65-animo-acid structured region of the ribosomal protein (S15) which deviated by 2.8 Å C_α root mean square deviation (RMSD) from the experimental structure obtained an average structure with only 1.8 Å C_α RMSD after 1 nsec of simulation. The difficulty is that on the time-scales a protein in water can be simulated currently, only limited structural arrangements are possible. This means that although simulations of 10 to 100 nsec may be useful for the refinement of structures close to their native conformation (Fan and Mark 2004), it is not possible to refine structures in which, for example, the global fold is incorrect (Lee et al. 2001b). The reason for this is that although the native structure of a protein may correspond to the global minimum in free energy at a given temperature in a specific environment, alternative partially folded states often correspond to local minima on the free energy surface and can remain metastable for extended periods. To address this problem, many investigators have turned to advanced sampling techniques such as replica exchange methods, multiple copy simulations, and/or the use of implicit representations of the solvent. However, these approaches have also met with only limited success. For example, although the use of an implicit solvent may extend the accessible timescale, it is not possible to correctly model short-range interactions with water by using a continuum electrostatic approach such as a generalized Born model. This means that such approaches stabilize existing elements of secondary structure and thus inhibit large-scale structural rearrangements.

The fact that proteins readily adopt metastable partially folded states is not just a problem for the prediction and refinement of protein structural models. It is also of critical importance in vivo to the overall viability of living cells. Thus, although most proteins, given sufficient time, can adopt their native fold spontaneously, a series of proteins, collectively referred to as molecular chaperones, have evolved with the primary role of assisting the folding of other proteins (Hartl and Martin 1995; Feldman and Frydman 2000). This is achieved in part by preventing aggregation and other unwanted interactions but also by specifically recognizing misfolded molecules and promoting productive folding in an ATP-dependent manner (Walter and Buchner 2002). Molecular chaperones are diverse and may be divided into several families (Bukau and Horwich 1998). Nevertheless, they share a number of structural and functional features. In particular, chaperones have a high affinity for unfolded or partially folded polypeptides that expose large areas of hydrophobic surface. Chaperones also induce specific conformational changes in the proteins to which they are bound. They are able to disrupt nonnative interactions, which leads to misfolded proteins becoming trapped in local energy minima. Finally, in an energy-dependent manner, whether by the binding and/or hydrolysis of ATP or the binding of additional chaperone associated proteins, the misfolded protein can be released (often into a protected environment), providing a new opportunity for the protein to fold correctly (Takagi et al. 2003). Repeated cycles of binding and release provide an efficient mechanism by which a given protein can undergo a series of structural rearrangement and eventually achieve their native conformation (Martin 1998).

Ab initio generated or homology-based protein structure models have many similarities to misfolded proteins that occur in vivo. The structures are normally compact and of low energy. Elements of secondary structure are often correctly formed, but there are errors in the packing and arrangement of these secondary structure elements. However, once a compact state has been reached, the flexibility and mobility within the structure are severely restricted. Rearrangements of the protein structure are extremely slow and difficult. In particular, hydrophobic interactions and hydrogen bonds (HBs), which drive the initial collapse of the structure, act as major obstacles to the adjustment of structural elements needed to reach the native state (Csermely 1999). It is by disrupting these interactions that chaperones can facilitate folding.

The action of chaperones is largely generic. A given set of chaperones can facilitate the folding of a wide variety of proteins that show little sequence or structural similarity. This indicates that it may be possible to mimic the action of chaperones in simulations using very simple principles. In fact, a number of workers have attempted to introduce some of the effects of chaperones into simulations of protein folding. To date, however, these have only involved simulations on a lattice or a coarse-grained representation of the protein with the primary aim being to understand how chaperones themselves function (Chan and Dill 1996; Sfatos et al. 1996; Betancourt and Thirumalai 1999; Fukunishi et al. 2002; Gorse 2002). In these studies, the chaperone cavity was modeled as a set of hydrophobic surfaces or as a box that could interact in various ways with the “protein” chain. Although simplistic, such studies indicate that an iterative annealing process can facilitate folding through variation of environment hydrophobicity (Todd et al. 1996). Here we focus specifically on the fact that in chaperone-assisted folding, the misfolded protein undergoes successive cycles of binding, unfolding, and refolding. Rather than providing a surface to which the misfolded protein could bind, we have chosen instead to mimic the action of the chaperone by modifying the solvent environment. Specifically, we cycle the environment by successively increasing, then decreasing the polarity of the solvent in order to first promote limited unfolding and then refolding of the protein structure. This effectively pumps energy into the system, allowing the protein to overcome barriers in the free energy landscape. By restricting the length of time the unfolding environment is applied, we affect primarily misfolded regions of the protein that are exposed to solvent. Of course, there are other aspects of chaperones that are very important in an in vitro context that we do not consider in current study. For one, chaperones help prevent aggregation and provide a sequestered environment. However, as in the simulations, we only deal with individual molecules in a restricted volume, prevention of aggregation is not relevant.

In current work, we investigate two questions. First, is it possible to promote large-scale structural rearrangements in MD simulations of misfolded proteins by mimicking computationally some aspects of molecular chaperones? Second, can such an approach can be used for the refinement of protein models that have been generated either ab initio or based on homology with known structures? The MD simulations described in this study were performed by using an atomic-based empirical force field in explicit solvent. The action of the molecular chaperone was mimicked by varying the charge distribution on individual solvent molecules during the simulation. The approach was tested by simulating structural models of three proteins generated by Baker and coworkers using the ROSETTA structure prediction algorithm (Simons et al. 1999, 2001) while inverting the hydrophobicity of the solvent environment at regular intervals. Key structural and energetic properties of the systems were then analyzed in order to assess objectively the ability to refine grossly misfolded protein structure models using this approach.

Results and Discussion

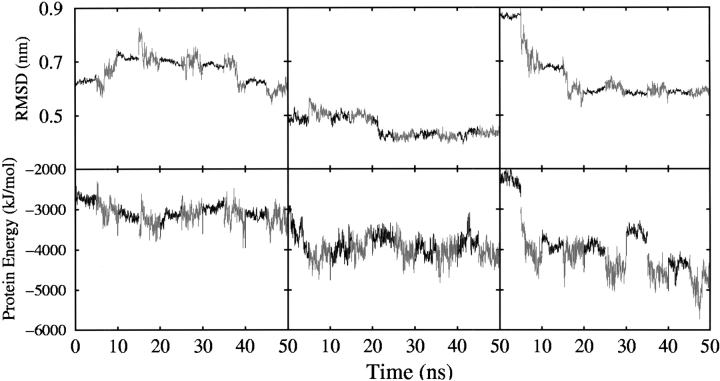
Figure 1 ▶ shows the positional RMSD of the backbone atoms from the respective experimental structure (NMR or X-ray) after a least-square best fit as a function of the simulation time. The RMSD between the corresponding experimental structure and the final refined model structure is also given in Table 1. The values in parentheses indicate the RMSD of the original ROSETTA models from the experimental structure. Also indicated in Table 1 are some structural properties of the proteins, including the number of residues involved in particular secondary structure elements. Comparing the RMSD of the models before and after five cycles of refinement, we see that for 1vcc, RMSD from native structure is unchanged at 0.59 nm. For 1a1z, RMSD from native structure of the initial model was 0.55 nm compared with a final RMSD of 0.46 nm. The largest change in RMSD was from 0.87 to 0.55 nm for the protein 1sro. However, the change in RMSD does not adequately reflect the improvement in the structures observed in the simulations, especially for 1vcc.

Figure 1.

(Top) The time evolution of the backbone positional root mean square deviation (RMSD) of the three ROSETTA models for the proteins 1vcc (left), 1a1z (center), and 1sro (right) after a least-square best fit on all backbone atoms of experimental structure. (Bottom) The time evolution of the internal potential energy of the three ROSETTA models for protein 1vcc (left), 1a1z (center), and 1sro (right).

Table 1.

Structural properties of the proteins after five chaperone cycles

						RG		SASA
PDBID	Nres	Exp.Nα	Exp.Nβ	RMSD	HB	Exp.	Model	Exp.	Model
1vcc	77	11	25	0.59 (0.59)	6 (8)	1.23	1.20 (1.30)	24.7/27.6	24.2/32.0 (29.4/32.3)
1alz	83	62	0	0.46 (0.55)	17 (13)	1.21	1.20 (1.33)	22.9/38.1	25.0/31.7 (31.4/29.5)
1sro	76	4	27	0.55 (0.87)	8 (11)	1.22	1.24 (1.31)	24.2/32.5	25.0/30.6 (27.8/32.1)

PDBID indicates Protein Data Bank identifier; N_res, number of residues; N_α, the number of helical residues; N_β, the number of strand residues; the backbone root mean squared deviation (RMSD) in nm with respect to the experimental structure after 50-nsec molecular dynamics (MD) simulation using five chaperone cycles starting from different initial configurations (the values in parentheses correspond to the RMSD of the starting model with respect to the experimental structure); HB, the number of native hydrogen bonds in a certain conformation while the native hydrogen bonds were defined as that occur with a frequency >0.9 during the last 1 nsec of the MD simulations started from the experimental structure; RG, radius of gyration; RG exp., RG of experimental structure; RG model, RG of predicted model structure (the value in parentheses correspond to the RG of the initial model); SASA, solvent-accessible surface area; SASA exp., hydrophobic and hydrophilic SASA of the experimental structure; and SASA model, hydrophobic and hydrophilic SASA of the predicted model structure (the value in parentheses correspond to the SASA of the initial model).

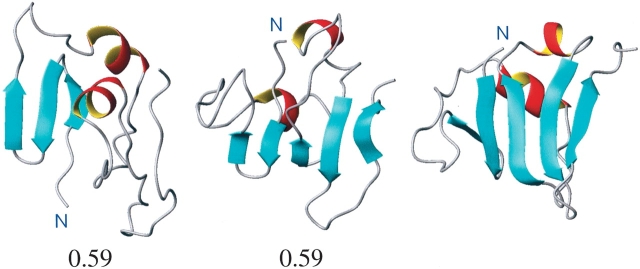
In Figure 2 ▶ is the initial ROSETTA model of 1vcc, the refined model, and the X-ray structure all orientated in a similar manner. As can be seen, the X-ray structure of 1vcc (Fig. 2 ▶, right) contains two short regions of α-helix and a five-stranded β-sheet. Note that in this orientation the N and C termini project up, toward the α-helices. In the initial ROSETTA model (Fig. 2 ▶, left), there is no recognizable secondary structure toward the C-terminal. There is a small region of triple-stranded β-sheet toward the N-terminal but not in the same region as observed in the experimental structure. Most notable, however, is the fact that the N terminus projects down and away from the regions of α-helix. After refinement (Fig. 2 ▶, center), it can be clearly seen that the N terminus now points in the correct direction and that although the β-sheet is not as extensive as in the X-ray structure, a five-stranded β-sheet with each strand in its correct relative position has begun to form.

Figure 2.

(Left to right) The initial ROSETTA model of the protein 1vcc, the final structure after 50 nsec of molecular dynamics (MD) simulation using five chaperone working cycles, and the structure of protein 1vcc as determined experimentally by using X-ray. The number below each figure corresponds to the backbone RMSD in nanometers from the experimental structure.

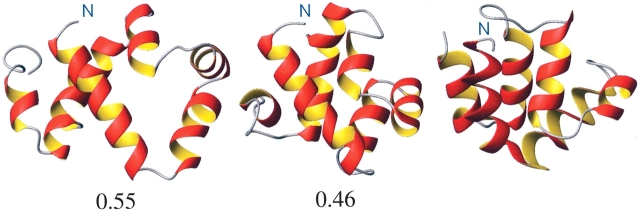
Figure 3 ▶ presents (from left to right) the initial ROSETTA model, the final refined structure, and the experimentally determined NMR structure for the protein 1a1z. In this case we see that compared with the experimental structure, the initial ROSETTA model is very loosely packed. There are also obvious differences in the relative orientation of certain helices. After refinement we see that the structure is more tightly packed and that there has been some improvement in the relative packing of the helices.

Figure 3.

(Left to right) The initial ROSETTA model of the protein 1a1z, the final structure after 50 nsec of MD simulation using five chaperone working cycles, and the structure of protein 1a1z as determined experimentally using NMR. The number below each figure corresponds to the backbone RMSD in nm from the experimental structure.

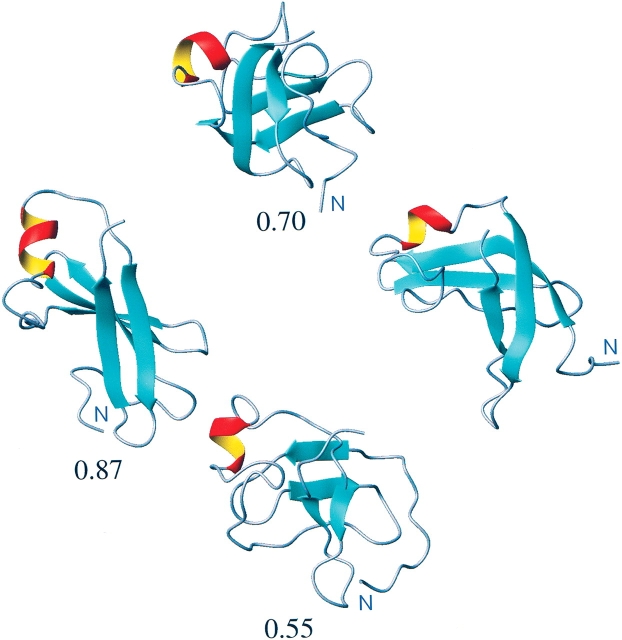
The ROSETTA model of 1sro used in this study was also used in a previous work in which we investigated of efficiency of classical MD simulations, performed in explicit water, for the refinement of structural models of proteins (Fan and Mark 2004). In that work, this model of 1sro was simulated for 400 nsec, and we were able to demonstrate limited refinement from 0.87-nm backbone RMSD to 0.7-nm backbone RMSD (with large fluctuations). The lowest RMSD from the native structure observed during 400 nsec was 0.68 nm. In Figure 4 ▶ we show the initial ROSETTA model (RMSD 0.87 nm; left), the final refined model after 400 nsec of simulation in water (RMSD 0.70 nm; top), the final refined model after 50 nsec of simulation in an oscillating environment (RMSD 0.55 nm; bottom), and the NMR structure of protein 1sro (right) determined experimentally. By comparing the initial model to the experimentally determined structure for 1sro, we can see that although the nature of the elements of secondary structure is similar, the overall fold is very different. In the ROSETTA model the two regions of β-sheet—one containing two strands; the other, three strands—are laying approximately in the same plain, whereas in the experimentally determined structure, the two regions of double-stranded β-sheet clearly lie perpendicular to each other. In the simulations the initial ROSETTA model is unstable. During the 400-nsec classical simulation in explicit water, the protein undergoes substantial structural rearrangements as shown in Figure 4 ▶ (top). There is an improvement in the relative orientation of the regions of β-sheet, which leads to a lower RMSD. However, if one follows the protein backbone from the N terminus, in the NMR structure and in the refined model, it can be seen that there remains an inappropriate pairing of β-strands. In contrast, after just 50 nsec, corresponding to five cycles of refinement, in which the environment is oscillated, we see that the inappropriate pairing of the β-sheet has been lost and the relative orientation of the structural elements is now largely correct (RMSD 0.55 nm). The primary differences between the refined model and the experimental structure are in the orientation of the N terminus and the extent to which the β-sheet has reformed. If we exclude the 11 N-terminal residues that are largely unstructured in the experimental structure from the fit and RMSD calculation, the backbone RMSD of the refined model with respect to the experimental structure is only 0.45 nm.

Figure 4.

The refinement of the protein 1sro. (Left to right) The initial ROSETTA model, the model after 400 nsec of classical MD simulation (top), the model after 50 nsec MD simulation using five chaperone cycles (bottom), and the NMR structure of protein 1sro. The number below each figure corresponds to the backbone RMSD in nm from the experimental structure.

In Figure 1 ▶ the intramolecular potential energy as a function of the simulation time is presented together with the RMSD values for each of the three proteins investigated. Although the intramolecular potential energy shows large fluctuations, it is clear that overall there is a systematic decrease with time. In each case the energy of the refined structure is significantly lower than that of the initial model. Furthermore, both the RMSD and the intramolecular energy show step-like behavior associated with the cycling of the properties of the solvent environment. The first stage of each cycle was characterized by a strongly polar environment that was intended to promote the disruption of intra-molecular hydrogen bonding and facilitate the rearrangement of elements of secondary structure. These stages were characterized by only small variations in RMSD, but in general, an increase in the intramolecular potential energy as exposed intramolecular HBs were lost in favor of interactions with solvent. The second stage of each cycle was characterized by a weakly polar environment to promote intramolecular hydrogen bonding, secondary structure formation, and the folding of the proteins. During this stage larger fluctuations in both the RMSD and the intramolecular potential energy are evident. The intramolecular potential energy is lower, and (in general) the most significant deceases in RMSD occur during this stage. The aim of including the more polar “unfolding” stage was to facilitate the crossing of barriers in the energy surface and thus facilitate the search for the native structure, in particular to promote the loss of poorly structured but metastable elements of secondary structure. It is evident that simply increasing the polarity of the solvent is only partly successful in this regard. Increasing the polarity of the solvent increases the hydrogen bonding capacity of the solvent and its interaction with exposed polar groups but also indirectly enhances hydrophobic interactions within the protein inhibiting major structural changes. Altering the charges also dramatically changes the structural and dynamic properties of the solvent itself. In particular, increasing the charges by 20% increases the dipole moment from 2.27 Debye (original SPC model) to 2.72 Debye. This is accompanied by a decrease in the diffusion constant (calculated for a box of pure solvent under the same conditions as those used for the refinement simulations) from 4.3 × 10⁻⁵ cm⁻² sec⁻¹ to 0.014 × 10⁻⁵ cm⁻² sec⁻¹. Conversely, decreasing the charges by 20% results in a dipole moment of 1.83 Debye and a diffusion constant of 11.325 × 10⁻⁵ cm⁻² sec⁻¹. Increasing the charges effectively results in the freezing of the solvent. Thus, although the enhanced interaction with the more polar solvent results in the local disruption of protein–protein interactions, large-scale motion or global unfolding is not possible.

Alternative measures to assess the degree of refinement in the simulations including the number of the native HBs, the radius of gyration (RG) and the nature of the solvent-accessible surface area (SASA) were also examined. HBs were determined based on geometric criteria. A HB was considered to exist if the donor-hydrogen-acceptor angle was <60 degrees and the distance between hydrogen and acceptor was <0.25 nm. To identify native HBs, we used the same criteria as in our previous work (Fan and Mark 2004). HBs were averaged over the last 1 nsec of a 5-nsec simulation of the protein started from the experimental structure. A HB was considered significant only if it occurred with a frequency of >0.9 over this 1-nsec period. This very strict criterion was adopted because in the simulations the HBs show rapid fluctuations with time and are sensitive to the details of the force field. The number of such native HBs in the final refined model together with the number in the initial model is listed in Table 1. Also listed in Table 1 are the RG and SASA calculated using the g_gyarte and g_sas tools in GROMACS (Groningen Machine for Chemical Simulation) package (Berendsen et al. 1995; Lindahl et al. 2001; van der Spoel et al. 2001) for the initial and refined models. Only for 1a1z did the number of native HB’s show a significant improvement, as is also evident in Figures 2 ▶ through 4 ▶. This reflects the fact that although there have been improvements in the relative orientations of the protein backbone, there is less extensive formation of secondary structure than in the experimentally determined structures. This indicates a final refinement stage in water to regularize the secondary structure may still be needed. For each of the three proteins, the RG of the refined models is closer to that of the native structure than the initial model, indicating the initial models are all loosely packed structures. For each protein there were also improvements in the values of the hydrophobic and hydrophilic SASA. There was a systematic decrease in the exposed hydrophobic surface area of the initial models. Only small changes in the polar surface area were observed with the value after refinement being closer to the experimental value in two of the three cases.

Conclusions

We have investigated whether it is possible to improve the efficiency by which classical MD simulation techniques can be used to promote the correct folding of protein structures by computationally mimicking some aspects of the action of molecular chaperones. The study was based on simulations of structural models of three proteins predicted by using the ROSETTA algorithm, each of which deviated significantly from the corresponding experimental structure (RMSD >0.50 nm). We find that although the function of a chaperone was mimicked in rather a crude fashion simply by raising and lowering the partial charges on the solvent molecules to provide an oscillating environment around the protein, significant refinement of the structures was observed in each of the three cases. Furthermore, this refinement was achieved within a small number of working cycles corresponding to simulation times in the order of tens of nanoseconds. In the case of the protein 1sro, chaperone-mediated refinement was shown to be much more effective than refinement using classical MD simulations in explicit solvent, even when performed on a much longer timescale (400 nsec). The work shows that chaperone assisted folding could be a very promising approach both to facilitate protein folding simulations as well as for the refinement of compact misfolded protein structures such as those predicted based on homology or generated ab initio.

We stress that the work presented here, although promising, is very much a preliminary study. We make no claim that this approach will assist in the folding of all proteins, and it is clear that although we have been able to achieve substantial improvements in the global fold of the proteins investigated, the final structures are still far from experimental resolution. The current approach is clearly not optimal. For one, the different protein structures show different sensitivity to the variation in the solvent environment. Second, the lengths of the refinement cycles have not been optimized, nor has a refinement step under native conditions been included in the protocol. In addition, simply altering the partial charges on the solvent dramatically affects the structural and dynamic properties of the solvent itself. In particular, increasing the charges on the solvent by 20% results in partial freezing of the environment, restricting large-scale structural changes in the protein. One obvious enhancement would be to only change the interactions between the protein and solvent. In fact it is remarkable that even limited success could be achieved with the crude approach used, and it is clear that many variations on this theme should now be investigated.

Materials and methods

Structure selection

The three proteins used in this study (Protein Data Bank numbers 1sro, 1vcc, and 1a1z) range in size from 76 to 83 amino acids (Sharma et al. 1994; Bycroft et al. 1997; Eberstadt et al. 1998). They were initially part of a test set used by Baker and coworkers to verify the structure prediction algorithm ROSETTA (Simons et al. 1999,2001). They were also used in a previous work by us aimed at assessing the efficiency of classical MD simulation techniques in structure refinement (Fan and Mark 2004). The proteins were chosen for these studies because they were small and do not contain disulphide bridges, and the experimental structures have been shown to be stable in simulations using the GROMOS96 force field (van Gunsteren et al. 1996; Fan and Mark 2003). The specific structural models used as the starting structures in this test were generated by using the ROSETTA procedure by Baker and coworkers obtained via their Web site (http://depts.washington.edu/bakerpg/decoys). The structures provided contained the peptide backbone and C_β atoms only. The side-chains were generated by using the program CORALL from the WHATIF package (Vriend 1990). The three initial protein models used in the current test are all compact and have extensive secondary structure, but errors in the global fold. In each case the backbone RMSD with respect to the corresponding experimental structure is >0.5 nm.

MD simulations

All simulations were performed in explicit solvent by using the GROMACS package (Berendsen et al. 1995; Lindahl et al. 2001; van der Spoel et al. 2001) in conjunction with the GROMOS96 43a1 force field for condensed phases (van Gunsteren et al. 1996). The simulations were performed at constant temperature and volume in a periodic truncated octahedral box. The minimum distance between any atom of the protein and the box wall was 1.0 nm. Nonbonded interactions were evaluated by using a twin-range method. Coulomb and van der Waals interactions within a short-range cutoff of 0.9 nm were evaluated every time step. Longer-range Coulomb and van der Waals interactions between 0.9 and 1.4 nm were updated every five time steps, together with the pairlist. To minimize the effects of truncating the electrostatic interactions beyond the 1.4 nm long-range cutoff, a reaction field correction (Tironi et al. 1995) was applied by using a relative dielectric constant of 78. To remove high frequency degrees of freedom, explicit hydrogen atoms in the force field were replaced by dummy atoms, the positions of which were constructed each step from the coordinates of the heavy atoms to which they are attached. This allows a time step of 4 fsec to be used without affecting the thermodynamic properties of the system significantly (Feenstra et al. 1999). Covalent bonds in the protein were constrained by using the LINCS algorithm (Hess et al. 1997). The SETTLE algorithm (Miyamoto and Kollman 1992) was used to constrain the geometry of the water molecules. To generate the starting configuration for each system, the following protocol was used. After energy minimization (EM) using a steepest descent algorithm, 10 psec of MD with position restraints on the protein (PRMD) was performed at 250 K to gently relax the system. Unrestrained MD was then performed at 300 K. During the simulations the temperature was maintained at 300 K by coupling to an external heat bath (Berendsen et al. 1984) with a relaxation time of 0.1 psec. The protonation state of ioniable groups in each of the proteins was set appropriate for pH 7.0, and no counter-ions were added to neutralize the system.

Chaperone refinement

To mimic the effect of the presence of a molecular chaperone, in particular its ability to interact with hydrophobic surfaces, the properties of the solvent environment were cycled during the simulation. One working cycle consisted of two separated stages, each of which was 5 nsec in length. In the first stage of a working cycle, the charges on the three atoms of the simple point charge (SPC) model for water (Berendsen et al. 1981) were increased by 20% (from the initial values), making the solvent more polar to increase the interaction between the peptide backbone. During the second stage of a working cycle, the charges on the solvent were decreased by 20%, making the solvent less polar and promoting secondary structure formation. Whenever the protein model was switched from one stage to the other, the solvent box was regenerated in the same shape but different size to ensure the minimum distance between the protein and the box wall was 1.0 nm. The new system was then energy-minimized and equilibrated as described above. A cycle was repeated five times for each protein, making each simulation 50 nsec in total.