The optimization principle in phylogenetic analysis tends to give incorrect topologies when the number of nucleotides or amino acids used is small

Abstract

In the maximum parsimony (MP) and minimum evolution (ME) methods of phylogenetic inference, evolutionary trees are constructed by searching for the topology that shows the minimum number of mutational changes required (M) and the smallest sum of branch lengths (S), respectively, whereas in the maximum likelihood (ML) method the topology showing the highest maximum likelihood (A) of observing a given data set is chosen. However, the theoretical basis of the optimization principle remains unclear. We therefore examined the relationships of M, S, and A for the MP, ME, and ML trees with those for the true tree by using computer simulation. The results show that M and S are generally greater for the true tree than for the MP and ME trees when the number of nucleotides examined (n) is relatively small, whereas A is generally lower for the true tree than for the ML tree. This finding indicates that the optimization principle tends to give incorrect topologies when n is small. To deal with this disturbing property of the optimization principle, we suggest that more attention should be given to testing the statistical reliability of an estimated tree rather than to finding the optimal tree with excessive efforts. When a reliability test is conducted, simplified MP, ME, and ML algorithms such as the neighbor-joining method generally give conclusions about phylogenetic inference very similar to those obtained by the more extensive tree search algorithms.

In phylogenetic inference some kind of optimization principle is commonly used for choosing the most probable tree. For example, in the standard maximum parsimony (MP) method (1, 2) the minimum number of mutational changes (M) that are required for explaining the evolutionary change of a set of DNA (or amino acid) sequences is computed for each topology (branching pattern), and the topology that requires the smallest M is chosen as the best tree. The theoretical basis of this method is William of Ockham’s philosophical idea that the best hypothesis to explain a process is the one that requires the smallest number of assumptions (3). In the MP method the number of assumptions is equal to the number of nucleotide substitutions assumed. If there are no backward and parallel mutations, this method is expected to generate the true topology as long as there are enough nucleotides examined, but otherwise there is no guarantee that the MP method gives the true topology.

The minimum evolution (ME) method (4–6) is a distance-based algorithm and chooses the topology that has the smallest value of the sum (S) of branch length estimates after these estimates are obtained from pairwise distances. Rzhetsky and Nei (7) showed that the expected value of S is smallest for the true topology when unbiased estimates of pairwise distances are used. However, this result does not mean that the topology with the smallest S value is the most probable tree (8). Another important method of phylogenetic inference is the maximum likelihood (ML) method (9, 10). In this method, the likelihood of observing a given set of data is maximized for each topology, and the topology that gives the highest maximum likelihood is chosen as the final tree. In this case, however, the parameters to be considered are not the topologies but the branch lengths for each topology, and the likelihood is maximized to estimate branch lengths rather than the topology. Therefore, it is unclear whether the ML principle gives the most probable tree (8, 11–15).

Another problem with phylogenetic inference based on the optimization principle is that it is very time-consuming, because the number of possible topologies is very large for a sizable number of nucleotide sequences (>15) and an enormous amount of computational time is required to find the optimal (MP, ME, or ML) tree. For this reason, various algorithms have been developed to speed up the search for the optimal or a near-optimal tree. However, the efficiency of these algorithms for finding the true topology is not well understood.

The purpose of this paper is to study these problems by computer simulation. We consider three major methods of phylogenetic inference based on the optimization principle—i.e., the MP, ME, and ML methods. We also examine the performance of simplified versions of the three methods to facilitate the computation. Since our interest is in examining the effects of sampling errors on MP, ME, and ML trees, we consider relatively simple model trees for simulation to avoid the problem of “inconsistency of estimation” of phylogenetic trees (16).

METHODS OF COMPUTER SIMULATION

Model Trees and Computation of Optimality Scores.

In this study we conducted a computer simulation to generate a given number of DNA sequences that evolved following a given model tree, and the DNA sequences generated in each replication of the simulation were used to construct phylogenetic trees by using the MP, ME, and ML methods. Details of the computer simulation are described in ref. 17. We then computed M, S, and the log likelihood value (A = −lnL, where L stands for the maximum likelihood) for MP, ME, and ML trees, respectively. We also computed M, S, and A for the correct topology, which is identical with that of the model tree. This allowed us to compare the M, S, and A for “estimated” topologies with those for the true topology. We also used simplified MP, ME, and ML methods (single-tree algorithms) to identify single optimal or suboptimal trees. The neighbor-joining (NJ) method (17) is a well established method to obtain a single potential ME tree (8), so we used this method for the ME method. There are several algorithms to obtain a single potential MP tree (18), but we used Kumar et al.’s (19) min-mini (MM) algorithm with search factor 0. This method is based on the idea of the branch-and-bound search algorithm and produces only one potential MP tree (or equally parsimonious trees if any). For the ML method we used the star-decomposition method (20, 21) and the stepwise addition method (21) and chose the topology showing a higher A value when two topologies were obtained by the two methods. We call this the two-tree (TT) method. Our preliminary study showed that this method improves the probability of obtaining the true topology compared with the case where only one of the two methods is used.

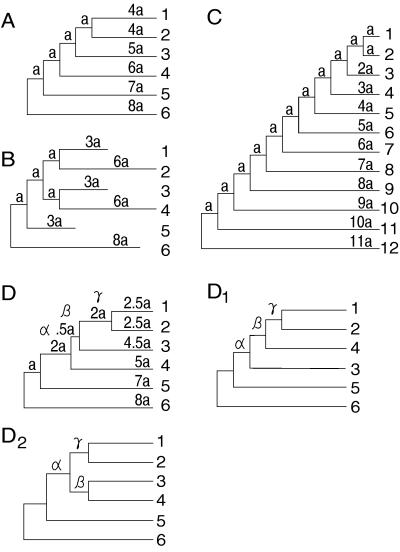
As mentioned above, it is very time-consuming to find the true optimal trees when the number of sequences used is relatively large. This is particularly so with the ML method. Since we had to find MP, ME, and ML trees for many replications, we used the model trees of six sequences given in Fig. 1 A and B. For a tree of six sequences there are only 105 unrooted topologies, so that we can determine the MP, ME, and ML trees by examining all the topologies in each replication.

Figure 1.

Model trees used for computer simulation. Trees A, C, and D represent cases of constant rate of evolution, and tree B represents a case of varying rate of evolution. Trees D₁ and D₂ are incorrect topologies reconstructed from simulated sequences by using model tree D. Branch lengths for model trees are expressed in terms of the expected number of nucleotide substitutions per site. Values of a were determined from the pairwise distances between the two most distantly related sequences (d_max).

The above exhaustive method of examining all possible topologies gives a clear-cut answer to our question, but in practice it is necessary to know what will happen when more sequences are used and only a fraction of all possible topologies are examined, because phylogenetic trees are usually constructed for a large number of sequences. There are many different heuristic algorithms of searching for potential MP, ME, and ML trees, and it is interesting to know how well these algorithms perform. We therefore studied this problem by using model tree C in Fig. 1. This tree consists of 12 sequences, so that there are 654,729,075 different unrooted topologies (9). For the MP method, we used the MM heuristic algorithm with a search factor of 30% (the difference between the local upper bounds of substitutions for two consecutive computational steps divided by the local upper bound for the earlier step) and examined up to 60,000 topologies per replication, depending on the extent of sequence divergence and the number of nucleotides examined. For the ME method, we used Rzhetsky and Nei’s (6) close-neighbor interchange (CNI) algorithm, examining about 200 topologies per replication. In the CNI algorithm the NJ tree is first constructed, and then all topologies different from the NJ tree by a topological distance (d_T) of 2 and 4 (22, 23) are examined to find a topology with an S smaller than that of the NJ tree. This process is repeated until no topology with a smaller S is found. For the ML method, the branch swapping (nearest neighbor interchange) option of the computer program molphy (21) was used.

The branch lengths (multiples of a) of the model trees in Fig. 1 represent the expected numbers of nucleotide substitutions per site. In trees A, C, and D the rate of nucleotide substitution remains constant throughout the evolutionary process, whereas in tree B the rate varies with branch. In all model trees we considered several levels of sequence divergence, the level of sequence divergence being measured in terms of the expected number of nucleotide substitutions per site between two most divergent sequences (d_max). The a values in the model trees were then determined in proportion to this d_max value. For example, when d_max = 1.0 for model tree A, a was 1/16.

Models of Nucleotide Substitution.

For generating a set of DNA sequences for any given tree, we have to use a certain model of nucleotide substitution. Since our purpose was to examine the effect of sampling errors on optimality scores, we used the simple Jukes–Cantor model (24). In the reconstruction of a tree by the ML method, we need a specific substitution model and used the same model as the one used for generating sequence data. For the ME method, some measures of pairwise sequence distances must be used. We used the proportion of different nucleotides (p-distance) as well as the Jukes–Cantor distance, because the latter distance has a larger variance than the former and may become undefinable when the distance value is large. The MP method does not require any specific model, and we used the standard unweighted parsimony method.

DISTRIBUTIONS OF RELATIVE OPTIMALITY SCORES

Model Tree A.

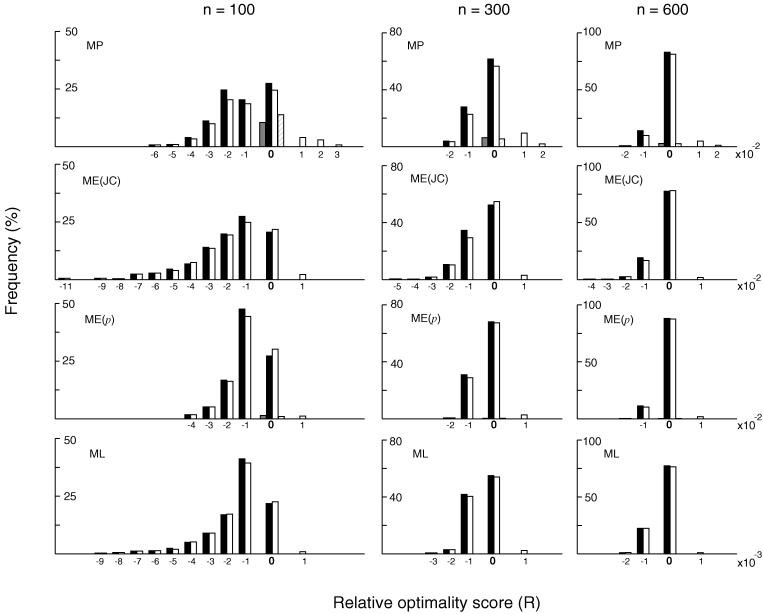
Fig. 2 shows the frequency distributions of relative optimality scores for MP, ME, and ML trees when 500 different data sets (replications) were examined by using model tree A. The relative optimality scores for an MP tree was computed by

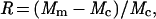where M_m and M_c stand for the M values (tree lengths) for the MP tree and the correct topology for a given replication, respectively. Therefore, if M_m = M_c, then R = 0. R becomes negative when M_m < M_c and positive when M_m > M_c. Similar relative optimality scores were used for the ME and ML methods by replacing M_m and M_c by the equivalent quantities (S_m, S_c, A_m, and A_c) in these methods.

Figure 2.

Distributions of relative optimality scores (R) of the MP, ME, and ML trees inferred by the exhaustive search (solid bars) and the single-tree search (open bars) algorithms. These results were obtained from 500 replications of computer simulation following model tree A in Fig. 1 with d_max = 1.0. n represents the number of nucleotides used. ME(JC) and ME(p) refer to ME trees with the Jukes–Cantor distance and the p-distance, respectively. R values for MP and ME (or NJ) trees are multiplied by c = 100, whereas those for ML trees are multiplied by c = 1,000. cR = 0 represents the case where the correct topology was obtained. Except for cR = 0, cR = x represents the cR values in the range of x − 1 < cR ≤ x for a positive integer x and in the range of x ≤ cR < x + 1 for a negative integer x. Thus, cR = 1 represents the cR values between 0 and 1 excluding cR = 0, cR = 2 represents the cR values between 1 and 2 excluding cR = 1, and cR = −1 represents the cR values between −1 and 0 excluding 0. We used c = 1,000 for ML trees, because the scale of R for ML trees was much finer than that for MP and ME trees.

Comparison of the distributions of R values for MP, ME, and ML trees is not always straightforward. For a given data set, the MP method may produce two or more equally parsimonious trees, one of which is the correct tree. It is not clear whether this case should be included in the class of the correct topology (23). In the present case we regarded 1/s of the case as the correct topology and (1 − 1/s) as incorrect topologies, where s is the number of equally parsimonious (tie) trees. In this case, all the tie trees have the same M value as that of the correct tree, so that R = 0 even for incorrect trees. In Fig. 2 the frequency of correct topologies with R = 0 is represented by a solid bar, whereas that of incorrect topologies with R = 0 is given by a gray bar. Tie trees were occasionally observed even for ME and ML trees partly because of rounding errors in the computation. When p-distance was used for constructing ME trees, the frequency of tie trees was appreciably high. When tie trees occurred, they were treated in the same way as in the case of MP trees. Except for R = 0, the abscissa of the histograms in Fig. 2 represents cR, where c is 100 for MP and ME trees and 1,000 for ML trees.

The solid bars of the histograms in Fig. 2 show the R values for the case of d_max = 1 (a = 1/16) when the number of nucleotides examined (n) was 100, 300, or 600. When n = 100, the exhaustive search of the MP tree identified the true topology in 28% of all cases (500 replications), whereas in about 10% of the cases incorrect topologies showed the same M value as that of the true topology. In all other cases (62%) the MP tree had an incorrect topology with R < 0. In other words, the topology with the smallest M was frequently an incorrect one. The same tendency was observed for the cases of n = 300 and 600, though the probability of obtaining the correct topology increased as n increased. Actually, when n = 1,200, all MP, ME, and ML methods produced the correct topology with a probability of nearly 100% when model tree A was used.

The results given in Fig. 2 establish the relationship R ≤ 0 for MP trees, but this relationship is obvious because M_m cannot be greater than M_c when all topologies are examined. In other words, if any incorrect topology has an M greater than M_c, this topology cannot be the MP tree when all topologies are examined. However, if it has an M smaller than M_c, then it may be the MP tree. Therefore, we have the relationship R ≤ 0. This relationship is of course a consequence of the definition of the optimal tree and applies to the ME and ML trees as well. Indeed, Fig. 2 shows that R ≤ 0 for both ME and ML trees when all topologies are examined. Actually, this relationship holds for any tree-building method based on an optimization principle, including the least-squares method (9, 25).

At the present time there seems to be a general consensus that in the absence of knowledge of the true topology the best tree is represented by the optimal (MP, ME, or ML) tree and that incorrect trees are often obtained when the algorithm used fails to identify the optimal tree (18, 19, 26–28). For this reason great efforts are made to obtain the optimal tree in most computer programs. However, the relationship R ≤ 0 does not support the current view and shows that the optimization principle tends to identify an incorrect topology when sample size (n) is small.

As mentioned earlier, we also used the MM algorithm with search factor 0 to identify a single MP or suboptimal MP tree (or trees). This algorithm can identify equally parsimonious trees. The relative frequencies of the R values for these trees are given by the open bars in the histograms of Fig. 2, whereas the frequency of incorrect tie trees with R = 0 is given by the hatched bars. The results obtained by this single-tree method are similar to those obtained by the exhaustive method, though the method does allow M_m to be greater than M_c. This suggests that at least with model tree A the single-tree algorithm works nearly as efficiently as the exhaustive search for identifying the true topology. Fig. 2 also shows that the single-tree algorithm such as the NJ and TT methods are almost as effective as the exhaustive search in obtaining the optimal tree. In the case of the NJ method the p-distance gives a slightly higher frequency of true topologies obtained than the Jukes–Cantor distance, despite the fact that the p-distance does not take into account multiple substitutions at the same nucleotide sites (17, 28–30). Another interesting result obtained from this simulation is that the topologies of the MP, ME, and ML trees for a given data set were usually the same or very similar to one another whether the topology obtained was correct or not. In other words, the inferred topology was affected more often by the data set used than by the tree-building method. This finding is consistent with Saitou and Imanishi’s (5) previous finding.

In the above computation we considered a relatively divergent set of DNA sequences with d_max = 1. However, our study of a case of low divergence (d_max = 0.25) gave essentially the same results except that in this case the frequency of tie trees with the correct topology was considerably higher for the MP method and the probability of obtaining the true tree was higher than that for the case of d_max = 1.0 in all methods (data not shown).

Model Tree B.

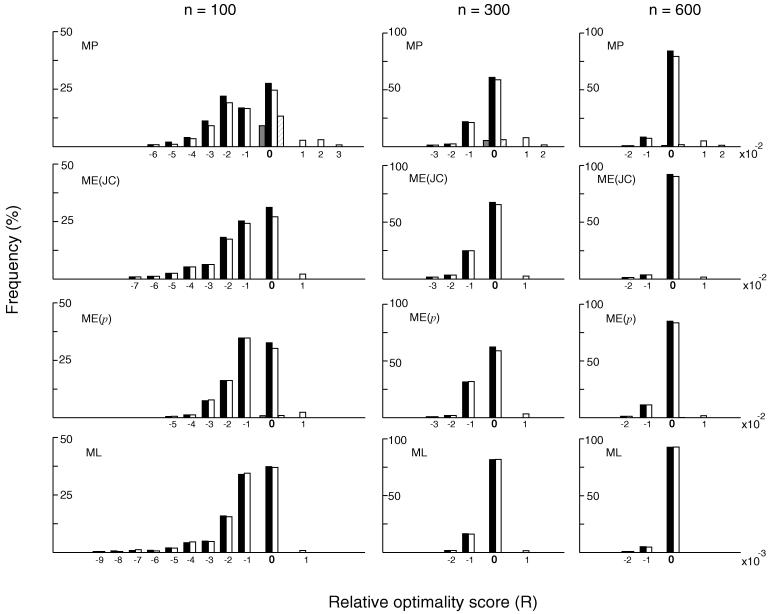
To see the effect of variation in substitution rate among different branches on optimality scores, we conducted another simulation using model tree B. We considered the cases of d_max = 1.0 and 0.25 and constructed the histograms of R for MP, ME, and ML trees. The results for d_max = 1.0 are given in Fig. 3. In all cases examined R is again equal to or smaller than 0 when the exhaustive search is used, indicating that the optimization principle tends to give incorrect topologies when n is small. In MP trees, the distribution of R is similar to that for model tree A in both the exhaustive and the single tree searches. In ME and ML trees the frequencies of true topologies obtained are somewhat higher than those for tree A, and the distributions of R is narrower partly because the sum of all branch lengths is smaller in this case. As in the case of tree A, the single-tree search algorithm is as effective as the exhaustive search in obtaining the correct tree for all tree-building methods. The results for the case of d_max = 0.25 were virtually the same as those of model tree A (data not shown). The single-tree MP, ME, and ML algorithms were also nearly as effective as the exhaustive search. Therefore, the magnitude of rate heterogeneity as considered in model tree B does not affect our conclusion seriously.

Figure 3.

Distributions of relative optimality scores (R) of the trees obtained by the MP, ME, and ML methods (solid bars) and the single-tree algorithms (open bars) when model tree B with d_max = 1.0 was used. See the legend of Fig. 2 for details.

Model Tree C.

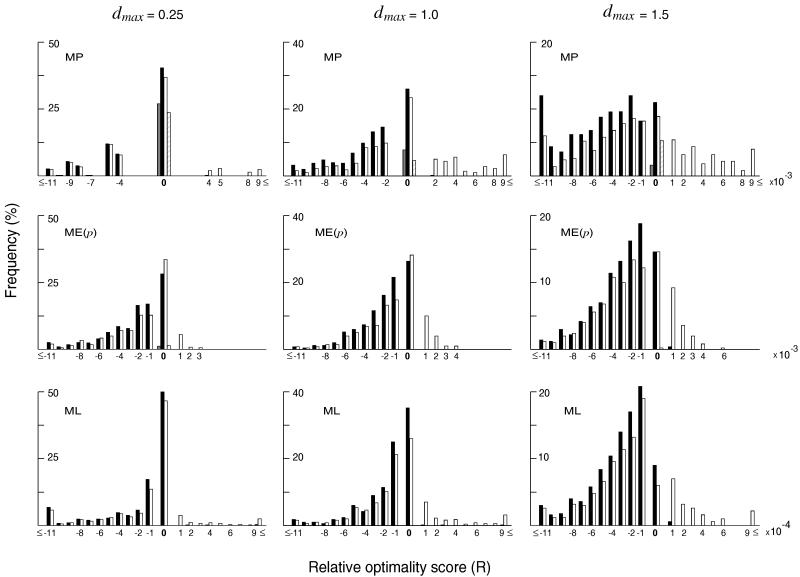
This tree was used to examine whether the above conclusion holds even when the number of sequences used is large and only a small fraction of all possible topologies is examined by using heuristic search algorithms. As mentioned earlier, we used the MM algorithm with a 30% search factor for obtaining MP trees. Fig. 4 shows the frequency distributions of R for the cases of d_max = 0.25, 1.0, and 1.5 with n = 300. The number of sequences is twice as many as that for tree A, so that we need to examine more nucleotides to obtain the correct tree with an appreciable probability. For MP trees the frequency of correct topologies obtained was highest (about 40%) for the sequence divergence of d_max = 0.25 and gradually declined as d_max increased, the frequency for d_max = 1.5 being about 10%. Even with this heuristic search algorithm, all MP trees showed an R that was either 0 or negative. In the case of d_max = 1.5 the frequency of correct topologies obtained was so small (about 10%) that most MP trees were incorrect. Essentially the same tendency was observed for the ME and ML trees obtained by the heuristic algorithms, though there were a few cases in which the correct topology was not examined and thus R was higher than 0. These results show that the heuristic algorithms used here for finding MP, ME, and ML trees all tend to identify incorrect topologies particularly when the extent of sequence divergence is high.

Figure 4.

Distributions of relative optimality scores (R) of the trees obtained by the MP, ME, and ML methods (solid bars) and the single-tree algorithms (open bars) when model tree C with n = 300 was used. When d_max = 1.5, the Jukes–Cantor distance was often undefinable so that p-distance was used. See the legend of Fig. 2 for details.

The open bars of Fig. 4 again represent the frequencies of R values obtained by the single-tree search algorithms. In the case of the ME method this algorithm (NJ) is as good as or slightly better in obtaining the true topology than the heuristic search algorithm (CNI), as in the case of model tree A. For MP and ML trees, however, the single-tree search algorithm is not as efficient as the extensive search algorithm for all values of d_max.

OPTIMALITY SCORES AND TOPOLOGICAL DIFFERENCES

One might think that the property of R ≤ 0 for optimality scores is contradictory with Rzhetsky and Nei’s (7) mathematical proof that in the case of ME trees the expected value of S for the correct topology is always smaller than that for incorrect topologies as long as unbiased estimates of nucleotide substitutions are used as distance measures. Actually, they are not contradictory at all. To see this point, we computed the S value for each of the 105 topologies when we searched for the ME tree with model tree A with d_max = 1.0 and n = 300. Since we determined the S value for each topology for 500 replications, we could compute the mean S values (S̄) for different topologies. The topological distance (d_T) of a tree from the true tree can be measured by considering sequence partitions (22, 31). For model tree A, there are one correct topology (d_T = 0), 6 topologies with d_T = 2, 24 topologies with d_T = 4, and 74 topologies with d_T = 6 (6, 23). The S̄ values for all the topologies with d_T ≥ 2 were greater than the mean (S̄_c) for the correct topology. The second row of Table 1 shows the means of S̄ values for topologies with different d_T values. The mean S̄ is smallest for the correct topology and increases as d_T increases. This confirms Rzhetsky and Nei’s theoretical prediction. However, S had a wide distribution, so that the S values for topologies with different d_T values overlapped extensively.

Table 1.

Mean optimality scores for trees with different d_T values

dT	Optimality principle
	MP	ME (JC)	ML
0	517.1  ±  0.7	738.9  ±  1.8	−2095.4  ±  1.4
2	522.8  ±  0.3	755.3  ±  0.8	−2097.4  ±  0.6
4	530.4  ±  0.2	778.2  ±  0.4	−2100.3  ±  0.3
6	540.6  ±  0.1	778.4  ±  0.2	−2104.1  ±  0.2

Results are from 500 replications of computer simulation using model tree A with d_max = 1.0 and n = 300. In each replication, optimality scores were first computed for all 105 topologies. Mean optimality scores and their standard errors for topologies with d_T = 0 (one correct topology), d_T = 2 (6 incorrect topologies), d_T = 4 (24 incorrect topologies), and d_T = 6 (74 incorrect topologies) were computed by pooling the optimality scores for all topologies in all replications for each value of d_T. ME (JC) refers to ME trees with Jukes–Cantor distance. 

For MP and ML trees there is no theoretical study that is equivalent to Rzhetsky and Nei’s, but computer simulations showed that essentially the same principle applies to these trees as well. Thus, the mean M and A for the correct topology were smaller than those for incorrect topologies (Table 1).

BOOTSTRAP CONSENSUS TREES

The finding that the optimization principle used in phylogenetic inference tends to give incorrect topologies when sample size (n) is small is disturbing, because it defies the current theoretical basis of phylogenetic inference. If this principle does not work, what kind of principle should we use in phylogenetic inference? This is a difficult question to answer. However, we note that the optimization principle works well if a sufficient number of nucleotides are examined and the inconsistency problem does not exist. The number of nucleotides required of course depends on the number of sequences used and the topology and branch lengths of the true tree, which are unknown. Note also that in real data analysis even if one happens to obtain the correct topology, it is not trustworthy unless the estimates of all or most interior branch lengths are significantly greater than 0 (6).

These observations lead to one solution to our problem concerning the optimization principle. That is, a tree obtained by an optimality criterion should be subjected to the interior branch test (6) or to the bootstrap test (32). We will then know reliable or unreliable interior branches or sequence clusters. Since most topological errors are caused by the erroneous branching patterns at weakly supported interior branches, a tree with an interior branch test for a given data set would give more or less the same conclusion whether the branching pattern obtained is correct or not (see below for some potential problems). Therefore, one simple solution to our problem would be to construct an optimal tree with the interior branch test or the bootstrap test and derive a conclusion about phylogeny based on this tree giving little weight to interior branches that have low statistical support.

A solid statistical test of interior branches is available for ME and NJ trees (6, 33), but it is dependent on the substitution model used and is time-consuming when the number of sequences is large. Furthermore, there is no equivalent test for MP and ML trees (8). By contrast, the bootstrap test, which is a crude way of testing interior branches, is applicable to all tree-building methods and is easy to use. Although this test has been shown to be conservative under certain theoretical frameworks (33–37), a conservative test is preferable in real data analysis, because the evolution of actual DNA (or protein) sequences almost never follows any mathematical model available (8). Therefore, the bootstrap test seems to be more convenient than the interior branch test of Rzhetsky and Nei (6).

To examine whether this approach is appropriate, we conducted another computer simulation using model tree D in Fig. 1. With this model tree, topological errors occur more often at interior branch β than at α and γ, because the expected branch length for β is 1/4 as long as that for α and γ. Therefore, the incorrect trees that occur frequently are topologies D₁ and D₂ in Fig. 1. We would therefore expect that when the incorrect topologies are obtained the interior branch β generally shows a lower bootstrap confidence value (P_B) than the branches α and γ. We would also expect a lower P_B for branch β even for the correct topology, because this branch is expected to have a smaller number of substitutions than other branches. In our simulation we used d_max = 1.0 (a = 1/16) with n = 600, so that the expected total number of substitutions for branch β was 0.5a × 600 = 18.75. With these parameters, the frequencies of correct topologies obtained for MP, ME, and ML methods were 78%, 77%, and 74%, respectively, when the exhaustive search was used and 78%, 79%, and 67% when the single-tree search algorithm was used.

Table 2 shows the P_B values for branches α, β, and γ for eight representative sets of simulated sequences that produced four incorrect and four correct topologies. (The total number of data sets examined was 200.) In all eight cases in Table 2 the topology of the bootstrap consensus tree (32) was identical with that of the tree obtained from the original data set. The bootstrap test was first conducted by the exhaustive search algorithms for MP, ME, and ML trees for each data set. For MP and ML trees, we used the branch-and-bound algorithm available in paup* (18). paup* does not have this algorithm for ME trees, so we used the full heuristic option in the software. The number of bootstrap replications was 1,000 for MP and ME trees, but it was 200 for ML trees because of the large computational time required. When the bootstrap test was conducted by using the single-tree method, we used the stepwise addition algorithm for MP and ML trees and the NJ algorithm for ME trees in paup*. In Table 2 the numbers before and after the/sign refer to the P_B values for the exhaustive search and the single-tree search, respectively.

Table 2.

Percent bootstrap confidence (P_B) values for three interior branches—α, β, γ—of the trees D, D₁, and D₂ in Fig. 1

Method	Interior branch			Interior branch			Interior branch			Interior branch
	α	β	γ	α	β	γ	α	β	γ	α	β	γ
	(a) Tree D1			(b) Tree D1			(c) Tree D2			(d) Tree D1
MP	97/93	46/59	100/100	100/100	66/54	100/100	100/97	63/60	100/100	100/100	82/69	100/100
ME (NJ)	99/98	55/55	100/100	100/100	57/58	100/100	100/100	66/62	100/100	100/100	46/47	100/100
ML	90/92	74/68	100/100	100/100	82/77	98/98	100/98	62/57	95/94	100/100	58/44	100/100
	(e) Correct topology			(f) Correct topology			(g) Correct topology			(h) Correct topology
MP	99/96	85/72	100/100	100/100	100/92	100/100	99/96	76/58	100/100	100/100	92/88	83/70
ME (NJ)	100/100	84/88	100/100	100/100	96/96	100/100	100/99	76/77	100/100	94/95	91/93	100/100
ML	92/90	55/50	100/96	100/98	100/94	100/99	80/82	61/56	100/100	62/62	91/88	100/100

Eight different sets of simulated sequence data generated from model tree D with d_max = 1.0 and n = 600 were subjected to the bootstrap test. Original data sets a–d produced incorrect topologies, whereas data sets e–h generated the correct topologies. P_B values before and after the / sign refer to those of the exhaustive search and the single-tree search bootstrap tests. The NJ tree was identical with the ME tree in all the eight cases. 

Table 2 shows that the P_B values for the exhaustive and the single-tree search algorithms are similar to each other, though the P_B values for the latter algorithm tend to be smaller than those for the former in MP and ML trees. This indicates that the bootstrap test can be done with the single-tree algorithm in the present case. When original data sets produced incorrect topologies, the P_B value for interior branch β is 44–82% and is always smaller than that for branches α and γ in all MP, ME, and ML trees. By contrast, the P_B values for branches α and γ are nearly 100%, though in the case of ML trees the P_B for branch α for data set a is 90–92%. This is true whether the topology obtained is D₁ or D₂. Therefore, if we use a type I error of 5% (P_B = 0.95) as the significant level, following Efron et al. (37), these results support our previous conjecture that incorrect interior branches receive a low P_B value, whereas correct branches generally have a high P_B except for ML trees for data set (a).

When the original data sets produced the correct topology, however, the relationships of P_B among the three interior branches are not as straightforward as those for incorrect topologies. In general, branch β shows a smaller P_B than branches α and γ, but the difference is often quite small (data sets e–h). Furthermore, there are several exceptions. In data set h, for example, P_B is lowest for the correct branch α of the ML tree and is lowest for the correct branch γ of the MP tree. At the present time, the reason for these unexpected P_B values is unknown. Our simulation record showed that the actual numbers of nucleotide substitutions that occurred for branches α, β, and γ in data set h were 69, 26, and 78, respectively, indicating that P_B is not necessarily correlated with the number of substitutions. Clearly, the bootstrap is a complex statistical test, and a detailed study on this subject is currently underway with respect to different tree-building methods. (So far no detailed study has been made on the bootstrap test of ML trees.) However, the strategy suggested above works relatively well at least for ME (NJ) trees, and therefore it can be used as a crude way of dealing with the problem raised by the deficiency of the optimization principle.

This strategy is conservative, but a conservative judgment is safer in phylogenetic inference because there are many disturbing factors in real data analysis. If the correct topology is not supported by a statistical test, one can increase the amount of data to confirm the initial tree. Note also that in this approach we do not have to make excessive efforts to find the true optimal tree if there is a simplified method for obtaining the correct tree with a reasonably high probability. In the present example, we have seen that a simplified method such as the stepwise addition or the NJ algorithm gives results similar to those obtained by the exhaustive search algorithms.

Nevertheless, the bootstrap is not almighty. When inconsistency of estimation of a topology occurs, the bootstrap may give a high P_B value for every interior branch when n is very large, and a wrong tree may look as though it were statistically confirmed (8). Therefore, it seems to be necessary to examine many independently inherited genes in the construction of reliable phylogenetic trees for different organisms.

DISCUSSION

The major finding in this paper is that the optimization principle used in current phylogenetic inference tends to give incorrect phylogenies when the number of nucleotides examined (n) is small. In the present study we considered relatively small values of n because the number of sequences used was small and the extent of sequence divergence was high. However, when a large number of closely related sequences are used, this problem would occur even if a large number of nucleotides were examined. Furthermore, in real DNA sequences there are highly conserved and highly variable sites, and the pattern of nucleotide substitution is much more complicated than the Jukes–Cantor model. Therefore, this problem seems to be quite serious in actual data analysis. For example, a number of authors attempted to construct the MP tree for the D-loop region of mitochondrial DNAs obtained from various human populations (38, 39). They spent a large amount of computer time because there were more than 100 sequences and the sequences were closely related, yet the results obtained were quite unreasonable in view of the population trees constructed from gene frequency data (40, 41) and later studies on the same subject (42).

Previously, Felsenstein (16) considered a tree-building method as an “estimator” of a tree topology and showed that the MP method can be an “inconsistent estimator.” (Note that the MP method is not a statistic.) If we are allowed to use a similar statistical terminology, we can say that all the MP, ME, and ML methods are “biased estimators.” In fact, when a large number of sequences are analyzed with a relatively small number of nucleotides per sequence, most of the trees obtained by these methods would be incorrect.

In the past great efforts have been made to find the MP or ML tree for a given data set by developing faster and faster algorithms under the assumption that the optimal tree is closest to the true tree (18, 19, 21, 27, 43). However, what is necessary is to develop an efficient method of finding the true topology. Ideally, it would be nice to develop a method that gives “unbiased estimators” of true topologies, though we do not know how to do it at this moment. At the same time, it is desirable to develop a simplified method of obtaining optimal trees to save computer time. In the case of the ME principle, the NJ method seems to be as efficient as or slightly more efficient than the ME method in finding the true topology, as shown by the present and previous studies (5, 44, 45). Therefore, unlike the suggestion made by Swofford et al. (26), there is no need to search for the ME tree. Particularly, if we construct a bootstrap consensus tree, both methods give essentially the same conclusion. For the MP and ML methods there is no simple algorithm like NJ. In the present study we used the single-tree MM and TT algorithms for convenience. For model trees A and B, they worked almost as well as the exhaustive search methods, but with model tree C they did not. Implementation of the CNI algorithm with a fewer number of cycles may improve the performance of the single-tree MP and ML algorithms.

In the present paper, we are not particularly concerned with the comparison of the efficiency of obtaining the correct topology among different tree-building methods, because this is a complex problem and depends on many factors (8, 46–48). When the extent of sequence divergence is low and the deviation from the constant rate of evolution is not large, MP, ME, and ML seem to be nearly equally efficient (5, 48–51). When the extent of sequence divergence is high and the evolutionary rate varies extensively with evolutionary lineage, ML usually gives a higher probability of obtaining the correct topology than other methods, provided that the patterns of nucleotide substitution used for generating simulated sequences and for inferring the phylogeny are the same (48, 50, 52).

However, the performance of ML is highly dependent on the pattern of nucleotide substitution, and the actual pattern of nucleotide substitution is very complex and apparently changes with time because different species often have different nucleotide frequencies and codon usages (53, 54). For this and other reasons, the mathematical model to be used in actual data analysis is often unclear (8, 15). By contrast, MP performs poorly when the heterogeneity of evolutionary rate is very high. However, as long as the extent of rate heterogeneity is no more extreme than that of model tree B, MP seems to work reasonably well. Note that if we consider the expected branch lengths rather than realized (observed) branch lengths, which are much more variable than the expected (M.N. and S.K., unpublished data), rate heterogeneity in most real data may not be much greater than that represented in model tree B (55–57). If we consider these factors, it is difficult to make any definitive conclusion about the relative efficiencies of different tree-building methods. The present study has shown that in phylogenetic inference simple methods are often as effective as complicated ones when the bootstrap test is used.

ABBREVIATIONS

MP

maximum parsimony

ME

minimum evolution

ML

maximum likelihood

NJ

neighbor joining

MM

min-mini

TT

two-tree

CNI

close neighbor interchange