Linkage disequilibrium mapping in isolated populations: The example of Finland revisited

Abstract

Linkage disequilibrium analysis can provide high resolution in the mapping of disease genes because it incorporates information on recombinations that have occurred during the entire period from the mutational event to the present. A circumstance particularly favorable for high-resolution mapping is when a single founding mutation segregates in an isolated population. We review here the population structure of Finland in which a small founder population some 100 generations ago has expanded into 5.1 million people today. Among the 30-odd autosomal recessive disorders that are more prevalent in Finland than elsewhere, several appear to have segregated for this entire period in the “panmictic” southern Finnish population. Linkage disequilibrium analysis has allowed precise mapping and determination of genetic distances at the 0.1-cM level in several of these disorders. Estimates of genetic distance have proven accurate, but previous calculations of the confidence intervals were too small because sampling variation was ignored. In the north and east of Finland the population can be viewed as having been “founded” only after 1500. Disease mutations that have undergone such a founding bottleneck only 20 or so generations ago exhibit linkage disequilibrium and haplotype sharing over long genetic distances (5–15 cM). These features have been successfully exploited in the mapping and cloning of many genes. We review the statistical issues of fine mapping by linkage disequilibrium and suggest that improved methodologies may be necessary to map diseases of complex etiology that may have arisen from multiple founding mutations.

Presently biomedical research focuses heavily on molecular genetics, that is, the elucidation of the molecular basis of disease. The driving force is the realization that not only accurate diagnosis, but also efficient therapy and prevention, will rely heavily on our knowledge of the pathogenetic pathways in the normal state and their abnormalities in the disease state.

One obvious way of getting a handle on physiologic, metabolic, and developmental pathways is to identify the proteins involved. Interestingly, in spite of major advances in protein chemistry during the second half of this century, only a few diseases had been clarified at the molecular level until the emergence of molecular genetics in the early 1980s. One key development was that hereditary phenotypes (diseases) could be genetically mapped by using natural variations in the DNA as markers (1). This finding opened the gates to a flood of research centering on the mapping of disease loci by linkage analysis using DNA markers. The era is by no means over. Microsatellite marker maps are already so dense (>5,000 markers with an average spacing of ≈1 cM) (2) that in Mendelian disorders almost any phenotype can be mapped by regular linkage analysis if samples from just a handful of nuclear families containing a few affected individuals are available. The high-tech aspect of gene mapping by linkage probably will soon become even more pronounced when solid-phase chip technologies enter the field (3, 4).

Once a locus has been convincingly mapped to a “critical” region, the sought-after gene can be cloned by efforts that have become known as positional cloning. The term implies that genes are identified in the region and a gene is shown to be mutated in patients but not in controls. Key to the success of positional cloning is to limit the size of the critical region in which the gene must reside. In not-so-common disorders, linkage analysis often does not allow the region to be made smaller than, say, 5–10 cM, even when a reasonable proportion of all multiplex families diagnosed worldwide is available for study. Positional cloning of a specific disease-causing gene in a 5-cM, approximately 5-Mb stretch of DNA, is a major effort even today, because on the average, this process will mean identifying and sifting through perhaps 150 genes.

Linkage Disequilibrium

The term refers to the fact that in loci that are close to each other certain alleles occur more often on the same chromosome than expected after random segregation. The more descriptive term allelic association covers the same situation; however, alleles at different loci can occur in nonrandom association for reasons other (usually functional) than close proximity of the loci. In panmictic populations linkage disequilibrium is supposedly not noticeable at genetic distances exceeding 1 cM, but, in fact, in parts of the genome linkage disequilibrium is seen at genetic distances as long as 1–2 cM, whereas for some markers, linkage disequilibrium is absent at very short distances (5). Recent work (6) may provide some justification for these observations.

Founder Mutations

For disease gene mutations, linkage disequilibrium can be expected only if single-origin founder mutations common to many living affected individuals occur. As will be discussed in more detail below, the extent of linkage disequilibrium around a disease locus harboring a founder mutation will depend mainly on the time that has elapsed since the mutation occurred. A classic example is provided by the CFTR gene responsible for cystic fibrosis (reviewed in ref. 7). Here, even though the disease is common and hundreds of segregating families were available for linkage analysis, it proved difficult to pinpoint the localization of the gene beyond 1–2 cM. However, linkage disequilibrium was observed with several markers and guided the positional cloning efforts. Indeed, after the CFTR gene had been cloned it turned out that a single mutation, ΔF508, accounted for 60–80% of all cystic fibrosis chromosomes in most populations. When polymorphic markers within the CFTR gene became available, it was possible to use mathematical models to attempt to calculate the age of the single founding mutational event leading to ΔF508. In one study (8) an age as high as 2,627 generations was suggested, corresponding to more than 50,000 years. Notably, for calculations of this type assumptions have to be made that cannot be verified. Thus other published estimates of the age of ΔF508 are one magnitude smaller, or approximately 5,000 years (7, 9).

Populations Favorable for Study

Linkage disequilibrium is a powerful tool in gene mapping whenever the population under study fulfills two major prerequisites: the present population should derive from a relatively small number of founders, and the expansion of the population should have occurred by growth rather than by immigration. Many human populations fulfill these criteria. However, to be as useful as possible for research into human disease, a number of additional characteristics are desirable. The population should be large enough to provide enough affected individuals to study. For high-resolution mapping, enough time should have elapsed since the founding to have produced critical crossovers. Conversely, for low-resolution mapping over larger genetic distances, only a few generations should have occurred between the founding and the present. Ideally, there should be genealogical records allowing common origins of the individuals living today to be searched for. Moreover, records showing geographical birthplaces of ancestors can help deduce similarities and dissimilarities in genetic origin. Finally, the standard of medical diagnostics and care should be high, and private, public, and professional attitudes toward research should be favorable.

The Finnish Population Structure

The above prerequisites are largely fulfilled by the 5.1 million population of Finland. Several original articles and reviews have been published on the population history of the Finns (10, 11). A brief synopsis of those findings follows: Present-day Finland was populated soon after the last glacial period, some 10,000 years ago. It remained populated with low density until about 2,000 years ago where after the number of people has grown rapidly. Although exact figures cannot yet be given, the “founding” population, that is the population that existed when the expansion began, must have been small. Immigration occurred during the period 0 AD through the first centuries of this millennium, whereafter immigration has been, and continues to be, quite small by almost any standard. Repeated population bottlenecks have occurred, the last one as late as the early 18th century. Up to the 1500s only the southwest and southeast corners and all coastal areas, were regularly inhabited (“old Finland”). Thereafter the rest of the country was settled by internal emigration from regions with population surplus to uninhabited areas. Once settlements in “new Finland” were established (for which there is documentation) they grew in isolation forming subisolates; the main reason for isolation being distance. Thus, in summary (Fig. 1, ref. 12), Finland’s 5.1 million people descend from a relatively small number of founders, with very little immigration having occurred during the 80–100 generations of expansion. The southern and western population can be viewed as panmictic, but regional clustering of several disease genes and markers shows that even here subisolates exist. The northern and eastern populations started expanding only 15–25 generations ago from founders that came from within Finland and is characterized by subisolates with 50,000 or fewer inhabitants.

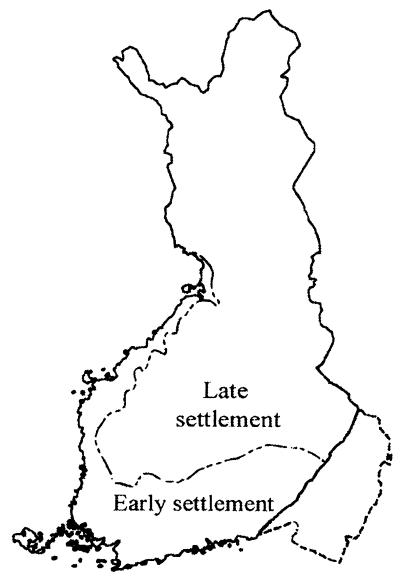
Figure 1.

Map of Finland showing the approximate extent of the early settlement (old Finland) in the south and west in which the population began to expand some 2,000–2,500 years ago, and the area of late settlement (new Finland) in the north and east in which population expansion started mainly after 1500. (Adapted from ref. 12.)

Several groups are conducting research into various aspects of the molecular genetics, clinical genetics, and genetic epidemiology in Finland. At the time a previous review was written (13) many disease gene projects had been started but were not completed. We summarize here some of the progress that has occurred since 1993 and provide a selective review of the literature pertaining to the topic.

Hereditary Disorders That Are Prevalent in Finland

Natural favorite targets of gene research in Finland are provided by those mainly autosomal recessive disorders and conditions that are highly prevalent in Finland and rare elsewhere (12). In most cases the relatively high gene frequency is caused by a founder effect and compounded by subsequent genetic drift (13). Table 1 summarizes most of these disorders (14–69). It can be seen that the responsible gene locus has been mapped in 29/34 cases and the gene itself identified in 14/34. In the following paragraphs a few disease examples highlighting the role of linkage disequilibrium in gene discovery are given.

Table 1.

Synopsis of the genetics of 30 autosomal recessive, two autosomal dominant, and two X-chromosomal recessive disorders that occur frequently in the Finnish population

Disease	McKusick no. (Locus)	Chrom. localiz.	Gene name	Gene symbol	References
Recessive inheritance
Aspartylglucosaminuria	208400 (AGU)	4q	Aspartylglucosaminidase	AGA	14
Autoimmune polyendocrinopathy-candidiosis-ectodermal dystrophy	240300 (APECED)	21q	Autoimmune regulator	AIRE	15, 16
Cartilage-hair hypoplasia; also metaphyseal chondrodysplasia	250250 (CHH)	9p			17, 18
Ceroid-lipofuscinosis, neuronal 1, infantile; also Santavuori disease	256730 (CLN1)	1p	Palmitoyl protein thioesterase	PPT	19, 20
Ceroid-lipofuscinosis, neuronal 2, late infantile type	204500 (CLN2)	11p	Ceroid-lipofuscinosis, neuronal 2	CLN2	21, 22
Ceroid-lipofuncinosis, neuronal 5	256731 (CLN5)	13q			23, 24
Cohen syndrome	216550 (COH1)	8q			25, 26
Congenital chloride diarrhea	214700 (CLD)	7q	Down-regulated in adenoma	DRA	27, 28
Congenital nephrosis; also Finnish nephrosis	256300 (CNF)	19q	Nephrin	NPHS1	29, 30
Cornea plana congenita	217300 (CNA2)	12q			31, 32
Diastrophic dysplasia	222600 (DTD)	5q	Diastrophic dysplasia sulphate transporter	DTDST	33, 34
Dibasicaminoaciduria II; also lysinuric protein intolerance	222700 (LPI)	14q			35
Disaccharide intolerance II; also congenital lactase deficiency	223000				36
Gyrate atrophy of choroid and retina; also gyrate atrophy with ornithine-delta-amino transferase deficiency	258870 (HOGA)	10q	Ornithine amino-transferase	OAT	37
Hydrolethalus syndrome	236680				38
Hyperglycinemia, isolated nonketotic, type I	238300 (NKH1)	9p	Glycine decarboxylase P protein	GCSP	39
Infantile-onset spinocerebellar ataxia	271245 (IOSCA)	10q			40, 41
Lethal congenital contracture syndrome; also Herva syndrome	253310 (LCCS)	9q			42, 43
Meckel syndrome	249000 (MKS)	17q			44
Megaloblastic anemia 1, also Imerslund-Gräsbeck syndrome	261100 (MGA1)	10p			45
Mulibrey nanism	253250 (MUL)	17q			46
Muscle-eye-brain disease; also MEB disease	253280 (MEB)				47
OHAHA syndrome (ophthalmoplegia, hypacusis, ataxia, hypotonia, athetosis)	258120 (OHAHA)				48
Ovarian dysgenesis, XX type	233300 (ODG1)	2p	Follicle-stimulating hormone receptor	FSHR	49, 50
PEHO syndrome	260565 (PEHO)				51, 52
Polycystic lipomembranous polycystic osteodysplasia; also Hakola syndrome	221770 (PLOSL)	19q			53, 54
Progressive epilepsy with mental retardation	600143 (EPMR)	8p			55, 56
Progressive myoclonus epilepsy, Unverricht-Lundborg type	254800 (EPM1)	21q	Cystatin B	CSTB	57, 58
Sialic acid storage disease; also Salla disease	268740 (SIASD)	6q			59
Usher syndrome, type III; also retinitis pigmentosa and congenital deafness	276902 (USH3)	3q			60, 61
Dominant and X-linked inheritance
Choroideremia	303100 (CHM)	Xq	Choroideremia	CHM	62, 63
Familial amyloidosis, Finnish type; also Meretoja syndrome; also amyloidosis V	105120 (FAF)	9q	Gelsolin	GSN	64, 65
Retinoschisis	312700 (RS)	Xp	X-linked retinoschisis 1	XLRS1	66, 67
Tibial muscular dystrophy, tardive	600334 (TMD)	2q			68, 69

Diastrophic Dysplasia (DTD)

Mapping by linkage in multiplex families allowed a resolution of 5 cM on chromosome 5 (70). When uniplex families were genotyped, in addition it became clear that one marker, and in particular one extended haplotype of markers, was almost uniquely associated with DTD-carrying chromosomes (33). Adapting formulas developed by Luria and Delbrück (33) for the genetic study of exponentially growing bacteria (see below), an attempt was made to calculate the genetic distance between the marker showing the highest degree of linkage disequilibrium and the putative DTD gene. For this calculation to be possible some variables needed to be defined, namely: μ = the mutation rate at the disease locus (for a rare disease such as DTD, the approximation of 5 × 10⁻⁶ was made); q = the disease gene frequency in this population, which can be directly calculated provided the frequency of newborn affected homozygotes is known (in Finland q could be estimated at 0.008); and g = the number of generations since founding. At the time when these studies were done this parameter was totally unknown, and to estimate g, genealogical data were leaned on heavily. First, it was shown that even when probands were traced back 5–10 generations, only occasional probands showed evidence of shared ancestry. This finding suggested a relatively distant common ancestor. Second, plotting the birthplaces of DTD carriers on the map of Finland (Fig. 2) showed it to be relatively evenly distributed, many cases belonging to the areas of early settlement (old Finland). This distribution could hardly have arisen unless the mutation was present at about the time of the beginning of the population expansion, that is, the time of founding. This being 2,000–2,500 years ago, the value of 100 was assigned to g.

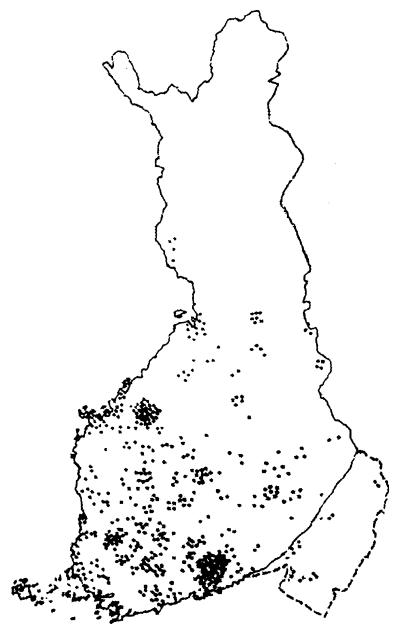
Figure 2.

Map of Finland showing the birthplaces of all known great-grandparents of patients with DTD studied. By using the birthplaces of great-grandparents putative biases stemming from the recent move of people from the north and east of the country to the south and west is avoided. However, of eight great-grandparents only two are actual carriers. See Fig. 5 for further comments. The distribution of birthplaces shown here is mainly in old Finland, suggesting that the putative ancestral founding DTD mutation was present in the population at the beginning of its expansion, some 2,000 to 2,500 years ago. Note also at least two local enrichments that are typical and stem from the existence, even in the panmictic older Finnish population of county-sized regional isolates in which local founder effects and genetic drift can occur. (Adapted from ref. 33.)

By using these parameters, the value of α = the proportion of mutations descending from the putative founding ancestor was calculated from the formula α = 1-μgq⁻¹ and turned out to be 0.94.

The Luria–Delbrück model (33) for calculating genetic distance (see Statistical Issues) was used for the marker considered to show the highest linkage disequilibrium. The distance of approximately 0.06 cM emerged from these calculations.

Outcome: Assuming a genetic distance of only 0.06 cM from the marker, the DTD gene was mainly searched for by physical mapping methods in the immediate vicinity (<100 kb) of the marker. Indeed this turned out to be correct in that the gene, named DTDST for DTD sulfate transporter, was located approximately 70 kb (sic) from the marker (34). Mutational analyses confirmed the existence of one major founding mutation, a splice site mutation in the 5′ untranslated region of DTDST, but the proportion of all DTD chromosomes carrying this mutation was somewhat lower (90%) than the predicted 94%. This difference is fully accounted for by the finding of two other mutations that occur on the same haplotype as the main one (J. Hästbacka, personal communication).

Progressive Myoclonus Epilepsy (EPM1)

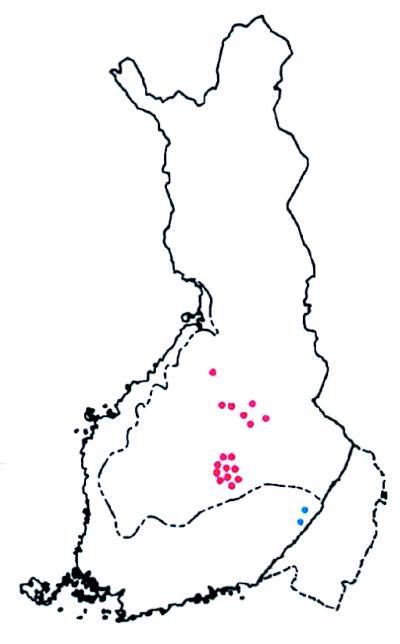
The locus was assigned to a 7-cM region by linkage in multiplex families (57). The value of g = 100 was used in linkage disequilibrium calculations because just as in the case of DTD, the mutation was widespread in old Finland (71). Luria–Delbrück calculations suggested a location 0.13–0.30 cM from the closest marker, PFKL (72). However, importantly, the EPM1 locus was assigned to a region that was unclonable in yeast artificial chromosomes (YACs) and therefore, the physical size of the critical region could not be determined, and there were few markers. Adjacent to but outside and centromeric of the presumed critical region was a marker (D21S141) that showed a relatively high degree of linkage disequilibrium (p_excess = 0.66; for a definition of this parameter of linkage disequilibrium, see below). This information and data on recombinations prompted physical mapping efforts to be targeted in the centromeric direction of the YAC-unclonable region (73).

Fig. 3 summarizes the physical and genetic mapping data that guided the search for CSTB, the gene that turned out to be responsible for EPM1. These data go a long way to emphasize the usefulness of linkage disequilibrium in disease gene mapping and equally the value of using multiple analytical methods in positional cloning.

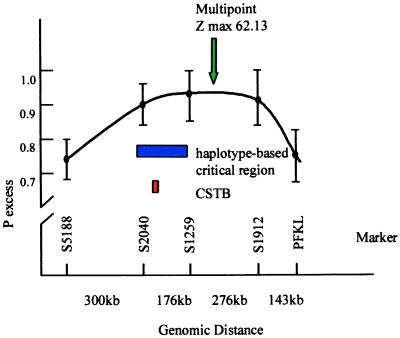
Figure 3.

Diagram of the CSTB region on chromosome 21q. The x-axis shows the location and physical distances (in kb) between five polymorphic markers. • indicate the degree of linkage disequilibrium (expressed as p_excess) calculated between EPM1 and the marker. Before CSTB was found (its location is shown in red), a minimal critical region (shown in blue) was defined based on the analysis of historical recombinations in the haplotypes of 88 EPM1-carrying chromosomes. The green arrow shows the point of highest multipoint linkage disequilibrium (z = 62.13) using these markers.

The founder mutation in Finland, a dodecamer minisatellite expansion in the promoter region, is the main mutation worldwide, accounting for greater than 85% of all EPM1 chromosomes (74–76). In Finland the proportion is 99%. Based on 88 disease-associated haplotypes we predicted that only one chromosome carries a mutation different from the main one (71) and that is indeed the case (ref. 75 and unpublished work).

Chloride Diarrhea (CLD)

The locus was assigned by linkage analysis to a 10-cM region, and every CLD chromosome in Finland occurred on the same, extended haplotype, suggesting a single founding mutation (α = 1) (27, 77). The critical region was narrowed to approximately 0.37 cM by linkage disequilibrium analysis, and this region contained two previously cloned genes, one of which, down-regulated in adenoma (DRA), turned out to be responsible for the disease (28). The Luria–Delbrück calculations (96) were done assuming a g of only 15–25 because most cases of CLD originated in new Finland (Fig. 4). The Finnish founder mutation is a 3-bp in-frame deletion that occurs on every CLD chromosome in Finland except one (78). Interestingly, when the Luria–Delbrück formula is used to calculate the age of the mutation (g) the other parameters including genetic distance being known, the average value of g obtained for five markers in the region turns out to be 19 (range 13–25). This figure is in full agreement with deductions from what is known of the geographical distribution of the gene and the population history of the Finns. Note, for instance, how few affected chromosomes in CLD homozygotes originate in the densely populated southwestern region of old Finland (Fig. 4).

Figure 4.

Map of Finland showing birthplaces of grandparents (red) and parents (blue) of 34 patients with CLD. The distributions are very similar, showing that recent moves from the eastern and north-central parts of the country to the south and west that would significantly distort the distribution have not occurred. Birthplaces are almost entirely confined to new Finland that is, regions populated after the 1500s. (Adapted from ref. 28.)

Founder Mutations in Cancer Predisposition

Dominantly inherited predisposition to hereditary nonpolyposis colorectal cancer (HNPCC) is caused by mutations in genes encoding mismatch repair proteins, mainly MLH1 and MSH2 (79, 80). Carriers of such mutations have an 80–90% lifetime risk of acquiring cancer, and the average age at onset at diagnosis of the first colorectal cancer is 42 years. Nevertheless, widespread recurrent mutations occur.

In Finland two founder mutations in the MLH1 gene deserve attention because they are so common that they account for approximately half of all HNPCC (81, 82). Extensive haplotype sharing over a genomic region as large as 18 cM indicated a relatively recent founding of the more prevalent mutation. By using a formula given by Risch et al. (83) the “age” of this mutation in most of the 19 kindreds studied could be estimated at 16–43 generations in keeping with historical records and compatible with a founding in a regional subisolate in new Finland in the early 1500s (81, 84). Interestingly, two kindreds with the same mutation shared only a ≈2-cM core haplotype with the rest of the kindreds. A glance at the map of Finland shows that these two kindreds share a different geographical location some 300 km southeast of the majority of kindreds (Fig. 5). Again, this feature is fully compatible with the population history of Finland, suggesting that the two kindreds in old Finland represent a first, more ancient founding bottleneck (perhaps some 43 generations ago), whereas the families in new Finland represent a second more recent founding bottleneck (perhaps some 16 generations ago).

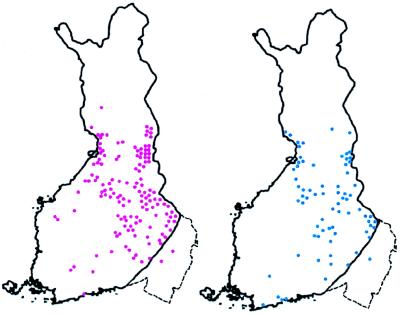
Figure 5.

Map of Finland showing birthplaces of ancestors of patients with HNPCC. The dotted line depicts the approximate border between old and new Finland. Each symbol depicts a kindred with several HNPCC patients. All of the kindreds share the same genomic deletion of exon 16 of the MLH1 gene. Based on linkage disequilibrium with numerous markers in and around the MLH1 gene, extensive haplotype conservation among kindreds marked in red suggests only a limited number of generations (perhaps 16) since founding. This finding is consistent with the population history of new Finland. In contrast, the two kindreds shown in blue share only a 2-cM core of the conserved haplotype with the other kindreds, suggesting a much older age of the mutation (perhaps 43 generations). This finding fits with their geographical location in old Finland. (Adapted from ref. 84.)

The message here is 3-fold. First, somewhat surprisingly, dominant founder mutations have spread and become highly enriched in specific populations even in cancer predisposition syndromes (as long as they do not significantly affect reproduction). Second, the incidence of some of these mutations is so high in some populations that they constitute a unique health problem. Third, as such mutations become known and characterized, they are usually relatively easily demonstrable even allowing them to be screened for at the population level if required.

Statistical Issues

The phenomenon of linkage disequilibrium was known to early genetics researchers (85, 86), but, only recently has technology enabled fine-scale mapping (87, 88). Genetic drift, selection, and other factors can complicate fine-scale mapping and produce unreliable estimates (89–91). However, the apparent success of linkage disequilibrium mapping in several diseases (33, 72, 77, 81, 92, 93) has demonstrated the feasibility of the approach in certain settings and inspired further methodological work.

The techniques can be roughly divided into three categories: single-marker analyses, multiple-marker analyses, and methods of detecting ancestral haplotypes. The first two categories are usually parametric in that they involve a specified model for ancestry. Another approach is to look for ancestral haplotypes that are present on disease-carrying chromosomes and absent on normal chromosomes (94). Such analysis may be performed nonparametrically, providing hope for identifying multiple mutations in populations with diverse ancestry.

Single-Marker Analyses

The isolated Finnish population provides several advantages in performing disequilibrium mapping (13, 91). For an expanding population, after disease introduction the expected degree of disequilibrium between the disease and a linked marker decreases geometrically with each generation. We assume that the ancestral marker allele associated with disease can be identified. Following previous notation (13, 72) the parameters are denoted as follows: p_normal = frequency of allele at a marker in normal chromosomes, p_affected = higher frequency of the same allele in disease chromosomes, α = proportion of current disease chromosomes descended from the disease mutation, g = generations since introduction of mutation, π = proportion of disease chromosomes that have never recombined between marker and disease gene, and θ = recombination fraction between disease and marker. As briefly derived in Lehesjoki et al. (72), assuming that p_normal has remained constant over time, p_affected = {π + (1 − π)p_normal}α + p_normal(1 − α), which yields

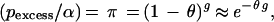1

where p_excess = (p_affected − p_normal)/(1 − p_normal). Estimates of p_normal and p_affected can be derived from samples of normal and disease chromosomes. Thus, if α and g are known, θ can be estimated from Eq. 1. Otherwise, the parameters are confounded and in this sense single-marker disequilibrium analysis is analogous to two-point linkage analysis (95). In the Finnish population, α and g may be estimated from historical and geographic considerations (13, 33). Hästbacka et al. (33) adapted the classical methods of Luria and Delbrück (96) to form a confidence interval for θ.

The Luria–Delbrück formulae, originally derived to estimate bacterial mutation rates, are naturally adaptable to populations such as the Finnish that have undergone rapid population expansion (91). The Luria–Delbrück results give the mean (essentially Eq. 1) and variance for the proportion of recombinants in the current generation, providing a point estimate and standard error for θ. To account for skewness in the recombinant proportion, Luria and Delbrück also derived formulae for what they termed the “likely” mean and variance. The simplest version of the approach was applied for the DTD gene and marker CSF1R (33), and implicitly assumed p_normal = 0, α = 1. Lehesjoki et al. (72) used a modified approach that explicitly incorporated p_normal and α.

Kaplan et al. (97) developed a likelihood-based method for estimating θ from the data by using a Poisson branching process. Likelihood methods often have desirable properties (98), and we and others (72) have conceded that when population ancestry is well understood likelihood approaches may be preferable. However, the observed data can arise from a huge number of possible ancestries, and the likelihood is difficult to evaluate. Kaplan et al. (97) developed a Monte Carlo rejection sampling scheme to estimate the likelihood, and found (97, 99) that the Luria–Delbrück bounds (33) would identify too narrow a region as containing the disease gene.

To understand the discrepancy, we outline the development of Hästbacka et al. (33). From Luria and Delbrück (96), the expected proportion of nonrecombinants is given in Eq. 1. π̂ is the observed proportion of nonrecombinant chromosomes in our sample. The “likely” SD for the proportion of disease chromosomes in the population that are not recombinant is θ/d, where d is the population growth rate per generation (33). However, only a small portion of the population of disease chromosomes typically is observed (especially for recessive diseases). For example, Hästbacka et al. (33) estimate that 80,000 DTD chromosomes exist in Finland, whereas only 152 were available for study. In creating the confidence intervals Hästbacka et al. treated the value θ/d directly as a standard error for π, ignoring the sampling variation. The variance of π̂ is approximately the sum of the sampling variation and the variance of the recombinant proportion in the population, or

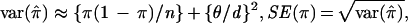2

where n is the sample size of disease chromosomes. Often the sampling variation will, in fact, contribute the greater part of the standard error of π. Hästbacka et al. (33) estimated θ = 0.00064, d = 0.085. Thus the original estimate SE(π) = θ/d = 0.0075 is now modified by using Eq. 2 to SE(π) = 0.020. Remarkably, none of the subsequent investigators (7, 91, 97, 99–101) appear to have noticed the oversight and instead attributed the small standard error to a failure of the moment method. Some of the confusion may stem from an error in equation 1 of ref. 33, in which π should be replaced by 1-π. This error was repeated in ref. 99 on page 1488. Interestingly, such sampling variation was explicitly considered by Luria and Delbrück (ref. 96, page 500), but in their setting was only of minor importance. Additional variations of the moment method are possible, but we argue that this modification of the original technique may be useful for simple inference.

Xiong and Guo (102) also obtained results based on more sophisticated population models, developing a Taylor approximation to the likelihood. Rannala and Slatkin (101) developed a likelihood procedure similar to that of Kaplan et al. (97) based on a continuous-time process. They also required Monte Carlo methods to evaluate high dimensional integrals in the likelihood.

Multiple-Marker Analyses

Fine mapping using single markers requires that the associated allele not be common among normal chromosomes, and that population parameters such as α and g be estimated from historical sources. The use of multiple markers in a synthesized analysis can improve the power and efficiency of linkage disequilibrium mapping (102–104) and provide estimates of the additional parameters of population ancestry.

An additional potential advantage to using multiple markers is that it may provide robustness to uncertainty in the conversion from genetic to physical distance. Regardless of the assumed map, a careful multiple marker analysis may still show the greatest disequilibrium at the marker nearest the disease gene (in a manner similar to linkage analysis; refs. 100 and 105).

Kaplan and colleagues (97, 99) provided a two-marker generalization to their technique. Terwilliger (103, 106) proposed a likelihood ratio test with a single free parameter (essentially p_excess). Terwilliger’s approach extends to multiple alleles and does not require a priori identification of the disease-associated allele. Terwilliger proposed a multilocus procedure by summing over the log-likelihoods contributed by each marker, producing a logarithm of odds-like curve to estimate the disease gene location. However, the proposed multilocus location score is not a true likelihood, as discussed below. Devlin et al. (104) proposed a method with explicit consideration of population history. They also used a multilocus summed log-likelihood procedure and clarified that this was an example of composite likelihood (107). Xiong and Guo (102) also used composite likelihood in their multilocus procedure. Recently Collins and Morton (7) detailed a similar approximate composite likelihood method with dichotomized allele classes. The lack of true likelihood procedures reflects the difficulty in modeling the dependence among marker alleles. Composite likelihood is generally efficient only when the markers are independent, i.e., in linkage equilibrium, which is certainly not expected to be true here. Furthermore, there is no simple procedure for creating confidence intervals for disease gene location (104). A simple support interval procedure (7, 103) adapted from likelihood theory is likely to produce optimistically small intervals (104), and in multilocus analyses the likelihood does not have a normal asymptotic shape (108). The recent paper by Lazzeroni (109) addressed this difficulty by estimating the marker covariances and performing bootstrapping (110) to obtain approximate confidence intervals. Although the composite likelihood procedures are potentially more powerful than single marker analyses, most of the applications have been for diseases (cystic fibrosis, Huntington’s disease) in which less formal methods had sufficed.

A simple example highlights one difficulty of multilocus analysis in detecting linkage disequilibrium. Suppose we examine two markers, A and B, and find that all disease chromosomes have either of two haplotypes AB or ab with equal frequency. Among normal chromosomes, the haplotypes AB, Ab, aB, and ab occur in equal frequency. This situation could arise if two founding mutations were introduced and no recombination had yet occurred between the markers and disease. This example is not entirely contrived, e.g., two founding haplotypes have been described in the HNPCC Finnish pedigrees (84).

For sufficient sample size, a comparison of haplotype frequencies with disease status (a 4 × 2 table) easily detects the haplotype-disease association. Note, however, that marginally the allele A appears in 50% of disease chromosomes and 50% of normal chromosomes, and thus we have no power to detect the association from marker A alone. The same holds true for B, and any of the composite likelihood methods applied to these data would fail to discover the obvious association [including multiple-mutation extensions proposed by Terwilliger (103)]. Among the methods described, only Lazzeroni’s (109) enables detection of this linkage disequilibrium through the marker covariances. However, one might imagine similar examples in which the association is present in the higher moments and not detectable by using covariances alone.

Detection of Haplotypes

As technology improves, analytic techniques are necessary to identify multiple founding mutations associated with disease. As the example illustrated, one approach is to examine the association of haplotypes (rather than marginal allele frequencies) with disease. This method may give rise to large, sparse contingency tables in which a few haplotypes may be strikingly associated with disease. If nonparametric tests are used, the degree of association and the number of disease mutations need not be specified in advance.

This type of analysis often is performed informally by researchers (71, 81). Ramsay et al. (94) have described a somewhat more systematic haplotype-based approach, and Sham and Curtis (111) examined nonparametric tests of association between disease and highly polymorphic alleles. The latter issue is of increasing importance, as in a haplotype-based analysis an “allele” represents the joint allele states at multiple marker loci. Recently Edwards (112) described related graphical methods for haplotype detection in recessive diseases, others (113) have used the length of shared haplotype among disease chromosomes as a linkage disequilibrium statistic.

For these techniques, a number of outstanding methodological questions remain. An important issue is how to choose the length of marker haplotypes as one scans for association across the genome. Another issue is the need for integrated methods to bridge the gap from haplotype detection to super-fine mapping in which a parametric model may be used. Finally, it should be noted that the methods described here assume that haplotypes may be deduced unambiguously from pedigree information. For more complex diseases, this circumstance generally will not be true, and methods are required in which phase-unknown genotype information can be used to effectively detect ancestral haplotypes (114).

ABBREVIATIONS

DTD

diastrophic dysplasia

EPM1

progressive myoclonus epilepsy

CLD

chloride diarrhea

HNPCC

hereditary nonpolyposis colorectal cancer