FoldMiner: Structural motif discovery using an improved superposition algorithm

Abstract

We report an unsupervised structural motif discovery algorithm, FoldMiner, which is able to detect global and local motifs in a database of proteins without the need for multiple structure or sequence alignments and without relying on prior classification of proteins into families. Motifs, which are discovered from pairwise superpositions of a query structure to a database of targets, are described probabilistically in terms of the conservation of each secondary structure element’s position and are used to improve detection of distant structural relationships. During each iteration of the algorithm, the motif is defined from the current set of homologs and is used both to recruit additional homologous structures and to discard false positives. FoldMiner thus achieves high specificity and sensitivity by distinguishing between homologous and nonhomologous structures by the regions of the query to which they align. We find that when two proteins of the same fold are aligned, highly conserved secondary structure elements in one protein tend to align to highly conserved elements in the second protein, suggesting that FoldMiner consistently identifies the same motif in members of a fold. Structural alignments are performed by an improved superposition algorithm, LOCK 2, which detects distant structural relationships by placing increased emphasis on the alignment of secondary structure elements. LOCK 2 obeys several properties essential in automated analysis of protein structure: It is symmetric, its alignments of secondary structure elements are transitive, its alignments of residues display a high degree of transitivity, and its scoring system is empirically found to behave as a metric.

Over the past few years, the rate at which new protein folds have been discovered has not kept pace with the rate at which protein structures have been determined and deposited into the Protein Data Bank (PDB; Berman et al. 2000). Although the set of proteins with structures that are solved is biased both by biological significance and by factors that contribute to the ease of structure determination, there has been some speculation that although many naturally occurring fold classes are now represented within the PDB, others have few or no representatives among known protein structures (Wang 1998; Zhang and DeLisi 1998; Govindarajan et al. 1999; Wolf et al. 2000). Just as our understanding of protein sequences has benefited from sequence alignment methods and classification schemes, so can our understanding of protein structures benefit from the continued development of methods for structure alignment, classification, and motif discovery. These types of structural analysis methods complement and extend sequence analysis in the detection of homologies and other evolutionary relationships among proteins. One of the goals of structural genomics initiatives is to discover all possible folds assumed by proteins (for reviews, see Sali 1998; Brenner 2001; Chance et al. 2002); methods for assessing structural similarity are essential to such endeavors. The large-scale nature of these efforts requires such methods to be both rapid and automated.

Both accurate structural alignments of distantly related structures and detection of commonly occurring and family-specific structural motifs have great potential to yield insight into questions such as the conservation of protein structure, the types of structural interactions “preferred” in nature, and the relationships among sequence, structure, and function (Russell et al. 1997; Martin et al. 1998; Orengo et al. 1999; Huang et al. 2000; Yang and Honig 2000b,c; Balaji and Srinivasan 2001; Todd et al. 2001). The identification of structural motifs facilitates and accelerates automated detection of structural homologies among both closely and distantly related proteins by focusing on regions of proteins that have been conserved in the evolution of protein structure (Holm and Sander 1998; Shindyalov and Bourne 2000; Liang et al. 2003). Motifs and core folds can also serve as templates for homology modeling and threading methods (Madej et al. 1995; Panchenko et al. 1999), and can provide guidance to ab initio fold prediction algorithms (Bystroff and Shao 2002). Comparisons of the abilities of structural motifs and structural alignment methods to find distantly related homologs strongly suggest that motifs provide for greater discrimination between homologs and analogs than do alignment methods that do not incorporate information from motifs (Matsuo and Bryant 1999; Orengo 1999).

Previous efforts to identify commonly occurring structural motifs can generally be divided into two categories: those that identify local motifs consisting of a relatively small number of residues, and those that capture the entire core fold common to a set of proteins. Many local methods use sequence information both to identify potential motif locations and to search structures for the presence of these motifs. Some such methods map previously known sequence motifs (Nevill-Manning et al. 1998; Henikoff et al. 1999, 2000; Huang and Brutlag 2001; Sigrist et al. 2002; Attwood et al. 2003) onto protein structures (Kasuya and Thornton 1999; Bennett et al. 2003), whereas others identify sequence and structure conservation simultaneously (Bystroff and Baker 1998; Jonassen et al. 2002). Inductive logic programming has been used to find protein “signatures,” which may be either local or global, by using structural characteristics such as the lengths and adjacencies of secondary structure elements (SSEs; Turcotte et al. 2001).

Global motif detection methods frequently perform multiple structure superpositions of known homologs and identify motifs and core folds as those portions of the structures that are aligned (Koch et al. 1996; Leibowitz et al. 2001). Some methods require further evidence such as low structural variability (Schmidt et al. 1997) or the presence of conserved structural properties (Orengo 1999) for inclusion of residues in a motif. Gelfand et al. (1998^; Stoyanov et al. 2000) find the core fold of immunoglobulin families by examining distances between α carbons and using a multiple sequence alignment to obtain correspondences among the residues of the structures, and thus avoid performing multiple structure alignments. Matsuo and Bryant (1999) also avoid the need for multiple structure alignments by defining the homologous core structure of a protein as those residues that are frequently aligned in pairwise structural alignments of homologs.

The problem of detecting global structural similarity is complicated by the presence of strong local structural similarities among proteins that have globally dissimilar structures. These regions of local structural homology tend to correspond to commonly occurring motifs consisting of a few SSEs that are not specific to any single fold or protein family. An analysis of the CATH structural classification hierarchy, for example, revealed a number of such local motifs that are found in a variety of families and folds (Orengo et al. 1997). This type of structural overlap can confuse classification efforts in regions of fold space that are not easily subdivided into distinct families (Orengo et al. 1997; Harrison et al. 2002). The requirement that a motif definition arise only from a given set of proteins identified as homologs by an outside standard can cause information from more distantly related structures to be ignored, and it is these distant relationships that are most likely to reveal information not easily gleaned from previously known evolutionary relationships. Because unsupervised motif discovery methods are unencumbered by the limitations of the existing protein classification systems from which sets of homologous proteins are typically obtained, they are perhaps more likely to discover previously unknown motifs and structural relationships than are supervised methods.

Here, we present an unsupervised motif discovery method, FoldMiner, that identifies motifs and core folds from pairwise structural alignments of a query structure to a database of target proteins. Neither multiple structure superposition nor sequence similarity is required. Because these alignments and motifs are determined purely from structure, they are ideally suited for analyses of the relationships among structure and other properties of proteins, such as sequence and function. The algorithm may also be run in a supervised fashion by limiting the target database to known homologs of the query structure.

As FoldMiner depends on pairwise structural alignments, it includes a structural superposition algorithm, LOCK 2, that is capable of detecting distant structural homologies. LOCK 2 is an improved version of Singh and Brutlag’s LOCK algorithm (Singh and Brutlag 1997). Although many structural alignment algorithms are capable of aligning structurally similar proteins, they tend to produce widely varying results in the more interesting cases of distantly related structures (Feng and Sippl 1996; Godzik 1996). Insertions and deletions of SSEs, for example, tend to result in either gapped or high root mean square deviation (RMSD) alignments (Grishin 2001). Such insertions in one protein with respect to another can occur both outside and within the core fold common to both structures. In the former case, alignment algorithms must be capable of detecting both global and local similarities, whereas in the latter case, they must be able to accommodate large gaps in the residue alignment. Changes in lengths and orientations of individual and groups of SSEs are also common (Mizuguchi and Blundell 2000) and require that scoring functions be flexible enough to detect such changes while still avoiding erroneous correspondences.

Most structural alignment algorithms use rigid body transformations and fall into one of two major categories: those that operate entirely at the level of individual residues (often restricted to C_α atoms) and those that operate at the level of SSEs, often using simplified representations of helices and strands to achieve an initial superposition that is later refined at the residue level. Among commonly used alignment methods that fall into the first category, the Structal algorithm is perhaps the most analogous to sequence alignment methods (Gerstein and Levitt 1996). It uses iterative dynamic programming to optimize a global alignment with a score that incorporates gap penalties and is based on interatomic distances between alpha carbons. Instead of using RMSD as a measure of structural similarity, Minarea minimizes the “soap film” surface area between the α carbon traces of the query and target structures (Falicov and Cohen 1996). DALI avoids rigid body transformations by aligning α carbon distance matrices (Holm and Sander 1993). More recently, the Combinatorial Extension (CE) algorithm was introduced; it builds alignments from small stretches of equivalent residues in the query and target structures (Shindyalov and Bourne 1998).

In contrast, both the Vector Alignment Search Tool (VAST; Gibrat et al. 1996) and LOCK 2 obtain an initial superposition by representing SSEs as vectors and optimizing their alignment subject to several scoring functions. VAST uses graph theoretic methods to find clusters of vectors in the query and target structures with similar relative orientations. LOCK 2 instead uses geometric hashing and dynamic programming to find a pair of vectors in the query and a pair in the target which, when aligned, bring the entire query and target structures into register (Singh and Brutlag 1997). LOCK 2 uses seven scoring functions to examine various distances and angles among query and target SSEs in order to find the best registration of the two proteins. After SSEs are aligned, both LOCK 2 and VAST refine the alignment at the residue level. LOCK 2 iteratively matches nearest neighbors, whereas VAST uses a Monte Carlo algorithm to explore the effects of moves such as extending or shortening aligned regions. Yang and Honig (2000a) have developed a similar method that aligns SSEs by considering their relative orientations in two structures. The residue alignment is then refined by using one round of dynamic programming followed by an iterative cycle of a rigid body superposition method introduced by Kabsch (1978) that terminates when the RMSD converges.

A recent algorithm introduced by William Taylor operates entirely at the level of SSEs (Taylor 2002). Taylor models interactions between SSEs by representing them as line segments and examining the overlap of each pair of segments. The interactions in each protein are represented as a graph, and the query and target structures are aligned via a bipartite graph-matching algorithm.

We have tested the ability of LOCK 2 to recognize distant structural relationships as defined by the Structural Classification of Proteins (SCOP; Murzin et al. 1995). We consider domains within the same SCOP fold to be structural neighbors even if they have no known evolutionary relationship. As even slight changes in orientations of SSEs in distant homologs make it difficult to achieve a correct, ungapped residue alignment, we believe it is both appropriate and necessary to assess structural homology at the level of SSEs (Mizuguchi and Blundell 2000). Accordingly, we have focused our efforts on increasing the accuracy and sensitivity of SSE alignment phase of LOCK 2. Unlike most structural alignment algorithms, LOCK 2 now reports the SSE alignment to the user in addition to the residue alignment.

FoldMiner provides several features that are of particular use in the automatic analysis of protein structures. In the process of performing a structural similarity search, FoldMiner not only reports statistically significant alignments but also detects the structural motif shared by the query and high-scoring target structures that is the basis for the structural similarity. Furthermore, its alignment scores are easily converted into distances between structures that are empirically found to obey the triangle inequality. Because LOCK 2 is a symmetric superposition algorithm, this distance is a metric that measures structural similarity between proteins. Pairwise alignments of protein structures that share a common fold are almost completely transitive at the level of SSEs and are nearly transitive at the residue level. That is, given three protein structures, two of the three possible pairwise alignments predict the third alignment. These properties allow users to take advantage of information contained within pairwise structural alignments in order to detect similarities across multiple structures. We validate FoldMiner in this study by comparing it to both VAST and the CE algorithm.

Results

Pairwise alignment scores and expectation scores

We have performed all unique pairwise alignments of structures in a database of 2448 SCOP domains, no two of which share >25% sequence identity. These domains were obtained from the ASTRAL compendium (Brenner et al. 2000) and represent 498 folds covering the mainly α, mainly β, α+β, and α/β SCOP classes as of release 1.55. We consider the structural neighbors of a given domain to be those structures in the same SCOP fold, as these domains generally have the same overall topology and connectivity of SSEs. Because some SCOP folds are quite diverse, however, we do not anticipate that structural alignment algorithms will attain 100% sensitivity.

To assess the statistical significance of LOCK 2 alignments, we have developed alignment scores based on the algorithm’s dynamic programming scoring functions. Briefly, the relative orientations of aligned SSEs with respect to both one another and the surrounding SSEs in the query and target structures determine the score as described by Singh and Brutlag (1997). The final alignment score is normalized to the larger of the query versus query and target versus target scores in order to favor alignments that are global with respect to both the query and target over alignments that are local with respect to one or both of the aligned structures. The score can then be converted into a distance between the two structures:

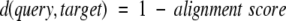(1)

These distances obey the triangle inequality within 5% error for all triples of over a set of three million alignments consisting of all pairwise superpositions of the 2448 structures described above. That is, for any three structures A, B, and C, the normalized scores almost always satisfy the following condition:

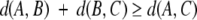(2)

Because LOCK 2 is a symmetric algorithm, the distance described in Equation 1 behaves as a structural similarity metric. This property will be useful in applications such as clustering and classification of proteins based on structural alignments.

To develop expectation scores for structural alignments, we have created background distributions of alignment scores for each SCOP fold. The distribution for a given fold consists of scores obtained from alignments of all structures within the fold to all structures outside of the fold’s SCOP class. It is necessary to exclude alignments of structures within the same SCOP class because many structural similarities cross SCOP fold boundaries. Structures in different SCOP classes, however, tend to have generally different compositions and arrangements of SSEs and normally do not align well at a global level (Murzin et al. 1995). This process is analogous to aligning random sequences in order to produce background distributions of scores for sequence alignment algorithms.

As is the case for alignments of random sequences, these structural alignment scores follow an extreme value distribution (Equation 3; Altschul et al. 1990^; Altschul and Gish 1996). The survival function of the extreme value distribution therefore gives the probability that an alignment score is achieved by chance, that is, the probability of obtaining a false positive (Equation 4).

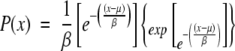(3)

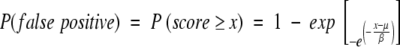(4)

We have fit the parameters of the extreme value distributions to our empirically derived background distributions to obtain expectation scores for LOCK 2 alignments (Fig. 1 ▶). Curve fitting was performed by using the S-PLUS 6 software package. Thus, LOCK 2 provides an assessment of the statistical significance of an alignment in the form of an expectation score, which allows us to control the number of expected false positives obtained in a database search in accordance with Equation 5:

Figure 1.

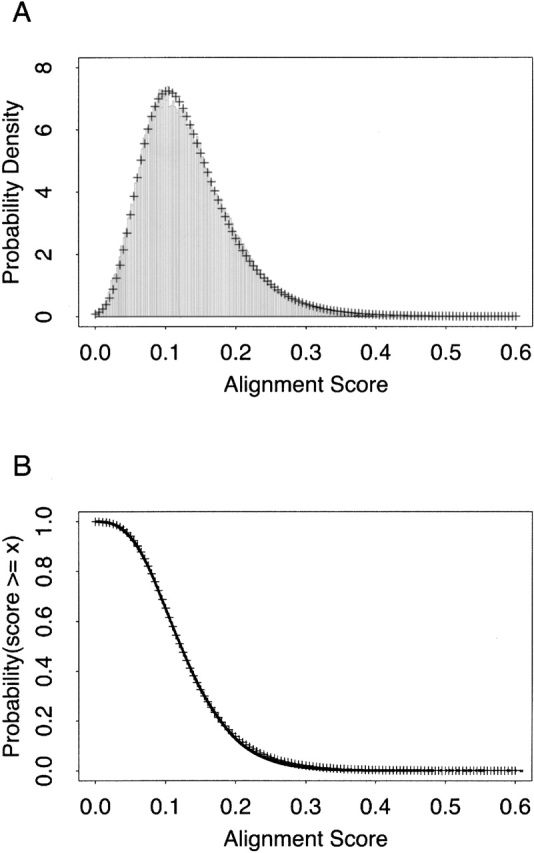
Statistical significance values and expectation scores for the ferredoxin-like SCOP fold. All SCOP ferredoxin-like domains (SCOP fold d.58) in a database of 2448 SCOP domains of <25% pairwise sequence identity were aligned by LOCK 2 to all other structures in the database that do not belong to this fold’s SCOP class. (A) The probability density of alignment scores is shown as bars. (B) The empirical CDF of the probability density (122,677 points plotted as dots) was fitted to an extreme value distribution, yielding a residual squared error of 0.004719. Fitted values are plotted as crosses (+) in both panels.

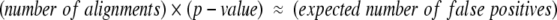(5)

We have chosen to produce a separate distribution for each fold because the probability of finding insignificant structural similarities varies with features such as compactness and secondary structure composition. In cases in which the query’s SCOP fold is unknown, we use a composite distribution for the query’s SCOP class. If the query’s SCOP class is also unknown, we use a background score distribution encompassing all folds in SCOP’s mainly α, mainly β, α+β, and α/β classes.

Structural similarity searches and motif discovery: The FoldMiner algorithm

Core folds and structural alignment

Expectation scores allow the user to align a single query structure to a database of targets at a statistical significance level determined by the size of the database and a desired upper bound on the false-positive rate (Equation 5). An expectation of 10, for example, implies that ~10 results will be false positives. For the database of 2448 structures used in this study, an expectation of 10 corresponds to a P value of 0.004. The amount of time required to perform all 2448 alignments varies among different query structures; the average time required to align a member of SCOP’s globin superfamily to the entire target database is 3.6 min on a 1.2-GHz Athlon processor. This corresponds to an average of less than a tenth of a second per alignment.

FoldMiner performs structural similarity searches using LOCK 2 to carry out the pairwise structural alignments. It differs from many other search algorithms in that it outputs not only a residue alignment but also the secondary structure alignment and a definition of the structural motif shared by the query and high-scoring targets. Matsuo and Bryant (1999) have previously reported improved discrimination between homologs and analogs by requiring that homologs align to a well-conserved core structure, compared to discrimination based on similarity measures such as the percentage of aligned residues and the RMSD. FoldMiner uses information about the structural conservation of the query’s SSEs learned from pairwise superpositions in order to achieve better discrimination between true and false positives that lie on the borderline of statistical significance. The motif is described probabilistically at the level of SSEs and may be viewed visually by coloring SSEs according to their observed conservations. Because LOCK 2 favors global structural alignments, FoldMiner motifs tend to be global as well, and often represent the core fold of the query protein and its homologs. This process is described in more detail below.

Analysis of the background distributions of alignment scores reveals that very few alignments attain >50%–60% of the maximum alignment score; we have observed this trend even among alignments of structures known to be homologous (data not shown). Many structures within the SCOP hierarchy contain a number of SSEs that are not part of the core motif common to all members of a given fold, and thus even global alignments will rarely encompass the entire query and target structures. An alignment that is global with respect to the core fold of the query structure may not appear to be statistically significant if the target structure is large, as the raw alignment score is normalized to a value that is proportional to the total number of SSEs in the larger of the query and target structures.

This problem can be overcome by detecting the core fold of the query structure via examination of high-scoring alignments and by using this information both to recognize more distantly related structural homologs and also to exclude false positives by requiring that targets align to this core fold. The core fold may be thought of as the structural motif shared by the query and high-scoring target structures. FoldMiner determines how well the position of each query SSE is conserved among the query protein and its homologs in order to find the regions of the query that are expected to align well to target structures. Hence, even when all query SSEs participate in the core fold, the structural conservation calculations identify both structurally variable and relatively invariant regions of the query protein. FoldMiner then permits a greater or lesser degree of variability, respectively, in the positions of aligned target SSEs when searching for homologous structures.

Data regarding the conservation of various regions of the query structure can be used to re-examine alignments and detect homologs not identified in the first pass of the structural similarity search. This is achieved both by placing less emphasis on those SSEs that are not part of the core fold or whose positions that are poorly conserved, and also by renormalizing raw alignment scores to a more reasonable value that reflects the size of the core fold and the expected structural variation among homologous structures. This process does not require prior knowledge of the motif or of the identities of any homologous structures within the target database. Furthermore, this approach increases both the sensitivity and specificity of the structural similarity search by using both the alignment score and the region of the query to which a target is aligned to discriminate between homologs and high-scoring false positives. As motif discovery and refinement of the structural similarity search do not require that additional alignments be performed and involve only parsing of alignment data, these processes are quite rapid.

Motif discovery and refinement of structural similarity searches

FoldMiner determines which of the query’s SSEs participate in the motif shared among the query and its structural neighbors by examining SSE alignments for high-scoring target structures. All statistically significant alignments are taken into account in this process. As LOCK 2 finds a global alignment whenever possible, these motifs are often consistent with definitions of core folds as described in SCOP when the target database consists of SCOP domains. Because the LOCK 2 algorithm assigns a score to each aligned SSE, FoldMiner can determine the conservation of the position of each query SSE by calculating an average SSE score across all targets with statistically significant homology with the query structure. This average is weighted such that highly significant targets contribute most heavily, and the impact of false positives, which are likely to be of lower statistical significance, is minimized. Thus, SSEs that frequently achieve high scores in statistically significant alignments to target structures are considered to be highly conserved. Insertions with respect to the core fold are easily detected because homologs lacking these insertions report SSE alignment scores of zero within the inserted regions, thus drastically decreasing the structural conservation values of the inserted SSEs.

Formally, the conservation of the i^th SSE, denoted c_i, is calculated by normalizing its weighted average score across the statistically significant alignments such that c_i lies on the interval [0, 1]. More details are provided in the Materials and Methods section. High values of c_i correspond to highly conserved SSEs. Instead of using a cutoff value to exclude certain helices and strands from the motif entirely, the conservation value determines the extent to which each SSE participates in the motif. Thus, the motif definition incorporates all query SSEs, but the user may wish to constrain the definition to those elements that are highly conserved. High conservation values identify SSEs in structurally invariant regions that are most useful for recognition of structural homology, whereas low conservation values are associated with structurally variable regions or insertions with respect to the core fold that are less useful for discrimination between homologs and analogs.

After obtaining a motif definition, FoldMiner uses this information to refine the structural similarity search. Although poorly conserved SSEs would not normally be considered to be part of the core fold, ignoring them entirely would decrease the specificity of the search because structures that are closely related to the query, and therefore likely share with it both the core fold and additional SSEs, would not be distinguished from more distantly related targets. Therefore, a new maximum SSE score is calculated for each query SSE by using both its conservation, as determined by the weighted average score described above, and a percentage of the original maximum score. This ensures that no maximum SSE score drops below a user-specified value. The value x in Equation 6, which lies on the interval [0, 1], determines to what extent the conservation affects the new maximum SSE score. The new maximum score for the i^th SSE (Equation 7) is calculated as a percentage p_i (Equation 6) of the original maximum SSE score, and the maximum score for the entire alignment can be calculated from the sum of the new maximum SSE scores.

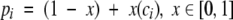(6)

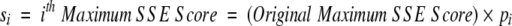(7)

By default, 75% of the new maximum SSE alignment score is derived from the conservation calculation (x = 0.75). We find that this value achieves good results across many folds, but it may need to be adjusted by the user in some cases. If the target database is small or if the structural similarity search reveals that it contains few examples of the query’s fold, the user should reanalyze the alignment results by lowering the value of x. This process is rapid, as no alignments are performed in the reanalysis of results with different search parameters.

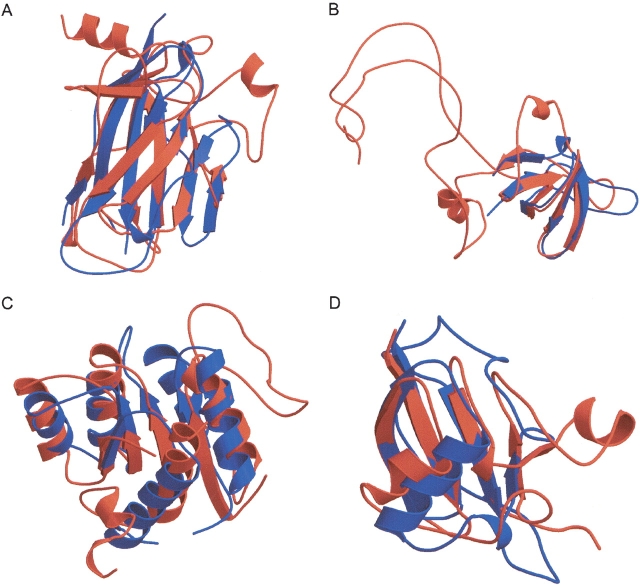
Now that the motif has been defined in terms of conservation values, FoldMiner uses this information to weight alignment scores for individual SSEs in order to determine a new alignment score for each target in the database. The more strongly conserved a SSE is, the more it will contribute both to the maximum alignment score and to an individual target’s score. The alignment results are refiltered both by weighting the score for each aligned SSE by p_i and by normalizing the total alignment score to the newly calculated, lower maximum score. To attain a high score, a target structure must now align well to a specific conserved region of the query. This process of calculating SSE conservations and new maximum scores is repeated until the maximum scores converge. Hence, FoldMiner provides not only a list of structures that are homologous to the query but also the definition of the motif or core fold used to detect these similarities in terms of the structural conservations of SSEs. When SSEs are colored by their conservations, the core fold and well-conserved SSEs can easily be identified by eye (Fig. 2 ▶).

Figure 2.

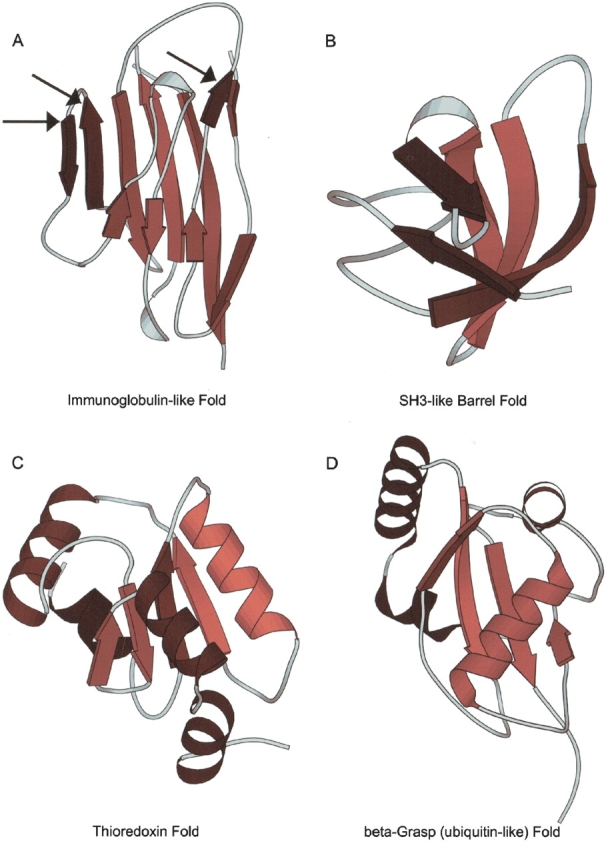
Visualizations of motifs from several SCOP folds. Structural similarity searches were performed by using members of four different SCOP folds as queries and a target database of 2448 SCOP domains of low sequence identity. In each panel, the query’s SSEs are colored according to their structural conservations (calculated as described in the text) with bright and dark colors representing high and low conservation values, respectively. (A) Arrows indicate strands of SCOP domain d1neu__ that are insertions with respect to the conserved core immunoglobulin fold (SCOP fold b.1). (B) Two strands of members of the SH3-like barrel fold (SCOP fold b.34) tend to be more highly conserved than are the remaining three strands. SCOP domain d1dbwa_ is pictured. (C) In general, strands are more conserved than are helices among members of the thioredoxin fold (SCOP fold c.47). One helix, however, is well conserved; SCOP domain d1kte__ is pictured. (D) One helix and the sheet it packs against are well conserved in domain d1eo6a_ of SCOP’s β-grasp fold (fold d.15), whereas the remaining helices are structurally variable with respect to the corresponding helices in the domain’s structural homologs. All cartoon diagrams were produced by MOLSCRIPT (Kraulis 1991; Esnouf 1997).

Validation of motifs across multiple structures

Although it seems likely that those query SSEs that routinely align well to target SSEs are part of a structurally conserved motif, we sought further proof that highly conserved SSEs in one structure correspond to highly conserved SSEs in other structures. That is, if FoldMiner does detect structural motifs, we would expect that the highly conserved SSEs in one structure would tend to align to highly conserved SSEs in other structures. These SSEs would then correspond to the most strongly conserved regions of the structural motif. To test this hypothesis, we examined the conservation values of pairs of aligned SSEs for structures in seven different highly populated and diverse SCOP folds (Table 1). For each fold, this analysis was restricted to statistically significant alignments of structures appearing in the low sequence identity database of 2448 SCOP domains used in this study.

Table 1.

SCOP folds selected for detailed analysis

SCOP fold	Fold name	Superfamiliesa	Domainsb	Domains in target databasec
a.1	Globin-like	2	35	16
b.1	Immunoglobulin-like	14	2673	116
b.34	SH3-like barrel	7	195	20
c.23	Flavodoxin-like	16	441	41
c.47	Thioredoxin fold	3	371	26
d.15	β-Grasp (ubiquitin-like)	9	279	30
d.58	Ferredoxin-like	36	584	73

^a Number of SCOP superfamilies in each SCOP fold.

^b Total number of protein domains in each SCOP fold.

^c Number of domains appearing in the target database, which consists of a set of SCOP domains with no >25% pairwise sequence identity obtained from the ASTRAL compendium (Brenner et al. 2000).

Because exact conservation values depend on the particular structure under consideration, they cannot be directly compared across multiple structures. The Kendall rank correlation test was therefore used to detect correlations in the conservation values. We have tabulated the percentage of query structures in each fold for which query SSE conservations are correlated with the conservations of the target SSEs to which they are aligned. The percentage of queries for which this correlation was significant at p = 0.01 is given in Table 2. In most of these folds, conservation levels are correlated across most fold members.

Table 2.

Conservations of secondary structure elements of domains in the same SCOP fold are correlated

SCOP fold	Fold name	Queries with significantly correlated conservation (%)
a.1	Globin-like	68.8
b.1	Immunoglobulin-like	88.8
b.34	SH3-like barrel	76.5
c.23	Flavodoxin-like	97.5
c.47	Thioredoxin fold	69.2
d.15	β-Grasp (ubiquitin-like)	43.3
d.58	Ferredoxin-like	43.8

^a The percent of protein domains for which the correlation of secondary structure element conservation values is significant, according to the Kendall rank correlation test at p = 0.01.

Although this correlation holds for many queries, it does break down in some cases. Examination of the structures for which the correlation does not hold in the immunoglobulin-like fold (SCOP fold b.1), for example, reveals that several have low secondary structure content and therefore lack the fold’s core structure as determined by secondary structure assignments. Two other uncorrelated immunoglobulin-like queries are members of the “Cu, Zn superoxide dismutase-like” SCOP superfamily, which has only three representatives in the target database in total. It is possible that the core motif of this superfamily is somewhat different than the motif discovered for the rest of the immunoglobulin-like fold. In some cases, the uncorrelated structures consist of entire superfamilies or families. This trend is particularly prevalent in the β-grasp fold (SCOP fold d.15), indicating that the superfamilies of this fold may be structurally divergent and perhaps can be distinguished by differences in their core folds.

Additional evidence for FoldMiner’s detection of a motif that is present in multiple structures comes from the high degree of transitivity among LOCK 2 assignments. That is, the alignment of structures A and B and the alignment of structures B and C predict the alignment of structures A and C. For statistically significant superpositions of structures within the same SCOP fold, this relationship holds ~95% of the time at the level of SSEs. The degree of transitivity at the residue level varies from ~40%–70%, depending on the fold of the structures under consideration. It should be noted that this analysis ignores cases with missing data (that is, cases in which the residues or SSEs under consideration were unaligned in one or more of the A versus B, B versus C, and A versus C alignments). Taken together with the correlation of conservation values, transitivity implies that FoldMiner identifies a structural core common to most or all members of a SCOP fold, that the same portions of this motif are highly conserved in all of the structures, and that the motif tends to be correctly aligned.

Detection of local motifs

Although the LOCK 2 scoring system is designed to favor global alignments, it is possible to detect local motifs in a query structure if the target database contains few globally similar structures. In this case, the conservation calculation will allow the search algorithm to focus on a smaller region of the query structure. We have performed a structural similarity search by using DNA topoisomerase III from Escherichia coli as the query structure. This protein belongs to a SCOP class excluded from our target database and therefore has no globally similar structural homologs within the database. Over the course of several iterations, the search algorithm detects five conserved SSEs out of the 42 SSEs of the topoisomerase. These five SSEs show strong homology with the “winged helix” DNA-binding domain family of SCOP’s DNA/RNA binding three-helical bundle fold (Fig. 3 ▶). This particular family contains two β strands in addition to the helical bundle.

Figure 3.

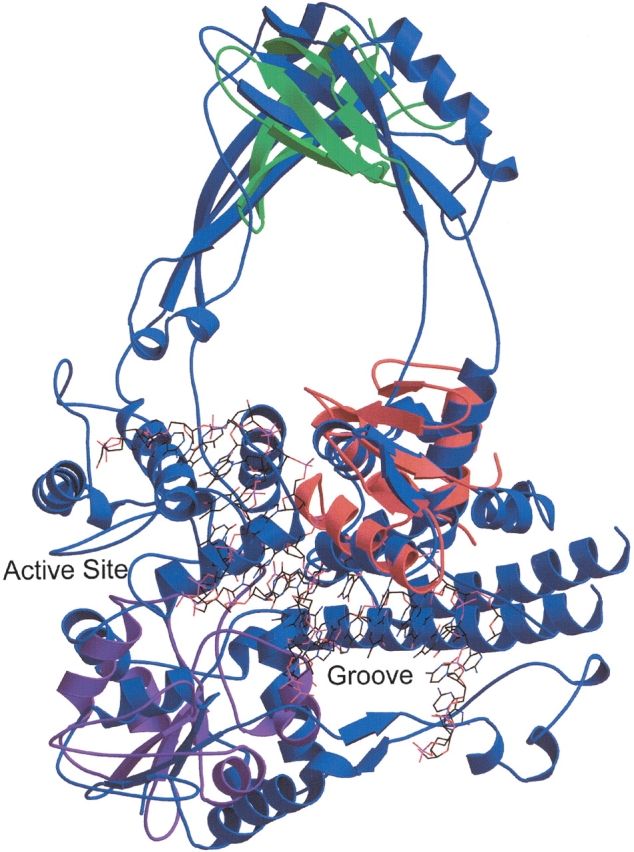
Topoisomerase III contains several small domains. A structural similarity search using DNA topoisomerase III of E. coli (SCOP domain d1d6ma_) as the query reveals local structural homology with the winged helix DNA-binding domain superfamily. The alignment of the topoisomerase (blue) to chain E of the transcription factor PU.1 of Mus musculus (SCOP domain d1puee_, shown in red), which is complexed with DNA (shown in wireframe), lends support to the hypothesis that the DNA could bind in the groove identified by Mondragon and DiGate (1999). The DNA reaches the active site of the topoisomerase as well. Repeated applications of the structural similarity search that exclude the SSEs of motifs already identified lead to the discovery of the additional motifs described in the text. The alignment of the topoisomerase to the C-terminal (UDP-binding) domain of UDP-glucose dehydrogenase (SCOP domain d1dlja3) is shown in purple, and an alignment of the major cold shock protein (SCOP domain d1c9oa_) is shown in green. This figure was produced by Molscript and rendered by Raster3D (Kraulis 1991; Merritt and Bacon 1997).

Some of the winged helix DNA-binding domains have been cocrystallized with DNA, and the superposition of the protein-DNA complex and the topoisomerase strongly supports the hypothesis of Mondragon and DiGate (1999) that the topoisomerase binds DNA in a groove formed by domains I and IV, located at the N and C termini of the protein, respectively. It is interesting to note that one of the helices of the topoisomerase’s three-helical bundle of topoisomerase is part of what Mondragon and DiGate identify as the fourth domain of the protein, whereas the remainder of the conserved SSEs are all part of the first domain. FoldMiner frequently identifies motifs consisting of SSEs that are not consecutive in sequence space.

If we now force FoldMiner to ignore the SSEs that are part of the DNA binding motif, we can detect other local motifs in the structure. The next motif discovered appears to occur in many types of structures across many SCOP folds; it consists of a small sheet against which several helices pack. Continuing to exclude SSEs that appear in motifs the search algorithm has already detected reveals the presence of a β barrel. The major cold-shock protein of Bacillus caldolyticus (SCOP domain d1c9oa|PV), a member of SCOP’s cold-shock DNA-binding domain-like family, aligns to a region of the topoisomerase that would likely be in close proximity to full-length bound DNA. Figure 3 ▶ shows alignments of the topoisomerase to these three SCOP domains.

Receiver operating characteristic curve analyses: Comparison of alignment algorithms

Differing philosophies behind different alignment algorithms make comparisons among them difficult, as the measure of alignment quality optimized by one algorithm cannot be fairly applied to the alignment produced by a different method designed to optimize a different statistic. Although LOCK 2 requires that all aligned residue pairs be no farther than 3.0Å apart, for example, other algorithms align a greater number of residues at the expense of the RMSD. Receiver operating characteristic (ROC) curves provide a means by which we can compare different search algorithms by using each method’s own measure of alignment quality to rank the relative similarities of a database of structures to a query structure (Swets 1988).

To validate the performance of the FoldMiner algorithm, we have compared ROC curves produced by FoldMiner, VAST, and the CE algorithm. Both FoldMiner and VAST provide alignment scores by which results can be ranked (although the methods by which these scores are obtained are different), whereas the CE algorithm ranks results according to Z scores. The CE algorithm does not provide statistical significance values, so we have chosen to discard alignments with low Z scores. We use the cutoff of 3.7 recommended by Shindyalov et al., who state in the CE software distribution that the interpretation of alignments with Z scores of <3.7 requires evidence beyond the alignment itself. VAST results with significance values greater than p = 0.004, the cutoff value used by FoldMiner to achieve an expectation of 10, were also discarded.

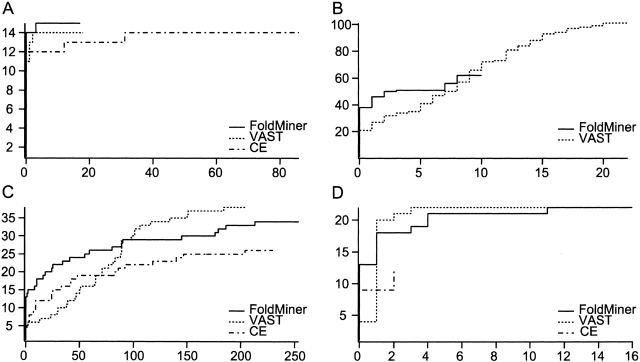
ROC curves measure the abilities of the three algorithms to rank structures within the queries’ respective SCOP folds, the true positives, ahead of structures outside their folds, termed false positives. For a given point on an ROC curve, the x value denotes the number of structures outside the query’s fold ranked ahead of the y^th true positive. Thus, steeper ROC curves indicate greater accuracy with respect to the definitions of true and false positives. We selected seven of the most populated and diverse SCOP folds for ROC curve analyses, two from each of the mainly β, α+β, and α/β classes, and one from the mainly α class (Table 1). ROC curves were produced for each structure in each fold; four representative curves are shown in Figure 4 ▶.

Figure 4.

Receiver operating characteristic (ROC) curves compare the performance of FoldMiner, VAST, and CE. Four representative ROC curves reveal trends observed in the full set of curves determined for all queries in seven different SCOP folds. VAST alignments are ranked by alignment score; minor changes occur if they are instead ranked by the number of aligned residues as described in the text. (A) The ROC curve for the globin query d1ew6a_ shows comparable performance of the three algorithms, although FoldMiner identifies one more member of the phycocyanin superfamily of the globin fold than do VAST and CE. (B) FoldMiner identifies more structural neighbors of the immunoglobulin query d1qfoa_ before it finds its first false positive than do the other algorithms, but finds fewer true positives overall than does VAST. CE returned no results with Z scores >3.7 in this particular case. (C) All three algorithms find a large number of false positives when the flavodoxin structure d5nul__ is used as the query, as the general motif of helices packing against both sides of a small β sheet is observed in many different folds. (D) FoldMiner and VAST perform equally well overall when the β-grasp structure d1vcba_ is used as the query, but FoldMiner more accurately ranks true positives ahead of false positives in early regions of the curve than does VAST.

In general, FoldMiner and VAST outperform the CE algorithm, which often returns fewer results than do the other two algorithms. In comparison to the CE algorithm, FoldMiner usually attains higher sensitivities without encountering tradeoffs in specificity. FoldMiner’s average sensitivity for each fold was consistently higher than was CE’s, and its average specificity was lower than was CE’s in only two of the seven folds (Table 3).

Table 3.

Average sensitivities and specificities for seven SCOP folds

		Average sensitivitya (%)			Average specificityb (%)
SCOP fold	Fold name	LOCK 2	VAST	CE	LOCK 2	VAST	CE
a.1	Globin-like	84	70	75	98	99	96
b.1	Immunoglobin-like	56	80	53	99	99	99
b.34	SH3-like barrel	57	64	16	98	99	100
c.23	Flavodoxin-like	83	80	47	89	93	94
c.47	Thioredoxin fold	60	90	53	100	99	99
d.15	β-Grasp (ubiquitin-like)	55	63	23	100	100	100
d.58	Ferredoxin-like	40	67	33	99	99	99

^a 100 × true positives/(true positives + false negatives).

^b 100 × true negatives/(true negatives + false positives).

Although VAST achieves higher sensitivities than does FoldMiner in all but one fold, in most cases FoldMiner initially ranks more true positives ahead of false positives in early regions of the ROC curve than does VAST. That is, FoldMiner more accurately identifies the query’s closest structural neighbors, but VAST generally identifies a greater number of the more distantly related structures than does FoldMiner.

The property of placing true positives ahead of false positives is not captured in the traditional metrics of sensitivity and specificity, which take into account only the total numbers of true and false positives identified, but is well described by the area under the ROC curve (Swets 1988). The ROC curve with the greatest area has most accurately ranked true positives ahead of false positives. When different algorithms achieve different specificities and sensitivities, however, the areas underneath their curves are not directly comparable. Hence, we define the crossover points of two ROC curves as the points at which the specificities and sensitivities of the two algorithms are equal (that is, the points at which the x and y values are equal). When more than one crossover point is present, we choose the one for which the sensitivity is greatest (that is, the crossover point with the greatest y value) and truncate the curves at this point. If no crossover point exists, this implies that the curve of one algorithm lies above the other curves at all points; in these cases this algorithm has outperformed the others. Finally, if the curves are exactly equal from the point (0,0) to the point at which the algorithm with the lowest overall sensitivity terminates, the algorithms have performed equally well. This last case can also be described in terms of crossover points, as a crossover point exists at all points on the ROC curves until the curve of the first algorithm terminates, and the areas underneath the curves at all of these crossover points are equal. The concept of truncating an ROC curve in order to focus on its most relevant region has been used by others (Gribskov and Robinson 1996), and is extended here in order to select the best truncation point for the purpose of comparing the area under two ROC curves. In this discussion, we refer to the area under an ROC curve as the area calculated for the portion of the curve lying between the origin and the last crossover point.

As the CE algorithm often achieves lower sensitivities than do VAST and FoldMiner, we have compared FoldMiner to the two other algorithms separately. For each query, we calculate the last crossover point (that is, the crossover point with the greatest sensitivity). For all queries in a single SCOP fold, we count the number of cases in which either a crossover point does exist and the FoldMiner ROC curve has a greater area than does the second algorithm, or in which no crossover point exists and FoldMiner’s curve lies entirely above the curve of the second algorithm. Results are tabulated separately for each fold and for comparisons between FoldMiner and each algorithm. The average numbers of true and false positives at which the crossover points occur are also noted (Table 4). The overall results do not change when VAST alignments are ranked by the number of aligned residues instead of the alignment score, although the performance of VAST does improve slightly (data not shown).

Table 4.

LOCK 2 ranks true positives ahead of false positives more accurately than do VAST and the CE algorithm

SCOP fold	Fold name	LOCK 2a	CEa	VASTa	Tiesb	False positivesc	True positivesc
Comparison of LOCK 2 and CE
a.1	Globin-like	7	3	—	6	19.7	11.5
b.1	Immunoglobulin-like	58	20	—	38	7.4	37.4
b.34	SH3-like barrel	6	0	—	11	0.2	3.3
c.23	Flavodoxin-like	18	7	—	15	42.8	11.3
c.47	Thioredoxin fold	7	1	—	18	0.5	11
d.15	beta-Grasp (ubiquitin-like)	5	4	—	21	0.4	6.5
d.58	Ferredoxin-like	25	9	—	39	3.2	12.6
	Totals	126	44	—	148
Comparison of LOCK 2 and VAST
a.1	Globin-like	6	—	7	3	13	10.9
b.1	Immunoglobulin-like	80	—	15	21	8.6	48.2
b.34	SH3-like barrel	10	—	0	7	4.7	6
c.23	Flavodoxin-like	34	—	2	4	101	23.4
c.47	Thioredoxin fold	6	—	1	19	0.5	13.8
d.15	beta-Grasp (ubiquitin-like)	7	—	8	15	2.3	11.8
d.58	Ferredoxin-like	33	—	15	25	2.3	17.5
	Totals	176		48	94

^a Number of times LOCK 2 or the second algorithm (CE or VAST) ranks true positives ahead of false positives more accurately than does the other.

^b Number of times LOCK 2 and the second algorithm rank true positives ahead of false positives equally well.

^c Average numbers of false and true positives at which the last crossover point between LOCK 2 and either CE or VAST ROC curves occurs.

For five of the seven folds, FoldMiner tends to have more area under its ROC curves (calculated only up to the crossover point) than does VAST. Out of a total of 318 ROC curves examined, FoldMiner achieves a greater area under its curve than does VAST in 176 cases, VAST achieves a greater area under its curve than does FoldMiner in 48 cases, and 94 cases are ties. When VAST alignments are ranked by the number of aligned residues instead of the alignment score, these numbers become 164, 62, and 92, respectively, for a net decrease of 26 cases in which the area under the FoldMiner curve is greater than the area under the VAST curve.

FoldMiner outperforms the CE algorithm in all seven of the examined folds. In the case of the CE algorithm, however, the crossover points tended to occur earlier in the ROC curve than was the case for VAST, and many results were ties that occurred at low sensitivities. This result captures the overall trends of the ROC curves discussed above, in that FoldMiner consistently performs better overall than does CE and tends to perform better than does VAST in early regions of the ROC curves. It does appear, however, that in the very early regions of the ROC curves, CE occasionally performs better than do FoldMiner and VAST (Fig. 4C ▶). Although VAST achieves greater overall sensitivities on average, it is perhaps more crucial that alignment algorithms distinguish between false positives and true positives that are closely related to the query structure than it is that they achieve high sensitivities overall, particularly given the wide scope of the definition of true positives (all structures within a query’s SCOP fold) used here.

The comparison of the area under ROC curves of the two methods may be biased against the algorithm with higher sensitivity, as this algorithm is on average more likely to place false positives ahead of true positives in any given portion of the ROC curve. If this tradeoff does exist, it seems to affect VAST to a much higher degree than it affects FoldMiner. VAST’s overall sensitivities is higher than that of FoldMiner, and, as would be predicted by this potential trend, FoldMiner performs better in the crossover point analysis than does VAST in five out of seven folds. Although the sensitivity of FoldMiner is consistently higher than that of CE, however, it still outperforms CE in the crossover point analysis for all seven folds.

Although all three alignment algorithms at times rank false positives ahead of true positives, some of these false positives exhibit strong structural similarity to the SCOP folds used in this study (Fig. 5 ▶). The immunoglobulin fold (SCOP fold b.1) shows a wide range of structural variation, particularly with respect to the angle between the two sides of the Greek key that defines the fold (Halaby et al. 1999). Other SCOP folds are comprised of Greek keys of different sizes, and it is not unusual for the relative orientation of the SSEs in structures from these folds to match the query structure more closely than do some members of the immunoglobulin fold itself (Fig. 5A ▶). This issue arises in part because some SCOP classifications are based on attributes such as function rather than on pure structural similarity (Murzin et al. 1995). The flavodoxin-like fold consists of three layers (αβα) in which two helices pack against each side of a five-strand β sheet; this pattern of SSEs appears to arise in a wide variety of folds and thus the ROC curve for the flavodoxin fold contains a large number of false positives (Figs. 4C ▶, 5C ▶). The flavodoxin-like fold may therefore represent a common theme in protein structure. Such structural similarities that cross SCOP fold boundaries make it difficult to analyze the high-sensitivity regions of the ROC curves, as the inclusion of false positives in the curves, even when they appear before some true positives, is potentially not incorrect on the basis of structure alone.

Figure 5.

LOCK 2 alignments frequently reveal structural similarities that cross SCOP fold and superfamily boundaries. (A) The immunoglobulin query d1neu__ (blue) aligns well to many Greek keys outside of the SCOP immunoglobulin fold; an alignment to d1ycsa_ (red) is shown. (B) An alignment of SCOP domain d1ckaa_ (blue), an SH3-domain, to d1d7qa_ (red), an OB-fold domain, reveals structural similarities between the two domains. Similarly, other SCOP folds that contain barrels frequently align well to domains in the SH3-like barrel fold. (C) Many members of the SCOP flavodoxin-like fold show strong structural similarity to the NAD(P)-binding Rossman fold. Here, a flavodoxin (d3chy__, shown in blue) is aligned to d1dih_1 (red). (D) An alignment of a human protein from SCOP’s ubiquitin-like superfamily (d1vcba_, shown in blue) to a 2E–2S ferredoxin from a cyanobacterium (d1czpa_, shown in red) reveals structural similarities between two superfamilies of SCOP’s β-Grasp (ubiquitin-like) fold. This figure was produced by Molscript and rendered by Raster3D (Kraulis 1991; Esnouf 1997; Merritt and Bacon 1997).

Discussion

FoldMiner is capable of detecting structural motifs in an unsupervised fashion given only a query protein and a database of target structures. It does so without using sequence information, without performing multiple structure alignments, and without prior classification of the target proteins into families. Instead, the algorithm uses pairwise structural superpositions performed by LOCK 2 to identify the query’s structural neighbors and to determine the structural conservation of each query SSE. Structural conservation values reflect the variability of each SSE’s position in the query and its structural homologs. To detect distant structural relationships and to improve discrimination between true and false positives, the motif definition is used to reanalyze alignment results by adapting the scoring system to focus on conserved regions of the query. This improves both the sensitivity and specificity of the structural similarity search both by requiring that a homolog align well to conserved regions of the query and by placing less emphasis on structurally variable regions and insertions to the query’s core fold. FoldMiner iteratively refines the motif definition from the current set of homologous structures in order to recruit more distantly related proteins and to discard false positives. This process ends when the motif definition converges.

Highly conserved SSEs in one protein domain tend to align to the highly conserved SSEs of other domains, indicating that the conservation values FoldMiner calculates are biologically relevant. The algorithm is also able to detect local structural motifs in structures that have no globally similar homologs in the target database. Sequential application of the motif discovery algorithm can result in the identification of multiple motifs; extension of the algorithm to identify multiple motifs in one pass is relatively straightforward.

To assess the performance of FoldMiner, we have compared it to VAST and the CE algorithm. Although VAST tends to achieve greater sensitivities overall, FoldMiner outperforms VAST at low sensitivities, as it is better able to distinguish between the query’s close structural neighbors and false positives than is VAST. The CE algorithm, however, often fails to detect structural similarities identified by FoldMiner and VAST.

All three algorithms at times consider structures in different SCOP folds to be more closely related to one another than are certain structures belonging to the same SCOP fold. Although we have labeled structures outside of a given protein’s SCOP fold as false positives, these results are not necessarily erroneous. It is important to note that structures that are members of different superfamilies within the same SCOP fold generally have no known evolutionary relationship (Murzin et al. 1995). Therefore, evolutionary relationships are not necessarily violated when structures outside of the query’s SCOP fold are ranked ahead of structures in different superfamilies within the query’s fold. Because FoldMiner identifies members of a query’s own superfamily with high accuracy (data not shown), most false positives fall into this category. Hence, the structural similarities identified by FoldMiner that cross SCOP fold boundaries suggest that protein structure classification systems such as SCOP that are based on attributes other than structure will in some cases fail to reveal structural relationships shared among distantly related proteins. Because FoldMiner is an unsupervised method that does not use predefined fold definitions, it easily detects remote homologies between members of different SCOP folds. An automatically created structural classification system based on FoldMiner results would be unbiased by such predefined fold definitions and may reveal distant structural similarities not readily apparent in manually created hierarchies.

Detection of structural motifs may aid in the classification of protein structures, as identification of motifs helps focus attention on the conserved regions of a fold. Structural differences within the motif may be more significant than are differences in other regions of protein structures and may help distinguish between members of different superfamilies or families that share the same overall fold. Cases in which the conservations of SSEs in an entire superfamily or family of structures are not correlated with the rest of the SCOP fold suggest that these groups of structures may be somewhat distantly related to other superfamilies or families in the fold. Correlation of SSE conservations may further assist in determining evolutionary relationships among protein structures. Structural conservation values calculated by FoldMiner may also play a role in fold prediction by identifying regions of a structural fold that tend to vary among its members and those whose positions remain relatively fixed.

FoldMiner superpositions are performed by an improved structural alignment algorithm, LOCK 2, which is capable of detecting more distant structural relationships than is its predecessor. We have placed increased emphasis on the alignment of SSEs and have modified our scoring functions to take into account such factors as differences in lengths and orientations of SSEs in distantly related proteins. Because the secondary structure alignment phase is critical for accurate detection of distantly related homologs, we now report the secondary structure alignment to the user. The algorithm is both symmetrical and nearly transitive, and its scoring system produces structural distances between proteins that obey the triangle inequality (Equation 2). This makes LOCK 2 suitable for the construction of an automated structural classification system using alignment scores converted into structural distances that obey the properties of a metric.

We have also developed statistical significance scores for LOCK 2 alignment scores. This is essential for the development of fully automated structural classification systems, and FoldMiner’s unsupervised identification of homologs and their common structural core is a first step in this direction. Where possible, statistical significance scores have been developed for individual SCOP folds. This improves their accuracies by taking into account features of certain folds, such as compactness, secondary structure composition, and the presence of internal repeats, that affect the probability of obtaining biologically insignificant alignments by chance. In cases in which a SCOP fold is only sparsely populated and a background distribution of alignment scores cannot be accurately produced, we use a composite distribution from the entire SCOP class of the fold. These composite distributions are also used when the query structure’s SCOP fold is unknown but its class is known. A distribution encompassing all folds in SCOP’s mainly α, mainly β, α+β and α/β classes is used when even the query’s SCOP class is unknown.

Because LOCK 2 alignments are transitive, there is enough information contained within pairwise alignments to begin to construct multiple structure superpositions, which would further enhance visualization of structural similarities and motifs. The correlation of conservation values among most structures in a given SCOP fold implies that the multiple structure alignment would also reveal the regions of the fold that are highly conserved. We are also exploring both global and local motif detection at the residue level.

Availability

FoldMiner is available on the Internet at http://fold.stanford.edu/FoldMiner and LOCK 2 is available at http://fold.stanford.edu/LOCK. Results for pairwise structural alignments, which are performed by LOCK 2, are generally returned in several seconds or less, and a PDB file containing the coordinates of the superimposed structures is supplied. FoldMiner results are generally obtained in 3 to 10 min, depending on the size and nature of the query. Search results include both a definition of the structural motif shared by the query and its structural homologs and also results for all pairwise alignments, including PDB files for each superposition. The motif is visualized by coloring query SSEs according to their conservation values. The freely available Chime plugin (http://www.mdlchime.com/chime/) is used to visualize both this motif and pairwise alignments; controls are provided to select, manipulate, and visualize the protein structures and the aligned regions. Source code is available royalty-free for not-for-profit institutions at http://motif.stanford.edu/software/ and from Stanford’s Office of Technology Transfer for for-profit institutions. The code has been tested on Unix and Linux platforms and is written in C and Perl.

Materials and methods

Nonredundant data set construction

A list of SCOP domains, no two of which share >25% sequence similarity, was obtained from the ASTRAL compendium (Brenner et al. 2000). We filtered the list to exclude any domain not in SCOP’s mainly α, mainly β, α+β, and α/β classes. As of SCOP version 1.55, this list contains 2448 structures from 498 different folds. SCOP classifications were used to determine the level of structural similarity of domains; we consider domains in the same SCOP fold to be structural neighbors.

The LOCK 2 algorithm

Secondary structure superposition

SSEs are reduced to vectors by computing the centroids of the first two and last two residues for strands and first four and last four residues for helices. A pair of SSE vectors from the query is superimposed on a pair of vectors from the target, and a dynamic programming algorithm scores the resulting superposition of the entire query and target structures. All possible vector pairs are used to obtain and score these initial superpositions; this geometric hashing algorithm and the dynamic programming scoring functions have been described in detail by Singh and Brutlag (1997). We have relaxed the assumption of the original LOCK program that either the query or target pair of vectors used in the geometric hashing must be sequential in sequence space and now attempt hashing with all pairs. However, a given superposition is not produced or scored if the relative orientations of the pairs of SSE vectors that would be used to produce it do not match well, and thus the time complexity of the algorithm tends to increase significantly only when many possible registrations of the query and target are possible. This typically occurs in cases involving compact structures and in structures with many internal repeats. The time complexity is not substantially increased in most other cases. This option may be disabled at the user’s discretion in order to decrease the number of initial superpositions that are tested.

We have also changed the scoring function that computes the distance between two aligned vectors in order to accommodate vectors of different lengths and orientations. We require at least a 25% overlap between the query and target vectors, where the overlapping region is defined as the longest continuous stretch of one aligned vector that is within 4 Å of the other. To avoid penalizing alignments of vectors of different lengths, the distance score does not increase with the extent of the overlap, but instead increases with decreasing distance between the vectors in the overlapping region. The values of 25% and 4 Å were selected by examining their impact on alignments of structures in different superfamilies of the same SCOP fold.

The previous version of LOCK did not permit gaps in the SSE alignment simultaneously in both the query and target structures. This restriction was implemented in order to restrict the alignment to the best locally aligned region. LOCK 2 favors ungapped secondary structure alignments, but if no such alignment is possible, it will attempt to achieve a global superposition by inserting as few gaps in the SSE alignment as possible.

For each aligned vector pair of the highest scoring initial superposition, the residues of the longer SSE are matched to the residues of the shorter SSE by finding their nearest neighbors. No distance cutoff is used at this stage. The quaternion transformation is used to superimpose the query and target structures (Horn 1997; Horn and Hilden 1998). Unlike the original LOCK algorithm, LOCK 2 assigns each residue pair a weight in the transformation procedure that is inversely proportional to the length of the SSE. This allows each aligned vector pair to influence the transformation approximately equally. The dynamic programming algorithm is repeated and the transformation is refined until the RMSD and dynamic programming score converge; the original LOCK algorithm did not require convergence of the dynamic programming score. If the dynamic programming score for the alignment obtained at the end of the secondary structure superposition phase is <90% of the score assigned to it directly after geometric hashing, or if fewer than three SSEs are aligned, we select a different initial transformation and repeat the refinement process. This also represents a change from the original version of LOCK.

Residue superposition

The remainder of the LOCK 2 algorithm considers only C_α atoms and remains relatively unchanged from the original version of LOCK. Loop residues no longer affect the transformation, but are considered aligned if they find each other as nearest neighbors within 3 Å after the final superposition is obtained. LOCK 2 also requires that aligned target residues be numbered in order with respect to the query over each SSE; the original version of LOCK required an in-order numbering over the entire structure. This change allows for more accurate residue alignments in cases such as circular permutations and β sheets of differing connectivity, although the alignment of these residues does not change the alignment score. This option may be disabled at the user’s discretion. After the final superposition is determined, the dynamic programming score is calculated and is normalized to the maximum of the query versus query and target versus target alignment scores.

Structural similarity searches: The FoldMiner algorithm

A structural similarity search consists of pairwise alignments of a query structure to all structures in a target database. A statistical significance threshold (P₁) is determined by the size of the target database and a user-specified expectation according to Equation 5 in the Results section. Only alignments meeting the statistical significance threshold P₁ are reported to the user. By default, the structural conservations of the query’s SSEs are calculated, and the alignment results are analyzed in an iterative fashion to identify additional structural homologs. This process is described below.

Calculation of SSE conservations and motif discovery

When a structural similarity search is performed (that is, when a query structure is aligned to a database of target structures), FoldMiner determines the structural conservation of the query’s SSEs and defines a structural motif in probabilistic terms. Both the statistical significance threshold P₁, described in the Structural Similarity Searches section above, and a more stringent threshold, P₂, are used to determine the structural conservation of each of the query protein’s SSEs. This second p value is calculated by default as P₂ = 0.1P₁ and may be adjusted by the user. All structural alignments are classified into three groups: alignments with p values that are less than P₂, alignments with p values that are between P₁ and P₂, and statistically insignificant alignments with p values that are above P₁. The numbers of alignments in these three classes are denoted n₁, n₂, and n₃, respectively.

Alignments are ranked in order of decreasing statistical significance, and a weighted average over all statistically significant alignments is calculated for each SSE according to Equations 8–10:

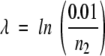(8)

(9)

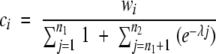(10)

The weighted average gives the greatest weight to alignments with statistically significant values that are less than or equal to P₂, the more stringent of the two significant thresholds, and invokes an exponential decay over the scores of the remaining statistically significant alignments. The alignment with the highest p value that is still less than or equal to P₁ is given a weight of 0.01. The value c_i, which lies on the interval [0,1], gives the conservation of the i^th SSE. High values of c_i correspond to highly conserved SSEs. The values of c_i therefore define a motif over the query SSEs in probabilistic terms.

To distinguish between alignments with similar scores that align to different regions of the query structure, new maximum SSE alignment scores are calculated from the c_i values. This score for the i^th SSE is defined as a percentage p_i of the original maximum SSE alignment score and is calculated according to Equations 6 and 7 of the Results section (reproduced below). The value of x is user-defined and is set to 0.75 by default.

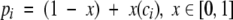(6)

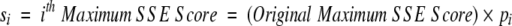(7)

The maximum score for a given alignment is then defined according to Equation 11, in which the original maximum alignment score is the maximum of the original query versus query and target versus target alignment scores.

(11)

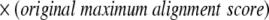New alignment scores are calculated for all alignments, including those with p values above P₁, by weighting SSE alignment scores by the p_i values. The sum of these weighted SSE alignment scores gives the new alignment score, which is normalized to the maximum alignment score calculated via Equation 11:

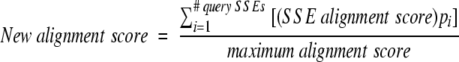(12)

The process of calculating conservation values and re-examining all alignment results iterates until the s_i values converge. The structural motif is defined by the final c_i values. The alignments determined to be statistically significant in the last iteration are reported to the user as the results of the structural similarity search along with the final c_i values.